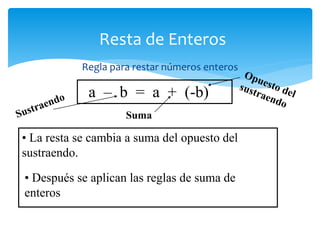
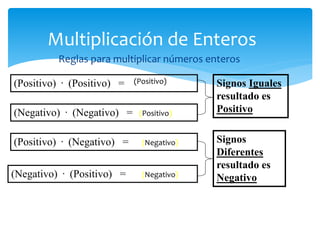
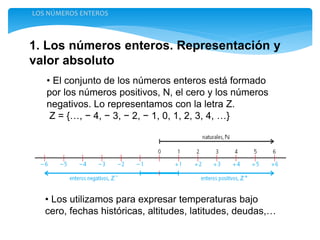
El documento presenta los números enteros. Explica que los números enteros incluyen los números positivos, cero y los números negativos. Describe cómo representar y ordenar los números enteros, y las propiedades de las operaciones como la suma, resta, multiplicación y división con números enteros. También cubre operaciones combinadas con números enteros usando el orden correcto de operaciones.

1. Universidad Interamericana de Puerto Rico
Recinto Metropolitano
Facultad de Ciencias y Tecnología
Propuesta LiNUS-MSP
Prof. Manuel Fernández

2. Los números enteros
1. Los números enteros. Representación y valor absoluto
2. Ordenación de los números enteros
3. Operaciones con números enteros
4. Propiedades de los números enteros
5. Operaciones combinadas

3. 1. Los números enteros. Representación y
valor absoluto
LOS NÚMEROS ENTEROS
• El conjunto de los números enteros está formado
por los números positivos, N, el cero y los números
negativos. Lo representamos con la letra Z.
Z = {…, − 4, − 3, − 2, − 1, 0, 1, 2, 3, 4, …}
• Los utilizamos para expresar temperaturas bajo
cero, fechas históricas, altitudes, latitudes, deudas,…

4. 1. Los números enteros. Representación y
valor absoluto
LOS NÚMEROS ENTEROS
El valor absoluto de un número entero es el mismo
número con signo positivo. Se expresa escribiendo
el número entre barras.
|+ a| = |− a| = a
|+ 12| = |− 12| = 12
Dos números enteros son opuestos o simétricos
si tienen distinto signo y el mismo valor absoluto.
|+ 7| = |− 7| = 7  op (– 7) = 7

5. 2. Ordenación de los números enteros
LOS NÚMEROS ENTEROS
• La forma más sencilla de ordenar los números
enteros es mediante su representación en la recta
numérica.
• Un número entero a es mayor que un número
entero b, a > b, si a está a la derecha de b en la
recta numérica, mientras que es menor si se
encuentra a la izquierda. También podemos decir
que :
a > b  a – b > 0 a < b  a – b < 0

6. 3. Operaciones con números enteros.
Adición y sustracción
LOS NÚMEROS ENTEROS
Para sumar dos o más números enteros del mismo
signo se suman los valores absolutos de los
sumandos y se deja el mismo signo. El resultado
siempre es un número entero.
(+8) + (+3) + (+5) = (+16)
(–6) + (–8) + (–9) = (–23)

7. 3. Operaciones con números enteros.
Adición y sustracción
LOS NÚMEROS ENTEROS
Para sumar dos o más números enteros de
distinto signo se suman por separado los del
mismo signo y después se restan sus valores
absolutos, el menor del mayor, y se pone el signo
del que tenga mayor valor absoluto. El resultado es
un número entero.
(–5) + (+4) + (–3) = (–5) + (–3) + (+4) =
= (–8) + (+4) = (–4)

8. 3. Operaciones con números enteros.
Adición y sustracción
LOS NÚMEROS ENTEROS
Para restar dos números enteros se suma al
minuendo el opuesto del sustraendo y se obtiene
así otro número entero.
(–7) – (–3) = (–7) + (+3) = (–4)

9. 3. Operaciones con números enteros.
Multiplicación y división
LOS NÚMEROS ENTEROS
Para multiplicar dos o más números enteros se
multiplican sus valores absolutos. El signo del
producto se obtiene mediante la regla de los
signos.
+ · + = + (+ 3) · (+ 5) = (+15)
+ · – = – (+ 4) · (– 5) = (– 20)
– · + = – (– 7) · (+ 2) = (– 14)
– · – = + (– 6) · (– 3) = (+18)

10. 3. Operaciones con números enteros.
Multiplicación y división
LOS NÚMEROS ENTEROS
Para dividir dos números enteros se dividen sus
valores absolutos. El signo de la división se
obtiene mediante la regla de los signos.
+ : + = + (+ 15) : (+ 5) = (+3)
+ : – = – (+ 18) : (– 2) = (– 9)
– : + = – (– 12) : (+ 4) = (– 3)
– : – = + (– 24) : (– 6) = (+4)

11. 3. Operaciones con números enteros.
Potencias y raíces
LOS NÚMEROS ENTEROS
La potencia de un número entero es otro número
entero que se halla multiplicando la base por sí
misma tantas veces como indique el exponente.
• Si la base es positiva, la potencia es siempre
positiva.
(+5)2 = 25
• Si la base es negativa, la potencia será positiva si
el exponente es par y negativa si el exponente es
impar.
(– 3)2 = (+9) (– 3)3 = (– 27)

12. 4. Propiedades de los números enteros
LOS NÚMEROS ENTEROS
La suma y la multiplicación de números enteros
tienen las siguientes propiedades:
Suma Multiplicación
Conmutativa (–3) + (+ 4) = (+ 4) + (–3) (–3) · (+ 4) = (+ 4) · (–3)
Asociativa [(+ 5) + (+ 7)] + (– 9) =
= (+ 5) + [(+7) + (–9)]
[(+ 5) · (+ 7)] · (– 9) =
= (+ 5) · [(+7) · (–9)]
Elemento neutro (–6) + 0 = (– 6) (+ 5) · 1 = (+ 5)
Elemento opuesto
o simétrico
(+3) + (– 3) = 0
Distributiva de la
multiplicación con
respecto a la suma
(–2) · [(+7) + (–3)] = (–2) · (+7) + (–2) · (–3)

13. 5. Operaciones combinadas
LOS NÚMEROS ENTEROS
Las operaciones entre paréntesis son las primeras
que debes realizar. También puedes eliminarlas de
la siguiente manera:
• Si delante del paréntesis hay un signo positivo, los
signos de los números que hayan dentro del mismo
no se modifican.
3 + (–7 + 6) = 3 – 7 + 6 = 2
• Si delante del paréntesis hay un signo negativo,
cambiarán de signo todos los números que se
encuentren dentro.
5 – (–3 + 8) = 5 + 3 – 8 = 0

14. 5. Operaciones combinadas
LOS NÚMEROS ENTEROS
Cuando hay varias operaciones juntas debes seguir el
siguiente orden:
1.º Efectuar las operaciones entre paréntesis y
corchetes.
2.º Calcular las potencias y las raíces.
3.º Realizar las multiplicaciones y divisiones en orden de
aparición.
4.º Efectuar las sumas y restas de izquierda a derecha.
[(– 5) – 3] · (– 2) + (– 8) : 22

15. 5. Operaciones combinadas
LOS NÚMEROS ENTEROS
1º ESO | UNIDAD 04 | MATEMÁTICAS
[(– 5) – 3] · (– 2) + (– 8) : 22 =
= (– 8) · (– 2) + (– 8) : 22 =
= (– 8) · (– 2) + (– 8) : 4 =
= (+16) + (– 2) = (+14)

16.  Los números racionales, son el conjunto de números
fraccionarios y números enteros representados por
medio de fracciones.
 Todos los números fraccionarios son números
racionales, y sirven para representar medidas.
Números Racionales

17. Es un conjunto infinito, ordenado y denso, donde
todos los números se pueden escribir como fracción,
es decir:
a
b
/ a y b son enteros, y b es distinto de ceroQ =
Ejemplos:
2; 17; 0; -6; -45; -2;
7
0,489; 2,18; -0,647-1;
8
14;
3
NO es racional
a: numerador y b: denominador
15
0

18. Repaso

19.  Son todos los números Cardinales a los
cuales se les ha añadido el reflejo de los
números Naturales en la parte izquierda
de la recta numérica, o sea, los puestos
de los números Naturales.
{…, - 4, -3, -2, -1, 0, 1, 2, 3, 4, …}
Números Enteros
-4 -3 -2 -1 0 1 2 3 4

20.  Son los números que se pueden escribir como una fracción,
en la cual el numerador y denominador son Enteros, excepto
el denominador que no puede ser cero.
Números Racionales

21.  Naturales:
 Para determinar si un número Natural es también Racional,
basta tomar un ejemplo.
 Tomemos como ejemplo el número 5.
 ¿Se puede escribir el 5 como una fracción que cumpla con
la definición de Racional?
 Si. El 5 se puede escribir como:
5
1
Ejemplos de Racionales

22.  Para determinar si un número Entero es también
Racional, con un ejemplo es suficiente.
 Por ejemplo un número negativo: -4
 ¿Se puede escribir el -4 como una fracción que cumpla
con la definición de Racional?
 Si. El -4 se puede escribir como:
−4
1
Enteros

23.  Propiedades:
 Cuando los números enteros tienen el mismo signo,
se suman y el resultado queda con el mismo signo de
los números sumados.
 Ejemplo:
 1+3+5+8=17
 -2-4-7=-13
Los números Enteros

24.  Cuando los números enteros tienen distinto signo, se
resta el mayor (en valor absoluto) con el menor (en
valor absoluto) y el resultado (en valor absoluto)
queda con el signo del mayor.
 Ejemplo:
 -5+3= -2
 6-2=4

25.  Si delante de un paréntesis, corchete o llave, no hay
nada o un signo positivo, entonces se considera que
hay un signo positivo que al retirar el paréntesis
mantiene el signo de los términos que estaban dentro
de el.
Ejemplo:
      54235423 
 5423 
5423 
0

26.  Si delante de un paréntesis, corchete o llave, hay un
signo negativo, entonces al retirar el paréntesis se
cambia el signo de los términos que estaban dentro
de el.
Ejemplo:
 412 
412 
1
      412412 

27.  Para sumar o restar números enteros:
 Eliminar los paréntesis, llaves y corchetes aplicando las
propiedades que correspondan.
 Sumar primero todos los positivos por un lado y los
negativos por otro poniéndoles el signo
correspondiente al resultado de cada uno.
 Restar ambos y pongo el signo del mayor al resultado.

28.  Resolver:
 Eliminar los paréntesis
 Sumar
 Restar
        853514952757 

29.  Resolver:
 Eliminar los paréntesis
 Sumar
 Restar
 Eliminé los primeros paréntesis
        853514952757 
      853514952757 

30.  Resolver:
 Eliminar los paréntesis
 Sumar
 Restar
 Eliminé los siguientes paréntesis
        853514952757 
      853514952757 
    853514952757 

31.  Resolver:
 Eliminar los paréntesis
 Sumar
 Restar
 Eliminé los últimos paréntesis
        853514952757 
      853514952757 
    853514952757 
853514952757 

32.  Resolver:
 Eliminar los paréntesis
 Sumar
 Restar
 Sumo los positivos y luego sumo el valor absoluto de los
negativos poniendo el resultado con signo negativo
        853514952757 
      853514952757 
    853514952757 
853514952757 
4327

33. Ejemplos de Suma:
5 + 7 =
(-5) + (-7) =
(-5) + 7 =
5 + (-7) =
12
(-12)
(-2)
2

34. Recordar el valor absoluto:
 | 7 | =
 | -7 | =
 | 0 | =
 | -3.1 | =
 | 0.85 | =
 | ¼ | =
 | - ½ | =
 | 5 - 4 | =
 | -9 | - | -2 | =
 - | -9 | =
7
7
0
3.1
0.85
¼
½
| 1 | = 1
9 – 2 = 7
- 9

35. Resta de Enteros
Regla para restar números enteros
a – b =
• La resta se cambia a suma del opuesto del
sustraendo.
a + (-b)
• Después se aplican las reglas de suma de
enteros
Suma

36. Ejemplos de Resta:
7 – (-2) =
(-7) – (-2) =
(-7) – 2 =
7 – 2 =
7 + 2 =
(-7) + 2 =
(-7) + (-2) =
7 + (-2) =
9
(-5)
(-9)
5

37. Multiplicación de Enteros
Reglas para multiplicar números enteros
(Positivo) . (Positivo) =
(Negativo) . (Negativo) =
(Positivo) . (Negativo) =
(Negativo) . (Positivo) =
Signos Iguales
resultado es
Positivo
Signos
Diferentes
resultado es
Negativo
(Positivo)
(Positivo)
(Negativo)
(Negativo)

38. Ejemplos de Multiplicación:
3 . 4 =
(-3) . (-4) =
3 . (-4) =
(-3) . 4 =
12
12
(-12)
(-12)

39. División de Enteros
Reglas para dividir números enteros
(Positivo) ÷ (Positivo) = (Positivo)
(Negativo) ÷ (Negativo) = (Positivo)
(Positivo) ÷ (Negativo) = (Negativo)
(Negativo) ÷ (Positivo) = (Negativo)
Signos
Iguales
resultado es
Positivo
Signos
Diferentes
resultado es
Negativo