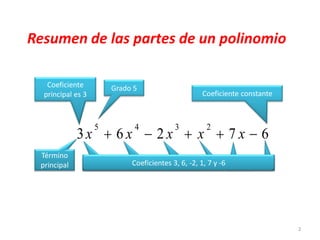
El documento resume conceptos clave sobre funciones polinomiales. Explica que las gráficas de polinomios de grado 0, 1 y 2 son parábolas y que a mayor grado es más complicada la gráfica. También define ceros de una función como los valores de x que hacen que la función sea igual a cero y muestra un ejemplo. Por último, resume los pasos para multiplicar y sumar/restar polinomios.

1. 1 Resumen Funciones polinomiales

2. 3 6 2 7 6
5 4 3 2
x  x  x  x  x 
Coeficiente
principal es 3
Grado 5
Término
principal Coeficientes 3, 6, -2, 1, 7 y -6
Coeficiente constante
Resumen de las partes de un polinomio
2

3. Gráfica de polinomios
Las gráficas de polinomios de grado 0 ó 1, y las gráficas de polinomios de grado 2 son parábolas. Mientras mayor sea el grado del polinomio, más complicada será la gráfica. Sin embargo, la gráfica de una función polinomial es siempre una curva lisa; es decir, no tiene discontinuidad en las esquinas.
3

4. 4
3
f ( x )  x  8
 
3
f (2 )  2  8  0
 
 
Los ceros de una función son
los valores de
D
efinic
tal q
i
ue 0.
ón
f x
x f x 
Ejemplo:
x  2 es un cero de la función.
Ceros de polinomios

5. Multiplicación de Polinomios
1.Multiplicación de un número por un polinomio
2. Multiplicación de un monomio por un polinomio
3. Multiplicación de polinomios

6. Suma y resta de Polinomios
Términos similares: Son Términos cuyas variables (y sus exponentes como el 2 en x2) son los mismos.
Sumar polinomios
Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.
Restar polinomios
La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.