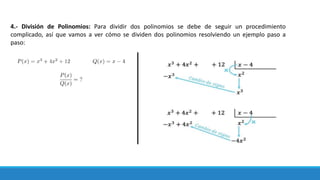
Este documento trata sobre monomios y polinomios. Explica que un monomio es una expresión algebraica formada por un coeficiente y una parte literal, y que un polinomio es una expresión formada por la suma de monomios. También describe las operaciones básicas que se pueden realizar con monomios y polinomios, como suma, resta, multiplicación y división. Finalmente, clasifica diferentes tipos de monomios y polinomios.

1. Sesión Nro. 04 – Monomios y Polinomios
Ing. WILMAR ORLANDO TABOADA PRINCIPE
RESOLUCIÓN DE PROBLEMAS MATEMÁTICOS II

2. MONOMIOS Y POLINOMIOS
Estas fórmulas forman parte de las expresiones algebraicas más sencillas
llamadas monomios en las cuales el valor particular se obtiene cuando
sustituimos la letra x por un valor concreto. Así por ejemplo si x = 4 cm,
tendremos que V = 43
= 64 𝑐𝑚3
y S = 6·42
= 96 𝑐𝑚2
.
Volumen V(x) = 𝐱𝟑
Superfície total S(x) = 𝒙𝟐
Del cubo de la figura podemos expresar su volumen y su superficie total en función de la medida de sus aristas (x):
A partir de estas expresiones, se pueden construir otras también sencillas
llamadas polinomios y a partir de ellos a su vez otras más complejas.

3. Un monomio es una expresión algebraica formada por una parte numérica (coeficiente) y una parte
literal.
El coeficiente del monomio es el número que aparece multiplicando a las variables.
La parte literal está constituida por las letras y sus exponentes.
I. MONOMIO

4. El grado de un monomio es la suma de todos los exponentes de las letras o variables.
❑ Tipos de grados del monomio
Grado relativo: es el tipo de grado que se origina de una visión parcial del monomio, y que toma en cuenta
únicamente el exponente de la variable que se escoge como guía.
Grado absoluto: por su parte, el Grado absoluto plantea una visión global del monomio, siendo el resultado de la
suma de cada uno de los exponentes a los que se encuentran elevados los literales del monomio.
𝑀(𝑥, 𝑦, 𝑧) = 4𝑥2
𝑦4
𝑧5
GR(x) = 2 GR(y) = 4 GR(z) = 5
𝑀(𝑥, 𝑦, 𝑧) = 4𝑥2
𝑦4
𝑧5
GA(x) = 2 + 4 + 5 = 11

5. 2.- MONOMIOS OPUESTOS: Dos monomios son opuestos si sus literales son semejantes y el coeficiente de uno
es el opuesto del coeficiente del otro.
5𝑥2
𝑦 − 5𝑥2
𝑦 Son monomios opuestos
II. TIPOS DE MONOMIOS
Ejemplo:
1.- MONOMIOS SEMEJANTES: Dos monomios son semejantes si tienen la misma parte literal. Por tanto, dos
monomios semejantes sólo se diferencian en el coeficiente.
2𝑎𝑥4
𝑦4
; −3𝑎𝑥4
𝑦4
; 4 𝑎𝑥4
𝑦4
Son monomios Semejantes
2𝑎𝑥3
𝑦; 2𝑏𝑥4
𝑦4
No son monomios Semejantes
Ejemplo:

6. 2.- MONOMIOS HETEROGÉNEOS : son los monomios que no tienen el mismo grado absoluto. Es decir, los
monomios heterogéneos son el contrario de los monomios homogéneos.
𝑥8
; 3𝑥2
𝑦 ; 7𝑎2
𝑏4
Ejemplo:
3.- MONOMIOS HOMOGENEOS: Dos monomios son homogéneos cuando su grado absoluto es equivalente.
2𝑥6
; −3𝑥3
𝑦3
Ejemplo:

7. III. OPERACIONES CON MONOMIOS
1.- SUMA Y RESTA DE MONOMIOS: La suma o la resta de monomios semejantes es otro monomio semejante
a ellos que tiene por coeficiente la suma o resta de los coeficientes.
2.- MULTIPLICACIÓN DE MONOMIOS: la multiplicación de dos monomios es otro monomio cuyo coeficiente
es el producto de los coeficientes de los monomios y cuya parte literal se obtiene de multiplicar las variables
que tienen la misma base, es decir, sumando sus exponentes.
5𝑥3
+ 2𝑥3
= (5 + 2) 𝑥3
= 7 𝑥3
5𝑥3
- 2𝑥3
= (5 − 2) 𝑥3
= 3 𝑥3
5𝑥2
. 2𝑥3
= (5 . 2) 𝑥2+3
= 10 𝑥5
Suma:
Resta:

8. ➢ Propiedad conmutativa: el orden de los monomios multiplicandos no altera el resultado de la
multiplicación.
➢ Propiedad asociativa: cuando se multiplican tres o más monomios, el resultado del producto es el
mismo independientemente de como se agrupen los factores:
➢ Propiedad distributiva: la suma de dos monomios multiplicada por un tercero es igual a la suma de
cada sumando por el tercer monomio.
3𝑥5
. 2𝑥4
= (3 . 2) 𝑥5+4
= 6 𝑥9
2𝑥5
. 3𝑥4
= (2 . 3) 𝑥4+5
= 6 𝑥9
( 2x . 4𝑥2). 3𝑥5 = (2.4.3) 𝑥1+2+5
= 24 𝑥8
2x . (4𝑥2
. 3𝑥5
) = (2.4.3) 𝑥1+2+5
= 24 𝑥8
4𝑥6
. (3𝑥4
+ 5𝑥4
) = 4𝑥6
. 3𝑥4
+ 4𝑥6
. 5𝑥4
= (4.3)𝑥6+4 + (4.5)𝑥6+4
= 12𝑥10
+ 20𝑥10
= 32 𝑥10

9. 4.- POTENCIA DE MONOMIOS: Para calcular la potencia de un monomio se debe elevar cada elemento
del monomio al exponente de la potencia. Es decir, la potencia de un monomio consiste en elevar su
coeficiente y sus variables (letras) al exponente de la potencia
(2𝑥4
)3
= (2)3
(𝑥4
)3
= 8 𝑥4.3
= 8 𝑥12
3.- DIVISIÓN DE MONOMIOS: El resultado de la división de monomios es otro monomio cuyo coeficiente
equivale al cociente de los coeficientes de los monomios y cuya parte literal se obtiene de dividir las variables
que tienen la misma base, esto es, restando sus exponentes.
6 𝑥7
/ 2𝑥3
= (6/2) 𝑥7−3
= 3 𝑥4

10. Un polinomio es una expresión algebraica de sumas, restas y multiplicaciones ordenadas hecha
de variables, constantes y exponentes.
Partes de un Polinomio
o Términos:
o Coeficientes: 5, 7, 3, y 9
o Grado: 3
o Variable o indeterminada: x
o Término independiente: 9
V. POLINOMIO

11. • Grado Relativo de un Polinomio: Estado dado por el mayor exponente de la variable referida.
• Grado Absoluto de un Polinomio: Esta dado por el monomio de mayor grado.
El primer término tiene como grado 5, el segundo tiene como grado 7 y el tercero tiene como grado 10, por
lo tanto:
GA(P) = 10

12. ➢ Monomio: Es un polinomio que consta de un sólo monomio.
➢ Binomio: Es un polinomio que consta de dos monomios.
➢ Trinomio: Es un polinomio que consta de tres monomios.
Los polinomios tienen su propia clasificación según sus características:
P(𝑥) = 2𝑥3
P(𝑥) = 2𝑥3
+ 3x
P(𝑥) = 2𝑥3
+ 3x + 5
Ojo: Más de tres términos: seguirán denominándose polinomios.

13. EJEMPLOS DE POLINOMIOS:
Para acabar de entender el concepto de polinomio, a continuación vamos a ver varios ejemplos de polinomios:
✓ POLINOMIO DE GRADO CERO:
✓ POLINOMIO DE SEGUNDO GRADO:
✓ POLINOMIO DE PRIMER GRADO:
✓ POLINOMIO DE TERCER GRADO:
P 𝑥 = 7
P 𝑥 = 4𝑥 + 1
P 𝑥 = 2𝑥2
+ 5𝑥 + 3
P 𝑥 = 2𝑥3
− 8𝑥 + 9

14. VI. TIPOS DE POLINOMIOS
1. POLINOMIO ORDENADO: Es aquel donde los exponentes de la variable van aumentando o disminuyendo.
2. POLINOMIO COMPLETO: Es aquel donde aparecen todos los exponentes de la variable, desde el mayor, hasta el
término independiente.
3. POLINOMIO INCOMPLETO: Es aquel polinomio que le falta como mínimo un término de algún grado.
P 𝑥 = 𝑥4
+ 5𝑥2
+ 4𝑥 − 9
P 𝑥 = 𝑥3
+ 2𝑥2
+ 6𝑥 + 4
P 𝑥 = 𝑥5
+ 5𝑥3
+ 2𝑥

15. 4. POLINOMIOS HOMOGÉNEO: Es aquel donde todos sus términos tienen el mismo grado absoluto.
5. POLINOMIO HETEROGÉNEO: Es aquel polinomio en el que no todos sus términos tienen el mismo grado.
6. POLINOMIO OPUESTO: Un polinomio es opuesto a otro si los coeficientes de los términos de igual grado son
del mismo valor pero de signo contrario.
P 𝑥 = 5𝑥3
+ 5𝑥2
𝑦 + 𝑦3
P 𝑥 = −3𝑥4
+ 𝑥2
− 4𝑥
P 𝑥 = 𝑥5
+ 7𝑥3
− 2𝑥 + 4
- P 𝑥 = − 𝑥5
− 7𝑥3
+ 2𝑥 − 4

16. 1. - SUMA DE POLINOMIOS: Para resolver la suma de dos o más polinomios se deben sumar los
términos de los polinomios que son semejantes. Es decir, la suma de polinomios consiste en
sumar los términos que tienen la misma parte literal (mismas variables y mismos exponentes).
SUMA VERTICAL
SUMA HORIZONTAL
VII. OPERACIÓN CON POLINOMIOS
P 𝑥 = 6𝑥4
+ 4𝑥3
+ 2𝑥 – 3
Q 𝑥 = 3𝑥4
− 7𝑥3
+ 6𝑥2
− 4𝑥 + 1
P 𝑥 +Q 𝑥 = 6𝑥4 + 4𝑥3 + 2𝑥 – 3 + (3𝑥4 − 7𝑥3 + 6𝑥2 − 4𝑥 + 1)
P 𝑥 +Q 𝑥 = 6𝑥4
+ 4𝑥3
+ 2𝑥 − 3 + 3𝑥4
− 7𝑥3
+ 6𝑥2
− 4𝑥 + 1

17. 2.- RESTA DE POLINOMIOS: Para hacer la resta de dos polinomios se deben restar los términos de
los polinomios que son semejantes. Es decir, la resta de polinomios se basa en restar los términos
que tienen la misma parte literal (mismas variables y mismos exponentes).
P 𝒙 − Q 𝒙 = 7𝑥𝟒 + 2𝑥3 + 5𝑥 – 4 - (4𝑥4 − 3𝑥3 + 8𝑥2 − 2𝑥 + 1)
P 𝒙 − Q 𝒙 = 7𝑥𝟒 + 2𝑥3 + 5𝑥 – 4 - 4𝑥4+ 3𝑥3 − 8𝑥2 + 2𝑥 − 1)
RESTA HORIZONTAL

18. 3.- MULTIPLICACIÓN DE POLINOMIOS
Q 𝑥 . P 𝑥 = 4𝑥2
. 𝑥3
+ 4𝑥2
. −𝟓𝒙𝟐
+ 4𝑥2
. 2𝑥 + 3𝑥. 𝑥3
+ 3𝑥 . −𝟓𝒙𝟐
+ 3𝑥. 2𝑥
P 𝑥 = 4𝑥2
+ 3𝑥
Q 𝑥 = 𝑥3
− 5𝑥2
+ 2𝑥
Q 𝑥 . P 𝑥 = (4𝑥2
+3𝑥) (𝑥3
− 5𝑥2
+ 2𝑥)

19. 4.- División de Polinomios: Para dividir dos polinomios se debe de seguir un procedimiento
complicado, así que vamos a ver cómo se dividen dos polinomios resolviendo un ejemplo paso a
paso:

20. DESARROLLO