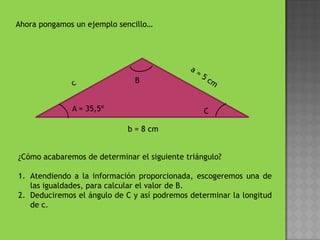
El teorema del seno establece que en cualquier triángulo, las longitudes de los lados son directamente proporcionales al seno de los ángulos opuestos. Para resolver un problema, basta con conocer tres términos (dos lados y un ángulo, o dos ángulos y un lado) para determinar el triángulo. El documento muestra un ejemplo de cómo usar el teorema del seno para calcular los ángulos y el lado restante de un triángulo dado dos lados y un ángulo.

1. teorema del senodosxdosTrigonometría

2. Matemáticamente hablando, el teorema del seno anuncia que…“ En todo triángulo, las longitudes de los lados son directamente proporcionales al seno de los ángulos que se oponen ”… que se resume a… c a B a = b = c msinAsinBsinCAC b *Nota: A la hora de solucionar problemas, sólo utilizaremos dos de las tres igualdades. Basta con que dispongamos de tres términos.

3. Ahora pongamos un ejemplo sencillo… c a = 5 cm B¿Cómo acabaremos de determinar el siguiente triángulo?Atendiendo a la información proporcionada, escogeremos una de las igualdades, para calcular el valor de B.Deduciremos el ángulo de C y así podremos determinar la longitud de c.A = 35,5ºC b = 8 cm

4. Disponemos de a, b y A. Lo único que podemos deducir es B: a = b m h h5 = 8 j sinAsinB sin35,5º sinBsinB = sin35,5º·8 = 0,92 5B = arcsin0,92 = 68,3º B= 68,3º2. C = 180º - (35,5º + 68,3º) = 76,2º C = 76,2º c = bsinC = 8sin76,2º = 8,36 cmsinB sin68,3 c = 8,36 cm