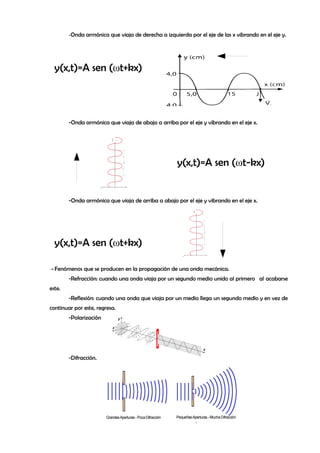
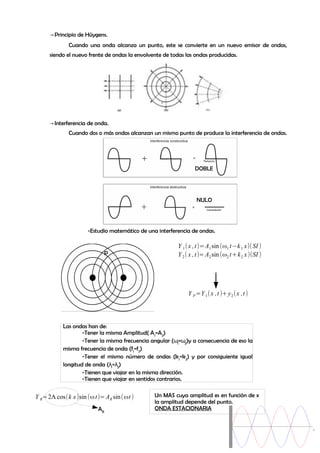
Este documento describe las características de las ondas mecánicas y electromagnéticas. Explica que una onda es una perturbación que se propaga a través de un medio, y que puede ser transversal, longitudinal o esférica dependiendo de su frente de ondas. Además, presenta la ecuación matemática que describe una onda armónica y los conceptos de interferencia, refracción, reflexión y difracción asociados con la propagación de ondas.

1. MOVIMIENTO ONDULATORIO.ONDAS.
· Onda: perturbación que se crea en un medio y que se propaga a todos los puntos de este.
(Sucesión de pulsos)
· Pulso: una sola perturbación.
· Onda armónica: aquella que se crea mediante un oscilador armónico.
→ Clasificación de las ondas.
-Según el frente de ondas:
~Onda circular si el frente es circular (piedra en piscina).
~Onda plana (palo en piscina).
~Onda esférica Si su frente es esférico, se propaga por el aire (música).
-Según el ángulo entre la vibración y el desplazamiento de la onda:
~Onda transversal: cuando la vibración y el desplazamiento forman un ángulo
recto.
~Onda longitudinal: cuando la vibración y el desplazamiento tienen la misma
dirección (ángulo 0).
-Según la influencia del medio
~Onda mecánica: perturbación relacionada con el movimiento de materia
(sonido) NO SE PROPAGAN POR EL VACÍO.
~Onda electromagnética: perturbación relacionada con dos campos, el magnético
y el eléctrico. SE PROPAGAN POR EL VACÍO.
→ Ecuación de una onda armónica.
ω
c= __
k
y(x,t)=A sen (ωt-kx)
Longitud de onda (m)
longitud en la que cabe
una onda completa.
Velocidad de avance o
propagación de onda
λ= c · T
Nº de ondas que caben en 2Π
m.
NO COINCIDE CON EL MAS.
Frecuencia de onda (Hz, s-1)
Nº de ondas por segundo.
f
→ Modificaciones de la ecuación de onda.
-Onda armónica que viaja de izquierda a derecha por el eje de las x vibrando en el eje y.
y(x,t)=A sen (ωt-kx)

2. -Onda armónica que viaja de derecha a izquierda por el eje de las x vibrando en el eje y.
y(x,t)=A sen (ωt+kx)
-Onda armónica que viaja de abajo a arriba por el eje y vibrando en el eje x.
y(x,t)=A sen (ωt-kx)
-Onda armónica que viaja de arriba a abajo por el eje y vibrando en el eje x.
y(x,t)=A sen (ωt+kx)
→ Fenómenos que se producen en la propagación de una onda mecánica.
-Refracción: cuando una onda viaja por un segundo medio unido al primero al acabarse
este.
-Reflexión: cuando una onda que viaja por un medio llega un segundo medio y en vez de
continuar por este, regresa.
-Polarización
-Difracción.

3. → Principio de Hüygens.
Cuando una onda alcanza un punto, este se convierte en un nuevo emisor de ondas,
siendo el nuevo frente de ondas la envolvente de todas las ondas producidas.
→ Interferencia de onda.
Cuando dos o más ondas alcanzan un mismo punto de produce la interferencia de ondas.
DOBLE
NULO
-Estudio matemático de una interferencia de ondas.
P
Y 1 ( x , t)=A1 sin (ω1 t−k 1 x)( SI )
Y 2 ( x , t)= A2 sin (ω2 t+k 2 x )(SI )
Y P =Y 1 ( x ,t )+ y 2 (x ,t )
Las ondas han de:
-Tener la misma Amplitud( A1=A2)
-Tener la misma frecuencia angular (ω1=ω2)y a consecuencia de eso la
misma frecuencia de onda (f1=f2)
-Tener el mismo número de ondas (k 1=k2) y por consiguiente igual
longitud de onda (λ1=λ2)
-Tienen que viajar en la misma dirección.
-Tienen que viajar en sentidos contrarios.
Y R=2A cos(k x )sin (ω t)= AR sin( ωt )
AR
Un MAS cuya amplitud es en función de x
la amplitud depende del punto.
ONDA ESTACIONARIA

4. ~Si AR es máximo es 2A por lo que el cos(kx)=1 entonces hay un vientre.
~Si AR es mínimo el cos(kx)=0 entonces hay un nodo.
→ Energía transportada por una onda armónica.
Y ( x , t)= Asin (ω t−k x)(SI )
v ( x , t)= Aω cos (ω t−k x)(SI )
1
1
Ec= m v 2 ( x , t)= m A2 ω2 cos2 (ω t−kx )
2
2
La energía transportada por una
onda es directamente proporcional
el cuadrado de la amplitud y al
cuadrado de la frecuencia.
1
1
Ec máx= m A2 ω 2= m A2 (2 Π f )2=2 m A2 Π2 f 2
2
2
→ Velocidad de las ondas en una cuerda tensa.
La c con que avanza la onda por la cuerda depende de T, de m y de L
√
√
T
T
c= μ =
m
L
c= f λ
√
T
m
c
L
f= =
λ 2L
Si:
-m aumenta c disminuye
-L aumenta c aumenta
-T aumenta c aumenta