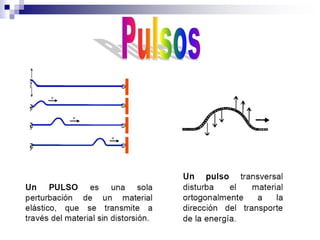
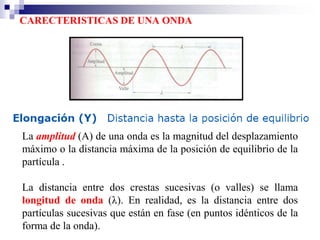
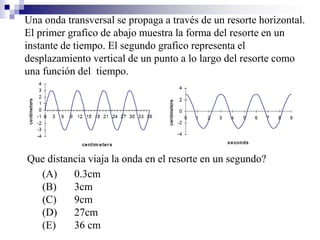
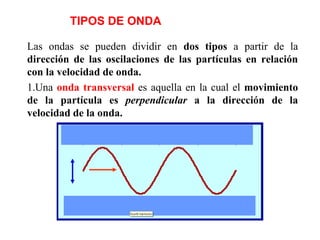
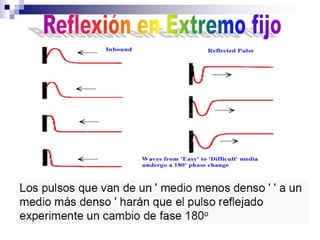
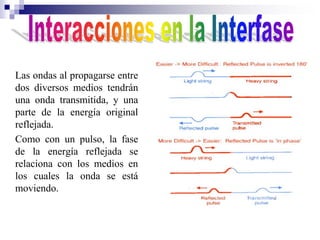
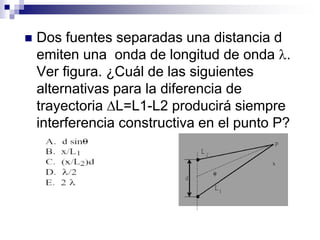
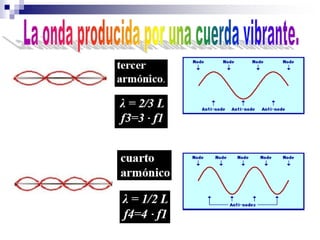
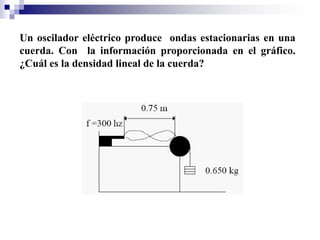
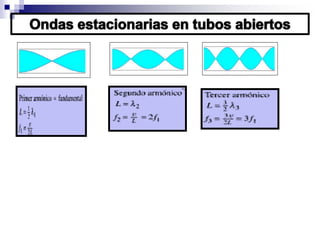
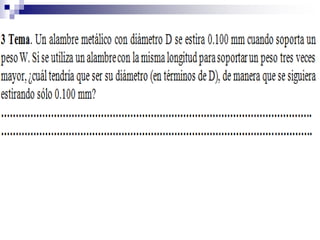
1) Los fenómenos ondulatorios se producen en todas las ramas de la física y se originan cuando una perturbación se propaga a través de un medio, transmitiendo energía pero sin transportar materia. 2) Las ondas electromagnéticas emitidas por una antena de radio son recibidas por un aparato de radio y convertidas en ondas sonoras. 3) Los fenómenos ondulatorios son una parte importante del mundo que nos rodea, a través de las cuales recibimos sonidos, luz e información.

2. Los fenómenos ondulatorios aparecen en todas las ramas de la
Física.
El movimiento ondulatorio se origina cuando una perturbación
se propaga en el espacio. No hay transporte de materia pero si
de energía.

3. La antena de la emisora emite las ondas electromagnéticas
que tu aparato de radio convierte en ondas sonoras.
Los fenómenos ondulatorios son parte importante del mundo
que nos rodea. A través de ondas nos llegan los sonidos, como
ondas percibimos la luz; se puede decir que a través de ondas
recibimos casi toda la información que poseemos.

4. Cuando un medio es perturbado, se le imparte energía. Esta
energía se propaga o se dispersa, por medio de interacciones
entre las partículas del medio.
Cualquier perturbación no sólo se propaga a través del
espacio, sino que puede repetirse una y otra vez en el tiempo,
en cada sitio a la largo del camino.
Una perturbación tal, regular, rítmica tanto en tiempo como en
espacio, se llama una onda viajera, y la trasferencia de energía
se dice que tiene lugar por medio de un movimiento de onda.

6. Una onda periódica, requiere de una perturbación constante
de una fuente de oscilación. En este caso, las partículas se
mueven continuamente hacia arriba y hacia abajo. El
movimiento de las partículas se puede describir como
movimiento armónico simple.
Tal movimiento tendrá forma senoidal (seno o coseno) tanto
en el tiempo como en el espacio.
Ser senoidal en el espacio significa que si se toma una
fotografía de la onda en cualquier instante (congelándola en
el tiempo), se podrá ver una onda de forma senoidal.
Sin embargo, si se ve un solo punto en el espacio al pasar la
onda, se verá una partícula del medio oscilando hacia arriba y
hacia abajo en forma senoidal con el tiempo, como la masa
suspendida de un resorte.

7. CARECTERISTICAS DE UNA ONDA
La amplitud (A) de una onda es la magnitud del desplazamiento
máximo o la distancia máxima de la posición de equilibrio de la
partícula .
La distancia entre dos crestas sucesivas (o valles) se llama
longitud de onda (λ). En realidad, es la distancia entre dos
partículas sucesivas que están en fase (en puntos idénticos de la
forma de la onda).

9. La frecuencia (f) de una onda es el número de ciclos por segundo,
esto es, el número de formas de ondas completas, que pasan por
un punto dado durante un segundo.
El periodo T = 1/f es el tiempo que se toma una forma de onda
completa (longitud de onda) pasar por un punto dado.

10. Velocidad de fase, relacionada con las características del medio
Como una onda se mueve, viaja una longitud de onda λ en el
tiempo de un periodo T.
Número de onda angular: k = 2π/ λ (rad/m)
Frecuencia angular: ω = 2 π/T (rad/s)

11. ECUACION DE UNA ONDA
Cada punto de un medio sobre el cual existe una perturbación
periódica está sometido a un movimiento armónico simple,
para expresar la dependencia con el tiempo del
desplazamiento de un punto del medio:
La dependencia espacial del desplazamiento en un momento
dado se representa mediante:

12. La fórmula matemática que describe una onda senoidal viajando
en la dirección de las x positivas es:
No podemos representar ésta ecuación en un diagrama plano
porque tenemos tres variables: y, x y t.
Para un valor fijo de t, la ecuación nos da y en función de x.
esta curva senoidal representa la forma del medio en un
momento dado (dominio espacial).
Para un valor fijo de x, o sea un punto dado de la cuerda, la
ecuación nos da y en función de t (domino temporal). Es un
movimiento armónico simple lo que llamamos vibración u
oscilación de una partícula.

14. Diagrama de cuerpo libre de un segmento de cuerda. La fuerza en cada extremo
de la cuerda es tangente a la cuerda en el punto de aplicación.

15. Una onda transversal se propaga por una cuerda tensa, de ecuación
Ordene la ecuación a la forma
Determine la frecuencia angular, el numero de onda, la longitud de
onda , el periodo y el ángulo de fase.
)02,04(6),( xtsentxy  
A=
k=
W=
θ=

16. De acuerdo a la ecuación de la onda
Determine:
La velocidad de propagación de la onda.
La velocidad máxima de la partícula
La aceleración máxima de la partícula.
En una posición de x=1 m y t=5 s.
Determine la velocidad y aceleración de la
partícula.
)02,04(6),( xtsentxy  

17. Un movimiento ondulatorio plano se propaga según la ecuación:
,t en segundos, x en cm.
Ordene la ecuación a la forma:
)54(),( xtsentx 
A. 4 cm/s y 5
B. 0,8 cm/s y 5
C. 1,26 cm/s y 0,64
D. 1 cm/s y 0,64
Determine su velocidad de propagación y número de onda es respectivamente:

18. Una onda transversal de esta forma se esta propagando a la
derecha a lo largo de una cuerda a una rapidez de 20 cm/s. la
grafica de arriba muestra un a instantánea de un segmento de
la cuerda tomada el tiempo t = 0 segundos medidos con un
cronometro.
¿Cuál es la longitud de onda de esta onda?
¿Cuál es el periodo de esta onda?

19. Una onda transversal se propaga a través de un resorte horizontal.
El primer grafico de abajo muestra la forma del resorte en un
instante de tiempo. El segundo grafico representa el
desplazamiento vertical de un punto a lo largo del resorte como
una función del tiempo.
Que distancia viaja la onda en el resorte en un segundo?
(A) 0.3cm
(B) 3cm
(C) 9cm
(D) 27cm
(E) 36 cm

20. En una cuerda colocada a lo largo del eje X, se propaga una onda
determinada por la función . El tiempo
que tardará la perturbación en recorrer 8m. Es de:
nota: primero ordene la ecuación de la onda de acuerdo a:
)48cos(02,0),( xttx 
A. 2 s.
B. 2,5 s.
C. 3 s.
D. 4 s.

21. TIPOS DE ONDA
Las ondas se pueden dividir en dos tipos a partir de la
dirección de las oscilaciones de las partículas en relación
con la velocidad de onda.
1.Una onda transversal es aquella en la cual el movimiento
de la partícula es perpendicular a la dirección de la
velocidad de la onda.

22. TIPOS DE ONDA
2.Una onda longitudinal es aquella en la cual el movimiento de
la partícula es paralelo a la dirección de la velocidad de la
onda.

23. TIPOS DE ONDA
 Las ondas mecánicas necesitan de un medio para
propagarse, mientras que las ondas electromagnéticas
no necesitan de un medio para su propagación.

24. FENOMENOS DE ONDAS
Frecuentemente se debe estudiar una onda que resulta de la
superposición de dos ondas. Estas pueden tener amplitudes,
frecuencias y fases diferentes.
Cuando dos movimientos ondulatorios se propagan por la misma
región del espacio, el efecto sumado de ambos sobre el medio se
denomina interferencia.
PRINCIPIO DE SUPERPOSICION:
En cualquier momento, la forme de onda combinada de dos o
más ondas que interfieren está dada por la suma de los
desplazamientos de las ondas individuales en cada punto del
medio.

25. )(
)(
02
01




tkxsenAy
tkxsenAy 




 





 

2
cos
2
sin2)sin()sin(
BABA
BA
21 yyy 
 )()(0   tkxsentkxsenAy




tkxba
tkxtkxba
22 



ba
tkxtkxba )(
)
2
(
2
cos2 0



 tkxsenAy Ec. de onda resultante
Principio de superposición

26. )
2
(
2
cos2 0



 tkxsenAy Ec. de onda resultante
2
cos2 0

AAR  Amplitud de la onda resultante
02
)4,2,0(1
2
cos
AA
parnn
R 
 

0
)5,3,1(0
2
cos


RA
imparnn 

Interferencia constructiva
Interferencia destructiva

27. Determine la ecuación de la
onda resultante de la
superposición de las siguientes
ondas.
)54(),( txsentx 
)3/54(),(   txsentx

28. Interferencia constructiva Se produce entre ondas de igual
frecuencia y longitud de onda cuando están en fase. El
resultado es una onda de igual frecuencia y longitud, pero con
una amplitud igual a la suma de las componentes
Interferencia destructiva Se produce entre ondas de igual
frecuencia y longitud de onda si tienen un desfase de media
onda. El resultado es una onda de igual frecuencia y longitud,
pero con una amplitud igual a la diferencia de las
componentes

29. Dos ondas de ecuaciones y
interfieren. Hallar la ecuación de las
ondas estacionarias resultantes:
)2501500(61 xtsenu 
)2501500(62 xtsenu 
A. U=24 cos 250 x sen 1500 t
B. U=12 cos 500 x sen 3000 t
C. U=12 cos 250 x sen 1500 t
D. U=24 cos 500 x sen 3000 t

30. En una cuerda interfieren dos impulsos de ecuaciones
cmty
cmty
)151500cos(3
)451500cos(2
2
1




La amplitud resultante será:
A. 1,61 cm
B. 2,65 cm
C. 4,36 cm
D. 4,84 cm

32.  Las ondas que viajan de
un medio ‘más denso’ a
un medio ‘menos denso’
harán que el pulso
reflejado este ‘EN
FASE’ con el pulso del
incidente.

33. Las ondas al propagarse entre
dos diversos medios tendrán
una onda transmitida, y una
parte de la energía original
reflejada.
Como con un pulso, la fase
de la energía reflejada se
relaciona con los medios en
los cuales la onda se está
moviendo.

35. Cuando emiten simultáneamente S1 y S2. El punto P describe un
M.A.S. que es la composición de dos M.A.S. de la misma
dirección y frecuencia. Los casos más importantes son aquellos
en los que los M.A.S. están en fase y en oposición de fase.

36. Dos M.A.S. están en fase
cuando la diferencia de
fase es un
múltiplo entero de 2π
21 krkr 

37.  Dos fuentes separadas una distancia d
emiten una onda de longitud de onda .
Ver figura. ¿Cuál de las siguientes
alternativas para la diferencia de
trayectoria L=L1-L2 producirá siempre
interferencia constructiva en el punto P?

38. Una onda de 493 hz de frecuencia tiene una velocidad
v = 353 m/s. ¿Qué distancia están separados dos
puntos que difieren en fase 55°?.

39. Ondas estacionarias Se produce
entre ondas idénticas viajando en
direcciones opuestas. En la onda
resultante hay puntos (vientres) que
vibran con una amplitud máxima
igual a la de las ondas componentes,
y puntos que permanecen en reposo
todo el tiempo (nodos)

40. )(
)(
02
01
tkxsenAy
tkxsenAy




YYY 21


41. Ec. de onda resultante
Amplitud de la inda resultante

42. Una cuerda sujeta por ambos extremos, vibra
de acuerdo con la ecuación Y= 3 sen(π x/3)
cos(50π t), donde x e Y se expresan en cm si t
viene en segundos. La distancia entre dos
nodos consecutivos es:
a) 6 cm
b) 3 cm
c) 10 cm
d) 8 cm

44. Onda fundamental o
primer armónico.
Segundo
armónico

46. Un oscilador eléctrico produce ondas estacionarias en una
cuerda. Con la información proporcionada en el gráfico.
¿Cuál es la densidad lineal de la cuerda?

47. En una cuerda tensa, sujeta por sus extremos, de 1m de longitud,
observamos la existencia de una onda estacionaria. La velocidad de
propagación de la perturbación vale 293,7 m/s, y observamos el armónico
cuya frecuencia es de 440 Hz.
a) ¿De qué armónico se trata: el fundamental, el 2°, el 3°,…?
b) ¿Cuántos nodos presenta? ¿Y cuántos vientres?
c) ¿Qué frecuencia tendría el 10 armónico o modo fundamental?

50. Una flauta es una cavidad resonante que puede
ser modelada como un tubo de longitud L, Abierto
en un extremo y cerrado en el otro, como se
muestra en la figura.
A) Estime la longitud esta flauta, si la velocidad del
sonido en el aire es 340 m/s y su frecuencia
fundamental es 80 Hz