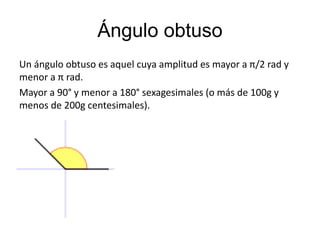
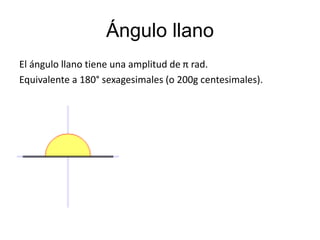
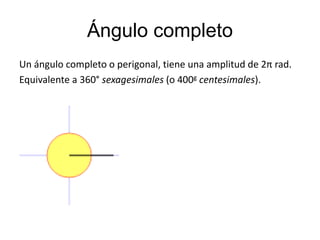
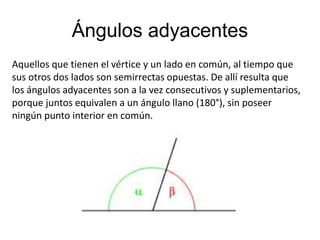
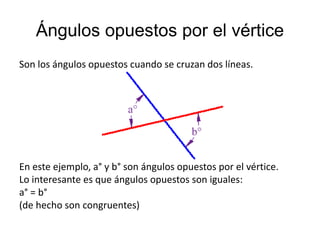
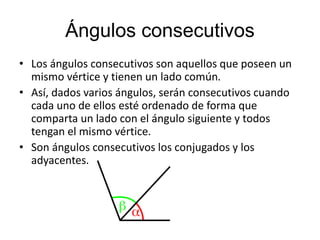
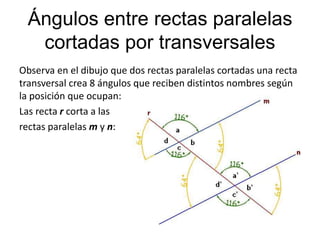
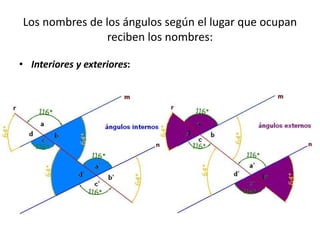
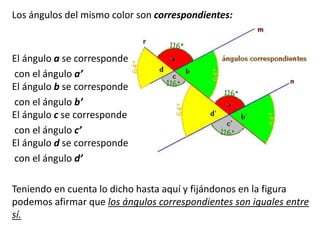
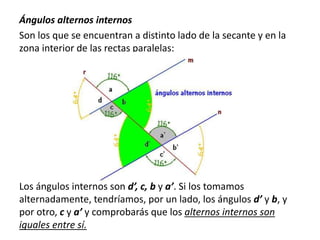
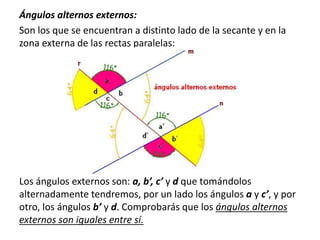
El documento explica los diferentes tipos de ángulos, incluyendo agudos, obtusos, rectos, llano y completo, así como sus medidas en radianes y grados. También se abordan conceptos relacionados como ángulos complementarios, suplementarios, adyacentes y opuestos por el vértice, así como las relaciones entre ángulos formados por rectas paralelas y una transversal. Se destacan las propiedades y las igualdades que rigen estos ángulos en diversas configuraciones.

1. “Ángulos en la vida”

2. ¿Qué es un ángulo?
Figura formada por dos semirrectas que
parten del mismo punto inicial. A las dos
rectas se les denomina lados del ángulo y al
punto inicial se le llama vértice del ángulo.
El símbolo del ángulo es <..

3. Ángulo agudo
Es el ángulo formado por dos semirrectas con amplitud mayor de
0 rad y menor de π/2 rad.
Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o
menor de 100g (grados centesimales).

4. Ángulo obtuso
Un ángulo obtuso es aquel cuya amplitud es mayor a π/2 rad y
menor a π rad.
Mayor a 90° y menor a 180° sexagesimales (o más de 100g y
menos de 200g centesimales).

5. Ángulo recto
Un ángulo recto es de amplitud igual a π/2 rad.
Es equivalente a 90° sexagesimales (o 100g centesimales).
Los dos lados de un ángulo recto son perpendiculares entre sí.
La proyección ortogonal de uno sobre otro es un punto, que
coincide con el vértice.

6. Ángulo llano
El ángulo llano tiene una amplitud de π rad.
Equivalente a 180° sexagesimales (o 200g centesimales).

7. Ángulo completo
Un ángulo completo o perigonal, tiene una amplitud de 2π rad.
Equivalente a 360° sexagesimales (o 400g centesimales).

8. Ángulos complementarios
Dos ángulos son complementarios si la suma de sus ángulos es
igual a 90º. Si conocemos un ángulo, su ángulo complementario
se puede encontrar restando la medida del mismo a 90º

9. Ángulos suplementarios
Dos ángulos son suplementarios si la suma de sus grados es igual
a 180º. Si conocemos un ángulo, su ángulo suplementario se
puede averiguar restando la medida del mismo a 180º.

10. Ángulos adyacentes
Aquellos que tienen el vértice y un lado en común, al tiempo que
sus otros dos lados son semirrectas opuestas. De allí resulta que
los ángulos adyacentes son a la vez consecutivos y suplementarios,
porque juntos equivalen a un ángulo llano (180°), sin poseer
ningún punto interior en común.

11. Ángulos opuestos por el vértice
Son los ángulos opuestos cuando se cruzan dos líneas.
En este ejemplo, a° y b° son ángulos opuestos por el vértice.
Lo interesante es que ángulos opuestos son iguales:
a° = b°
(de hecho son congruentes)

12. Ángulos consecutivos
• Los ángulos consecutivos son aquellos que poseen un
mismo vértice y tienen un lado común.
• Así, dados varios ángulos, serán consecutivos cuando
cada uno de ellos esté ordenado de forma que
comparta un lado con el ángulo siguiente y todos
tengan el mismo vértice.
• Son ángulos consecutivos los conjugados y los
adyacentes.

13. Ángulos entre rectas paralelas
cortadas por transversales
Observa en el dibujo que dos rectas paralelas cortadas una recta
transversal crea 8 ángulos que reciben distintos nombres según
la posición que ocupan:
Las recta r corta a las
rectas paralelas m y n:

14. Los nombres de los ángulos según el lugar que ocupan
reciben los nombres:
• Interiores y exteriores:

15. Ángulos correspondientes
Son los que se encuentran en el mismo lado de la secante, un
ángulo en la parte interior y otro en el exterior de las paralelas.

16. Los ángulos del mismo color son correspondientes:
El ángulo a se corresponde
con el ángulo a’
El ángulo b se corresponde
con el ángulo b’
El ángulo c se corresponde
con el ángulo c’
El ángulo d se corresponde
con el ángulo d’
Teniendo en cuenta lo dicho hasta aquí y fijándonos en la figura
podemos afirmar que los ángulos correspondientes son iguales entre
sí.

17. Ángulos alternos internos
Son los que se encuentran a distinto lado de la secante y en la
zona interior de las rectas paralelas:
Los ángulos internos son d’, c, b y a’. Si los tomamos
alternadamente, tendríamos, por un lado, los ángulos d’ y b, y
por otro, c y a’ y comprobarás que los alternos internos son
iguales entre sí.

18. Ángulos alternos externos:
Son los que se encuentran a distinto lado de la secante y en la
zona externa de las rectas paralelas:
Los ángulos externos son: a, b’, c’ y d que tomándolos
alternadamente tendremos, por un lado los ángulos a y c’, y por
otro, los ángulos b’ y d. Comprobarás que los ángulos alternos
externos son iguales entre sí.

19. Ángulo obtuso

20. Ángulo agudo

21. Ángulo recto

22. Ángulo llano.

23. Ángulo completo

24. Ángulo suplementario

25. Ángulo complementario