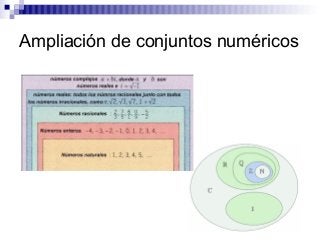
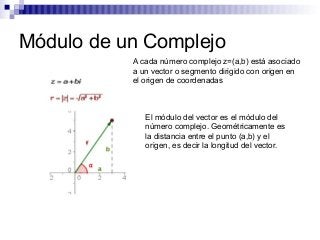
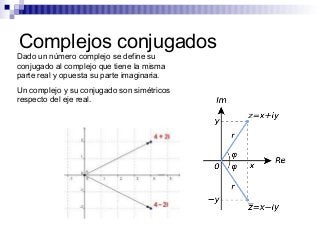
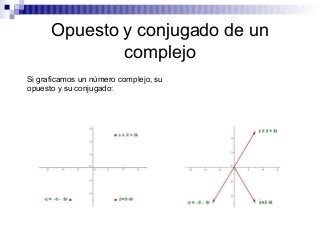
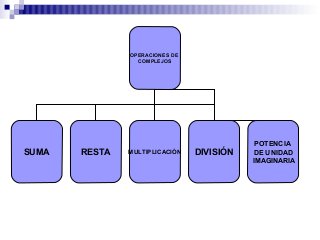
El documento introduce los números complejos, definidos como pares ordenados de números reales (x, y) donde x es la componente real y y la componente imaginaria. Explica que los números complejos permiten calcular cualquier raíz de índice par de radicando negativo, ampliando así el conjunto de los números reales. Describe las operaciones básicas con números complejos como suma, resta, multiplicación y división.