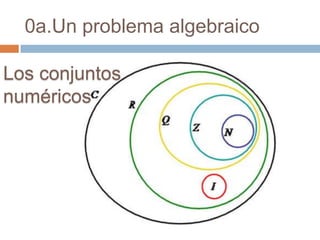
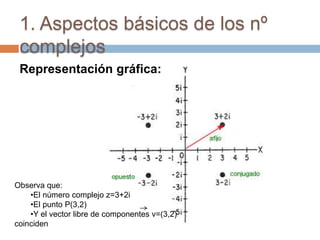
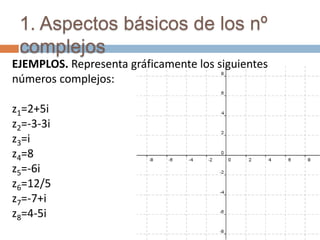
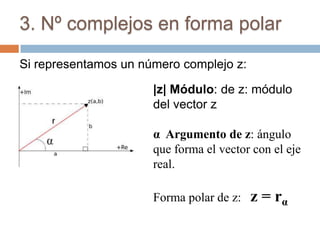
Este documento introduce los números complejos. Explica que se necesitó introducir este nuevo conjunto numérico para resolver ecuaciones como x2 = -1 que no tenían solución en los números reales. Define los números complejos como conjuntos de la forma a + bi, donde a y b son números reales y i = √-1. Describe las operaciones básicas con números complejos como suma, producto, cociente y representación en forma polar.

1. LOS NÚMEROS
COMPLEJOS
Imagen tomada del blog de Alberto Montt http://www.dosisdiarias.c

2. 0a.Un problema algebraico
La NECESIDAD de resolver ecuaciones ha
dado lugar a los distintos CONJUNTOS
NUMÉRICOS
Resolviendo ecuaciones…
 x-1=0 x=1 solución en N
 x+1=0 x=-1 solución en Z
 2x=3 x=2/3solución en Q
 x2=3 x=√3 solución en I

3. 0a.Un problema algebraico
¿La ecuación
x2 = -1
tiene solución en R?
No
Por eso se introduce un nuevo conjunto:
C, los números Complejos
i = √-1

4. 0a.Un problema algebraico
Los conjuntos
numéricos

5. 0b. Algo de historia
S. I a. de C. Herón de Obtiene raíces negativas
(En el Maediterráneo se Alejandría resolviendo pirámides
extiende el Imperio Romano)
S. XVI Tartaglia y Obtienen raíces negativas
Felipe II Cardano al resolver ecuaciones
Miguel de Cervantes
Nicolás Copérnico
polinómicas de grado 2 y
3
S. XVII Descartes Introduce el término
Último Austria (Carlos II) “Número imaginario”
Francisco de Quevedo
Isaac Newton
S. XVII Euler Introduce la notación “i”
Último Austria (Carlos II)
Francisco de Quevedo
Isaac Newton
S. XIX Gauss Extiende su uso
Guerras Napoleónicas
Gustavo A. Becquer
Louis Pasteur

6. 1. Aspectos básicos de los nº
complejos
Unidad imaginaria: i = √-1
2 → i = -1
Números complejos:
C = {a+bi, a,b números reales}
Ejemplos: 3-5i, -7+i, 2+4i…
a es la parte real (es un nº real)
b es la parte imaginaria (también es un número rea

7. 1. Aspectos básicos de los nº
complejos
z=a+bi es la forma binómica de un número complej
 si b = 0 z=a es un número real.
Luego todos los reales son nº complejos
si b ≠ 0 → z=a+bi es un número imaginario
 si a = 0 →z=bi es un número imaginario puro

8. 1. Aspectos básicos de los nº
complejos
Igualdad: Dos números complejos son iguales cuando
sus partes reales son iguales y la imaginarias también:
z=a+bi y z’=a’+b’i
z=z’ ↔ a=a’ y b=b’
Opuesto: el opuesto de z=a+bi es –z=-a-bi
Conjugados: a+bi y a-bi se llaman conjugados

9. 1. Aspectos básicos de los nº
complejos
EJEMPLOS:
Números imaginarios: 2-3i, -5+√3i, 1+iπ…
Números reales: 2+0i, π, 2/3…
Números imaginarios puros: 3i, πi, -1234i…
Sea z=-3+5i
El opuesto es: -z = -(-3+5i) = 3-5i
El conjugado es: z = -3-5i
¿Cuánto deberían valer las letras para que estos números
complejos sean iguales?
z=3-bi y z’=a+5i
z=z’ ↔ a=3, b=-5

10. 1. Aspectos básicos de los nº
complejos
Representación gráfica:
a es un número real: lo representamos
en el
eje horizontal (Eje Real)
b es un número real: lo representamos
en el
eje vertical (Eje Imaginario)
A cada punto del plano le corresponde un
ºn complejo z = x+yi y viceversa
Por eso se habla del PLANO COMPLEJO

11. 1. Aspectos básicos de los nº
complejos
Representación gráfica:
Observa que:
•El número complejo z=3+2i
•El punto P(3,2)
•Y el vector libre de componentes v=(3,2)
coinciden

12. 1. Aspectos básicos de los nº
complejos
EJEMPLOS. Representa gráficamente los siguientes
números complejos:
z1=2+5i
z2=-3-3i
z3=i
z4=8
z5=-6i
z6=12/5
z7=-7+i
z8=4-5i

13. 1. Aspectos básicos de los nº
complejos
Resolución de ecuaciones en C:
En el conjunto de los números complejos, las
ecuaciones polinómicas de segundo grado sin
solución real tienen dos soluciones complejas
conjugadas
Ejemplo:

14. 2. Operaciones con nº complejos
SUMA
Ejemplos:
(3-5i)+(2+9i) = 5+4i
(-2+i)-(6-2i) = -8+3i
2+(1-i) = 3-i

15. 2. Operaciones con nº complejos
PRODUCTO
Ejemplo:
(3-5i)·(2+9i) = 6+27i-10i-45i2=6+45+27i-10i=51+17i
¿Qué pasa si multiplicamos un número por su
conjugado?
(a+bi)·(a-bi) =a.a-abi+bia-bbi2 = a2-b2

16. 2. Operaciones con nº complejos
COCIENTE:
Se multiplica y divide por el conjugado del
denominador
No se puede dividir por cero

17. 2. Operaciones con nº complejos
PROPIEDADES DE LAS OPERACIONES:
• El 0 es el elemento neutro de la suma
z+0=z
• El opuesto de a+bi es -a-bi
• El inverso de a+bi es
El 0 no tiene inverso
En la práctica, operamos con los complejos como
si fueran reales, teniendo en cuenta que i2 = -1

18. 2. Operaciones con nº complejos
• Las potencias de i son:
i0 = 1
i1 = i
i2 = -1
i3 = i2 · i = -i
i4 = i2 · i2 =1
i5 = i4 · i = i
in ·= i(resto de dividir n entre 4)

19. 3. Nº complejos en forma polar
Si representamos un número complejo z:
|z| Módulo: de z: módulo
del vector z
α Argumento de z: ángulo
que forma el vector con el eje
real.
Forma polar de z: z = rα

20. 3. Nº complejos en forma polar
Paso de forma binómica a polar:

21. 3. Nº complejos en forma polar
Paso de forma polar a binómica:

22. 3. Nº complejos en forma polar
Algunos ejemplos:
¿Cuál es la forma polar de los siguientes complejos?
z=1 = 10º
z = -1 = 1180º
z=i = 190º
z = -i = 1270º

23. 4. Operaciones en forma polar
Producto:
El módulo es el producto de los módulos
El argumento es la suma de los argumentos
Ejemplo:
Observa que
Multiplicar = estirar (o encoger) el vector (r·r’) y girarlo
(α+β)

24. 4. Operaciones en forma polar
Producto:
Multiplicar por un complejo de módulo 1 es realizar
un giro de amplitud β

25. 4. Operaciones en forma polar
Cociente:
El módulo es el cociente de los módulos
El argumento es la resta de los argumentos
Ejemplo:

26. 4. Operaciones en forma polar
Potencia:
El módulo se eleva al exponente
El argumento se multiplica por el exponente
Ejemplo:

27. 4. Operaciones en forma polar
Potencia:
Si aplicamos las operaciones con potencias a un
complejo de módulo 1 obtenemos:
Por otra parte:
Con lo que obtenemos la fórmula de Moivre, que
relaciona las razones de nα con las de α:

28. 4. Operaciones en forma polar
Raíz n-sima de un nº complejo :
El módulo es la raíz n-sima del módulo
El argumento es el argumento dividido por n
Con k=0, 1, 2,…n-1
Por lo tanto, un número complejo tiene n raíces n-ésimas,
todas con el mismo módulo y diferentes argumentos
Si n>2 los puntos afijos de las n raíces de un número
complejo son los vértices de un n-ágono regular con
centro en el origen de coordenadas

29. 4. Operaciones en forma polar
Raíz n-sima de un nº complejo :
Vamos a calcular las tres
raíces cúbicas de 8i
Llamaremos a la raíces z1 z2 y z3

30. 4. Operaciones en forma polar
Raíz n-sima de un nº complejo : Si representamos las
raíces vemos que ocupan los vértices de un triángulo equilátero