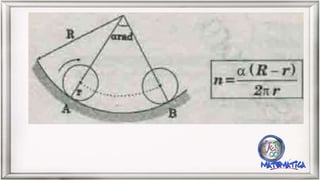
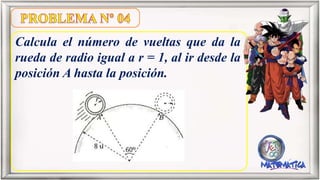
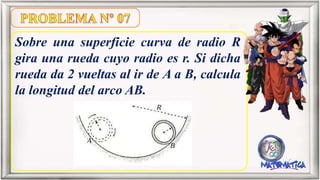
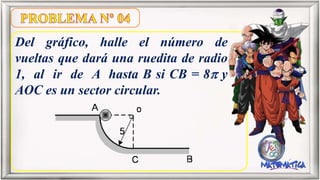
El documento contiene varias fórmulas y problemas relacionados con el cálculo del número de vueltas que dan ruedas al desplazarse sobre superficies planas y curvas. Se proporcionan ecuaciones para calcular el número de vueltas en función del radio de la rueda, la longitud recorrida y el ángulo barrido. También se explican las relaciones entre el número de vueltas y radios de ruedas unidas por una correa o eje común.

2. Si en la figura mostrada la
rueda de radio r se desplaza sin
resbalar de ‘A’ hasta ‘B’. El
número de vueltas ‘‘n’’ que da
dicha rueda se calcula así:

3. A
B
e
r
r
r
Ln e
2

e: Trayectoria descrita
por el centro de la rueda.
Le: Trayectoria descrita
por el centro de la rueda.
Pero también, si el ángulo girado por la
rueda es  rad, entonces:


2
n
R
L


4. RODANDO SOBRE UNA SUPERFICIE
CURVA:

6. RELACIONES ENTRE RUEDAS Y POLEAS:
a) Unidas por una franja de trasmisión o en contacto
en un punto.
P’
P
L1 θ1
θ2
L2
r1
r1
r2
r2
(1)
(2)
Q
Q’
P’
P
L1
θ1
r1
r1
(1)
θ2
L2
r2
r2
(2)
Q
Q’
LL 21  rr 2211   rnrn 2211 

7. b) Concéntricas o unidas por un eje que
pasa por sus centros:
r1
r1θ1 θ2
r2 r2
(1)
(2)
P’
P
QQ’
Eje
θ1
θ2
L1
L2
P’
P
Q’
Qr2
r2
r1
r1
(1)
(2)
 21  nn 21 

9. Si la rueda que se muestra en el gráfico
barre un ángulo de 750º al ir de A hasta
B, calcula el radio de la rueda.

10. Determina el número de vueltas que dará
la rueda de radio 8u al desplazarse desde
A hasta tocar la pared vertical ( = 22/7)

11. Los radios de las ruedas de una bicicleta
son entre sí como 3 es a 5. Calcula el
número de vueltas que da la rueda menor
cuando la rueda mayor barre un ángulo
de 216 radianes.

12. Calcula el número de vueltas que da la
rueda de radio igual a r = 1, al ir desde la
posición A hasta la posición.

13. En la figura, se muestra una rueda que gira sobre
una superficie circular. Determina el número de
vueltas que ha dado la rueda para ir desde P hasta
Q si su radio es 1/6 del radio de la superficie
circular sobre la cual se desplaza.

14. Dos ruedas de radios R y r, tal
que R > r, recorren la misma
longitud L sobre una pista plana.
Si la diferencia del número de
vueltas de la menor y la mayor es
L/R. Calcula R/r.

15. Sobre una superficie curva de radio R
gira una rueda cuyo radio es r. Si dicha
rueda da 2 vueltas al ir de A a B, calcula
la longitud del arco AB.

16. Las ruedas de radios 1u y 4u dan 10 y 3
vueltas, respectivamente, desde su
posición inicial hasta el instante en que
se separan. Calcula la distancia que las
separa.

17. En el gráfico, determina el número de
vueltas que da la rueda de r = 1u, al ir
desde A hasta C. Considere que AB =
12u y BC = 8u.

18. Una rueda de radio a metros da 10
vueltas para recorrer un tramo de
longitud L metros. Otra rueda de
radio (a2 + 62a – 3) metros gira 60º
para recorrer el mismo tramo.
Calcula a2 + 2a en metros.

20. Se tiene una bicicleta cuyas
ruedas tienen por radios R1 y
R2 (R1 < R2); cuando la rueda
menor gira º la mayor gira
g. ¿En qué relación se
encuentra los radios?

21. Se tienen dos ruedas conectadas por
una faja; si hacemos girar la faja, se
observa que las ruedas giran
ángulos que suman 144º. Determina
la diferencia de los números de
vueltas que dan estas ruedas si sus
radios miden 3 m y 5m.

22. En el sistema mostrado, si la rueda A
da 3/4 de vuelta, entonces la longitud
recorrida por la rueda C es:
2 6
A
C
8
B

23. Del gráfico, halle el número de
vueltas que dará una ruedita de radio
1, al ir de A hasta B si CB = 8 y
AOC es un sector circular.

24. Halla el número de vueltas que da la
rueda de radio (r = 1) al ir de la
posición A hasta la posición B.
r o
rBoA
20

25. La rueda de radio «r», gira
sin resbalar sobre la
superficie de radio 240r.
¿Cuál es la longitud
recorrida por el centro de la
rueda hasta que el punto B
este en contacto con la
superficie de la curva, si:
mAOB = 120º, r = 18u?
A
r
B
B
A240 r

26. Sobre una superficie
curva de radio “R” gira
una rueda cuyo radio es
“r” (ver figura). Si dicha
rueda da una vuelta al ir
de “M” a “N”. Calcula
la longitud del arco MN.
(son centros).
r
o
M
N
R
O