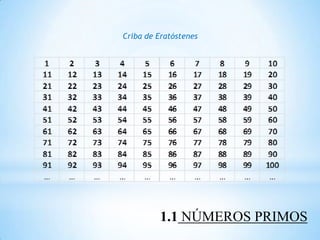
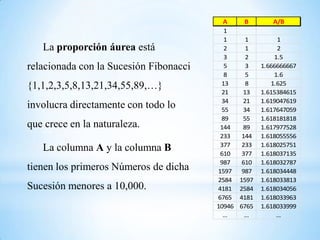
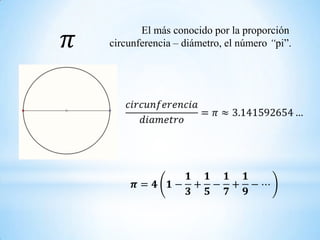
Este documento introduce los números irracionales, que son aquellos números reales que no pueden expresarse como la división de dos números enteros. Explica que los irracionales se dividen en dos categorías: los irracionales algebraicos, que son las raíces de polinomios con coeficientes reales; y los trascendentes, como pi, que no son soluciones de ninguna ecuación polinómica. También cubre temas como números primos, fracciones y la sucesión de Fibonacci en relación con la proporción áurea.

1. NÚMEROS IRRACIONALES

2. INTRODUCCIÓN
En general cualquier NÚMERO REAL que
no sea RACIONAL

3. INTRODUCCIÓN
Clasificación: Tras distinguir los números
componentes de la RECTA REAL en tres categorías:
(naturales, enteros y racionales), podría parecer que
ha terminado la clasificación de los números, pero aún
quedan "huecos" por rellenar en la recta de los
números reales.

4. INTRODUCCIÓN
Los Números Irracionales son los elementos de
dicha recta que cubren los vacíos que dejan los números
racionales.
Los Números Irracionales son los elementos de
la recta real que no pueden expresarse mediante el
cociente de dos enteros y se caracterizan por poseer
infinitas cifras decimales no periódicas.

5. CAPÍTULO 1:
El CONJUNTO DE
LOS NÚMEROS NATURALES.

6. Criba de Eratóstenes
1.1 NÚMEROS PRIMOS

7. 1 Descartamos a la unidad.
2 Se busca el número
menor, que en éste caso es el 2.
3 Se descartan los múltiplos
de 2.

8. 4 Se busca el número
menor, que en éste caso es el 3.
5 Se descartan los múltiplos
de 3.
6 Se busca el número
menor, que en éste caso es el 5.
7 Se descartan los múltiplos
de 5.

9. Y así sucesivamente…

10. Así. Los primeros 25 números primos, que por cierto son
TODOS menores que 100:
{
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61,
67, 71, 73, 79, 83, 89, 97 }

11. 1.1.1 PRIMOS ENTRE SI
Se dice que dos Números Enteros a y b si tienen
como único factor común la unidad entonces son primos
entre sí.
15 y 52 SI son primos entre si
15 y 63 NO son primos entre si
(ya que tienen como factor común al 3)
52 y 63 NO son primos entre si
(ya que tienen como factor común al 2)

12. 1.2 NÚMEROS NEGATIVOS
1.3 NÚMEROS ENTEROS

13. CAPÍTULO 2. NÚMEROS RACIONALES
• 2.1 Números Fraccionarios
• 2.2 Fracción Irreducible

15. CAPÍTULO 3. IRRACIONALES
Que solo pueden expresarse como un número con
infinitos decimales no periódicos (ya que se desconoce la
cantidad y secuencia).

16. 3.1 TIPOS DE IRRACIONALES.
Los Números Reales pueden subdividirse en
conjuntos según muchos criterios de clasificación por
ejemplo: Algebraicos y Trascendentes.
Así:
 Racionales
• Números Algebraicos
 Irracionales
• Números Trascendentes

17. 3.1.1 IRRACIONAL ALGEBRAICO

18. En general un Número Algebraico son las raíces
“n-ésimas” resultados de un polinomio de cualquier
grado con coeficientes Reales, que no sea un Número
Complejo.
Si una raíz de un polinomio además de no ser
complejo tampoco es un Número Entero, entonces es
Irracional Algebraico.
…………………….

19. En particular, éste es un ejemplo
de un Número Irracional
Algebraico, que además es conocido de
varias formas…
 Número Áureo
 Proporción áurea
 Razón dorada
 Número de oro

21. La proporción áurea

22. A B A/B
1
1 1 1
La proporción áurea está 2 1 2
3 2 1.5
relacionada con la Sucesión Fibonacci 5 3 1.666666667
8 5 1.6
{1,1,2,3,5,8,13,21,34,55,89,…} 13 8 1.625
21 13 1.615384615
34 21 1.619047619
involucra directamente con todo lo 55 34 1.617647059
89 55 1.618181818
que crece en la naturaleza. 144 89 1.617977528
233 144 1.618055556
377 233 1.618025751
La columna A y la columna B 610 377 1.618037135
987 610 1.618032787
tienen los primeros Números de dicha 1597 987 1.618034448
2584 1597 1.618033813
Sucesión menores a 10,000. 4181 2584 1.618034056
6765 4181 1.618033963
10946 6765 1.618033999
… … …

23. 3.1.2 NÚMERO TRASCENDENTE
Los Números Trascendentes son los Números
Reales que no son solución de ninguna ecuación
polinómica de coeficientes Racionales.
Por lo que:

24. El más conocido por la proporción
circunferencia – diámetro, el número “pi”.

27. Considerado como una verdadera “Proeza de
Alquimia Matemática” por Marcus Du Sautoy. Escritor y
presentador de “Los límites del espacio”, 3er capítulo de los
documentales La historia de la Matemática co-producido por
la BBC en 2008

28. CONCLUSIÓN

29. BIBLIOGRAFÍA.
1. (19-01-2009). Números algebraicos y trascendentes. Recuperado el (12-04-
2012), de (http://gaussianos.com/numeros-algebraicos-y-trascendentes-los-15-
numeros-trascendentes-mas-famosos/)
2. (Copyright 2012). Números Irracionales. Recuperado el (12-10-2012), de
(http://numerosirracionales.com/)
3. Angoa, J J, Contreras, A, Ibarra, M, Linares, R y Martínez, A. (2008).
Matemáticas Elementales, México, Puebla: Dirección de Fomento Editorial.
4. Du Sautoy, M. (2008). La historia de las Matemáticas, El lenguaje del Universo,
E.U.A: BBC.
5. Purcell, E, Varberg, D y Rigdon S. (Copyright 2000). Cálculo. U.S.A Prentice-
Hall