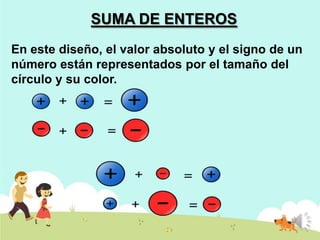
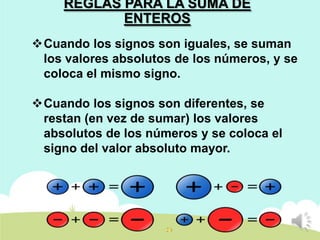
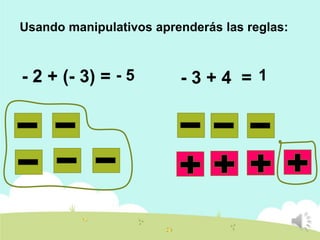
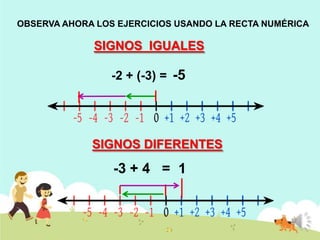
Este documento presenta una lección sobre números enteros. Explica la definición de números enteros, incluyendo positivos, cero y negativos. Describe el inverso aditivo, valor absoluto y comparación de números enteros. También cubre las reglas para sumar números enteros, ya sea con signos iguales o diferentes.

1. DEPARTAMENTO DE EDUCACIÓN DE PUERTO RICO
DISTRITO ESCOLAR DE PONCE
AÑO ESCOLAR 2012-2013
NÚMEROS ENTEROS
Por: Merielle K. Ortiz
Maestra de Matemáticas
Esc. Manuel González Pató

2. ESTÁNDAR DE CONTENIDO 1:
NUMERACIÓN Y OPERACIÓN
El estudiante es capaz de
entender los procesos y
conceptos matemáticos al
representar, estimar, realizar
cómputos, relacionar
números y sistemas
numéricos.

3. EXPECTATIVA E INDICADOR
2.0 Modela las operaciones, realiza
cómputos con fluidez y resuelve
problemas con números enteros.
N.SO.7.2.1 Modela la suma, resta,
multiplicación y división con
números enteros, describe las
relaciones entre estas operaciones y
aplica el orden de operaciones.

4. INTRODUCCIÓN

En esta presentación se trabajará con la historia y la
definición del conjunto de los números enteros, el
inverso aditivo, el valor absoluto, comparación de
números enteros y la suma de números enteros.

El nombre de enteros se justifica porque estos
números ya sean positivos o negativos, siempre
representaban cantidades en unidades enteras (por
ejemplo, piedras, palillos, nudos en
sogas, personas, etc.). Su utilidad, aunque con
diversas notaciones de acuerdo a la cultura, se
remonta a la antigüedad.

5. INTRODUCCIÓN Continuación
• No fue sino hasta el siglo XVII que tuvieron
aceptación en trabajos científicos
europeos, aunque matemáticos italianos
del renacimiento como Tartaglia y Cardano
los hubiesen ya advertido en sus trabajos
acerca de solución de ecuaciones de tercer
grado. Sin embargo, la regla de los signos
ya era conocida previamente por los
matemáticos de la India.

6. 
Al ser humano se le presentaron diferentes
situaciones; como indicar temperaturas bajo
0, diferenciar alturas y profundidades de la
tierra y como expresar que se queda debiendo
algo, entre otras.

Al no poder dar respuesta a estas situaciones
utilizando los números naturales, surgió la
necesidad de crear un nuevo conjunto de
números: los enteros.

7. DEFINICIÓN
El conjunto de los números
enteros incluye a los
números positivos, el cero
y los números negativos.
Los enteros negativos, como
−1 o −3 (se leen «negativo
uno», «negativo tres»), son
menores que todos los
enteros positivos (1, 2, ...) y
que el cero. Los números
enteros no tienen parte
decimal.
.

8. DEFINICIÓN continuación
Para resaltar la diferencia
entre positivos y negativos, a
veces también se escribe un
signo «positivo» delante del
número: +1, +5, etc. Cuando
no se le escribe signo al
número se asume que es
positivo. El conjunto de todos
los números enteros se va a
representar en este ejemplo
con la letra Z = {..., −3, −2,
−1, 0, +1, +2, +3, ...}.

9. USO DE ENTEROS PARA REPRESENTAR
CANTIDADES
Podemos usar signos para representar cantidades.
Ejemplos:

9 grados sobre 0 y 9 grados bajo 0.

Un 9 positivo representa una temperatura de
+9 grados y un 9 negativo representa una
temperatura de -9 grados.

El incremento se representa con un
número positivo y una disminución con un
número negativo.

10. HAZ LA PRUEBA
a. Una pérdida de 5 lbs
-5
Un aumento de 6 lbs
6
b. 3 pisos hacia arriba
3
2 pisos hacia abajo
-2
c. 7 pasos hacia adelante
7
4 pasos hacia atrás
-4
d. Una ganancia de $21
Una pérdida de $14
21
-14

11. INVERSO ADITIVO DE UN NÚMERO
ENTERO
Cuando extiendes la recta numérica a la
izquierda, puedes representar números
negativos. Aquellos números menores que
cero siempre se escriben con un signo
negativo. Los números opuestos como 9 y -9,
están a la misma distancia de cero en la recta
númerica.
El CERO se toma como punto de origen, ya
que no es positivo ni negativo.
Inverso aditivo(opuesto)

12. VALOR ABSOLUTO DE UN NÚMERO
ENTERO
El valor absoluto de un número es la distancia
que lo separa del cero. El valor absoluto se
representa mediante el símbolo y siempre
es positivo.

13. HAZ LA PRUEBA
Escribe el opuesto
-5
5
10
-10
12
-12
Halla el valor absoluto
|-7|
|15|
7
15
|-35| 35
0
1
|21|
-7
|1|
21
7
No tiene

14. COMPARACIÓN DE NÚMEROS ENTEROS
Cuando los números se alejan hacia la izquierda, su
valor disminuye
Cuando se alejan a la derecha, su valor aumenta
I I I I I I I I I I I I I I I I I I I
-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
Números negativos
Números positivos
ORIGEN
Puedes comparar números enteros utilizando
símbolos de comparación: <, >, ≤, ≥ ó =

15. HAZ LA PRUEBA
a) -3
<
b) -4
>
-7
d) 3
e) -5
f) 4
g) 0
<
c)
<
>
>
>
2
-7
7
5
-8
-9
-2

16. SUMA DE ENTEROS
En este diseño, el valor absoluto y el signo de un
número están representados por el tamaño del
círculo y su color.

17. REGLAS PARA LA SUMA DE
ENTEROS
Cuando los signos son iguales, se suman
los valores absolutos de los números, y se
coloca el mismo signo.
Cuando los signos son diferentes, se
restan (en vez de sumar) los valores
absolutos de los números y se coloca el
signo del valor absoluto mayor.

18. Usando manipulativos aprenderás las reglas:
- 2 + (- 3) = - 5
-3+4 = 1

19. EJEMPLOS
SIGNOS IGUALES





SIGNOS DIFERENTES
-5 + (-4) = -9

-3 + 8 = 5

6 + (-9) =-3

4 + (-1) = 3

-10 + 5 = -5

8 + (-9) =-1
2 + 7 =9
-5 + (-3) = -8
8 + 9 = 17
-3 + (-7) = -10
RECUERDA LAS REGLAS PARA
SUMAR NÚMEROS ENTEROS

20. OBSERVA AHORA LOS EJERCICIOS USANDO LA RECTA NUMÉRICA
SIGNOS IGUALES
-2 + (-3) = -5
SIGNOS DIFERENTES
-3 + 4 = 1

21. Copyright 2012, Todos los derechos reservados - Prohibida la
reproducción parcial o total de esta presentación, en cualquier lugar del
mundo, para fines lucrativos. Se puede utilizar estrictamente para
propósitos educativos.
AGRADECIMIENTOS

Superintendente de EscuelasSra.Edmée Lugo Meléndez

Director Escuela Manuel González
Pató- Sr. Wilberto Báez Rodríguez

Especialista Tecnología EducativaProf. Josefina Hernández

Facilitadora Docente de MatemáticaProf. Ana A. Silva Luciano

22. REFERENCIAS
Scott Foresman-Addison Wesley, MATEMÁTICAS
INTERMEDIAS CURSO I, Scott ForesmanAddison Wesley, MATEMÁTICAS
INTERMEDIAS CURSO II.
Diseños recuperados del Buscador Google. Com., el
27 de octubre de 2012
Microsoft Office. Com Clipart
http://es.wikipedia.org, recuperado el 27 de octubre
de 2012

23. FIN
Revisado por:
Ana A. Silva Luciano
Facilitadora Docente de Matemáticas
29 de noviembre de 2012