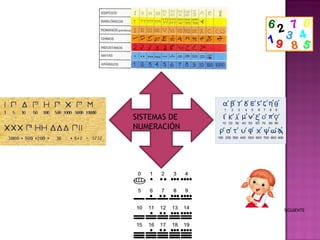
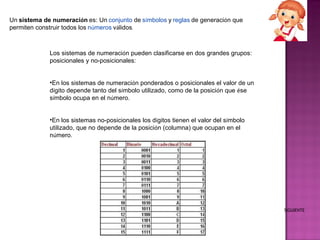
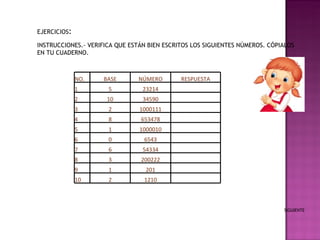
El documento describe diferentes sistemas de numeración, incluyendo el sistema decimal y otros sistemas posicionales y no posicionales. Explica que en los sistemas posicionales el valor de cada dígito depende de su posición, mientras que en los sistemas no posicionales como el romano el valor es independiente de la posición. Además, detalla los pasos para realizar sumas y restas con numeración romana convirtiendo primero a una notación única antes de aplicar las reglas de la suma y resta romanas.

1. MATEMATICAS 1 BLOQUE 1 SECUENCIA 1.Sistemas de numeración. • DESCRIPCIÓN: Identificar las propiedades del sistema de numeración decimal y contrastarlas con las de otros sistemas numéricos posicionales y no posicionales. 1.1 El sistema decimal SIGUIENTE

2. ¡HOLA! SOY TELERINA! TE INVITO A DESCUBRIR EL MÁGICO MUNDO DE LOS SISTEMAS DE NUMERACIÓN! SIGUIENTE

3. SIGUIENTE SISTEMAS DE NUMERACIÓN

4. SIGUIENTE Un sistema de numeraci ó n es: Un conjunto de s í mbolos y reglas de generaci ó n que permiten construir todos los n ú meros v á lidos . Los sistemas de numeraci ó n pueden clasificarse en dos grandes grupos: posicionales y no-posicionales: En los sistemas de numeraci ó n ponderados o posicionales el valor de un d í gito depende tanto del s í mbolo utilizado, como de la posici ó n que é se s í mbolo ocupa en el n ú mero. En los sistemas no-posicionales los d í gitos tienen el valor del s í mbolo utilizado, que no depende de la posici ó n (columna) que ocupan en el n ú mero.

5. Sistemas de numeraci ó n posicionales El n ú mero de s í mbolos permitidos en un sistema de numeraci ó n posicional se conoce como base del sistema de numeraci ó n. Si un sistema de numeraci ó n posicional tiene base b significa que disponemos de b s í mbolos diferentes para escribir los n ú meros, y que b unidades forman una unidad de orden superior. ESTO SIGNIFICA QUE: ASÍ QUE: DEL SIGUIENTE CONJUNTO DE NÚMEROS ¿CUÁLES ESTÁN BIEN ESRITOS? SIGUIENTE BASE VALORES PERMITIDOS 2 (BINARIA) 0,1 3 (TERNARIA) 0,1,2 4 (CUATERNARIA) 0, 1, 2, 3 5 (QUINARIA) 0,1,2,3,4 . . . . . . 10 (DECIMAL) 0,1,2,3,4,5,6,7,8,9 BASE NÚMERO 2 24 3 110111 10 2764 5 176 6 2166 1 10000 RESPUESTAS El número 24 está mal escrito, puesto que en base 2 solamente se permite hasta el número 1 El número 110111 está bien , puesto que en base 3 se permite hasta el número 2. El número 2764 está bien escrito, ya que todos son menores que 9 en base 10. El número 176 está mal escrito, ya que en base 5 sólo se permiten valores hasta 4. El número 2166 de base 6, también está mal escrito, por permitirse hasta el valor 5. Por último el número 10000 , está mal escrito, ya que no existe la base 1.

6. EJERCICIOS : INSTRUCCIONES.- VERIFICA QUE ESTÁN BIEN ESCRITOS LOS SIGUIENTES NÚMEROS. CÓPIALOS EN TU CUADERNO. SIGUIENTE NO. BASE NÚMERO RESPUESTA 1 5 23214 2 10 34590 3 2 1000111 4 8 653478 5 1 1000010 6 0 6543 7 6 54334 8 3 200222 9 1 201 10 2 1210

7. SIGUIENTE AHORA VAMOS A VERIFICAR TUS RESPUESTAS! INTERCAMBIA TU CUADERNO CON UN COMPAÑERO DE CLASE. AQUÍ TIENES LA CLAVE DE RESPUESTAS! NO. CLAVE 1 SI 2 SI 3 SI 4 NO 5 NO 6 NO 7 SI 8 SI 9 NO 10 NO

8. Sistemas de numeraci ó n no posicionales Estos son los m á s primitivos se usaban por ejemplo los dedos de la mano para representar la cantidad cinco y despu é s se hablaba de cu á ntas manos se ten í a. Tambi é n se sabe que se usaba cuerdas con nudos para representar cantidad. Tiene mucho que ver con la coordinabilidad entre conjuntos. Entre ellos est á n los sistemas del antiguo Egipto, el sistema de numeración romana, y los usados en Mesoamérica por mayas , aztecas y otros pueblos . EGIPCIO ROMANO MAYA SIGUIENTE

9. SIGUIENTE De manera que el sistema no posicional es cuando tiene el mismo valor, sin importar qu é posici ó n o lugar ocupe, eso pasa con los n ú meros romanos. X = 10 lX = 1 - 10 = 9 XXX = 10+10+10 = 30 XC = 100-10 = 90 En todos los ejemplos la X vale siempre 10.

10. Aritm é tica con Numeraci ó n Romana Todas las operaciones aritm é ticas realizadas con numeraci ó n romana, al tratarse de un caso particular de numeraci ó n entera, pueden ser descompuestas en sumas y restas. Suma Numerales romanos en un manuscrito del siglo XVI. 116 + 24 = 140 CXVI + XXIV = 140 Donde: SIGUIENTE Paso Descripción Ejemplo 1 Eliminar la notación substractiva IV -> IIII 4 = 4 2 Concatenar los términos CXVI + XXIIII -> CXVIXXIIII 116 + 24 = 140 3 Ordenar los numerales de mayor a menor CXVIXXIIII -> CXXXVIIIII 4 Simplificar el resultado reduciendo símbolos IIIII -> V; VV -> X; CXXXVIIIII -> CXXXX 5 = 5: 10 = 10: 140 = 140 5 Añadir notación substractiva XXXX -> XL 40 = 40 6 Solución CXL 140

11. Solución: CXVI + XXIV = CXL RESUMEN: El primer paso decodifica los datos posicionales en una notaci ó n ú nica, lo que facilita la tarea aritm é tica. Con ello, el segundo paso, al tener una notaci ó n ú nicamente aditiva puede entrar en funcionamiento. Tras eso, es necesaria una reordenaci ó n, pues los dos sumandos mantienen sus ordenaciones respectivas, lo que no es problema al no estar presente anotaci ó n substractiva. Una vez reordenados los s í mbolos, se agrupan los s í mbolos y se introduce de nuevo la notaci ó n substractiva, aplicando las reglas de numeraci ó n romana. Ahora, anota los siguientes ejercicios en tu cuaderno. No olvides hacer los cálculos con números romanos y dar el resultado en números romanos. SIGUIENTE 1.-LXXV + LXX = 2.-CCLXXIX + LIX = 3.-XCVIII + CCXCIV =

12. B)Intercambia tu cuaderno con un compañero y revisa las respuestas. RESPUESTAS: 1.- CXLV, 2.- CCCXXXVIII, 3.- CCCXCII SIGUIENTE ¡Lo has hecho muy bien! ¡Hasta la próxima!