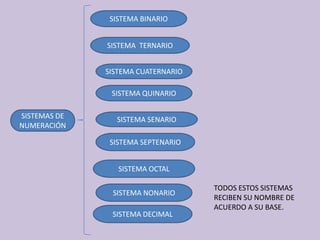
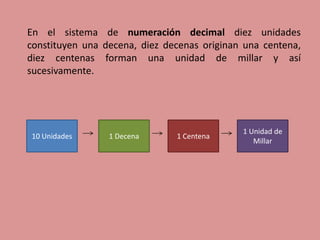
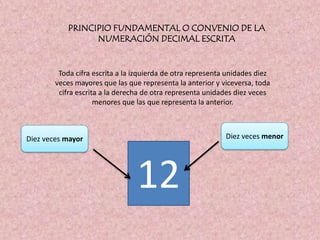
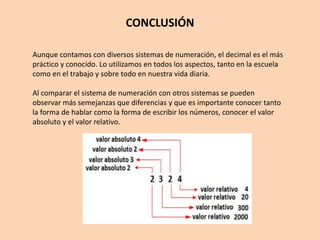
El documento describe el sistema de numeración decimal, que es el sistema que utilizamos habitualmente. Explica que se trata de un sistema de base 10, donde cada cifra representa unidades de un orden de magnitud, siendo el cero un valor posicional. También compara este sistema con otros y señala que aunque existen diferencias en las bases, todos los sistemas comparten características como el uso de un conjunto de reglas y la representación de valores relativos según la posición de cada cifra.

1. Sistema de Numeración
Decimal

2. A lo largo de la historia las civilizaciones han utilizado diferentes
sistemas de numeración, de algunos de los cuales todavía quedan
algunos vestigios: seguimos utilizando números romanos para señalar
las horas en algunos relojes, para numerar los siglos o los capítulos de
algunos libros; utilizamos el sistema sexagesimal de numeración de la
antigua Babilonia cuando medimos el tiempo. Sin embargo el sistema
que utilizamos de modo habitual es el sistema de numeración decimal.

3. La numeración es la parte de la Aritmética que enseña a expresar y a escribir los
números.
Dicha numeración puede ser hablada o escrita;
Numeración hablada (NH): nos enseña a expresar los números
Numeración escrita (NE) : nos enseña a escribir los números.
Por ejemplo;
NH = DIEZ NH = TRESCIENTOS OCHENTA Y CINCO
NE = 10 NE = 385

4. CIFRAS O GUARISMOS
Estos son los símbolos que representan una cantidad o número.
NÚMERO DIGITO
Son los que constan de una sola cifra. 1,2,3,4,5,6,7…
NÚMERO POLIDIGITO
Son los que constan de dos o más cifras. 25, 369, 4566…
SISTEMA DE NUMERACIÓN
Es un conjunto de reglas que sirven para expresar y escribir los números, estos constan
de una base.
BASE
Es el número de unidades que forman de un orden que forman una unidad del orden
inmediato superior.

5. SISTEMAS DE
NUMERACIÓN
SISTEMA BINARIO
SISTEMA TERNARIO
SISTEMA CUATERNARIO
SISTEMA QUINARIO
SISTEMA SENARIO
SISTEMA SEPTENARIO
SISTEMA OCTAL
SISTEMA NONARIO
SISTEMA DECIMAL
TODOS ESTOS SISTEMAS
RECIBEN SU NOMBRE DE
ACUERDO A SU BASE.

6. La numeración arábiga o decimal es la que comúnmente
utilizamos y son los números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Este sistema
fue desarrollado por los hindúes, posteriormente lo introducen
los árabes en Europa, donde recibe el nombre de sistema de
numeración decimal o arábigo.
Es decir, de base 10.
El cero no tiene valor por sí mismo, sino únicamente valor
posicional, es decir, por el lugar que ocupa. Recibe el nombre de
cifra no significativa o cifra auxiliar .
Valor Posicional
0
10
100
1000

7. Cuando utilizamos el sistema decimal creamos ORDENES.
1 2 3 4
ORDENES
Unidad (1) = Unidad de primer orden.
Decena (10) = Unidad de segundo orden.
Centena (100) = Unidad de tercer orden.
Millar (1,000) = Unidad de cuarto orden.
Decena de millar (10,000) = Unidad de quinto orden.
Centena de millar (100, 000) = Unidad de sexto orden.
M C D U

8. En el sistema de numeración decimal diez unidades
constituyen una decena, diez decenas originan una centena,
diez centenas forman una unidad de millar y así
sucesivamente.
10 Unidades 1 Decena 1 Centena
1 Unidad de
Millar

9. VALOR ABSOLUTO Y VALOR RELATIVO
VALOR ABSOLUTO: es el valor que adquiere el digito sin importar el lugar que
ocupe, es el valor por si solo.
432
VALOR RELATIVO: Es el valor posicional, es decir, cada digito tiene un valor de
acuerdo el lugar que ocupa en la cantidad.
432
400 30 2
4 3 2

10. PUNTO DECIMAL
El punto decimal es la parte más importante de un número decimal. Está
exactamente a la derecha de la posición de las unidades. Sin él, estaríamos
perdidos y no sabríamos cuál es cada posición.
Ahora podemos seguir con valores más y más pequeños,
como décimas, centésimas, y más, como en este ejemplo:

11. 12
PRINCIPIO FUNDAMENTAL O CONVENIO DE LA
NUMERACIÓN DECIMAL ESCRITA
Toda cifra escrita a la izquierda de otra representa unidades diez
veces mayores que las que representa la anterior y viceversa, toda
cifra escrita a la derecha de otra representa unidades diez veces
menores que las que representa la anterior.
Diez veces mayor Diez veces menor

12. DIFERENCIAS Y SEMEJANZAS CON OTROS SISTEMAS
DE NÚMERACIÓN

13. SEMEJANZAS
-Todos los sistemas de numeración cuentan con una base.
-Todos reciben un nombre de acuerdo a la base que lo conforma.
-En todo sistema, un número de unidades de cualquier orden, igual a la base,
forma una unidad del orden inmediato superior.
-En todo sistema, con tantas cifras como unidades tenga la base, se pueden
escribir todos los números.
-En todo sistema una cifra escrita a la izquierda de otra representa unidades
tantas veces mayores que las que representa la anterior, como indique la
base.
-Ningún sistema puede utilizar su base dentro de una cantidad.
-Todos los sistemas tienen en común las cifras 0 y 1.

14. DIFERENCIAS
-Todos los sistemas de numeración tienen diferente base.
-Todos reciben diferente nombre.
-Cada sistema utiliza diferente número de dígitos.
SISTEMA BINARIO
DIGITOS = 0 Y 1
SISTEMA TERNARIO
DIGITOS = 0, 1 Y 2

15. CONCLUSIÓN
Aunque contamos con diversos sistemas de numeración, el decimal es el más
práctico y conocido. Lo utilizamos en todos los aspectos, tanto en la escuela
como en el trabajo y sobre todo en nuestra vida diaria.
Al comparar el sistema de numeración con otros sistemas se pueden
observar más semejanzas que diferencias y que es importante conocer tanto
la forma de hablar como la forma de escribir los números, conocer el valor
absoluto y el valor relativo.

16. http://www.fismat.umich.mx/~elizalde/curso/node111.html
http://www.slideshare.net/rutmoritaharry1/semenjanzas-
y-diferencias
http://www.gpdmatematica.org.ar/publicaciones/Ana_Br
essan_Sistemas_y_Bases_de_Numeracion.pdf
http://www.escolares.net/matematicas/sistema-de-
numeracion-decimal/
http://www.disfrutalasmatematicas.com/numeros/decimal
es.html
BIBLIOGRAFÍA
Aritmética teórico practica, A. Baldor, Publicaciones Cultural.
Páginas 26-44