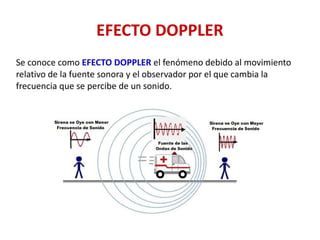
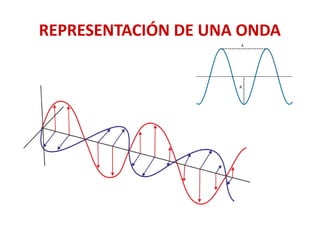
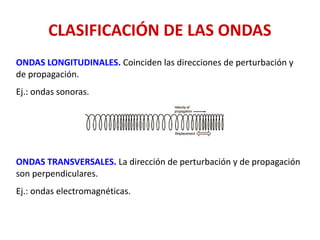
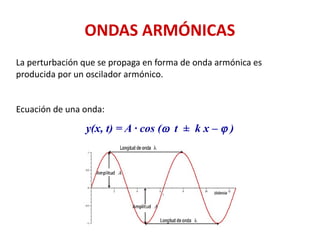
Este documento trata sobre ondas. Explica que una onda representa la propagación de una perturbación de un punto a otro sin transporte de materia, y que existen ondas mecánicas y electromagnéticas. Describe las características de las ondas armónicas como la longitud de onda, período, frecuencia y velocidad. También cubre conceptos como interferencia, ondas estacionarias y propiedades de las ondas sonoras.

1. TEMA 2 ONDAS

2. CONCEPTO DE ONDA
Una ONDA representa el movimiento de propagación de una
perturbación de un punto a otro sin que exista transporte neto de
materia. En una onda se propaga energía.
TIPOS DE ONDA:
- ONDAS MECÁNICAS. Son aquellas que necesitan un medio material
para transmitirse. Ej.: el sonido.
- ONDAS ELECTROMAGNÉTICAS. No requieren un medio material para
su propagación y pueden transmitirse en el vacío. Ej.: ondas de radio, la
luz.

3. REPRESENTACIÓN DE UNA ONDA

4. CLASIFICACIÓN DE LAS ONDAS
ONDAS LONGITUDINALES. Coinciden las direcciones de perturbación y
de propagación.
Ej.: ondas sonoras.
ONDAS TRANSVERSALES. La dirección de perturbación y de propagación
son perpendiculares.
Ej.: ondas electromagnéticas.

5. ONDAS ARMÓNICAS
La perturbación que se propaga en forma de onda armónica es
producida por un oscilador armónico.
Ecuación de una onda:
y(x, t) = A · cos (w t ± k x – j )

6. ONDAS ARMÓNICAS
y(x, t) = A · cos (w t ± k x – j )
PARÁMETROS CONSTANTES DE UNA ONDA ARMÓNICA
LONGITUD DE ONDA (l). Distancia entre dos puntos consecutivos que se
encuentran en idéntico estado de perturbación.
PERÍODO (T). Tiempo que tarda un punto cualquiera en repetir un
determinado estado de perturbación u oscilación.
FRECUENCIA (f). Número de veces que un determinado punto repite
cierto estado de perturbación u oscilación por unidad de tiempo. La
frecuencia es la magnitud inversa del período.

7. ONDAS ARMÓNICAS
y(x, t) = A · cos (w t ± k x – j )
PARÁMETROS CONSTANTES DE UNA ONDA ARMÓNICA
VELOCIDAD DE PROPAGACIÓN (v). Desplazamiento efectuado por la
onda en la unidad de tiempo.
NÚMERO DE ONDA (k). Número de longitudes de onda que hay en una
distancia 2p.
v = l · f
k =
2p
l

8. ENERGÍA TRANSMITIDA POR
LAS ONDAS ARMÓNICAS
Eo
= · k · A2
= · m · w 2
· A2
=
= · m · 4p2
· f 2
· A2
= 2 · m · p 2
· f 2
· A2
1
1
1
2
2
2
I = =
E
S t
P
S

9. ESTUDIO CUALITATIVO DE ALGUNAS
PROPIEDADES DE LAS ONDAS
PRINCIPIO DE HUYGENS:
Todo punto de un medio hasta el cual llega una perturbación se
comporta como un foco emisor de ondas secundarias que se propagan
en la dirección de la perturbación.
La superficie tangente (envolvente) a todas las ondas secundarias en un
instante dado constituye el siguiente frente de ondas.

10. ESTUDIO CUALITATIVO DE ALGUNAS
PROPIEDADES DE LAS ONDAS
PRINCIPIO DE HUYGENS:

11. ESTUDIO CUALITATIVO DE ALGUNAS
PROPIEDADES DE LAS ONDAS
REFLEXIÓN:
Cuando una onda que se propaga por un medio llega a la superficie de
separación con otro medio distinto, parte de la onda se refleja y sigue
propagándose por el mismo medio, mientras que la otra parte pasa a
propagarse por el otro medio, donde, al ser distinto, lo hará con diferente
velocidad.
La primera fracción de la onda recibe el nombre de ONDA REFLEJADA, y
la segunda se denomina ONDA REFRACTADA.

12. ESTUDIO CUALITATIVO DE ALGUNAS
PROPIEDADES DE LAS ONDAS
REFRACCIÓN:
si v' > v si v' < v

13. ESTUDIO CUALITATIVO DE ALGUNAS
PROPIEDADES DE LAS ONDAS
REFRACCIÓN:
Ley de Snell de la refracción:
=
sen i
sen r
v
v'

14. ESTUDIO CUALITATIVO DE ALGUNAS
PROPIEDADES DE LAS ONDAS
DIFRACCIÓN:
Se llama difracción al fenómeno por el cual una onda modifica su
dirección de propagación al encontrarse con aberturas u obstáculos.
Este fenómeno adquiere importancia cuando las dimensiones de la
abertura o las del obstáculo que se va a sortear son comparables con la
longitud de onda.

15. PRINCIPIO DE SUPERPOSICIÓN EN
EL MOVIMIENTO ONDULATORIO
La perturbación producida en un punto por dos o más ondas es igual a la
suma algebraica de las perturbaciones producidas en dicho punto por
cada una de las ondas consideradas de modo aislado.
FENÓMENO DE INTERFERENCIA

16. INTERFERENCIA ENTRE
ONDAS ARMÓNICAS
y1
= A · cos (w t – kx)
y2
= A · cos (w t – kx – d )
A' = 2 A · cos d / 2
AMPLITUD DE LA
ONDA RESULTANTE

17. INTERFERENCIA ENTRE
ONDAS ARMÓNICAS
CASO 1.- LAS ONDAS ESTÁN EN CONSONANCIA DE FASE (d = 0)
A' = 2 A · cos 0 = 2 A
Cuando dos ondas en consonancia de fase (desfase nulo) interfieren
entre sí, lo hacen de manera constructiva.

18. INTERFERENCIA ENTRE
ONDAS ARMÓNICAS
CASO 2.- LAS ONDAS ESTÁN EN OPOSICIÓN DE FASE (d = p)
A' = 0
Cuando dos ondas en oposición de fase interfieren entre sí, lo hacen de
manera destructiva.

19. INTERFERENCIA ENTRE
ONDAS ARMÓNICAS
CASO 3.- DIFERENCIA DE LA DISTANCIA RECORRIDA ENTRE DOS FUENTES
La interferencia será constructiva cuando la diferencia entre las
distancias por las ondas sea un múltiplo entero de la longitud de onda.
En los puntos en los que se satisfaga esa condición, se producirán
máximos. Así pues, la condición de los máximos es:
Dd = n · l
donde n es igual a 0, 1, 2, etcétera.

20. INTERFERENCIA ENTRE
ONDAS ARMÓNICAS
CASO 3.- DIFERENCIA DE LA DISTANCIA RECORRIDA ENTRE DOS FUENTES
La interferencia será destructiva si la diferencia entre las distancias es de
media longitud de onda o un múltiplo impar de ella. En los puntos en los
que se satisfaga esa condición, las ondas se anularán mutuamente,
dando lugar a mínimos. Así pues, la condición de los mínimos es:
Dd = (2n + 1) · l
2

21. INTERFERENCIA ENTRE
ONDAS ARMÓNICAS
RECUERDA:

22. ONDAS ESTACIONARIAS
Si un tren de ondas se encuentra con una frontera, la parte reflejada
interfiere con la parte incidente del tren de ondas.
Cuando se confinan las ondas en una región del espacio mediante
fronteras, estas ondas se reflejan hacia delante y hacia atrás en dichas
fronteras, y se originan ondas estacionarias.

23. ONDAS ESTACIONARIAS
Por tanto, se considera estacionaria la onda que resulta de la
interferencia de dos ondas idénticas que se propagan en la misma
dirección pero en sentido contrario.
Estas ondas reciben el nombre de estacionarias porque el perfil de la
onda no se desplaza debido a que existen puntos fijos o nodos, N, para
los cuales la amplitud es cero y otros, llamados vientres, V, para los
cuales es máxima.

24. ONDAS ESTACIONARIAS
Ecuación de la onda estacionaria:
y = (2 · A · sen k x) · cos w t
La amplitud es función de la posición x, de modo que determinados
puntos oscilan con amplitud máxima y otros no oscilan.
La frecuencia es igual a la de las ondas armónicas que se superponen.

25. ONDAS ESTACIONARIAS
Localización de los nodos:
sen k x = 0
k x = 0, p, 2p, 3p …
x = n · , n = 0, 1, 2, 3...
l
2

26. ONDAS ESTACIONARIAS
Localización de los vientres:
sen k x = 1
k x = , , , …
x = ( 2n + 1 ) · , n = 0, 1, 2, 3...l
4
p 3p 5p 7p
2 222

27. EJERCICIO 1 EvAU
Una onda armónica transversal de frecuencia angular 4p rad/s se
propaga a lo largo de una cuerda con una velocidad de 40 cm/s, en la
dirección positiva del eje X. En el instante inicial t = 0, en el extremo
de la cuerda x = 0, su elongación es de +2,3 cm y su velocidad de
oscilación es de 27 cm/s. Determine:
a) La expresión matemática que representa la onda.
b) El primer instante en el que la elongación es máxima en x = 0.

28. EJERCICIO 2 EvAU
La función matemática que representa una onda transversal que
avanza por una cuerda es
y(x, t) = 0,3 · sen (100pt – 0,4px + j)
donde todas las magnitudes están expresadas en unidades del SI.
Calcule:
a) La separación entre dos puntos cuya diferencia de fase, en un
determinado instante, es de p/5 radianes.
b) La diferencia de fase entre dos vibraciones de un mismo punto del
espacio separadas por un intervalo de tiempo de 5 ms.

29. EJERCICIO 4 EvAU
Una onda armónica transversal, de longitud de onda 1 m y amplitud
A, se propaga en el sentido negativo del eje X. En el instante inicial,
para el punto situado en x = 0, la elongación es y = - A y la velocidad
de oscilación es nula y 2 s después, su velocidad alcanza (por
primera vez) el valor máximo es 0,5 m/s.
a) Calcule la frecuencia y la velocidad de propagación de la onda.
b) Escriba la expresión matemática de la onda.

30. EJERCICIO 8 EvAU
Una onda armónica transversal se propaga en el sentido negativo del
eje X con una velocidad de 10 m/s y con una frecuencia angular de
p/3 rad/s. Si en el instante inicial la elongación en el origen de
coordenadas es 6/p cm y la velocidad de oscilación es 1 cm/s,
determine:
a) La expresión matemática que representa la onda.
b) La velocidad de oscilación en el instante inicial en el punto situado
en x = l/4.

31. EJERCICIO 10 EvAU
La perturbación asociada a una onda viene descrita por la expresión
y(x, t) = 10-8
· sen (2765t + 1,85x)
donde y y x se expresan en metros y t en segundos.
a) Indique su dirección y sentido de propagación, y calcule su
longitud de onda y su frecuencia.
b) Obtenga la velocidad de propagación de la onda y la velocidad
máxima de oscilación.

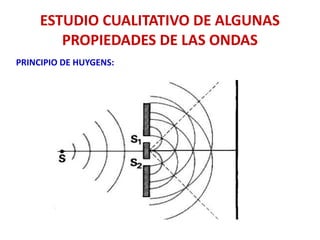
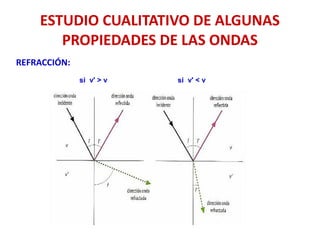
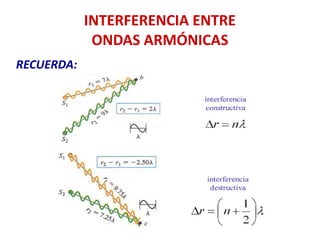
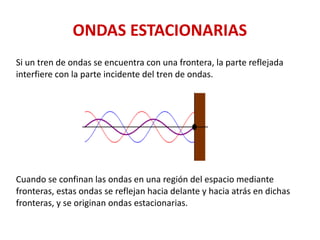
32. EJERCICIO 11 EvAU
En el extremo izquierdo de una cuerda tensa y horizontal se aplica
un movimiento armónico simple perpendicular a la cuerda, y como
consecuencia, por la cuerda se propaga una onda transversal con la
siguiente expresión:
y(x, t) = 0,01 · sen [p(100t + 2,5x)]
en unidades del Sistema Internacional. Calcule:
a) La velocidad de propagación, frecuencia, longitud de onda y
número de onda.
b) La aceleración y velocidad máxima de un punto cualquiera de la
cuerda.

33. ONDAS SONORAS
Todo cuerpo que oscile con una frecuencia comprendida entre 20 y
20.000 Hz crea una onda sonora en el medio circundante, con
independencia de que este sea sólido, líquido o gaseoso.
Las ondas sonoras se propagan a través de los medios materiales
mediante variaciones alternadas de la densidad del medio.
En medios gaseosos, dichas variaciones de densidad equivalen a una
secuencia alternada de compresiones y enrarecimientos.

34. INTENSIDAD DEL SONIDO
I =
I =
E
S · t
P
4p r2

35. INTENSIDAD DEL SONIDO
Las ondas sonoras son esféricas.
La intensidad del sonido es proporcional al cuadrado de la
amplitud y al cuadrado de la frecuencia.
La intensidad del sonido disminuye al alejarse del foco
puntual emisor a tenor de 1/r2
, siguiendo la ley del inverso
del cuadrado de la distancia.

36. SENSACIÓN SONORA
Como receptor de sonidos, el oído humano abarca un amplísimo
espectro de intensidades, que van desde los casi imperceptibles 10-12
W/m2
, considerados como umbral de audición, hasta aproximadamente
1 W/m2
, que correspondería a una sensación auditiva dolorosa.
Cuando percibimos los sonidos, podemos distinguir entre sonidos fuertes
y débiles, esta percepción está relacionada con la intensidad.
Debido al amplio rango de intensidades que abarca el oído humano,
suele emplearse una escala logarítmica de intensidades relativas llamada
escala de nivel de intensidad.

37. SENSACIÓN SONORA
Se define el nivel de intensidad, b, de una onda sonora como:
Los niveles de intensidad se miden en decibelios (dB).
I: intensidad de la onda sonora.
IO
: nivel de referencia que se denomina intensidad umbral (10-12
W/m2
)
b = 10 · log I
IO

38. EFECTO DOPPLER
Se conoce como EFECTO DOPPLER el fenómeno debido al movimiento
relativo de la fuente sonora y el observador por el que cambia la
frecuencia que se percibe de un sonido.

39. EFECTO DOPPLER
FUENTE SONORA EN MOVIMIENTO Y OBSERVADOR EN REPOSO
La fuente se acerca:
La fuente se aleja:
f '= f (
v
v−vF
)
f '= f (
v
v+vF
)

40. EFECTO DOPPLER
FUENTE SONORA EN REPOSO Y OBSERVADOR EN MOVIMIENTO
El observador se acerca:
El observador se aleja:
f '= f (
v+vo
v
)
f '= f (
v−vo
v
)

41. EFECTO DOPPLER
FUENTE SONORA Y OBSERVADOR EN MOVIMIENTO
Fuente y observador se acerca al
mismo tiempo:
Observador y fuente se alejan a la
vez:
f '= f (
v+vo
v−vF
)
f '= f (
v−vo
v+vF
)

42. EJERCICIO 12 EvAU
En un punto situado a igual distancia entre dos fábricas, que emiten
como focos puntuales, se percibe un nivel de intensidad sonora de
40 dB proveniente de la primera y de 60 dB de la segunda.
Determine:
a) El valor del cociente entre las potencias de emisión de ambas
fábricas.
b) La distancia a la que habría que situarse respecto de la primera
fábrica para que su nivel de intensidad sonora fuese de 60 dB.
Suponga en este caso que solo existe esta primera fábrica y que el
nivel de intensidad sonora de 40 dB se percibe a una distancia de
100 m.

43. EJERCICIO 13 EvAU
Para determinar la profundidad de una cueva se emite una onda
sonora esférica de 10 W y se observa que al cabo de 3 s se escucha
el eco. Admitiendo que la cueva es suficientemente amplia para
despreciar las reflexiones en las paredes laterales, determine,
despreciando los efectos de absorción:
a) La profundidad de la cueva.
b) La intensidad de la onda sonora al llegar al fondo de la cueva.

44. EJERCICIO 15 EvAU
Dos altavoces de 60 W y 40 W de potencia están situados,
respectivamente, en los puntos (0, 0, 0) y (4, 0, 0). Determine:
a) El nivel de intensidad sonora en el punto (4, 3, 0) m debido a cada
uno de los altavoces.
b) El nivel de intensidad sonora en el punto (4, 3, 0) m debido a
ambos altavoces.