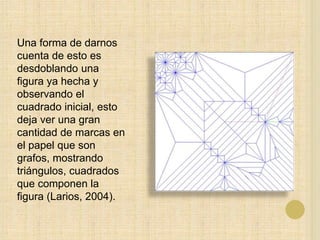
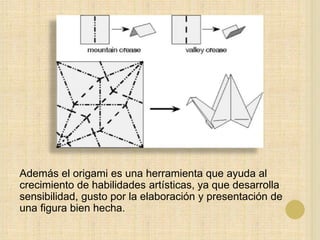
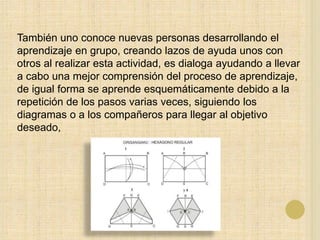
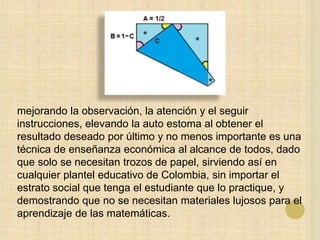
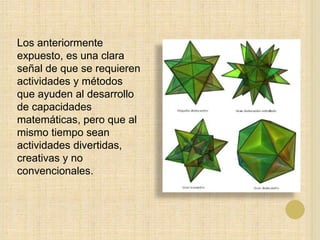
Este documento discute cómo la técnica del origami (papiroflexia) puede implementarse en la enseñanza de las matemáticas en Colombia para mejorar los resultados deficientes del país en pruebas internacionales. El origami promueve el desarrollo de habilidades matemáticas, lógicas y espaciales a través de la manipulación de figuras geométricas. Al ser una actividad creativa y divertida, motiva más a los estudiantes que los métodos tradicionales.

1. EL ORIGAMI: PIEZA FUNDAMENTAL EN
EL DESARROLLO
DEL PENSAMIENTO MATEMÁTICO
GEYNER ORLANDO HERNANDEZ LESMES
ALEJANDRO CASSIANI BAQUERO
UNIVERSIDAD AUTÓNOMA DE COLOMBIA

2. En los últimos años,
Colombia ha logrado
grandes avances en la
educación con proyectos
como Colombia aprende,
vive digital, ingles para
todos, entre otros; sin
embargo, el nivel de
formación que se está
brindando no alcanza
para competir a nivel
internacional.

3. El Gobierno tiene
planteado como meta
ubicar a Colombia entre
los países con mejores
índices de formación,
pero al momento de
evaluar qué tan bien
preparados están los
estudiantes por medio de
pruebas como las PISA
(Programa Internacional
de Evaluación de
Estudiantes, por su sigla
en inglés), nos va mal.

4. Esta prueba es un estudio internacional comparativo de
evaluación educativa liderada por la OCDE (Organización para la
Cooperación y el Desarrollo Económico), que tiene como
propósito principal valorar en qué medida los jóvenes de 15 años
de edad han adquirido los conocimientos y habilidades esenciales
para su participación en la sociedad, a fin de identificar elementos
que contribuyan al desarrollo de competencias y sea posible
establecer diálogos sobre los aspectos que debe atender las
políticas educativas de los países (ICFES, 2015). La prueba se
lleva a cabo cada tres años desde el 2000, y cada vez se enfatiza
en una materia: lectura, ciencias naturales y matemáticas.

5. En el año 2012, la
prueba PISA tuvo
como énfasis el área
de matemáticas, los
resultados de estas
fueron deficientes
para el país, ya que
quedó clasificado en
el puesto 61 entre
los 65 países
evaluados,
obteniendo un
puntaje de 376.

6. En matemáticas, el 74% de los estudiantes colombianos se ubicó
por debajo del nivel 2 y el 18%, en el nivel 2. Esto quiere decir
que solo dos de cada diez estudiantes pueden hacer
interpretaciones literales de los resultados de problemas
matemáticos; además, emplean algoritmos básicos, fórmulas,
procedimientos o convenciones para resolver problemas de
números enteros, e interpretan y reconocen situaciones en
contextos que requieren una inferencia directa. En contraste,
apenas 3 de cada mil alcanzaron los niveles 5 y 6. Quienes están
en estos niveles tienen pensamiento y razonamiento matemático
avanzados: pueden seleccionar, comparar y evaluar estrategias
de resolución de problemas; conceptúan, generalizan y utilizan
información; aplican conocimientos en contextos poco
estandarizados; reflexionan sobre su trabajo y pueden formular y
comunicar sus interpretaciones y razonamientos. (ICFES, 2013,
p8, original en cursiva)

7. Si bien se podría cuestionar el modelo de medición del
aprendizaje, Colombia no está al nivel de educación
internacional mostrando una amplia distancia con respecto a
los resultados obtenidos por los primeros puestos, los cuales
son países asiáticos (Shanghái-China, Singapur, Hong Kong-
China, Corea, Japón), posiblemente esto se deba a que en
esos países utilizan técnicas de aprendizaje que motivan a los
estudiantes a ser mejores en sus labores diarias como son el
aprendizaje con música, series de ejercicios mentales que
sirven para estimular el aprendizaje, actividades manuales de
enseñanza, más capacitación a los docentes con sustentos del
gobierno, gran apoyo extraacadémico por parte de los padres,
el trabajo individual, para la enseñanza en áreas matemáticas
como la geometría y se benefician de todos los efectos
positivos que trae practicar estas técnicas y de incluirlas en los
procesos educativos.

8. Es claro que las
metodologías
pedagógicas tradicionales
que se utilizan en el país
actualmente como: la
memorización, la
repetición de lecciones, la
poca participación de los
estudiantes, deben tener
un cambio; ya que los
estudiantes se distraen
con facilidad, perdiendo el
interés en las clases
lineales.

9. Hay estudios en pedagogía infantil que plantean la
importancia del juego como una herramienta de desarrollo
que estimula todos los procesos de formación en el
aprendiz tal como lo plantea la UNESCO:
Todos los niños del mundo juegan,
y esta actividad es tan
preponderante en su existencia
que se diría que es la razón de ser
de la infancia. Efectivamente, el
juego es vital; condiciona un
desarrollo armonioso del cuerpo,
de la inteligencia y de la
afectividad. (1980, p 5, original en
cursiva)

10. Por tal razón, expertos en
el área del desarrollo
cognitivo, empiezan a
fusionar la construcción
de figuras basadas en la
geometría y la habilidad
manual al concepto de
“juego” en el proceso de
formación matemática,
obteniendo resultados
favorables en los
estudiantes.

11. A partir de lo anterior, podemos
ver que si unimos el juego, al
conocimiento se pueden
implementar técnicas de
aprendizaje no tan utilizadas y
divertidas como el origami o
papiroflexia, palabra que
proviene de los términos ORU
(doblar) y KAMI (papel), antes
llamada orukata (ejercicios de
doblado) y con el paso del
tiempo origami, conocido
también en Europa sobre todo en
España como papiroflexia, de
donde deriva de los términos
PAPIRO (papel) y FLECTERE
(doblar) con la misma
composición lingüística que la
palabra japonés (Royo, 2002)

12. Un arte preciso de hacer
coincidir bordes y realizar
dobleces para crear
figuras de todo tipo,
desde las más simples
hasta las más complejas
imaginables. Siendo los
árabes los que lo llevaron
a Europa y aplicaron esta
técnica a los principios de
la geometría,
investigando las
propiedades del plegado
del cuadrado.

13. Mi propuesta es que la técnica del origami se implemente en la
enseñanza básica y media de las matemáticas, ya que posee
muchas ventajas en diversos niveles, los cuales contribuyen al
desarrollo de habilidades matemáticas, lógicas, espaciales,
artísticas, pedagógicas, psicológicas y sociales. Esta técnica
promueve la comprensión y el uso de conceptos geométricos,
como son la diagonal1, la media2, el vértice3, la bisectriz4, la
concepción volumétrica5, entre otras, permitiendo a los estudiantes
crear y manipular figuras geométricas como rectángulos,
cuadrados, y triángulos de distintas clases.
1. Diagonal [línea recta] Que en un cuerpo geométrico une dos ángulos que no están en la misma cara.
2. Media de algunos números es la relación de la suma de todos los números a sus cantidades.
3. Vértice punto en el que coinciden los dos lados de un ángulo o de un polígono.
4. Bisectriz semirrecta que parte del vértice de un ángulo y lo divide en dos partes iguales.
5. Concepción volumétrica de la medición de volúmenes o relacionado con ella.

14. Una forma de darnos
cuenta de esto es
desdoblando una
figura ya hecha y
observando el
cuadrado inicial, esto
deja ver una gran
cantidad de marcas en
el papel que son
grafos, mostrando
triángulos, cuadrados
que componen la
figura (Larios, 2004).

15. Además el origami es una herramienta que ayuda al
crecimiento de habilidades artísticas, ya que desarrolla
sensibilidad, gusto por la elaboración y presentación de
una figura bien hecha.

16. Hace algunos años participe a un grupo de origami ubicado
en la ciudad de Bogotá y gracias a esta experiencia puedo
decir que, el origami es un recurso el cual se puede utilizar
en la aulas de clase ya que estimula el desarrollo de las
capacidades intelectuales, genera interés y perseverancia
cualidades que están haciendo falta en algunos de nuestros
estudiantes, desarrolla la comprensión espacial, igualmente
es importante en el aprendizaje de la simetría ya que en
muchas figuras lo que se realiza en un lado se repite en el
otro, esto se puede usar en algebra para las ecuaciones.

17. Otra ventaja del uso
del origami en el
proceso educativo,
es el poder generar
varias figuras y
luego unirlas para
construir un módulo
tridimensional con el
cual se puede
interactuar y aplicar
propiedades
matemáticas.

18. También uno conoce nuevas personas desarrollando el
aprendizaje en grupo, creando lazos de ayuda unos con
otros al realizar esta actividad, es dialoga ayudando a llevar
a cabo una mejor comprensión del proceso de aprendizaje,
de igual forma se aprende esquemáticamente debido a la
repetición de los pasos varias veces, siguiendo los
diagramas o a los compañeros para llegar al objetivo
deseado,

19. mejorando la observación, la atención y el seguir
instrucciones, elevando la auto estoma al obtener el
resultado deseado por último y no menos importante es una
técnica de enseñanza económica al alcance de todos, dado
que solo se necesitan trozos de papel, sirviendo así en
cualquier plantel educativo de Colombia, sin importar el
estrato social que tenga el estudiante que lo practique, y
demostrando que no se necesitan materiales lujosos para el
aprendizaje de las matemáticas.

20. Los anteriormente
expuesto, es una clara
señal de que se requieren
actividades y métodos
que ayuden al desarrollo
de capacidades
matemáticas, pero que al
mismo tiempo sean
actividades divertidas,
creativas y no
convencionales.

21. Por ello, el origami es
una técnica práctica y
viable para cumplir
eficientemente con el
objetivo educativo, el
cual no ha sido
explotado en su
totalidad, dejando
abiertas un gran
número de posibles
opciones para
aprender de una
manera más
agradable.

22. Por lo tanto, la
implementación del
origami sería un gran
aporte al mejoramiento
del desempeño en el área
de matemáticas, y
ayudaría al progreso de
las capacidades
intelectuales de los
estudiantes, lo que traería
como consecuencia
resultados favorables y
avances en el desarrollo
educativo del país.

23. Los invito a reflexionar sobre la ayuda educativa que nos
brinda el origami si fuera usada en más instituciones de
educación.

24. Referencias
ICFES. (2015). Instituto Colombiano para la Evaluación de la
Educación ICFES . Recuperado el 07 de mayo de 2015, de
Instituto Colombiano para la Evaluación de la Educación ICFES :
http://www.icfes.gov.co/investigacion/evaluaciones-
internacionales/pisa
Larios Osorio Victor, (2004): Buckiedros, geometría del espacio y
origami modular, Educación Matemática, vol. 16, Querétano,
México, Ed. Santillana.
Royo Prieto, J. I. (2002): Matemáticas y papiroflexia, Madrid, Ed.
Sigma.
Unesco. (1980). unesco.org. Obtenido de El niño y el juego
No34, Recuperado el 08 de mayo de 2015, de
http://unesdoc.unesco.org/images/0013/001340/134047so.pdf