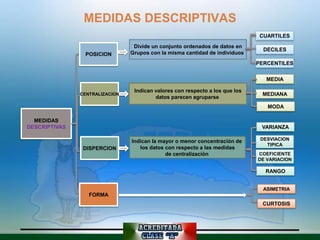
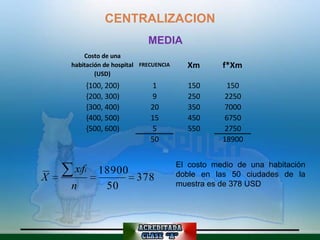
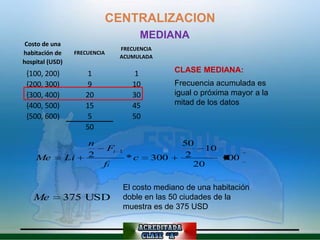
Este documento describe diferentes medidas descriptivas como cuartiles, deciles, percentiles, media, mediana, moda, varianza, desviación estándica, coeficiente de variación, rango, asimetría y curtosis. Explica cómo calcular e interpretar cada una de estas medidas para datos agrupados y no agrupados, y cómo indican valores centrales, dispersión y forma de una distribución de datos.

1. pcespoch
MEDIDAS DESCRIPTIVAS
WILMER FABIAN N
[AlienWfabi]

2. MEDIDAS DESCRIPTIVAS
CUARTILES
Divide un conjunto ordenados de datos en
DECILES
POSICION Grupos con la misma cantidad de individuos
PERCENTILES
MEDIA
Indican valores con respecto a los que los
CENTRALIZACION MEDIANA
datos parecen agruparse
MODA
MEDIDAS
DESCRIPTIVAS VARIANZA
Indican la mayor o menor concentración de DESVIACION
TIPICA
DISPERCION los datos con respecto a las medidas
de centralización COEFICIENTE
DE VARIACION
RANGO
ASIMETRIA
FORMA
CURTOSIS

3. POSICION


4. Ejemplo:

xi ni Ni
0 14 14
1 10 24
2 15 39
3 26 65
4 20 85
5 15 100
n=100

5. CENTRALIZACION
DATOS NO AGRUPADOS

6. CENTRALIZACION
Nos dan un centro de la distribución de frecuencias, es un valor que se puede tomar como representativo de todos los datos.
Hay diferentes modos para definir el "centro" de las observaciones en un conjunto de datos. Por orden de importancia, son:
MEDIA
(Media aritmética o simplemente media). es el promedio aritmético de las observaciones, es decir, el cociente entre la suma
de todos los datos y el numero de ellos. Si xi es el valor de la variable y ni su frecuencia,
X
X
n
Ejemplo:
Calcule el valor medio (o promedio) del ingreso anual de una muestra de empleados de la empresa “CLARO”:
10.500, 8.720, 11.350, 9.520 y 12.350 USD.
10500 8720 11350 9520 12350
X
52440 5
X
5
X 10488USD

7. CENTRALIZACION
MEDIANA
1) Cuando hay valores extremos (muy grandes o pequeños) la media puede no ser
representativa.
2) Mediana corresponde al punto medio de los datos después de ordenarlos.
3) 50% de las observaciones son mayores que la mediana y 50% son menores.
4) Si el número de datos es par, la mediana es la media aritmética de los datos situados en la
mitad.
n
Pos med
2
5) Si el número de datos es impar, la mediana es el valor que se sitúe justo en la mitad.
n 1
Pos med
2

8. EJEMPLO
Edades de una muestra de 8 Edades de una muestra de 9
estudiantes de Estadística. estudiantes de Estadística.
(PAR) (IMPAR)
8 9 1
Pos med 4 Pos med 5
2 2
23 23
23 23
24
24 Mediana
25
28 28 30
29 28 Mediana
30 2 30
32 32
34 34
41 41

9. CENTRALIZACION
MODA
Valor que aparece con mayor frecuencia.
EJEMPLO:
Edades de personas que asisten a una tienda de videos de un centro
comercial a las 10 am.
12 8 17 21 11 17 14 8 17 21 28
Moda

10. CENTRALIZACION
DATOS AGRUPADOS

11. CENTRALIZACION
MEDIA
FORMULA
xifi
X
n
MEDIANA
CLASE MEDIANA: clase cuya frecuencia acumulada es igual o próxima mayor a la mitad de los datos.
FORMULA
n
Fi 1
Me Li 2 *c
fi
DONDE:
 Li: límite inferior de la clase mediana.
 n: Es el numero de datos de la muestra.
 : Es la semisuma de las frecuencias absolutas.
 n i-1: frecuencia acumulada anterior a la clase mediana.
F
2
 fi: frecuencia absoluta de la clase mediana.
 c: Es la amplitud o intervalo de la clase.

12. CENTRALIZACION
MODA
CLASE MODAL: clase que contiene la mayor frecuencia
FORMULA
fi fi 1
Mo Li * ai
( fi fi 1) ( fi fi 1)
DONDE:
 Li: límite inferior de la clase modal.
 fi: Frecuencia absoluta de la clase modal.
 fi-1: frecuencia absoluta anterior a la clase modal.
 fi+1: frecuencia absoluta posterior a la clase modal.
 ai: Es la amplitud de la clase.

13. CENTRALIZACION
EJEMPLO:
En una muestra de 50 ciudades de EEUU con poblaciones que se encuentran entre 100.000 y
1´000.000 habitantes, se encontró la siguiente distribución de frecuencias para el costo diario
de una habitación doble en un hospital.
Costo de una
habitación de hospital FRECUENCIA
(USD)
{100, 200) 1
{200, 300) 9
{300, 400) 20
{400, 500) 15
{500, 600) 5
50

14. CENTRALIZACION
MEDIA
Costo de una
habitación de hospital FRECUENCIA Xm f*Xm
(USD)
{100, 200) 1 150 150
{200, 300) 9 250 2250
{300, 400) 20 350 7000
{400, 500) 15 450 6750
{500, 600) 5 550 2750
50 18900
El costo medio de una habitación
xifi 18900 doble en las 50 ciudades de la
X 378
n 50 muestra es de 378 USD

15. CENTRALIZACION
MEDIANA
Costo de una
FRECUENCIA
habitación de FRECUENCIA
ACUMULADA
hospital (USD)
{100, 200) 1 1 CLASE MEDIANA:
{200, 300) 9 10 Frecuencia acumulada es
{300, 400) 20 30 igual o próxima mayor a la
{400, 500) 15 45 mitad de los datos
{500, 600) 5 50
50
n 50
Fi 1 10
Me Li 2 *c 300 2 100
fi 20
El costo mediano de una habitación
Me 375 USD doble en las 50 ciudades de la
muestra es de 375 USD

16. CENTRALIZACION
MODA
Costo de una
habitación de FRECUENCIA
hospital (USD)
{100, 200) 1
{200, 300) 9 CLASE MODAL
{300, 400) 20
Mayor frecuencia
{400, 500) 15
{500, 600) 5
50
fi fi 1 20 9
Mo Li * ai 300 100
( fi fi 1) ( fi fi )
1 20 9 20 15
El costo modal de una habitación
Me 369 USD doble en las 50 ciudades de la
muestra es de 369 USD

17. DISPERCION
VARIANZA
Podemos definirla como el promedio del cuadrado de las diferencias de todas las puntuaciones respecto a la media
aritmética. La varianza es la distancia media entre puntuaciones.
Propiedades de la varianza:
 Una varianza puede valer cualquier cosa, es decir, no tiene límites numéricos. Su valor dependerá de las categorías
de las variables.
 Una varianza jamás puede ser negativa, y siempre tendrá un valor positivo o igual a O.
 Se ve afectada por la modificación de cualquiera de las puntuaciones.
 Si multiplicamos un conjunto de puntuaciones por una constante, la desviación típica y la varianza quedarán
multiplicadas por la constante y por el cuadrado de esa constante.
 Si sumamos un conjunto de puntuaciones a una constante, la desviación típica y la varianza no se verán afectadas.
 Para datos agrupados en intervalos, el valor depende de la amplitud de los intervalos, el número de ellos y los límites
fijados.
 No debe calcularse en situaciones en que tampoco debe calcularse la media.
( Xi x) 2
FORMULA Para datos no agrupados S2 i 1
n 1
fi ( Xi x) 2
Si los datos están agrupados utilizamos la siguiente formula. S2 i 1
n 1

18. DISPERCION
DESVIACION TIPICA
 Se define como la raíz cuadrada de la varianza, tomada con signo positivo. Dado que antes hemos elevado las
puntuaciones al cuadrado para que nos saliesen distancias negativas, ahora le haremos la raíz a la varianza para
devolver los datos a su estado original
 La desviación típica es el índice de dispersión más importante.
 Las propiedades de la desviación típica son similares a las de la varianza.
FORMULA Para datos no agrupados. S S2
FORMULA Para datos agrupados. 2 fi ( Xi x) 2
S
n 1
COEFICIENTE DE VARIACION
 Es un coeficiente que se usa para comparar variabilidad entre dos grupos o más grupos.
 Cuanto más alto es este coeficiente, más dispersión, más variabilidad, y más distintos serán los sujetos entre sí.
 El Coeficiente de variación (CV) es una medida de la dispersión relativa de un conjunto de datos, que se obtiene dividiendo
la desviación estándar del conjunto entre su media aritmética:
se expresa para una muestra. S
CV (1 0 0)
x
CV (1 0 0)
se expresa para la población. x

19. DISPERCION
Los coeficientes de variación tienen las siguientes características:
 Puesto que tanto la desviación estándar como la media se miden en las unidades originales, el CV es una medida
independiente de las unidades de medición.
 Debido a la propiedad anterior el CV es la cantidad más adecuada para comparar la variabilidad de dos conjuntos de datos.
 En áreas de investigación donde se tienen datos de experimentos previos, el CV es muy usado para evaluar la precisión de
un experimento, comparando en CV del experimento en cuestión con los valores del mismo en experiencias anteriores.
RANGO
 Podemos definirlo como la distancia que existe entre la máxima y la mínima puntuación de una distribución.
FORMULA
Re = xmax – xmin
Donde:
R = Recorrido, rango o amplitud
Xmax = Valor máximo de los datos de un conjunto
Xmin = Valor mínimo de los datos de un conjunto

20. DISPERCION
EJEMPLO:
En seis sábados consecutivos un operador de taxis recibió 9, 7, 11, 10, 13 y 7 llamadas a su sitio para su
servicio. Calcule:
a) Amplitud.
b) Media.
c) Desviación estándar.
d) Varianza.
e) Coeficiente de variación.
a) Para calcular la amplitud.
Valor máximo 13
Valor mínimo 7
A = 13 - 7 = 6

21. b) Para calcular la media.
xifi

X
n
xifi 9 7 11 10 13 17 57
X 9.5
n 6 6
c) Para calcular la desviación estándar.
fi ( Xi x) 2
S
n 1
Se puede utilizar la siguiente tabla:
Al sustituir los valores se obtiene:
27.5 27.5 5.5
S 2.3452
6 1 5

22. d) Para calcular la varianza:
( Xi x) 2
S2 i 1
n 1
S2 ( 2.3452 2
)
S2 5.5
e) Para calcular el coeficiente de variación:
S
CV (100)
x
2.3452
CV
9.5
CV 0.2468

23. FORMA
Comparan la forma que tiene la representación gráfica, bien sea el histograma o el diagrama de barras de la distribución, con
la distribución normal.
MEDIDA DE ASIMETRÍA
 Diremos que una distribución es simétrica cuando su mediana, su moda y su media aritmética coinciden.
 Diremos que una distribución es asimétrica a la derecha si las frecuencias (absolutas o relativas) descienden más
lentamente por la derecha que por la izquierda.
 Si las frecuencias descienden más lentamente por la izquierda que por la derecha diremos que la distribución es asimétrica
a la izquierda.
 Existen varias medidas de la asimetría de una distribución de frecuencias. Una de ellas es el Coeficiente de Asimetría de
Pearson:
Su valor es cero cuando la distribución es simétrica, positivo cuando existe asimetría a la derecha y negativo cuando existe
asimetría a la izquierda.

24. FORMA
MEDIDA DE APUNTAMIENTO O CURTOSIS
 Miden la mayor o menor cantidad de datos que se agrupan en torno a la moda.Se definen 3 tipos de
distribuciones según su grado de curtosis:
 Distribución mesocúrtica: presenta un grado de concentración medio alrededor de los valores centrales
de la variable (el mismo que presenta una distribución normal).
 Distribución leptocúrtica: presenta un elevado grado de concentración alrededor de los valores
centrales de la variable.
 Distribución platicúrtica: presenta un reducido grado de concentración alrededor de los valores
centrales de la variable.

25. GRACIAS POR SU ATENCION