Este documento presenta un resumen de los capítulos de un libro de física fundamental. Incluye 13 capítulos que cubren temas como análisis dimensional, vectores, estática, cinemática, dinámica, trabajo-energía, cantidad de movimiento, fluidos, movimiento armónico, gravitación, calor, termodinámica, electrostática y electromagnetismo. El objetivo del libro es ayudar a los estudiantes a comprender las leyes físicas fundamentales y aplicarlas en la resolución de problemas.

2. Hecho el depósito legal, Ley N° 26905.
BEG. N° 15013298-1124
Prohibida la reproducción parcial o total de la obra,
sin la previa autorización escrita del Editor de la misma.
Aníbal Jesús Paredes Galván - Editor
Jr. Natalio Sánchez 220 - Otic 304 - Jesús María
Impreso en Perú__________________ Printed in Perú
Composición, diagramación y montaje:
Editorial San Marcos
RUC. 11029221

3. A mi familia
porsu compresión
porsupaciencia.
A 'DiegoPérezContreras
mihijo.

4. PROLOGO
El presente trabajo es frutode varios años en ladocencia y está dirigido
a los estudiantes que inician el estudio de la FISICA FUNDAMENTAL.
El objetivo de la obra es, la comprensión de las leyes físicas funda­
mentales y el desarrollo en los estudiantes del hábito de utilizarlas en los
diferentes problemas.
Aprovecho laoportunidad,parasaludaramiscolegas,profesores de las
diferentes Academias y Centros Pre universitarios del medio, por la noble
labor que realizan.
Finalmente, pero no con menos calor, quiero saludar a los alumnos,
jóvenes de nuevo tipo, que gracias a su inquietud y espíritu de desarrollo, he
podido elaborar los temas que contiene este libro.
EL AUTOR
NOTAS DEL EDITOR
FísicaTeoríay Problemas desarrolla todoel curso de Física válidopara
losexámenes de admisión a las diferentesuniversidadesde nuestro país; tiene
un contenido de 655 páginas, encontrando en cadacapítulo la teoría expuesta
en forma clara y objetiva, además de un gran número de problemas tipo
resueltos, empleando métodos directos y sencillos de solución, comple­
mentados con un gran número de problemas propuestos.

5. CONTENIDO
Prólogo
CAPITULO 1
ANALISIS DIMENSIONAL
Pág.
1
1. Sistema Internacional (S.ll Magnitudes.
2. Ecuación Dimensional Dimensión de las Magnitudes.
3- Principio de Homogeneidad Dimensional.
1 Vector: Elementos de un Vector.
2 Suma de dos Vectores. Método de Paralelogramo.
3. Suma de "n" Vectores. Método del Póligono.
4. Descomposición Rectangular. Descomposición Poligonal
5. Vectores Unitarios Cartesianos.
6. Vector Unitario. Vector como par ordenado.
1. Fuerza. Tensión. Comprensión. Fuerza Elástica
2. Leyes de ISiewton. Ley de Hooke
3 Diagrama del Cuerpo Libre.
4 Primera Condición de Equiliorio.
5. Teorema de Lamy o de las tres fuerzas.
6. Momento de una Fuerza. Torque. Cupla.
7 Equilibrio de un Cuerpo Rígido.
8 Segunda Condición de Equilibrio.
9. Sistema Física Sistema Aislado. Fuerzas internas.
10. Teorema de Varignon.
11 Centro de Gravedad Centro de masa.
12 Cupla o Par de Fuerzas
13. Rozamiento. Coeficiente de rozamiento
CAPITULO 2
ANALISIS VECTORIAL 17
CAPITULO 3
ESTATICA

6. CAPITULO 4
CINEMATICA
1. Sistema de Referencia Inercial.
2. Movimiento Mecánico. Velo'cídad Media.
3. Movimiento Rectilíneo Uniforme (M.R.U.)
4 Ley de Kepler para el M R,U
5. Movimiento Rectilíneo Uniformemente Variado (M.R.U.V.)
7. Movimiento Relativo. Velocidad y aceleración relativa.
8. Movimiento Compuesto. Composición de velocidades
9. Movimiento Parabólico. Tiempo de Vuelo.
10. Movimeiento Circular. Aceleración Centrípeta.
11. Ley de Kepler para el M C U.
CAPITULO 5
DINAM ICA.......... ......... ........ ..............................................
1 Dinámica Lineal. Segunda Ley de Newton.
2. Sistema de Referencia Inercial y No Inercial.
3. Principio de D'Alambert. Fuerza Inercial.
4. Principio de Equivalencia (Albert Einstem).
5. Dinámica Circular Sistema de Referencia Rotacional.
6. Péndulo Cónico. S.stema de Referencia Rotacional
7. Fuerza Centrífuga. Aceleración Relativa.
CAPITULO 6
TRABAJO - ENERGIA - POTENCIA ................... ........... .
1 Trabaio Mecánico de una Fuerza Constante.
2. Gráfica, Fuerza Versus Posición
3. Energía Energía Cinética.
4. Teorema de la Energía Cinética.
5. fcnergía Potencial Gravitatona.
6. Principio de Conservación de la Energía Mecánica
7 Teorema del Trabajo y la Energía Mecánica.
8. Energía Potencial Elástica Ley de Hooke.
9. Potencia Mecánica. Potencia de un motor.
10. Rendimiento o Eficiencia de una máquina
201
241

7. CAPITULO 7
CANTIDAD DE MOVIMIENTO Y CHOQUES 275
1. Cantidad de Movimiento. Impulso.
2. Sistema aislado (S.A). Fuerzas externas.
3. Principio de Conservación del Momentum Lineal.
4. Velocidad de! Centro de Masa.
5. Teorema de la Cantidad de Movimiento.
6. Colisiones o choques. Choque frontal.
7 Coeficiente de Restitución.
8. Clasificación de los Choques. Choque Elástico.
9. Ley de Reflexión en los Choques.
CAPITULO 8
ESTATICA DE FLUIDOS ............................. ........ .......................................... 301
1 Densidad, Presión . Isóbaras.
2. Principio de Pascal.
3. Prensa Hidraúlica. Vasos Cominicantes.
4 Presión Hidrostátic Presión absoluta.
5. Principio Fundamental de la Hidrostática.
6 Principio de Arquímedes. Empuje.
7 Presión Atmosférica Experimento de Torricelli
8. Manómetro Barómetro.
9 Principio de Arquímedes en los gases
CAPITULO 9
M.A.S Y PENDULO SIMPLE .. . ................................................ .............. 329
1. Movimiento L Armónico Simple.
2 Elongación Amplitud. Fuerza recuperadora.
3. Período Energía Total del Sistema.
4. Asociación de resortes: Serie y Paralelo.
5 Período del Péndulo simple.
CAPITULO 10
GRAVITACION Y MOVIMIENTO PLANTETARIO ..................... .......... . 342
1 Ley de Gravitación Universal
2 Campo Gravitatorío. Intensidad del campo gravitatorio

8. 3. Variación de la aceleración de la gravedad con la altura.
4. Energfa potencial de Interacción gravitatoria
5. Leyes del movimiento Planetario Leyes de kepler.
CAPITULO 11
CALOR ................................................................ ........... .......... ..................... 355
1. Temperatura. Escalar Termométricas.
2. Dilatación Lineal, superficial y volumétrica.
3. Variación de la densidad con la Temperatura.
4. Calorimetría, Cantidad de Calor
5 Capacidad Calorífica Calor específico.
6. Equilibrio Térmico o Ley cero de la Termodinámica.
7. Calorímetro de mezcla. Equivalente en agua.
8. Cambio de Fase. Termodinámica.
9. Punto Triple. Calor Latente.
CAPITULO 12
TERMODINAMICA ................... .................................................................. 369
1. Gas Ideal Ecuación de Estado Teermodinámico.
»
2. Proceso Termodinámico. Energía Interna.
3. Trabajo. Pumera Ley de la Termodinámica.
4. Proceso Isobárico. Isócoro, Isotérmico y Adiabático.
5. Segunda Ley de la Termodinámica.
6. Máquina Térmica. Ciclo de Carnot Entropía.
CAPITULO 13
ELECTROSTATICA...... ......... . ... ___ ____ ____ __ _____________ 391
1 Carga Eléctrica. Cuantización de la carga.
2, Ley de Conservación de la carga eléctrica.
3. Fenómenos de Electrización.
4 Ley de Coulomb. Campo Eléctrico.
5. Intensidad del campo eléctrico. Líneas de Fuerza.
6, Energfa Potencial ELéctríca. Campo Eléctrico Homogéneo.
1 Potencial Eléctrico. Diferencia de Potencial
8. Superficies Equipotenciales Equilibrio Electrostático.
9 Potencial y Campo Eléctrico en un esfera conductora
10 Energía Portencial de Interacción Eléctrica.

9. 11. Capacidad Eléctrica. Condensadores.
12. Asociación de Condensadores. Teorema de la Trayectoria.
13. Ley de Coulomb en un medio Dieléctrico.
14- Condensador con dieléctrico. Leyes de Kirchhoff.
ELECTRODINAMICA...................... .'................................................................. 475
1. Corriente eléctrica Resistencia eléctrica. Ley de Ohm.
2. Asociación de Resistencias. Fuentes de Energfa Eléctrica.
3. Fuerza Electromotriz. Potencia Eléctrica.
4. Dilatación Lineal de los conductores. Ley de Joule - Lenz.
5. Teorema de la Trayectoria. Leyes de Kirchhoff.
7. Ley de Conservación de la Energía.
MAGNETISMO .................................................................................................. 548
1. Historia de Magnetismo Natural. Imán natural.
2. Leyes del Magnetismo. Campo Magnético. Líneas de Fuerza.
3. Intensidad de campo magnétco. Flujo magnético.
4. Inducción Magnética. Permeabilidad magnética.
5. Magnetismo Terrestre.
ELECTROMAGNETISMO ........................................................................ ..... 560
1 Efecto Oersted. Campo magnético creado por unacorriente.
2. Ley de Biot - Savart.
3. Campo magnético creado por una corriente circular.
4. Campo magnético creado por un Arco conductor.
5 Acción del Campo magnético sobre un conductor.
6. Acción y Reacción entre dos corrientes.
7. Fuerza de Lorentz. Movimento de las partículas cargadas en los campo eléctricos y
magnéticos.
8. Campo magnético creado por una carga eléctrica en movimiento
9. Campo magnético creadopo un Solenoide
10. Campo magnético producido por un Toroide
11. Inducción Electromagnética. Ley de Lenz.
12 Imágenes Electrostáticas.

10. 1. Naturaleza de la Luz. Velocidad de la Luz
2. Optica geométrica . Indice de refracción.
3. Ley de Reflexión y Refracción. Ley de Smell.
4. Angulo Límite y Refracción Total
5. Lentes convergentes y divergentes.
6. Principio de Fermat. El camino más rápido.
TEORIA ESPECIAL DE LA RELATIVIDAD.......................
1. Contracción de la longitud. Transformación de Lorentz.
2. Sistema de Referencia Inercial
3. Dilatación del Tiempo. La masa aumenta.
4. Energía cinética de la partícula relativista.
5. Ley de Interacción de la masa y la energía.
644

11. CONCEPTO.
Es una parte auxiliar de la Física que
estudia las relaciones entre las magnitudes
fundamentales y derivadas, principalmente
el Sistema Internacional de Unidades
MAGNITUD.
Es todo aquello que es susceptible a ser
medido y que se puede percibir por algún
medio. Por consiguiente magnitud, es todo
aquello que se puede medir.
MEDIR.
Es comparar una magnitud dada, con
otra de su misma especie asumida en forma
arbitraria como unidad o patrón.
Ejemplo: Para medir el largo de la
pizarra, comparamos con un
metro patrón.
CLASIFICACION DE LAS MAGNITUDES
A) Por su origen
1. Magnitudes Fundamentales.
2. Magnitudes Derivadas.
B) Por su naturaleza:
1. Magnitudes Escalares.
2. Magnitudes Vectoriales.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
MAGNITUDES FUNDAMENTALES.
Son aquellas elegidas arbitrariamente
como base para establecer las unidades de
un SISTEMA DE UNIDADES y en función de
las cuales se expresan las demas magni­
tudes
MAGNITUDES DERIVADAS.
Son aquellas magnitudes que se expre­
san en función de las magnitudes asumidas
como fundamentales.
MAGNITUDES ESCALARES.
Son aquellas que enunciado su valor
seguido de su correspondiente unidad
quedan perfectamente definidas, a veces
afectado de un signo negativo convencio­
nalmente elegido
Ejemplo: La temperatura: - 15o C
Son magnitudes escalares: Longitud,
masa, tiempo, volumen, densidad, trabajo,
potencia, energía, carga eléctrica, intensidad
de corriente eléctrica, potencial eléctrico, ilu­
minación.
MAGNITUD VECTORIAL.
Son aquellas que además de conocer su
módulo o valor, es necesario conocer su
dirección y sentido para que esté plenamente
definida.
Son m agnitudes vectoriales: Des­
plazamiento, velocidad, aceleración, fuerza,
torque, impulso, cantidad de movimiento, in­
tensidad del campo eléctrico, inducción
magnética

12. SISTEMA INTERNACIONAL DE UNIDADES (S.I.)
MAGNITUD UNIDAD s ím b o l o
Longitud metro m
Masa kilogramo kg
Tiempo segundo s
Intensidad de corriente eléctrica ampere A
Temperatura kelvin K
Intensidad luminosa candela cd
Cantidad de sustancia mol mol
Angulo plano radián rad
Angulo sólido estereoradián sr
En la X conferencia de Pesas y Medidas
(1954), se establecieron las unidades y mag­
nitudes fundamentales del S.I. Este sistema
fue complementado en la XIV Conferencia de
Pesas y Medidas, realizado en Francia en
1971, el S.I. considera siete magnitudes fun­
damentales y dos au-xiliares:
ECUACION DIMENSIONAL.
Es aquella igualdad matemática que
muestra la relación que existe entre una
magnitud derivada y las que asumen como
magnitudes fundamentales.
La DIMENSION de una “magnitud física"
se representa del siguiente modo:
Sea A la magnitud física,
[A ]: dimensión de la magnitud física"A“,
o ecuación dimensional de A.
Ejemplos:
1. [longitud] = L
2. [masa] = M
3. [tiempo] = T
4 [intensidad de corriente] = I '
5. [temperatura] = 0
*
*
#
4t
#
*
f¡
$
*
*
*
♦
*
#
*
*
*
#
♦
*
m
*
m
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
6- [intensidad luminosa] = J
7. [cantidad de sustancia] = N
8. [número) - 1
PRINCIPIO DE HOMOGENEIDAD DIMEN­
SIONAL.
Si una fórmula física es correcta, todos
los términos de la ecuación deben ser dimen-
síonalmente iguales.
Sea la fórmula física:
A = B + C . D
[A] = [B] = [C.D]
Ejemplos: Analicemos !a fórmula para
determ inar la altura en
caída libre.
h = V0
I I
m
rn
s
Luego: Todos los términos tienen uni­
dad de longitud.

13. 1ra. PROPIEDAD:
Los ángulos, funciones trigonométricas,
funciones logarítmicas y en general
cualquier número son adimensionales
Convencionalmente la dimensión de un
número es igual a la unidad.
Ejemplos:
[30o] = 1
[Sen 30o] = 1
*
*
*
*
*
*
*
*
*
*
FINES Y OBJETIVOS DEL ANALISIS DI­
MENSIONAL.
1 Expresar las magnitudes derivadas en
función de las denominadas magnitudes
fundamentales
2. Comprobar la veracidad de las fórmulas
físicas mediante el principio de homo­
geneidad dimensional
* 3
*
*
*
Determinarformulas empíricas a partirde
datos experimentales.
C PROBLEMAS RESUELTOS
;
PROBLEMA Nfi 01
Determinar la ecuación dimensional
de las principales magnitudes derivadas.
SOLUCION
1. [área] = L2
2. [volumen] = [área x h] = L
3. [densidad] = [ m /v ] = M .L-3
4. [velocidad] = [ e / 1] = LT 1
5. [aceleración] = [ A V / 1] = L.T"2
6. [fuerza] = [ m . a ] - M .L T 2
7. [trabajo] = [ F d ] = M . L 2 .T“ 2
8. [potencia] = [ W / 1] = M.L2 . T ”3
9. [energía] = [ m . c2] = M.L2 T ‘
10 [cantidad de calor] = [energía]
=M.L2 . T 2
11 [presión] = [F/A] = M.L-1 T 2
12. [velocidad angular] =[0 / 1] = T 1
13 [período] = T
14. [frecuencia] = T-1 *
PROBLEMA Ne02
Determinar las unidades de "E" en el
Sistema Internacional.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
$
*
*
*
*
*
*
*
*
E =
D.V
D: densidad
V: velocidad lineal
g: aceleración de la gravedad
SOLUCION
Del principio de homogeneidad dimen­
sional.
[E
]= L.P.U
V
.2
J
tJ lg]
[E] =
M . L~3 . L2 . T 2
L T 2
[E] = M . L
Luego; E se mide en: kg . rrf2
PROBLEMA N®03
Hallar la dimensión de “S" en la
siguiente ecuación dimensionalmente co­
rrecta.
V.S. = A Cos 60° + UP . Ln 2
A : aceleración centrípeta
V : velocidad lineal

14. Del principio de homogeneidad dimen­
sional.
[V.S] = [ a Cos60°]
[V][S] = [A 12]
L / r ’ .ts] = l 1/2. t
Luego: [S] = L
-1/2
Para la solución del problema no es ne­
cesario conocer el tercer termino.
PROBLEMA N204
En la siguiente fórmula física, indique
las dimensiones de "Y"
Y = w . A . Cos (w.t)
donde:
A = longitud; t = tiempo
SOLUCION
1. La dimensión del ángulo es igual a
la unidad:
[w . t] = 1
[w]. T = 1
[w] = T 1
2 La dimensión de la función coseno
es igual a la unidad:
[Cos (wt) ] = 1
[Y] = [w] [A] [Cos (wt) ]
[Y] = T L . 1
Luego: [Y] = L . T 1
PROBLEMA N205
La velocidad "V" del sonido en un gas
depende de la presión “P" del gas y de la
densidad "D" del mismo gas, y tiene la
siguiente forma:
*
*
«
i*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
Hallar la fórmula física para determinar
la velocidad del sonido en cualquier gas.
SOLUCION
Del principio de homogeneidad dimen­
sional:
[V] = [Px] . [Dy]
L . T 1= Mx . L~x . T 2x . My. L 3y
M °L 1. T 1= Mx+y. Lx_3y . T 2x
A bases iguales le corresponden expo­
nentes iguales.
1 .
T : -1 = -2x —
> x = —
M : 0 = x+ y
Reemplazando:
Luego:
1
2
V =P1/2. D~1/2
PROBLEMA N206
Sabiendo que el Impulso es I =F.t, en­
contrar las dimensiones de "Z" para que
la siguiente ecuación sea dimensional­
mente correcta.
. W ,
Y + m Z
W : trabajo
m : masa
SOLUCION
F : fuerza
t : tiempo
Del principio de homogeneidad dimen­
sional
[l] = [Fj-[t]
[I] = M . L . T 2 .T = M . L . T _1
De la ecuación:

15. i i = M
[Z]
[ m ] [ Z ]
Reemplazando:
M. L. T 1 = M. [Z ]
Luego: [ Z ] = L . T
Compruebe Ud., el mismo resultado con
la otra igualdad.
PROBLEMA Ns 07
Dimensionalmente, la siguiente ex­
presión es correcta y su respectiva
ecuación dimensional es la unidad.
[U N A u n i] =1
donde; U = m.C2
m : masa de un fotón
C : velocidad de la luz
I : radio de la Tierra
Hallar la dimensión de N
SOLUCION
Cálculo de la dimensión de U
[U] = [m] [c ]
[U] = M . L2 . T -2 (1)
La dimensión de un exponente siempre
es igual a la unidad.
[ü] [N] [I] =1
M.L2 .T _2.[N]L =1
[N] - M _1 . L-3 . T2
PROBLEMA Ne 08
El período de oscilación de un péndulo
depende de la longitud ( l ) de la cuerda y
.de la aceleración de la gravedad (g) y tiene
la siguiente forma:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Hallar la fórmula física correcta
SOLUCION
Por principio de Homogeneidad
[ T ] = U x] [g y ]
T = Lx . Ly 1_2y
L ° j1= L**y . T -2y
A bases iguales le corresponde exponen­
tes iguales.
L : O = x + y
T : 1 = -2y
Resolviendo:
x = +
y=~
Reemplazando en la formula:
PROBLEMA Ne 09
Un chorro de agua con densidad (D) y
velocidad (V), choca contra un área (A).
La fuerza que ejerce el chorro de agua
contra la superficie tiene la siguiente
forma:
F = ^ Vx . Ay . D2
Hallar la fórmula física correcta.
SOLUCION
Por principio de Homogeneidad
t F ] = [ V x] [ Ay ] [ Dz ]
LMT “2 = LxT x ,L2y .Mz L~3z
L1. M 1. T 2 = Lx+2y_3z MZ.T X
A bases ¡guales le corresponde exponen­
tes iguales.
L : 1 = x + 2y - 3z

16. M : 1 = z
T -2 = -x
Resolviendo
x = 2
y = z = 1
F = V2 V2 A . D
PROBLEMA N® 10
La velocidad de un satélite artificial
terrestre (Sputnik) que se desplaza no le­
jos de la superficie terrestre depende de
la distancia al centro de la tierra o radio de
curvatura R y de la aceleración de la
gravedad "g” en la superficie equipoten­
cial en que se mueve el satélite.
Determinar una fórmula empírica que
permita calcular el valor de la velocidad.
C = 1 = constante adimensional.
SOLUCION
1. De la condición del problema:
V = C.RX.gy
2. Por el principio de homogeneidad
dimensional.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
i»
*
*
*
*
*
*
*
*
*
*
[V] = [C] [R]x [g]v ....(2)
3. Sabemos que:
[V] = L.T -1 , IR] = L
[C] = 1 , [g] =L . T
4. Reemplazando en (2):
L.T -1 = 1. L*. Ly. T _2y
L1.T _1= L x+y j _2v
Identificando exponentes:
L: 1 = x + y
T -1 = 2y .
.... (3)
1
En (3) X = 7
5. Reemplazando en (1).
V=R . g V = VR7g
...a esta velocidad del satélite se le llama
también VELOCIDAD ORBITAL
PROBLEMAS RESUELTOS Y PROPUESTOS DE
ANALISIS DIMENSIONAL
MAGNITUD UNIDAD S.I. SIMBOLO DIMENSION
Longitud metro m L
Masa kilogramo kg M
Tiempo segundo s T
Temperatura kelvin K O
Intensidad de corriente eléctrica ampere A I
Intensidad Luminosa candela cd J
Cantidad de Sustancia mol mol N

17. La siguiente es un fórmula física co­
rrecta:
KF = mV
donde: m = masa
F = Fuerza
V = Velocidad
Determinar qué magnitud representa K.
SOLUCION:
Por principio de Homogeneidad dimen­
sional
[ K . F ] = I m . V ]
I K ] [ F ] = [ m ] [ V ]
[ K ] L M T 2 = M L T 1
[ K ] = T
K representa un tiempo
PROBLEMA Nfi 02
En la siguiente fórmula física:
PK = m g h
donde: P = Potencia
m = masa
g = aceleración
h = altura
¿Qué magnitud representa K ?
a) Longitud b) Masa
c) Tiempo d) Area
e) Volumen
PROBLEMA Nfi 3
La siguiente expresión es dimensio­
nalmente correcta y homogénea:
KF = mV2
donde: F = Fuerza
m = masa
V = Velocidad
¿Qué magnitud representa K?
SOLUCION:
Por principio de homogeneidad dimen­
sional
[ K.F] = [ m . V2 ]
[ K ] [ F ] = [ m ] [ V 2 ]
[ K ] L M T -2 = M L 2T~2
[ K ] = L
K representa una longitud
PROBLEMA Ns4
La siguiente fórmula física es dimen­
sionalmente correcta y homogénea.
KV = mc2A
donde: V = Volumen
m = masa
c = velocidad
A = Area
Determinar que magnitud representa K
a) Longitud b) Masa
c) Tiempo d) Fuerza
e) Densidad
PROBLEMA N®05
En la siguiente fórmula física:
E = AV2 + BP
donde: E = Energía
V = Velocidad
P = Presión
Determinar qué magnitud representa
A/B
SOLUCION
Por principio de homogeneidad
[E] = [A.V2] = [B.P]
L2 MT ~2 = [A] L2T ~2 = [B]L"1MT ~2
------0 ) -----
------------ - (2)
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
$
#
&
&
#
*
*
#
$
$
#
*
*
$
*
*
$
*
*
*
*
s
í?
4
5
*
*
*
m
*
*
*
«
C
*
*
❖

18. de (1) [A] = M
de (2): [B] = L3
de donde: = ML
<-3
entonces — representa una densidad.
l5
PROBLEMA N®6
En la siguiente fórmula física.
KX = A d + i- BP
donde
K = Constante Física ( M T~2)
X = Longitud
d = Longitud
p = momentum lineal (M LT ~1)
Hallar qué magnitud representa A.B.
a) Masa b) Tiempo
c) Velocidad d) Aceleración
e) Fuerza
PROBLEMA Ns 7
La siguiente fórmula es dimensional­
mente correcta y homogénea:
E = AW2 + BV2 + CP
donde: E : Energía
W : Velocidad Angular
V : Velocidad Lineal
P : Presión
Hallar:
■ m
SOLUCION:
Por principio de Homogeneidad:
[E] =[AW2] = [BV2] = [CP]
L2M1 = [A] "2=[B]L21 ‘2 =[C]L"1M T 2
J
— ------- (2) --------1
-(3).
*
*
*
4)
%
*
*
*
«
¡i
*
*
*
*
*
*
# '
*
*
*
*
0
*
*
«
fe
*
*
*
*
*
i¥
*
Ü
f
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ü
*
*
*
*
de (1)
de (2)
de (3)
entonces:
[A] = L M
[B] = M
[C] = L3
PROBLEMA Ne8
La posición de una partícula móvil so­
bre el eje X está dada por:
X = K1+K2 T + * K3 T2
donde:
Hallar:
X . distancia
T tiempo
K52
c) M
Kl . K3
a) L4 b) T
d) M °L°T° e) N.A.
PROBLEMA N2 9
La fórm ula que determina la altura
máxima h alcanzada por una partícula que
es lanzada verticalmente hacia arriba con
una velocidad inicial Vo tiene la siguiente ‘
forma:
y
h =-
xg*
siendo:
g = aceleración de la gravedad
Hallar la fórmula física correcta.
SOLUCION:
Por principio de Homogeneidad:
x g y

19. L =
(L T 1)X
(L r2)y
L1T 0 = |_*“y>T 2y~x
de donde: x - y = 1 ....(1)
2y - x = 0 ....(2)
Resolviendo.
x = 2 ; y = 1
entonces:
h =
Vo
2g
PROBLEMA Ns 10
La presión P que un fluido ejerce sobre
una pared depende de la velocidad V del
fluido, de su densidad D y tiene la
siguiente forma:
Hallar la fórmula física correcta
a) P =V2 V2 D2 b) P =V2 V2 D
c) P =V D
e) N.A.
PROBLEMA N® 11
Dada la ecuación:
d) P = V D
F = nx ry v2
donde:
F = Fuerza
n = Viscosidad
masa
; Longitud x tiempo
r = radio (Longitud)
v = velocidad
Hallar: (x + y + z)
SOLUCION:
Por principio de Homogeneidad:
*
*
*
*
*
*
*
*
*
&
*
m
*
%
*
*
*
fj*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
$
*
♦
¡fe
*
*
*
■
&
*
•3*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
[F] = [n]x [r]y [V]z
LMT-2 = (ML~1T _1)x(L)y (LT “ ’)
L1M1T _2=L~x+y+z M* T ~x_z
de donde:
- x + y + z = 1
x = 1
-x - z = -2
Resolviendo.
x = 1; y = 1 ;
entonces:
(1)
(2)
- - O )
z = 1
x + y + z = 3
PROBLEMA Ne 12
La siguiente es una fórmula física di­
mensionalmente correcta y homogénea:
P = K Dx gy hz
siendo:
Hallar.
a) -1
d) 3
K = Adimensional
P = Presión
D = Densidad
g = aceleración
n = altura
(x + y + z)
b) i
e) N.A.
c) 2
PROBLEMA Ne 13
La fórmula para hallar la rigidez de una
cuerda es:
donde:
Q = carga (newtons)
R = Radio (metros)
d = Diámetro (metros)
S = Rigidez (newtons)

20. Hallar las ecuaciones dimensionales
de las magnitudes a y b.
SOLUCION;
Desarrollando:
por P.H.D.:
[ S ] = [ a ] = [bd2]
LMT “ 2 = [a] L ! MT ' 2 = [b] L2
(1)
(2)
[a] = L-1
[b] = L~1M T-2
de (1):
de (2):
PROBLEMA Ns 14
En la siguiente expresión:
donde: F = Fuerza
V = Velocidad
Hallar la ecuación dimensional de la mag­
nitud "b“
a) M ~1T b) MT “ 1
c) M T d) LT
e) N A.
PROBLEMA Ns15
Dada la siguiente fórmula física:
P = KW2 Tg e
donde:
P = Potencia
W = Velocidad Angular
Hailar la unidad de la magnitud K en el
sistema internacional.
*
*
*
*
«
*
*
*
*
SOLUCION:
[P] = [K] [W]2 [Tg6]
La M T 3 = [K] T ’ 2 1
[K] = L2M T “ 1
La unidad de K será:
Kg . n f . s 1
* PROBLEMA N« 16
*
*
*
*
*
*
*
$
*
$
*
*
*
#
*
*
#
*
*
La siguiente es una fórmula física di­
mensionalmente correcta.
Q = K A V2gh
donde Q = Caudal (Se mide en m /s)
A = Area
g = aceleración de la gravedad
h = altura.
Hallar la unidad de la magnitud K en el
sistema internacional de unidades
a) L b) L¿
-1
d) No tiene unidades
PROBLEMA Ns 17
c) LT
e) N.A.
Dada la siguiente fórmula física, di­
mensionalmente correcta y homogénea:
Q = m.Ce.AT
*
f
t
*
*
donde:
Q = Cantidad de calor
m = masa
AT = Variación de Temperatura
Hallar la ecuación dimensional del
calor específico Ce.
SOLUCION:
[O] = [m] [Ce] [AT]
L2 M T-2 = M [Ce] 6
[Ce] = L2T ”2 6 " 1

21. Hay que señalar que el calor Q es una
forma de energía
PROBLEMA N® 18 .
Si la longitud final de una barra al di­
latarse, está dada por la siguiente re­
lación:
Lf = L0 (1+ ccA T)
AT: Variación de la Temperatura.
Determinar la ecuación dimensional
del coeficiente de dilatación lineal a
1
a) L6
d) 0
PROBLEMA N9 19
b) L 6 '
e) N.A.
c) L-1 e
La entropía S de un gas, se define
matemáticamente por la siguiente re­
lación:
AS -
AQ
donde:
AS increm ento de Entropía (Si - So)
AQ =Cantidad de Calor absorbido.
T =Temperatura
Hallar la ecuación dimensional de la
entropía "S".
SOLUCION.
[AQ]
[AS] =
m
[S] =
L2 M T 2
*
*
*
*
*
*
*
*
*
*
*
*
*
$
&
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
#
*
*
*
donde'
K = Constante de Boltzman
T = Temperatura Absoluta
Determinar la ecuación dimensional de la
constante de Boltzman.
a) L M T ~2 6 -1
c) L2 M T -2e
b) L M T e
d) L2M T _2e
e) N.A.
PROBLEMA N®21
La siguiente es la ecuación universal
de los gases ideales
PV = n R T
donde:
P = Presión
V = Volumen
n = Número de moles
T = Temperatura
Hallar la ecuación dimensional de la
constante universal de los gases R.
SOLUCION:
[P] [V] = [n] [R] m
L-1 MT ~2 . L3 = N [R] 6
[R) = L2 M T_2e V 1
PROBLEMA N®22
La energía interna, por mol, de un gas
ideal depende únicamente de la tempera­
tura, como lo indica la siguiente fórmula.
*
[S] = l2 m r 2e~1 *
*
*
*
U=f RT
PROBLEMA N® 20
La siguiente fórmula física nos deter­
mina la energía cinética promedio de una
molécula monoatómica de un gas ideal.
E = f KT
*
*
#
*
donde:
R = Constante Universal de los gases
T = Temperatura.
Determinar la ecuación dimensional de la
energía interna U.

22. b) MLT “2 N“ 1
d) ML2 T ~2 N
a) ML2T~2N _1
c) ML2T -1N ~1
e) N.A.
PROBLEMA Ne23
La cantidad de calor Q que atravieza
una lámina de Area A y espesor b, desde
una temperatura Ti hacia una tempera­
tura T2 , en un tiempo t está dada por la
siguiente fórmula:
<
*
II
0
fT s -T i 1
" b 1
l D J
donde:
K = Conductividad térmica del mate­
rial.
Hallar la ecuación dimensional de K
SOLUCION:
[Q] = [ K ] [ A ] ^ [ t ]
L2MT~2 = [Kj L2 . ® .T
[K] = LMT -3 6 ~1
PROBLEMA Ne 24
El calor latente de fusión de una sus­
tancia está definido por la siguiente re­
lación:
r Q
C l =~r
m
donde:
Q = Cantidad de calor entregado,
m = masa de la sustancia
Hallar la ecuación dimensional del calor
latente CL
a) L2t '
c) L2T 2
e) N.A.
b) LT
d) L T 1
-2
*
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
O
f
*
*
*
*
*
¡h
*
*
*
*
*
*
*
Si la intensidad de corriente eléctrica
se define por la siguiente relación:
1=
donde:
Q = Carga Eléctrica
t = Tiempo
Hallar la ecuación dimensional de la
carga eléctrica "Q"
SOLUCION:
[11 =
M
[t]
[Q] = I T
La unidad de carga eléctrica es el cou­
lomb (c) en honor a Charles A. de Cou­
lomb (1736 -1806) que fue el primero que
midió las fuerzas eléctricas y magnéticas.
Según ésto:
1c= 1A.S
PROBLEMA N926
Si el potencial eléctrico V define por la
siguiente relación:
V —
w
o
donde: W = trabajo
Q = Carga Eléctrica
Hallar la ecuación dimensional del po­
tencial eléctrico V.
a) L2M T ^ r 1
c) LMT~3r 1
e) N.A.
b) L2M T~2 r 1
d) LMT 2 1
-1

23. La ley de Ohm, se expresa matemáti­
camente por la siguiente relación:
AV = IR
donde:
AV = Diferencia de Poten­
cial
I = Intensidad de Co­
rriente Eléctrica
R = Resistencia Eléctrica
Hallar la ecuación dimensional de la
resistencia eléctrica "R".
SOLUCION:
m = [t][R ]
L2M T_3I“ 1 = I [R]
[R] = L 2M T ~ 3 r 2
Para la ecuación dimensional del poten­
cial electrico V se ha utilizado el resul­
tado del problema anterior.
La unidad de resistencia eléctrica es el
Ohm (Li) en honor a Georg S Ohm
(1787 - 1854) quien formuló la ley de
Ohm. según ésto.
1 0 = 1 m2KgS“3 A~2
PROBLEMA N9 28
Si la capacidad eléctrica de un con­
ductor se define matemáticamente como:
C =7
donde: Q = Carga Eléctrica
V = Potencial Eléctrico
Hallar la ecuación dimensional de la ca­
pacidad eléctrica C
a) L-1M -1 T 4 1
2
c) L-2 M -1 T 4I
e) L_2.M~1T 4 . 1
2
b) L-1M~1T 4 I
d) L-2 M, T 4 I
*
m
m
«¡6
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
+
*
*
*
#
*
*
#
*
*
*
*
*
*
*
üt
*
*
*
*
*
La fuerza F que actúa sobre un alam­
bre, por el cual circula una corriente I, está
dada por la siguiente relación:
F = I L B
donde:
L = Longitud del alambre
B = Densidad de flujo magnético ex­
terno.
Hallar la ecuación dimensional de "B".
SOLUCION:
[*=] = [ l ] [ L ] [ B ]
LMT -2 = I L [ B ]
[B] = M T
-2,-1
La unidad de densidad de flujo magnético
es la TESLA (T) en honor de Nickola
Testa (1856-1943) quien demostró el
valor de la corriente alterna. Según ésto:
1T = 1Kg.s~2A_1
PROBLEMA N®30
Si el flujo m agnético, se define
matemáticamente por la siguiente re­
lación:
<
}>= BA Cos 6
Donde:
B = D ensidad de flujo
magnético
A = Area
Hallar la ecuación dimensional del flujo
magnético <
J
>
a) L M T -2 I _1
c) L2 M T “2 1
e) N.A.
b) L M T ^ I
d) L2 M T 2 I”1

24. Si la inductancia de un bobina está
dada por la siguiente relación:
I
donde:
N = Número de vueltas del arro­
llamiento
$= Flujo magnético
I = Intensidad de corriente
Hallar la ecuación dimensional de la
inductancia “L"
SOLUCION:
[N] m
[L i­
li]
[L] -
l2 m t ~2 r 1
[ L ] = L2M T “2r 2
Hay que hacer notar que el número de
vueltas N es adimensional y la dimensión
del flujo magnético <
¡>se ha tomado del
problema anterior. La unidad S.l. de In-
ductancia es el Henry (H) en honor a
Joseph Henry (1797 -1878) que realizó
experimentos que condujeron al
telégrafo eléctrico. Según esto:
1H = 1m2 . Kg . s-2 A-2
PROBLEMA Nfi 32
La energía W que almacena una bo­
bina en forma de campo magnético tiene
la siguiente forma:
W J - i x Ly
x
donde:
I = Intensidad de corriente
L = Inductancia de la bobina
Hallar (x+y)
*
*
*
*
s
k
i
*
sis
#
m
m
*
*
m
*
*
*
*
*
s
is
<
¡f
*
*
<
¡f
*
$
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
a) 1 b) 2
d) 4 e) 0
PROBLEMA Ne33
La intensidad de Campo Eléctrico E,
está definida matemáticamente por la
siguiente relación:
E = ^
q
donde:
F = Fuerza Eléctrica
q = Carga eléctrica de
prueba
Hallar la unidad S.l, de "E" (1voltio
(V) = m2 Kg s~3 A-1 )
SOLUCION:
[El J f l
11 L
q]
[E
]
LMT
= |T
[E] = LMT ~3 1_1
Según ésto la unidad S I de la intensidad
de campo Eléctrico es:
m . K g . s~3A-1
pero por definición:
1V = m2 Kg . s-3 A-1
entonces la unidad de E es:
1 V/m
PROBLEMA Nfi 34
La fuerza de Lorentz, que es la fuerza
que actúa sobre una partícula que se mue­
ve con una velocidad V en una región
donde existe un campo eléctrico E y un
campo magnético B, está dada por la si­
guiente relación.
F = XE + Y V . B
Hallar las unidades S.l. de las magni­
tudes X e Y. (1 coulomb (c) = 1 A.S)

25. a) 1c ;1A b) 1c ; 1c
c)1c;1A.S d )1 c .s ;1 c
e) N.A.
PROBLEMA Ne35
La densidad de flujo magnético B,
originado por una corriente rectilínea I, a
una distancia radial r, está dada por la
siguiente relación:
B =
2n
Hallar la unidad S.l. de la permeabili­
dad magnética n .(1Henry(H)=1m .Kg.s-2.A-2)
SOLUCION:
,111
[B] =[H]
[ r ]
lv i = LM T-2r 2
Según ésto la unidad S.l.de la permea­
bilidad magnética es:
m . Kg . s ~2A-2
p _p o
Pero por definición: 1H =m Kgs A
entonces la unidad de n es: 1H/m
PROBLEMA Nfi 36
La intensidad de campo magnético H
se define matemáticamente como:
donde: B = Densidad de flujo
magnético
u = Perm eabilidad m ag­
nética
Hallar la unidad S.l. de “H"
a) A m b) A/m c) m/A
d) A e) N.A.
*
*
s|í
*
$
*
*
#
*
*
*
*
#
#
*
*
*
*
*
#
s
je
*
*
+
*
*
#
#
*
*
#
*
*
*
*
¡Se
*
*
*
*
*
*
*
*
*
$
Determ inar la velocidad de propa­
gación de una onda mecánica en una
cuerda tensa sabiendo que depende de la
fuerza de tensión F a la cual está sometida
y de su densidad lineal de masa n (masa /
longitud). La constante numérica de pro­
porcionalidad es la unidad.
SOLUCION:
La velocidad de propagación V puede
expresarse de la siguiente manera:
V = K
siendo K la constante numérica de pro­
porcionalidad.
Por principio de homogeneidad dimen­
sional.
[V] = [F]x [|o.]y
L T 1 = (LM“
r 2)x(ML-1)y
L1M °T _1 = Lx-y Mx+yT “2*
A bases iguales le corresponden expo­
nentes iguales.
L :
M :
T :
Resolviendo:
Por lo tanto:
1
1 = x —y
0 = x + y
-1 = —
2x
e y = -
PROBLEMA Ns 38
La aceleración centrípeta es una mag­
nitud física vectorial que mide el cambio
que experimenta la velocidad en direc­
ción y sentido. Se representa por un vec­
tor que indica en todo instante al centro
de curvatura.
Su valor depende déla velocidad lineal
"V" y del radio de curvatura "R" de la
trayectoria. Hallar la fórmula empírica
para calcular el valor de la aceleración
centrípeta ac-

26. La constante numérica de proporcio­
nalidad es la unidad.
a) ac = V¿R
c) ac = V ~2R
e) N.A.
PROBLEMA N939
b) ac = VR
d) ac = V^R-1
La cantidad de calor "Q“ que disipa un
conductor cuando por él circula una co­
rriente eléctrica, depende de la intensidad
de corriente "I" que por ella circula, del
valor de su resistencia "R" y del tiempo
"t" transcurrido. Si la constante numérica
de proporcionalidad es k = 1, hallar la
fórmula empírica de la cantidad de calor
Q.
SOLUCION
La cantidad de calor Q puede expresarse
de la siguiente manera:
Q = K I x R y t z
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
siendo K la constante numérica de pro­
porcionalidad.
Por P..H.D. tenemos que:
[O] = [ I f [ R ] y [ t ] z
l2m t "2 = i*(l2m t ~3 r 2) y t 7
L2M1T -2 |0= L2yMy T - 3y+zr 2y
A bases iguales, le corresponden expo­
nentes iguales.
L 2 = 2y
M : 1 = y
T : -2 = -3y + z
I 0 = x - 2 y
Resolviendo:
x = 2 ; y = 1 ; z = 1
Luego.
Q = r R T

27. Es un ente matemático, que se repre­
senta mediante un segmento de recta
orientado, dentro det espacio euclidiano tridi­
mensional. En física, el vector, sirve para
representar a las magnitudes físicas vecto­
riales.
_ L írie < i de
i c c i 6 r
x
Se representa con cualquier letra del al­
fabeto, con una pequeña flecha en la
parte superior de la letra.
—
»
A ; se lee : vector A
O : origen del vector
P : extremo del vector
—
) —
>
También se denota : A = OP
ELEMENTOS DE UN VECTOR
7. Módulo
Indica el valor de la magnitud vectorial.
Geométricamente es el tamaño del vec­
tor.
*
*
*
*
*
#
*
*
*
*
*
*
*
i
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
IAI = y2
|A| = V42 + 32 = 5p
2. Dirección
Es la orientación que tiene el vector, res­
pecto al sistema de coordenadas carte­
sianas. En el plano se define mediante
el ángulo que forma al vector respecto del
eje (+)
tge = *
M x
* 3. Sentido
Indica hacia que lado de la dirección
(Línea de acción) actúa el vector. Gráfi­
camente se representa por una cabeza
de flecha
A = OP

28. Sentido de A :
O hacia P
CLASIFICACION DE LOS VECTORES
1. Vectores Colineales.
Son aquellos dos o más vectores que
tienen una misma linea de acción o todos
ellos están contenidos en una misma
recta
Los vectores a ; b y c son colineales.
2. Vectores Paralelos.
Son aquellos vectores que tienen sus
lineas de acción respectivam ente
paralelas.
Si, Li es paralelo con , entonces-
a es paralelo con el vector b
a es paralelo con el vector c
3. Vectores Opuestos.
Dos vectores serán opuestos cuando
tienen igual dirección, igual módulo, pero
sentidos opuestos.
La suma de dos vectores opuestos es
igual al vector nulo (Tamaño igual a cero).
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
#
M
í
#
*
*
*
S
í!
*
*
*
*
*
$
*
*
*
*
*
$
*
*
*
#
*
*
s
¡»
*
*
*
*
*
*
*
*
%
*
*
s
H
*
- - L2
Si, L, es paralelo con L2; o son iguales
lal = Ibl y sentidos opuestos a +b = 0
4. Vectores Iguales.
Dosvectoresserán iguales, cuandotienen sus
tres elementos respectivamente iguales.
-----------------------2---------------- L,
L2
Igual dirección Li // L2
Igual modulo lal = Ibl
Igual sentido : -»
5. Vectores Coplartares.
Dos o más vectores se denominan copla-
nares, cuando todos ellos están conteni­
dos en un mismo plano.
6. Vectores Concurrentes.
Dos o más vectores se denominan con­
currentes, cuando todos ellos tienen un
mismo punto de aplicación o sus líneas
de acción se intersectan en un mismo
punto.
a ; b y c son vectores coplanares y
concurrentes.

29. OPERACIONES CON VECTORES
SUMA DE VECTORES COLINEALES Y
PARALELOS.
Dado que todos los vectores tienen la
misma dirección, entonces el vector re­
sultante también tendrá la misma direc­
ción, por consiguiente la suma se realiza
algebraicamente teniendo en conside­
ración los signos (sentidos)
I
a + b = (2) + (4) = +6
a + c = (2) + (-3) = -1
(-): sentido a la izquierda.
2 PRODUCTO DE UN ESCALAR POR UN
VECTOR.
En principio una cantidad escalar es todo
número real, positivo o negativo, entero
o fracción. Cuando se multiplica un es­
calar por un vector, el vector resultante es
otro vector de igual dirección. Si la can­
tidad escalar es positiva también tiene el
mismo sentido, pero si la cantidad esca­
lar es negativa el sentido es opuesto al
vector inicial.
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
2A
-A
L
3. SUMA DE DOS VECTORES
(Método del Paralelogramo)
Para sumar dos vectores que tienen el
mismo origen, se construye un paralelo-
gramc, trazando por el extremo de cada
vector una paralela al otro. Geométri­
camente el módulo del vector resultante
se obtiene trazando la diagonal del para­
lelogramo desde el origen de los vec­
tores.
El módulo del vector resultante se deter­
mina del siguiente modo:
R = Va 2 + B 2+ 2 . A . B. Cose
i) A y B representan el tamaño de los
vectores.
ii) R es el tamaño del vector resultante.
es el opuesto de *
*
*
*
iii) 0 es el ángulo que forman los vec­
tores.
DEMOSTRACION

30. Teorema de Pitágoras:
R2 = (B + pf + q2
R2 = B2 + 2pB + p2 + q2
Pero: p = A.Cos 0
p2 + q2 = A2 .... (2)
Reemplazando (2) en (1):
R2 = B2 + 2(ACos 0) B + A2
(1)
R2 = A2 + B2 + 2A.B Cos 0
PROBLEMA N9 01
¿Qué ángulo deben formar dos fuer­
zas de 27N y 45N para que actúen sobre
un cuerpo como una sola fuerza de 63N?
SOLUCION
Método del Paralelogramo.
R? = A2 + B2 + 2A.B. cos 0
(63)2=(27)2+(45)2+2 (27) (45) cos 6
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
92.72 = 92 32 + 92.52+2(9.3)(9.5)Cos 0
49 = 9 + 25 + 30 . Cos 0
Cos 0 = —
Luego; las fuerzas forman un ángulo: •
0 = 60°
CASOS PARTICULARES
1. RESULTANTE MAXIMA
La resultante de dos vectores es máxima,
cuando forman entre sí un ángulo igual a
cero, por consiguiente tienen igual direc­
ción y sentido.
Rmax —a +b
2. RESULTANTE MINIMA
La resultante de dos vectores es mínima,
cuando forman entre si un ángulo igual a
180° por consiguiente tienen sentidos
opuestos.
Rrmn —3 —b
3. La resultante de dos vectores se obtiene
mediante el Teorema de Pitágoras, cuan­
do forman entre sí un ángulo igual a 90°
R = Va2
a*+b

31. La resultante de dos vectores de
módulo constante, varía al hacer girar uno
de ellos. El mínimo módulo de la resul­
tante es 2 y el máximo 14. Determinar el
módulo de la resultante, cuando los vec­
tores forman ángulo recto.
SOLUCION
Resultante mínima:
a - b = 2 .....(1)
Resultante máxima:
a + b = 14 .... (2)
Sumando las Ec. (1) y (2)
a = 8 y b = 6
Cuando forman ángulo recto
R2 = a2 + b2
R2 = 64 + 36
R = 10
PROBLEMA Ns03
La figura muestra tres vectores de
módulos iguales. Hallar la medida del án­
gulo "6" para obtener la resultante
mínima.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
El módulo de la resultante no se altera si
giramos los vectores un ángulo “ 6 “ en
sentido anti-horario.
Los vectores a y b se puede reem­
plazar por el vector S
La resultante de sumar los vectores
—
> —
>
c y S será mínimo cuando forman un
ángulo de 180°.
45° + 90° + 20 = 180°
0 = 22,5°
4. SUMA DE "n" VECTORES
(Método del Polígono)
Consiste en construir un polígono con los
vectores sumandos, manteniendo constan­
tes sus tres elementos (módulo, dirección y
sentido), uniendo el origen del segundo vec­
tor con el extremo del primero, el origen del
tercero con el extremo del segundo, así
sucesivamente hasta el último vector El
módulo del vector resultante se determina
uniendo el origen del primero con el extremo
del último vector.

32. Calcular el vector resultante, de los vec­
tores mostrados.
POLIGONO CERRADO
Si el polígono vectorial resulta cerrado,
entonces el módulo del vector resultante
es igual a cero.
!a + b + c + d | = 0
CASO PARTICULAR (TRES VECTORES)
A + B + C = 0
Se cumple la ley de Senos
B
*
*
*
Ü
f
*
*
*
*
*
*
«
e
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
fe
*
*
*
*
*
*
*
*
*
*
*
<
¥
Sen a Sen p Sen y
PROBLEMA Ne 04
La figura muestra una circunferencia de
—
)
centro "O". Escribir el vector x en función de
—
> —
>
los vectores a y b .
SOLUCION
El punto “O", es el punto medio del mó-
—
> —
>
dulo de los vectores a y b
Del método del Polígono:

33. ( b - a )
> D
c + d
Pero: AD = 4 n
Luego:
*
PROBLEMA NB05
En la figura los puntos A,B,C,D,E y F
determinan un exágono regular de lado
2|x. Hallar el módulo del vector resultante,
en el sistema vectorial mostrado.
SOLUCION
Trazamos los vectores manteniendo
constante su módulo, dirección y sentido
El vector AF ocupa la posición CD y el
vector AB ocupa la posición ED.
Si , "G" es el baricentro del triángulo
AOB y M es punto mudio de AB. Escribir
el vector x en función de los vectores
—
► —
>
a y b.
Ia + b + c + d l = 8 | i
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
5
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
#
*
#
*
*
*
*
*
0
?
*
#
0
SOLUCION
Sea, p un vector auxiliar
—
> —
» —
*
AOAB : a + 2 p = b
—
> —
>
”* b - a
P ■ (1)
AOAM : 3 x = a + p .... (2)
Reemplazando (1) en (2):
x =
a + b
PROBLEMA Nfi 07
—
*
Expresar el vector x en términos del
-> ->
vector a y b, sabiendo que ABCD es un
paralelogramo, además M y N son puntos
medios de AB y CD respectivamente.

34. *
*
*
SOLUCION
Del método del paralelogramo:
-» -> ->
x = 2 (p + . ..(1)
-> -» ->
Del ADAM: 2 p + q = a ... (2)
—
> —
* —
*
Del ADCN : 2 q + p = b ... (3)
sumando:
^ (a + b )
P + q = • 3
Reemplazando en (1):
x = - { a + b }
5. DIFERENCIA DE DOS VECTORES
*
La diferencia de dos vectores que tienen
el mismo origen se consigue uniendo los
extremos de los vectores E! vector dife­
rencia D indica al vector minuendo A.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
-+
*
*
*
Del método del Polígono:
-> -» -»
B + D = A
D = A - B
El modulo del vector diferencia se deter­
mina aplicando la Ley de Cosenos
D = V a 2+ B2 - 2 A.B. Cos G
PROBLEMA N908
dos los vepto
= 6N X 2 O
0
Dados los vectores a = 5N
, b
/ 73o
Calcular la - b I
SOLUCION
Llevamos los orígenes a un punto común
" O " .

35. a - b
Cálculo del vector diferencia :
—
> —
> -»
D = a - b
D2 = a2 + b2- 2(a) (b) Cos 53°
D2 = 25 +36 -2 (5 ) ( 6 ) |
b
la - b I = D = 5N
6. DESCOMPOSICION RECTANGULAR
En principio un vector se puede escribir
en función de dos o mas componentes.
En este caso particular escribiremos en
función de dos componentes que forman
entre sí un ángulo recto.
'
!
A. Sen
l : - ________ ~
Cos
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
=
ü
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Ax : Componente de A en el eje x
Ay : Componente de A en el eje y
De la figura: Cos 0 =—
<
ii
X
<
. Cos
6I
Sen B :. Ay
" A
| Ay = A . Sen
lJ
Para determinar la resultante de un
sistema de vectores por este método, se
sigue los siguientes pasos:
1.
2.
3.
4.
Cada vector se descompone rectan­
gularmente, respecto de un sistema
de ejes coordenados arbitraria­
mente elegido.
Se determina la resultante en cada
eje cartesiano:
Rx : Resultante en el eje x
Ry : Resultante en el eje y
El modulo del vector resultante se
halla aplicando el Teorema de
Pitágoras.
| R = V ~ R f + Ry |
La dirección, del vector resultante,
respecto del eje x se determina me­
diante la función tangente:
PROBLEMA Ne 09
Si las componentes rectangulares de
un vector F en el sistema de coordenadas
x e y son Fx = 5 ; Fy = 5 VíT
Hallar las componentes del vector en
el sistema de coordenadas x’ e y’, que con
respecto al primero ha sido rotado un
ángulo de 23 .
r..

36. Calculo del módulo del vector F
F=V F
?+F
p =10
Cálculo del ángulo “ 9 " que forma el
—
>
vector F con el eje x.
tge = | * = V3 =>
r x
0 = 60°
El vector F forma un ángulo de 37° con el
eje x'.
Cálculo de las componentes en el sis­
tema x’ e y'
FX-=F cos37° = 10. ~
Fx
I!
03
Ll!
II
se n 37°
Fy
II
O)
3
5
PROBLEMA Ne 10
La figura muestra un cuadrado ABCD
de 4cm de lado, donde M es el punto
medio del segmento BC. Determinar el
valor del ángulo “ G“, tal que el módulo de
la resultante vectorial sea igual a .221 cm.
*
*
*
*
*
*
&
*
I
*
*
*
*
#
*
jfi
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
#
$
#
*
*
*
*
#
*
*
$
#
*
*
*
*
*
m
*
*
*
*
*
#
#
*
#
*
*
#
#
*
SOLUCION
Descomponiendo los vectores rectangu­
larmente:
4Tg8
Cálculo de la resultante en los ejes x
e y.
Rx = 10
Pero:
Ry = 8 + 4 tg 0
R2 = R2 + R2
221 = 100 + (8 + 4.Tg G)2
121 = (8 + 4Tg 0)2
T9 e= f
0 =37°
7. VECTORES UNITARIOS CARTESIA­
NOS
Son aquellos vectores cuyo módulo es la
unidad de medida y se encuentran en los
ejes coordenados cartesianos.
y

37. i : vector unitario en el eje x
j : vector unitario en el eje y
Representación de un vector en función
de los vectores unitarios cartesianos:
PROBLEMA N9 11
Determinar el módulo del vector resul­
tante del conjunto de vectores mostrados
en la figura. El lado de cada cuadrado es
la unidad.
SOLUCION
Escribimos los vectores en función de los
vectores unitarios
->
A = (-1; 2) = - i + 2j
B =(-2;-2) = —
2¡ —2j
C = ( 1; -1) = ¡ - j
D = ( 2 , 1 ) = 2¡ + j
$
sü
sü
*
*
*
*
*
*
*
*
*
*
*
$
*
*
»
v
*
H
j
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
ü
*
$
s
ü
*
#
*
*
*
*
*
*
*
*
#
*
*
*
*
*■
*
*
*
*
sü
*
*
#
S
ü
sü
*
sü
*
*
*
Sumando:
—
>
R = (0 ; 0) = Oi + O
j
.-. R = vector nulo
R = 0
Módulo de la resultante igual a cei ^
8. VECTOR UNITARIO
Es aquel vector cuyo módulo es la unidad
de medida y tiene por misión indicar la
dirección y sentido de un determinado
vector El vector unitario se define como
la relación del vector A entre su módulo.
Por definición:
Despejando:
-i -»
A = A . M
MODULO
J V
LO / DIRECCION'Y SENTIDO
Cualquier vector, se puede escribir como
el producto de su módulo por su corres­
pondiente vector unitario.
PROPIEDAD
Dos vectores paralelos o colineales (del
mismo sentido) tienen e¡ mismo vector

38. unitario, por consiguiente los vectores
serán directamente proporcionales a sus
módulos.
Si, Li es paralelo con L2
-» _ L
A
8 1
Tamaño de A Tamaño de B 1
PROBLEMA Ne 12
Los puntos A, B, C y D determinan un
cuadrado. Escribir el vector x en función
de los vectores a y b
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*■
*
*
*
*
*
*
*
*
Comparando los gráficos. El vector x es
colineal con el vector suma (a+b)
a + b
(Tamaño x ) Tamaño (a + b)
-> -> -»
a + b
PROBLEMA Ne 13
Los puntos P, Q, R y S determinan un
cuadrado donde M y N son puntos medios
de PQ y QR respectivamente. Relacionar
-» —
» —
»
el vector x con los vectores a y o .

39. Los triángulos SPM y PQN son congruen­
tes.
Luego:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
a + p = 90°
Los triángulos rectángulos POM y POS
son semejantes, cuyos lados están en la
razón de 1 a 2.
Luego : SO = 4 x
Método del polígono, en el ASPM

40. PROBLEMAS RESUELTOS Y PROPUESTOS DE
ANALISIS VECTORIAL
PROBLEMA Ns 1
Hallar el módulo del vector resultante
de dos vectores de 15 y 7 unidades que
forman entre sí un ángulo de 53°
SOLUCION:
Sabemos
R = A2 + B2 + 2 AB Cos 0
R = V 152 + 72+ 2 (15) (7) Cos 53
R = 20
PROBLEMA N2 2
Se desea extraer un clavo de una ma­
dera mediante la acción de dos fuerzas de
30 y 50 Newtons que forman entre sí un
ángulo de 127°. Hallar el efecto neto que
producen las dos fuerzas actuando sobre
el clavo.
a) 20 N b) 30 N c) 40 N
d) 50 N e) 60 N
PROBLEMA N2 3
Si la resultante máxima de dos vec­
tores es 17u y la resultante mínima es 7u,
determinar el módulo de la resultante
cuando los vectores formen entre sí un
ángulo de 90°.
m
*
*
*
*
*
N
i
*
*
*
*
*
S
lí
#
*
*
*
*
$
*
*
*
*
*
*
*
* Rmax —A + B —17
Rmin = A — B = 7
Resolviendo
A = 12 ; B = 5
Cuando los vectores forman un ángulo de
90°, su resultante se determina por:
R = ^ A2 + B2
R = V l 2 2+ 52
R = 13
PROBLEMA Ne 4
Si la resultante máxima de dos vec­
tores es 8u y la resultante mínima es 2u,
determ inar el módulo de la resultante
cuando los vectores formen entre sí un
ángulo de 60°
a) 4u b) 5u c) 6u
d) 7u e) N.A.
PROBLEMA Ns 5
Hallar el ángulo que forman dos vec­
tores de igual módulo, si su vector resul­
tante tiene el m ism o m ódulo que los
vectores componentes.
SOLUCION :

41. R =Va 2+ B2 + 2 AB Cos 9
pero por condición del problema:
A = B = R, entonces:
A = ÍA 2+ a 2+ 2A¿ Cos 0
A2 = 2A2 + 2A2 Cos 0
Cos 0 = -
1
0 = 120°
*
*
*
*
*
*
slí
*
*
*
*
*
<
!=
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
PROBLEMA NB6
Determinar el módulo del vector resul­
tante de los tes vectores mostrados en la
figura:
PROBLEMA Nfi 7
En la figura, determinar el modulo del
vector resultante del conjunto de vec­
tores mostrado, si el radio de la circun­
ferencia es de '-'S unidades y O es su
centro.
*
*
*
*
*
<
t*
*
*
*
*
*
*
*
*
*
*
#
sis
*
*
#
#
Utilizando la conclusión del problema re­
suelto anteriormente deducimos que la
—
* —
»
resultante de los vectores P y Q es el
—>
vector B de móduloVÉT y forma 60° con
el vector Q. Ahora el problema se reduce
—
» —
>
a hallar la resultante de A y B.
R2 = A2 + B2 + 2AB Cos 0
R2 = V Ír + ^ + 2 (a
/5)2 Cos 127
R2 = 10+ 10 ( - f )
5

42. Dado el conjunto de vectores mos­
trado en la figura, hallar el valor de 6 para
obtener la resultante máxima.
a) 5o
d) 20°
b) 10°
e) 30°
c) 15°
i y
PROBLEMA Ne 9
—
> —
> —
*
Si dados los vectores A, B y C se
cumple que:
A + B + C = 0
SOLUCION :
Si la resultante de los tres vectores
mostrados es CERO el módulo de la
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
resultante de dos de ellos tendrá igual
módulo que el tercero según esto.
C =a/a2+ b 2 + 2 a b Cose
13 =^J?2+ 82 + 2 (7) (8; Cos 6
169 = 113+ 112Cos6
Cos 0 = 7
T
9 = 60°
PROBLEMA N® 10
Si la resultante de los tres vectores
coplanares mostrados en la figura es
CERO, hallar el módulo del vector O, si:
a) 5 b) 7 c) 8
d) 10 e) N.A.
PROBLEMA Nfi 11
La figura adjunta muestra dos vecto­
res A y B, siendo:
—
V
i A I = 20

43. SOLUCION :
Sabemos:
1A - B I=Va*+ B 2- •2AB Cos 0
IA - B l=^202+72-2 (20)(7)Cos 37
(A - B )
IA - B 1= 15
PROBLEMA Nfi 12
-> ->
Dados los vectores A y B mostrados
en la figura, determinar:
—
> —
►
IA - 2 B I
Si se cumple que:
I A l= 5
—
>
I B l= 3
a) 4 b) 5 c) 6
d) 8 e) 20
PROBLEMA Ne 13
Si el módulo de la suma de dos vec­
tores de igual módulo es dos veces del
*
#
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
$
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
slí
#
*
*
#
*
*
*
4
=
*
*
módulo de su diferencia, hallar el ángulo
comprendido entre dichos vectores.
SOLUCION :
Sea: A = B = x
* S2 = A2 + B2 +2AB Cos 0
S2 = 2X2 + 2x2 Cos 6
* D2 = A2 + B2- 2AB Cos 0
D2 = 2X2- 2x2. CosG
Pero:
S2 = 4D2
2X2 +2X2 Cos 6=4(2x2 - 2X2 Cos 0)
1 + Cos 0 = 4 ( 1 - Cos 0)
Cos 0 = §
o
0 = 53°
PROBLEMA Ne14
Si el módulo de la suma de dos vec­
tores de igual módulo es el triple del mó­
dulo de su diferencia. Hallar el ángulo
comprendido entre dichos vectores.
c) 45°
a) 30° b) 37°
d) 53° e) 60°
PROBLEMA N9 15
Dado el conjunto de vectores mos­
trado en la figura, determinar el módulo de
su vector resultante

44. SOLUCION :
Utilizando el método del triángulo reem­
plazamos cada par de vectores conse­
cutivos por su respectivo vector
resultante.
Entonces:
R : 2 + 4 + 6 + 8
R = 20
PROBLEMA N® 16
Determinar el módulo del vector resul­
tante de los vectores mostrados en la
figura, sabiendo que ABCD es un trape-
ció, donde: AB = 14.; DC = 22.
a) 4
b) 8
c) 16
d) 20
e) Faltan datos
PROBLEMA N9 17
Hallar el módulo de la resultante del
conjunto de vectores mostrados en la fi­
gura, si el lado de cada cuadrado pequeño
es de 1 unidad de longitud.
*
*
*
*
♦
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
■
>
$
*
*
*
*
*
*
*
*
*
*
*
s
is
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
SOLUCION :
De donde:
R = V2
PROBLEMA N®18
En la figura, determinar el módulo de
la resultante del conjunto de vectores
mostrado, si el lado de cada cuadrado
pequeño es de 2 unidades de longitud.
a) 1u
b) 2u
c) 3u
d) 4u
e) N.A.
PROBLEMA N9 19
Hallar el módulo de la resultante de los
vectores mostrados en la figura.

45. De donde: R = 5 + 5
R = 10
PROBLEMA Ns20
Hallar el módulo del vector resultante
de los tres vectores mostrados en la figu­
ra.
HafHar el vfector x en función de ios
—
» —
»
vectores A y B, sabiendo que Mes punto
medio de su respectivo lado.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
m
*
#
*
*
m
*
*
Sis
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
B + x + 2x - A
B + 3x = A
x =
A - B
G Baricentro del triángulo rectángulo
isósceles.
PROBLEMA N®22
En el paralelogramo mostrado M y N
son puntos medios de sus respectivos
lados. Hallar el vector:( x + y ) en fun-
—
» —
»
ción de los vectores A y B.
a )¿ ( A + B )
*
*
*
tjs
*
stí
*
*
*
*
*
*
í¡*
*
*
*
*
*
*
*
♦
b) A + B
3 “* Á
c ) | ( A + B ) A
PROBLEMA Ns23
Si dados los vectores A , B y C mos­
trados en la figura se cumple que:

46. A + B + C = O
Siendo:
IAI = 7
IB! =15 ; IC l= 20
Hallar los ángulos 6 y a, si 6 es agudo
y a es obtuso.
SOLUCION
Siempre que la resultante de tres vec­
tores es CERO, se cumple que el módulo
de cada uno de ellos es directamente
proporcional al seno de su ángulo
opuesto, según ésto:
A B
Sena Sen143° Sen 9
15 20
Sen a 3 /5 Sen 0
7
* Sen a =
25
a =164°
De donde:
9 =53°
* Sen 9 = —
5
PROBLEMA N924
Si la resultante de los tres vectores
mostrados es CERO, hallar el ángulo 0 si
es agudo (P = 18 ; Q - 15).
*
■
»
$
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
m
*
*
ff!
m
$
*
*
#
*
*
4
>
*
SN
*
*
*
*
*
#
*
*
#
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
«
¡í
*
*
♦
*
*
*
a) 53°
b) 60°
c) 67°
d) 75°
e) 80°
PROBLEMA N925
Si en el trapecio mostrado en la figura,
M es punto medio de su respectivo lado,
hallar el módulo de la resultante de los
dos vectores mostrados en la figura.
SOLUCION:
Descompongamos cada uno de los vec­
tores en las direcciones indicadas
De la figura es fácil darse cuenta que los
vectores oblicuos se anulan y, en con­
secuencia, resultante del conjunto de
vectores es:
R = 4 + 8
R = 12

47. Dado el paralelogramo ABCD mostra­
do en la figura, hallar el módulo del vector
resultante de los tres vectores indicados.
Donde:
a) 8
AB = 4 y BC =3,5
*
*
*
*
*
*
*
*
«
*
*
* Ry = SVy = 25
R = 25^2
PROBLEMA Ne28
Determinar el módulo del vector resul­
tante de los tres vectores en la figura si
La figura muestra un cuadrado cuyo
lado es de 10 unidades. Determinar el
módulo de la resultante de los tres vec­
tores mostrados si M y N son puntos me­
dios de sus respectivos lados.
M
*
*
*
*
*
PROBLEMA Ns29
Hallar el módulo del vector resultante
de los cuatro vectores mostrados en la
figura si: A b 2 ^ ; B = 10 ; C = 4 ;
D = 10^2
SOLUCION:
Descompongamos cada uno de los vec­
tores en sus componentes rectangulares.
M
. N
*
*
*
*
*
*
*
#
*
m
*
*
*
*
*
SOLUCION :
Rx = X Vx = A + B .Cos37° - C. Sen 60°
Rx = —
2
Ry = £Vy = B. Sen 37° + C. Cos 60° -
Ry = —
2
- D. Sen 45°
- D. Cos 45°

48. R =*I Rx + Ry
R = 2>/2
PROBLEMA Ns30
Dado el conjunto de vectores mostra­
dos en la figura, determinar el módulo de
su vector resultante, si A = 10; B = 20;
C = 6 ; D = 13.
a) 13
b) 26 V2
C)39^
" >
^ 37°
d) 52>/2 r 5 x
e) N.A.
i
PROBLEMA N® 31
Determinar la dirección del vector re­
sultante del conjunto de vectores mos­
trado en la figura.
20
45°
y
j ’
í
2 J2 x
J r
- 5/2
SOLUCION :
’ Rx = ZVX= 2 y¡2--10^2
Rx = - 8 ' 2
*
*
<
i=
*
*
*
*
*
*
s
t¡
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
m
*
*
*
*
Ry = I Vy = V 2 + 1 0 a/2 - 5 V2
R v = 6 ^ 2
De donde se deduce que:
6= 143°
PROBLEMA Ne32
Determinar la dirección del vector re­
sultante del conjunto de vectores mostra­
dos en la figura.
a)30° 10.'2u
b) 37°
c) 45° _ 4f>
d) 53°
e) 60° 10lJ
PROBLEMA N9 33
En el gráfico mostrado, hallar el valor
de A para que el vector resultante de
los tres vectores indicados esté sobre el
eje x.

49. SOLUCION:
Por condición de! problema:
*
*
$
*
*
SOLUCION:
Por condición ael problema:
Ry = ZVy = 0 *
$ Rx = Ry
*
AV3 Sen 60 + AV2 Sen 45 - 1 0 = 0
A = 4
PROBLEMA Ns34
Si el vector resultante del conjunto de
vectores mostrados está en el eje y, hallar
el ángulo 6
a) 30°
b) 37°
c) 45°
d) 53°
e) 60°
4y
y'3y
PROBLEMA Ne35
Hallar el módulo del vector A mostra­
do en la figura sabiendo que el vector
resultante del conjunto de vectores
mostrado forma 45° con el semieje posi­
tivo de las x.
(B = 4 ; C = 10nÍ2; D = 2 V3)
y
4 V
^ 6 0 °
S i l 0
^ A
2 / 3
X
1 0 / 2 " /
$
*
*
o
»
*
$
*
$
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
d
e
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
¡fs
*
*
*
*
*
*
*
*
*
*
♦
*
$
*
*
A Sen 37° +B Cos 60° - C Cos45°
á ^
^ A - 10 = f A - 8
5 5
5 A = 2
A = 10
PROBLEMA Ne36
—
>
Determinar el módulo del vector A
mostrado er> la figura, si el vector resul­
tante del conjunto de vectores indicado
forma 37° con el semieje - positivo de las
x. (B = 2 V2 , C = 7)
a) 5
y
S
/ 1
b) 10 X
c) 15 45° / 53°
d) 20
e) N.A
t
PROBLEMA N237
Determinar el módulo de la resultante
de los tres vectores mostrados en la
figura, si: A = 10 ; B = 10; C = 4'J2.
<

50. Tomemos un sistema de coordenadas
adecuado y utilicemos el procedimiento
para determinar la resultante analítica­
mente
4/2
y A
/
10 '
/
/
x , 450 a . 'S ” ' . r
i—,1
1 10
Rx = I Vx
Rx = 10 Cos 53 - 4 V2 Sen 45
Rx = 2
Ry — iV y
Ry = 10 Sen 53 + 4^2 Cos 45° - 10
Ry = 2
R = V" Rx + Ry
PROBLEMA Ne38
Determinar el módulo de la resultante
del conjunto de vectores en la figura.
*
*
*
#
*
*
*
d
e
*
$
s
ü
*
*
*
*
*
#
#
#
*
$
*
*
*
0
»
#
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
<
n
Hallar el módulo de la resultante del
conjunto de vectores mostrados en la fi­
gura.
1 ;9)
14 ; - l )
SOLUCION :
Expresemos cada uno de los vectores en
forma de par ordenado:
A = (1 ; 9)
B = (-5 ; 5)
C = (-6 ; -5)
D = ( 4 ; —
1 )
Entonces :R = A + B + C + D
R =(1; 9) + (-5; 5) + (-6; -5) + (4; -1)
R = (-6 ; 8)
I r | = V (—
G)2 + (8f
IR 1= 10
PROBLEMA Ne40
Dado el siguiente conjunto de vecto­
res:
A = (1; -2)
B = (-1 ; 2)
C = ( - 2 ; 3)
Hallar el módulo del vector:

51. E = 2A + 3B — C
a) -42 b) 2 v2 c) 3 <2
d) 4 <2 e) 5'i2
PROBLEMA NE41
Dado el conjunto de vectores mostra­
dos en la figura, determinar el módulo del
vector:
E = A - B + C - D
SOLUCION : i-_*------1
Expresando cada vector en forma de par
ordenado
A = (-1 ; 2)
B = (2 ; 2 )
C = (1 ; —
1)
D= (—
2 ;-1)
Entonces.
-4
E = A - B + C - D
E = (-1 ; 2) + (2 ; 2) -t
(1 ;-1)-(-2,-1)
E = ( 0 , 0 )
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
•
<
<
*
*
*
*
*
*
*
#
*
«
i
*
*
$
*
*
*
$
*
*
*
&
*
Si dados los vectores A, B y C mostra­
dos en la figura se cumple que:
m.A + n.B + p.C = 0
Donde m, n y p son números reales,
hallar el valor numérico de:
E =
mn
c) 3
a) 2 b) 2,5
d) 3,5 e) N.A.
PROBLEMA N®43
Dados los vectores mostrados en la
figura, determinar el módulo de su vector
resultante. El radio de la circunferencia
es de 25 unidades.
IE I = 0 *
*

52. Para utilizar el método de los componen­
tes rectangulares y trabajar con ángulos
notables, efectuemos una rotación anti­
horaria al sistema de ejes coordenados
en ángulo 5o.
Rx= IVx
Rx = 25 Cos 16o - 25 Sen 37°
Rx = 9
Ry = I Vy
Ry = 25. Sen 16° + 25 cos 37°
Ry = 27
R = V r ? + r S
R = 9 'fW
PROBLEMA Ns 44
Dado el conjunto de vectores mos­
trado, determinar el mínimo valor que
puede tomar el módulo de su resultante.
Hallar el módulo de la resultante del con­
junto de vectores mostrados en la figura
De la figura obtenemos la siguiente re­
lación vectorial:
A +~B + (-C) +~D + E +(—
F) = O
A+ B + f) + E = C + F .... (*)
Nos piden:
R = A + B + C + D + E + F
R = (A+B+D+E) + (C+F)
R = 2 (C +T)
En módulo: iR i =2 IC + F |
I RI = 2 V c 2+ F 2
ÍRI = 10
PROBLEMA Ns 46
Hallar el módulo del vector resultante
del conjunto de vectores mostrados en la
figura sabiendo que: IA I = 5u; IC I = 8u

53. Dado el conjunto de vectores mostra­
dos en la figura, determinar el módulo del
vector.
P = A —B + 2 C - 2 D
Si: |C| = 6V3
De la figura vemos que:
Á + (—
B) + C + (-D) = 0
Á - B + C -'D = 0 . . . (*)
Entonces:
P = A - B + 2C —2D
P = ( A - B + C - D ) + C - Ü
P = C —D
De la figura : ÍFl = 6^J3 Cos 30
P = !
PROBLEMA Nfi 48
Dados los vectores mostrados en la
figura, hallar el módulo del vector x, si:
*
<
¡
>
*
*
*
*
*
$
■
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
$
*
$
#
*
#
*
*
*
*
*
$
*
$
*
#
$
>
$
$
*
*
#
$
*
*
*
*
*
*
*
x = P + Q —R + S —T
SOLUCION
Donde:
a) 24 b) 48 c)30
d) 60 e) N. A.
PROBLEMA NB
49
Determinar el módulo del vector resul­
tante del conjunto de vectores mostrados
en la figura.
a/2 a/2
f, ---------------------------

54. R = af2 + a ^2
R = 2aV2
PROBLEMA Nfi 50
Determinar el módulo del vector resul­
tante de los vectores mostrados en la
figura, "a" es el lado del cubo
PROBLEMA Ne51
La figura muestra un cuadrado de
5cm. de lado. Donde el segmento CE es
tangente a la semicircunferencia en el
punto T. Escribir el vector x en función
de los vectores A y B.
Considere: Tg(53°/ 2) = 0,5
S
K
4
=
*
*
*
*
*
*
*
*
*
$
*
*
#
*
*
* *
*
m
*
, $
*
a *
, *
*
*
. *
i *
*
*
*
*
*
*
*
*
*
*
#
*
$
*
♦
a) ( B - 3A )/5 b) ( B + 3A )/5
c) ( B - 2A )/5 d)Faltan datos
e) N.A.
PROBLEMA Ne 52
-» -> -»
Encontrar x en función de A y B.
MNOP es un cuadrado.
4 Í ; _ I
5 v 2
c ) l
C) 5 2 )
e) Ninguna
b ) ^ |A
i(:
«iM
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*■
*
4
*
*
+
*
*
*
*
*
*
*
* NP : Cuadrante
PROBLEMA NB53
La figura muestra un rombo ABCD de
lado 2cm, determinar el módulo de la re­
sultante de los vectores mostrados.
Ar — /-— T —/
o0
Dl - 1 - ‘
a)^30 cm b) V5T cm c) V32 cm
d) ^40 cm e) Faltan datos.

55. CONCEPTO.
Es parte de la mecánica que estudia al
sistema de Fuerzas que actúan sobre un
cuerpo material en equilibrio.
FUERZA.
Es una magnitud física vectorial, se de­
fine como la causa de los movimientos y de
la deformación de los cuerpos.
La acción de una fuerza sobre los cuer­
pos depende de su módulo, dirección (línea
de acción), sentido y punto de aplicación.
La fuerza en el SI se mide en newtons
(abreviado N).
F = 50 newtons
F = 50 N
FUERZAS INTERNAS
Son aquellas fuerzas de origen electro­
magnético, que se manifiestan en el inte­
rior de los cuerpos flexibles y rígidos,
cuando éstos son sometidos a la acción
de fuerzas externas que tratan de defor­
marlo por alargamiento o estiramiento y
por aplastamiento o compresión. Según
ésto las fuerzas internas se clasifican en:
Tensión, compresión, torsión y fuerza
elástica.
TENSION (T)
Es aquellafuerza generada internamente
en un cuerpo (cable, soga, barras) cuan­
do tratamos de estirarla. Para graficar la
tensión se realiza previamente un corte
imaginario.
La tensión se caracteriza por apuntar al
punto de corte. Si el peso de la cuerda
es despreciable, latensión tiene el mismo
valor en todos los puntos del cuerpo.
t. __
_ -J
Corte
El bloque de peso W se encuentra en
equilibrio.
IF y = 0
T - W = 0
La tensión en la cuerda es igual al del
bloque.

56. COMPRESION (c)
Es aquella fuerza interna que se opone a
la deformación por aplastamiento de los
cuerpos rígidos.
Para graficar la compresión se realiza
previamente un corte imaginario, se
caracteriza por alejarse del punto de
corte. Si el peso del cuerpo rígido es
despreciable, la compresión es colineal
con el cuerpo y tiene el mismo valor en
todos los puntos.
CORTE IMAGINARIO
La compresión "C" se opone a la fuerza
deformadora “F“.
FUERZA ELASTICA
Es aquella fuerza interna que se mani­
fiesta en los cuerpos elásticos o defor-
mables, tales como los resortes. La fuer­
za elásiica se opone a la deformación
longitudinal por compresión o alarga­
miento, haciendo que el resorte recupere
su dimensión original.
Ley de Hooke:
" La fuerza generada en el resorte
es directamente proporcional a la
deformación longitudinal"
F = K . X
K
X :
Constante de elasticidad del
resorte, se mide en (N/m).
Deformación longitudinal,
mide en (m).
se
1) F : Como tensión
*
*
■
é
*
*
*
*
*
*
1
»
*
*
*
*
*
*
*
«I
*
«
S
í
*
*
*
*
*
*
*
*
#
■*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
s
ts
*
*
*
*
*
*
«
ft
*
■
*
*
*
*
*
*
*
*
*
*
*
*
Diagrama de fuerzas sobre el bloque:
F = KX
E1
V J
2) F: Como Compresión
Diagrama de fuerzas sobre el bloque:

57. LEYES DE NEWTON
lera. Principio de Inercia
"Todo cuerpo material permanece en re­
poso relativo o se mueve con velocidadcons­
tante en línea recta, si sobre él actúa una
fuerza resultante igual a cero"
V
Ejemplo: Desde una nave cósmica que
se mueve con velocidad V=500 m/s, se
abandona un objeto. Si la nave se en­
cuentra en una zona de ingravidez, ace­
leración de la gravedad igual a cero, en­
tonces la nave y el objeto marchan para­
lelamente con la misma velocidad.
2da. Ley de Aceleración
"Todo punto material sometido a la ac­
ción de una fuerza resultante diferente de
cero, adquiere necesariamente una acele­
ración en la misma dirección y sentido de la
fuerza resultante, elmódulo de la aceleración
es directamente proporcional a la fuerza re­
sultante e inversamente proporcional a su
inercia (masa)".
Aceleración =
Fuerza Resultante
masa
Ejemplo: Un cuerpo en caída libre ace­
lera en virtud a la fuerza resultante (peso)
que ejerce la tierra sobre el cuerpo, el
peso y la aceleración de la gravedad
tienen la misma dirección y sentido.
T ierra
i r
$
*
*
*
*
*
*
*
*
$
4
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
3
*
*
*
*
*
*
*
3era. Principio de Acción y Reacción
"Cuando dos cuerpos A y B interactúan,
a la acción de A se opone una reacción de
B, en la misma dirección, con la misma inten­
sidad, pero en sentido opuesto".
Acción + Reacción =0
Ejemplo: En la figura mostrada, el bloque
A se encuentra apoyado sobre una su­
perficie horizontal B.
II*.. .....
(B)
OBSERVACIONES:
1) Para graficar las fuerzas de acción
y reacción, se realiza previamente
una separación imaginaria de los
cuerpos.
2) Si las superficies en contacto son
lisas, entonces las fuerzas de reac­
ción son perpendiculares a las su­
perficies.
3) Las fuerzas de acción y reacción
actúan en cuerpos diferentes.
□
B/A
SEPARACION^
I M A G I N A R I A
A/B
R A/B = R B/A

58. Diagrama del Cuerpo Libre (D.C.L.)
Consiste en aislar imaginariamente un
cuerpo o parte del sistema mecánico en
estudio, donde se grafican todas las fuer­
zas externas que actúan sobre la parte
aislada. Las fuerzas internas, ai sistema
físico en estudio, no se grafican.
1) D.C.L. de la polea central.
i
T i: tensión en la cuerda "1"
T2: tensión en ia cuerda "2"
W: peso de la polea central.
2) D.C.L (bloque de peso Q)
1
3) D.C.L (bloque + cuerda *1" + polea
central).
S I S T E M A
F I S I C O
W + Q :ío so Total
Nota : La tensión en la cuerda (t) no se
dibuja porque pasa a ser una fuerza in­
terna, al sistema físico elegido.
lera. CONDICION DE EQUILIBRIO
(Equilibrio de Traslación)
Un punto material o cuerpo rígido, per­
manece en reposo relativo o se mueve con
velocidad constante en Línea recta, si la
fuerza resultante que actúa sobre él es igual
a cero. El reposo, es un estado particular del
movimiento.
* E Fx = 0
* ZFy= 0
El sistema de fuerzas, que actúan sobre
el cuerpo en equilibrio de traslación, deben
formar un polígono cerrado

59. ( PROBLEMAS >
PROBLEMA N« 1.
La figura muestra un bloque de peso
W = 10N, en equilibrio. Si el peso de cada
polea es P ~2N, determinar la lectura en el
dinamómetro “D” instalado en el cable.
La lectura en el dinamómetro, indica la
tensión en la cuerda, que se transmite a
lo largo de la cuerda
D.C.L (Poiea móvil):
T T
O
SFy = 0 2T = P + W
Reemplazando:
T = 6 N
PROBLEMA N®2.
Los bloques A y B se encuentran en
equilibrio en la posición mostrada. Si se
retira lentamente el bloque A de peso 20N,
¿Qué distancia ascenderá el bloque B?
Constante elástica del resorte.
N
K = 100
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
ü
¡
>
*
*
*
$
*
*
*
$
o
*
*
¿
ti
$
*
*
4»
*
*
*
*
#
♦
*
*
*
*
$
*
*
*
*
♦
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
$
*
*
SOLUCION :
El peso del bloque A, produce una defor­
mación "x" en el resorte.
Ley de Hooke:
F = K. X 20 N = 100 — . (X)
m
X = 0,2m
Luego:
Al retirar el bloque A, el bloque
B ascenderá 20 cm
PROBLEMA NB3
Se tiene un sistema de dos bloques
como muestra la figura. El peso del blo­
que A, excede al peso del bloque B en 6N.
Determinar la fuerza de Reacción en­
tre los bloques A y B.
SOLUCION:
1) D.C.L. (A + B)
A

60. II
' .
■- - ----------
W
A + W
B
ZFy = 0
4T = Wa + Wb
Wa + Wb
T = •
4
2) D.C.L (bloque a)
ZFy = 0
R + 2 T = WA - . ( 2)
Reemplazando (1) en (2):
R =
Del dato:
Wa - W b
R = 3N
*
*
*
*
*
*
*
«*
*
*
*
*
*
*
«
¡
=
*
*
PROBLEMA Ne4
La figura muestra una esfera de radio
"r" y peso W = 6 N, apoyado en una super­
ficie cilindrica de radio de curvatura "R“.
Hallar la reacción sobre la esfera en el
punto A, sabiendo que R = 3r.
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
5
*
*
m
*
*
*
*
*
*
SOLUCION:
D.C.L. (esfera)
>j
Ra W
Ra = 23 N

61. La figura muestra dos esferas A y B de
pesos 6 N y 2 N respectivamente, en equi­
librio. Determinar la reacción de la pared
lisa sobre la esfera B y la tensión en la
cuerda.
*
*
*
*
*
*
*
*-
*
$
*
*
s
i»
*
*
*
a
te
*
"Si tres fuerzas coplanares actúan sobre
un cuerpo en equilibrio, estas necesariamen­
te son concurrentes El módulo de cada
fuerza es directamente proporcional al seno
del ángulo opuesto".
SOLUCION
1) D.C.L. (A + B)
2) Formando el polígono cerrado:
*
*
*
*
*
*
*
*
*
*
*
*
*
m
$
*
*
*
*
*
*
*
*
*
*
*
#
*
Fi f 2 P3 |
Sen a Sen |i Sen y 1
Polígono Cerrado- Fuerza Resultante
igual a cero.
La relación anterior se obtiene, aplicando
la Ley de Senos, al triángulo de fuerzas.

62. Si, a = P = y = 120°
Entonces:____
Fi = F2 = F3
SOLUCION:
Diagrama del cuerpo libre del Nudo "O".
Teorema de Lamy:
W Ti
Sen 90° Sen 150°
W 40 N
1
W = 80 N
*
*
*
*
*
*
PROBLEMA Nfi 6
En el sistema mecánico mostrado, la
tensión en la cuerda (1) es de 40 N, deter­
minar el peso del bloque.
Determinar la reacción que ejerce el
plano inclinado sobre la esfera de peso
20 N. No hay fricción.
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION :
Diagrama de fuerzas sobre la esfera:
Teorema de Lamy:
R W
Sen (90 + 0) Sen (90 + 0)
R = W
R = 20 N
PROBLEMA Nc 8
Un bloque se encuentra sostenido co­
mo muestra la figura. Calcular la medida
del ángulo " 6 ”, para el cual la tensión en
la cuerda “1" resulte ser mínima.

63. SOLUCION
D.C.L. (del nudo)
Teorema de Lamy:
T i W
Sen150° Sen (1 2 0 - 6)
T 2W
Ti =
e = 30°
*
*
*
*
Sen (1 2 0 -0 )
T1t será mínima, cuando la función Seno
tome su máximo valor, es decir igual a la
unidad.
Sen (120o- 0) = 1
Entonces: 12O °-0 = 9O°
Luego:
PROBLEMA Ne9
Sí la reacción en "A" de la pared lisa
sobre la barra es de 5 newtons y la barra
uniforme y homogénea AB pesa 12 new­
tons. Hallar la magnitud de la fuerza hori­
zontal "F” que mantiene en equilibrio a la
barra.
*
♦
*
*
m
*
»
*
SOLUCION .
Diagrama de cuerpo líbre, de la barra.
Equilibrio de Traslación: Fuerza resul­
tante igual a cero.
Teorema de Pitágoras:
F2 = W2 + N2
F2 = 144 + 25
F = 13 N

64. Una barra homogénea de longitud L =
2m se apoya en una pared vertical y una
superficie cilindrica de radio R = V7 m.
Hallar “ 8 No hay fricción.
L Serv
I
+
En el A ACO, P es punto medio, por con­
siguiente:
OB = BC = L. Sen 0 .. (1)
Teorema de Pitágoras en el á ACO.
R2 = (L Cos O)2 + (2 L Sen fl)2
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Del teorema de Lamy, las tres fuerzas
concurren en el punto "P“.
o
L Sen
Sen 6 = 2
t í
0 = 30°
MOMENTO DE UNA FUERZA
r z a |
CONCEPTO.
La experiencia muestra que un cuerpo
rígido sometido a la acción de una fuerza,
además de trasladarse, puede girar alrede^
dor de un punto. El efecto rotatorio de una
fuerza se caracteriza por su momento.
*
*
*
$
*
«
i*
*
*
*
*
El momento de una fuerza, es una mag­
nitud física vectorial y tiene los siguientes
elementos:
t) Módulo: La medida cuantitativa del
efecto rotatorio, es igual al producto de la
fuerza, por la distancia trazado desde el
centro de giro, perpendicularmente a la
línea de acción de la fuerza.
M6= F. d.
R2 = L2 Cos2 0 + L2. Sen2 0 +
+ 3 L2. Sen2 0
R2 = L2 + 3. L2. Sen2 0
Sen2 0 = - — y ~
3L
*
*
*
*
*
2)
"Momento de la fuerza F respecto al
centro O"
Unidades: N.m
Dirección: Es perpendicular al plano de
rotación, determinado por la línea de ac­
ción de la fuerza y el centro de giro.

65. 3) Sentido: Se determina aplicando el mé­
todo de la mano derecha, los dedos indi­
can el sentido de giro y el pulgar el
sentido del vector momento. Tiene la
misma dirección y sentido, de la veloci­
dad angular.
SIGNOS
El momento es positivo si el giro es anti­
horario y negativo si el giro es horario.
,F
M
( + )
" 7
/
r~ ~~7
/ r r > / /
L ____ L ____
( - )
(ANTIHORARIO)
PROPIEDADES:
(HORARIO)
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
1) El momento de una fuerza no varía
cuando el punto de aplicación de ésta se
traslada a lo largo de su línea de acción.
2) El momento de una fuerza con respecto
al centro "O" es igual a cero, solamente
cuando la fuerza es igual a cero o cuando
la línea de acción de la fuerza pasa por
el centro de giro "O" (el brazo es cero).
3) El módulo del momento de una fuerza se
expresa numéricamente por el doble del
área del triángulo OAB
= 2.área (OAB)
Si, Area (OAB) = ^ vAB).d
Luego:
donde:
= (AB).d
AB = F = magnitud
2da. CONDICION DE EQUILIBRIO
"Todo cuerpo rígido sometido a la acción
de un sistema de fuerzas no gira, si la suma-
toria de momentos con respecto a cualquier
punto es igual a cero'.
I M = 0
EQUILIBRIO DE UN CUERPO RIGIDO
Cuando las fuerzas están actuando so­
bre un cuerpo rígido, es necesario considerar
el equilibrio en relación tanto a la traslación
como a la rotación. Por tanto se requieren
las condiciones siguientes:
1 ) P rim era cond ició n (E q u ilib rio de
traslación): La suma de todas las fuerzas
debe ser cero.
I F x= 0 y
2) Segunda condición (Equilibrio Ro­
tacional): La suma de momentos con res­
pecto a cualquier punto debe ser cero.
PROBLEMA ^ 01
La barra quebrada en forma de "L", es
homogénea de peso "3W“. Determinar
la magnitud de la fuerza "F“ , para man­
tener el segmento BC en posición verti­
cal. BC = 2. AB .
SOLUCION :
El peso de los lados AB y BC, son propor­
cionales a su longitud respectiva.
*
*
*
*
*
*
*
*
*
*
*
#
*
2L
C t
L

66. Diagrama de fuerza sobre la barra. *
$
*
Equilibrio de Rotación
I M a = 0
m f m W . ..2W
MA = M A + M A
F.L = W . | + 2W . L
F = f W
SOLUCION:
Diagrama de Fuerzas, sobre la barra.
PROBLEMA Ne02
Si la barra homogénea que muestra la
figura tiene un peso de 80N, hallar la
tensión en la cuerda. Los ángulos a y p son
complementarios.
*
*
*
*
$
*
*
*
$
*
*
*
*
*
#
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
$
f
*
*
£ M a = 0
mt mw
m a = m a
T. (2 L Sen P) = W. (L Cos a)
T = 40 N
CONCEPTOS ADICIONALES
1) SISTEMA FISICO:
Es el cuerpo o conjunto de partículas
consideradas en estudio, elegido en
forma arbitraria.
I./*-
(1)

67. La figura (1) muestra una esfera de peso
w, y un bloque de peso w2 unidos me­
diante una cuerda de peso despreciable.
Elegimos nuestro sistema físico:
(esfera + cuerda + bloque).
2) FUERZA EXTERNA AL SISTEMA :
Es aquella fuerza que actúa sobre el
sistema con cuerpos o partículas exter­
nas al sistema.
En la figura (2) se indica las fuerzas ex­
ternas al sistema físico elegido, ellos
son: Los pesos w1 y w2, la tensión en la
cuerda (T1) que une la esfera con la viga.
3) FUERZA INTERNA AL SISTEMA :
Es aquella fuerza debido a la interacción
de cuerpos o partículas considerados
dentro del sistema físico. La sumatoria
de todas las fuerzas internas siempre es
igual a CERO.
La figura (3) muestra la fuerza interna (T)
al sistema físíco elegido.
4) SISTEMA AISLADO :
Es aquel sistema físico cuya resultante,
de fuerzas externas, es igual a CERO.
Ejemplo: Consideramos nuestro sis­
tema físico al planeta tierra
más su satélite LA LUNA co­
mo muestra la figura:
1) La fuerza "F , debido a la intersec­
ción entre la tierra y la luna, es la
tuerza interna al sistema físico en
eStud¡0- LUNA
T r
Tierra
bol
2)
*
*
*
*
*
*
*
*
*
*
*
*
£
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
o
s
*
*
*
*
*
*
*
*
*
*
*
*
Sistema Físico *
La fuerza “F2", debido a la interac­
ción entre la Tierra y el Sol es una
fuerza externa al sistema físico en
estudio.
La figura muestra una estructura en for­
ma de “T" de peso despreciable En los
extremos de la estructura se encuentran sol­
dados dos esferas de pesos 14N y 17N res­
pectivamente. Determinar el valor del án­
gulo ' 0 " que define la posición de equilibrio.
*
*
*
*
*
*
*
*
Realizamos el diagrama del cuerpo libre,
del sistema físíco (estructura + esferas).
Z M0 = 0 M 14N = M 17N
O O
14.a(Cos 0 - Sen 0)=17. (2a. Sen 0)
7 Cos 0 - 7 Sen 0 = 17 Sen 0
7 Cos 0 = 24 Sen 0
7
Tg 0 =
24
0 = 16°

68. • A ► .....^
4 ROZAM IENTO
CONCEPTO
La figura (1) muestra un bloque de peso
“W" sobre una superficie plana horizontal y
rugoso, al cual se le apiica una fuerza externa
F variable desde cero hasta un valor máximo
cuando el bloque se encuentra en movimien­
to inminente (pronto a moverse).
Cuando realizamos el diagrama del
cuerpo libre del bloque, la fuerza de reacción
"R" ya no es perpendicular a la superficie en
contacto, como ocurría con las superficies
lisas (ideales), sino que esta fuerza es obli­
cua respecto al plano en contacto.
Al ángulo “ 0 “ de desviación que experi­
menta la reacción “R" respecto a la normal o
perpendicular al plano, se le llama "ángulo de
rozamiento".
A medida que la fuerza externa aumenta
su valor, el ángulo 1
1 0 “ también incrementa
su valor, siendo máximo cuando el bloque
está pronto a moverse.
Respecto a la figura (2), la fuerza de
reacción "R" que ofrece la superficie sobre el
bloque, se puede descomponer en función
de dos fuerzas mutuamente perpendicula­
res, una componente perpendicular a la su­
perficie en contacto llamada "Reacción Nor­
mal" denotado con la letra ”N,r y la otra com­
ponente tangencial a la superficie en con­
tacto llamada “fuerza de rozamiento".
Por consiguiente la "fuerza de rozamien­
to" es un componente de la reacción “R",
tangente a la superficie en contacto.
La fuerza de rozamiento por deslizamien­
to se debe a la interacción entre las molécu­
las de los dos cuerpos en contacto.
COEFICIENTE DE ROZAMIENTO^)
Es aquella magnitud adimensional que -
se define como la tangente trigonométrica
del ángulo máximo de rozamiento
De la figura (2):
H = Tg0 = ~ ,...(1)
Leyes de Rozamiento p or Deslizamiento
lera. Ley: o
"La fuerza de rozamiento se opone
al movimiento o posible movimiento rela­
tivo del cuerpo respecto a la superficie en
contacto".
2da. Ley:
"La fuerza de rozamiento es direc­
tamente proporcional a la reacción nor­
mal’1
. De la ecuación (1):
3ra. L ey:
"El módulo de la fuerza de rozamiento
es independíente del tamaño de las su­
perficies en contacto”.
CLASES DE ROZAMIENTO
Rozamiento Estático (f s)
Es aquella fuerza de rozamiento que se
opone al posible movimiento relativo del
cuerpo respecto a la superficie en con­
tacto. Su módulo es variable, desde cero
hasta un valor máximo, cuando el cuerpo

69. se encuentra en movimiento inminente
(pronto a moverse).
0 < f < fs .... (1 )
Cuando el cuerpo está pronto a moverse,
se cumple que:
f s = H s ■N I .... (2)
|j$ = coeficiente de rozamiento
estático.
Tangente del ángulo " 6 ” máximo.
fs = fuerza de rozamiento estático max.
Rozamiento Cinético (f k)
Es aquella fuerza de rozamiento que se
opone al movimiento relativo del cuerpo
respecto a la superficie en contacto
Para movimientos lentos y uniformes su
módulo se considera constante.
fk = Uk- N .... (3)
|ik : coeficiente de rozamiento cinético
OBSERVACIONES :
I) Experimentalmente se demuestra
que la fuerza de rozamiento cinético
es menor que la fuerza de rozamiento
estático máximo, por consiguiente el
coeficiente de rozamiento cinético es
menor que el coeficiente de roza­
miento estático.
Si, f k < f s
Entonces: n k < H s —■(4)
II) La fuerza de rozamiento por desli­
zamiento puede disminuir debido, a la
humedad, calor, aceites, grasas y en
general cualquier lubricante.
GRAFICA DE LA FUERZA DE ROZA­
MIENTO VERSUS LA FUERZA EXTERNA:
La figura muestra un bloque de peso
"W “, sobre un plano horizontal rugoso, el
cual es sometido a la acción de una Fuerza
Externa variable desde cero hasta un valor
máximo, cuando el bloque se encuentra en
movimiento.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
♦
*
*
*
&
*
*
*
*
*
*
*
*
$
*
w
—
I F (ext.)
U J .
i
N
I e
R
~
Donde: 1
F (ext.) = 0; 1; 2; 3; 4; 5; .... n, (N)
f = fuerza de rozamiento, variable
6 = ángulo de rozamiento, variable.
R = reacción de la superficie.
De la condición de equilibrio, la fuerza de
rozamiento estático, (f) tiene el mismo valor
de la fuerza externa hasta cuando el bloque
se encuentra todavía en reposo relativo
La fuerza de rozamiento estático es
máximo cuando el cuerpo está pronto a mo­
verse.
Cuando el cuerpo logra moverse por ac­
ción de la fuerza externa, la fuerza de roza­
miento disminuye y se hace constante el
módulo, como indica la figura.
f fuerza de rozamiento
F(ext.}
TEOREMA DE VARIGNON
*
*
*
*
*
*
*
P Varignon (1 654 - 1 722) es un desta­
cado científico francés, matemático y me­
cánico. En su libro "Proyecto de una
Mecánica Nueva” (1687) explicó los funda­
mentos de la Estática.

70. Sistema Real
*
*
*
*
*
*
*
*>
*
*
*
*
■*
*
*
*
*
*
*
*
*
*
*
*
*
Sistema Equivalente
"El momento producido por la fuerza re­
sultante de un sistema de fuerzas res­
pecto de un punto dado, es igual a la
suma de los momentos de las fuerzas
con respecto al mismo punto”.
1 ) Cálculo del momento resultante
respecto del punto “O”, en el sistema
real.
Y , Mo = Mo' + Mo?+ Mo3 +.... Mf " .... (1)
En la sumatoria de momentos se ten­
drá en cuenta los signos:
2) Cálculo del momento producido por la
fuerza resultante respecto del punto
"0", en el sistema equivalente.
La fuerza resultante será:
F r = Fi + F2 + F3 +.... Fn .... (2)
3) Luego, el momento producido por la
luerza resultante.
MÜR= FR .d ....(3)
donde, "d” es el brazo o distancia de
la fuerza resultante.
4) De la condición (hipótesis) las ecua­
ciones (1) y (3) son equivalentes.
Mo1 + M02+ Mo-
*+ + M0° —
MoR - (4)
5) De otro modo:
Mo = Fr . d ... (5)
6) El brazo de la fuerza resultante será
X Mo
d = -
Fr
d =
Sumatoria de M om entos
Fuerza resultante
*
♦
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
PROBLEMA Ns 1
La figura muestra una barra ingrávida
AB, de longitud 2,5 m. ¿A qué distancia
del punto “A", se encuentra aplicando la
fuerza resultante?
80N
2.5m
¿ÜN
SOLUCION :
Cálculo del momento resultante, respec­
to del punto "A".
M a = - 50 N. m
( - ) : giro horario
Cálculo de la fuerza resultante
F r =100 N
Teorema de Varignon:

71. F
R
M * = M a
- Fr , d = M a
-(100N) x = —50 N.m
, X
f- — -r-
A B
100N
x = 0,5 m
PROBLEMA NB2
¿A qué distancia de “B" se debe colo­
car ei apoyo fijo para que la barra de peso
despreciable y 3m de longitud, permanez­
ca en equilibrio. Poleas ingrávidas.
« W t= 4 N y W2 =10N
SOLUCION :
1 ) D C.L. de la barra AB.
(3-X)
D
B 6N
2N
•V ,
8N
Equilibrio de Rotación.
£ M o = 0 lA p7 -
2N en
M o = M o
2N (3 - x ) = 8N(x)
x = 0,6
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
$
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
2) Aplicando el Teorema de Varignon:
Cálculo del momento resultante, sin
considerar a la reacción en el apoyo.
M B= 6 N.m .... (1)
Cálculo de la fuerza resultante en el
eje y .
Fy = 10 N
La fuerza resultante en el eje V , no
produce momento respecto de "B“.
M e = £ Mb
Fy.(x) = Z M b
Reemplazando
10N (x) = 6 N*m
x = 0,6 m
I) Para calcular V :
F
* I
II) Para calcular "d"
CONCEPTO.
Se denomina así a dos fuerzas paralelas
de magnitudes iguales pero sentidos opues­
tos que actúan sobre un mismo cuerpo.
SISTEMA (1)
[

72. SISTEMA (2)
El momento producido por la cupla o par
de fuerzas.
M = cupla = F d ....(1)
La fuerza resultante de una cupla es Iguai
a cero, esto quiere decir que no produce
traslación del cuerpo rígido, sólo produce
rotación o giro.
I F r = 0
£ M * 0
El momento producido por una cupla es
el mismo respecto a cualquier punto, como
se puede comprobar en el sistema (2)
Calculamos el momento producido por la
cupla respecto de un punto arbitrario "O"
M = L Mo = F.x + F.y = F (x+y) ....(2)
pero de la figura: x + y = d ....... (3)
Reemplazando (3) en (2):
M = F. d .... (4)
La cupla produce un momento en sentido
antihorario (+) en este caso.
PROBLEMA Ns 1
Reemplazar el PAR de fuerzas mos­
trado en la figura, por otro equivalente, de
tal manera que las fuerzas que la generan
también estén aplicadas en A y B, pero
sean de módulo mínimo.
*
*
*
*
*
$
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
El momento producido por el nuevo “par"
es 45 N.m, es decir *
/
sro.
En (1):
r. d = 45
F. d:
Pero, d = (5) Sen G
9
Sen 6
.... (2)
Analizando la Ec. (2), F será (mínimo),
cuando la función Sen 6 es máximo:
Sen G= 1 6 = 90®
Reemplazando en (2):
F (mínimo) —9 N
PROBLEMA NB2
Una palanca está doblada de tal modo
que sus íados AB, BC y CO son iguales y
forman entre sí ángulos rectos (Ver fig.).
El eje de la palanca AB está en el punto
“B“. Una fuerza P esta aplicada en el

73. punto “A" perpendicularmente al brazo de
la palanca AB. Determinar el valor
mínimo de la fuerza que es necesario apli­
car en el punto "D", para que la palanca
se encuentre en equilibrio. El peso de la
palanca es despreciable.
cla
SOLUCION :
Suma de momentos, respecto de B, igual
a cero.
i- i-
Mb = Mb
F.d = P.a ....(1)
Pero: d = a 2 . Sen G
p 2
En (1) F = —
——
— - ....(2)
2 .(Sen 0)
i
l
B /
Analizando la Ec. (2), *F” será mínimo,
cuando, “Sen 0” sea máximo, es decir la
unidad
En (2):
V2"
F (mín) - P g
$CENTRO DE GRAVEDAD
CONCEPTO.
Es aquel punto geométrico ubicado den­
tro o fuera de un cuerpo, por el cual pasa la
línea de acción de la fuerza resultante, de las
fuerzas de gravedad que actúan sobre cada
una de las partículas que forman el cuerpo.

74. 3)
PESO (W) es una magnitud vectorial.
Se define como lafuerza resultante que
ejerce la tierra sobre los cuerpos que lo
rodean, se representa por un vector
que indica en todo instante al centro de
la tierra.
Peso = m.g (1)
2)
4)
El centro de gravedad (G) puede ser
considerado como el punto donde está
concentrado el peso de un cuerpo, y
sobre el cual se debe aplicar una fuerza
numéricamente igual al peso para es­
tablecer el equilibrio.
Respecto de la figuras (1), (2) y (3),
cuando sesostiene un cuerpodepuntos
diferentes, se puede notar que el centro
de gravedad se localiza debajo del
punto de suspensión. Si se prolongan
las líneas de suspensión vemos que
éstas se cortan en el punto donde se
encuentra el centro de gravedad (G) del
cuerpo.
Para un cuerpo constituido por "n”
componentes cuyos centros de gra­
vedad están determinados, el centro
de gravedad del sistema se deter­
mina aplicando el Teorem a de
Varignon, respecto de un sistema de
coordenadas.
W = W i + W2 + W3
5) Teorema de Varignon, respecto de!
eje "Y".
*
*
*
«
*
*
*
*
*
*
$
«
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
W .X =Wt X1+W2. X2 +W3 . X3
_ Wi.X1 + W2-X2 + W3-X3
W i + W2 + W3
x : abscisa del centro de gravedad
Teorema de Varignon, respecto del
eje “ x "
W.g = W 1.Y1 + W2.Y2 + W3.Y3
W 1-Y1 +W &Y2 + W 3 Y3
W1 +W 2 + W3 }
Y : ordenada del centro de
gravedad *
6) Para cuerpos linealmente homogé­
neos, como muestra la figura (4), el
peso se puede escribir en función de
su longitud. El peso es directamente
proporcional a su longitud.
W i = K. L1 ; W2 = K.L2 ; W3 = K.L3
Reemplazando en las ecuaciones (2)
y (3)
L1 .X 1 + L 2 .X 2 + L3 .X 3
x = --------- :------:------:------------ ... (4)
Y =
L| H 1-2 + L3
Li .Y i+ I- 2 . Y2 + L3.Y3
L| + L2 + L3
7) Para cuerpos superficialmente homo­
géneos (densidad constante e igual
espesor), el peso es directamente
proporcional al área.
W1 =K. Ai, W2 = K. A2 , W3 = K. A3
Reemplazando en las ecuaciones (2)
y O)
_ Al .X i+ A a -X g f A3.X3
A1 + A 2 + A3
Y_ A i ■Yi+ A2 ■V A3 ■Y3
A i + A2 + A3
8) Para un sistema de cuerpos de igual
específico.
Peso =Peso específico x volumen

75. W, = K.V1 , W2 = K V2 , W3 = K V3
Reemplazando en las ecuaciones (3)
y (2).
v _ Vi . Xi s
- Vg . Xgj- V3 X3 /m
V
!+v2+v3 "A
b}
w Vi .Y 1+ V 2 . Y2+ V 3 . y3
Y =-------- ------ —
-----:----------- ...(9)
Vi + V2 + V3
£L
CENTRO DE MASA
CONCEPTO.
Es aquel punto geométrico donde se con­
sidera concentrado la masa de un sistema de
partículas. Aplicando el Teorem a de
Varignon se puede hallar la posición del cen­
tro de masa respecto de un sistema de coor­
denadas.
¡i 'I „
t
: I I 1
*
*
*
*
*
*
*
*
#
*
Ü
S
*
*
*
Sistema real
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
1) La posición del centro de masas
(C.M) está definido por las coorde­
nadas (x,y)
2) De las ecuaciones (2) y (3), además:
Peso = m.g
X = 1711 ~Xl r m g -X 2 '
~m 3 ■
*3 ,1qj
mi + m2 + m3
y = mi . Yi+ m2 . Y2+ m3 ■Y3
mi + m2 + ms
3) Las fórmulas (10) y (11) se puede
generalizar para un sistema de “n"
partículas.
* 4) En general:
Zm¡
*
*
*
Ü
s
*
*
*
*
*
*
*
*
3Ü
*
*
*
*

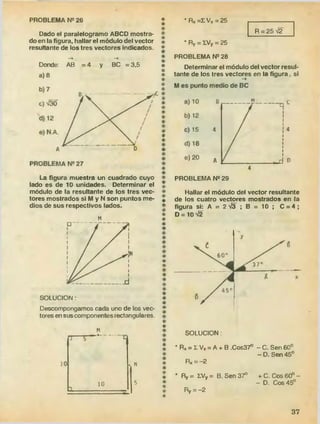
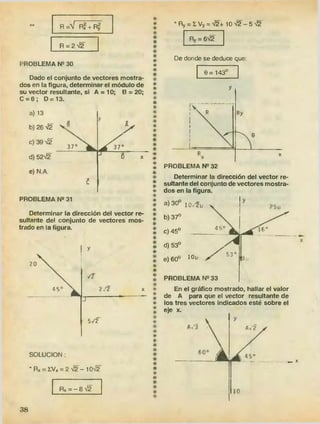
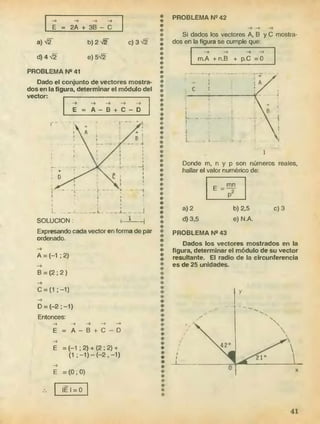
76. NOMBRE FIGURA X 7
Triángulo h r
g
^ c : 1 —
^ n. y
h
3
Cuarto de Circun­
ferencia
1 « > •
2R
K
2R
n
Semi­
circunferencia
0 2R
k
Cuarto de
Círculo
B ‘ « - Y . / - * ■
* ; M iT ( ■ ■ i
L j " 8
?
4 R
3 rc
4 R
3 ’ 7t
Semi­
círculo
0 4 R
3 ' 7
T
Arco de
Circunferencia
r/ V b
Á G ] X b G I
j * Ñ r — '
! x L x X '
R . Sen 0
e
0
Sector
Circular
2R.Sen 0
30
0

78. c
- ______ _— __
PROBLEMRS RESUELTOS
PROBLEMA N® 1
En los vértices de un cuadrado de lado
2r. se han colocado cuatro partículas pun-
tu i es. Determinar el centro de masa (CM),
respecto del sistema de coordenadas.
Sea:
mi = 1 kg
ma = 3 kg
nri2 = 2 kg
m4 = 4 kg
Consideremos laposición : r =(X ; Y)
ri = (0 ;2) r2 = (2 ;2)
r3 = (2;0) r4 = (0 ;0)
Xi.m i +Xa.m2 + X31T13 + X4rru
X = -
X =
rn1 + rr¡2 + m3 + m4
(0)( 1) + (2)(2) + (2)(3)+ (0)t4)
1 + 2 + 3 + 4
.... (1)
X = 1,0m
Y=
Y =
Yi . m i+ Y2 m?+ Y3 . rri3+ Y4 . m4
mi + m2 + m3 + m4
2(1) + 2(2) + (0)(3) + (0)(4)
1 + 2 + 3 + 4
.... (2)
Y = 0,6 m
Luego: C,M = (1,0 ; 0,6)
*
*
«
H
*
*
PROBLEMA Ne 2
Hallar el centro de gravedad del alam­
bre mostrado en la figura, con respecto al
sistema de coordenadas que se indica.
Considere conocido *R".
«
■
*
*
*
>
S
í
♦
*
*
*
*
*
*
*
*
*
0
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
1
Dividimos el alambre en tres longitudes
de semicircunferencias:
Li = n R L2 = L3 = n.
G1 = (R ; —— )
7t
- fR . R'l , _ (3 _ . R1
• ° 3’ 2 R ,_ 7 j
- X1 L1 + X 2 .L 2 + X3 .L 3
X = —
L1 + L2 + L3
R(nR) +
X = -
(B lf—
2 2
V /
3RYnR^
2 2
R + itR
... (1)
Y =
'tiR')
J í
^ -r YjiR
2 n R
y = - r-
71
-i

79. El centro de gravedad estará ubicado en $
PROBLEMA Nfi 3
Hallar el centro de gravedad, de la
figura sombreada , siendo R = 36 cm y
r = 18 cm.
Y =~
n (R2—r2)
Y = 30 cm
El centro de gravedad será:
G = (36 ; 30) cm.
*
*
i
Por simetría de la figura, la absisa del
centro de gravedad estará en:
X = R = 36 cm.
Consideremos como área total el circulo
de radio (R) y el área por restar el círculo
de radio (r)
Ai = ji. R2 ; A2 = n. r2
Gi = (R ;R) ; G2 (R ; R+ r)
Yt . Ai - Y2 . A2
A 1 - A 2
Reemplazando:
R (71. R2) - (R + r) (7t r2)
PROBLEMA Ns4
En un cilindro de radio “R" y altura “H"
se realiza una perforación cónica. El
cono tiene su base en la parte superior del
cilindro y su vértice cae en el centro
geométrico de la base del cilindro. Deter­
minar el centro de gravedad del cuerpo
que queda.
*
*
*
*
*
$
*
*
*
*
$
*
*
*
*
*
*
*
*
*
$
*
*
*
&
*
*
*
*
$
*
*
*
SOLUCION .
Consideremos el cilindro como el cuerpo
total (1) y el cono como el volumen (2)
que tenemos que restar.
Vi= 71. R2 , H ; V2= ~ 71 R2 . H
O
Gi= (0 ; H/2) ; G2= (0; 3H/4)
Por simetría de la figura, el centro de
gravedad estará en el eje del cilindro.
Y =
Yi .V i- Y a .V z
V1 - V 2
Y—
(H/2)(7i R2 H) - (3H/4)(7t R2 H/3)
2 k R2 H /3
y=i H
El centro de gravedad se encuentra a una
altura 3 H/8, respecto de la base, del
cuerpo resultante.
PROBLEMA NB5
La figura (1) muestra una lámina ho­
mogénea (densidad constante) ABC de
forma triangular. Sabiendo que el lado
AB permanece en posición horizontal (m.
AB = 20 cm), hallar el valor de " m.AP ”

80. P : es el punto donde está atado la
cuerda vertical.
SOLUCION :
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
, luego: x = 2cm _(1)
El centro de gravedad de una lámina
homogénea de forma triangular se en­
cuentra en el baricentro del triángulo,
esto quiere decir en la intersección de las
medianas.
Del diagrama del cuerpo libre, la tensión
(T) y el peso (W), son vectores opuestos,
tienen igual magnitud y dirección, pero
sentidos opuestos. Por consiguiente la
línea de acción de la tensión pasa por el
"centro de gravedad", en la posición de
equilibrio.
Por semejanza de triángulos:
AMPG ~ AMQC
x + 4 3a
M es el punto medio del segmento AB
luego: m.AM = 10 cm
De la figura: Z = m.AM + x .... (2)
Reemplazando datos en (2):
Z = 10 cm + 2 cm
m. AP = 12 cm
PROBLEMA Ne6
La figura muestra un cono recto de
altura 40 cm y radio 20 cm, suspendido
desde el punto P.
Si P es punto medio del radio, determi­
nar el ángulo " tí “ que forme el eje del
cilindro con la vertical.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
En la posición de equilibrio, el peso (W) y
la Tensión (T), son colineales, por con­
siguiente los puntos P y G, se encuentran
en la misma vertical.
Del dato:
OP = 10 cm
OG = ^ (h )= 10 cm

81. 6 = 45°
PROBLEMA Nfi 7
Una semiesfera de 16 newtons de peso
se encuentra apoyada sobre una pared
vertical lisa. Determinar la fuerza de reac­
ción normal de la pared sobre la semies­
fera.
G : centro de gravedad de la semies­
fera
O : centro geométrico de la semiesfera
R : radio de curvatura
° g = | r
SOLUCION :
Sobre la semiesfera actúan tres fuerzas
coplanares y concurrentes, que son, el
peso (W), la reacción normal (N) y la
reacción (F) en la rótula.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*t¡
*
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
De la 2da. condición de equilibrio, res­
pecto del punto A.
I Ma = 0
N W
M a - M a = 0
N. R - W. OG = 0 ....(2)
del dato: OG =-r. R
O
.... (3)
Reemplazando datos en (2)
N .R - ( 1 6 ) .|.R = 0
8
Luego:
N = 6 newtons
PROBLEMA Ne8
La figura (1) muestra tres ladrillos
idénticos de longitud mayor “L", colo­
cados de manera peculiar, determinar el
máximo valor de "x“, de tal modo que el
conjunto permanezca en equilibrio.
Fig.(i)
!
í
1
1 3 III
1 2 ' I I
re-fe
l | | , l i l i ||
*4t

82. SOLUCION: •
D.C.L. del sistema de dos ladrillos.
I—
W
I - J
L
_ "
u
— -
N
La experiencia que el 1er ladrillo (el que
está en contacto con el plano horizontal)
no puede girar, por consiguiente cuando
se produce el desequilibrio el 2do ladrillo
gira con respecto al extremo derecho del
1er ladrillo.
Cuando analizamos al sistema (ladrillo
#2 y #3), la reacción normal "N" se con­
centra en el extremo del 1er ladrillo.
IFy = 0 , entonces: N = 2 W ___ (1)
Esto quiere decir que la “fuerza resul­
tante" de todos los pesos se concentra en
el extremo derecho del 1er ladrillo.
La figura muestra el D.C.L. del sistema
de dos cuerpos (ladrillos # 2 +# 3).
i )
l r¿
(L-X)
4 -
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
S
K
$
*
*
*
*
O
s
*
*
*
*
*
$
$
S
lí
*
■4
?
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
%
*
*
*
*
De la 2da condición de equilibrio:
ZM0 = 0
M n - M W- M W= 0
N.(L-x)-W
.... (2)
0 .... (3)
Reemplazando (1) en (3)
2W (L-x) - W Hr
en (3)
(k)-w(h )-«
2 L -2 X —| —| - x = 0
2L - 3x = 0, entonces :
- . (4)
L
J l ü
La figura (2) muestra "n" ladrillos idénti­
cos de longitud mayor "L" colocados de
manera peculiar, determinar el máximo
valor de "x“, de tal modo que el conjunto
permanezca en equilibrio.
f- X
X X
T
F íq .(2)
1
•
J
• t ,
*
i K!
- r r - — .
. , n . ¡ l l i
fi ■ :¡fl
i ;
i ¡
i
i ... r .
i !
i r 3 ■ iu
as . 1 l
-
i
l
!r
lili i .....................................
Análogamente al problema anterior se
demuestra que, x es igual a:
L
x = —
n
Donde: n = 2, 3, 4, 5, 6 ..
PROBLEMA N«9
Sobre un plano que forma con la hori­
zontal un ángulo de 37®, se apoya un cil­
indro recto de radio 30 cm. ¿Qué altura
máxima (H) podrá alcanzar el cilindro sin
perder el equilibrio? Existe suficiente
rozamiento para no resbalar.

83. SOLUCION
Mientras la línea de acción del peso pase
por el plano de sustentación (AB), el cilin­
dro no volcará. La máxima altura lo en­
contraremos cuando la línea de acción
pasa por "A".
La reacción que ejerce el plano sobre el
cilindro, es vertical y se concentra en el
punto A.
De la geometría; la altura maxima será:
H = 80 cm
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
4
c
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
PROBLEMA N5 10
La figura muestra una placa cuadrada
homogénea en posición de equilibrio,
donde el punto "O" es el punto de suspen­
sión. Si G= 53°, hallar:
*
*
*
*
*
*
*
SOLUCION
En el diagrama de fuerzas, aplicadas al
cuerpo, en la posición de equilibrio: "La
tensión en la cuerda y el peso del cuerpo,
deben ser colineales".
Consideramos el lado cuadrado “8a', en­
tonces:
AM = 4a ; MO = 3a , OB = a
Luego: AO = 7a
AO
OB
= 7

84. PROBLEMA Nfi 1
La figura muestra un bloque de 20
newtons de peso en posición de equili­
brio. Si el peso de cada polea es de 4
newtons, determ inar la tensión en la
cuerda "1
SOLUCION
Hagamos D.C.L, de todo el sistema­
.. ’ f‘ '
XFy+—£Fy -
4T = 24
T = 6N
I I
lii '
.
i i
f
l
l
'24
Hagamos D.C L. de la polea móvil
EFyj, = ZFy-
2T = T, + 4
12 = Ti + 4
Ti = 8N
a) 20N
d) 35N
b) 25N
e) 40N
*
*
*
*
*
<
¡*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
H
e
*
*
*
*
H
*
*
*
*
*
*
*
*
*
*
PROBLEMA Nfi 2
Determinar la tensión en la cuerda “1“
si el bloque que pesa 70 newtons y cada
una de las poleas móviles pesa 10 new­
tons.
PROBLEMA Ne3
Si la esfera mostrada en la figura pesa
80N, determinar la tensión en la cuerda y
la fuerza de reacción en la pared vertical.
No existe rozamiento.
SOLUCION:
Haciendo D.C.L. de la esfera y cons­
truyendo el triángulo de fuerzas
[*) W=80

85. Resolviendo el triángulo rectángulo nota­
ble:
T = 100N
R = 60N
PROBLEMA Ne4
La figura muestra una esfera maciza
de 60 newtons de peso apoyada sobre
dos planos inclinados completamente
lisos. Determinar la fuerza de reacción en
los puntos de contacto A y B.
a) 75N ; 45N b) 45N ; 75N
c) 80N; 75N d) 100N ; 80N
e) N.A.
PROBLEMA Ns5
La barra AB mostrada en la figura, de
12 N de peso, se encuentra en equilibrio
apoyado en una pared vertical y en un
plano inclinado completamente liso. Si la
fuerza de reacción en el apoyo A es de 5N
hallar la fuerza de reacción en el apoyo B.
SOLUCION:
Haciendo D.C.L. de la barra y constru­
yendo el A de fuerzas:
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
de donde, por Teorema de Pitágoras de­
ducimos que:
Rb = 13N
PROBLEMA N9 6
Si la barra AB mostrada en la figura, de
17,3 newtons de peso, se encuentra en
equilibrio apoyado en un plano inclinado
completamente liso, siendo la fuerza de
reacción en el apoyo A de 15 Newtons,
hallar la tensión en la cuerda BC paralela
al plano inclinado.
PROBLEMA Ns 7
Si la barra AB mostrada en la figura
pesa 48 newtons y la tensión de la cuerda
CD que la sostiene es de 52 newtons,
hallar la fuerza de reacción en el pasador
A, sabiendo que esta fuerza es horizontal.

86. SOLUCION- *
*
Haciendo D.C.L. de la barra y constru- *
yendo el A de fuerzas. *
*
*
4
»
*
=
t*
*
*
*
de donde, aplicando T. de Pitagoras, de- *
ducimos que: *
*
*
*
*
*
Ra = 20N
PROBLEMA Ns 8
Si la barra AB y el bloque Q pesan 20N *
y 5N respectivamente y la tensión de la *
cuerda que mantiene el sistema en equili- *
brío es de 30 N, determinar la fuerza de *
reacción en el pasador (A).
*
*
*
*
*
*
*
$
*
*
*
*
*
*
PROBLEMA N99 |
Si el peso de la esfera mostrada en la $
figura es de 10N, hallar la tensión de la |
cuerda y la fuerza de reacción que ejerce *
el plano inclinado sobre la esfera.
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
T = 10 N
R = 12 N
a) RA = 50 ; Rb = 30
b) Ra = 50 ; Rb = 40
c) Ra = 30 , Rb = 40
d) Ra = 40 ; RB = 30
e) N.A.
Haciendo D.C.L y construyendo A de
fuerzas:
Por ley de Senos: ^
1 Sen53 Sen53
Sen 74
De donde despejando:
PROBLEMA Ne 10
Si la esfera mostrada en la figura pesa
14 newtons, hallar las fuerzas de reacción
en los puntos de apoyo A y B.
Dar respuesta en newtons.
lu

87. Si el sistema mostrado en la figura se
encuentra en equiiibrio, hallar la tensión
en la cuerda BC,_y la fuerza de compren­
sión en la barra AÉ, de peso despreciable,
sabiendo que: SB = 3m; ETC = 4m
Haciendo D.C.L de una "porción”
barra y graf¡cando el A de fuerzas:
C K
de
Como el A de fuerzas es semejante al A
geométrico ABC, se tiene la siguiente
razón de proporcionalidad:
8 _T___ C_ I = I = C
AC ~ BC ~ AB ^ 2 43
De donde:
T = 16N C = 12N
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
PROBLEMA Nfi 12
Si el sistema mostrado en la figura se
encuentra en equilibrio, siendo el peso del
bloque Q 15 Newtons, determinar la ten­
sión en la cuerda AE y la fuerza de com­
p re n s ió n en la b a rra AC de peso
despreciable.
(AB = 40 cm ; AÜ = 60 cm.)
30cm
a)T = 20 N ; C =15N
b) T = 20 N C = 30 N
c) T = 60 N ; C = 15 N
d) T = 60 N ; C = 30 N
e) N A.
PROBLEMA Ne13
Si el sistema mostrado en la figura se
encuentra en equilibrio, hallar las tensio­
nes en las cuerdas A y B. El bloque pesa
200 newtons.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
¥
*
Haciendo D.C.L. del nudo y aplicando el
Teorema de Lamy tenemos:

88. Sen 53 Sen 164 Sen 143
200
4 =
5
De donde:
Ta = 70 N
Tb =150 N
£FX= 0
T3 Sen30° = T2 ... (2)
T3 = 8N
*
*
*
*
*
*
*
*
*
*
*
*
*
<
ü
*
*
*
*
*
*
*
*
*
*
+
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
PROBLEMA NB16
Determinar el peso del bloque Q sa­
biendo que el sistema mostrado se en­
cuentra en equilibrio y que las tensiones
en los cables AB y ÜD son respecti­
vamente 130N y 120 f2. La cuerda BÜ es
horizontal.
b) 100 N
c) 120 N
d) 140 N
e) 160 N
PROBLEMA Ns 17
Si en el sistema físico mostrado en la
figura, el peso del bloque Q es de 100N,
determinar la tensión en la cuerda verti­
cal.
PROBLEMA Ne 14
En el sistema en equilibrio mostrado
en la figura determinar las tensiones en
las cuerdas A y B si el peso del bloque es
de 200 N.
a) 50 N . 146 N b)50 N; 173 N
c) 100 N ; 146 N d)100 N;173 N
e) N.A.
t ROBLEMA Nfi 15
Si el sistema físico mostrado en la
figura se encuentra en equilibrio, siendo
BC una cuerda horizontal, determinar la
tensión en la cuerda CD.
SOLUCION:
Haciendo D.C.L del nudo B:
Haciendo D.C.L. del nudo C:
Fr = 0
T2 = 4N ...(1)

89. SOLUCION:
Haciendo D.C.L. del nudo A:
Ti = t 2 = 100N
Haciendo D.C.L. del nudo B:
IF y =0
T=T2 Cos60°
de donde:
T = 50N
PROBLEMA Ns18
Si el sistema físico mostrado en la
figura se encuentra en equilibrio, determi­
nar los pesos de los bloques P y Q.
W = 200N.
a) 100N; 200N b)200N ;100N
c) 300N ; 346N d)346N ;200N
e) N.A.
PROBLEMA N® 19
Si el sistema mostrado se encuentra
en equilibrio, determinar la tensión en la
cuerda oblícula "A”. El bloque Q pesa 40
newtons.
*
$
SOLUCION:
Haciendo D.C.L. de la cuerda MN:
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
T. Fy =0
Ta Sen 53 = 40
Ta =50 N
PROBLEMA N®20
Si el bloque Q pesa 25 newtons, deter­
minar el peso del bloque P para que el
sistema se encuentre en equilibrio en la
posición indicada.
*
*
*
*
*
a) 15N
d) 50N
b) 25N c) 25 V3 N
e) N.A.

90. Si en el sistema físico mostrado en la
figura, el peso del bloque Q es de 20
newtons y en la polea fija no existe
rozamiento, determinar la tensión en la
cuerda horizontal.
Haciendo D.C.L de la cuerda AB;
Si el sistema físico mostrado en la
figura se encuentra en equilibrio y sabi­
endo que la tensión en la cuerda SB es de
10 newtons, determinar la tensión en la
cuerda horizontal CD. P = 2N y Q = 4N.
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
i
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
é
*
*
*
*
*
*
*
*
*
*
*
a) 4 N
d) 10 N
PROBLEMA Ne23
b) 6 N c) 8 N
e) Faltan datos
Si la barra imponderable AB se en­
cuentra en equilibrio en la posición indi­
cada, hallar la fuerza de reacción en el
gozne A. El peso del bloque Q es 4 new­
tons.
SOLUCION:
Haciendo D.C.L. de la barra AB y cons­
truyendo el A de fuerzas:
de donde:
Ra = 4 N
Conviene señalar que hemos deducido
que la dirección de RAes horizontal, por­
que las tres fuerzas que actúan sobre la
barra deben ser concurrentes.
PROBLEMA N524
Calcular la fuerza de reacción en el
gozne si el sistema está en equilibrio y el
peso de la barra doblada es despreciable.
P = 30N y O = 40N.

91. Por teorema de Pitágoras deducimos
que:
Ra = 21 N
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
S
i»
*
*
*
*
*
*
í¡*
*
*
*
*
*
#
$
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
#
*
*
s
i»
*
*
*
*
*
*
*
#
*
*
*
#
*
*
*
*
*
*
*
*
*
s
5
í
*
*
*
*
a) 30 N
b) 40 N
c) 50 N
d) 60 N
e) N.A.
PROBLEMA Ns 25
SOLUCION:
Hagamos D.C.L. de la barra AB conside­
rando que las tres fuerzas que actúan
sobre ésta deben ser concurrentes.
PROBLEMA Nfi 26
En el sistema mostrado en la figura, el
peso de la barra AB, uniform e y ho­
mogéneo, es de 30 newtons. Sabiendo
que el sistema se encuentra en equilibrio
y que M es punto medio de AB, hallar la
tensión en la cuerda y la fuerza de reac­
ción en el gozne.
a) T = 40 N ; R = 40 N
b) T = 40 N ; R = 60 N
c) T = 80 N : R = 40 N
d) T = 40 N ; R = 50 N
e) N.A.
PROBLEMA N« 27
La barra AB mostrada en la figura se
encuentra en equilibrio por acción de la
cuerda horizontal. Sabiendo que el peso
de la barra es de 40N y que la tensión en
ia cuerda es numéricamente igual a la
reacción en el punto A, determinar la reac­
ción en B. No existe rozamiento.
Si el peso de la barra uniforme y ho­
mogénea AB es de 72N y la tensión en la
cuerta CD es de 75 N, hallar ia fuerza de
reacción en el pasador (C es punto medio
de AB).
SOLUCION:
Haciendo D.C.L. de la barra:
(w
+ra)

92. Resolviendo el triángulo.
RA= T = 120 N
Rb = 200 n
Haciendo D.C.L. de la polea móvil:
I Fy+ = Z Fy -
2T = 60
T = 30N
m
60
*
*
*
PROBLEMA Ns 28
'Determinar el valor de la fuerza hori­
zontal F aplicada a la esfera de 2 newtons
de peso sabiendo que la fuerza de reac­
ción en el punto de contacto B es el
cuádruple que la del punto de contacto A.
No existe rozamiento.
PROBLEMA N9 29
En el siguiente sistema en equilibrio,
hallar la fuerza de reacción del piso sobre
la esfera. Se sabe que no existe roza­
miento y que el peso del bloque A y de la
esfera B son de 60 N y 100 N respecti­
vamente (La polea móvil es de peso des­
preciable). F = 24 N.
* IF x + = IF x -
24 = 30 Cos e
Cos e = %
e =37s
* £ F y + = I F y -
R +30 Sen 37a= 100
R = 82 N
PROBLEMA Ne30
Sabiendo que el sistema mostrado se
encuentra en equilibrio y que F = 40N y
Q = 20N, determinar las tensiones en las
cuerdas A y B.
*
$
*
*
*
*
*
S
U
*
*
a) 20N ; 40N b) 40N ; 20N
c) 60N ; 40N d) 40N ; 60N
e) N.A.
PROBLEMA Ne31
La figura muestra una barra AB uni­
forme y homogénea de 2 newtons de pe­
so, apoyada en una pared vertical lisa yen
una superficie horizontal rugosa. Deter­
minar las fuerzas de reacción en los pun­
tos de apoyo A y B.

93. SOLUCION:
Haremos el D.C.L de la barra teniendo
presente el criterio de concurrencia de las
tres fuerzas actuantes.
A 0
V
¡ °
2x . .. K . .Rn
KA 1
X X
Como el triángulo de fuerzas es seme­
jante al OBM tenemos que.
_2_
2x
Ra Rb
x x-45
Ra = 1N Rb =V5Ís
T
PROBLEMA Ne32
La barra AB uniforme y homogenea
mostrada en la figura pesa 3 mewtons. Si
no existe rozamiento en la pared vertical,
hallar la fuerza de reacción en la rótula A.
a) V5N"
b) >/§Ñ
c)V8FT
d) VT3Ñ"
e) N.A.
PROBLEMA NE33
Determinar el punto de aplicación de
la fuerza resultante del conjunto de fuer­
zas mostrado en la figura. Dar la distancia
al punto A.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
N
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
«
N
*
*
*
*
*
*
*
*
m
*
*
*
*
*
SOLUCION:
El modulo de la resultante se determina
por:
Re = IF -> Re = 50 —20 - 1 0
Re = 20N
Su punto de aplicación se determina por
teorema de Varignon:
ZON
T 50N i Re
pl
2m Zm
, *
n
Re F
M a = X M fl
20x = 50(2) -
20x = 60
10(4)
1CN
x = 3m
PROBLEMA N934
Determinar el módulo de la fuerza
equivalente al conjunto de fuerzas apli­
cadas sobre la barra AB mostrada en ia
figura. Dar su punto de aplicación.

94. a) 20 N : en A b)140N en C
c) 40 N : en D d) 10 N : en D
e) N.A.
PROBLEMA Ne35
'_a figura muestra una placa, que tiene
la forma de un exágono regular de 10 cm
d< ado, sobre el cual se encuentran ac­
tuando cuatro fuerzas. Encontrar el mo­
mento resultante con respecto al punto
"O ".
Re __
M 0 =126 (5 V3) —15 (10 y¡3) -
—
48 (10V§) +14 (5) + 20 (5)
de donde:
Re
M 0 = 170cm.N
Re
M 0 =1,7 m.N
Determinar el momento resultante del
sistema de fuerzas mostrado en la figura,
respecto del punto A. La placa cuadrada
tiene como lado 1m de longitud.
a) 480 m N
b) 960 m.N
c) 1000 m.N
d ) 1120 m.N
e) 1200 m N
PROBLEMA N®37
Si la barra horizontal AB es de peso
despreciable y el peso del bloque Q es de
90N, hallar la fuerza de reacción en el
apoyo A y en el apoyo B.
4m, , Im , 4m
SOLUCION
Haciendo D.C.L. de la barra:
.R.
- ¡
7 ‘
5i;i
90N
Por segunda condición de equilibrio:
Rb (9) - 90 (5) = 0
Rb = 50N
Por pnmera condición de equilibrio:
IF = 0

95. Ra = Rb —90 = O
Ra = 40N
SOLUCION:
* D.C.L. de la barra izquierda:
Ft (4) —T (1) = O
T = 4Fi ....(1)
PROBLEMA N938
Si la barra doblada ABC es de peso
despreciable y el peso del bloque P es de
50 newtons. Hallar la tensión en la cuerda
vertical BD. Sabiendo que existe equili­
brio.
(AB = BC = 5m)
a) 10 N
b) 30 N
c) 70 N
d) 90 N
Si el sistema mostrado en la figura se
encuentra en equilibrio, hallar en qué re­
lación se encuentran los módulos de las
fuerzas horizontales Fi y F2 aplicadas.
PROBLEMA Ne 39
*
*
*
st>
*
*
*
*
*
*
*
*
*
#
*
$
*
*
*
*
EM = 0
o2
T (2 ) -F Z (6) = 0
T * 3 F2
De (1) = (2))
4Fi = 3 F2
*
(2)
F i = 3
F2 4
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
D«
PROBLEMA N940
Si el sistema físico mostrado en la
figura se encuentra en equilibrio, determi­
nar la fuerza de reacción en el apoyo A.
Considerar ei peso de las barras despre­
ciable. Q a: 10N.
a) 30N
b) 35N
c) 40N
d) 45N
e) 50N
FT
*
*
*
*
*
*
*
*
*
*
PROBLEMA N®41
El sistema físico mostrado en la figura
se encuentra en equilibrio. Si la estruc­
tura es de peso despreciable y la esfera A
pesa 50N, hallar la tensión en la cuerda
horizontal Bü.

96. Haciendo D.C.L. del sistema:
I M o = 0
T (2) - 50(1) = 0
T = 25N
PROBLEMA N942
El sistema físico mostrado en ia figura
se encuentra en equilibrio. Si la estruc­
tura es de peso despreciable, determinar
la reacción del piso sobre la barra en A si:
F = 12 N
3m
a) 9N -
b) 12N ■ C B i
C) 15N
j .
d) 18N 4m
e) N.A.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
4
=
*
*
*
*
*
*
*
*
*
¡t*
*
*
«
b
*
<
¡
>
*
*
*
*
*
Si la barra uniforme y homogénea AB
mostrada en la figura pesa 10 newtons,
determinar las tensiones en las cuerdas
- |- y « 2 Q = 3N
(1) (2)
A R
r — i - " - - ^
A-, 8u
SOLUCION:
Haciendo D.C.L. de la barra
3N
l : H
1 2u
5u
* c t <í ION
Por 2da. condición de equilibrio:
( Í M b + = I M b
3(10)+ 10(5) = Ti (8)
|T i = 10N
Por lera, condición de equilibrio:
£Fy+= X
F
y
—
Ti + T2 = 3 + 10
T2 = 3N
PROBLEMA Nfi 44
Hallar las fuerzas de reacción en los
puntos de apoyo A y B si la barra uni­
forme y homogénea AÜ pesa 100 newtons
(AB = 5BÜ), Q = 10N.
t
B
I

97. a) Ra = 20 N ; Rb = 90N
b) Ra = 40 N ; RB= 70N
c) Ra = 50 N ; RB = 60N
d) Ra = 38 N ; RB = 72N
e) Ra = 30 N ; Rb = 80N
PROBLEMA Ne45
Si la barra horizontal AB, uniforme y
homogénea pesa 40 newtons, determinar
la fuerza de tensión en la cuerda " 1 El
peso de la polea móvil es despreciable.
(i)
SOLUCION:
Haciendo D.C.L. de la barra:
(1)
<J
fr /2 c-
a
40N
Por 2o condición de equilibrio:
IM 0 C r = £Mo O
T (3a) (2a) = 40a
T = 10N
..J
PROBLEMA Ns46
Si la barra AB, uniforme y homogénea
pesa 5 N y se encuentra en equilibrio,
determinar la tensión en la cuerda "1 El
peso de la polea móvil es de 2N.
$
*
*
$
*
*
«
n
*
*
*
*
*
*
*
*
*
*
*
*
*
*
PROBLEMA N®47
La figura muestra una barra AB uni­
forme y homogénea de 5 newtons de peso
y 4m de longitud. Si la esfera de 10 new­
tons de peso se encuentra apoyada sobre
la barra, hallar la fuerza de reacción entre
la barra y la esfera.
*
*
B, |
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
é
*
m
*
*
i
lm
SOLUCION:
Haciendo D.C.L. de todo el sistema:
1
M
--------- ►
1 2
5 N
*
*
$
0
*
*
*
$
Por 2° condición de equilibrio:
I M a '+ )= T M a
T(1) + T(4) = 10(1) + 5(2)
T = 4N
Haciendo D.C.L. de la esfera y aplicando
la 1o condición de equilibrio:

98. R = 6N
PROBLEMA Nfi 48 .
Si la barra horizontal AB de 4N de peso
y Sm de longitud se encuentra en equili­
brio, en la forma que muestra la figura,
hallar la tensión en la cuerda " 1 (Peso
del bloque Q = 8N).
*
t*
*
*
*
*
4
>
*
*
*
*
$
*
*
*
a) 1 N
b) 2N
c )3 N
d) 4 N
(1)
*
*
*
3m 3m
PROBLEMA N9 49
La figura muestra una barra ÜA uni­
forme y homogenea de 5 newtons de peso
y 15 metros de longitud en estado de
equilibrio. Si el peso del bloque Q es de
10 newtons, hallar la tensión de la cuerda
horizontal BÜ. (OS = 10m).
SOLUCION:
Haciendo D.C.L. de la barra:
Por 2o condición de equilibrio:
IM o = £M0
T(6) = 5 (6 )+ 10(12)
'• l T = 25N I
*
#
>
*
*
*
*
$
*
«
I*
*
*
*
*
*
*
#
*
*
*
*
*
*
«
tí
PROBLEMA N951
Si el sistema mostrado en la figura se
encuentra en equilibrio, los pesos de la
barra AB y el bloque Q de 60 N y 30 N
respectivamente, hallar la tensión del ca­
ble que sostiene a la barra.
E
j D
PROBLEMA N950
Si el peso de la barra DA uniforme y
homogénea es de 40 newtons y el bloque
W pesa 20 newtons, determinar la tensión
de la cuerda B£ (Aó = 3A3).
d) 80 N
a) 50 N
b) 60 N
c) 70 N
e) 100 N

99. SOLUCION:
Haciendo D.C.L. de la barra:
-Olí
, O j T/ 2 ^ , t r¿
—
-----
a j a l a
60N T —
€
30N
Por la 2da. condición de equilibrio:
I M a = 0
|( a ) + |( 3 a ) = 60(2a) + 30(4a)
T = 120 N
PROBLEMA N« 52
Si la barra AB uniforme y homogénea
que muestra la figura pesa 28 newtons,
hallar la tensión de la cuerda que lo
sostiene.
PROBLEMA Ne53
Si la barra doblada en forma de T es de
peso despreciable y en sus extremos
están soldados dos esferillas de pesos W
y 6W, hallar el ángulo 0 que define la
posición de equilibrio del sistema
*
*
*
*
*
*
4 *
*
m
+
*
*
*
*
*
*
*
■
i»
*
*
*
*
*
$
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
+
*
*
*
*
*
*
*
*
f
*
*
*
+
*
6W
SOLUCION:
Haciendo D.C.L. de todo el sistema:
Por 2o condícion de equilibrio:
M&^ = M0^ )
6 (L Cos 0 -- L Sen 0) = 2L Sen 0
3 Cos 6 = 4 Sen 0
tge
ÍÍLSene
(LCosn-LSeno)
0 =37°
PROBLEMA Ns54
Hallar el ángulo 0 que define la posi­
ción de equilibrio del sistema formado por
dos barras uniformes y homogéneas sol­
dados en la forma que muestra ía figura.
a) 16°
PROBLEMA N5 55
Si el peso de la barra horizontal AB,
uniforme y homogénea es de 45N, deter­
minar la tensión de la cuerda que lo sos­
tiene. Q = 10N

100. SOLUCION:
Haciendo D.C.L. de la barra:
(TI 31 C 4T
A 4T 3T B
"* Z
L J
L
ION 'r (L 45N l e
¡
Por 2o condición de equilibrio:
£ M b ( + = I M b
10(4a) + 45(2a) = 3T(3a) + 4T(a)
T = 10
5T = 50N
Debemos aclarar que hemos asumido,
por conveniencia, que la tensión de la
cuerda es 5T
PROBLEMA Ne 56
Si la barra AB uniforme y homogénea
que muestra la figura pesa 16 newtons y
el bloque Q pesa 4 newtons, determinar
las tensiones en las cuerdas ”1” y "2".
#
&
s
»
*
*
$
*
m
*
*
*
$
*>
<
¡*
*
*
*
*
*
*
*
*
*
*
*
a) 10N ; 6N b)10N ;8N
c) 9N ; 9N d) 6N ; 6 N
e) 5N ; 1N
PROBLEMA NB57
Si el sistema mostrado en la figura se
encuentra en equilibrio, determinar el
peso del bloque B. El peso del bloque A
es de 150N y las barras rígidas son de
peso despreciables.
SOLUCION:
Haciendo D.C.L. de la barra oblicua:
4 m C
IM c (T = IM C'£)
150(4) = R (2,5)
R = 240 N i
Haciendo D.C.L. de la barra horizontal:
2 tn _2 m
D

101. Por 2o condición de equilibrio:
X M d ( T = £ M d ^ )
192(2) = WB (2)
WB = 192N
Conviene señalar que en ninguno de los
D.C.L. se han graficado las fuerzas de
reacción que actúan a sus respectivas
rótulas ya que al tomar momentos en
éstas y dichas fuerzas se anulan.
PROBLEMA Ne56
La barra AB de peso despreciable se
apoya sobre ta barra idéntica ÜD en la
forma que muestra la figura. Si sobre la
barra AB actúa una fuerza F en forma
perpendicular a ésta, determinar la ten­
sión en la cuerda EP, M es punto medio de
AB.
a) 2F b) 4F c)%
(3 F
d) 4 V3 F e) N.A.
PROBLEMA Ns59
Si el peso de la esfera mostrada en la
figura es de 10 newtons y el peso de la
barra AB uniforme y homogénea es de 8
newtons, determinar la tensión en la
cuerda horizontal BC. M es punto medio
de AB.
$
*
$
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
m
*
*
*
*
*
*
i#
¡#
«
*
*
*
*
¡¡N
*
*
*
*
SOLUCION-
Haciendo D.C.L. de la esfera y cons­
truyendo el A de fuerzas tenemos:
10
de donde. R = 20 N
Haciendo D.C.L de la barra:
l JT |
Por 2o condición de equilibrio:
I M a + ) = X M a C i
T(L V3) = 8 (|) + 20(L)
T = 8>Í3 N
PROBLEMA Nfi 60
La barra AB mostrada en la figura pesa
25N y mide 20cm. Determinar el valor de
la fuerza horizontal F para que el sistema
se mantenga en equilibrio en la posición
indicada. No existe rozamiento. Q = 32N.

102. a) 6N
d) 50N
PROBLEMA Ne 61
b) 12N
e) Ninguna
c) 20N
El sistema físico mostrado en la figura
consta de una barra AB uniforme y ho­
mogénea de 200 N de peso y 2m de longi­
tud cuyo extremo lleva soldado una
esferilla metálica de 500 N de peso. Si el
sistema se encuentra en equilibrio en la
posicion indicada por acción del resorte
cuya longitud natural es de 0.8m, determi­
nar la constante elasticidad del resorte. M
es punto medio de AB
SOLUCION:
Debemos señalar que la tuerza recupera­
dora en un resorte es directamente pro­
porcional a su deformación (Ley de
Hooke) cumpliéndose que:
F = KX - > F = K (0,3)
Haciendo D.C L de la barra:
*
*
$
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
*
*
*
*
«
*
*
#
*
#
*
*
*
*
Por 2o condición:
IM a +)= £Ma3
0,3K(L) = 200L + 500(2L)
K = 4000 N/m
PROBLEMA NB62
La barra AB mostrada en la figura es
de peso despreciable y se encuentra sus­
pendido por dos resortes ideales dis­
puestos en posición vertical. Si se
suspende del punto medio de la barra un
bloque Q, su extremo A desciende una
distancia doble que el extremo B. A que
distancia de A debe suspenderse el blo­
que para que el extremo B descienda una
distancia doble que el extremo A.
a) 6m
b) 7m
c) 8m
d) 9m
e) N.A. lt m
PROBLEMA N263
El bloque Q de 100N de peso mostrado
en la figura es presionado en la pared
vertical por acción de una fuerza horizon­
tal F. Si el coeficiente de rozamiento
estático entre el bloque y la pared es 0,5
determinar el mínimo valor de F que per­
mite al bloque conservar su estado de
equilibrio.

103. F = 200 N
* ZFx + = £Fx -
MN = Q Sen 0 ... (2)
Reemplazando (1) a (2)
H Q Cos 6 = Q Sen 0
Tge = n
Reemplazando
dato : 9 = 37°
*
sis
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
t
*
*
*
#
«tí
*
*
*
*
*
#
#
*
*
*
*
&
*
*
*
*
*
4¡
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
s
i»
*
*
*
*
d
*
*
*
*
*
*
*
*
Si el coeficiente de rozam iento
estático entre el bloque Q y el plano incli­
nado es 0,75, determinar el máximo án­
gulo 6 con la condición de que el bloque
no resbale sobre el plano.
Reemplazando (1) en (2)
0.5F = 100
PROBLEMA Ne64
Si el peso del blcqua Q mosir? ■
en ia
figura es de 10 Newtons, hallar el mínimo
valor de fuerza F que se debe aplicar al
bloque con la condición de que se con­
serve su estado de equilibrio estático. El
coeficiente de rozamiento estático es (i =
0,5.
a )8 N
b) 10 N
c) 12 N
d) 14 N
e) 16 N
SOLUCION:
Haciendo D.C.L. del bloque en el ins­
tante que está a punto de deslizarse.
* XFx+ = XFx-
* £Fy+ = IF y -
|iN = 100 ... (2)
SOLUCION
Haciendo D.C.L. del bloque en el ins­
tante que está a punto de deslizarse y
aplicando la primera condición de equili­
brio tenemos:
* IF y + = ZFy -
N =Q CosG .... (1)

104. Si los pesos de los bloques A y B
mostrados en la figura son de 10N y 5N
respectivamente y el coeficiente de
rozamiento entre todas las superficies en
contacto es n = 0,2, determinar el máximo
ángulo 6 con la condición que el bloque
B no resbale por el plano inclinado.
ROBLEMA Ne 67
En la figura, si los pesos de los blo­
ques A y B son de 10N y 20N respectiva­
mente y el coeficiente de rozamiento está­
tico entre todas las superficies en con­
tacto es 0,2, determinar la mínima fuerza
horizontal F capaz de iniciar el movimien­
to de B.
SOLUCION
Haciendo D.C.L de A y aplicando la 1c
condición de equilibrio: j
LFy + — £Fy —
Ni = 10N
fi = 2N
Haciendo D.C.L. de B y aplicando la 1o
condición de equilibrio:
* ZFV + = SFV -
f2 = 6N
*
&
*
*
*
*
*
¡je
*
*
*
*
*
<
f¡
*
S
f>
*
*
*
S
H
*
*
*
*
*
£
*
*
*
*
m
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*SFX + = SF* -
F =fi+f2
F = 8N
f
1
30
F
n ' . t i !¡:>1 -
f2
n 2
PROBLEMA Ne68
En la figura, si los pesos de los blo­
ques A y B son de 16N y 20N respecti­
vamente y el coeficiente de rozamiento
estático entre todas las superficies en
contacto es de 0,25, determinar la mínima
fuerza horizontal F capaz de iniciar el
movimiento de B.
Si los bloques A y B del sistema
mostrado en la figura son de 15N y 45N de
peso y el coeficiente de rozamiento entre
todas las superficies planas en contacto
es de 0,4, determinar el máximo valor que
puede tomar la fuerza horizontal F con la
condición que el sistema se encuentre en
reposo.

105. Haciendo D.C.L de A y aplicando la 1ra.
condición de equilibrio:
* ZFy += ZFy - ' 15
T
N = 15N —
ti = 6N 1
*’ ZFX+ = ZFx------ > T = 6N
Haciendo D.C.L. de B y aplicando la 1ra.
condición de equilibrio:
* IF y + = ZFy -
N2 = 60N
1
6U
f2 = 24N
ZFX+ = ZFX-
F = fi + T + f2
F = 36 N
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
m
-$
&
*
*
*
$
PROBLEMA Ns70
En el sistema mostrado en la figura,
ios pesos de los bloques A y B son de 50N
y 70N respectivamente y el coeficiente de
rozamiento estático entre todas las super­
ficies planas en contacto es de 0,5. Deter­
minar la mínima fuerza horizontal F capaz
de iniciar el movimiento del sistema.
a) 70 N
b) SON
c) 90 N
d) 100 N
e) N. A.
*
*
*
*
*
*
*
*
PROBLEMA N®71
Si el bloque Q que muestra la figura
pesa 35N y es presionado en la pared ver­
tical de coeficiente de rozamiento 0,75 de­
bido a la acción de la fuerza oblícula F,
determinar el intervalo en que puede variar
el valor de dicha fuerza manteniéndose el
equilibrio.
*
*
*
Hallaremos el máximo valor de F anaii-
zando el estado en que el bloque está a
punto de moverse hacia arriba.
f
* I F x - = ZF* +
N = F Sen 37°
--(1 )
N = 0,6F
** ZFy + = ZFy —
F Cos 37° = 35 + 0,75 N
0,8F = 35 + 0,75 N (2)
Reemplazando (1) en (2) y resolviendo:
Fmax = 100N
Para hallar el mínimo valor de F se
analiza el estado en que el bloque está a
punto de moverse hacia abajo. Este pro­
cedimiento es análogo al seguido en el
caso anterior obteniéndose las siguien­
tes ecuaciones:
N = 0,6F ....(1)
0,8 F = 35 - 0.75N .... (2)
De donde resolviendo obtenemos que:
= 28 N
El intervalo en que se encuentra F será
en consecuencia:

106. Calcular en qué intervalo se encuentra
el valor de la fuerza horizontal F con ia
condición que el bloque de 55N de peso
se encuentre en equilibrio. El coeficiente
de rozamiento estático en el plano incli­
nado es 0,5.
Haciendo D.C.L. de A y aplicando la 1ra
condición de equilibrio:
*£Fy += ZFy -
N = W + 10
h = 0,6 (W + 10)
a) [10, 70]N
c) [30 ; 70]N
e) N A.
PROBLEMA N« 73
b) [10 ; 110]N
d) [30 ; 110]N
Los bloques A y B mostrados en la
figura se mueven hacia la derecha con
velocidades constantes de 2m/s y 3m/s
respectivamente. Si el peso del bloque A
es de 10N y el coeficiente de rozamiento
entre todas las superficies en contacto es
0,6, hallar el valor de F.
2F
£ A
H L
SOLUCION;
Como el movimiento relativo de B res­
pecto de A es hacia la derecha la tuerza
de rozamiento (cinético) que actúa sobre
B es hacia la izquierda. Haciendo D.C.L.
de B y aplicando la 10condición de equili-
bno: _
w
IFy + = ZFy -
N = W
fi = 0,6W
F + fi = f2
F + 0.6W = 0,6(W + 10)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
F = 6N
PROBLEMA N974
En el sistema mostrado en ia figura los
pesos de los bloques A y B son de 20N y
40N respectivamente v el coeficiente de
rozamiento estático entre todas las super­
ficies planas en contacto es de 0,5. Deter­
minar la mínima fuerza horizontal F capaz
de iniciar el movimiento del sistema. No
existe rozamiento en las poleas.
I ! “ h —
_ . _ í 3 i
— B ______
a) 25N
d) 4CN
b) 30N
e} 45N

107. La figura muestra un sistema formado
por dos poleas solidarias de radios R =
80cm. y r = 40cm. apoyado en una super­
ficie horizontal de coeficiente de roza­
miento ¡i = 0.25 y en una pared vertical
completamente lisa. Determinar el máxi­
mo peso permisible del bloque Q man­
teniéndose el equilibrio, sabiendo que el
peso del sistema es de 14N.
Haciendo D.C.L. del sistema y aplicando
condiciones de equilibrio:
*£ F y + = IF y -
N = 14 + Q ....(1)
’ £ M0 "+) = Z M 0 ( ^
f (2r) = Q(r)
0,5N = O .... (2)
Reemplazando (1) en (2):
0,5(14+ Q) = Q
*
*
*
*
*
*
*
é
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
La figura muestra un sistema formado
por dos poleas solidarias de radios
R = 80cm. y r = 40cm. apoyado en una
superficie horizontal de coeficiente de ro­
zamiento n = 0.25 y en una pared vertical
completamente lisa. Determinar el má­
ximo peso permisible del bloque Q man­
teniéndose el equilibrio, sabiendo que el
peso del sistema es de 14N.
a) 1N '
b) 2N
c) 3N
d) 4N
e) N.A.
PROBLEMA N977
Si la barra AB uniforme y homogénea
mostrada en la figura pesa 1GN y el coefi­
ciente de rozamiento entie éste y el blo­
que Q es 0,8, determinar el mínimo peso
de Q para que el sistema se conserve en
equilibrio.
Q = 14N
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
Haciendo D.C.L. del bloque Q y aplican­
do la 1o condición de equilibrio:
* IF y + = IF y —
N = Q
' 2 Fx +=£ Fx -
T = 0,8N
T = 0,8Q .... (1)

108. Haciendo D.C.L. de todo el sistema y
aplicando la 2o condición de equilibno:
* I M b < T =
(Q + 10)2 = T(4) + T(1)
e
-
¡}— í
l T
2 1
L 1 L ~
(0 +10)
2Q + 20 = 5T .... (2)
Reemplazando (1) en (2):
2Q + 20 = 4Q
Q = 10N
*
$
1
*
*
*
*
i
*
*
*
*
*
#
«
0
*
*
#
*
*
PROBLEMA Nfi 78
Si el sistema mostrado en la figura se
encuentra en equilibrio, hallar el máximo
peso permisible del bloque Q, mantenién­
dose el estado de equilibrio. El peso de la
barra horizontal AB, uniforme y homo­
génea, es de 9N y el coeficiente de roza­
miento estático entre la barra y la polea
mayor es 0,25 (R =2r).
d) 6N e) 7N
PROBLEMA N®79
La barra AB uniforme y homogénea
que muestra la figura se encuentra apo­
yado en una superficie horizontal de coe­
ficiente de rozamiento p = 0,5 y en una
pared vertical completamente lisa. Deter­
minar el mínimo ángulo 6 * 0o conser­
vando la barra su estado de equilibrio.
SOLUCION:
Hacemos el D.C.L. de la barra teniendo
presente el criterio de concurrencia:
Se cumple que:
$
#
*
*
m
*
*
*
*
*
*
*
Demoninándose a " £,", ángulo de roza­
miento. En este caso.
T g^ = |
T g^ =
de donde:
Tg0 =
2x
2x
2x
Tge = 1
0 = 45°

109. La barra AB uniforme y homogénea
mostrada en la figura se encuentra
apoyado en una superficie horizontal y en
una pared vertical rugosa. Si el coefi­
ciente de rozamiento entre todas las su­
perficies en contacto es 0,5, determinar el
mínimo ángulo 6 conservando la barra su
estado de equilibrio ( 0 * 0 ) .
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
#

110. ..-y..-.::.........V. . - ....... ,f
PROBLEMAS ESPECIALES DE ESTATICA
TEMA : SEGUNDA CONDICION
DE EQUILIBRIO
p p :b le m a Ne 1
Se tiene una esfera de radio 60cm y de
peso 2N, del punto "0“ se suspende me­
diante una cuerda un bloque P de peso
10N, haciendo que la esfera se desvie con
respecto a su posición inicial. Si la longi­
tud de la cuerda que ata la esfera es 40cm.
calcular la medida del ángulo " 6 " que
define la posición de equilibrio. No hay
rozamiento.
SOLUCION:
Consideramos nuestro tísico, a la esfera
más una porción de cuerda que bordea
la esfera. Realizamos el diagrama de
fuerzas del sistema físico elegido.
*
*
i*
m
#
*
*
*
*
*
*
m
*
*
*
*
*
*
#
*
*
#
&
*
a = 100 Sen 0
b = 6 0 - 100 Sen 0
La suma de momentos respecto del
punto “0" es igual a cero
I M o = 0
w P
M 0= M 0
w. a = P. b
2N(100Sen 0) = 10N(60- 100 Sen 0)
Sen 0 = "
0 = 30°
PROBLEMA N®2
Determinar la medida del ángulo " 0 ",
para que el sistema mostrado se encuen­
tre en equilibrio. Se trata de dos esferas
de igual tamaño, unidos por un hilo de
peso despreciable y se encuentran sobre
una superficie cilindrica carente de fric­
ción.
Wi = 15Ny W2 = 7N
SOLUCION:
Consideremos nuestro sistema físico, las
dos esferas más la cuerda.

111. La suma de momentos respecto del cen­
tro de curvatura "0", es igual a CERO.
XM0 = 0
w1 w2
M 0 = M „
w i. L Cos 0 = W2 L Cos a
15. Cos 0 = 7Cos (1 2 7 -0 )
15Cos0 = 7 Sen (0 -3 7 ° )
-i o 24
Tg0 = —
0 = 74°
m
*
&
PROBLEMA N®3
En la figura mostrada hallar la medida
dei ángulo " 0 " que define la posición de
equilibrio. Si OB = 2m, el radio de la
esfera homogénea es 1,0m y la longitud
de ia barra uniforme y homogénea es 4m.
Donde "O” es en centro de la esfera y
ambos cuerpos tienen pesos iguales.
*
*
*
%
*
*
*
*
*
*
*
$
#
*
*
*
*
#
*
*
Consideremos nue:;tro sistema físico, la
esfera, más, ia barra y la cuerda El dia­
grama de fuerzas del sistema físico.
Suma de momentos respecto del punto
”B' es igual a CERO.
£MB = 0
O G
m b = m b
w. 2 Sen (30° - a) = w. 2 Sen a
Sen (30° - a) = Sen a
3 0 ° - a =a
Luego: a = 15
0 = 75°
«
ti
PROBLEMA NB4
La figura muestra dos esferas de igual
radio, unidos por barra de peso despre­
ciable, apoyados sobre una superficie ci­
lindrica. Si el peso de las esferas son:
wi = 6N y W2 = 5N, determinar la me­
dida del ángulo" 0" que define la posición
de equilibrio del sistema mecánico. No
existe rozamiento.

112. Reemplazando el valor de * p "
SOLUCION:
Sea nuestro sistema físico, las dos es­
feras (w1y w2) unidos con la barra.
Diagrama del cuerpo libre, del sistema
físico escogido.
De la segunda condición de equilibrio:
IM 0 = 0
w1 w2
= M ,
(6). | = (5) . xSen (3
Senp = |
P= 37°
Entonces:
Del diagrama del cuerpo libre:
3 0 °+a + 6 = 90° . . . (1)
(a - 0) + P = 90° .. . (2)
De: (1) —(2)
e = 3,5°
PROBLEMA N®5
En la figura mostrada las esferillas son
de igual radio "r“, donde A, B y C tienen
pesos iguales a 4N cada una. Hallar el
peso de la esferilla D, tal que el sistema se
encuentre en equilibrio del modo indi­
cado, sabiendo que descansan sobre la
superficie semiesférica de radio ”5r".
*
*
*
*
*
*
*
*
«i
*
*
*
*
*
*
*
SOLUCION
Consideramos nuestro sistema físico, las
cuatro esferas. Diagrama del cuerpo li­
bre del sistema físico elegido
Lsen2i
/
La suma de momentos respecto del cen­
tro de curvatura “O1
' es igual a CERO
ZMo = 0

113. M q — M q+ M q + M q
P. L Sen a = w. L Sen a +w. L Sen a +0
P Sen a = 2w Sen a Cos a +w Sen a
P = w (1 + 2 Cosa) ...(1 )
En el triángulo isósceles formado:
Ley de cosenos:
7
Cos a = —
O
Reemplazando en (1):
P = —-w
4
P = 11IM
#
*
*
*
*
*
*
*
*
*
*
*
#
*
*
s
i»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
PROBLEMA Ns 6
La figura muestra dos esferas del
mismo materia! de radios a = 3 cm. y b =
2 cm., sobre una superficie esférica de
radio de curvatura R = 11 cm. No existe
rozamiento.
............ . Sen a _
Hallar la razón: —
— - = ?
Sen p
SOLUCION:
Sea nuestro sistema físico, las dos es­
feras de radios a y b.
*
*
$
*
*
*
*
«
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Diagrama del cuerpo libre.
, "'■'X . (R -b)S ení
(R -a )se n a ' 1 ^ '
La sumatoria de momentos respecto del
centro geométrico de la superficie es­
férica, es igual a Cero
ZMo = 0
«i
w .(R - a) Sen a = w . (R - b) Sen p
1 2
* D.g.v^R-aJSen a = D.g.v2 (R - b) Sen p
a3.(R-a)Sen a = ~ b3 (R-b) Sen p
Sen a b (R - b)
Sen p a3.(R - a)
Reemplazando valores
Sen«
Sen p 3
PROBLEMA Ne7
Tres pequeñas esferas sólidas y rígi­
das de pesos: wi = 1N; W2 = 2N; W3 = 3N,
que pueden moverse en un aro circular
liso, están enlazados por tres varillas de
pesos despreciables y de igual longitud.
Calcular la medida del ángulo " 6 " que
define la posición de equilibrio. Las tres
esferas están contenidas en un plano ver­
tical.

114. Consideramos nuestro sistema físico, los
tres cuerpos esféricos y las varillas.
Diagrama del cuerpo libre:
W
,
La sumatoria de momentos respecto del
centro de curvatura ”0 ' es igual a CERO.
M,
EMo = 0
Wo %
+ = M,
w i.r Sen (60 - 0)+W3.r Sen 0=W2 r(60 + 0)
1 . Sen(60 - 0) + 3Sen 0 = 2. Sen (60 + 0)
*
*
*
*
*
*
*
•*
♦
*
*
*
*
#
*
*
#
*
#
*
*
*
*
*
*
*
*
*
Cotg 0 = y¡3
0 = 30°
PROBLEMA Ne8
Una rueda de peso 100 N gira sobre su
cubo (riel circular) ascendiendo sobre la
superficie curvilínea por acción del peso
del bloque de 25 N que pende de una
cuerda enrrollada en su superficie. Deter­
minar la medida del ángulo " 0" al cual se
detiene la rueda, suponiendo que el
rozamiento es suficiente para impedir el
deslizamiento, a = 6 cm y b = 15 cm.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
Realizamos el diagrama del cuerpo libre,
de la rueda. Las fuerzas que actúan so­
bre la rueda son los pesos de 100 N; 25
N, además la fuerza de reacción "R" del
cubo representado por una fuerza verti­
cal.
La sumatoria de momentos respecto del
punto "A" es igual a CERO.

115. i m a = o
m a = m a
100. 6 Sen 0 = 25. (15 - 6 Sen 0)
24 Sen 0 = 15 —6 Sen 0
Sen 6 = x
0 = 30°
PROBLEMA Ne9
Una varilla uniforme y homogénea de
longitud “4a" está sujeta a un collarín en
B y descansa sobre un cilindro liso de
radio "a". Sabiendo que el collarín puede
deslizarse libremente a lo largo de la guía
vertical, hallar la medida del ángulo “ 6 "
correspondiente al equilibrio.
*
#
¡i»
#
¡i»
*
*
*
*
*
*
*
*
SOLUCION:
Realizamos el diagrama de fuerzas sobre
la barra homogénea de peso "w".
Fuerza Resultante igual a cero:
TgG = P
Suma de momentos respecto del i 'jntro
de curvatura "0" es igual a cero
XMo = 0
M o = M o
w. 2a Cos 0 = F. a Sec 0
I r 2 Cos2 0 ....(2)
Luego: 2 Cos3 0 = Sen 0
Resolviendo;
0 = 45°
*
#
*
%
*
*
*
PROBLEMA N9 10
La figura muestra una esfera homo­
génea y lisa de peso 4N. El sistema
en equilibrio presenta tres cuerdas, hallar
la magnitud de la fuerza "F", de modo
que la cuerda BM se devía un ángulo
0 = are Sen (1/7) hacia la derecha res­
pecto a la vertical. E¡ bloque P tiene un
peso de 8N.
Además: OM = BM.
SOLUCION;
Consideramos nuestro sistema físico, la
esfera más la porción de cuerdas que
bordean la esfera.

116. La suma de momentos respecto del
punto "B" es igual a CERO:
IMb =0
F W P
M e = M B + M B
F.b = w a + P . (a + R) .... (1)
Pero: BM = MO = R
a = 2R Sen 0
b = R(1 - 2 Sen 0)
Sen 0 = j
Reemplazando en (1):
F = 16N
PROBLEMA Ne 11
La figura (1) muestra una barra uni­
forme y homogénea de peso igual al doble
del peso del bloque "w". Despreciando el
rozamiento, hallar el valor del ángulo “ 9 "
que define la posición de equilibrio.
#
*
*
*
*
*
*
#
*
*
m
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
$
*
m
*
*
$
#
*
♦
*
*
*
*
*
*
*
*
#
*
*
#
*
*
#
*
*
Figura (2) D.C.L. (barra)
SOLUCION.
La figura (2), muestra el diagrama del
cuerpo libre de la barra uniforme y ho­
mogénea de peso “2w".
Del teorema de Lamy, las fuerzas peso
(2w), reacción normal (N) y la tensión en
la cuerda (T=w),deben ser concurrentes.
De la sequnda condición de equilibrio
£ Ma = 0
Sumatoria de momentos respecto al
punto A igual a Cero.
M a + M a = 0
2 w . L Cos a - w. 2L Sen 2 0 = 0
Sen 2 0 = Cos a
Entonces:
2 0 + a = 90° .. (1)
De la le ra , condición de equilibrio
(Teorema Lamy)

117. Ley de Senos:
w 2 w
.... (2)
Sen 0 Sen 30
Sen 30 =2. Sen G
Desarrollando:
3Sen 0 - 4 . Sen3 0 = 2. Sen 0
Sen 0 = 4 Sen3 0
? 1 1
Sen 0 = —, entonces: Sen 0 = —
4 2
Por lo tanto:
0 = 30°
Figura (3 )
Debe observar Ud,, que la relación (1j se
ha utilizado en el D.C.L , figura (2).
PROBLEMA Ne 12
Una barra homogénea de 100cm.
es doblada en un ángulo recto tal
que AB = 40cm. y BC = 60cm. Calcular
la distancia "x" del cual debe sostener,
para mantener el lado AB en posición
horizontal.
*
«
w
*
*
*
$
#
*
*
*
m
*
«t
*
a
*
*
*
*
*
*
*
»!
#
*
+
*
m
*
*
*
*
*
*
*
*
*
*
*
#
$
*
*
*
*
*
#
$
$
*
*
*
~VLjsas¡smr
SOLUCION
D.C.L. (barra homogénea)
< 2 0 - x ) _ J
4K
20cm.
6K
Los pesos de los lados AB y BC son
proporcionales a su longitud respectiva
£M = 0
I,
4
k
■M0 = M 0
i '
I ¡
4K.(20 - x) = 6K.(x)
i
2 (20 - x) = 3x
x = 8 cm
PROBLEMA Ne13
Una varilla de 40 cm. de longitud es
doblada en su punto medio ( B ) formando
un ángulo agudo. Hallar el valor de "x",
para que el lado BC permanezca en posi-

118. ción vertical. La varilla es de un material
uniforme y homogéneo.
Los lados AB y BC, tienen igual tamaño,
por consiguiente igual peso "W“.
El peso de cada lado actúa en su centro
geométrico G1y G2, respectivamente.
D.C.L. (Varilla doblada)
Suma de momentos respecto del punto
“O” igual a cero.
AB BC
M o = M o
w. (x-10) Cos a = w. (20-x) Cos a
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
fe
f
*
*
*
*
*
0
*
o*
*
♦
*
*
*
*
*
*
*
*
0
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
u
*
*
*
$
*
x = 15 cm
PROBLEMA N® 14
La figura muestra una barra homo­
génea doblada en forma de “L". Hallar la
medida del ángulo " 6 “ que define la
posición de equilibrio, si se cumple que:
a2 + 2ab - b2 = 0
SOLUCION:
El peso de los lados AB y BC, son direc­
tamente proporcionales a sus longitudes.
Peso = K. Longitud
El peso de cada lado actúa en su centro
geométrico G, y G2, respectivamente.
D.C.L.(barra homogénea)
IM a - 0
M, M,
ka. —Sen 0 = kb, —Cos 0 - a Sen 0

119. 0 = 45°
PROBLEMA N9 15
La figura muestra tres esferas A; B y C
en equilibrio. Cada varilla es ingrávida
(peso despreciable). Determinar la ten­
sión en la cuerda (1), sabiendo que la
esfera A pesa 6N.
Tapasraesair
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
#
*
*
*
*
*
«
o
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
Analizando la varilla inferior:
2m 3f
í
i
6N
ZMp = 0 -» W b = 4 N
I F y= 0 -» T2 = 10N
Analizando la varilla superior:
T i = 18N
IM o = 0 -> Wc = 8N
£F y = 0 -
PROBLEMA 1*
Una barra homogénea de peso vr
17N,
ha sido doblada en tres partes iguales, tal
como indica la figura, si se mantiene en
equilibrio, determinar la reacción del piso
rugoso sobre la barra.
^ CUERDA

120. SOLUCION
D.C.L. (barra)
±>
2a
2a
o
R.
y
Equilibrio de Rotación y traslación:
* IF x = 0 -» R* =T
*
♦
*
*
*
*
*
*
♦
*
♦
*
♦
*
*
*
IM o = 0
M 0 = M 0
T(4a) = W(a)
W
T =
Rx =
4
W
Del teorema de Pitágoras-
2 2 2
R = Rx + Ry
R = ~ r < r í
4
Del dato:
R = 4,25 N
:
a

121. c
ftp
n
ru
L
04
Va
r»
CINEMATICA
| nal) en cada instante de tiempo con respecto
i a un sistema de referencia
CONCEPTO.
Es parte de la mecánica que estudia las
propiedades geométricas del movimiento
mecánico que describen los cuerpos pres­
cindiendo de su inercia (masa) y de la inter­
acción con otros cuerpos (fuerzas
aplicadas).
SISTEMA DE REFERENCIA.
Es aquel cuerpo o lugar del espacio en
donde se ubica un observador en forma real
o imaginaria para analizar y describir el
fenómeno físico en el tiempo. Para describir
el fenómeno del movimiento mecánico es
necesario asociar con el observador un
sistema cualquiera de coordenadas (sistema
cartesiano) y un reloj.
También llamado radio vector, determi­
na la posición de un cuerpo ( o punto mate-
¡ DESPLAZAMIENTO ( d ).
3
¡
}
í
* Es una magnitud vectorial que se define
J como el cambio de posición que experimenta
$ un cuerpo (o punto) con respecto a un
f sistema de referencia.
*
*
*
*
*
d = A r
—
>
A r : Cambio de posición.

122. Movimiento Rectilíneo
“Es el cambio de posición que experi­
menta un cuerpo con respecto a un sistema
de referencia en el tiempo".
Elementos del movimiento mecánico
1) M ó v il: Se denomina así a todo cuerpo
(o punto) en movimiento, respecto a un
sistema de referencia.
2) Trayectoria : Es aquella línea continua
que describe un punto m aterial en
movimiento respecto a un sistema de
referencia. Si la trayectoria es una línea
recta, el movimiento se llama rectilíneo y
si es una curva, curvilínea
3) Espacio recorrido ( e ): Es la longitud de
la trayectoria entre dos puntos conside­
rados.
Distancia : Es una magnitud escalar,
que se define como el módulo o tamaño
del vector desplazamiento. Su valor no
depende de la trayectoria que sigue la
partícula, sólo es necesario conocer su
posición inicial y final.
*
$
%
*
&
*
*
*
*
*
*
*
*
$
*
£
&
m
&
*
*
$
&
*
$
*
*
%
*
*
*
'Si la partícula se mueve en línea recta y
en el mismo sentido, entonces el espacio y
la distancia tienen el mismo valor"
e = a
II)
Medidas del movimiento
Velocidad. Es una magnitud física vec­
torial. Mide la rapidez del cambio de
posición, que experimenta la partícula
respecto de un sistema de referencia.
Aceleración. Es una magnitud física
vectorial. Mide la rapidez de cambio que
experimenta el vector velocidad en mó­
dulo, dirección y sentido, respecto de un
sistema de referencia
Velocidad Media (Vm)
La relación entre el vector desplaza­
miento del punto material y el intervalo de
e: es mayor que: d

123. tiempo correspondiente, determina la magni­
tud vectorial que se llama "Velocidad media”
del punto material.
V m : Velocidad media
d : Vector desplazamiento
A t: intervalo de tiempo
La velocidad media y el vector des­
plazamiento tienen la misma dirección y
sentido.
m cm km
h
Unidades: — : — ; -7—
Movimiento Rectilíneo Uniforme
(M. R. U.)
Concepto. Es aquel tipo de movimiento
que tiene como trayectoria una línea recta,
sobre el cual los espacios recorridos por el
móvil son directamente proporcionales a los
intervalos de tiempo empleados Se carac­
teriza por mantener su velocidad constante
(módulo, dirección y sentido) durante todo el
movimiento
. . . . . Espacio recorrido
Velocidad = ------------ ;— ~
Tiempo empleado
1) e = V t
2)V = |
3) t ■
e
V
*
«
•
*
s¡s
*
♦
*
*
*
$
*
*
!¡*
*
*
$
$
♦
*
*
*
LEY de KEPLER para el M.R.U.
Todo punto material que tiene movimien­
to rectilíneo uniforme, recorre espacios
iguales en tiempos iguales, por consiguiente:
”EI vector posición describe áreas
iguales en tiempos iguales
*
*
*
"AREAS IGUALES EN
TIEMPOS IGUALES"
PÓsÍCIo T uF l'ÑA PARTICULA
La posición de una partícula o cuerpo se
determina respecto de un sistema de refe­
rencia arbitrariamente eiegido
El desplazamiento que experimenta una
partícula en el eje X, es igual al cambio de
posición.
*
«
s
*
*
*
*
Para el instante (t - 0) la posición se
denomina inicial (xo)
d = xf - x0

124. Posición de la partícula en cada instante
de tiempo o posición final:
xf = xo + d
El sentido de los vectores posición y des­
plazamiento se representa por los signos,
positivo (+) a la derecha y negativo (-) a la
izquierda.
rara el M.R.U.
xf = Xo + V. t
Signos del vector velocidad:
(+V): Movimiento a la derecha, sentido
del eje x positivo.
(- V ): Movimiento a la izquierda, sentido
del eje x negativo.
Y
V
rnov 0
---------- f)>
0
1
1
1
• 1
l
1
r i
«
Xo
D>- (+ x )
GRAFICAS DEL MOVIMIENTO
Relaciona matemáticamente, la posición,
velocidad y aceleración de una partícula en
cada instante de tiempo, haciendo uso de un
sistema de coordenadas cartesianas.
Para el movimiento rectilíneo uniforme:
1) Posición vs Tiempo. Muestra gráfica­
mente la relación, entre la posición de
una partícula en cada instante de tiempo.
*
*
*
*
*
*
*
*
*
*
*
»
*
*
*
*
*
*
*
*
*
*
*
«i*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
I) La pendiente de la recta es igual a
la velocidad de la partícula.
V = Tg0
II) La recta corta el eje de ordenadas
en un punto que nos da la posición
inicial de la partícula.
2) Velocidad vs Tiempo. Muestra gráfica­
mente la relación, entre la velocidad que
tiene la partícula en cada instante de
tiempo.
IV(m/s)
t(s)
I) El área bajo la recta, es igual al
espacio recorrido por la partícula.
A = espacio recorrido
II) En general, el área bajo la recta es
igual al cambio de posición que ex­
perimenta la partícula, en un inter­
valo de tiempo.
U = x ^ 7 ]
PROBLEMA Ne 1
Una persona sale del punto A en auto
a una velocidad de 12 km / h, llega a B y
desea regresar caminandoa 4 km / h
(siguiendo el mismo camino) si todo el
recorrido duró 6 horas. ¿Durante cuánto
tiempo estuvo caminando?
SOLUCION:
El espacio recorrido es el mismo
e - V i. ti = V2 . 12
(12) ti =(4) te
te = 3 ti .... (1)
Pero: 11 + 12 = 6h .... (2)
Resolviendo (1) y (2):

125. 11 = 1,5 h
12 = 4,5 h
Estuvo caminando durante 4,5 horas.
PROBLEMA N92
Un móvil que va a 15 km / h llega a su
destino a la hora "t". Si va a 10 km / h se
demora 2 horas más. ¿A qué velocidad
tiene que ir para llegar a la hora (t + 1)?.
SOLUCION:
La longitud del camino es el mismo en los
tres casos:
e = 1 5 t= 1 0 ( t + 2)
Resolviendo: t = 4 h .... (1)
Entonces la longitud del camino será:
e = 60 km
En el tercer caso:
e 60 km
*
V —
(t + 1) 5 h
V = 12 Km/h
PROBLEMA N93
Una partícula se mueve con M.R.U. en
un plano x - y, con velocidad igual a 4
m/s. Sabiendo que el vector posición
describe una área de 12m7 en cada se­
gundo, determinar la distancia mínima
que se acerca al origen del coordenadas.
SOLUCION:
“Ley de Kepler”
La partícula recorre 4 m en cada
segundo. El área que descubre el vector
posición, en cada segundo será:
A = £ . b . h
12 = 2 (4) d
d = 6 m
*
*
*
#
*
*
*
*
$
*
$
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*■
S
fc
«
i?
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
d distancia mínima al origen de coor­
denadas.
PROBLEMA N®4
Un auto viaja desde una ciudad A has­
ta otra B distante 2 km. empleando 50
segundos. En uno de los viajes (de A
hacia B) después de 20 segundos de ha­
ber iniciado su movimiento sufre un des­
perfecto que lo obliga a detenerse 15 se­
gundos. ¿Cual debe ser el módulo de la
velocidad con que debe continuar el viaje
para que llegue a B sin ningún retraso?.
SOLUCION:
Cálculo de la velocidad normal del móvil.
w a 2000 m ,
V = —= —zr------ = 40 m/s
t 50 s
Espacio recorrido en 20 segundos:
e = V t = (40.20)
e = 800 m
La distancia que le falta recorrer (1 200
m) lo tendrá que hacer en t = 15 segun­
dos, para llegar a B sin retraso.
, _ d _ 1200 m
t “ 15 s
U = 80 m/s
El auto continua su viaje con una veloci­
dad de 80 m/s, duplicando su velocidad
normal.
PROBLEMA N° 5
Un automóvil durante la primera mitad
del tiempo que estuvo en movimiento
llevó la velocidad de 80 km/h y durante la
segunda mitad del tiempo la velocidad de
20 km/h, en línea recta.
¿Cuál es la velocidad media de este
móvil en todo este tiempo?

126. Consideramos los desplazamientos dt y
d2, recorridos en un tiempo T cada uno
di = V i . t y d2 = V2 . t
La velocidad media será:
di + d¿ V i f + V2 .t
*
*
Vm—
Vm —
t + t
V
i+v2
2t
Reemplazando:
Vm = 50 km/h
PROBLEMA NB6
Si un móvil se mueve con una veloci­
dad constante de 5 m/s y en el instante
t = 3 s, se halla en la posición x - 25 m .
Hallar su posición inicial (t = 0).
SOLUCION:
La posición de una partícula en el M. R.
U está definido del siguiente modo:
xF = xG + V . t
Para: t = 35
25 = xq + 5(3)
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
xq : posición inicial (t = 0)
PROBLEMA Ne7
Dos automóviles A y B se desplazan
en una misma carretera. El gráfico mues­
tra la posición de cada uno en relación al
comienzo de la carretera y en función del
tiempo.
Hallar la ecuación de la posición de los
móviles A y B.
SOLUCION;
La pendiente de las rectas nos da la
velocidad.
Va = Tg a =
90 km
3 h
VA = 30 Km/h ....(1)
. , , T n 30 km
VB= T9 P = - 3 t r
V e= 10 Km/h ....(2)
Posición de una partícula en el M.R.U.
* (t) = Xo + V t
Para el móvil “A"
*
$
Xq = 10m *
xA = 3 0 1
*
*
Para el móvil "B"
Xq = 60 + 10 t
*
*
*
m
*
*
í PROBLEMA Nb8
f Un automóvil va de Lima a La Oroya
| (200 km de separación) en cuatro horas y
j el regreso lo hace en dos horas.
| Hallar la velocidad media del recorrido
* total (ida y vuelta).

127. La velocidad media se define como la
relación del desplazamiento entre el
tiempo empleado.
* Si el móvil regresa a su posición inicial,
$ su desplazamiento e.s nulo.
*
ífí
« Por consiguiente en este caso ía veloci-
* dad media del automóvil es igual a cero.
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
#
m
*
*

128. ....
1. MOVIMIENTO RECTILINEO UNI­
FORME (M.R.U)
PROBLEMA N° 01
Una persona debe llegar a un determi­
nado lugar a las 12m y observa que cami­
nando a razón de 3km/h llega 5 horas
después y caminando a Skm/h llega 5
horas antes. ¿Con qué velocidad debe
caminar para llegar a las 12m?
SOLUCION:
distancia = velocidad x t
L = Vi . ti = Va . t2
L =3. (T +5) = 6 .(T - 5) ... (1)
T = 15 horas
Reemplazando en (1): L = 60Km
L 60 Km
T ~ 15 h
PROBLEMA Ne02
Un camino se puede recorrer en 16
horas con cierta velocidad medido en
Km/h y se puede recorrer en 6 horas
menos aum entando su velocidad en
6Km/h. ¿Cual es la longitud del camino?
a) 16 Km b) 32 Km
c) 160 Km d) 320 Km
e) N.A
PROBLEMA N®03
Dos móviles A y B se mueven en sen­
tidos contrarios sobre rectas paralelas Li
y L2 separados entre sí una distancia de
3m. Si después de 1,5s del instante que
m ue stra la fig u ra , la d is ta n c ia de
*
*
*
*
*
*
s
fc
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
#
*
s
fl
*
*
*
*
*
*
*
$
*
separación entre los móviles es de 3 !2
m. Determinar después de que intervalo
de tiempo la distancia de separación es de
5m. Cada uno de los móviles se mueven
con la misma rapidez.
A
«O-
SOLUCION:
De la figura deducimos:
2 . v . t = 3m
pero t = 1,5s
v = 1m/s
La distancia de separación será 5m,
cuando la suma de sus espacios sea
igual a 4m.
2 v . ti = 4m
pero: v = 1 m/s
ti = 2 segundos
V

129. Dos móviles se mueven en sentidos
contrarios acercándose con velocidades
constantes de 4m/s y 2m/s respecti­
vamente. Si inicialmente estaban separa­
dos 18m. ¿Al cabo de cuánto tiempo
estarán separados por segunda vez 12m?
a) 3s b) 4s c) 5s
d) 6s e) N.A.
PROBLEMA Ne 05
Un tren con M. R. U., de largo "L" pasa
un túnel de 200m de largo en 28 segun­
dos. Una mosca fija en el tren, tarda 25
segundos en pasar al túnel. ¿Cuál es el
largo del tren?
SOLUCION:
. 200 tn
. , l
___L
A * . A
B i ' i
J | t u n e F !i i 1111ilu
■
<
C
*5 « !> V fí®
Ktj ■"¿.i---- r» r .i.
Cálculo de la velocidad de ia mosca:
e 200 m
Vm:
t 25 s
= 8m/s
La velocidad del tren y la mosca, son
iguales:
Vtren = 8m/s
Cada punto (A) del tren experimenta un
desplazamiento de (L + 200m) para que
el tren atraviese completamente el túnel.
e = V . t -> (L + 200) = 8 x 28
L = 24 m
PROBLEMA NE06
Un tren demora en pasar frente a un
alumno (muy cerca a él) 8 segundos y
luego recorre íntegramente un túnel de
160m de largo en 48 segundos con velo­
cidad constante . ¿Cuánto mide el largo
del tren?.
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
■
t*
*
*
*
*
*
*
*
«
H
£
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
d) 48 m e) N.A.
PROBLEMA NB07
Se tiene 2 velas (1) y (2) de tamaños
iguales, las cuales tienen una duración de
Ti = 4 horas y T2 = 3 horas, emitiendo
energía luminosa. Si las velas empiezan a
emitir luz al mismo instante. ¿Después de
cuánto tiempo el tamaño de una de ellas
es el doble que el de la otra?
SOLUCION
) ~ ~ r
1 ■ ■ * '"
1
1
(L-2h )
1 2h
t ____ ________ ___
(L - h )
(1 ) (2 )
Consideremos las velas de longitud ,,L''
Velocidad de consumo de las velas:
T i 4
V2 = ^
2 T2 3
.... (2)
Después de un tiempo T , consideremos
las alturas de las velas "2h” y "Ir
e = v . t
vela (1):
(L -2 h ) = | . T
vela (2):
< L -h ) = t . T
Dividiendo: (3) i (4)
(L -2 h ) _ 3
( L -h ) ~ 4
(3)
.... (4)

130. Reemplazando en (4):
T - 2,4 horas
PROBLEMA N908
Si la vela se consume uniformemente
a razón de 0,6 cm/s. ¿Con qué velocidad
se desplaza el extremo de la sombra que
se proyecta en la pared vertical debido al
obstáculo frente a la vela?.
a) t ,2 cm/s b) 1,8 cm/s
c) 1,5 cm/s d) 0,9 cm/s
e) Ninguna
Un automóvil se dirige de una ciudad
"A' a otra ciudad "B", la mitad de su
camino recorre con una velocidad de
30Km/h y la otra mitad a 70Km/h, en línea
recta. Determinar la velocidad media del
automóvil entre A y B
SOLUCION:
L L
*
*
distancia _ L + L *
tiempo ~ ti ^ t£ *
~ + —■ *
V, V2 *
Reemplazando:
Vm = 2_£30M70>
Vm = 42 km/h
PROBLEMA N® 10
Un ciclista se dirige de una ciudad A
hacia otra ciudad B en linea recta, divi­
diendo su trayectoria en tres partes igua­
les. El primer tercio de su camino lo re­
corre con una rapidez de 60Km/h, el se­
gundo tercio con 30Km/h y el último con
20 Km/h.
Determinar la velocidad media del ci­
clista entre A y B.
a) 36,66 Km/h b) 35 Km/h
c) 30 Km/h d) 25 Km/h
e) Ninguna
PROBLEMA Nfi 11
Un avión se airige de B hacia C, el
ruido del motor emitido en B, alcanza al
observador en A en el instante en que el
avión llega a C. Sabiendo que la velocidad
del sonido es de 340 m/s, determinar la
velocidad del avión.
I •
/ _
SOLUCION:
Del gráfico podemos afirmar que el des­
plazamiento del avión es la mitad del
desplazamiento del sonido, en un mismo
inteivalo de tiempo por consiguiente la
velocidad del avión es la mitad de la
velocidad del sonido.

131. Vavion 170 m/s
PROBLEMA N9 12
Un avión se dirige de B hacia C, el
ruido del motor emitido en B, alcanza ai
observador en A en el instante en que el
avión llega a C. Sabiendo que la velocidad
del sonido es de 340 m/s, determinar la
velocidad del avión.
a) 104 m/s
b) 180 m/s
c) 204 m/s
d) 272 m/s
e) N.A.
PROBLEMA Nfi 13
7 J B
l3T/
Dos personas A y B están separadas
una distancia "x”. En cierto instante la
persona “A" dispara una bala con una
velocidad de 170 m/s (horizontalmente)
en dirección del "blanco" que se encuen­
tra junto a la persona ’B''. Sabiendo que
"B" escucha el disparo y 3 segundos des­
pués percibe el impacto con el blanco,
determinar “x".
Velocidad del sonido en ei aire = 340
m/s
SOLUCION:
*
*
*
i
*
S
¡»
*
*
*
♦
*
*
&
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
La velocidad del proyectil es la mitad de
la velocidad del sonido, por consiguiente
cuando el sonido llega a "B" el proyectil
habrá recorrido (x/2), entonces en 3
segundos recorre la otra mitad
e = v , t
x
2
1 7 0 ^ . (3s)
x = 1 020 m
PROBLEMA N® 14
Un niño se encuentra en reposo a una
distancia de 85m de una montaña. En
cierto instante el niño silba. ¿Al cabo de
qué tiempo escucha el eco?
Velocidad del sonido en el aire = 340
m/s.
a) 0,1 s b) 0, 25 s
c) 0,5 s d) 2,0 s
e) N.A.
PROBLEMA Ne 15
Una persona ubicada entre dos mon­
tañas, emite un grito y percibe el primer
eco a los 3 segundos y el siguiente a los
3,6 segundos correspondiente a la otra
montaña. Determinar la distancia de
separación entre las montañas.
Velocidad del sonido en el aire = 340
m/s.
SOLUCION:
El sonido demora en llegar a la montaña
"A” 1,5 segundos y a la montaña "B” 1,8
segundos
distancia = Velocidad . tiempo
Montaña "A" x = (340)(1,5)
x = 510 rri

132. Montaña "B ": y = (340)( 1,8)
y = 612 m
Luego (x +y) = 1 122 m
PROBLEMA N9 16
La distancia de separación entre dos
montañas es 7 980 m. Un automóvil
que se mueve con velocidad constante
V = 17m/s, por una carretera rectilínea que
une las montañas, toca la bocina justo en
el instante que pasa por el punto medio
entre las montañas. Hallar el espacio re­
corrido por el automóvil en el intervalo de
tiempo comprendido entre la percepción
del primer y segundo eco provocado por
las montañas.
Velocidad dei sonido en el aire = 340
m/s.
a) 20m
c) 10Om
e) N A,
PROBLEMA Ns 17
b) 40m
d) 500m
De la figura: x + y = 1 020 m . (1)
distancia = velocidad . tiempo
En (1): 340 . t + 340.(t - 2) =1020
#
*
*
*
*
*
*
•*
i
Dos relojes electrónicos están separa­
dos 1 020 m, cuando dan la hora, uno de
ellos se adelanta 2 segundos. ¿A qué dis­
tancia del reloj adelantado una persona
oirá a los dos relojes dar la hora al mismo
instante?
Velocidad del sonido en el aire = 340
m/s.
SOLUCION.
Resolviendo:
t = 2,5 segundos
Luego:
x = Vs . t = 340 — . 2,5 s
s
x - 850 m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
PROBLEMA Ns 18
Un automovil se mueve con una velo­
cidad constante V = 54 Km/h, en línea
recta dirigiéndose a uná montaña, en
cierto instante el chofer toca la bocina y 8
segundos después percibe el eco. Calcu­
lar la distancia de separación entre el auto
y la montaña, en el instante que el chofer
tocó la bocina.
Velocidad del sonido en el aire = 340
m/s.
a) 1 200 m b) 1 420 m
c) 2 840 m d) 2 420 m
e) N.A.
PROBLEMA N®19
Dos móviles A y B parten simultá­
neamente de un punto común con veloci­
dades V y 2V. A 900 metros parte un
móvil C en el mismo instante y en sentido
contrario con una velocidad 1,5V. Si
transcurridos 10 segundos, B equidista
de A y C. ¿Cuál es la velocidad del móvil
A?
SOLUCION:
2V
1,5V
-•C
*
*
*
De la figura:
x = eB -eA .... (1)
También:
eD+ x + e„ = 900
D L
-

133. 2eB + ec - eA = 900
2 (2V t) + 1,5 V t - V .t = 900
4,5 V . t = 900
Pero: t = 10s
Luego:
V = 20 m/s
PROBLEMA N9 20
Dos móviles A y B se mueven desde
un mismo punto simultáneamente con
velocidades constantes de 20 m/s y 30m/s
respectivamente. En ese instante a una
distancia de 1 300 m, otro móvil C sale al
encuentro de los anteriores con velocidad
constante de 40 m/s.
Determinar despues de qué tiempo el
móvil C equidista de A y B.
a) t = 15 s b) t = 20 s
c) t = 25 s d) t = 28 s
e) Ninguna
PROBLEMA N® 21
Determinar la gráfica: posicion versus
tiempo, de una partícula que se mueve en
el eje X, con velocidad constante V = 1
m/s. Inicia su movimiento en la posición
X0 = - 2 m.
SOLUCION:
La posición de una partícula, en el tiempo
que se mueve con velocidad constante
está definida del siguiente modo:
XF = X0 + V . t
XF = - 2 + 1 t
Xf = t - 2 (1)
Graficando la función (1):
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
a
*
ü
*
*
*
*
*
*
*
M
f
»
$
*
*
Ü
E
sis
*
*
*
*
«
U
S
U
*
*
*
*
*
*
*
Propiedad : La pendiente de la recta es
igual a la velocidad de la partícula.
V = Tg6
PROBLEMA Ne22
La figura muestra la gráfica, posición
versus tiempo, de una partícula que se
mueve en el eje X. Determinar la posición
de la partícula en el insianie i = 5 s
PROBLEMA N®23
Determinar la gráfica, posición versus
tiempo, de una partícula que se mueve en el
eje X, con velocidad constante Vx=-1 m/s (en
el sentido negativo del eje X). Inicia su
movimiento (t =0) en la posición Xo =+ 2 m.
SOLUCION:
La posición de una partícula, en el tiempo
que se mueve con velocidad constante
está definida del siguiente modo:
XF = Xo + V t

134. Xf = 2 —t - (1)
t X
0 2
1 1
2 0
3 - 1
4 -2
5 -3
Graficando la fundón (1)
V = Tg a. = - Tg 0
a) X = - 2 m
c) X = - 6 m
e) N A.
b) X = - 4 m
d) X = - 8m
#
*
*
*
#
*
«
*
*
*
*
Propiedad: La pendiente de la recta es
igual, a la velocidad de la partícula.
PROBLEMA NB24
La figura muestra la gráfica, posición
versus tiempo, de una partícula que se
mueve en el eje X. Determinar la posición
de ia partícula en el instante t = 5 s.
Una partícula se mueve con M. R. U. en
un plano x - y . Si la rapidez del móvil es
V = 3 m/s, determinar la distancia mínima
que se acerca al origen de coordenadas,
sabiendo que el radio vector (vector posi­
ción) describe un área de 6 m2 en cada
segundo.
SOLUCION:
*
*
*
*
*
*
*
*
*
*
*
*
$
$
*
*
■
f
e
*
<
*
*
*
#
*
*
*
*
*
*
*
i
*
Ley de Kepler para el M. R. U.: "En todo
movimiento rectilíneo uniforme, el vector
posición describe áreas iguales en tiem­
pos iguales”.
El espacio recorrido en cada segundo, es
3 metros. Por consiguiente la base del
triángulo es 3m en cada segundo.
A = | . b . h
b = ¿ (3) (d)
d = 4 m
PROBLEMA Nfi 26
Dos partículas A y B se mueven con M.
R. U., en un plano x - y (positivos). Las
trayectorias son paralelas y ambas tienen
la misma rapidez, V = 5 m/s. El vector
posición de A describe un area de 15 m2
y el de B un área de 20 m2, en cada
segundo, respecto del origen de coorde­
nadas. Determ inar la distancia de
separación entre las trayectorias.

135. X
a = 6 m
b = 8 m
*
*
$
4
5
#
*
$
❖
*
*
*
*
*
*
£
*
*
*
*
*
*
*
*
*
*
*
#
*
*
♦
$
#
*
*
*
*
*
*
♦
#
*
♦
*
*
*
v
*
*
s
js
*
*
3
!»
*
*
*
*
*
o
»
*
#
*
*
*
♦
*
*
#
*
♦
+
#
«
I
*
d) 2,0 m e) 3,0 m
PROBLEMA NB27
Dos partículas A y B se mueven con M.
R. U„, en un plano x - y, iniciando un
movimiento en un mismo punto: X = 10m,
con velocidades de 4m/s y 3m/s respec­
tivamente. El vector posición de cada
partícula describe un area de 12 m en
cada segundo, respecto del origen de co­
ordenadas.
Determinar el ángulo que forman las
trayectorias de A y B.
SOLUCION:
Identificando en el triángulo:
a = 37°
Analizando la partícula "B". De la Ley de
Keplerpara el M.R. U La base del triángulo
es igual a 3 m en cada segundo.
Area =
Analizando ia partícula "A” De la Ley de
Kepler para el M. R. U. la base del trián­
gulo es igual a 4m en cada segundo.
' ~ 0
p = 53°
Rpta.: El ángulo que forma la trayec­
toria es 16 .
PROBLEMA Ns28
Una partícula se mueve con M. R. U. en
el plano x - y. La rapidez del móvil es 4
m/s, iniciando su movimiento en el punto
(10 ; 0). El vector posición describe un
área de 12 m2, en cada segundo, respecto
del origen de coordenadas.
Determinar la ecuación de la trayecto­
ria que describe la partícula.
a )y = 3 x -1 0 b )y = 4 x -1 ü
c)y = | ( 1 0 - x ) d )y = |( 1 0 —x)
e) N.A.
PROBLEMA Ne29
El gráfico mostrado representa la
posición de un automóvil en el tiempo.
a) ¿Cuál era la posición del auto al principio
del movimiento (t = 0)?
b) ¿Cuál era la posicion en el instante que
t = 1h?
c) ¿Qué velocidad desarrolló en esta
primera hora de viaje?
d) ¿En qué posición y por cuánto tiempo
permaneció parado?
e) ¿Cuál es su posición a las 4 horas de
viaje?
f) ¿Cuál es su velocidad en el viaje de
regreso?

136. SOLUCION:
a)
b)
c)
Al principio del movimiento el auto
se encuentra en el kilómetro 10.
El auto avanza y después de una
hora (t = 1h) se encuentra en el
kilómetro 30.
La pendiente de la recta que corres­
ponde a la primera hora de viaje nos
dará la velocidad.
Ax 3 0 -1 0
" At “ 1 - 0
V = 20 km/h
d) P erm aneció detenido en
kilómetro 30, durante una hora.
f)
e) A las 4 horas de viaje el auto se
encuentra en el origen (x = 0).
El automóvil llegó hasta la posición
x = 30 km, y a partir de esta posición
el auto comenzó a regresar, la pen­
diente de la recta que corresponde
al intervalo de tiempo <2 , 4> h nos
dará la velocidad:
V =
Ax 0 -3 0
At 4 - 2
V = 15 km/h
El signo ( - ) indica que el auto está
de regreso.
PROBLEMA N930
El movimiento rectilíneo de un móvil
está representado por:
*
*
*
*
*
*
*
*
*
*
*
%
*
*
el *
*
*
*
*
*
*
«
n
*
*
*
*
*
*
m
*
#
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Entonces se puede afirmar que.
I) La velocidad en el intervalo de tiempo;
(0, 2) segundos, es 0,5 m/s.
II) La velocidad media en el intervalo de
tiempo <2 ; 6) segundos, es -1 ,0 m/s.
III) El móvil permanece en reposo (V = 0)
en el intervalo (6; 8) segundos.
a) Sólo I y II son verdaderas
b) Solo II y III son verdaderas
c) Sólo I y III son verdaderas
d) Sólo III es verdadera
e) Todas son verdaderas.
PROBLEMA Ns31
Un avión se dirige de B hacia C, el
ruido del motor emitido en B, alcanza al
observador en A en el instante en que el
avión llega a la posición C. Sabiendo que
la velocidad del sonido es de 340 m/s
determinar la velocidad del avión.
SOLUCION:
De la geometría elemental podemos es­
tablecer una proporción entre los lados
del AABC
El tiempo empleado por el avión y el
sonido son iguales:

137. t =
6 avión es
Vs
Vavión =119 m/s
PROBLEMA Ne 32
¿A qué distancia de la orilla y sobre la
superficie del agua, estalla una bomba; si
la diferencia del tiempo empleado entre el
sonido transmitido por el agua y por el
aire es de 45,5 segundos?
Velocidad del sonido
en el aire
Velocidad del sonido
= 340 m/s.
= 1 250 m/s.
b) 21,25 km
d) 23,25 km
a) 100 m
c) 150 m
e) Ninguna
b) 125 m
d) 180 m
MOVIMIENTO RECTILINEO UNIFORME­
MENTE VARIADO
*
*
*
*
*
*
en el agua
a) 20,25 km
c) 22,25 km
e) N.A.
PROBLEMA NE33
Una lancha patrullera de vigilancia
está a 60 km de otra de la que se sospecha
lleva contrabando. La primera inicia su
persecución a 50 km/h, la otra lancha que
estaba parada se percata 20 minutos des­
pués, de que van en su busca y emprende
la huida en la misma dirección y sentido
de su perseguidora con una velocidad de
30 km/h.
¿Qué espacio recorre la lancha hasta
el instante de ser alcanzada por la Sancha
patrullera?
ACELERACION LINEAL (a).
Es una magnitud física vectorial, mide la
rapidez de cambio que experimenta la velo­
cidad en módulo.
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
¡*
*
*
*
*
*
*
V0 : Velocidad inicial
Vf : Velocidad final
t : Intervalo de tiempo
UNIDADES:
m cm
Convencionalmente el movimiento
puede ser:
ACELERADO.- Si la velocidad aumenta
progresivamente, el movimiento se de­
nomina "acelerado1
'. La aceleración se
representa por un vector que tiene la
misma dirección y sentido de la veloci­
dad. En las fórmulas tendrán signos
iguales.
-------------- ..« O .
RETARDADO.- Si la velocidad disminu­
ye progresivamente, el movimiento se
denomina retardado. La aceleración se
representa por un vector que tiene la
misma dirección pero sentido opuesto
que la velocidad. En las fórmulas tendrán
signos opuestos.
(M. R. U. V)
CONCEPTO.
Es aquel tipo de movimiento en el cual la
velocidad cambia en módulo aumentando o
disminuyendo progresivamente, por lo cual
los espacios recorridos en tiempos iguales
serán diferentes, por consiguiente la par­
tícula se mueve con aceleración constante.
*
*
$
*
*
*
*
#
*
---- —
— f f®

138. Posición de una Partícula en el M.R.U.V.
La posición de la partícula en el instante
de tiempo T , que se mueve en el eje x. será:
”
1 o
x f = Xo + Vo . t + ~ a . t
xo: Posición inicial (t = 0)
Vo : velocidad inicial (t = 0)
GRAFICAS DEL M.R.U. V.
1) Posición vs Tiempo. Muestra giáfíca-
mente la relación, entre la posición de
una partícula en cada instante de tiempo.
*
*
*
*
*
n
2)
Características:
I) La curva es una parábola
II)La pendiente, de la recta tangente
trazada a la curva, es igual a la
velocidad de la partícula en un ins­
tante de tiempo
Velocidad vs Tiempo. Muestra gráfica­
mente la relación, entre la velocidad que
tiene la partícula en cada instante de
tiempo.
V = Tq 6
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
«
t»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
>
1
=
*
*
*
La pendiente de la recta, es iguai a
la aceleración de la partícula.
II)
III)
El área bajo la recta, es igual al
espacio recorrido por la partícula en
un intervalo de tiempo.
En general, el área bajo la recta es
igua! al cambio de posición que ex­
perimenta la partícula, en un inter­
valo de tiempo.
[ A - X2 - xi |
3) Aceleración vs Tiempo. Muestra gráfi­
camente la relación, entre la aceleración
que tiene una partícula en cada instante
de tiempo.
ia(m/s2)
t'.s)
Características:
I) Si la aceleración e~ instante, la
recta paralela al r». uviporal.

139. El área bajo la recta, es igual al
cambio de velocidad que experi­
menta la partícula en un intervalo de
tiempo.____________
A = Vf - V 0
VELOCIDAD MEDIA (Vm)
La relación entre el ve cto r des­
plazamiento de la partícula y el intervalo de
tiempo correspondiente, determina la magni­
tud vectorial que se llama "velocidad media"
de la partícula.
Para el M.R.U.V.
Vm = . - O)
El desplazamiento que experimenta la
partícula, es igual al área bajo la recta
(inclinada).
d = A = área del trapecio
.... (2)
(Vo + Vf) .
d = — —------t
Reemplazando en (2) en (1):
Vm —
Vo + Vf
La velocidad media, se puede interpretar
como aquella velocidad constante que
debe tener un móvil, para recorrer el mis­
mo espacio (e = d) en el mismo intervalo
de tiempo, que otro móvil que tiene acele­
ración constante. Siempre y cuando el
móvil no invierta el sentido de su mo­
vimiento.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
¡h
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
#r
#
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Deducción de fórm ulas que
gobiernan el M.R.U.V.
En principio consideramos una partícula
que se mueve en línea recta, sin invertir
el sentido de su movimiento, por con­
siguiente el espacio recorrido y la distan­
cia tienen el mismo valor.
Disponemos de dos ecuaciones iniciales:
Vf - V o
a = ■
Vm=
t
V o - V f
Secuencia:
1) De la ecuación (1):
at = vF- Vo
2) En el M.R.U.
e = Vm t
(Vo + Vf>
..(1)
•(2)
.... (3)
- (4)
e = - A ...(5 )
Reemplazando (4) en (5):
(Vo + Vo + at)
e = . t
3) M u ltip lica n d o las ecuaciones
(3) y (5):
( v : - v i )
a Le = -----g-----
t Z 2
V F = V 0 + 2 a e
PROBLEMA Ne 1
Dos autos que están separados 100 m
uno delante del otro, parten del reposo en
el mismo sentido y en el mismo instante.
El primero con una aceleración de 5m's2
y el segundo con una aceleración de 7
m/s9. ¿Al cabo de cuánto tiempo el se­
gundo alcanza al primero?

140. A
lOOm eB
Suponiendo que A alcanza a B en el
punto “E“.
e A -e s = 100 m
| ( a A - a B)t2 = 100
Reemplazando datos:
t = 10s
A alcanza a B luego de 10 segundos.
PROBLEMA Ne 2
Un auto corre en una pista horizontal
con una aceleración de 2 m/s2 , después
de 5 s de pasar por un punto "P", posee
una velocidad de 72 km/h. ¿Qué velocidad
tenía el auto cuando le faltaban 9 m para
llegar al punto "P"?
SOLUCION:
t=5s
t 9m
En el tramo PB.
Vp = Vo + a t
(20) = Vp + 2 (5)
Vp = 10m/s ..
En el tramo AP:
V ¡ = V 0 + 2 a e
100 = V * + 2 (2) (9)
(1)
Va = 8 m/s
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Vb=2Om/s *
Un auto parte del reposo con un
M.R.U.V. y recorre entre dos puntos A y
B de su trayectoria la distancia de 1,0 km
durante 10 segundos, si al pasar por B su
velocidad es el triple de la que tuvo en A.
Calcular el espacio que recorrió entre el
punto de partida y el punto A.
SOLUCION:
En el tramo AB:
Vo + V f
e - — _—
1000 =(2V)(10) V = 50 m/s ... (1)
Cálculo de la aceleración:
Vf - Vo 2V
a = -
t t
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
a = 10 m/s
En el tramo OA:
Vp = Vo + 2 a e
Reemplazando (1) y (2)
V2 = 2 a(x)
(2)
x = 125 m
* No necesita el dato t = 10 s
PROBLEMA Nfi 4
Un automovil parte del reposo y re­
corre una trayectoria recta de 270 m. La
trayectoria durante los tres primeros
segundos tiene una aceleración constan­
te, luego con la velocidad adquirida hace
nula la aceleración del móvil durante 6
segundos más, con la cual completa su
recorrido. Hallar la aceleración del móvil
durante el primer segundo.
SOLUCION:
Construyendo la gráfica V - 1

141. El área del trapecio es igual al espacio
recorrido por el móvil
270 = Area = | (15) V
V = 36 m/s ...(1)
La pendiente de la recta nos da la acele­
ración.
a = Tg a
V 36
3 - 3
a = 12 m/s
PROBLEMA N95
Un automóvil de carrera parte del re­
poso con una aceleración constante de
0,8 m/s2 , apenas termina de acelerar em­
pieza a frenar a razón de 0,4 m/s2. Si en
total todo el movimiento duró 5 minutos,
hallar la máxima velocidad que alcanzó el
automóvil.
SOLUCION:
Construyendo la gráfica V - 1
t(s )
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
5
t=
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
La pendiente de la recta nos da la aceler­
ación.
T g a = ^ = 0,8
Tge =^ =0.4
■* T1 - 0,8
-* T2 = o í
De la condición:
Ti + T2 = 300
Reemplazando-
V V
~ + -^7 = 300
0,8 0,4
V = 80 m/s
PROBLEMA Ne6
Un móvil parte del reposo y acelera a
razón constante de 5 m/s2 durante un
tiempo de 20 s luego con la velocidad
adquirida comienza a "desacelerar" a ra­
zón de 2 m/s2 hasta que se detiene com­
pletamente. Calcular el espacio total re­
corrido por el móvil.
SOLUCION:
Construyendo la gráfica V - 1
La pendiente de la recta nos da la aceler­
ación.
T v
g° =20
v
Tge =~ = 2
V = 100 m/s
T2 = 50 s

142. El área bajo la curva nos da el espacio
recorrido.
Area = ^ ( T n - T 2)V
e = -~ (70 s) (50 m/s) V
e = 3,5 km
PROBLEMA N* 7
Un policía de tráfico ve que un auto­
móvil se le aproxima a una velocidad
no permitida de 100 km/h (instante).
En el instante que pasa frente a él,
monta en la moto y sale en su per-
secusión La moto después de acele­
rar durante 10 segundos alcanza su
velocidad tope de 120 km/h. Calcular
cuanto ha tardado ai policía en alcan­
zar al auto.
SOLUCION:
Construyendo la grafica v - 1
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
w
$
*
*
*
*
#
slí
#
*
*
*
*
*
*
*
*
*
En el instante que el policía alcanza
al auto los espacios recorridos, desde
(t = 0) que inicia la persecusión, serán
iguales.
e (auto) = e (moto)
Pero el espacio recorrido es igual al área
bajo la curva.
100 T =
2T
1
360
120
Resolviendo: T = — - h
120
T = 30 segundos

143. *
*
*
2. Movimiento Rectilíneo Uniforme- £
mente Variado (M.R.U.V.)
Signos:
(+) = cuando aumenta la velocidad
(-) = cuando disminuye la velocidad,
(*) = excepto para la formula (2)
PROBLEMA N201
Un ratón se dirige a su hueco en línea
recta con velocidad constante de 2m/s,
cuando le faltan 5 metros para llegar, pasa
por el lado de un gato que se encuentra
en reposo. Si el gato acelera a razón de
2m/s en dirección del ratón. ¿El gato
logra alcanzar al ratón?, si lo alcanza ¿A
qué distancia de su agujero?.
SOLUCION:
ratón
Suponiendo que si lo alcanza en el punto
" B l o s espacios recorridos por el gato y
el ratón serán iguales:
©gato = eratón
1 *2 , , 2V
—. a . t = v . t t = —
t =
2 (2)
t=2segundos
Espaciorecorridoporelratónen:
t = 2s
eratón = V t —
» eratón —2 . (2) = 4m
x = 5 - 4 —
» x = 1 m
Respuesta: El gato alcanza al ratón a 1
metro desuagujero.
PROBLEMA Ns02
Un automóvil, violando las reglas de
tránsito se mueve a 72 km/h en una zona
donde la velocidad máxima es de 40 km/h
Un policía motociclista arranca en su per-
secusión, del reposo, justo cuando el auto
pasa enfrente de él. Si la aceleración
constante del policía es de 0,5 m/s2. ¿Que
sucederá?

144. a) No lo llega a alcanzar.
b) Lo alcanza después de media hora de
persecución
c) Lo alcanza después de 2 minutos
d) Lo alcanza a los 2 km. de distancia.
e) Lo alcanza a 1 600 m de distancia
PROBLEMA Ne 03
Un leopardo africano puede lograr
desde el reposo una aceleración de 80
m/s1 Si va a la caza de una gacela que
puede lograr una aceleración de 4 m/s , y
si ésta inicia la huida desde el reposo en
el mismo instante en que el leopardo está
a 18 metros de ella. ¿Cuánto tardará el
leopardo en atrapar a la gacela?, ¿Cuánto
habrá recorrido la gacela antes de ser
atrapada?, ¿A qué velocidad correrá el
leopardo antes de atrapar a la gacela?
SOLUCION:
1eopa rdo(1)
18 m g a c e l a ( 2 )
$
*
*
*
*
*
*
*
#
m
*
*
a) De la figura: ei - e2 = 18m ... (*)
Pero: e = VQ. t + —. a . t
En (*):
| . (8). t2 - 1 . (4). t2 = 18
Resolviendo, t = 3 segundos
b) Espacio recorrido por la gacela en
t = 3 s, será:
e = j . a . t2 -» e2 = ~ (4) (9)
ez = 18 metros
c) Velocidad del leopardo instante antes
de atrapar a la gacela:
V f =V0 +a. t. -> V f =0 + 8(3)
*
*
*
y
*
*
*
*
*
*
*
*
*
■
f*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
Un zorro plateado, puede lograr desde
el reposo una aceleración de 3 m/s '. Si va
a la caza de un conejo que puede lograr
una aceleración de 1 m/s3 y si éste inicia
la huida desde el reposo en el mismo
instante que el zorro está a 36 m de él.
¿Qué afirmación es falsa?
a) Lo alcanza después de 6 segundos
b) La velocidad del zorro es 18 —
s
instante que atrapa al conejo.
en el
c) La velocidad del conejo es 6 — , en el
instante que es atrapado.
d) El zorro recorre 54 m, antes de atrapar al
conejo.
e) El conejo recorre 20 m, antes de ser
atrapado
PROBLEMA Ne 05
Un móvil parte del reposo y se mueve
con M.R.U.V. sobre el eje X. Sí transcurri­
do un tiempo "t” posee una velocidad "V"
y luego recorre 15 metros en 3 segundos,
siendo su velocidad en ese instante “4V".
Hallar el intervalo de tiempo "t".
SOLUCION:
1) Consideramos tres puntos A; B y C,
sobre el eje X:
VA = 0 VB = v VC=4V
2) En el tramo BC:
(Vo+ Vf)
e = - . t
15 = ^ . 3
Resolviendo- V = 2 m/s
Cálculo de la aceleración:
Vf = 24 m/s
a = -
Vf - Vo
t
a -

145. a = 2 m/s
3) En el tramo SB:
V f = Vo + a . t
2 = 0 + 2 . t
t = 1 segundo
PROBLEMA Ne06
Un móvil viaja de "A“ hacia "B" dis­
tante ”L" metros en línea recta; parte del
reposo con aceleración constante "a"
(m/s2); en el mismo instante sale otro
móvil de B hacia A con velocidad cons­
tante “V" (m/s). ¿Cuál es el valor de la
velocidad de B para que ambos móviles
se crucen a la mitad de la distancia entre
A y B?
1
b) V = ~ -
4
d) V = VaTT
a) V = —. VL/a
c) V = ^ . va .L
e) Ninguna
PROBLEMA Nfi 07
Los extremos de un tren de 350m de
longitud pasan por el costado de una per­
sona (fijo en la Tierra) con velocidades de
5 m/s y 9 m/s respectivamente. Determi­
nar la aceleración del tren y el tiempo que
demora en pasar por el costado de esta
persona.
s
3 5 0 m
SOLUCION:
1) Sabemos que:
( V o + V f ) .
e = t
350 = ^ . t
t = 50 segundos
$
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
#
*
ó
»
*
*
*
*
*
*
*
*
*
*
*
*
2) Cálculo de la aceleración:
( V f - V o )
a =
a =
t
( 9 - 5 )
50
a = 0,08 m/s
PROBLEMA Nfi 08
Los extremos de un tren de 300 m de
longitud pasan por el costado de un poste
de luz con velocidades de 6 m/s y 9 m/s,
respectivamente.
Determinar la aceleración del tren.
a) 0,025 m/s2 b) 0,035 m/s2
c) 0,075 m/s2 d) 0,098 m/s2
e) N.A.
PROBLEMA N2 09
Una partícula con M.R.U.V. tiene una
velocidad Vi = 10m/s en el instante
ti = 2 s y una velocidad V2 = 30 m/s en
el instante t2 = 7s. Determinar la distan­
cia recorrida por la partícula desde el ins­
tante t = 0, hasta el instante t = 10s.
SOLUCION:
Tabla tiempo versus velocidad:
POSICION TIEMPO VELOCIDAD
A t = 0 V
B t = 2 10
C
II
30
D t = 10
1) Cálculo de la aceleración en el
tramoBÜ:
V f - V o (30-10) „ , P
a= ----- -----= ——- - = 4m/s
t (7-2)
2) Cálculo de la velocidad inicial en el
tramo AB:
VF = V0 + a. T
10 = V + 4 ( 2 - 0 )
V= 2m/s (velocidad inicial).

146. 3) Cálculo de la distancia en el tramo
m
e = V o. T + | . a . T2
e = 2(10)+ j . (4)(100)
e = 220 m
PROBLEMA Ns10
Una partícula con M.R.U.V., en el ins­
tante t = 2 s tiene una velocidad de
14 m/s y en el instante t = 5 s su velo­
cidad es de 2S m/s. Determinar el espacio
recorrido por la partícula desde el ins­
tante t = 0 , hasta el instante t = 8 s.
a)162m b)192m c)200 m
d) 232 m e) N.A.
PROBLEMA Ne 11
Una partícula se lanza desde el punto
"A" hacia arriba sobre un plano inclinado
con una velocidad inicial V0 = 20m/s, Si
después de 9 segundos la partícula se
encuentra bajando con una velocidad
V = 16m/s, hallar a qué distancia "d" se
encuentra del punto de lanzamiento en
ese instante. Considerar que ia partícula
en todo momento se mueve con acele­
ración constante.
SOLUCION:
1) Cálculo de la aceleración:
V f = V0 - a . t
(-16) = 20 - a . (9)
a = 4 m/s
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
*
>
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Convensionalmente el signo de la veloci­
dad es positivo hacia arriba y negativo
hacia abajo.
2) Cálculo de la distancia "d":
2 2
VZ = V —2 a . d
F o
(-16)2 = (20)z - 2 (4) . d
d = 18 m
PROBLEMA Ns12
Desde un punto “A'' sobre el plano
inclinado, se lanza una partícula hacia
arriba (t = 0) con una velocidad inicial
V0 = 12m/s. Si después de 5 segundos la
partícula se encuentra bajando con una
velocidad V = 8 m/s, determinar en qué
instante “t“ la partícula pasará por su
posición inicial.
a) t = 3 s b) t = 5 s c)t =5.5 s
d) t = 6 s e) N.A.
PROBLEMA N9 13
Un automóvil que parte del reposo se
mueve con una aceleración constante
a = 1 m/s2en línea recta dirigiéndose hacia
una montaña. Al partir el chofer emite una
señal sonora y cuando ha recorrido 32
metros recibe el eco. Determinar la dis­
tancia de separación inicial ( t = 0) entre
el auto y la montaña.
Velocidad del sonido en el aire = 340
m/s.
SOLUCION:
El intervalo de tiempo empleado por el
auto en desplazarse 32m, es el mismo
tiempo que emplea la onda sonora en ir
y regresar a ia montaña con una rapidez
de 340 m/s.

147. (X - 32)
1 ?
Para el auto: e = VQ. t + —a . r
32 = 0 + 1 ( 1 ) t2
jji
t = 8 segundos
Para el sonido
espacio —Vsonido t
x + (x - 32) = 340 (8)
x = 1 376 m
PROBLEMA Ne 14
Un automóvil que inicialmente se en­
cuentra en reposo^ sale con aceleración
constante a = 1 m/s2en línea recta, aleján­
dose de una montaña. En el instante que
sale, el chofer toca la bocina y cuando a
recorrido 18m percibe el eco. Hallar la
distancia de separación inicial entre el
auto y la montaña.
Velocidad del sonido en el aire = 340
m/s.
a) 1 011 m b) 1 022 m
c) 1 033 m d) 1 044 m
e) N.A.
PROBLEMA Ns 15
Determinar la gráfica, velocidad ver­
sus tiempo, de una partícula que se mue­
ve en el d e X, con aceleración constante
a*= 1 m/s~ inicia su movimiento (t = 0) con
una velocidad V0 = - 2 m/s (en el sentido
negativo del eje X).
SOLUCION:
Sabemos que: V f = V Q + a . t
Reemplazando
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
$
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Luego.
V f = t —2 (1)
t V
0 -2
1 -1
2 0
3 1
4 2
5 3
Graf¡cando la función (1):
Ks)
1° PROPIEDAD: La pendiente de la recta
es igual, a la aceleración de la partícula.
2o PROPIEDAD : El área bajo la curva
es igual, al cambio de posición que ex­
perimenta la partícula en un intervalo de
tiempo.
[(Xf - X o) = Ai - A 2
* Se considera el signo del área
Vf = - 2 + 1 t

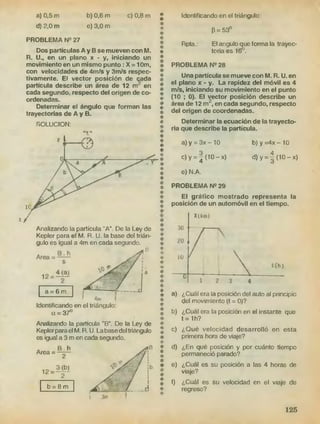
148. 3 PROPIEDAD: El espacio recorrido
por la partícula es igual, al área bajo la
curva (en general) sin considerar los sig­
nos.
espacio = Ai + A2
PROBLEMA N® 16
La figura muestra, la gráfica V - t de
una partícula que sale del origen (X = 0),
moviéndose en línea recta.
¿Cuál(es) de las siguientes afirmacio­
nes son verdaderas?.
I) Del instante t = 2 a t = 3 s. la partícula se
encuentra en reposo.
II) En el intervalo de tiempo [0 ; 5] segun­
dos, el espacio recorrido por la partícula
fue de 5 metros.
III) En el instante t = 4,5 s, el móvil estaba
de regreso a su posición inicial,
IV) En el instante t = 4 s, el móvil se en­
cuentra a 2 metros del origen.
a) Sólo I y II b) Sólo III
c) Sólo I , II y IV d) Sólo II y III
e) Todas son verdaderas
PROBLEMA Nfi 17
Una partícula se mueve sobre el eje
X. En el instante t = 0, su posición es
X0 = - 2m. La figura muestra sus gráfica
V - t .
Determinar su posición en el instante
t = 6 s.
*
*
*
#
*
*
*
$
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
$
*
*
*
«i
*
*
*
*
*
*
s¡*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION
El cambio de posición que experimenta
la partícula es igual al área bajo la recta;
en la gráfica V - 1
(Xf - X0) = área del trapecio,
(3 + 9) ^
(Xf - X0) = — g— . 6
XF- (—2) = 36
XF = 34 m
PROBLEMA Ns 18
Dos móviles A y B parten al mismo
tiempo, si en el instante t = 0, sus posi­
ciones son: Xa = - 2 m y Xb = 4 m,
respectivamente. Calcular en qué ins­
tante de tiempo “t" se encuentran, si sus
gráficas V - t son las siguientes:
Vü(m/s)

149. Nota: A y B se mueven sobre el eje X.
a )t = 2 s b )t = 4 s
c) t = 6 s d) t = 8 s
e) N.A.
PROBLEMA Ne 19
Una partícula se mueve sobre el eje X,
en el instante t = 0, su posición es
Xo= 0- La figura muestra su gráfica V - 1.
Determinar su posición en el instante
t = 6 s y el espacio recorrido en el inter­
valo de tiempo [0 ; 6] segundos.
SOLUCION:
El cambio de posición, que experimenta
la partícula es igual al área bajo la recta,
en la gráfica V - 1
:
- Cálculo del área:
Ai = 16m y A2 = 4m
Luego: (Xf - X0) = Ai - A2
Xf - 0 = 16- 4 m
XF = + 12m
y 1
J L
16 m ¡
. --- ------- ¿t=4
0
iH --- ^ ^ ^
4 m
,=6
- Cálculo del espacio recorrido:
e = Ai + A2
e = 16 m + 4 m
e = 20m
PROBLEMA NB20
La figura muestra, la gráfica V - t, de
una partícula que se mueve en el eje X, en
el instante t = 0, la posición del móvil es:
Xo = +2 m.
¿Cuál(es) de las siguientes afirmacio­
nes son verdaderas?
I) En el instante t = 4s, la partícula se en­
cuentra en el origen de coordenadas: (X
= 0).
II) En el intervalo de tiempo [0; 4] segundos,
el espacio recorrido por la partícula fue
de 10 metros.
III) En el intervalo de tiempo { 2 ; 3 ) segun­
dos, la velocidad y aceleración tienen
igual sentido (a la izquierda, respecto del
sistema de referencia).
*
*
*
*
*
*
*
*
*
*
*
*
*
»
!>
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
#
*
*
*
*
*
*
*
*
*
*■
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

150. IV) En el instante t = 3,5 s el rhóvil estaba de
regreso a su posición inicial.
a) Sólo I y II b) Solo II y III
c) Sólo I, II y IV d) Sólo IV
e) Todas son verdaderas.
PROBLEMA Ne21
La gráfica velocidad versus tiem ­
po, describe el movimiento de una par­
tícula. Si para t = 24 segundos, el espacio
recorrido es 96m. ¿Qué velocidad máxima
alcanzó la partícula?
t ( s )
La velocidad máxima es igual a la altura
del triángulo
El espacio recorrido por la partícula es
igual al área del triángulo, en la gráfica
V - t :
b x h
e = -
96 =
2
(24) .V
Vmax = 8 m/s
PROBLEMA Ne22
La figurs muestra, la gráfica V - 1 de
una partícula que se mueve en el eje
X. Inicia su movimiento en la posición
Xo = 12 m, (t = 0)
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
+
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
¿Cuál(es) de las siguientes afirmacio­
nes son verdaderas?
I) En el instante t = 2s, el móvil se encuentra
en el origen ( X = 0)
II) En el instante t = 4s, el móvil se encuentra
en su posición inicial (X = 12m).
III) En el intervalo de tiempo [0; 5] segundos,
el espacio recorrido por el móvil fue 28
metros.
IV) En el instante t = 3s, el móvil se encuentra
a 4 metros del origen (X = 4m).
a) Solo I y II b) Sólo II y III
c) Sólo III y IV d)Sólo I, II y III
e) Todas son verdaderas
PROBLEMA Ne 23
Un auto está esperando que cambie la
luz roja, cuando la luz cambia a verde, el
auto acelera a razón de 2 m/s2 durante 6
segundos, después del cual se mueve
con velocidad constante, en el instante
que el auto comienza a moverse un ca­
mión que se mueve en la misma dirección
con velocidad constante de 10 m/s, lo
pasa. ¿En qué intervalo de tiempo y a qué
distancia se encontrarán nuevamente el
auto y el camión?
SOLUCION:
1) Analizando el movimiento del auto:
VF = Vo + a . t
Vf = 0 + 2 (6) = 12

151. La velocidad máxima alcanzada es:
12 m/s
Espacio recorrido = Area del trapecio
(b+ B)
e auto =
2
(T - 6 + T)
12 = (2T —6) 6 ... (1)
2) Espacio recorrido por el
auto = 10. T (2)
3) Cuando el auto alcanza al camión, los
espacios recorridos serán iguales;
igualando (1) y (2)
(2T - 6)6 = 10T
T = 18 s
X = 180m
Cálculo de la distancia, reemplazan­
do en (2):
X = 10T
X = 10(18) ->
PROBLEMA Ne 24
Un auto y un camión se mueven por
una carretera a 72 km/h, cuando el auto
está a 5m detrás del camión comienza a
acelerar hasta colocarse 55m delante de
él. ¿Cuál será el tiempo mínimo que de­
mora la operación, si la máxima acelera­
ción del auto es de 2,5 m/s2 y sabemos
que su máxima velocidad alcanzada es
igual a 90 km/h?
a) 12s b) 13s c) 14s
d) 15s e) N A.
PROBLEMA Ne25
La aceleración de una partícula, que se
mueve en línea recta, varía mediante la
siguiente ley:
l~aF=~i
:3q + C . t i
*
«
ü
#
*
*
*
*
*
*
*
s
i*
$
*
$
*
*
*
*
*
sis
*
s|*
*
*
*
*
*
*
*
*
S
Ü
*
>
!*
*
*
*
*
*
*
*
*
*
*
sí¡
a0: aceleración inicial (t = 0)
C : celeridad o plus aceleración (m/s3)
Si la partícula inicia su movimiento
con una aceleración de 2 m/s2y celeridad
constante C = 1 m/s3. Determinar la grá­
fica aceleración versus tiempo.
*
*
*
*
*
*
*
*
*
*
«
i*
*
*
*
*
*
*
*
SOLUCION:
De la fórmula:
3F = So + C . t
aF = 2 + (1) t
ap = 2 + 1
t a
0 2
1 3
2 4
3 5
4 6
Graficando la función (1):
1o PROPIEDAD: La pendiente de la recta
es igual, a la celeridad (plus aceleración)
de la partícula_________
~ C = Tg 6 j
2o PROPIEDAD: El área bajo la curva es
igual, al cambio de la velocidadcjue ex­
perimenta la partícula en un intervalo de
tiempo.

152. 1 (VF- y 0) = A i - A 2 ~ j
* Se considera el signo del área.
PROBLEMA N* 26
La figura muestra, la gráfica a - 1de una
partícula que inicia su movimiento (t = 0)
con una velocidad V0 = +9 mis, en el eje X.
¿Cuál (es) de las siguientes afirmacio­
nes son verdaderas?
I) En el instante t = 2 s, la velocidad del
móvil es cero (V = 0).
II' En el intervalo de tiempo (2;3) segundos,
el móvil se encuentra en reposo.
III) En el instante t = 4 s. la velocidad del
móvil es 3m/s.
IV) En el instante t = 5 s, ia velocidad del
móvil es 6 m/s.
a) Sólo I b) Sólo II
c) Sólo III d) Sólo I, II y IV
e) Todas son verdaderas.
PROBLEMA Nfi 27
Se tiene el gráfico a - t de un móvil
que se mueve en línea recta. Si en el
instante t = 0 su velocidad es “V” y para
t = 4 s la velocidad es "3V", determinar su
velocidad para t = 6s.
*
*
#
*
*
*
♦
*
*
*
*
*
*
*
*
*
1) En el intervalo de tiempo: [0 ; 4) se­
gundos, el área bajo la recta es igual
al cambio de la velocidad.
(Vf - Vo) = área del triángulo
( 3 V - V ) = | . ( 4 ) (5)
V = 5 m/s
2) En el intervalo de tiempo: [4;6) segun­
dos.
VF = V0 + a. t
Vf = (15) + 5(2)
*
*
*
*
*
*
*
*
+
*
*
*
*
*
*
*
*
*
*
*
i
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Vf = 25 m/s
PROBLEMA N928
Se tiene el gráfico a - 1de una partícula
que se desplaza en línea recta. Si en el
instante t = 0 su velocidad es "3V", deter­
minar su velocidad para t = 6 s.
a) 20 m/s
c) 64 m/s
e) Ninguna
b) C0 m/s
d) 84 m/s

153. Una partícula que se mueve en línea
recta inicia su movimiento (t = 0) con una
velocidad V0= 3 m/s. La figura muestra su
gráfica a - 1. Determinar su velocidad en el
instante t = 8 s.
a(m/s )
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
a(m/sZ )
2 ------
PROBLEMA Ne31
Una partícula se mueve en el eje X,
mediante la siguiente ley:
Xp —
Xo +Vot +2 ao • +g ■C . t3
Sus gráficas v - t y a - t , son:
SOLUCION:
El cambio de velocidad que experimenta
la partícula es igual al área bajo la curva,
en la gráfica a —t:
(Vf - V0) = área del trapecio
( V f - V o ) = ^ . 2
Vf - 3 =12
Vf = 15 m/s
PROBLEMA Ne30
Una partícula que se mueve en línea
recta, inicia su movimiento (t = 0) con una
velocidad V0= -12 ,5 metros por segundo.
La figura muestra su gráfica a - t . ¿En
qué instante "t" su velocidad es nula?.
a) 3 s
d) 7 s
b) 4 s
e) N A
c) 6 s
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Si la partícula inicia su movimiento
(t = 0) en la posición X0= - 2m, determinar
su posición en el instante t = 4s.
SOLUCION.
1) De la gráfica V - t , la velocidad inicial
(t = 0) es: Vo = 3 m/s.
2) De la gráfica a - t, la aceleración
inicial (t = 0) es: a0 = 2 m/s*1 La
celeridad es igual a la pendiente de la
recta:

154. 3) Reemplazando en la ley del
movimiento:
Xf =(-2)+3(4)+|(2)(16) + 1 (3)(64)
XF = 58 m
PROBLEMA Ns 32
La ley de movimiento, de una partícula
que se mueve en el eje X, se define del
siguiente modo:
Y _ X 0 t1 t2 t3
F “ O! + V o i , + a °2 ! + C 3Í
Sus gráficas V - 1 y a - 1, son:
Si la partícula inicia su movimiento
(t = 0) en el origen (X =0), determinar su
posición en el instante t = 5s.
a) Faltan datos
c) X = 125 m
e) Ninguna
b) X = 100 m
d) X = 625 m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
slí
5tí
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Ü
í
*
¡f=
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Un perro se encuentra echado sobre el
piso. A 32 m de él un motociclista arranca
y sale del reposo (V = 0) con una acelera­
ción constante a = 1 m/s2. Determinar la
mínima velocidad constante del perro, tal
que puede alcanzar al motociclista.
SOLUCION:
i 32 m
a *
’-.p v rw ; 'M
motocicli sta(2
1
perro (1)
De la figura: 32 + e2 = ei
Reemplazando:
32 + | . a . t2 = V . t
Luego:
1
. r - V . t + 32 = 0
Resolviendo:
t = V ± V V 2 - 6 4
Pero: 'T e su n númeroreal positivo
Entonces:
V2- 64 > 0
V(míninno) —8 m/s
PROBLEMA Nfi 34
Un leopardo africano se encuentra
“muerto de hambre’ ,a 81 metros de él una
gacela sale del reposo en línea recta con
una aceleración constante de 2 m/s2. De­
term inar la mínima, velocidad media
(constante) del leopardo, tal que pueda
alcanzar a la gacela.
a)imposible,elleopardoestámuerto
b) 18 m/s
c) 16 m/s
d) 14 m/s
e)Ninguna anterior

155. Un perro corre detrás de un automóvil
con una rapidez de 6m/s, cuando se en­
cuentra a 64 m de él sale el auto del
reposo con una aceleración constante
a = 0,5 m/s . Determinar después de qué
tiempo a partir de ese Instante el perro
alcanza el automóvil. Si no lo alcanza,
determinar la distancia mínima que el
perro se acercó al auto.
SOLUCION:
a u t o ( 2 )
¡"64 m*
d = | | - 6 | +28
La distancia "d” es mínima cuando:
t = 12 s
Luego:
drninima = ?8 m
perro (1)
Suponemos que no lo alcanza, donde
"d" es la distancia mínima que el perro
se acerca al auto:
Del gráfico:
ei + d = 64 +
d = 62 - ei +64
d— . a . t 2—V . t + 6 4
d = | . (0,5).t2 - 6 t + 64
completando cuadrados:
d = |-~| - 2 I - H . 6 + 36 + 28
Dos móviles A y B desde las posicio­
nes mostradas en la figura salen del re­
poso (V = 0), con aceleración constante
8A = 6m/s2 y aB = 8 m/s2, a través de dos
carreteras que se cruzan formando un
ángulo recto. Hallar la mínima distancia
que se acercan los móviles A y B durante
su movimiento.
„ ____ 8
a) 1,8 m ** '
A «
=t¿=
b) 2,8 m Ü'OV
*
*
♦
*
*
*
♦
*
*
*
*
*
*
mov
c) 3,8 m
d) 4,8 m
e) N.A.
PROBLEMA Ne37
A partir de la gráfica V - t, se pide
determinar la velocidad media, dei móvil,
en el intervalo 4 ; 12 segundos
V ( m / s )
t i s )
*
*
*
*
*
*
0| 4
SOLUCION:
El desplazamiento que experimenta el
móvil en el intervalo 4 ; 12 segundos,
es igual al área bajo la curva.
d = area = 60 m Por definición:
Vm =
A t
60m
(1 2 -4 )
Vm= 7,5 m/s

156. Hallar la velocidad media entre t = 1 s
y t = 2 s, de un móvil que se desplaza en
línea recta con la siguiente ley de movi­
miento:
X = 7 1
2 +2t - 2
X : posición (m)
t : tiempo (s)
a) 13 m/s b) 15 m/s
c) 18 m/s d) 23 m/s
e) N.A.
PROBLEMA Ne39
El gráfico V - t mostrado nos repre­
senta el movimiento de dos móviles A y
B. Si ambos móviles se encuentran en el
instante t = 6 s , ¿Qué distancia los
separaba inicialmente?
SOLUCION:
La distancia de separación inicial, es
igual a la diferencia de espacios recorri­
dos.
*
*
<
*
*
*
♦
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
m
*
*
*
*
*
*u
*
*
*
*
*
d = 16 m
PROBLEMA Ns40
Se tienen el gráfico V - 1 de un móvil
que se mueve sobre el eje X y que en el
instante t = 0 su posición es X0 = 5 m.
¿En qué instante pasará por segunda
vez por el origen?
SOLUCION:
Posición de una partícula, en el M.R.U.V:
XF = Xo + Vot + | . a . t 2
0 = 5 - 1 0 1 ♦ i f f ' 1
| t2 - 2 t + 1 = 0
Resolviendo:
ti = ( 3 - V 6 )
t2 = (3 + V6)
1ra. vez
: 2da vez

157. Ü
M OVIM IENTO DE CAIDA LIBRE
CONCEPTO.
Es aquel tipo de movimiento, que tiene
como trayectoria una línea vertical. Todos los
cuerpos abandonados cerca de la superficie
común, denominada aceleración de la
gravedad "g".
g = 9,8 m/s2
CONSIDERACIONES:
La máxima altura alcanzada por un cuer­
po es suficientemente pequeña como para
despreciar la variación de la gravedad con la
altura.
La velocidad máxima alcanzada por el
cuerpo es suficiente pequeña para despre­
ciar la resistencia del aire.
Bajo estas consideraciones se deduce
que el movimiento de caída libre es un
M.R.U.V. donde la aceleración de la gra­
vedad "g“ permanece constante.
En las ecuaciones escolares, se consi­
dera al signo positivo cuando el cuerpo baja
(movimiento acelerado) y el signo menos
cuando el cuerpo sube (movimiento retar­
dado).
b .#vb=0
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
¡t
*
*
*
*
*
*
*
*
*
»
*
*
*
*
*
*
*
*
*
*
*
tf
*
$
*
*
*
*
*
*
*
*
*
*
*
*
Cuando un cuerpo lanzado hacia arriba,
alcanza su altura máxima, su velocidad in­
stantánea es igual a cero y su aceleración es
igual a ''g”.
La velocidad de lanzamiento en "A" es
igual a la velocidad de llegada en "C", en
módulo y dirección.
El tiempo de subida en el tramo AB es
igual al tiempo empleado de bajada en el
tramo BC.
La velocidad en los puntos M y N son
iguales en módulo y dirección pero sentidos
opuestos.
FORMULAS ADICIONALES
Dos partículas A y B, son lanzadas
simultáneamente en caída libre.
P'
1­
!-
i-
TIEMPO DE ENCUENTRO
t =
H
V a + V b
TIEMPO DE ALCANCE
t =
V a - V b

158. Dos cuerpos iguales se encuentran a
una altura de 20 m; uno se deja caer y
simultáneamente el otro se lanza hacia
abajo con una velocidad de 15 m/s. Calcu­
lar la diferencia de tiempo en llegar al
piso .
%= 10 m/s2
SOLUCION:
Apliquemos la siguiente fórmula:
h = Voy. t + l . g t2
20 = 0 + ^ (10). t2
ti = 2 s
Segunda piedra:
(1)
20= 15. t+ ^ (10) t"
Í2 = 1 S
Luego, la diferencia de tiempos es igual
a 1,0 segundo,
PROBLEMA N®2
Se lanza un cuerpo verticalmente
hacia arriba; si a la mitad del recorrido de
su altura máxima, su velocidad es de 10
V2 m/s. Calcular la velocidad con que se
lanzó el cuerpo,
g = 10 m/s2.
SOLUCION;
V=Q © C
10 2
m a
H/2
H/2
Tramo BC:
v ‘ = Vo = 2gh
*
*
♦
*
*
5
#
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
m
*
m
#
*
*
*
*
*
*
*
*
*
*
*
»
*
*
*
*
*
+
$
*
*
«
i*
*
*
*
*
*
*
*
#
*
*
#
*
*
*
I
*
*
#
*
*
*
*
*
H = 20 m .... (i)
Tramo AC:
2 O
V F = V F- 2 g h
0 = V ¡,-2(10)(20)
V0 = 20 m/s
PROBLEMA N* 3
Desde el penúltimo piso de un edificio
se deja caer (V = 0) una piedra, al mismo
tiempo (t = 0) que del último piso se lanza
hacia abajo otra piedra con una vefocidad
inicial de 4 m/s. la distancia entre cada
piso es 7 m. Calcular al cabo de qué
tiempo estarán separadas las piedras 3 m.
Dar como respuesta el tiempo mínimo.
g = 10 m/s2
SOLUCION:
- 8
l
~T
7m
A # -
i
A’ •--4
3m
De la figura:
hB + 3 = hA + 7
hB-hA = 4 .'...(1)
Reemplazando en (1):
4 t + | g . t 2 - ^ g . t 2 = 4
4 1= 4
t= 1,0s

159. En el segundo caso B’ se encuentra 3 m
delante de A'.
PROBLEMA Na4
Dos cuerpos A y B se encuentran en
una línea vertical separados por una dis­
tancia de 100 m. El cuerpo "A" (está ar­
riba) se deja caer y simultáneamente el
cuerpo "B” (está abajo) se lanza hacia
arriba con una velocidad de 50 m/s. ¿En
qué tiempo chocarán los cuerpos?
SOLUCION:
Cálculo del tiempo de encuentro:
d
t =
Va + Vb
Va y Vb : velocidad inicial de A y B.
Reemplazando:
100
t = -
0 + 5 0
*
*
*
*
*
*
Se lanza verticalinente hacia arriba
una piedra con velocidad de 20 m/s. Cal­
cular el tiempo que demora en alcanzar
una velocidad de 6 m/s por segunda vez.
g = 10 m/s2.
SOLUCION:
v f = V o + g . t
— 6 = 2 0 - 1 0 t
t = 2.6 s
o
¡t6m/s
20m/s^
t = 2,0 S
Chocan los cuerpos A y B, despues de 2
segundos.
( - ) : El signo negativo se debe al sentido
hacia abajo de la velocidad final

160. 1 M OVIM IENTO VERTICAL O
MOVIMIENTO DE CAIDA LÍBRE
ECUACIONES ESCALARES:
1) h = v 0t ± 1 . g t 2
2) h = v Ft ± g t2 .... n
3)
<
T
I
II
<
O
1
+
<o
t
4)
2
v F = Vo ± 2 . g . h
5) h =
ÍV0+ VF
.t
2
>
Signos: (+). cuando el cuerpo baja.
(-)• cuando el cuerpo sube.
(*): excepto para la formula (2)
PROBLEMA Ns 01
Un globo m etereológico desciende
con una velocidad constante V = 5 m/s,
cuando se encuentra a una altura de 60 m
sobre la superficie, desde el globo se
abandona una piedra. ¿Qué tiempo de­
mora la piedra en llegar al suelo?.g =10
m/s2
SOLUCION:
La velocidad inicial de la piedra es la
misma que la del globo.
V0 = 5 m/s
De la fórmula:
h = Vo t + . g . t2
60 = 5 , t + | (10). t2
#
*
*
*
*
*
*
*
#
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
S
U
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
12 = t + 1
'
Resolviendo: t = 3 s
PROBLEMA Nfi 02
Un globo se eleva verticalmente con
una velocidad constante de 5 m/s, aban­
dona un lastre en el instante en que ei
globo se encuentra a 30 m sobre ei suelo.
¿Al cabo de cuántos segundos de ser
abandonado el lastre, llegaré a la Tierra?
g = 10 m/s2
a) 1 s b) 2 s
c) 3 s d) 4 s
e) N.A.
PROBLEMA ^ 03
En cierto planeta se observa que un
cuerpo cayendo cerca de la superficie, en
caída libre, duplica su velocidad luego de
recorrer 81 m etros en la que tarda 3
segundos. Calcular la aceleración de la
gravedad en este planeta que no tiene
atmósfera.
SOLUCION.
Cálculo de la velocidad:
. (Vo + Vf)
^ _ _ t
(V + 2V)
81 = (3)
V = 18 m/s

161. Cálculo de la aceleración de la gravedad
(Vf - Vo) (36 -1 8 )
g =
t
g = 6 m/s
PROBLEMA NB04
En cierto planeta se observa que un
cuerpo cayendo verticalmente cerca de la
superficie, triplica su velocidad durante
un recorrido de 20 m en el que tarda 2
segundos.
¿Podría este planeta ser la Tierra?
a) No, la aceleración es muy pequeña.
b) Falta mayor información para de­
cidir
c) No, la aceleración es muy grande.
d) Si. podría ser la Tierra
e) Se necesitarán cálculos muy com­
plicados para determinar la acele­
ración de la gravedad.
PROBLEMA Ns 05
Se deja caer un objeto desde la azotea
de un edificio. Cuando pasa cerca a una
ventana de 2,2 m de altura, se observa que
el objeto invierte 0,2 segundos en recorrer
la altura de la ventana.
¿Que distancia existe entre la cima del
edificio y la parte superior de la ventana?
g = 10 m/s2
*
*
*
*
*
*
*
*
$
*
*
*
*
*
$
*
s
fe
$
*
$
♦
*
*
*
*
*
$
#
*
*
*
*
*
*
*
*
*
♦
$
s
fr
$
s
fe
$
#
*
*
*
♦
$
$
*
*
*
*
*
*
(H + 2,2) = ~ . g . t2
En el tramo /ÍB:
H = l . g . ( t - 0 , 2 ) 2
(2) en (1):
t = 1,2s
Reemplazando en (2):
H = —
■
(10) (1,2 —0,2)2
-..(1)
... (2)
H = 5 m
PROBLEMA Ns 06
Se deja caer un objeto desde la azotea
de un edificio. Cuando pasa cerca a una
ventana de 1,05 m de altura, se observa
que el objeto invierte 0,1 segundo en re­
correr la altura de la ventana.
¿Qué distancia existe entre la cima del
edificio y la parte superior de la ventana?
p
g = 10 m/s
a) 6 m b) 4 m c) 5 m
d) 3 m e) N.A.
PROBLEMA Nfi 07
Dos piedras A y B están separadas por
una distancia de 200 m, como indica la
figura, se ponen simultáneamente en
movimiento, la de arriba (A) se suelta y la
de abajo (B) se lanza verticalmente hacia
arriba con una velocidad Vb = 40m/s. ¿Al
cabo de qué tiempo chocan las piedras?.

162. 200 m
*
#
SOLUCION:
De la figura:
200 m
A
«V ,
ijv
'
h! + h2 = 200 .... (1)
De la formula:
h = V0 1 + ^ . g . t2
En(1):
^ . g . t2 + VB.t - ^ . g . t2 = 200
VBt = 200
40.t = 200
t = 5 s
PROBLEMA Nfi 08
Dos piedras A y B es’án separadas por
una distancia de 20 m, tal como indica la
figura, se ponen simultáneamente en mo­
vimiento, la de arriba (A ) se lanza verti-
caimente hacia abajo con una velocidad
de 5 m/s y la de abajo se suelta (V = 0). ¿Al
cabo de qué tiempo chocan la piedras?.
20 re j 1
,í
- ---------- i-
B ' 1
i
i
!
■
v i
*
*
*
♦
*
*
*
♦
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
«
*
n
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«i
$
*
#
*
#
a) No llegan a chocar las piedras.
b) Chocan en el infinito.
c) Chocan si consideramos:
g = 19,6 m/s2.
d) Chocan en el instante, t = 3 s
e) Chocan en el instante, t = 4 s
PROBLEMA N* 09
Un cuerpo "A" se de|a caer a partir del
reposo desde una cierta altura y después
de 2 segundos otro cuerpo “B" se lanza
verticalmente hacia abajo desde el mismo
lugar de donde se dejó caer "A”, con una
velocidad inicial de 25 m/s. Hallar a qué
distancia del nivel de lanzamiento se pro­
ducirá el encuentro de los cuerpos.
■ g = 10 m/s2.
SOLUCION:
Sea V el tiempo que estuvo en movi­
miento "B" hasta alcanzar al móvil "A".
B
'f 25 m/s
(t+2)
i:
De la fórmula:
h = Vo T + i g . T 2
Para “A":
H = 5 (t + 2) .... (1)

163. Para "B“
H = 25 . t + 5 . t2 .... (2)
(1) = (2): 5 (t + 2)2 = 25 . t + 5t2
Resolviendo: t = 4 s
Reemplazando en (1):
H = 180 m
PROBLEMA Nfi 10
Se deja caer una piedra y un segundo
después, del mismo punto, se lanza otra
piedra verticalmente hacia abajo con una
velocidad de 15 m/s. ¿A qué distancia por
debajo del punto de lanzamiento, alcanza
la segunda piedra a la primera?.
g = 10 m/s2
a) 15 m b) 20 m c) 25 m
d) 30 m e) N.A.
PROBLEMA Ns 11
Se lanza un cuerpo verticalmente ha­
cia arriba, desde la superficie de la Tierra,
con una cierta velocidad inicial "V" que
permite alcanzar una altura maxima "H".
Si dicha velocidad inicial se duplicara, su
altura máxima aumentaría en 60 m. Hallar
■H".
SOLUCION:
1) En el primer caso:
V f2 = V02 —2g H
Pero: V f = 0
V = 2gH .,..(1)
6 0 iti
O
i
I
2 V
CASO (1) CA50 (2 )
2) En el segundo caso;
Vf2 = Vo2 - 2g.h
*
*
*
*
*5
&
#
*
í¡¡
♦
*
*
*
*
*
*
*
*
*
m
*
*
*
m
*
*
*
*
$
s
d
*
*
*
*
#
*
*
*
*
#
%
*
*
*
*
*
*
•i*
*
*
*
*
*
*
*
#
*
*
»
*
*
0 = (2V) - 2g(H + 60) ....(2)
Reemplazando (1) en (2):
H = 20 m
PROBLEMA N®12
Una pistola dispara un proyectil verti­
calmente hacia arriba, alcanzando u>.a al­
tura máxima H. Si el disparo se realiza en
la Luna, cuya aceleración de la gravedad
es la sexta parte de la aceleración de la
gravedad de la Tierra. ¿A qué altura lle­
gará, considerando que la variación d@la
gravedad en nada influye en ei fun­
cionamiento de la pistola?.
, H
a ) 6
d) H %Í6/6
b) H ^6 c) 6H
e) Faltan datos
PROBLEMA He 13
En cierto planeta la aceleración de la
gravedad es la cuarta parte de la acele­
ración de la gravedad en la tierra. En la
tierra se abandona una moneda desde
una altura "h" y demora eh llegar al piso
un tiempo ti = 3 s.
Si repetimos la misma experiencia en
este planeta, ¿cuánto tiempo demora la
moneda en llegar al piso?
SOLUCION
En general, en cualquier planeta se cum­
ple que:
h = Vo t + - . g. t2
En la tierra:
h = ¿ . g r - t i 2
En el planeta:
h 4 j - T g l
2 4
.... (1)
.... (2)
Igualando las ecuaciones (1) y (2):
t2 = 2 . ti
T2 = 6 s

164. En la Luna la aceleración de la gra­
vedad es la sexta parte de la aceleración
de la gravedad en la Tierra. En la Tierra
se abandona una piedra desde una altura
"H” y demora en llegar al piso un tiempo
ti = '¡6 segundos. Si repetimos la misma
experiencia en la Luna. ¿Cuánto tiempo
demora la piedra en llegar al piso?.
a) 2V6 s b) 3^6 s
c) 5 s d) 6 s
e) N.A.
PROBLEMA NB15
Una moneda se lanza verticalmente
hacia abajo con una velocidad de 15 m/s,
en caída libre.
¿Qué espacio recorre la moneda en el
QUINTO segundo de su movimiento?,
g = 10 m/s2
SOLUCION:
El espacio recorrido por una partícula en
el n-ésimo SEGUNDO de su movimiento
será:
X = V0± ~ . g . ( 2 n - 1 )
(+ ): cuando baja
( - ) : cuando sube
En este caso: V0 = 15 m/s ; n = 5
Reemplazando: X = 15 + ~ (10) (9)
PROBLEMA Ne 16
Un cuerpo cae libremente desde una
determinada altura, recorre 35 metros en
el último segundo de su caída. ¿Desde
qué altura se abandonó el cuerpo?.
g = 10 m/s
a) 70 m
d) 85 m
b) 75 m c) 80 m
e) Ninguna
*
o
*
*
♦
*
*
o
?
*
o
*
&
*
*
*
*
*
o
*
Oí
Oí
*
Oí
o
?
Oí
Oí
Oí
Oí
0*
*
Oí
Oí
Oí
Oí
*
0
*
Oí
$
$
*
*
Oí
$
*
*
*
Oí
Oí
O
í
O
í
*
$
♦
0
*
O
í
o
»
0
»
O
í
o
*
Oí
Oí
0
6
*
#
Oí
Oí
O í
Oí
Oí
0
4
Oí
*
O
í
*
0
?
Oí
*
Oí
Oí
0
«
Oí
De un caño cae una gota cada 0,1 se­
gundo, si cuando está por caer la tercera
gota se abre la llave y sale un chorro de
agua, ¿con qué velocidad debe salir dicho
chorro para que alcance a la primera gota,
justo cuando llegue al piso?
El caño se encuentra a una altura de
7,2 metros del piso.
g =10 m/s2
SOLUCION:
7,2
0,2 s
1) Para la primera gota:
h = “ . g . t2
2 y
Reemplazando:
7.2 = 5 (T + 0,2)
Resolviendo:
T = 1 s
2) Para el chorro:
1 o
h = Vo. t + 2 - g • t
Reemplazando:
7.2 = V0(1) + 5(1)
.... (1)
V0 = 2,2 m/s
PROBLEMA N918
Un cuerpo que se encuentra cayendo
libremente choca con la superficie de la
Tierra, con una velocidad de 40 m/s. De­
terminar el tiempo que tarda en recorrer
los últimos 60 m.
g = 10 m/s2

165. SOLUCION:
Aplicamos la siguiente fórmula:
1
h = vF
.t± ¿ g t2 (1)
(+) : cuando sube (retardado)
( - ) : cuando baja (acelerado)
Reemplazando datos en (1)
60 = 40 t - ~ . (10) .t2
12 = 8 . t - t 2
Resolviendo;
t = 2 segundos
t 0 1 2 3 4 5 6 7 8
V 40
O
C
O
20 10 0 -10 -20 -30 -40
»
*
*
*
El signo ( - ) significa que el sentido de la
velocidad es hacia abajo.
PROBLEMA Nfi 19
Un niño lanza una pelota verticalmente
hacia arriba, después de 0,5 segundos
impacta con el techo con una velocidad
de 2 m/s.
¿Qué altura recorre la pelota hasta el
impacto?
g = 10 m/s2
a) 2,15 m b) 2,25 m
c) 2,35 m d) 2,45 m
e) Ninguna
PROBLEMA Ns 20
Una partícula se lanza verticalmente
hacia arriba (t = 0) con una velocidad de
40 m/s. Considerando la aceleración de la
gravedad g = 10 m/s2, determ inar la
gráfica v - t , hasta el instante que regresa
a su posición inicial.
SOLUCION:
De la fórmula:
Vf = V0 - g . t
Reemplazando:
VF = 40 - 10 . t ....(1)
Graficando la función (1):
*
*
*
*
*
&
0
El siguiente es un diagrama v - t de
una partícula que se mueve en linea recta
en el eje Y.
En el instante t = 0 está en Y = 5 m.
*
m
#
*
*
*
*
*
*
*
*
*
*
*
*
*
I) La aceleración del móvil es cero
II) En el instante t = 5 s, el móvil está
en Y = 30 m.
III) El diagrama Y - 1es una recta.
IV) En el instante t = 5 s, el móvil se
detiene.
Son ciertas:
a) Sólo I b) Sólo II
c) Sólo II y IV d) Sólo III
e) Todas son ciertas

166. Una partícula se lanza verticalmente
hacia arriba con una velocidad V0=40 m/s
(t = 0). Considerando la aceleración de la
gravedad g = 10 m/s2, determinar la
gráfica, altura (h) versus tiempo (t).
SOLUCION
1) Cálculo del instante "t" en que el
cuerpo alcanza su altura maxima.
Vf = V0 - g . I
0 = 4 0 - 1 0 . t
t = 4 s
2) De la fórmula
h = V0t - | , g . t 2
Reemplazando:
h = 40 t —5 . t2 .... (1)
Grafícando la relación (1):
t 0 1 2 3 4
1
5 6 7 8
h 0 35 60 75 80 75 60 35 0
PROBLEMA ^ 23
El siguiente es un diagrama h - t de
una partícula que se mueve en caída libre,
g = 10 m/s2. Determinar la posición de la
partícula en el instante t = 5 s.
*
$
»
*■
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ü
s
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
♦
#
*
*
*
#
<
¡>
*
*
«
*
*
*>
*
*
*
*
*
*
*
*
*
#
*
*
*
*
♦
*
*
*
*
a) h = -1 0 m b)h = -1 5 m
c) h = 20 m d) h = -25 m
e) Ninguna
•PROBLEMA N®24
Analice los siguientes diagramas e in­
dique el que no puede corresponder a un
movimiento rectilíneo uniforme (M.R.U.),
en el eje X.
a) b)
c) d)
e)

167. En eí movimiento rectilíneo uniforme, en
el eje X:
Velocidad = constante (positivo o nega­
tivo),
aceleración = 0 = cero.
Rpta. D, no corresponde.
PROBLEMA N925
Un paracaidista se arroja desde un
avión que vuela horizontalmente con una
velocidad V = 340 m/s a 1 km de altura.
¿Cuál de los gráficos representa mejor la
magnitud de la velocidad vertical "Vv“ en
función da tiempo “t
E)
*
*
*
*
<
¡¡
*
m
*
*
*
*
*
*
m
*
♦
#
*
t*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
4
>
#
*
*
*
*
*
*
*
#
¡
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
&
*
*
*
*
*
Un cuerpo se lanza verticalmente
hacia arriba desde el borde de un acanti­
lado de 60 m de altura, con una rapidez
inicial V0. ¿Después de qué tiempo de
haber sido lanzado el cuerpo está a una
altura de 35 m acercándose a la Tierra con
una rapidez 1,5 V0?
SOLUCION:
1) Calculo de "V0“ sabemos que:
VF2 = V¡2 -2 g h
donde ’ h" es ei desplazamiento de
la partícula con respecto al nivel de
lanzamiento, h >0 cuando el móvil
se encuentra sobre el nivel de lan­
zamiento, en caso contrario (bajo el
nivel) h < 0.
Entonces:
(-1.5Vo
)2= V 2o- 2 . 10(25)
1,25Vo2 = 500
V0 = 20 m/s
V
e
-
n i
i
. ¡ Ni v el de la n z a m ie n to
í
■
:
1
60 m
i
i
T 1,5V0
25 m
1
T
i
35 m
■
»!'■ rrei-tsr
2) Cálculo del tiempo Y :
Sabemos que: V f = V ¡ - g . t
donde " V f " es la velocidad fina! del
móvil V f > 0 , cuando el movimiento
todavía es retardado (el cuerpo aún
se mueve hacia arriba). V F < 0 ,
cuando e! movimiento es acelerado
(el cuerpo se mueve hacia abajo).

168. Entonces:
(-30) = 20 - 10.t
t = 5 s
PROBLEMA N®27
Dos piedras se lanzan verticalmente y
en el mismo instante desde A y B con
velocidades de: 12,5 m/s y 20 m/s respec­
tivamente.
¿A qué altura h sobre el nivel B se encuen­
tran las piedras?
g = 10 m/s2.
a)h = 8m b) h = 1 0 m
c) h = 20 m d) h = 30 m
e) Justo al caer a Tierra.
PROBLEMA Nfi 28
Se lanza una piedra desde la superficie
de la Tierra con unaveíocidad inicial de 50
m/s. Si después de un tiempo "t" la piedra
se encuentra acercándose a la Tierra con
una velocidad de 30 m/s, hallar "t“.
9 7
g = 10 m/s .
SOLUCION:
Convencionalmente el signo de la veloci­
dad es positivo (+) hacia arriba y nega-
tivo(-) cuando tiene sentido hacia abajo.
#
*
*
*
«
*
$
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
V f = V0 - g . t
(-30) = (50) - (10). t
t = 8 seoundos
PROBLEMA N®29
Un cuerpo es lanzado a Tierra con una
velocidad V0 hacia arriba y alcanza una
altura H.
¿Qué afirmaciones son verdaderas?
Nota: Suponer el experimento en el
vacío.
Q
P<
¡■« S
U -TO
W
P
C
T
B
g
*
*
♦
*
#
*
<
*
*
*
*
*
*
*
*
*
*
*
I) El tiempo en ir a P a Q, es el mismo que
emplea de Q a S.
II) En P la aceleración gravitatoria tiene el
mismo sentido que en S.
III) La aceleración del cuerpo en Q es igual
a cero.
IV) En P la velocidad tiene el mismo sentido
qilte la velocidad en S
a) Todas son verdaderas.
b) Sólo I
c) Sólo I y II
d) Sólo I y IV
e) Sólo I, II y III

169. MOVIMIENTO RELATIVO
Hasta ahora hemos estudiado al
movimiento de una partícula respecto de un
solo sistema de referencia dado. Sin em­
bargo, hay casos en los que es razonable, y
a veces necesario, examinar el movimiento
de una partícula simultáneamente respecto
de dos sistemas de referencia, uno de los
cuales se considera convencionalmente in­
móvil (Tierra) y el otro se mueve de un modo
determinado respecto del primero. Entonces,
es importante saber la forma en que están
relacionadas las observaciones hechas por
personas de diferentes sistemas de referen­
cia.
LA TRAYECTORIA ES RELATIVA
El piloto, de un avión que vuela horizon­
talmente, abandona un proyectil respecto del
avión. La trayectoria que describe el proyec­
til respecto de un hombre que se encuentra
fijo en la tierra, es una parábola.
>
V
Para el piloto, que se mueve con veloci­
dad constante, la trayectoria que se des­
cribe el proyectil es una línea recta.
o
o
#
*
*
*
*
*
s
i»
*
*
*
*
*
*
*
*
*
*
Ü
í
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
s
i»
*
*
*
*
*
0
»
*
*
*
#
>
8
*
*
*
*
*
*
*
*
*
«
I»
s
i»
*
*
*
O
*
*
#
sis
*
*
*
*
#
S
tf
*
*
VELOCIDAD RELATIVA
Consideremos dos Asteroides A y B que
se mueven en línea recta con velocidades Va
y Vb respecto de un observador fijo en la
tierra.
..... -.......... <(!
La velocidad del asteroide "A" respecto
de un observador ubicado en el asteroide
”6“, es igual a la diferencia vectorial de sus
velocidades respecto de la tierra.
Va/b = Va - VB
Va/b : velocidad A respecto de B.
"Todo movimiento Mecánico es relativo’
En general, las partículas A y B pueden
tener cualquier dirección y sentido en su
movimiento.
ACELERACION RELATIVA
Considerando dos Asteroides A y B que
se mueven en línea recta con aceleraciones
aA y aB respecto de un observador fijo en la
tierra.
La aceleración del asteroide "A” respec­
to de un observador ubicado en el asteroide
“B”, es igual a la diferencia vectorial de sus
aceleraciones respecto de la tierra
a A / B = a A—aB
a A/B : aceleración de “A“ respecto de
"B".

170. En general, la aceleración de A y B pue­
den tener cualquier dirección y sentido.
PROBLEMA NB1
Dos autos que se desplazan en cami­
nos perpendiculares viajan hacia el norte
y el este respectivamente. Si sus veloci­
dades con respecto a la tierra son de 60
Km/h y de 80 Km/h, calcular su velocidad
relativa, uno respecto del otro.
SOLUCION:
Vi =80 Km/h
V2 = 8 0 km/h
Consideremos las velocidades V, y V2.
Cálculo de la velocidad del móvil "1” res­
pecto del móvil "2", V1/2:
2 2 2
v 1
/2= v , + v 2
Reemplazando.__________
V1/2 = 100 Km/h
PROBLEMA Nfi 2
Un hombre que guía su auto/nóvil a
través de una tormenta a 100 Km/h ob­
serva que las gotas de lluvia dejan trazos
en las ventanas laterales haciendo un án­
gulo de 53® con la vertical. Cuando el
hambre detiene su auto, observa que la
lluvia esta cayendo realmente en forma
vertical. Calcular ia velocidad de la lluvia
respecto de ia tierra.
SOLUCION:
mov.
Consideremos la velocidad del auto ha­
cia la derecha, "Va".
Del diagrama de velocidades:
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
«
«
*
*
*
«
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Tg 37a=
Vll
Va
VLL = Va . Tg 37®
Reemplazando:
V l l = 7 5 Km/h
PROBLEMA N« 3
La bandera situada en el mástil de un
bote a vela flamea haciendo un ángulo de
60°, como se muestra en la figura, pero la
bandera situada en una casa a la orilla del
río se extiende 66° al suroeste.
Si la velocidad del bote es de 10 Km/h,
calcular la velocidad del viento y la velo­
cidad aparente del viento para un obseF-
vador situado sobre el bote.
mov.
SOLUCION:
De la composición vectorial de veloci­
dades se deduce que:
Vbote —Vviento = 10 Km/h
Cálculode la velocidad de) viento respecto de
un observadorubicadoen el bote.
De la ley de cosenos
Vv/b= 10 V3 Km/h

171. 4. M O V I M I E N T O R E L A T I V O
M O VIM IENTO COM PUESTO
Cuando está parado sobre la escalera
en movimiento demora en llegar 60 se­
gundos. ¿Qué tiempo demora en llegar si
camina sobre la escalera en movimiento?
PROBLEMA N®01
Un ascensor de 4,9 metros de altura
(entre el techo y el piso) está subiendo
con una velocidad constante de 5 m/s.
Calcular el tiempo que demora en llegar al
piso del ascensor un perno que se des­
prende del techo del mismo ascensor.
SOLUCION'
Fijamos nuestro sistema de Referencia
dentro del ascensor. La velocidad inicial
del perno respecto de nuestro observa­
dor es igual a cero.
h = V0y . t + 1 . g . t2
4,9 = 0 + -(9,8) t2
t = 1 s
"El tiempo transcurre de igual modo para
todos los sistemas de Referencia"
PROBLEMA N2 02
Un ascensor de 6 metros de altura
(entre el techo y el piso) está subiendo
con aceleración constante a razón de 2,2
m/s2. Calcular el tiempo que demora en
llegar al piso del ascensor un foquito que
se desprende del techo del mismo ascen­
sor.
a) 1 s
d) 4 s
PROBLEMA N» 03
b) 2 s
e) Ninguna
c ) 3 s
Un muchacho caminando sobre una
escalera mecánica detenida se demora en
llegar arriba 90 segundos.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
m
*
*
*
*
*
m
*
m
*
*
*
*
*
*
*
SOLUCION:
Sea, L la longitud de la escalera
Velocidad del hombre respecto a la es­
calera:
Vh/E = 90
Velocidad de la escalera respecto a la
Tierra:
V e =
60
Velocidad del hombre respecto a la
Tierra:
VH = V e + VH/e
V h =— + —
h 60 90
"El hombre demora en desplazarse la
distancia L, 36 segundos".
PROBLEMA Ne 04
Dos pueblos amazónicos se encuen­
tran a la orilla de un rio, separados por
una distancia de 36 km, para movilizarse
los pobladores usan una lancha que siem­
pre se mueve con la misma velocidad
constante respecto al agua. Cuando se
mueve río abajo demora 1,0 hora y cuando
se mueve río arriba se demora 2,0 horas,
entre ambos pueblos. Hallar la velocidad
de la corriente del río.

172. a) 6 Km/h b) 7 Km/h
c) 8 Km/h d) 9 Km/h
e) Ninguna
PROBLEMA Nfi 05
Sobre la plataforma de un ferrocarril
que sstá corriendo a razón de 12 Km/h, un
ho rbre camina con una velocidad de 5
Km n respecto a la plataforma, en direc­
ción perpendicular a la dirección de los
rieles. La verdadera velocidad del hom­
bre respecto al suelo firme es igual a:
SOLUCION:
En el movimiento compuesto, la veloci­
dad resultante se consigue sumando
vectorialmente la velocidad del tren, más
la velocidad de! hombre respecto del tren.
Del Teorema de Pitágoras;
V h = 13 Km/h
PROBLEMA N» 06
Un hombre se encuentra parado sobre
una plataforma móvil que se mueve hori­
zontalmente con una velocidad constante
de 7 m/s. Si e! hombre sostiene en sus
manos un rifle. ¿En qué dirección, de­
finido por el ángulo " 0 “ debe hacer el
disparo, en el instante que el hombre pasa
frente a un poste para hacer blanco en
éste. Velocidad de la bala = 25 m/s, res­
pecto del rifle.
© POSTE
d) 20° e) Ninguna
PROBLEMA N®07
A través del cristal de la ventana de un
coche de ferrocarril, un pasajero ve caer
las gotas de la lluvia paralelamente a la
diagonal del marco. ¿Con qué velocidad
cae realmente, si no hay viento, y el tren
está corriendo al 60 Km/h?. El ancho de la
ventana es el doble de la altura.
SOLUCION:
Nos piden determinar la velocidad de la
lluvia respecto de la Tierra. De la con­
dición del problema, la velocidad de la
lluvia respecto del tren es paralela a la
diagonal del marco.
De la semejanza de triángulos:
V l l = V t
a 2a
V l l = 3 0 Km/h
PROBLEMA Nfi 08
Sobre las ventanas laterales de un
automóvil que se desplaza a 60 Km/h se
observa los trazos que dejan las gotas de
lluvia. Si los trazos en las ventanas for­
man un ángulo de 37° con la vertical y si
las gotas de lluvia se observan que caen
verticalmente cuando el auto está dete­
nido, ¿cuál será la velocidad de las gotas
de lluvia respecto a la tierra?
a) 30 Km/h b) 60 Km/h
c) 80 Km/h d) 90 Km/h
e) Ninguna
*
#
*
*
*
*
*
s*
#
*
*
*
*
*
*
*
sjí
*
s
i»
*
#
*
s
i»
*
*
*
*
*
*
*
*
*
sis
*
*
S
í
*
*
*
*
*
*
*
*
s
H
+
*
*
»
*
+
S
I»
s
H
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
«
1
S
ií
*
*
*
m

173. Un coche de ferrocarril se desplaza
rectilíneamente a velocidad constante de
5 m/s. Un perro que se encuentra fuera de
la línea férrea se dirige en todo instante al
coche con velocidad constante en mó­
dulo. El perro observa que el tren pasa
frente a él (perpendicularmente) con una
velocidad de 4 m/s. Hallar la velocidad del
perro.
fPERRO
TREN
SOLUCION
El perro cambia de dirección en cada
instante respecto a la Tierra, pero man­
teniendo constante el módulo de su velo­
cidad.
El perro dirá que el tren pasa frente a él
cuando la velocidad del perro es perpen­
dicular a la velocidad relativa del tren
respecto al perro.
Del diagrama de velocidades se deduce,
que la velocidad del perro es:
Vp = 3 m/s
PROBLEMA N9 10
Las gotas de lluvia caen con una velo­
cidad constante de 10 m/s formando un
ángulo de 37° con la vertical. Hallar la
velocidad con que debe moverse el hom­
bre con sombrero de charro para mojarse
lo menos posible.
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
S
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
a) 3 m/s
d) 6 m/s
b) 4 m/s
e) 8 m/s
/
A
PROBLEMA N9 11
Un hombre en un bote debe ir de A
hacia B que están en orillas opuestas del
río. Las dimensiones son AC = 80 m y
BC = 60 m. La velocidad de la corriente
del río es 5m/s. Hallar la mínima veloci­
dad del bote relativa al agua, para lograr
su objetivo.
C B
RIO
SOLUCION:
La velocidad del bote respecto a la Tierra
debe tener la dirección AB. Pero la velo­
cidad resulta de sumar vectorialmente la
velocidad del río, más la velocidad del
bote respecto del agua (río).

174. Vb = V r + Vb/R
La velocidad del bote respecto del río,
pueden ser:
O P ; O Q ; O S ; .. .
_a velocidad de menor módulo, es
aquel vector perpendicular al seg­
mento AB.
Luego:
Vb/R = 4 m/s
"Velocidad mínima del bote respecto del
agua (río)”
PROBLEMA Ne 12
Un hombre puede nadar en aguas tran­
quilas con una velocidad de 5 m/s. Si se
tiene un río de 24 m de ancho, cuyas
aguas se mueven con una velocidad cons­
tante de 3 m/s; hallar el tiempo que tardará
en cruzar el río, sabiendo que quiere hacerlo
de A hacia B.
a) Es imposible cruzar en forma perpen­
dicular.
b) t = 3 s
c) t = 4 s
d) t = 6 s
e) Ninguna
24 m
*
RIO
PROBLEMA Ns 13
Una bandera ubicada en el mástil
de un bote flamea haciendo un ángulo
de 60° como se muestra en la figura,
pero la bandera situada en ia orilla se
extiende al sur 30° oeste. Encontrar la
velocidad del viento respecto a la
tierra, si el bote se mueve con una
rapidez de 10 km/h.
4
»
t-
*
*
*
*
*
*
*
*
*
*
*
*
*
$
<
¡*
«
is
*
s
t»
*
*
*
#
*
*
s
u
*
s
jt
*
SOLUCION:
La bandera ubicada en el mástil del
bote flamea en dirección de la veloci­
dad relativa del viento respecto del
bote.
Vv/b —V v —Vb
Resolviendo el triángulo:
Vviento = 5 Km/h
En ausencia del viento, la bandera ubi­
cada en el mástil del bote flamea en el
sentido de Oeste a Este, opuesto al
movimiento del bote.

175. Por un río del punto A al punto B que
se encuentra en la orilla opuesta, a lo
largo de ¡a recta AB, navega un bote. La
bandera ubicada en el mástil del bote fla­
mea en la misma dirección del río. El
viento sopla con una velocidad de 6 m/s
en dirección perpendicular a la orilla, de
A hacia C. Si AC = 3 km y CB = 4 km.
Determinar la velocidad del bote respecto
de la orilla.
C B
W
J»v 1. i - p j i ..-A C.-."ra
il, i
RIO
a) 8 m/s b) 9 m/s
c) 10 m/s d) 12 m/s
e) Ninguna
PROBLEMA Nfi 15
Una lancha a motor que va río arriba se
encontró con un bote que flotaba a aguas
abajo. Pasada una hora después de este
encuentro. La reparación de ésta duró 30
minutos y durante todo el tiempo la lancha
seguía libremente la corriente del río. Arre­
glado el motor, la lancha comenzó a ir río
abajo con la misma velocidad con relación
a la corriente del agua y alcanzó al bote a
una distancia igual a 7,5 km del punto del
primer encuentro. Determinar la velocidad
de la corriente del río, considerándola cons­
tante.
SOLUCION:
Fijamosnuestrosistema de referenciainercia!
S’enelbote, deahíobservamosquelalancha
se aleja una distancia X’ en una hora.
-SUS
*
*
*
*
*
«
*
#
S
í
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
♦
*
s
H
*
*
*
&
s¡*
m
*
*
*
s
H
$
*
*
*
$
*
*
*
*
*
*
♦
*
*
*
*
Pasada media hora, en que el motor de
la lancha paró, la distancia X' no se altera
debido a que ambcs cuerpos tienen la
misma velocidad del río. Arreglado el
motor la lancha regresa con la misma
rapidez respecto del agua, por con­
siguiente pasada una hora más da al­
cance al bote.
El tiempo total transcurrido será: 2,5 h.
El tiempo transcurre de igual modo para
todos los sistemas de referencia Ahora
fijamos nuestro sistema de referencia S
en la Tierra.
S ( ¿ 7 TIERRA
wr.A-.u.^- MLiStttfii.rr.r
TRAYECTORIA
7 ,5 km
■ j
DE LA LANCHA
TRAYFCTORIA
DEL BOTE
Observamos que la lancha le da alcance
al bote a 7,5 km de! punto de su primer
encuentro.
El bote en 2,5 h se ha desplazado 7,5 km
con la velocidad del río, respecto a Tierra
e = V . t
7,5 = V (2,5)
V = 3 Km/h
PROBLEMA N®16
Una lancha "A" se mueve río abajo con
una rapidez de 3 Km/h respecto al río y
otra lancha "B" río arriba con 5 Km/h
respecto al río. Parten del mismo punto y
al mismo instante; B se mueve durante 2
horas y reforma río abajo con una rapidez
doble respecto al río 4 horas más al cabo
del cual se detiene el motor. La lancha "A ”
que mantiene su dirección y sentido le da
alcance a 6 ‘ 50 Km más abajo del punto
de partida. Hallar la velocidad del río.

176. a) 1 Km/h b) 2 Km/h
c) 3 Km/h d) 4 Km/h
e) 5 Km/h
PROBLEMA N« 17
Dos trenes corren en sentidos con­
trarios y con velocidades Vi = 36 Km/h y
V2= 54 Km/h.
Un pasajero del primer tren (ol de Vi),
observa que el tren (2) demora en pasar
por su costado 6 segundos. ¿Cuál es la
longitud dei segundo tren?. Se supone
que el pasajero está inmóvil en el primer
tren mirando a través de la ventana.
SOLUCION:
El pasajero (sistema de referencia) ob­
serva pasar al segundo tren con una velo­
cidad (V, + V2):
Vi = 10 m/s y V2 = 15 m/s
Para el pasajero:
e = V2/1 t
L = (V, + V2) . t
Reemplazando:
L = (10 + 15). (6)
L = 150 m
V2/1 : velocidad del móvil (2)
respecto del móvil (1)
PROBLEMA Ne 18
Dos trenes corren en sentidos iguales
en trayectorias paralelas con velocidades
Vi = 54Km/h y V2 = 36Km/h.
Un pasajero del primer tren (se en­
cuentra fijo en su asiento mirando a tra­
vés de la ventana) observa que el segun­
do tren demora en pasar por su costado
18 segundos. ¿Cual es la longitud del se­
gundo tren?.
a) 98 m b) 95 m c) 90 m
d) 80 m e) N.A.
PROBLEMA Ne 19
Para cruzar un río de 200 m de ancho,
se emplea un bote, que se mueve siempre
perpendicularmente a la corriente del
agua, con una velocidad de 4 Km/h. Si la
velocidad de la corriente es de 3 Km/h. ¿A
qué distancia, medida desde el punto de
partida, se encuentra el punto de llegada
del bote.
SOLUCION
En el movimiento compuesto, la veloci­
dad resuitante se consigue sumando
vectorialmente la velocidad del río, más
la velocidad del bote respecto del agua.
La trayectoria que sigue al bote tiene la
misma dirección del vector velocidad.
c B
Del triángulo rectángulo de velocidades
se deduce que el ángulo “ 0 " mide 53°.
En el triángulo rectángulo ACB
d = AB = 250 m
PROBLEMA Ns20
Un hombre puede nadar en aguas tran­
quilas con una velociaad de 4 m/s. Si se
tiene un río de 12 m de ancho cuyas aguas
se mueven con una velocidad constante
de 5 m/s. hallar el tiempo que tardará en
cruzar el río, sabiendo que quiere llegar
alejado del punto de partida una distancia
mínima.
*
*
*
*
#
s
is
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
#
*
*
S
ü
*
*
*
*
*
*
*
*
*
*
*
s
í*
*
4
*
*
*
*
*
*
*
m
*
*
*
S
*
s
lí
#
*
*
*
*
*
*
*
*
*
*
O
f
*
&
*
*
*
S
*
*
*
*
*
sí

177. RIO
PARTIDA
a) 3 S
d) 8 s
b) 5 s
e) N.A
c) 6 s
,iíiiitn
n
S
M
»M.mitii -n
.-itt.A
U
»
..-.■
■
■
■
■
•:
■ ■
■ A W -.*
MOVIMIENTO COMPUESTO
Es aquel movimiento que resulta de la
composición de dos o más movimientos sim­
ples, éstos pueden ser el M.R.U., M.R.U.V.,
M.C.U,, M.C.U.V. y otros.
Ejemplo:
Un hombre pretende cruzar una piscina
de 30 m de ancho, nadando con una
velocidad de 3 m/s respecto del agua.
Respecto de la tierra el hombre M.R.U.
e = V, t
30 m = 3 m/s t
entonces:
t= 10s
30m |VH=3m/ s
A
fig- (i)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
❖
*
*
*
#
*
#
*
m
*
*
*
*
*
#
*
#
*
*
*
*
El hombre demora en cruzar la piscina 10
segundos.
Supongamos ahora que el hombre, man­
teniendo la misma velocidad respecto
del agua, se mueve en un río de 30 m de
ancho y que tiene una corriente de rapi­
dez de 4 m/s respecto de la tierra.
Cálculo de la velocidad de hombre res­
pecto de la tierra
VHombre —Vrjo + Vh/R
(
j
✓
/
30ni j
j • ^ i
vH/R=3n,Zs::
n—
i « fo '' VR=4m/s
¡
H-'YfJ J
v
;.- -i.,,
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
S
í
*
*
*
*
*
#
*
*
H
fiq . (2)
Aplicando el teorema de Pitágoras
2 2 2
V H = V R + V RH
Vh = 5 m/s
"El hombre se traslada diagonalmente
respecto de la tierra"
El desplazamiento del hombre es
AB = 50m
e = V. t
50 m = 5 m/s . t
t = 10s
.. El hombre demora en cruzar el río
10 segundos.
El desplazamiento a lo largo de río es
d = 40 m, como muestra la figura del
M.R.U.
e = V. t
40 m = 4 m/s . t
t= 10s
Luego, se concluye que: el tiempo trans­
curre de igual modo jjara cada movi­
miento componente.
PRINCIPIO DE INDEPENDENCuToE
LOS MOVIMIENTOS
Fue enunciado por Galileo:
Cada movimiento componente es un fe­
nómeno físico independiente de los demás
movimientos.

178. El parámetro común de los movimientos
componentes es el intervalo de tiempo, para
cada uno de ellos transcurre de igual modo.
MOVIMIENTO PARABOLICO
-itm ^
.ICO
*
«
I»
*
*
*
*
CONCEPTO.
Es aquel movimiento compuesto que
tiene como trayectoria una línea curva de­
nominada parabólica- Todo cuerpo que es
lanzado con una velocidad “Vo" formando
con la horizontal un ángulo " 0 ” describe un
movimiento parabólico.
Empecemos por encontrar las fuerzas
aplicadas al móvil. Sobre éste actúa sola­
mente la fuerza de gravedad (peso) por esta
razón, en la dirección horizontal el cuerpo se
mueve a velocidad constante, la fuerza resul­
tante en el eje "x” es igual a cero, mientras
en el eje vertical su movimiento es uniforme­
mente acelerado a razón de 9,8 m/s2.
*>
*
*
*
ü
*
3*
*
*
*
*
0
$
*
*
*
*
ta
*
*
*
*
*
*
MOVIMIENTOS COMPONENTES:
En el eje “x" se cumple el M.R.U.
Vx = constante
En el eje "y" se cumple el M.R.U.V.
ay = g = 9,8 m/s2
CONSIDERACIONES
El alcance horizontal ”D“ es suficiente­
mente pequeño como para despreciar la cur­
vatura de la tierra.
La altura máxima alcanzada es suficien­
temente pequeña para despreciar la
variación de la gravedad g.
FUNCIONES DEL MOVIMIENTO
PARABOLICO
TIEMPO DE VUELO
En el tramo AB:
Vfy = Voy —g . t
0 = V0 . Sen 0 - g t
V0 . Sen 6
tAB —
Tvuelo —
2V0 . Sen 0
ALTURA MAXIMA (H)
En el tramo AE:
v : = v ; - 2 . g . h
0 = V* . Sen 0 - 2 gH.
V c .Sen2e
2g
.... (2)
ALCANCE HORIZONTAL (D)
En del tramo ABC:
e = Vx . t
,,, ^ 2 v o • Sen 0
D = (V0 Cos 0). —
2 V
D =- Sen 0 . Cose O)
*
*
*
*
*
*
#
*
m
#
*
s¡*
*
$
*
RELACION ENTRE H Y D
Dividiendo miembro a miembro las
ecuaciones (2) y (3):
T r, 4H
Tg 0 = —
w D
RELACION ENTRE H Y T
Dividiendo: (1)2 4(3)
h . s t *

179. De lo alto de una torre, se lanza una
piedra con una velocidad de 40m/s.
Sabiendo que la piedra estuvo en
movimiento 3,0 segundos:
- ¿Cuál es la altura de la torre?
- ¿A qué distancia del pie de la torre la
piedra alcanza el suelo?
- ¿Con qué velocidad la piedra alcanza
el suelo?
g = 10 m/s2
SOLUCION:
H = 0 + ¿(10)(9)
H = 45 m
En la horizontal:
D = Vx . t
D = (40 m/s)(3 s)
Ds =120 m
Cálculo de la velocidad en la vertical:
Vy = Voy + g . t
Vy = 0 + 10(3)
Vy = 30 m/'s
#
#
*
*
*
*
0
»
*
*
*
*
*
$
*
*
*
Del teorema de Pitágoras:
V2 = V2X+ V2y
V2 = 1 600 + 900
V = 50 m/s
V : velocidad de la piedra cuando llega
al suelo.
PROBLEMA Nfi 2
Un futbolista comunica a una pelota la
velocidad de 10 m/s con un ángulo de 37°
con la horizontal, encontrándose a 8 m de
distancia de una portería (arco) de 2,5 m.
¿Había posibilidad del gol?
SOLUCION:
2,&m
*■’ i ^ u .m 'VV-: y
."-
8™
En la horizontal:
D = (Vo Cos 37°) t
ti*4 /0s
En la vertical:
h = (V0 S en37°)t —| . g . t 2
h =¡ 10 - 5 | l ) - 2 {9'8)(1)
*
*
*
*
*
*
*
*
%
*
*
*
*
*
h - 1 ,1 , m
¿Hay posibilidades de gol?
Si, h < 2,5 m
PROBLEMA Ns 3
Un avión vuela horizontalmente con
velocidad de 100 m/s, se deja caer une
piedra respecto del avión y recorre una
distancia horizontal de 1 000 m. antes de
llegar al suelo.

180. - ¿Cuál es la altura a la que se encuen­
tra el avión?
- ¿Con qué ángulo llegó la piedra so­
bre el suelo respecto de la horizontal?
g = 10 m/s2.
SOLUCION:
*
*
*
*
*
d
*
*
*
s
k
á
*
*
*
*
*
*
«l
*
*
*
*
*
*
*
*
*
*
*
*
0
*
*
En el horizontal:
D = (Vx) . t
1 000 = (100) t
t = 10s
Cálculo de la velocidad en la vertical:
Vy = Voy + g . t
Vy = 0 + 10(10)
Vy = 100 m/s
Cálculo del ángulo de impacto:
Tg 6 = 1
6 = 45°

181. 5. MOVIMIENTO PARABOLICO
i) Tiempo de vuelo:
T = — — Sene
g
ii) Altura máxima:
H =
V i . Sen2 6
~2g
iii) Desplazamiento horizontal:
Vo
D = — . Sen 2 6
9
iv) Relación entre H y D
-r « 4H
9 D
v) Relación entre H y T
| _ f l T 2
H :
8
PROBLEMA Nfi 01
Respecto del movimiento parabólico,
determinar la medida del ángulo de lan­
zamiento ” e ", tal que el alcance horizon­
tal sea el triple de la* altura máxima
alcanzada.
SOLUCION:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
El ángulo de lanzamiento " 0 " , la altura
máxima “IT y el alcance horizontal "D”,
se relacionan del siguiente modo:
Pero: D = 3H tg 0 =
4H 4
3H 3
PROBLEMA Nfi 02
Un proyectil es lanzado con una velo­
cidad inicial "Vo” formando un ángulo de
45° respecto de la longitud.
Si la altura máxima alcanzada es 4 m,
determinar el alcance horizontal hasta lle­
gar al plano.
a) 1 m
d) 16 m
PROBLEMA Ns 03
b) 2 m c) 8 m
e) Ninguna
Dos proyectiles "A" y "B" lanzados
con inclinaciones de 53° y 37° respecti­
vamente alcanzan iguales alturas máxi­
mas. El proyectil “A" experimenta un al­
cance horizontal de 9 metros, ¿qué al­
cance horizontal experimenta "B"?
SOLUCION

182. 4H
D
Proyectil "A":
Proyectil "B":
4 _ 4H
3 _ 9
I H = 3 m
4(3)
x
x = 16 m
PROBLEMA Ne 04
Dos proyectiles A y B son lanzados
con inclinaciones de 37° y 53° respecti­
vamente, experimentan iguales alcances
horizontales. El proyectil A alcanza una
altura máxima de 4,5 m. ¿Qué altura má­
xima alcanza B?
a) 2 m b) 4 m c) 6 m
d) 8 m e) Ninguna
PROBLEMA Ne 05
Un futbolista patea la pelota, la cual
describe una trayectoria parabólica, si
permanece en el aire un intervalo de 6
segundos, ¿qué altura máxima alcanzó la
pelota?, g = 10 m/s2
SOLUCION:
En un parabólico, el tiempo de vuelo “T"
y la altura máxima alcanzada "H", se
relacionan del siguiente modo:
H = 8 (*)
pero: g = 10 m/s y T = 6 s
Reemplazando en (*):
H = y (36)
H = 45 m
*
*
*
*
*
*
<
¡*
$
*
*
*
*
*
*
*
PROBLEMA Ne 06
Un futbolista impulsa la pelota desde
el piso, la cual describe un movimiento
parabólico, alcanzando una altura máxi­
ma de 20 metros. Determinar el tiempo de
vuelo de la pelota,
g = 10 m/s'
a) 2 s b) 3 s
d) F.D. e) N.A.
PROBLEMA N907
Un bombardero que vuela horizontal­
mente a una altura de 125 m y con una
velocidad de 10Om/s, trata de atacar a un
barco que navega a una velocidad de 20
m/s, en la misma dirección y sentidos
opuestos.
¿A qué distancia “d” se debe dejar
caer una bomba para lograr un impacto
sobre el barco?
g = 10 m/s2
*
*
*
*
*
*
*
*
*
*
$
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1
SOLUCION
1
I25m
C1 2
Cálculo del tiempo de vuelo del proyectil:
1 o
h = Vo. t + —. g . r , pero V0 y = 0
125 = 0 + ^ (10) t2 t = 5s
De la figura:
d = ei + e2
d = V i. t + V2 .«
d = 100(5)+ 20(5)
d = 600 m

183. Un bombardero que vuela horizontal­
mente a una altura de 180 m y con una
velocidad de 100 m/s, trata de atacar un
barco que navega a una velocidad de 20
m/s, en la misma dirección y sentido. ¿A
qué distancia "d" se debe dejar caer una
bomba para lograr un impacto sobre el
barco?
g = 10 m/s2
a) 280 m b) 380 m
c) 480 m d) 580 m
e) Ninguna
PROBLEMA Nfi 09
Calcular la velocidad del móvil en el
punto "P". El cuerpo es lanzado horizon­
talmente desde el punto A y llega al punto
B como indica la figura, g = 10 m/s
20 m
80 g
i
6U m
SOLUCION'
Analizando en la vertical:
h = V0y t + ^ . g , t 2
80 = 0 + (10). t2
Analizando en la horizontal: M.R.U.
x 60 _ , ...
Vx = - = — =15 m/s ....(1)
Cálculo de la velocidad en el punto "P".
Componente Vertical:
V2Fy = V2oy + 2.g.h
V2y = 0 + 2 (10)(20)
Vy = 20 m/s .... (2)
Luego: V = V v 2 + v | = 25 m/s
PROBLEMA N9 10
Calcular la velocidád del móvil en el
punto "P”. La partícula es lanzada hori­
zontalmente en el pupto "A" y llega al
punto "B" como indica
g = 10 m/s2.
♦
*
#
*
*
#
<
«í
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
72 m
a) 10 m/s b) 24 m/s
c) 26 m/s d) 28 m/s
e) Ninguna
PROBLEMA N911
Una partícula se lanza horizontalmen­
te con una velocidad inicial V* = 40 m/s,
desde lo alto de una torre, ¿Qué ángulo
forma el vector velocidad de la partícula
con respecto a la horizontal, luego de 3
segundos?,
g = 10 m/s2
SOLUCION:
El vector velocidad, es tangente a la tra­
yectoria de la partícula en cada instante
de tiempo.

184. Vy = 30
La velocidad instantanea, tiene dos com­
ponentes, en x e y.
Eje x . V* = 40 m/s
Eje y : Vy = Voy + g.t
Vy = 0 + 10(3) = 30 m/s
Del triángulo rectángulo de velocidades
se deduce que:
PROBLEMA N® 12
Se deja caer una bomba desde un
aeroplano que vuela horizontalmente a
una altura de 320 m con una velocidad de
216 Km/h. ¿Cuál será la dirección de la
velocidad respecto a un eje horizontal en
ci momento del impacto?
g = 10 m/s
-* ? r --------
a) e=-45°
c) e = -53°
e) Ninguna
b) 6 = -37°
d) 0 = Tg-1(-2)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Una partícula se lanza con una veloci­
dad inicial de 20 m/s, haciendo un ángulo
de 53° con la horizontal.
Hallar al cabo de qué tiempo su velo­
cidad formará un ángulo de 37° con la
horizontal,
g = 10 m/s¿
SOLUCION:
En todo movimiento parabólico la veloci­
dad tiene un componente en el eje X,
constante, "Vx"
- 12
Vo = 9
V, = 16
*
*
*
*
*
*
<
¡*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
+
i»
!
*
*
*
+
s
js
*
*
*
*
Analizando en el eje Y.
Vf = V0 - g.t
9 = 16 - 10.1
t = 0,7 s
PROBLEMA Ns 14
Una partícula se lanza con una veloci­
dad inicial V0 = 15 m/s formsndo un án­
gulo de 53° con la horizontal. ¿En qué
instante "t” su velocidad formará un án­
gulo de 45° con la horizontal?
g = 10 m/s2
a) t = 0,1 s b) t = 0,2 s
c) t = 0,3 s d) t = 0,4 s
e) Ninguna
PROBLEMA Ns 15
Un dardo es lanzado desde "A“ con
una velocidad V0 = 10 m/s formando un
ángulo de 53° con la horizontal y se in­
crusta en el punto "B" perpendicular­
mente al plano inclinado. Calcular el
tiempo en movimiento del móvil,
g = 10 m/s2

185. SOLUCION:
En todo movimiento parabólico, la com­
ponente de la velocidad en el eje X, es
constante en el tiempo.
(A
(B)
V2 = 6
Analizando en la vertical:
VFy = V0y - g t
6 = 8 - 1 0 t
t = 0,2 s
PROBLEMA N9 16
Un dardo es lanzado desde el punto A
con una velocidad V0 = 15 m/s formando
un ángulo de 53° con la horizontal y se
incrusta en el punto B perpendicularmen­
te al plano inclinado. Calcular el tiempo
en movimiento del dardo,
g = 10 m/s2
*
&
*
*
*
*
*
*
*
<
¥
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
fs
*
*
*
*
*
*
a*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
a) 0,3 s
d) 2,1 s
PROBLEMA Ns 17
b) 0,6 s
e) Ninguna
c) 1.8 s
Dos esferitas A y B inician su mo­
vimiento simultáneamente, A es lanzada
horizontalmente y B verticalmente. Hallar
la distancia "x" si se sabe que los cuerpos
chocan a una altura H/2. Tienen igual ve­
locidad de lanzamiento.
A
V
T
T
T
g
n
n
re
T
P
T
tcmr—
iT
7■
> y rsTmnm
_______ __________ m-i
H/2
H/2
SOLUCION:
Los cuerpos A y B tienen igual velocidad
(módulo) de lanzamiento.
Analizando en la vertical:
h = V0 t ± ~ . g . t2
Para "A":
... (1)
Para "B“:
| = V . t - | . g . t 2 ....(2)

186. (1) +(2): H =V. t .... (3)
Para "A" en la horizontal, M R U.
x = V . t .... (4)
de (3) y (4):
x = H
PROBLEMA N® 18
Dos esferitas A y B inician su mo­
vimiento simultáneamente. A es lanzada
horizontalmente con una velocidad “V" y
B verticalmente con una velocidad "2V .
Hallar la distancia "x“ si se sabe que los
cuerpos chocan en el punto P.
®«=-
8 m
1
P
L
-.V
Z
T
? V 1
4 m
'cmufan
B
a) 2 m
d) 5 m
PROBLEMA N9 19
b )3 m
e) Ninguna
c) 4 m
En la figura mostrada, en el mismo
instante que se abandona la esferita "A"
se lanza la esferita "B“ con una velocidad
“Vo", determinar el ángulo " 6 de lan­
zamiento, tal que, las esferitas A y B coli­
sionen en el punto P.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
»
*
*
*
*
*
sis
*
*
*
*
*
*
*
*
*
40 m
Vo
'P
30 m
Analizando en la vertical:
h = Voy.t ± | . g . t 2
Para "A”:
a = | g - t2 ( 1)
Para "B":
b = V0 . Sen 6. t - ^ g . t2
(1) + (2):
40 = Vo . Sen 6. t .... (3)
Analizando en la horizontal: M.R.U.
30 = Vo .C o s e .t ...(4 )
(3)í (4) : f = Tg0
(2)
e = 53
PROBLEMA N920
En la figura mostrada, la esferita A se
lanza horizontalmente con una velocidad
"Vi ”, simultáneamente se lanza la esferita
B con una velocidad "V2 " formando un
ángulo de 45° con la horizontal. Sabiendo
que chocan en el aire durante su movi­
miento, determinar el desplazamiento ho­
rizontal que experimenta "A" hasta la co­
lisión.

187. b) 15 m c) 20 m
e) Ninguna
Vi . Sen a = Va . Sen p .... (3)
2) D esplazam iento h o rizo n ta l
(M.R.U.): e = Vx . t
Para “A " V i. Cos a . t = d
Para "B": V2 . Cos p . t = 2d
2 V i. Cos a = V2 . Cos ¡i .... (4)
Dividiendo las ecuaciones- (3) r (4)
a) 10 m
d) 25 m
PROBLEMA N2 21
Hallar la relación entre la tangente de
los ángulos a y p con que se lanzan los
dos proyectiles simultáneamente, si coli­
sionan en el aire durante su movimiento.
«
s
>
*
0
0
0
*
*
5¡S
S
¡*
*
*
*
0
*
*
*
*
Tg a
Tgp
= 2
PROBLEMA Nfi 22
Dos proyectiles A y B se lanzan simul­
táneamente, como indica la figura. Hallar
la medida del ángulo “ 0 ”, si los proyec­
tiles colisionan en el punto "P“durante su
movimiento.
SOLUCION:
1) Si ambos proyectiles alcanzan al­
turas iguales.
h = Voy. t - ^ . g . t 2
Para "A":
H =Vi S e n a .t- l.g .t2 ....(1)
Para "B”:
H=V2.S e n p .t-| g.t2 ... (2)
Igualando: (1) = (2)
*
*
fe
*
$
*
#
m
$
&
&
*
$
&
#
*
*
a) e =30° b) 0 =37° c) 6 =53°
d) 6 = 60° e) Ninguna
PROBLEMA N2 23
Desde un globo que asciende con una
velocidad U = 6 m/s, se lanza una piedra
horizontalmente (respecto del globo) con
una velocidad Vx = 5 m/s. La piedra ex­
perimenta un alcance horizontal de 15 me­
tros hasta llegar al suelo. ¿Desde qué
altura H se lanzó la piedra?
g = 10 m/s2

188. 1) En el eje horizontal se cumple en
M.R.U.:
t e 15 m
Vx 5 m /s
t = 3 s
tiempo en
movimiento
2) En el eje vertical, tomamos como
referencia el punto de lanzamiento.
-h = V0y . t - ^ . g . t2
H = 27 m
PROBLEMA Ne 24
Desde un globo que asciende a 5 m/s,
se lanza un objeto con una velocidad V0 =
5 m/s (respecto del globo) formando un
ángulo de 53° con la horizontal. El objeto
experimenta un alcance horizontal de 12m.
¿Desde qué altura H se lanzó al objeto?
g = 10 m/s2
i i
i I
I !
i !
r-n» k
7
1
’L
.Z
'’:v ,f*V'WKlgWlM^IJy'*
■
— 12 m----------—
I
*
*
*
*
*
*
*
*
*
*
*
*
*
*
n
>
s
t*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
4
»
*
*
*
*
*
*
*
*
*
*
*
*
*
a) H = 24 m
c) H = 44 m
e) Ninguna
PROBLEMA N225
b) H = 34 m
d) H = 54 m
En ia figura el campo gravitatorio se
representa mediante líneas de fuerza. Se
lanza una pelota perpendicular a la super­
ficie con una velocidad V0= 20 m/s. Hallar
la altura máxima que alcanza la pelota
respecto a la superficie.
La intensidad del campo gravitatorio
es: g = 10 m/s2
SOLUCION:
Descomposición rectangular de la inten­
sidad del campo gravitatorio:
q x = 5 ' ¡ 3
gy = 5 m/s
En el eje "y“ :
Vf2 = Vo2 - 2 gy . h
Reemplazando en (1):
0 = 400 - 2(5)H
.... ( 1)
H = 40 m
PROBLEMA N226
La figura muestra un campo gravitato­
rio representado mediante líneas de fuer­
za de intensidad g = 10 m/s2. Se lanza un
proyectil perpendicularmente a la super­
ficie con velocidad V0 = 40 m/s. Determi­
nar el desplazamiento a lo largo del plano.

189. a) x = 100 m
c) x = 300 m
e) x = 500 m
PROBLEMA N927
b) x = 200 m
d) x = 400 m
¿Cuál es la diferencia entre las alturas
máximas alcanzadas por un proyectil dis­
parado con una velocidad V0 = 2 m/s,
cuando varía su ángulo de tiro de 30° a
60o?. El módulo de la velocidad de lan-
. o
zamiento es constante, g = 10 m/s .
a) 0,1 m b) 0,2 m
d) 0,4 m e) Ninguna
c) 0,3m
4
M O V IM IE N T O C IR C ULA R
CONCEPTO.
Es aquel tipo de movimiento que tiene
como trayectoria a una circunferencia.
Elementos del m ovimiento circular
1) Desplazamiento Lineal (S).
Es la longitud de arco de la circunferencia
que recorre el móvil o punto material, entre
dos puntos considerados de la trayectoria.
2) Desplazamiento angular ( 6).
Es el ángulo central correspondiente al
arco descrito por el móvil, se mide en ra­
dianes.
Relación entre los desplazamientos li­
neal y angular:
El ángulo medido en radianes es igual al
cociente de la longitud de arco entre el radio
de curvatura.
RV-'e'v'R
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Luego:
" f 1
1"
s = e .R |
(1)
$ 3) Velocidad lineal o tangencial (Vj).
* Es una magnitud vectorial, se define
J como la longitud de arco recorrido por el
* móvil por cada unidad de tiempo. Se repre-
% senta por un vector tangente a la trayectoria.
i
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
... (2)
4) Velocidad angular (W).
Es una magnitud vectorial, se define co­
mo el desplazamiento angular que experi­
menta la partícula por cada unidad de tiem­
po. Se representa por un vector perpendicu­
lar al plano de rotación; el sentido se deter­
mina mediante la regla de la mano derecha,
los dedos indican el sentido de giro y el pulgar
el sentido de la velocidad angular,
W =
6
.... (3)

190. Unidades:
rad rad rad
s ’ min ' hora
Relación entre las velocidades tangen­
cial y angular
S
i) Sabemos que: V t = — .... (2)
pero: S = 6 R .... (1)
ii) Reemplazando (1) en (2):
0 , R
VT =
t
.... (4)
0
pero: W = - - - (3)
Reemplazando (3) en (4):
VT = W . R | .... (5)
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
#
*
t
#
*
*
*
*
♦
*
«
*
#
4
*
i»
#
#
♦
#
í
*
*
♦
*
*
*
*
*
*
CONCEPTO.
Es aquel movimiento que tiene como tra­
yectoria una circunferencia, en el cual la par­
tícula recorre arcos iguales, por consiguiente
barre ángulos en tiempos iguales, esto quie­
re decir que la velocidad angular permanece
constante. En este caso el movimiento de la
partícula es periódico, y la partícula pasa por
cada punto de la circunferencia en intervalos
de tiempos iguales.
1) Periodo (T).
Es el intervalo de tiempo constante que
demora una partícula en recorrer la misma
trayectoria. Su valor indica el tiempo em­
pleado por cada vuelta o revolución.
j tiempo empleado
“ número de vueltas
Unidades
s ., min , hora , años
2) Frecuencia (f).
Se define como la inversa del período.
Su valor indica el número de vueltas que
describe la partícula porcada unidad de tiem­
po.
f _ 1 número de vueltas
- T tiempo empleado
Unidades
1 1
____ 1_
s ' min ’ hora
— R.P.S. = Hertz.; -4 = R.P.M.
s min
t
hora
= R.P.H.
El término usual de la frecuencia es
(R.P.S.) revoluciones por segundo o Hertz.
La unidad fue llamada Hertz en honor al físico
alemán H.R. Hertz (1 857 - 1 894), quien fue
el primero en demostrar experimentalmente
la existencia de ondas electromagnéticas.
3. Relaciones entre la velocidad angular
el período y la frecuencia.
0
i) Sabemos que: W = ■• .... (1)
ii) Pero, cuando la partícula da una
vuelta sobre la trayectoria el ángulo
barrido es: 6 = 2 n rad. y el tiempo
empleado es igual al período.
iii) Luego: 0 = 2 n rad y
t = período = T ... (2)
iv) Reemplazando (2) en (1):
.... (3)

191. v) Además sabemos que: *
♦
.... (4)
vi) Reemplazando (4) en (3):
W = 2 n. f .... (5)
4) LEY de KEPLER para el M.C.U.
Toda partícula o punto material que tiene
movimiento circular uniforme, describe areas
iguales en tiempos ¡guales, respecto de un
sistema de referencia ubicado en el centro de
la circunferencia".
Ley de áreas:
“Areas iguales en tiempos iguales"
*
*
*
*
»
*
*
*
*
*
*
*
*
*
CONCEPTO.
Es aquel movimiento que tiene como tra­
yectoria una circunferencia, en el cual la par­
tícula aumenta o disminuye su velocidad an­
gular progresivamente, por consiguiente se
mueve con aceleración angular constante.
1) Aceleración Angular ( a ). Es una mag­
nitud vectorial que mide la rapidez de
cambio de la velocidad angular que ex­
perimenta una partícula. Se representa
por un vector perpendicular al plano de
rotación.
*
*
*
*
*
*
*
*
$
*
*
Fig. 1
AW
Unidades:
rad
„2
rad
- 2
min
Dimensionalmente:
[ a ] = T
-2
.... (3)
2) En el M.C.U.V., la velocidad lineal o tan­
gencial cambia en módulo, dirección y
sentido. A la medida de la rapidez de
cambio de la velocidad lineal se le llama
"aceleración lineal" que es diferente a la
"aceleración angular".
3) Descomposición rectangular
aceleración lineal
de la
La aceleración lineal se puede escribir en
función de dos componentes mutuamen­
te perpendiculares llamados: aceleración
tangencial y aceleración centrípeta.

192. 4)
5)
Fig 2
Aceleración Tangencial ( a t). Es una
magnitud vectorial, mide la rapidez de
cambio que experimenta la velocidad li­
neal en módulo. Es la componente de la
aceleración lineal paralela o colíneal a la
velocidad instantánea, por consiguiente
se representa por un vector tangente a la
trayectoria. Su valor es igual a:
.... (4)
De la figura (2) se puede escribir la acel­
eración tangencial como una componen­
te de la aceleración linea! “a".
L®¡= a . Sen 6 (5)
Acelereración centrípeta ( ac )■ Es una
magnitud vectorial, mide la rapidez de
cambio que experimenta la velocidad en
dirección (y sentido). Es la componente
de la aceleración lineal, radial, por con­
siguiente se representa por un vector que
apunta en todo instante al centro de la
circunferencia. Su valor es igual al cua­
drado de la velocidad instantánea entre
el radio de curvatura de la circunferencia.
.... (6), pero:
V = W . R ....(7)
Reemplazando (7) en (6):
ac = W . R (8)
*
*
*
*
*
*
*
*
*
*
*
*
+
*
*
*
*
*
*
*
*
*
*
*
*
+
$
*
*
*
$
*
*
*
*
*
#
♦
*
*
*
*
#
ftf
*
#
»
*
#
*
m
*
0
*
O
f
*
*
*
#
*
*
*
*
*
#
*
#
*
*
*
*
*
V = Velocidad lineal instantánea
W = Velocidad angular instantánea
R = radio de curvatura, constante
De la figura (2) se puede escribir la ace­
leración centrípeta como una compo­
nente de aceleración lineal "a".
ac = a Cos G 1 - . O )
6) Relación entre la aceleración angular
y la aceleración Tangencial.
Sabemos que: Vt = W . R ; en cada
instante
Luego: V f = W f .R : V0 = W0 R . (i)
Además; la aceleración angular:
W f-W o
a = ■
t
Reemplazando e ( i ) en
V f - V o
at = -
t
.... (ii)
.... (iii)
WF. R - Wo- R (WF - W0) „
3 i " t R
De (ii): at = ce, R
.... (iv)
... (v)
Debe observarse que la aceleración an­
gular (a) y la aceleración tangencial ( a ,)
son vectores mutuamente perpendicu­
lares.
LINEAL
S = V0 t + | a , . t 2
V f = V o + 3 t . t
V2f = V20 + 2 . a ,. S
s = (Vo + Vq t

193. ANGULAR
e = Wo . t + ~ . a . t2
Wf = W0 + a . t
W2f = W20 + 2 . a .6
PROBLEMA Ne 01
Una esfera hueca de radio 1,0 m gira
alrededor de un eje vertical que pasa por
su centro. Un proyectil se desplaza con
una velocidad de 400 m/s perpendicular­
mente al eje, perforando la esfera en un
punto cuyo radio forma 30° con el eje.
Hallar la mínima velocidad angular que
debe tener la esfera para que el proyectil
entre y salga por el mismo agujero.
SOLUCION:
Proyectil:
e = V . T
*
*
*
*
m
%
*
$
*
*
*
#
$
$
*
*
*
*
*
o
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
1 m :
T =
400
400
m
Esfera:
W- ! - ±
400
W = 400 n rad/s
PROBLEMA N2 02
Dos satélites A y B decriben trayecto­
rias circulares concéntricas de radios de
curvatura R y 2R, respectivamente. Si los
vectores posición, respecto del centro de
curvatura de A y B describen áreas igua­
les en tiempos iguales, determinar la re­
lación entre sus velocidades angulares.
SOLUCION:
el mismo tiempo.
*
*
*
*
*
#
w
*
*
*
*
*
#
El proyectil atraviesa el cuerpo esférico
haciendo un solo agujero cuando la es­
fera gira un ángulo de 180° (mínimo) en *
*
*
*
Igualando Areas:
A(A) = A(b)
| a R 2 = | p (2R)2
a =4 p
Por consiguiente:
WA = 4 WB

194. Dos móviles A y B parten de dos pun­
tos diametralmente opuestos de una pista
circular, desplazándose en el mismo sen­
tido con velocidades angulares de n!2 y
n/3 rad/s; respectivamente. ¿Después de
cuánto tiempo se encuentran juntos?
SOLUCION:
#
i
Desplazamiento angular:
6 a - 6 B = n
(WA - Wb) t = n
Reemplazando:
§ - § ! « ■
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
En qué tiempo se detiene una rueda
que giraba a 1200 RPM; si es frenada
logrando dar 200 vueltas hasta que se
detiene.
SOLUCION:
Considerando un movimiento con ace­
leración angular constante:
o _ (W0 + Wf) t
Pero:
W0 = 2 ic f y WF = 0
Reemplazando:
v 2rc(1200) „
200 ( 2 n ) = — --------- t
t = —
imin
u
*
t = 6 s
*
*
t = 2 0s

195. 6) MOVIMIENTO CIRCULAR UNI­
FORME (M.C.U.)
PROBLEMA N®01
La figura muestra tres discos tangen­
tes entre sí, de radios de curvatura:
_ R R ,
R ; — ; — respectivamente.
Cuando el disco de mayor radio gira 4
vueltas, ¿cuántas vueltas girará el disco
de menor radio?.
$
*
*
*
*
*
*
*
*
$
♦
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
%
$
*
♦
*
♦
$
*
♦
*
SOLUCION:
Los puntos periféricos de los discos tan­
gentes, tienen igual velocidad lineal
VA = VB = Vc
Wa - R = WC - j
3W a =W C
3 fA = fe
3(4v) = fe
fe = 12 vueltas
’EI número de vueltas que gira uno de los
discos tangentes es inversamente pro­
porcional a su radio de curvatura".
PROBLEMA N9 02
Se tiene "n" discos giratorios todos
ellos tangentes el uno a continuación el
otro tal como se muestra en la figura, sus
radios son:
_ R R R
R* 2 * 3 * 4 *
de mayor radio con velocidad angular
"w", ¿cuál será la velocidad angular del
disco n-ésimo?
#
*
*
*•
*
*
*
a) w
d )(n - 1 ) w
b) nw
e) N.A
c)
w

196. Un disco gira con una velocidad angu­
lar constante. Si los puntos periféricos
tienen el triple de velocidad que aquellos
puntos que se encuentran 5 cm. más cer­
ca al centro del disco, calcular el radio del
disco.
SOLUCION
3 V
Los puntos A y B tienen igual velocidad
angular "w".
La velocidad lineal será:
Vi = w Ri
Para "A” :
3 V = w . R ... (1)
Para ”B ':
V = w . (R - 5)
Dividiendo:
3 R
.... (2)
1 (R - 5)
Resolviendo:
R = 7,5 cm.
PROBLEMA Ne 04
Un disco gira con una velocidad angu­
lar constante. La velocidad lineal de los
puntos periféricos del disco es 6m/s y la
velocidad lineal de los puntos situados a
una distancia de 0,15 m más cerca al eje
es 5,5 m/s. Determinar el radio del disco.
a) 2,8 m b) 2,4 m c)1,8 m
d)1,2m e) Ninguna
*
4
»
*
4
»
*
*
*
*
*
♦
4*
4
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
#
4»
#
>
*
#
*
*
4»
i»
!
*
*
*
*
4*
*
«s
*
4»
*
*
#
4»
4*
#
*
*
*
*
#
*
La figura muestra dos poleas concén­
tricas de radios de curvaturas a = 20 cm y
b=30 cm. Si las poleas giran en sentido
horario con velocidad angular constante
w = 4 rad/s. Hallar la velocidad relativa de
alejamiento entre los bloques A y B.
SOLUCION-
La velocidad de cada bloque, es igual a
la velocidad lineal de los puntos periféri­
cos de las poleas respectivas:
V = w . R
Para "A":
Va = (4) (20) = 80 cm/s .... (i)
Para “B":
VB = (4) (30) = 120 cm/s
En cada segundo los bloques se alejan
en 40 cm.
Vrelativa = (Vb ~ Va) = 40 cm/s
PROBLEMA Nfi 06
La figura muestra un sistema de po­
leas concéntricas, entre las poleas tan­
gentes no hay deslizamiento. Si el bloque
P baja con una velocidad de 5 cm/s, deter­
minar la velocidad del bloque Q. Los ra­
dios son los siguientes:
a = 60 cm
x = 40 cm
b = 30 cm ;
y = 20 cm

197. a) 3 cm/s b) 5 cm/s
c) 7 cm/s d) 9 cm/s
e) Ninguna
PROBLEMA Ns07
La figura muestra dos poleas con­
céntricas de radios a = 20 cm y b = 10
cm, respectivamente. La polea móvil se
encuentra sostenida mediante una cuer­
da cuyos extremos están enrrollados a
las poleas fijas.
Si las poleas con centro fijo giran con
velocidad angular constante de 4 rad/s en
sentido horario, hallar la velocidad del
bloque unido a la polea móvil.
*
*
*
0
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
o
»
$
*
*
*
*
*
*
$
*
SOLUCION
La velocidad de los puntos (1) y (2) en la
cuerda, es igual a la velocidad lineal de
los puntos periféricos de las poleas res­
pectivas:
2
V = w . R
Para (1)
Vi = (4) (10) =40 cm/s
Para (2):
V2 =(4) (20) = 80 cm/s
Propiedad de la polea móvil:
Reemplazando:
V3 = 60 cm/s
PROBLEMA Nc08
La figura muestra tres poleas concén­
tricas de radios de curvatura a = 10 cm;
c = 30 cm. Si el sistema de poleas gira con
velocidad angular constante igual a w = 4
rad/s, en sentido horario, hallar ia veloci­
dad con que se mueve el bloque “E''.
a) 0,5 m/s
c) 0,8 m/s
e) Ninguna
b) 0,7 m/s
d) 0,9 m/s

198. La figura muestra dos poleas concén­
trica de radios a = 20 cm y b = 10 cm,
respectivamente. Si las poleas giran en
sentido antihorario con velocidad angular
constante w = 6 rad/s, hallar la velocidad
del bloque que se encuentra unido a la
polea móvil.
SOLUCION
1) Cálculo de la velocidad lineal de los
puntos A y B de la cuerda.
-I
''N
r
i .
2) Sabemos que. V = w.R
Punto “A“ ;
VA = (6) (20) = 120 cm/s ( i)
Punto "B“:
VB = (6) (10) = 60 cm/s (T)
Propiedad de la polea móvil:
Va + Vb
Vc = -
2
Reemplazando
(-120)+ (60)
y _ - -
Vc = -30 cm/s ( -:b a ja )
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
>
!<
»
l*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
#
*
<
¡»
fe
*
*
*
*
*
*
*
*
*
*
*
*
*
*
0
*
*
*
«
i*
*
*
*
*
*
*
*
*
La figura muestra dos poleas concén­
tricas de radios a = 156 cm y b = 10 cm,
respectivamente. Si las poleas giran en
sentido horario con velocidad angular
constante w = 4 rad/s, hallar la velocidad
lineal del bloque que se encuentra unido
a la polea móvil.
c)7cm/s
a)3 cm/s b)5 cm/fe
d)9 cm/s e) Ninguna
PROBLEMA Nfi 11
Un disco que tiene un agujero a 50 cm
de su centro geométrico, gira con veloci­
dad angular constante en un plano hori-
zontal.Respecto a un eje vertical, desde
una altura H = 1,25 m se abandona una
bolita en el instante en que el agujero y la
bolita están en la misma línea vertical.
Hallar la mínima velocidad angular del
disco, tal que, la bolita pueda pasar por
el agujero.

199. SOLUCION
El tiempo que demora la bolita en reco­
rrer H = 1,25 m, es el mismo tiempo que
demora el disco en dar una (1) vuelta.
En la vertical:
h = V o . t + | g . t2
Reemplazando:
125 = 0 + “ (10). t2
Resolviendo:
t = 0.5 segundos
Para el movimiento circular del disco:
6 2 n
w ~ t ~ o,5
w = 4 n rad/s
constante, cuya frecuencia es de 1900
R.P.S. respectivo de un eje vertical. Se dis­
para un proyectil horizontalmente, de tal
modo que pasa por e¡ centro geométrico del
campo esférico. Calcular la máxima veloci­
dad del proyectil, tal que, atraviese haciendo
un solo agujero.
PROBLEMA NB12
Si la bala atraviesa el orificio del
disco mostrado con una velocidad lineal
V = 314,16 m/s hacia arriba, ¿Cuál debe
ser la mínima velocidad angular cons­
tante con ta que debe estar girando el
disco, para que ia bala de regreso pase
por el mismo orificio? g = 10 m/s.
W I n
c b
a) 0,01 rad/s b) 0,02 rad/s
c) 0,10 rad/s d) 0,20 rad/s
e) Ninguna
PROBLEMA Ns 13
Un cascarón esférico de radio de curva­
tura R = 0,5 m gira con velocidad angular
De la conoición del problema el proyectil
hace un solo agujero:
0=7t ; 3 n ; 5 n ; ......
Si la velocidad del proyectil es máximo,
entonces el desplazamiento angular del
agujero es n radianes. El tiempo em­
pleado por el cascarón en dar 1/2 vuelta
es el mismo empleado por el proyectil en
recorrer el diámetro igual a 1 metro.
El agujero da 100 vueltas en 1 segundo,
por consiguiente gira 1/2 vueíta en 1/200
de segundo.
El proyectil:
e 1m
v=_ =_ _
200 S
v = 200 m/s
PROBLEMA Ns 14
Un cilindro hueco (vacío) de radio de
curvatura R =0,4 m gira a una velocidad
angular constame,cuya frecuencia es 150
R.P.S. respecto de un eje vertical.
SOLUCION

200. Se dispara un proyectil horizontalmente,
de tal modo que pasa por el eje de rotación.
Calcular la máxima velocidad del proyectil,
tal que, atraviese haciendo un solo agujero
al cilindro.
a) 200 m/s
c) 240 m/s
e) Ninguna
PROBLEMA N® 15
b) 220 m/s
d) 280 m/s
Sobre un eje que gira con una frecuen­
cia de 1 200 R.P.M., se tiene montado dos
discos separados a una distancia de 25
cm. Se dispara un proyectil paralelamente
al eje, tal que perfora los dos discos,
notándose que el segundo agujero se
desvía 12a respecto al primero. Determi­
nar la velocidad del proyectil.
25 cm
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
#
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
si*
*
*
*
*
*
*
SOLUCION
El tiempo que demora el proyectil en des­
plazarse del 1er al 2do agujero, es el mismo
tiempo que emplean los discos en girar un
ángulo de 12® ó rc/15 radianes.
t J > = J L
<
ú 2jtf
t =
n
15
2k 1200
t = S
600
Analizando el movimiento del proyectil
que tiene M.R.U.
e
t
25 cm
600 S
V (bala) = 150 m/s
PROBLEMA N2 16
Un cilindro hueco de 3 m de largo gira
alrededor de un eje horizontal con veloci­
dad angular constante a razón de 180
R.P.M. Una bala disparada paralelamente
al eje de rotación perfora las bases en dos
puntos, cuyos radios forman un ángulo
de 89. Calcular la velocidad de la bala.
a) 105 m/s
c) 305 m/s
e) Ninguna
PROBLEMA N9 17
b) 205 m/s
d) 405 m/s
Se tiene una barra horizontal en reposo
cuya longitud es de 1m, sostenida por dos
cuerdas enrrolladas a dos poleas de ra­
dios, a = 2,5 cm y b = 7,5 cm, respecti­
vamente.
Si las poleas empiezan a girar a razón de
2 rad/s en sentido horario, ¿en cuánto tiem­
po los cables que sostienen la barra estarán
en posición vertical, como indica la figura?
*
*
*
*
*
¡¡t

201. 6 0 ,
3 7 °
UYJ
De la figura:
(L + Si) - ( L - S2) = 60 cm
Si + S2 =60 cm .... (1)
Si. longitud de cuerda que cede la po­
lea "a"
S2: longitud de cuerda que enrolla la
polea ”b"
En (1): wat + wbt = 60 cm
Reemplazando:
t.w (a + b) = 60 cm
t . (2) (10) =60
t = 3 s
PROBLEMA Ns 18
Dos poleas solidarias giran en sentido
antihorario con velocidad angular cons­
tante w = 0,3 rad/s. Si el tiempo se mide
desde el instante que muestra la figura,
hallar al cabo de qué tiempo las cuerdas
que sostienen a la barra AB, de longitud
50 cm, estarán nuevamente en posición
vertical.
*
*
*
*
*
*
*
<
K
*
*
*
*
*
*
*
*
*
*
«
*
*
*
♦
#
*
*
#
#
*
#
*
*
*
*
*
*
*
«
H
*
*
*
*
#
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
c) t = 4 s d) t = 5 s
e) Ninguna
PROBLEMA N® 19
Se tiene un reloj de agujas. ¿A qué
hora entre las tres y las cuatro, el horario
y el minutero formarán un ángulo del 180s.
SOLUCION
I
12
Velocidad angular del horario:
cüh = 7 rad/h
O
Velocidad angular del minutero:
com = 2k rad/h
De la figura:
0 M - 0 H = 2 r
c .... (1)
Pero: 0 = tú . t
E n (1): 6 ' t~2rc - 1= | ti
Luego:
Respuesta
t = — horas
3h 49 min 5,45 s
PROBLEMA N920
Se tiene un reloj de agujas, ¿A qué
hora entre las tres y las cuatro, el horario
y el minutero formarán un ángulo recto.
a) 3h 32min
c) 3h 33min 50s
e) Ninguna
b)3h 32min 43,6s
d)3h 38min 9s

202. Un móvil recorre la trayectoria ABC,
con módulo de la velocidad constante pa­
ra el tramo AB y para el tramo BC. Se sabe
que la aceleración en AB es 6 m/s2 y en
BC 5 m/s2.
Hallar el intervalo de tiempo que de­
mora en el recorrido total ABC.
1 La aceleración centrípeta en cada
tramo:
V 2
ac = -R - (1)
V2
En AB: 6 = - ^ V a b = 6 m/s
6
V2
En BC: 5 = ^ - Vac = 5m /s
5
2. Calculo del tiempo en cada tramo:
_ . _ , r t . 6
En AB: Iab = =n s
o
r- 7
1■5
En BC: tBC - c = n s
D
Tiempo total = 2n s
PROBLEMA Ns 22
¿Con qué velocidad deberá volar un
avión en el Ecuador de Este a Oeste, para
que a sus pasajeros les parezca que el Sol
está fijo en el firmamento?
Radio de órbita del avión = 6396 Km
' i '
SOLUCION SOL
La velocidad angular del avión debe ser
igual a la velocidad angular de la tierra,
pero en sentido opuesto.
£D= y = — rad/h co= — rad/h
La velocidad lineal del avión respecto de
la Tierra:
V = (o.R
V = ^ (6 396)
V = 1673,62 Km/h
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
&
*
+
*
*
*
*
*
*
*
*
*
%
*
*
*
$
*
*
*
*
#
#
*
*
*
#
*
»
*
*
*
*
*
*
*
*
$
*
*
*

203. 7. MOVIMIENTO CIRCULAR UNIFOR­
MEMENTE VARIADO (M.C.U.V.)
AnGULAR.
*
*
*
*
*
éf
*
*
*
*
*
s
fs
*
*
*
*
*
#
»
*
*
*
#
*
*
*
*
PROBLEMA Ns 01
La hélice de un ventilador gira a razón
de 240 R.P.M., si al desconectarlo se de­
tiene al cabo de 10 segundos, con acelera­
ció n a n g u la r co n sta n te . C alcu la r el
número de vueltas que ha dado hasta
detenerse.
SOLUCION:
Cálculo de la velocidad angular inicial:
240
«o = 2 7
1í = 2 E .
60 s
o)= 8h rad/s
cúf = 0 .... la hélice se detiene
Cálculo del desplazamiento angular:
„ ( “ o + CO F, .
i ‘
e = i.8ft + 0) (1ü) = 40;t ra)j
Cálculo del número de vueltas:
J L _
2n~ 2n
N° de V = 20 vueltas
N° de V =
* PROBLEMA Ns 02
*
*
*
*
*
*
*
*
*
*
$
*
m
*
*
*
*
*
*
Una hélice gira a razón de "a" R.P.M.,
si da "b" vueltas antes de detenerse, con
aceleración angular constante. ¿Qué
tiempo tarda en detenerse?
. a .
a) -m in
.. 2b
b) — min
a
,2a
c)— min
^ b
d) — min
' 2a
e) Ninguna
PROBLEMA NB03
La velocidad de un automóvil aumenta
uniformemente en 10 segundos de 19
km/h a 55 km/h. Si el diámetro de sus

204. ruedas es 50 cm, ¿cuál es fa aceleración
angular de las mismas?
SOLUCION
Cálculo de la aceleración lineal:
_(Vf - Vo) (5 5 -1 9 ) 1000 m
t
aT=
10s 3600 s
3t =1 m/s
Pero: ar = a . R
1 m/s = a (0,25 m)
Luego: a = 4 rad/s
PROBLEMA N®04
La velocidad de un automóvil aumenta
uniformemente en 5 segundos de 36 km/h
a SOkm/h. Si el diámetro de las ruedas es
60 cm, ¿cuál es la aceleración angular de
las llantas?.
a) 5 rad/s/J b) 10 rad/s2
c)15 rad/s2 d) 18 rad/s2
e) Ninguna
PROBLEMA N® 05
Dos ruedas parten de un mismo punto
en sentidos opuestos con velocidades
angulares iguales a roo= 5 rad/s; una man­
tiene un M.C.U.V. acelerando a razón de 2
m/s2.
Calcule la suma de los radios de am­
bas ruedas, si después de 4 segundos
están distanciados 156 metros.
SOLUCION:
M.C.U.V
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
»
*■
*
*
*
*
*
Cálculo del desplazamiento lineal:
M C U :
51 = V t = «o - r . t
M.C.U.V.:
52 = V0 . t + ^ . a i . t2
1 9
S2 = íúo . R . t + —. aT. t
Pero: Si + S2 = 156 m
too. t (r + R) + —. aT - 1
2 = 156 m
5(4). (r+ R )+ 1(2)(16) = 156
Luego: (r + R) = 7 m
PROBLEMA N« 06
Dos ruedas parten de un mismo punto
en igual sentido con velocidades angu­
lares iguales a c
ü
0 = 2 rad/s, una mantiene
un M.C.U. y la otra un M.C.U.V. acelerando
a razón de 4 m/s2. Determine la diferencia
de los radios de ambas ruedas, si des­
pués de 5 segundos están separadas 80
metros.
a) 1 m
d) 4 m
PROBLEMA N®07
b) 2 m
e) Ninguna
c) 3 m
Una partícula realiza un M.C.U.V. a par­
tir del reposo (V = 0) con aceleración an­
gular constante de 0,25 rad/s2. Si se sabe
que el radio de la trayectoria es de 2 metros
y el cambio de la velocidad en módulo, es
igual, al cambio de la velocidad en dirección
y sentido en un determinado instante. De­
termine el tiempo de movimiento de la
partfcua hasta ese instante.
SOLUCION:
1) La aceleración centrípeta, es igual a
la aceleración lineal, en modulo.
M.C.U
3 >
i

205. V2 = a . R2
Reemplazando:
V2 = (0 , 25)(4)
V = 1 m/s - ( 1 )
2) Cálculo de la aceleración lineal o
tangencial.
aT = a . R a-n=(0 , 25)(2)
ar = 0,5 — (2)
s
3) Cálculo del intervalo de tiempo:
Vf = V0 + At t
1= 0 + (0, 5). t
Luego:
t = 2 s
*
*
&
*
*
*
*
*
*
*
*
$
*
*
«ti
*
*
*
PROBLEMA N908
Una partícula realiza un M.C.U.V. a par­
tir del reposo con aceleración angular
constante de 1,0 radianes/s2. Si se sabe
que el radio de la trayectoria es R = 2 m y
el cambio de la velocidad en dirección y
sentido, es igual, al cambio de la veloci­
dad en módulo en un determinado ins­
tante.
Determinar el tiempo en movimiento
de la partícula hasta ese instante.
a) t = 0,1 s b) t = 8 s
c )t = 0.8s d )t= 1 ,0 s
e) Ninguna
PROBLEMA N809
En la figura se muestra una partícula
moviéndose en sentido antihorario sobre
una circunferencia de radio P = 5 m. La
magnitud de su velocidad es variable. En
un determinado instante el vector acele­
ración de módulo a = 20 ^¡2 m/s2, forma un
ángulo de 135° con el vector velocidad.
Halle Ud. el valor de la velocidad y el tipo
de movimiento en dicho instante.
*
*
*
*
*
m
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
&
£
SOLUCION:
Descomponiendo la aceleración rectan­
gularmente:
Cálculo de la aceleración centrípeta:
42
ac=a .Cos 45°= 20 y¡2 =20 m/s2
Pero:
ac=-R
V¿
20 = T
Luego.
V = 10
m
s
El movimiento de la partícula es retar­
dado, V y aT tienen sentidos opuestos.
PROBLEMA N9 10
En la figura se muestra una partícula
moviéndose en sentido horario sobre una
circunferencia de radio R = 0,4 m. La
magnitud de su velocidad es variable. En
un determinado instante el vector acele­
ración de módulo a = 50 m/s2 forma un
ángulo de 127° con el vector velocidad.
Entonces, la partícula se mueve con una
velocidad instantánea de módulo..........y
el tipo de su movimiento e s .................
"acelerado"
“retardado":
la velocidad aumenta,
la velocidad disminuye.

206. V
a) V = 4 m /s; acelerado
b) V = 4 m/s ; retardado
c) V = 6 m/s , acelerado
d) V = 8 m/s ; retardado
e) Ninguna
PROBLEMA Ne 11
Un móvil parte del reposo y comienza
a moverse con M.C.U.V. con una acele­
ración angular constante de2 rad/s .
Sabiendo que un ciertointervalo de
tiempo, el móvil ha barrido con ángulo
central “6" y 2 segundos después ha ba­
rrido un ángulo donde se cumple que;
6 _ e
4 “ 5
Hallar el ángulo “ e "
SOLUCION:
1)
0 = | a l2
2)
3)
Luego
6 + e = (t +2Y
De la condición:
2
— (2)
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
S
fí
*
*
*
#
*
*
*
*
*
Llamaremos T al tiempo que tarda
el móvil en barrer el ángulo central “
0 Analizando el tramo inicial del
movimiento:
A nalizando el tram o total del
movimiento:
(0 + e.) = | . a (t+2)2
Luego:
e + 0 9
e " 4
Reemplazando (1) y (2) en (3):
t = 4 s
e = 16 rad
e = 20 rad
PROBLEMA Ns 12
Un móvil parte del reposo (o = 0) con
M.C.U.V., después de un tiempo "t" se
observa que barre un ángulo central " 0 "
y 5 segundos después barre un ángulo
* e ", donde se cumple que:
Si la aceleración angular es de 4
* rad /s2, determine el ángulo total barrido
i (6 +e).
a) 200 rad b) 300 rad
| c) 400 rad d) 500 rad
S e) 800 rad
PROBLEMA Nfi 13
La figura muestra dos poleas concén­
tricas de radios x = 20 cm y = 30 cm,
sabiendo que las poleas giran en sentido
horario con aceleración angular constan­
te = 4 rad/s2, hallar la aceleración lineal
con que baja el bloque unido a la polea
móvil.
*
*
*
*
*
*

207. La aceleración lineal de los puntos A y B, es
igual a la aceleración lineal de tos puntos
periféricos de las respectivas poleas:
a = a . R
Para “A ":
aA = 4 (20) - 80 cm/s2 (1)
Para "B ":
aB = 4(30) = 120 cm/s2 (1)
Reemplazando:
(80+120)
*
*
*
*
0
W
*
*
*
*
*
*
*
$
*
c) 0,4 m/s2 d) 0,8 m/s2
e) Ninguna
PROBLEMA Ns 15
Una partícula sale del reposo, descri­
biendo una trayectoria circular, con acele­
ración angular constante de
a = ^ rad/s2'
5
Hallar el desplazamiento angular que
describe la partícula en el OCTAVO se­
gundo de su movimiento.
SOLUCION:
El desplazamiento angular que describe
la partícula en el n-ésimo SEGUNDO de
su movimiento será:
<
j>= a>o+ ^ a . ( 2 n - 1 )
coo : velocidad angular inicial
a : aceleración angular
Reemplazando en (*):
.... (*)
cm/s'
- « ♦ 5 i
(15)
2 *
ac = 1 m/s2
*
* Luego: <
t>= | ji rad = 270°
$
*
PROBLEMA N® 14
La figura muestra dos poleas concén­
tricas de radios x = 15cm e y=25 cm.
Sabiendo que las poleas giran en sentido
horario con aceleración angular constan­
te a = 2 rad/s2, hallar la aceleración lineal
con que baja el bloque "E"
í PROBLEMA Ns 16
*
*
$
*
*
*
*
*■
*
*
*
*
*
*
*
*
*
*
Una partícula inicia su movimiento
(t = 0) con una velocidad angular coo = rc/4
rad/s y aceleración angular a = n/9 rad /s2.
Hallar el ángulo que barre la partícula
en el quinto segundo de su movimiento.
a) 120°
d) 150°
PROBLEMA Ns 17
b) 135°
e) Ninguna
c) 143°
La figura muestra dos poleas concén­
tricas de radios x = 20 cm. y b = 10 cm.,
respectivamente. Si las poleas giran en
sentido antihorario con aceleración angu­
lar constante igual a 0,2 rad/s2; hallar la
aceleración lineal del bloque que se en­
cuentra unido a la polea móvil.

208. SOLUCiON:
La aceleración lineal de los puntos A y B,
es igual a la aceleración lineal de ¡os
puntos periféricos de las respectivas po­
leas.
a = a . R
Para "A ":
aA = (0 , 2) (20) = 4 cm/s2 (i)
Para' B" :
aB = (0 , 2) (10) = 2 cm/s2 (1)
1
*. t
T
•1
Propiedad deja polea móvil:
ac = -
aA + aB
Reemplazando:
. (-4) + (2)
a c = ----------- ■ ■
Luego:
ac = -1cm/s
( - ) : sentido hacía abajo
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
#
*
*
*
#
*
*
*
*
*
*
En el sistema mecánico mostrado, el
bloque Q sube con aceleración lineal
constante igual a 0,6m/s2. Sabiendo que
los radios de curvatura de las poleas con­
céntricas son x = 10 cm e y = 20 cm,
determinar la aceleración lineal del blo-
d) 0,6 m/s
PROBLEMA N5 19
e) Ninguna
Un disco experimenta un movimiento
de rotación variado, cuya velocidad angu­
lar versus tiempo, es la que indica la fi­
gura. Determinar el número de revolu­
ciones que gira en los 6 primeros segun­
dos.
SOLUCION:
El desplazamiento angular que experi­
menta el disco, es igual al área de la
curva, en la gráfica (ú- 1 :
0 = área del trapecio

209. e = ^ . h
e =
2
(2 + 6)
7t = 47C
Número de vueltas = -7- = ~ = 2
2 71 2tc
# V = 2
PROBLEMA N920
La gráfica, velocidad angular versus
tiempo, describe el movimiento circular
de una partícula.
Determinar el número de vueltas que
describe hasta el instante t = 8 s
a) 2 V
d) 8 V
b) 4 V
e) N.A.
c) 6 V
La figura, muestra la gráfica: a - t de
una partícula que describe una trayecto­
ria circular. Si en el instante t = 0 su
velocidad angular es “ co“ y para t = 4 s la
velocidad angular es "3ü)", determinar su
velocidad angular para t = 6 s.
*
*
*
*
*
*
*
£
*
*
*
$
$
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
$
2)
En el intervalo de tiempo [0 ; 4) se­
gundos, el área bajo la recta es igual
al cambio de la velocidad angular.
(cüf - túo) = área del A
(3co-co) = | (4) (8)
co= 8 rad / s
En el intervalo de tiempo [4 ; 6] se­
gundos.
c ü f = ©o + c t. t
cof = 24 + 8 (2)
c ü f = 40 rad/s
para t = 6 s
PROBLEMA NS 22
Se tiene la gráfica a - t de una
partícula que se mueve describiendo una
trayectoria circular. Si en el instante t = 0
su velocidad angular es "co" y para t = 4 s
su velocidad angular es "3co", determinar
su velocidad angular para t = 8 s.
a) 31 rad/s b) 41 rad/s
c) 51 rad/s d) 61 rad/s
e) Ninguna
PROBLEMA Ns23
Una rueda durante su recorrido ne­
cesita 3 segundos para girar un ángulo de
234 radianes. Su velocidad angular al ca­
bo de este tiempo es de 108 rad/s. Deter­
minar su aceleración angular constante.

210. SOLUCION:
De la fórmula:
Q_ (C
O
q + C
O
F) t
Reemplazando:
234 = í í ^ . ,3)
.-. (úo = 48 rad/s
Cálculo de la aceleración angular:
Wf-CÜo
a = -
t
a =
1 0 8 -4 8
a = 20 rad/s2
PROBLEMA Ne24
Una partícula gira en una circunferen­
cia de 3 m de diámetro. Inicia su movi­
miento (t=0) con una rapidez de 6 m/s, 3
segundos después su rapidez es de 9 m/s.
Determinar el ángulo que describe la
partícula al cabo de 6 segundos.
£
*
*
*
*
*
*
*
*
a
»
+
n
a
*
*
*
*
*
*
*
<
t>
*
*
*
*
*
m
*
*
m
*
a)12rad b)18rad c) 36 rad #
d) 48 rad e) Ninguna
PROBLEMA Ne25
En el sistema mecánico mostrado, el
bloque A sube con una aceleración igual
a 1,5 m/s2, determinar la aceleración del
bloque B.
a) 1 m/s b) 2 m/s
c) 4 m/s2 d) 8 m/s2
e) Ninguna
PROBLEMA N« 26
En el sistema mecánico mostrado, el
bloque a sube con una aceleración igual
a 1,0 m/s2, determinar la aceleración del
bloque B.
*
*
*
*
*
*
#
*
*
*
$
*
*
*

211. V -
DINAMICA LINEAL
CONCEPTO.
La dinámica es parte de la mecánica,
estudia las relaciones el movimiento y la
causa (fuerza). En este caso ei movimiento
rectilíneo.
2da. Ley de Newton (1 672)
(Ley de Aceleración)
“Todo cuerpo material sometido a la ac­
ción de una fuerza resultante diferente de
cero adquiere necesariamente una acele­
ración en la misma dirección y sentido de la
fuerza resultante. El módulo de la acele­
ración es directamente e inversamente pro­
porcional a su inercia (masa)"
Aceleración =
F (resultante)
masa
1) a = —
m
2) m ~
a
3) F = m.a.
Para un sistema de varios cuerpos, que
tienen aceleración común "a".
*
*
*
*
*
<¡s
¡Sí
*
#
*
*
*
*
$
*
*
*
*
rjs
*
*
*
*
*
*
*
*
*
*
F = ( I m) a
F = (mi + rri2 + rri3) a
La fuerza resultante y la velocidad, no
siempre tienen !a misma dirección y sentido,
como podemos observar en el movimiento
parabólico. La velocidad instantánea V se
representa por un vector tangente a la trayec­
toria El peso (fuerza resultante) y la acele­
ración de la gravedad (g) tienen la misma
dirección y sentido.
Vi
Aplicando la 2da. Ley de Newton, en el
eje vertical.
XFy —m . ay
Inercia
Es un atributo de la materia. Todo cuerpo
material se opone al cambio. En mecánica
decimos que la inercia es la "Terquedad de
los cuerpos al cambio de la velocidad”.
Masa
Es la medida cuantitativa de la inercia
En mecánica se define como la relación entre
la fuerza resultante y la aceleración que ad­
quiere, se mide en kilogramos. La masa es
una magnitud escalar de módulo constante.

212. F 2F 3F
masa = —= — = —-
a 2a 3a
Peso(W)
Es una magnitud física vectorial. Se de­
fine como la fuerza resultante que ejerce la
tierra sobre los cuerpos que lo rodean. Se
representa por un vector que indica en todo
instante al centro de la tierra.
Todo cuerpo abandonado cerca de la
superficie terrestre, cae con una aceleración
constante, a = g. En caída libre la única
fuerza que actúa sobre el cuerpo es su peso
(F = W).
p is o
De la segunda Ley de Newton:
]
F = m a -» W = m . g
SISTEMAS DE REFERENCIA
1) Sistema de Referencia Inercial
Se denomina de este modo al sistema de
referencia que se encuentra fijo a la tierra
(reposo relativo) o se mueve con velocidad
constante en línea recta respecto a un siste­
ma de referencia fijo a la tierra.
2) Principio de D’Alambert (1 850)
(Sistema de Referencia No Inercial)
Es aquel sistema de referencia con movi­
miento acelerado respecto a otro (a la tierra
en este caso particular).
El sistema de referencia puede tener ace­
leración tanqencial y/o aceleración centrí­
peta.
Realicemos el D.C.L. de la esfera de
masa "m" respecto de! sistema de referencia
Inercial S (fijo a la fierra).
Realicemos ahora el D.C.L. de la esfera
de masa “m" respecto dei sistema de refe­
rencia No Inercial S’ (ubicado en el carro).
Para nuestro observador el cuerpo se en­
cuentra en reposo, por consiguiente la fuerza
resultante es igual a cero.
Para el observador S la fuerza resultante
de T y mg es igual al producto de la masa por
la aceleración.
Para el observador S la fuerza que pro­
duce el equilibrio es F’ (fuerza de inercia).
Luego:
La fuerza de inercia, tiene sentido opues­
to a la aceleración del sistema respecto de la
Tierra.

213. La fuerza de inercia, tiene sentido físico
sólo para sistemas de referencia acelerados
PRINCIPIO DE EQUIVALENCIA
(Albert Einstein 1 915)
*
*
#
*
Todos los sistemas de referencia No iner-
cial, con aceleración “a"respecto a la tierra,
tienen un campo gravitacional local, equiva­
lente al campo gravitatorio creado por la tie­
rra, satélites y estrellas.
A la intensidad del campo gravitatorio
local se le denomina "gravedad efectiva".
La gravedad efectiva es igual a la suma
vectorial, de la aceleración de la gravedad g
creado por la tierra, más la aceleración del
sistema de referencia, pero con sentido
opuesto (-a), como muestra la figura.
El principio de equivalencia, es una
cantidad del principio de D’Alambert (fuer­
za de inercia). La fuerza de inercia fue
propuesto por los físico s franceses
D’Alambert y Larange (1 850) y el principio
de equivalencia fue desarrollado por Albert
Einstein (1915) una proposición que consti­
tuye la base del Principio General de la Re­
latividad.
“Las Leyes de la naturaleza deben ser
expresadas de modo que sea imposible dis­
tinguir entre un campo gravitacional uniforme
y un sistema de referencia acelerado”.
*
#
*
*
*
#
*
*
#
*
$
*
«i
*
*
*
*
#
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
Para nuestro observador ubicado en el
carro, con movimiento acelerado, la grave­
dad efectiva se representa por un vector que
está dirigido de arriba hacia abajo. Por consi­
guiente el concepto de arriba y abajo es
relativo.
En la posición de equilibrio relativo, el
cuerpo humano se encuentra alineado con la
dirección de la gravedad efectiva.
Unidades de Fuerza
I) Newton (N)
Se define como la fuerza resultante que
actúa sobre un (1) kilogramo masa, pro­
duciéndole una aceleración de 1,0 m/s2.
2da Ley de Newton;
Fr = m a
Albert Einstein

214. II) Kilogramo Fuerza (kg - f)
Se define como la fuerza que ejerce la
tierra por cada kilogramo de masa que lo
rodea
Equivalencia :
Cuando un cuerpo es abandonado cerca
de la superficie terrestre, cae con la ace­
leración constante a =g, en caída libre.
Consideremos un cuerpo de masa un
kilogramo, entonces la fuerza que ejerce
la tierra será:
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
2da Ley de Newton :
F = m . a
1.0 kg - f = 1,0 kg . 9,8 m/s2
1.0 k g - f = 9,8 N
Valor de aceleración de la gravedad
g = 9,8 m/s2
g = 9,8 N/kg
PROBLEMA Ns 1
En el techo de un ascensor se encuen­
tra suspendido un bloque de masa 6
kg, sabiendo que el ascensor baja con
aceleración constante a = 1,8 m/s . Ha­
llar la tensión en la cuerda que sostiene al
bloque.
2da. Ley de Newton:
Fr = m a
mg - T = m a
T = m (g - a)
SOLUCION:
D.C.L (bloque)
, i
E
s
ÍIKJ
Reemplazando.
T = 48 N
PROBLEMA Ns 2
Un muchacho que pesa 300 N en una
balanza, se pone de cuclillas en ella y
$
*
*
#
*
*
*
*
$
*
*
*
*
*
#
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
S
i*
*
*
*
*
*
*
salta repentinamente hacia arriba. Si la
balanza indica momentáneamente 450 N
en el impulso, ¿cuál es la máxima acele­
ración del muchacho en este proceso?
g = 10 m/s2
SOLUCION:
D.C.L. (muchacho)
2da. Ley de Newton:
Fr = m . a
W
N - W = — . a
9
_ f N i
a - ( w -
Reemplazando :
a = 5 m/s
PROBLEMA Ns 3
Una fuerza Fi sobre una masa "M"
produce una aceleración ai = 3 m/s2. Otra

215. fuerza F2 sobre una masa “2M" produce
una aceleración a¿ = 2 m/s'‘ Determinar
la aceleración que producirán Ft y F2 ac­
tuando sobre una masa “5M", en direccio­
nes perpendiculares entre s í :
Aplicando la 2da. Ley de Newton:
1er. caso : F1 = M . ai
F1 =3M ...
2do. caso : F2 = (2M) a2
F2 = 4 M .
3er. caso : 2da. Ley de Newton.
F r = (5M) a
5M = (5M) a
(1)
(2)
a = 1 m/s
PROBLEMA Nfi 4
Determinar la fuerza de reacción entre
los bloques A y B de masas 3 kg y 2 kg
respectivamente. No hay rozamiento.
Fi = 60 N F2 = 40 N
SOLUCION:
Analizando el sistema (A+B)
2da. Ley de Newton:
(F1 - F2) = (mA + itib) .a
20 = 5(a)
*
*
i
*
*
*
2da Ley de Newton:
(Ft - R) = ida • a
(60 - R) = 3 (4)
R = 48 N
a = 4 m/s'2
*
*
*
*
*
*
*
m
*
*
*
S
s
*
*
Slí
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
PROBLEMA N25
Determinar la tensión en la cuerda que
une los bloques A y B de masas 2 kg y 3
kg respectivamente. La magnitud de la
fuerza aplicada es F = 25N.
Desprecie la fuerza de fricción.
rasuramtw
SOLUCION:
Sistema (A+cuerda +B)
2da. Ley de Newton:
F = (mA + itib) . a
25 = (5) a
p
a = 5 m/s
D.C.L.(bloque A)
T = mA - a
T = 2(5)
íí

216. En el techo de un carro se encuentra
suspendido una esferita, que debido a la
inercia se desvía el hilo respecto de la
vertical e = 45°. Hallar la aceleración del
carro.
SOLUCION:
D.C.L. (esfera)
Eje X : Fr = m a
T . Sen 0 = m . a
Eje Y : IF y = 0
T . Cos O = m . g
Dividiendo (1) í (2)
T9 6 = f
.... (2)
| a = g . Tge~
Reemplazando: a = 9,8 m/s
PROBLEMA Ns 7
Si el punto "J" de la cuerda baja con
una aceleración "g", pero el punto K sube
como una aceleración g/4. ¿Qué tensión
soporta la cuerda que une el centro de la
polea móvil, con el bloque de peso 16 N.
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
m
$
*
*
*
*
*
*
*
=
¡í
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
S
jt
*
*
#
*
*
*
*
*
*
*
*
J t
Z' N
'
SOLUCION:
Cálculo de la aceleración del bloque o de
un punto en la cuerda (B). Propiedad de
la polea móvil.
ae —
aj + aK
aB = g (baja)
D.C.L. (bloque):
T
as =
..(1)
- g + ^
s 4
2da. Ley de Newton :
(W —T) = ^ . a B .-.(2)
Reemplazando (1) en (2):
T = § W
T = 10
T = 10 N
PROBLEMA N98
Si el sistema mostrado en la figura
está libre de todo rozamiento hallar la
aceleración del carrito de masa M . Los
bloques A y B tienen igual masa “m" cada
uno.
TSPTXTT

217. D.C.L. (bloque A)
2da. Ley de Newton
T = m . ai .... (1)
m
g
D.C.L (bloque B)
2da. Ley de Newton
mg - T = m.a2 .... (2)
D.C.L. del carrito:
2da. Ley de Newton
FR =m.a
2T =M.a .... (3)
ir,q
I
Í n ’
Analizando cinemáticamente el movi­
miento del carrito
*
*
*
*
*
s
t*
$
*
$
*
*
$
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
f c
a = 31 ^ 82 (Vectorialmente)
a = -
2
- ai + a2
- (4)
Resolviendo las ecuaciones (1),(2), (3), y
(4):
a =
m
(M + 2m)
PROBLEMA Nfi 9
Una masa de 4kg reposa sobre un pla­
no horizontal, con el cual el coeficiente de
fricción estático es 0,2. Se le aplica una
fuerza horizontal F =5N. Determinar la
fuerza de fricción del piso sobre el cuer­
po- 2
g = 10 m / s
SOLUCION:
D.C.L. (bloque)
Cálculo de la fuerza de rozamiento está­
tico máximo.
Fs(máx) = Hs • N
Fs(máx) = 0,2 (40) =8
El bloque se encontrará en movimiento
inminente cuando la fuerza externa F sea
igual a 8N.

218. Por consiguiente el bloque está en re­
poso.
SFx = 0
Fs = F = 5N
FS= 5N
PROBLEMA Ns10
Un bloque de masa 4 kg se encuentra
en reposo sobre un piso rugoso, con el
cual pk = 0,3 y M
s = 0,4. Se le aplica una
fuerza horizontal F = 18N. Determinar la
fuerza de fricción ejercida sobre el blo­
que. g = 10m / s2
SOLUCION:
D.C.L. (bloque)
Cálculo de la fuerza de rozamiento está­
tico máximo.
Fs (máx) = nEN = 16
Pero, F >16, entonces el bloque está en
movimiento
Fk = Hk N
Fk = 0,3 (40)
Fk = 12 newtons
PROBLEMA Ne 11
Un bloque se desliza sobre un piso
horizontal, con aceleración de 4m/s . El
bloque pesa "Q" y las fuerzas externas
son Fi = F2 = Q.
Calcular el coeficiente de rozamiento
cinético g = 10 m/s2.
#
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
■
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
D.C.L. (bloque)
"H L ll
20
o a
N
IFy = 0
N = 2Q ....(1)
Fuerza de rozamiento cinético:
fk = HkN = nk(2G).... (2)
2da. Ley de Newton
IF x = m . a
( Q - f k ) = | . a .... (3)
Reemplazando (2) en (3):
Hk---0,3
PROBLEMA Nfi 12
Determinar la máxima aceleración del
sistema mostrado, tal que el bloque de
masa ”m" no resbale sobre la plataforma.
Coeficiente de rozamiento estático 0,6.
g = 10 m / s2.

219. SOLUCION:
D.C.L (bloque):
mgi
1»
£Fy = 0
N = ring .... (1)
IF X= m.a
us (mg) = m.a
3max = Us . g
Reemplazando:
amóx —6 m/s
PROBLEMA N9 13
El bloque de 2kg de masa se mueve
sobre una superficie de horizontal, cuyo
coeficiente de rozamiento cinético es 0,5.
La fuerza oblicua F es de 10N. Deter­
minar la aceleración del bloque.
g = 1 0 m /s 2.
SOLUCION:
D.C.L. (bloque)
*
*
*
*
*
#
*
*
*
s¡*
*
*
*
*
*
*
#
IF y = 0
N =14
fk=H k. N = 0.5(14)
fk = 7
2da. Ley de Newton:
(8 - f k) = m . a
1 = 2 (a)
a= 0,5 m/s
* PROBLEMA Ns 14
*
m
*
*
*
*
*
*
5
*
*
*
*
#
*
$
Slí
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
■*
*
*
En la figura mostrada el bloque de
masa “ M“ tiene una aceleración doble de
masa "2W . Existe rozamiento en todas
las superficies en contacto. Calcular el
valor de "(i "cinético.
SOLUCION:
Sistema (M + cuerda + M), consideramos
que se mueve con una aceleración (2a)
Mg
p M g
'Mg
2da Ley de Newton-
(Mg - |i Mg) = (2M) (2a)
a = g (1 -n )/4 . ..(1 )

220. : (MS 9upold) J.O.Q
f " '
3Mg
m r 2 M T T 1
nMg'í
V
N, J
2da Ley de Newton : Fr = m.a
PROBLEMA NB15
La barra uniforme y homogénea AB,
de longitud "2L", se deja en libertad, a
partir del reposo, de la posición vertical
que muestra la figura. Sabiendo que la
superficie horizontal es completamente
lisa, hallar la ecuación de la trayectoria
que describirá el extremo "A" hasta cuan­
do la barra llegue al piso.
trayectoria
del extremo
SOLUCION:
Haciendo D.C.L. de la barra AB cuando
se encuentra cayendo:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
#
*
*
*
£
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Al aplicar ia 2da. Ley de Newton a un
cuerpo rígido, la aceleración "a" que es
producido por ia fuerza resultante “FR“,
es la de su centro de masa (c.m)
Por la 2da. Ley de Newton:
Fr = m . a
Fr // a
Pero como la " FR " es un vector vertical
(N y mg son vertical), entonces la acele­
ración "a" de su C.M. será también verti­
cal, por consiguiente el C.M. de la barra
uniforme homogénea se moverá vertical­
mente y hacia abajo. Hallar la ecuación
de la trayectoria que describe un punto,
con respecto a un cierto sistema coorde­
nado de referencia, es encontrar una re­
lación entre la abscisa “X" y la ordenada
"y" de un punto.
Y
A(X;Y)
De la figura; por Teorema de Pitágoras:
(2L)2 = (2x)2 + y2
Y = 2 V l2 —x2
"Ecuación de un arco de Elipse”
PROBLEMA Ns 16
Hallar la aceleración de los bloques de
masas mi = 1kg , m2 = 2kg ym a = 3kg, si
las poleas son de masa despreciable y el
sistema está libre de todo rozamiento.
g = 10 m / s2

221. SOLUCION:
Haciendo D.C.L. del bloque mi :
Por 2da. Ley de Newton :Fr = m . a
iru g -T = m ia i
1 0 -T = ai . . . (1)
r
blui
1
í
^0
l i
(*) Obsérvese que hemos asumido que
el bloque "m i’ se mueve acelerada­
mente hacia abajo.
Haciendo D.C.L. del bloque ''nrte":
Por 2da. Ley de Newton F r = m . a
2T = tTi2 . a2
T = a2 ....(2)
N
im
J
i
f
J F
lm
29
Haciendo D.C.L. del bloque "mg1:
Por la 2da Ley de Newton F r = ma
rri3g - T = nri3 . a3
30 - T = 3 a3 .... (3)
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
i
♦
*
*
*
*
Analizando cinemáticamente a la polea
móvil:
De la propiedad de la polea móvil,
a n-a3
a2 = -
2a2 = ai + a3 .... (4)
Resolviendo las Ecuaciones:
Reemplazando (2) en (1):
ai = 1 0-a2 .... (I)
Reemplazando (2) en (3):
30 —a2 = 3a3
30 - a2
83 = .... (II)
Reemplazando (I) y (II) en (4):
_ , 3 0 - 3 2
2a2 = (10 - a2) + — - —
donde:
ai = 4m/s
a¿ = 6m/s2
83 = 8m/s2
El resultado positivo que hemos obtenido
para "a,” al resolver las ecuaciones, nos
indica que el sentido de la aceleración del
bloque "m," que habíamos asumido ini­
cialmente (hacia abajo) es correcto.

222. En qué relación deben estar las masas
M y m para que el cuerpo A esté en reposo
con respecto del cuerpo B. No existe ro­
zamiento.
Masas: A = D = m y B = C = M
SOLUCION
Haciendo D.C.L, de A:
Como la aceleración es horizontal, enton­
ces:
TCosG = mg ....(1)
Por 2da. Ley de Newton: F r = m . a
T Sen 0 = ma
Haciendo D.C.L. de B
Por 2da. Ley de Newton
F r = m . a
T + T - T Sen 0 = M a ....(3)
*
*
*
*
*
$
*
%
*
*
*
*
*
*
*
*
*
*
*
♦
#
*
*
*
*
*
*
*
*
*
*
*
ü
*
*
*
*
*
#
#
*
*
♦
#
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
u Haciendo D.C.L. de C
Por 2da. Ley de Newton:
Mg - T = M a
T = M(g —a ).... (4)
■ Haciendo D.C.L. de D
Por 2da. Ley de Newton:
m g -T = ma -— (5)
Resolviendo las ecuaciones:
Sumando (3) y (5)
mg + T - T Sen = (M + m) a
Reemplazando las ecuaciones (2) y (4)
en la anterior.
mg + M (g - a) - ma = (M + m) a
g(M + m) = 2(M + m) a
a = g/2
Sumando (1)2+(2)2:
t 2 m2_2. __,2 2
T = m g +m a
T = m^/a2^- g'
Igualando las ecuaciones (4) y (6)
M(g - a) = m
(6)
! - a) = m Va2-*-g2
PROBLEMA Np18
Si el sistema mostrado se deja en liber­
tad a partir del reposo, hallar el tiempo
que tarda el bloque A de masa 2kg, en
recorrer la distancia d = 5 metros sobre él
móvil C de masa 6kg. Los bloques A y B
tienen igual masa. No hay rozamiento y
las poleas tienen peso despreciable.
(g = 10m/s2)

223. SOLUCION:
Aplicando la segunda Ley de Newton, a
cada bloque
Bloque "A ":
T = m . aA
T = 2 aA -..(1 )
mg - 2T = m . aB
10 - T = aB ..(2)
Bloque “B ":
T = m . aA
T = 2 aA . • ■(1)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
#
*
*
slí
*
*
*
*
*
♦
#
*
*
*
&
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Bloque "C“ :
T = Mac
Analizando cinemáticamente la polea
móvil:
De (1) = (3): aA = 3ac
Reemplazando (3) en (2):
10 - 6ac = aB
Reemplazando en (4):
20 —12. ac 3ac + ac
5 , 2 1 5 / 2
ac = - m /s y ha = m /s
Analizando el movimiento relativo (A con
respecto a C).
a reí = a a/c = aA - ac
a reí = 2,5 m/s2
Del M.R.U.V.:
1 o
e = Vo-1 + - . a reí ■t
Reemplazando

224. t = 2s
PROBLEMA N319
Calcular la máxima aceleración que
podrá tener el carrito, para que el bloque
rio vuelque. Existe suficiente rozamiento
para que el bloque no resbale
g = 10 m/s2
0 ,4 m
SOLUCION:
D.C.L. para un observador ubicado en el
carro (Sistema de referencia NO inercial)
2da condición de equilibrio.
Mh
5 r MAm9 = 0
*
*
*
*
*
*
«
te
%
*
*
#
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ma (0 ,4 )= mg (0 , 2)
1
a = 2 9
amax —5 m/s
PROBLEMA N320
Una barra uniforme y homogénea se
encuentra suspendida en el techo de un
carro, que se mueve con aceleración
constante. Debido a la inercia la barra se
desvia un ángulo 6 = 37° respecto de la
vertical. Hallar ia aceleración del carro,
g = 10 m/s2
SOLUCION: i
D.C.L. de la barra, respecto de un obser­
vador ubicado en el carro.
*
*

225. 2da. condición de equilibrio.
Z M a = 0
' F
A
mg (L Sen 0) - F ’ (L Cos 0) = 0
mg Sen 0 = m . a
Tg0 = ¡
Reemplazando:
a = 7,5 m/s
PROBLEMA N9 21
La figura muestra una carro que se
mueve con aceleración constante "a", en
línea recta. En el interior del carro se
encuentra una estructura imponderable
en forma de “ T ”, en sus extremos se
encuentran fijos 2 esferas de pesos "W" y
“6W”. Hallar el valor de la aceleración, tal
que 0 = cero. g = 10m/s
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
S
ü
*
*
*
*
*
*
*
*
*
2da. condición de equilibrio:
ZMa = 0
6 - a . L + - a (2L) = 6 W.L
g g
a = 4 ‘ 9
a = 7,5 m/s
PROBLEMA N9 22
Hallar la aceleración de los bloques de
masa M y m con respecto al carrito, sa-
SOLUCION:
D.C.L. de la estructura, para un obser­
vador fijo en el carro, sistema de referen­
cia no Inercial.
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
Haciendo D.C.L. de los bloques desde un
sistema de Referencia NO Inercial, fijo al
carrito.

226. Haciendo D.C.L. del bloque "m"
Por 2dá Léy de Newton: *
T - m "s/a2+ g2 = m .arei .... (1)
Haciendo D.C.L. del bloque “M":
M . Va2+ g¿ - T = M arei .... (2)
Resolviendo las ecuaciones:
Sumando (1) y (2):
(M -m ) a 2+ g 2= (M+m) a reí
PROBLEMA N®23
En el sistema mostrado hallar la magni­
tud de la fuerza "F" con la finalidad de que
los bloques de masa "2m " y "m ” per
manezcan en reposo con respecto del carro
de masa "M ". No hay rozamiento.
Considere: m = 10kg , M = 90kg
g = 10m/s
*
*
*
*
*
#
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
#
*
*
*
*
*
*
*
#
*
*
#
*
*
S
É
*
*
*
*
«
t»
*
*
*
*
H
e
*
#
*
#
*
*
*
*
*
*
*
Aplicando la 2da. Ley de Newton a todo
el sistema
F = (M + 2m + m) a
F = (M + 3m) a
F = 120 a ,.,.(1)
Para un observador NO Inercial, ubicado
en el carro "M".
D.C.L del bloque (2m):
SFx = 0
T = F '
T = (2m) a
T = 20 a (2)
D.C.L. del bloque (m).
Fr = 0
T = m Va2+ g2
T = 10 Va2+ g2 ....(3)

227. 2a = 'a 2+ g2
V3
3 '
Reemplazando en (1):
F = 400 y¡3 N
PROBLEMA NE24
Un ascensor de 6 metros de altura
(entre el techo y el piso) esta subiendo
con aceleración constante igual a 2,2
m/s2.
Calcular el tiempo que demora en lle­
gar al piso del mismo ascensor un foquito
que se desprende de! techo del mismo
ascensor.
SOLUCION:
Ubicamos nuestro observador en el as­
censor, para él existe un campo equiva­
lente al cam po g ra v ita to rio , de
intensidad
9ef = - ( g + a )j gef = 12 m/s
*
*
*
*
*
*
*
*
S
K
*
*
*
*
*
*
*
*
*
#
*
*
*
*
#
*
*
*
*
*
#
♦
♦
*
$
#
*
*
*
*
*
*
*
*
*
*
*
<
¡í
*
*
*
*
El móvil mostrado de-masa ”M" que
tiene un agujero cilindrico de radio de
curvatura R = 1,6m, se encuentra sobre
una superficie horizontal con aceleración
constante “a". Si en cierto instante se
desprende de la parte superior un clavo
de masa “m“, hallar la velocidad relativa
del clavo respecto de M, cuando ci oca
con la superficie cilindrica.
g = 10 m/s2
SOLUCION:
Fijemos nuestro sistema de referencia en
el móvil, para nuestro observador el clavo
inicia su movimiento desde el reposo en
dirección de la gravedad efectiva
Del triángulo vectorial
Caída libre: *
*
H - V0y . t + g gef í¿
6 = 0 + 1 (12 ) _t2
iii
*
*
*
t= 1s. «
H
*
Pero : h = AB = 2R (Cos 6)
C
8l<=c i é (1>
De la Ecuación cinemática
V^ = V^+ 2 gef h ....(2)

228. = 0 + 2 — . (2R Cos 6)
F Cose
Vp = 2VgR"
"Velocidad de m respecto de M"
Vf = 8 m/s
PROBLEMA N2 26
La figura muestra un cascarón de peso
“P", que en su interior lleva una esfera
maciza también de peso "P". Todas las
superficies en contacto son lisos. Hallar
el valor de la fuerza"F", tal que los centros
geométricos del cascarón esférico y la
esfera se mantengan en dirección hori­
zontal. Considere: 6 = 30°
SOLUCION
D
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
De la condición del problema para
un sistema de Referencia NO Iner­
cial. la gravedad efectiva “gef" den­
tro del cascarón debe tener direc­
ción horizontal.
Luego:
Sen 6 = fl
2) Aplicamos la 2da. Ley de Newton al
sistema físico (cascarón + esfera)
respecto de un observador en la
tierra. Paralelo al plano inclinado:
F (Resultante) = m . a .... (2)
.?£ 9
(F+ 2 P Sen 6) =
g Sen 6
Luego:
F = 2p
1
-- Sen 6
Sene
Para 6 =30°, entonces F =3P
.... (3)
*
*
#
*
*
*

229. CONCEPTO
Es parte de ia mecánica que estudia a las
fuerzas que originan el movimiento circular.
1) Aceleración centrípeta (ac)
Es una magnitud física vectorial. Mide la
rapidez de cambio que experimenta la
velocidad en dirección (y sentido). La
aceleración centrípeta se representa por
un vector que apunta al centro de cur­
vatura en todo instante. Su valor se de­
termina como el cuadrado de la velocidad
entre el radio de curvatura de la trayecto­
ria.
... (1)
v = velocidad lineal
R = radio de curvatura
N
Pero de cinemática sabemos que;
v = w .R ....(2)
Reemplazando (2) en (1):
a c = w2 . R ... (3)
donde; w = velocidad angular
2) Fuerza centrípeta (Fc)
Es la fuerza resultante de todas las fuer­
zas en dirección radial que actúan sobre
un cuerpo en movimiento circular.
Fc =£ fuerzas hacia el centro
£ fuerzas hacia afuera
La fuerza centrípeta es la responsable
del cambio de la velocidad en dirección
(y sentido).
La fuerza centrípeta (fuerza resultante)
está siempre dirigida a centro de cur­
vatura de la trayectoria.
De la 2da. Ley de Newton:
*
$
*
*
*
#
$
*
*
*
F = (resultante nn dirección radial)
= masa x a (centrípeta)
Fc = m . ac .... (4)
Pero de (2) y (3) en (4):
Fc = m . -k-
Fc = m . w . R
En la figura (1), la fuerza centrípeta será:
*
* Fc = mg. Cos 0 - N
# donde: N = reacción normal
i
J 3) Aceleración Tangencial (at)
Es una magnitud física vectorial. Mide la
rapidez de cambio que experimenta la
velocidad en módulo. Es la componente
de la aceleración neta paralela a la velo­
cidad instantánea, por consiguiente se
representa por un vector tangente a la
trayectoria.
Su valor es igual a:
*
*
*
*
*
*
s
t>
at =-
V f - V o
t
.... (5)

230. De la figura (2) se puede escribir la acete -
ración tangencial como una componen­
te en dirección tangente a la trayectoria.
ai = a . SenG .(6)
Del mismo modo la aceleración centrí­
peta se puede escribir como una compo­
nente de la aceleración neta, en dirección
radial.
ac = a . Cose .... (7)
donde "a" es la aceleración neta.
4) Fuerza Tangencial (Ft)
Es la fuerza resultante de todas las fuer­
zas en dirección tangencial respecto ala
trayectoria que actúan sobre un cuerpo
en movimiento circular, en general se
cumple para culalquier movimiento cur­
vilíneo.
La fuerza tangencial es responsable del
cambio en la magnitud de la velocidad
De la 2da. Ley de Newton.
—
>
p (resultante en dirección tangencial)
= masa, a (tangencial).
-» -i
Ft = m . at .... (8)
La fuerza tangencial y la aceleración tan­
gencial tienen la misma dirección y sen­
tido.
En la figura (1) la fuerza tangencial será,
una componente del peso
Ft = m . g . Sen 6 .... (9)
Reemplazando en la ecuación (8), ob­
tenemos el valor de la aceleración tan­
gencial.
m. . g. Sen 6 = m . a t
Luego:
at = g . S e n 6 ....(10)
g = aceleración de la gravedad.
*
m
*
*
*
*
*
*
*
*
PENDULO CONICO
, Una masa "m" suspendida de un punto
fijo por una cuerda de longitud “L" y peso
despreciable que gira alrededor de la vertical
con velocidad angular constante "w"; a este
sistema se le llama "PENDULO CONICO”.
1) Realizamos el D C.L. de la masa pendu­
lar, respecto de un observador fijo en la
tierra (sistema de Referencia Inercial).
Las fuerzas que actúan sobre el cuerpo
son el peso (mg) y la tensión (T) en la
cuerda.
La fuerza resultante es igual a la fuerza
centrípeta (Fc), como muestra la figura.
N.
2) Ahora realizaremos el D.C.L. de la masa
pendular, respecto de un observador que
gira con la misma velocidad angular del
péndulo (Sistema de referencia No Iner­
cial). Respecto del "observador giratorio”
el cuerpo de masa “m“ se encuentra en
equilibrio (reposo relativo), por con­
siguiente la fuerza resultante es igual a
cero.

231. Las fuerzas que actúan sobre la masa
"m" son el peso (mg), la tensión (T), y una
tercera fuerza (F ’) que anula a la fuerza
resultante de sumar el peso, más, la ten­
sión (T), como indica la figura (4)
Figura (4)
4) Comparando las figuras (3) y (4), la
fuerza "F y !a fuerza centrípeta son
iguales en módulo y dirección pero senti­
dos opuestos,
-> —
»
F’ = - m . a c ....(11)
F’ = se llama “fuerza inercial", es el
opuesto de la fuerza centrípeta.
*
*
*
*
*
#
m
*
#
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
$
#
*
*
*
*
*
*
*
*
m
♦
*
*
*
#
*
*
*
m
5) A estafuerza inercial debido a la rotación,
se le llama en mecánica "FUERZA CEN­
TRIFUGA",
6) La fuerza inercial debido a la rotación,
que actúa sobre el cuerpo, es igual al
producto de la masa del cuerpo por la
aceleración centrípeta del cuerpo, pero,
con sentido opuesto.
F* = F inercial = m . (— acent(ipeta) —(12)
7) La “fuerza inercial” se grafica sólo para
sistemas de referencia NO inercial (que
tienen movimiento acelerado)
8) Para sistemas de referencias inerciales
(están en equilibrio relativo), la fuerza
inercial ”no existe".
FUERZA CENTRIFUGA (Fcg)
Es la fuerza inercial, que tiene el mismo
valor de la "fuerza centrípeta”, igual direc­
ción, pero con sentido opuesto.
Fcg —— F centrípeta ... (13)
La "Fuerza Centrífuga" tiene sentido
físico sólo para sistemas de referencias de
rotación.
c
■ ü
PROBLEMAS RESUELTOS
PROBLEMA N9 01
Un automóvil se desplaza sobre un
puente circular de radio de curvatura 125
metros. Hallar la velocidaad con que se
mueve el auto, sabiendo que, cuando
pasa por el límite superior del puente la
reacción normal sobre el auto es igual a
50% de su peso, g = 10 m/s2
SOLUCION:
D.C.L del auto:
*
*
*
*
*
*
#
*
*
m
*
*
f
1 "S
v
X 1 N
t
1
V 0 J

232. 2da. Ley de Newton:
£ Fradiales = m . a c
-2
mg - N = m .
v_
R
■
2
ma V'
2 _ m R
v2 = ¿ - g . R
V = 25 m/s
Reemplazando:
PROBLEMA Nc02
¿Qué velocidad angular debe tener el
sistema mostrado para que la tensión en
la cuerda (A) sea 1,6 veces la tensión en
la cuerda “A" es 25 cm.
g = 10 m/s2
SOLUCION:
D.C.L. (esfera):
1.6 T
m
g
XFy = 0
T = mg .... (1)
£ Fradiales = m . ac
1,6T = m . w 2.R .
Reemplazando (1) en (2)
p
1,6 mg = m w R
(2)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Ü
t
*
*
O
í
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*»
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
M i W
Luego: w = 8 rad/s
PROBLEMA Ne03
Determinar la tensión en la cuerda AC
si la esfera tiene una masa de 16 kg y la
estructura gira con una velocidad angular
de 2 rad/s.
Además: AB = 4m
g 10 m/s^
SOLUCION:
D.C.L.(esfera)
I F y = 0
T1 . Cos 6 = m . g
Tí = 200 N .... (1)
£ F(radiales) = m . 3c
T2 +Ti Sen 6 = m . w2 . R
Reemplazando: R = AC- - *¡m

233. T2 + (200)~ = 16(4)5
o
Luego: T¿ = 200N
PROBLEMA N2 04
Un disco horizontal gira alrededor de
un eje vertical que pasa por su centro
geométrico "0". La ranura es lisa y con­
tiene un bloque de masa 2kg, sujeto a un
resorte.
El bloque está a 20 cm. del centro,
cuando el disco no gira.
Calcular la constante elástica del re­
sorte, si se deforma 5cm. cuando el disco
gira a 4 rad/s.
SOLUCION:
D.C.L (bloque)
kx = m . w . R
Luego:
(0,05m) = 2 kg j
K = 1 60 ^
m
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
H
»
#
*
*
*
*
*
*
*
*
*
*
*
*
*
#
#
*
*
*
*
*
*
*
*
«
S
¡
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
El sistema mostrado gira con veloci­
dad angular constante w = n rad/s. calcu­
lar la reacción de la pared vertical sobre
las esferas de masas m = 2 kg.
2 2
Considere: g = ti m/s
SOLUCION:
D.C.L. de la esfera izquierda
'1 L -
1 E
i J
JE
Equilibrio vertical: I Fy = 0
Ni . Sen 45° = mg
Fuerza centrípeta:
N - Ni . Cos 45°=m. w2.R
Sumando; (1) y (2)
N = m (g + w2 R)
Reemplazando:
~ ( 1)
.... (2)
N = 4n newtons
PROBLEMA N®06
El sistema mostrado acelera a razón
de a = 10 'fc m /s 2. La esfera de masa 0,5

234. kg, gira con una velocidad constante de
12 rad/s descubriendo una circunferencia
de radio 1,0 m respecto de carro. Hallar la
tensión máxima en ia cuerda que sostiene
la esferita.
g = 10 m/s2
SOLUCION
Realizamos el D.C.L. de la esfera res­
pecto de un observador ubicado en el
carro (sistema de referencia NO Inercial).
"PRINCIPIO DE EQUIVALENCIA"
■“ S e f .
Cálculo de la gravedad efectiva.
*
*
i*
*
*
*
*
<
}
<
*
$
*
*
*
*
#
*
*
#
*
%
*
$
*
<
¥
*
*
*
*
9ef =Vg2+ a
gef = 20 m/s
La tensión en la cuerda será máxima,
cuando la esfera pase por su posición más
baja respecto del “Campo Efectivo"
2da. Ley de Newton:
£Fradiales = m . 3c
T - m. gei = m. w R
T - (0,5) 20 = (0,5). 144.(1)
T = 82 N
* PROBLEMA N907
*
*
*
*
*
Ü
>
*
*
*
*
#
*
#
*
*
*
*
*
*
*
*
*
*
*
*
A
*
*
*
*
*
*
La figura muestra dos esferas de masa
“M" y “m" unidos mediante una cuerda
ABC de longitud "L“, en B se encuentra
B
c

235. una polea pequeña que no ofrece roza­
miento. Si el sistema gira con velocidad
angular constante, hallar BC (X)
SOLUCION
D.C.L. (esfera M):
2da Ley de Newton
Fc = m. ac
T. Sen a = M. w2 . R
T. Sen a = M. w2 . (x. Sen a)
T = M .w2 .x ...(1)
D.C.L (esfera m):
Análogamente, se tiene:
T = m. w2. (L - x) .... (2)
_ ■ - A
T
: t . eos e
T. Sen e
V | mg J
Igualando (1) y (2)
m ,
x = ----------- L
(M + m)
PROBLEMA N® 08
Un balde es atado a una cuerda de
longitud 200 cm y gira formando una cir-
cunferencia.Las gotas de agua que caen
«
i»
¡i»
«
H
*
*
*
*
*
*
*
*
*
*
*
*
■
fe
*
*
n
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
4*
*
*
*
*
4
*
*
*
4
*
m
*
♦
4*
*
4*
del balde forman una circunferencia de
radio “a" en el piso. Determinar "a", cuan­
do 6 = 37°.
SOLUCION
D.C.L. del balde
LFy = 0
T. Cos 0 = m.g
2da Ley de Newton
V2
T. Sen 0 = m -¡=r
H
(i)
T. Sen 0 =
De (1) y (2):
m .
L . Senil
- (2)
v ='/g. L. Tg0. Sen 0
120 cm
1
T Cos 0
--------------------- 7T
/ 9 !
/ 1
1 A
£ » £ r
T Sen 6
m
g
Reemplazando:
v = 3 m/s
I6ücm
Además sabemos que cada gota de agua
sale tangente a la trayectoria con velocidad
V , para luego describir un movimiento para­
bólico.

236. *
#
m
dad angular que puede girar el sistema sin
que se rompa la cuerda, g = 10 m/s
Analizando en la vertical
h = V o - t + l - g . t 2
0,45 = 0 + 1 (10) t2
t = 0,3 s
Luego: d = v. t =0,9 m
Observando desde arriba:
! = ^/r ^+
2 - d2
Reemplazando:
a = 1,5 m
PROBLEMA N909
En la figura la barra AB es mantenida
en posición vertical por m edio de la
cuerda CD cuando gira el sistema alrede­
dor del eje vertical que muestra la figura.
El pin en "A" es liso y la barra en AB tiene
una masa de 40 kg. Si la máxima tensión
que puede soportar la cuerda CD es de
1500 N, hallar el valor de máxima veloci-
D
*
*
*
*
*
*
*
&
$
*
*
#
*
#
*
*
*
*
*
*
*
*
*
*
$
*
*
*
m
*
&
#
$
*
*
*
*
*
Haciendo el D.C.L. de la barra desde un
sistema de referencia rotacional que gira
con velocidad angular constante "w pa­
ra nuestro observador la barra AB estará
en equilibrio.
Por2da. condición de equilibrio.
EMa = o
Fcg (0,3) =T. (0,4) Sen 37*
m w2 R (0,3) = T. (0,24)
Reemplazando datos:
w = 5 -J2 rad/s

237. <
t E! sistema mecánico mostrado en la
figura gira alrededor de su eje de rotación
vertical. Hallar el valor de la velocidad
angular constante"w", tal que, la parte AB
de la barra imponderable en forma de "T",
articulada en A, esté en posición vertical.
En los extremos B y D se encuentran dos
esferas puntuales de masas M y m respec­
tivamente (M =4m).
Donde: CA =CB =CD =L =1 metro
SOLUCION
Haciendo el diagrama del cuerpo libre del
sistema físico formado por la barra en
forma de "T" y las esferas en forma de "M"
"m”, desde el sistema de referencia ro­
tacional, que rota a velocidad angular
constante "w" En este sistema de refer­
encia el sistema físico se encuentrá en
reposo (Equilibrio).
*
$
*
*
&
*
#
*
$
#
*
*
*
#
*
*
mg
Por 2da. Condición de Equilibrio.
I M a = 0
2mw? L (L) +Mw2 L (2L) =mgL
2 w2 L (M +m) =m.g
Pero:
,=)H
™Ipo
Y(M + m) I 2L j
M =4m , L = 1, g =10
w=1 rad/s
$ PROBLEMA Ns 11
*
*
*
sd
*
*
*
*
*
*
*
*
*
*
*
»
m
*
m
*
*
*
#
*
*
*
$
*
*
*
*
*
íd
*
«d
#
*
#
♦
El sistema m ecánico m ostrado en la
figura, gira alrededor de su eje vertical.
Hallar el valor de la velocidad angular
"w", tal que, la parte AB de la barra
uniform e y homogénea en form a de “ L",
articulada en A, esté en posición ve rti­
cal. Donde:
AB =2m , BC - 1m
L. =1m , g =10 m/s2
w
a) 1 rad/s
c) 3 rad/s
e) Ninguna
b) 2 rad/s
d) 4 rad/s

238. T E M A : D IN A M IC A L IN E A L Y
C IR C U LA R
PROBLEMA NE01
En nuestro planeta un hombre pesa 900 N.
¿Cuánto pesaría en la luna cuya acele­
ración de la gravedad es la sexta parte de
la gravedad en la tierra?.
SOLUCION:
Peso en la tierra:
P = m g ,..(1)
Peso en la luna:
Pl = m. gu = m . f
Pl =
Reemplazando:
PL =150 N
PROBLEMA Ne 02
Del techo de una cabina de ascensor,
cuelga una masa de 4 kg. Calcular la
aceleración para que la tensión sea 35 N.
El ascensor sube con m ov.......
con aceleración de módulo.......
(g = 10 m/s2).
a) retardado; 10 m/s
b) retardado; 10 m/s2
c) retardado; 5 m/s2
d) acelerado; 1,25 m/s2
e) retardado; 1,25 m/s2
*
<
*
<
*
*
*
*
#
#
#
í-
$
$
#
m
#
*
*
*
*
*
#
*
*
#
*
*
*
*
*
»
*
#
*
t»
#
*
*
*
*
<
K
*
*
*
*
*
*
#
*
*
*
*
PROBLEMA Ne03
Determinar la magnitud de la fuerza
"F" que se debe aplicar a un bloque de
peso 5N, de tal modo, que el cuerpo acele­
ra hacia arriba a razón de a = 9,8 m/s2.
SOLUCION:
D.C.L (bloque)
2da. Ley de Newton
Fr = m . a
w
(F —w) = — . a
g
F = w (1 + —
)
g
F = 10 N
Reemplazando:
PROBLEMA Ne04
Un bloque reposa sobre un pisoJiori-
zontal y se le aplica una fuerza vertical
hacia arriba igual al doble de su peso.
¿Qué altura sube en 1 segundo?.
a) Falta el peso
b) menos de 5 m.
c) mas de 5 m.
d) más de 10 m.
e) más de 15 m.

239. Si en el interior de un ascensor se halla
una persona sobre una balanza. ¿Cuánto
registrará ésta si el ascensor baja con una
aceleración de 4,9 m/s2?, sabiendo que el
hombre pesa 600 N.
SOLUCION:
2da. Ley de Newton
F r = m . a
., w
w - N — .a
g
N = w (1 - —)
9
Reemplazando:
N = 300 newtons
PROBLEMA N9 06
Un hombre se encuentra sobre una
balanza móvil sobre un plano inclinado
que forma un ángulo 6 = 45° con la hori­
zontal. Si la lectura en la balanza indica
300 N. ¿Cuánto pesa realmente el hom­
bre? No hay rozamiento sobre el plano
inclinado.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
a) 400 N b) 500 N c) 600
d) 700 N e) Ninguna
PROBLEMA Ne07
En el sistema mecánico mostrado, de­
terminar la aceleración de los bloques y la
tensión en la cuerda. La polea no ofrece
rozamiento.
*
*
*
*
*
*
*
*
SOLUCION:
D.C.L. (bloque A)
2da. Ley de Newton
nriA . g - T = mA . a ....(1)

240. 2da. Ley de Newton
T - mB . g = m e. a .... (2)
Sumando: (1) + (2)
(nriA - mB) • g = (mA + m B ). a
(mA - mB)
a = - ----- . g
(mA + mB)
Reemplazando en (3):
a = 6 m/s2
Reemplazando en (1):
T = mA (g - a)
.... (3)
T = 16 N
*
*
■
*
*
*
*
*
*
Determinar la aceleración del sistema
mecánico, tal que el bloque menor de ma­
sa “m" permanezca en reposo respecto
del carro en forma de cuña. Considere
$ = 37® y g = 10 m/s¿. No hay rozamiento.
PROBLEMA N° 08
En la figura mostrada, determinar la
aceleración de los bloques de masas
iguales. El coeficiente de rozamiento ci­
nético entre el bloque y la superficie hori­
zontal es 0,5.
g = aceleración de la gravedad.
*
*
*
*
E F x = m . a
NSen<}> = rrt a .... (1)
Eje vertical:
L Fy = 0
N. Cos (¡>= m . g ... (2)
Dividiendo (1)r (2)
Tg <!>=-'-
a = g Tg <
¡
>
Reemplazando:

241. PROBLEMA N® 10 *
r á
?
Determinar la aceleración del sistema, *
sabiendo que no existe fricción en nin- *
guna superficie en contacto. *
d) g/2 e) g/6
PROBLEMA NB11
Determinar la aceleración mínima del
sistema mecánico mostrado, tal que el
bloque de masa "m" no resbale respecto
del bloque mayor "M". El coeficiente de
rozamiento estático es de 0,8.g =10 m/s2.
SOLUCION:
(1)
.... (2)
2da. Ley de Newton, en el eje x.
N = m . a
Z F y = 0
fs =m g
(1)en (2):
Us (m a) = mg
am in = - ^ *
„ Us
Reemplazando:
amin —12,5 m/s
PROBLEMA Ne 12
Si al bloque mostrado le aplicamos
una fuerza horizontal F = 10N y no se
mueve, entonces es cierto que:
*
*
*
*
*
*
*
*
*
i
*
*
*
*
*
*
*
*
r
r -
. . . _
V. . v
a) La fricción estática máxima es 10N
b) La fricción estática es mayor que 10N
c) La fricción estática es 10N
d) El peso del cuerpo es mayor que 20N
e) El peso del cuerpo es menor que 10N
PROBLEMA N913
En la figura mostrada, hallar la acele­
ración de los bloques A y B, de masas
iguales m = 10 kg; F = 60N. El coeficiente
de rozamiento cinético es 0,2 entre las

242. SOLUCION:
D.C.L. de todo el sistema mecánico.
2da. Ley de Newton
(F - 2|j mg) = (2m)a
Reemplazando:
a = 1 m/s'
.2
PROBLEMA Ne 14
Una masa de 3 kg. reposa sobre un
piso horizontal, con el cual el coeficiente
de fricción estática es 0,2. Se le aplica
una fuerza horizontal de 4N. Determinar
la fuerza de fricción del piso sobre el cuer­
po. ( g = 10 m/s2).
a) 6N
c) 0,6N
e) 0,4N
PROBLEMA N -15
b) Faltan datos
d) 4N
La figura muestra dos bloques de ma­
sas A = 3 kg y B = 2 kg. Hallar el mínimo
valor del coeficiente de rozamiento " n ”
tal que el bloque “B“ no resbale respecto
"A", sabiendo que no existe rozamiento
entre el bloque “A" y el piso horizontal. La
magnitud de la fuerza constante aplicada
ai bloque ”A“ es F = 10N. g = 10 m/s2.
g = 10 m/s2
SOLUCION
D.C.L. del sistema físico ( A +B):
2da. Ley de Newton
F = (n riA + i t i b ) . a
10 = (5) a
■l_L
*
*
#
*
*
*
*
*
*
*
*
*
*
#
s
i»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
.*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
a = 2 m/s
D.C.L. del bloque B.
2da. Ley de Newton
fs = me - a
(i . rriB ■g = mB a
....(1)
PROBLEMA Nfi 16
Determinar la aceleración de los blo­
ques, sabiendo que las masas son:
A = 2 kg, b = 3 kg. El coeficiente de
rozamiento cinético entre los bloques y la
superficie es 0,5. Ademas: F = 50N.
g = 10 m/s2
a) 3m/s2
b) 4m/s2
o
c) 5m/s
d) 6m/s2
e) N.A.

243. Las superficies de los bloques en con­
tacto son rugosas n = 0,5 y la superficie
horizontal donde descansan es lisa. Ha­
llar la relación de las aceleraciones entre
los bloques A y B.
*
*
*
*
*
*
*
*
*
*
*
.img 2m
*8l
* 2da. Ley de Ngwton
¿mg
SOLUCION:
Analizando el movimiento de los bloques
de masas "m“.
*
*
*
•*
<
j£
s
i*
*
*
*
*
*
3 *
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
2da. Ley de Newton
(mg - n mg) = (2m) aA
aA = í l ^ - . g - .(1 )
Analizando el movimiento de los bloques
de masas "2m“
(2mg - ¡i
3
(
Q
II
'4m) a B
a B
( 2 ­
4 - - ( 2 )
Dividiendo las ecuaciones (1) y (2):
a A 2(1 - | i )
a B ( 2 - ■u)
a A 2
aB 3
PROBLEMAS N9 18
El peso de B es el doble del peso de A
y ambos se mueven con velocidad cons­
tante. El coeficiente de fricción entre B y
el piso es: (Despreciar el peso de las
poleas lisas).
#
*
*
*
*
S
i*
a) 0,25
d) 0,40
b) 0,50
e) 0,20
c) 0,35

244. Se jala con una fuerza horizon­
tal F = 88N dos bloques de masa iguales
a ”m" unidos por un elástico de masa
despreciable. En un momento dado se
mide las aceleraciones de los extremos A
y B de la liga encontrándose que:
aA = 3 . as
Para el mismo instante calcular la ten­
sión en el elástico a lo largo de éste. No
hay Rozamiento.
f
m lB A
ni
F
V
•i.j“
•"
."
.[ü
iic
j
i .wwi1
, 'ivíw
1
J
#
*
*
*
*
*
Ü
¡
4*
<
*
*
*
*
SOLUCION:
D.C.L. (bloque B)
2da. Ley de Newton
(F -T ) = m (3a)
(1) en (2)
F - T = 3T
T = s
Reemplazando:
(2)
Se jala con una fuerza horizontal cons­
tante dos bloques de masas iguales a “m"
unidas por un elástico de masa desprecia­
ble. En un momento dado se mide las
aceleraciones de los extremos A y B de
liga encontrándose que:
aA = 2 . aB
Para este mismo instante calcular la
tensión en el elástico a lo largo de éste.
El p iso es l i s o .
a) T = F
c) T = F/3
e) T = F/5
b) T = F/2
d) T = F/4
PROBLEMA Ne 21
Un avión realiza un clavado a una velo­
cidad de 108 km/h, en el punto más bajo
(cuando comienza a elevarse) el piloto
siente que pesa 6 veces lo normal.
¿Cuál es el radio de la trayectoria?.
g = 10 m/s2
SOLUCION:
D.C.L. (hombre)
T = 22N
*
4<
*
#
4
»
sis
*
*
*
4*
*
*
2da. Ley de Newton
Fc = m . ac
Pero: N = 6 mg
5 mg = m .
m
q

245. r =í t
5g
Reemplazando:
R = 18m
PROBLEMA N9 22
Por un carta torcido en forma circular
de radio R = 100 cm.; se desliza sin fric­
ción una esfera de masa “m". ¿A qué
altura"h” se encontrará el cuerpo, si el riel
gira uniformemente con velocidad angu­
lar constante w = 5 rad/s.
g = 10 m/s'
I
a) 20 cm b) 40 cm c)60 cm
d) 80 cm e) Ninguna
PROBLEMA Ne 23
La figura muestra un péndulo cónico
de masa "m " y altura "h", que gira con
velocidad angular constante. Hallar la
velocidad angular.
*
*
*
*
*
*
$
*
sK
*
*
*
*
*
*
*
*
#
ílf
*
Sis
*
*
*
*
*
*
*
si»
*
*
*
#
*K
*
*
*
*
*
*
*
2da. Ley de Newton:
£Fradiales = m . Q
c
T . Sen 9 =m.w2.R
ZFy = 0
T Cos 0 = mg
(1 )f(2 );
Tg 0 =
Pero: R = h , Tg 0
Luego: w2 =
- - d )
.... (2)
w2
g
PROBLEMA Ns 24
En la figura mostrada el ascensor sube
con una aceleración a = 3g. ¿Qué ángulo
" 0 " formará el péndulo cónico con la
vertical cuando gira a razón de 2 n rad/s?.
La longitud de ia cuerda es 2 metros.

246. b) 6 = 37°
d) e = 60°
a) 6 =30°
c) 0 = 45°
e) Ninguna
PROBLEMA Nfi 25
En el sistema mecánico mostrado,
el eje vertical mantiene su velocidad
angular constante. Un hombre se en­
cuentra dando vueltas suspendido de una
cuerda de longitud "L" que forma un án­
gulo de 37° con el eje. Calcular la nueva
longitud "x" de la cuerda, tal que, el hom­
bre manteniendo la misma velocidad an­
gular constante, la cuerda forme un án­
gulo de 53c con la vertical.
SOLUCION:
Propiedad : "La velocidad angular de un
péndulo cónico depende
únicamente de la altura"
*
Ü
*
«
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
N
i
*
*
*
¡it
*
Por consiguiente ambos péndulos cóni­
cos tienen la misma altura.
h = x . Cos 53° = L . Cos 37°
Despejando: -
PROBLEMA Ne26
El sistema físico mostrado acelera ho­
rizontalmente a = 4m/s Hallar la máxima
velocidad angular "w" del disco, tal que,
el bloque "m" que se encuentra a una
distancia R = 25 cm. del eje, no resbale.
|i8 = 0,5
g = 10 m/s2.
a) 1 rad/s b) 2 rad/s
c) 3 rad/s d) 4 rad/2
e) Ninguna
PROBLEMA Ne27
La figura muestra una esfera de ma­
sa “m" en movimiento circular con ra­
dio de curvatura "R". La esfera y el
bloque de masa "M“ se encuentran
unidos mediante una cuerda que pasa
por un agujero del plano horizontal
liso. Determinar la velocidad angular
constante de la esfera.

247. SOLUCION:
D.C.L de la esfera y del bloque:
El bloque se encuentra en equilibrio
IF y = 0 —
> T = M . g .... (1)
Analizando ia esfera:
radiales = m - 3c
T = m . w2 . R ....(2)
Igualando: (1) y (2)
Mg = m . w2 . R
PROBLEMA NB28
El ascensor sube con una aceleración
constante (a = g). Hallar la máxima velo­
cidad angular "w" con que se puede girar
al disco, tal que un bloque de masa "m"
ubicada a una distancia R = 10cm., no
salga disparado. |is = 0,5.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
g = 10 m/s
!
a) 10 rad/s b) 12 rad/s
c) 14 rad/s d) 16 rad/s
e) Ninguna.
PROBLEMA N» 29
Un automóvil se desplaza por una ca­
rretera de radio de curvatura 180m. Sa­
biendo que el coeficiente de rozamiento
estático entre las llantas y la pista hori­
zontal es 0,5. Hallar la máxima velocidad
del auto, tal que la llanta no resbale,
g = 10 mis2.

248. El diagrama de fuerzas sobre el auto,
visto de frente.
XFy = 0 - » N = mg
X Fradiales = m. ac
ír = m ac
m(mg) = m . —
vmáx = Vu g. R
Vmax = VMU. JE. R
Reemplazando:
Vmáx = 3 0 m/s
a) 10 m/s
c) 20 m/s
e) Ninguna
b) 15 m/s
d) 3 0 m/s
*
*
PROBLEMA N9 30
Un automovil ingresa a una curva de
30 metros de radio y 37° de ángulo de
peralte. Determinar la velocidad del auto,
tal que la fuerza de rozamiento sobre las
-lantas sea igual a cero,
g = 10 m/s2.
Calcular la velocidad del cilindro de
radio R = 10m, tal que, el bloque de masa
"m" no resbale. El coeficiente de roza­
miento estático es 0,25 entre el bloque y
la pared vertical.
*
*
*
*
*
*
♦
*
*
*
#
$
*
♦
*
*
*
*
*
#
*
*
*
*
S
d
*
*
sis
*
*
*
*
*
*
*
*
*
*
*
mg
SOLUCION:
D.C.L. del bloque:
X Fradiales = m . ac
N = m . w2 . R
L Fy = 0 • --------
fs = m .g
2 f s
Hs(m . w . R) = m . g
|is - R
Reemplazando:
PROBLEMA N9 32
Se muestra un auto venciendo la gra­
vedad. El radio de curvatura de la super­
ficie esR = 40m y el coeficiente de roza­
miento estático entre las llantas y la pista
es 0,25. Hallar la mínima velocidad del
auto, para que no caiga,
g = 10 m/s2.

249. a) 20 m/s b) 30 m/s
c) 40 m/s d) 50 m/s
e) Ninguna
PROBLEMA N9 33
Una piedra atada a una cuerda gira
uniformemente (velocidad angular cons­
tante) en un plano vertical. Encontrar la
masa "m" de la piedra si la diferencia
entre la tensión máxima y mínima en la
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
#
*
*
*
$
*
*
♦
$
*
*
+
m
p v2
Fc = m . ~
V2
Tmin + mg = m . — ....(a)
V2
Tmáx-mg = rn— .... (P)
(a) = (P)
Tmax —mg = Tmín + mg
Tmáx —Tmín = 2 m . g
-------w
------ /
19.6N = 2m (9,8) m/s2
m = 1 kg
PROBLEMA N9 34
Un carrito se mueve con velocidad
constante en módulo sobre una pista cur­
vilínea, como indica la figura. ¿En qué
posición la reacción normal sobre las
llantas es máxima? (Considerar fricción
nula).

250. T R A B A J O Y P O T E N C I A

251. c
fip
rru
L
Qi
CONCEPTO.
El trabajo existe en muchas formas, mien­
tras que el calor, solamente en una En el
trabajo de cualquier forma siempre participan
dos: el sistema y la fuente de trabajo.
Por ejemplo, la mano del hombre (la fuente
de trabajo) comprime un recorte (el sistema),
eleva un bloque "m” (el sistema). El agüa en un
matraz (la fuente de trabajo), que se dilata al
evaporarse; vence la inercia del tapón (el sis­
tema): el tapón, que inicialmente se encuentra en
¡
—
d F
lllllllll !1T l
- l
l
l
l
É
o j «
O
« GAS
C o
0 • j
Estado
Inicial
Estado
Final
1) Los ejemplos han sido apropiados del
matemático e ingeniero militar francés J.
Poncelet ( 1 788 -1 867). El fue el que
introdujo el término "TRABAJO” en el año
1 826
2) "Realizar trabajo mecánico significa ven­
cer o eliminar resistencias, tales como las
fuerzas moleculares, la fuerza de los re­
sortes, la fuerza de gravedad, la inercia
de la materia, etc. Desgastar un cuerpo,
rectificarlo, dividirlo en partes, elevar car­
gas; arrastrar un carro por la carretera,
comprimir un resorte, todo esto significa
realizar trabajo, significa vencer en cierto
intervalo de tiempo una resistencia que
se restablece continuamente".
3) Más ejemplos Realizar trabajo significa
vencer la presión del gas liquido, cristal.
Comprimir un gas, liquido o cristal sign-

252. fica realizar trabajo. Vencer la fuerza
electromotriz de un acumulador significa
realizar trabajo. Cargar un acumulador
significa realizar trabajo.
4) Todos los fenómenos semejantes como:
elevación de bloques, comprensión del
cías, desplazamiento de carro, compren­
; ión del resorte, carga de acumulador,
'tan sido denominados con una misma
palabra: "TRABAJO"
5) El trabajo está relacionado "con la supe­
ración de resistencia" No importa, que es
lo que crea y que es lo que vence la
resistencia.
6) La resistencia se vence “durante el movi­
miento": el bloque se eleva, el carro se
mueve, los portadores de las cargas eléc­
tricas se desplazan en determinada di­
rección, etc.
7) Durante el movimiento sin superación de
resistencia, no hay trabajo. No importa
que movimiento es, lo esencial es el pro­
pio movimiento.
8) El trabajo está relacionado no con cual­
quier movimiento, sino que sólo con el
movimiento ordenado. Toda la masa del
bloque se eleva. Todo el émbolo se des­
plaza en el cilindro en una dirección. To­
do el carro se mueve por el suelo en una
dirección. Al cargar el acumulador las
partículas cargadas de un mismo signo
se mueven en una dirección determina­
da. El movimiento ordenado de las par­
tículas se sobrepone a su movimiento
caótico. (Al comprimir el gas el movi­
miento ordenado de todo el gas en una
dirección determinada se sobrepone el
movimiento caótico de las moléculas, de
las cuales está compuesto el gas).
9) Para el trabajo siempre se necesitan dos
participantes:
a) Uno crea la resistencia
b) Y el otro la vence
*
*
s*
*
s*
*
*
*
*
*
slí
*
slí
*
slí
*
slí
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
S
U
slí
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
S
ü
slí
*
*
slí
*
*
slí
Slí
st>
slí
slí
#
*
slí
S
ü
MOVIMIENTO DE IONES
(Movimiento Ordenado)
10) La mano del hombre ejerce una fuerza
"F“ sobre el émbolo, lo desplaza en el
cilindro y comprime el gas, venciendo su
resistencia
11) Las participantes pueden cambiar de
papel. El gas se expansiona y vence la
presión que ejerce la mano del hombre
que impide la expansión. No importa que
participantes son. Es necesario que ellos
sean dos.
12) Definitivamente:
“EL TRABAJO ES LA TRANSMISION
DEL MOVIMIENTO ORDENADO DE UN
PARTICIPANTE A OTRO CON SUPE­
RACION DE RESISTENCIA".
13) Cuando la mano ejerce presión sobre el
émbolo y comprime el gas en el movi­
miento. Para vencer la resistencia hace
falta la FUERZA.
TRABAJO MECANICO REALIZADO POR
UNA FUERZA CONSTANTE
Matemáticamente, el trabajo realizado
por una fuerza constante sobre un cuerpo
que se mueve en línea recta, es igual al
producto del módulo de la fuerza por la dis­
tancia, por el coseno del ángulo que forma el
vector fuerza con el vector desplazamiento

253. 1) De la figura obsérvase que no hay trans­
misión de movimiento en el eje vertical,
por consiguiente las fuerzas perpendicu­
lares al movimiento realizan trabajo.
w f Sene = C E R Q
Fáene
2) De la figura, la fuerza que transmite movi­
miento es la componente "F , Cos 8'', por
consiguiente solamente realizan trabajo
mecánico las fuerzas paralelas al movi­
miento
w f = w fcos e = Cos 0) d (2)
CASOS PARTICULARES
1) Las fuerzas que tienen la misma direc­
ción y sentido del movimiento, realizan
trabajo Positivo. En este caso ,9 = 0 °
Wh = F.d - ¿ . J T
2) Las fuerzas que tienen dirección perpen­
dicular al movimiento no realizan trabajo.
En este caso, 0 = 90°
WF= 0
_ = ca i
3) Las fuerzas que tienen igual dirección»
pero sentido opuesto al movimiento, rea­
lizan trabajo negativo.
En este caso, 0=180°
W = -F d
4) El trabajo neto o total realizado sobre un
cuerpo, es igual a la suma algebraica de
los trabajos realizados por las diferentes
fuerzas aplicadas al cuerpo.
Wneto =
i= 1
v r
Si el trabajo neto es igual a cero, el
cuerpo se mueve con velocidad cons­
tante.
Si el trabajo neto es negativo, el mo­
vimiento del cuerpo es retardado, dis­
minuyendo la velocidad.
Si el trabajo neto es positivo, el movi­
miento del cuerpo es acelerado, aumen­
tando la velocidad
Unidades de trabajo y la Energía en el Si
Un joule(J) se define como el trabajo rea­
lizado por la fuerza F = 1N, actuando sobre
un cuerpo que se mueve la distancia d = 1m
en la dirección de la fuerza.
*
*
*
*
*
*
*
*
*
*
m
m
*
$
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Wf = F d
1 joule = 1 newton metro
1J= 1 N .m
El nombre "joule" fue escogido en honor
a James Prescott Joule (1 816 - 1 869),
científico británico, famoso por sus investi­
gaciones sobre los conceptos de calor y
energía.
GRAFSCA FUERZA VERSUS POSICION
La figura muestra la gráfica fuerza versus
posición. La fuerza "P de magnitud variable
aplicado a un cuerpo que se mueve en direc­
ción del eje "x".

254. El trabajo realizado por la fuerza sobre un
cuerpo en dirección del eje "x" es igual al
AREA bajo la curva, entre dos puntos de su
posición.
Ejemplo:
1) La figura muestra un sistema mecánico,
un bloque de masa “m“ acoplado a un
resorte de constante de elasticidad "K”.
2) En la gráfica, fuerza vs posición, la pen­
diente de la recta nos da el valor de “K"
K = Tg 0 =
F = K . X
(1)
(2)
«
¡
6
*
*
*
*
*
*
«
j»
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
#
*
*
*
*
*
»
3) Al bloque se le aplica una fuerza externa
"P (variable) que vence a la resistencia
que ofrece el resorte, logrando deformar­
lo una distancia "x".
4) De la ecuación (2). La fuerza externa
varía directamente proporcional a la de­
formación "x” del resorte.
5) Despreciando la fuerza de rozamiento.
El trabajo realizado por la fuerza externa
sobre el sistema es igual al área del trián­
gulo.
6) Luego: WF = área del triángulo
WF= (base)(altura)= } . x . F . .(3)
Reemplazando la ecuación (2) en (3)
WF= | . x .(k . x) = ~ . k . x2
Por lo tanto:
K = constante de elasticidad del re­
sorte (N/rn)
x = deformación de resorte (m)
Ci
-a—
PROBLEMAS RESUELTOS
PROBLEMA N®01
Un muchacho jala un bloque sobre
una superficie horizontal en línea recta
con velocidad constante. Sabiendo que
la fuerza de rozamiento que actúa sobre
el bloque es 36 N, calcular el trabajo reali­
zado por el muchacho cuando logra des­
plazar el bloque una distancia de 10 me­
tros.
SOLUCION
Realizamos el D.C.L. del bloque
*
*
*
*
*
He
*
De la lera. Ley de Newton

255. Luego: F.Cos 0 = 36 newtons ...(1)
Cálculo del trabajo realizado:
WF= F d.Cos 0 = (F.Cos 0) d
Wf = (36)(10)
WF= 360 J
PROBLEMA N®02
En la figura mostrada, un bloque de
peso 40 N, es sometido a la acción de un
sistema de fuerzas donde: Fi = F2 = F3 =
F4 = 20N, Calcular el trabajo realizado por
todas las fuerzas sobre el cuerpo, para un
desplazamiento de 5m.
F4 : fricción cinética.
SOLUCION:
Las fuerzas perpendiculares al movi­
miento no realizan trabajo, por consi­
guiente, el peso, la normal y la fuerza F3,
No realizan trabajo. La suma de los tra­
bajos realizados por las fuerzas F1 y F4
es igual a cero.
Luego
Wneto = Wf2
Wneto = (F2) d. Cos 53°
Wneto = (20N) (5m) f | '
Wneto = 60 J
*
*
*
*
*
*
*
*
*
$
*
*
*
*
s
t»
*
*
*
*
*
*
*
¡>
*
*
*
*
S
U
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
PROBLEMA Ne 03
Un bloque de masa 8 kg. se empuja
una distancia de 5m sobre un plano hori­
zontal, con coeficiente de rozamiento ci­
nético 0,4; por una fuerza constante "F"
paralela al plano a velocidad constante.
Calcular el trabajo realizado por "F“. g =
1 0 m/s2
SOLUCION:
Diagrama del cuerpo libre, del bloque:
XFy = 0 N i= 8 0 = mg
fk = U|<. Ni = ( 0 , 4 ) (80)
fk = 32 newtons . . . . ( 1 )
1era. Ley de Newton:
Si el bloque se mueve con velocidad
constante, la fuerza resultante es
igual a cero.
F = fk = 32 N
Trabajo realizado por "F"
WF= F.d = (32 N) (5m)
WF = 160 J
PROBLEMA Na04
Un bloque de peso 80 N se desplaza
por acción de la fuerza F = 5QN Sabiendo
que el coeficiente de rozamiento cinético
es 0 ,2 entre el bloque y el piso horizontal,
determinar el trabajo realizado por "F" al

256. cabo de 4 segundos de estar actuando. El
bloque inicia su movimiento desde el re­
poso. g = 10 m/s,
SOLUCION:
Cálculo del desplazamiento que experi­
menta el bloque en t = 4.
30
40
80
fk = u . Ni = (0,2) (110)
fk = 22 N .... (1)
FR 18 N
m
a =
8 kg
a = —m/s2 .. (2)
4
v y
(16)
e = 18m ....(3)
Cálculo del trabajo realizado por "F"
WF= (F Cos 37°).d
WF = (40N) (18 m)
Wr = 720 J
PROBLEMA N® 05
Determinar el trabajo neto que se rea­
liza sobre un bloque de peso 180N, para
un desplazamiento de 5 m en la vertical.
*
*
*
«i
*
#
*
*
#
*
*
*
*
*
*
%
*
*
*
*
*
*
♦
*
d
e
*
*
*
*
*
*
*
*
«
t¡
*
*
*
m
*
#
*
*
*
*
*
*
*
*
*
*
*
*
La magnitud de "F" es 100N, y el coefi­
ciente de rozamiento cinético es 0,7 entre
el bloque y la pared.
SOLUCION:
Cálculo de la fuerza resultante en el eje
vertical.
180
80
60
N^eo
fk
fk = Uk. Ni = (0,7) (80) = 56
El peso del bloque es mayor que la com­
ponente de F en la vertical 180) 60, por
consiguiente el bloque desciende
Z F y = 180 - 6 0 -fk
I Fy = 64 N
Wneto = (£ Fy) (d)
Wneto = (64 N) (5m)
Wneto = 320 J
PROBLEMA Ne06
En la figura mostrada un bloque de
peso 90N, es sometido a la acción de un
sistema de fuerzas, donde:
Fi = SON y F2 = 40N
Calcular el trabajo que desarrolla F2
para un recorrido "D", sabiendo que Fi
realiza un trabajo de + 400 J.

257. SOLUCION:
Cálculo de la distancia "d"
WF, = (Fi) d. Cos 37
400 J = (50N)d ^
3
d = 10 m
Cálculo del trabajo realizado por F2
WF2 = (F2) d. Cos 120°
Wf 2 =(40) (10) ( - | )
*
$
WF2 = - 200J
*
&
#
*
*
*
*
*
*
*
*
*
*
$
*
*
«í
*
*
PROBLEMA NB07
Al estirar un resorte una longitud
x = 0,8 m, la fuerza externa varía desde
cero, hasta F = 50N. Calcular el trabajo
desarrollado sobre e! resorte.
SOLUCION:
En toda gráfica F- x, el área bajo la recta,
es igual al trabajo realizado por la fuerza
*p
WF = área del triángulo
Wf = |( F ) (x)
WF (50N) (0,8 m)
WF = 20 J
íPOTENCIA MECANICA
i CONCEPTO.
Es una magnitud física escalar que nos
expresa la medida de la rapidez con la cual
se transfiere movimiento ordenado. Tam­
bién se puede expresar como el trabajo rea­
lizado por cada unidad de tiempo.
Sabemos que: W = F . d
r _ W F.d
~ t t
P = F. v
La potencia desarrollada por una fuerza,
sobre un cuerpo, será igual al producto de la
fuerza por la velocidad.
Unidad de la Potencia en el SI
Un "watt” es la potencia de una maquina
que efectúa trabajo con la rapidez de un joule
por cada segundo.
Iw a tt.- U S Ü f-
segundo
1 W = 1 -
s
— El nombre "watt" fue escogido en honor
del ingeniero británico James Watt (1 736
- 1 819) quien mejoró la máquina de
vapor con sus inventos.
RENDIMIENTO O EFICIENCIA DE UNA
MAQUINA (n)
Concepto.
Es aquella magnitud adimensional que
nos expresa el grado de perfeccionamiento
de una máquina térmica con respecto a la
potencia que consumen. Su valor se define
como el cociente de la potencia útil entre­
gada por la máquina, entre la potencia con­
sumida por la máquina

258. *
*
*
*■
*
*
*
*
*
*
$
*
*
*
<ts
*
*
*
*
*
La potencia perdida, se experimenta du­
rante el funcionamiento de la máquina.
Eficiencia(n) =
Potencia Util
Potencia consumida
tual.
La eficiencia expresada en forma porcen-
Eficiencia=-:
Potencia Util
Potencia consumida
donde: 0 % < n < 100%
x 100%
cPROBLEMAS RESUELTOS
PROBLEMA N®01
Determinar la potencia del motor de un
ascensor cuando levanta la cabina con un
peso total de 15 000 N, a la velocidad de
1,2 m/s.
SOLUCION.
La potencia desarrollada por el motor es:
P = F.v
P = (15 000 N)(1,2 m/s)
P = 18 000 watts
P = 18 kw
PROBLEMA Ne 02
E¡ m otor de una lancha le hace desa­
rrollar a esta una velocidad constante de
36 km/h, venciendo la fuerza de resisten­
cia del agua de 3 000 N. Determinar la
potencia desarrollada por el motor.
SOLUCION:
La fuerza desarrollada por el motor, sirve
para vencer a la fuerza de resistencia dei
agua de magnitud 3 000 N.
P = F . v
P = (3 000 N)(10 m/s)
P = 30 000 w
P = 30kw
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
■*
*
*
*
*
*
*
*
*
*
*
PROBLEMA Nfi 03
El motor de un bote tiene una potencia
de 3 000 watts y lo lleva a una velocidad
de 2,5 m/s. ¿Cuál es la fuerza de resisten­
cia del agua que se opone al movimiento
del bote?
SOLUCION:
ZFX= 0 , Velocidad = cte.
F - fa ....(D
Pero: P = F . v
3 000 = F . (2,5)
f =1,2 kN
"La fuerza desarrollada por el motor,
es igual a la fuerza de resistencia del
agua"
PROBLEMA Ne04
Un ciclista cuyo peso total es 800 N,
sube con velocidad constante de 36 km/h,
sobre un plano inclinado que forma 30°
con ia horizontal. Determinar la potencia
desarrollada por el ciclista. Desprecie la
fuerza de oposición del aíre.

259. La fuerza desarrollada por el ciclista, es
igual a la componente del peso paralelo
al plano.
P = F . v
P = (400 N) (10m/s)
P = 4 kW
PROBLEMA Nfi 05
¿Cuál es la potencia desarrollada por
una fuerza “F" que actúa sobre un cuerpo
de masa 50 kg, que le hace variar su velo­
cidad de 16 m/s a 20 m/s, en 10 segundos.
Liso
SOLUCION
Del teorema de la Energía Cinética, el
trabajo realizado por la fuerza "F" es igual
a la variación de la energía cinética que
experimenta la masa.
wF = 2 m í VF “ 'o
W = 3 600 J .... (1)
Potencia desarrollada por la fuerza "F"
WF _ 3600J
t " lO s
P =
P = 360 W
*
*
m
fc
*
fc
*
*
*
*
*
fc
*
fc
*
fc
fc
#
fc
*
fc
fc
#
fc
*
fc
fc
fc
#
*
*
*
fc
fc
s*
fc
fc
*
*
fc
*
fc
#
PROBLEMA Ns06
Cuando una lancha a motor se des­
plaza a velocidad constante la fuerza de
resistencia del agua al desplazamiento
del cuerpo es directamente proporcional
a la velocidad. Si para mantener una velo­
cidad de 36 km/h desarrolla una potencia
de 3 KW, ¿Qué potencia se requiere para
mantener una velocidad de 72 km/h?.
SOLUCION:
La fuerza desarrollada por el motor, es
igual a la fuerza de oposición del agua
F = k . v , k- constante
Pero: P = F . v = (k . v ) . v
P = k . v2 ....(1)
La potencia desarrollada por el motor es
proporcional al cuadrado de la velocidad.
2
P i
p2 2
v 2
Reemplazando datos:
Pi = 3 KW
P2 = 12 KW
PROBLEMA Ns07
Hallar la eficiencia de una máquina;
sabiendo que la potencia perdida equivale
al 25% de la potencia Util.
SOLUCION:
Pe = Pu + Pp
Pe = Pu + ~ Pu
Pe = fP u - ( 1)
F = W Sen 30°
F = (600 N) = 400 N
Cálculo de la Potencia.

260. Sabemos que:
n =
Pu
Luego, de (1):
n = 0,8 ó
n = 80%
SOLUCION:
Sabemos:
280 J
n =
Wu
We
0,7:
We
We = 400 J
Wp = We-Wu
Wp = 400 J - 280 J
Wp = 120 J
*
*
*
*
*
*
*
PROBLEMA NB08
La eficiencia de un motor es de 0,70, si
se sabe que puede efectuar un trabajo útil
de 280 joules, ¿qué cantidad de trabajo se
pierde en vencer ciertas resistencias?
Wu : Trabajo Util
We : Trabajo Entregado
Wp : Trabajo Perdido
PROBLEMA N909
Un automóvil que tiene un motor de 9
kwatt de potencia, se mueve en línea recta
sobre un plano horizontal alcanzando una
velocidad máxima de 108 km/h. Determi­
nar la fuerza resultante que ejerce el aíre
sobre el auto.
Despreciar las pérdidas de energía de­
bido al rozamiento.
SOLUCION:
El motor del automóvil realiza trabajo me­
cánico positivo, en virtud a la variación de
su "Energía interna” (combustible). Eltra-
bajo realizado por el aire, es negativo.
Cuando el auto alcanza su velocidad má­
xima se mueve con velocidad constante,
por consiguiente el trabajo neto es igual
a cero. Luego, la fuerza desarrollada por
el motor es igual a la fuerza del aire.
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
#
*
*
*
#
#
*
*
*
*
*
*
*
*
#
*
*
*
*
#
*
*
♦
*
*
P = F . V
9 000 W = F (30 m/s)
F = 300 N
PROBLEMA Ns 10
¿Qué potencia tiene el motor de uno
bomba que eleva 18 000 litros de agua por
cada hora desde un lago hasta una altura
de 60 metros? g = 10 m/s2
SOLUCION:
W _ m g h
t t
En el SI
P =
18000. (10). 60
3600
P = 3 000 W
P = 3 KW
PROBLEMA Ne11
Un obrero levanta cajas de masa 3 kg
cada uno, sobre una plataforma de altura
2 metros respecto del piso a razón de 10
cajas por cada minuto.
Calcular la potencia mecánica desa­
rrollada por ei obrero.
g = 1Q/s2

261. „ W m g h
T = t ~
En el SI P =
30.(10) 2
60
P = 10 watts
CONCEPTO.
La energía es una magnitud física escalar
que sirve de medida general a las distintas
formas de movimiento de la materia que es­
tudian en la física.
1. La energía, es la medida cuantitativa del
movimiento en todas sus formas.
2. La energía, es la medida cuantitativa de
la forma principal de existencia de la ma­
teria (movimiento)
3. En física, para analizar las formas cuali­
tativamente distintas del movimiento y las
interacciones que le corresponden, se
introducen diversas formas de energía:
Energía mecánica, interna o intrínseca
electromagnética, nuclear, atómica, calo­
rífica, .etc.
4 La Energía Mecánica está constituida por
la energía cinética y la Energía Potencial
en sus diversas formas.
5. La energía potencial puede ser: gravita-
torio (campo gravitatorio), eléctrico (cam­
po eléctrico), elástica.
6. En mecánica, la energía se define como
la capacidad que tiene un cuerpo para
realizar trabajo en virtud a su movimiento
mecánico y la posición que ocupa en el
campo gravitatorio, respecto a un sis­
tema de referencia.
ENERGIA CINETICA (Ek)
CONCEPTO. Es aquella magnitud física
escalar que sirve para expresar la medida
cuantitativa del movimiento de los cuerpos o
partículas en virtud a su velocidad, respecto
de un sistema de referencia
#
#
*
*
*
*
*
*
*
*
*
#
*
*
*
*
#
*
m
*
*
*
*
#
$
*
*
*
*
*
*
*
*
*
*
*
*
*■
*
*
*
*
*
n
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Ek = ~ . m . v2
Ek: “Fuerza viva"
¿Z
/
r
“Se da el nombre de ENERGIA CINE­
TICA de un cuerpo a la energía de su
movimiento mecánico".
TEOREMA DÉ LA ENERGIA CINETICA
o de las fuerzas vivas
"La variación de la Energía cinética de un
sistema mecánico es igual a la suma alge­
braica de los trabajos de todas las fuerzas
externas e internas que actúan sobre dicho
sistema"
LWex’ + LWím= AEk (i)
(INICIAL)
L
I
E
.
¿
I
A
1
'l-..'■
I
3 -w M iy v w w O
(hl!MAL)
“La variación de energía cinética del sis­
tema (bloques + resorte) mecánico es
igual a la suma algebraica de los trabajos
de todas las fuerzas internas que actúan
sobre dicho sistema”.

262. 1. A la Energía cinética también se le llama
“fuerza viva".
2. A !a cantidad de movimiento (p = m . v),
también se llama "Fuerza muerta”.
3. La figura muestra un sistema mecánico
compuesto de dos bloques idénticos uni­
dos mediante un resorte de constante de
elasticidad “k" y masa despreciable, apo­
yados sobre un plano horizontal que no
ofrece rozamiento.
4. Inicialmente el resorte se encuentra com­
primido una deformación "x". se man­
tiene en esta posición por la acción de un
hilo.
5. Cuando se corta el hilo, las masas se
liberan y los bloques se alejan con una
velocidad V respecto de su posición de
equilibrio. Las fuerzas externas que ac­
túan sobre el sistema es igual a cero,
entonces las fuerzas que realizan trabajo
son las fuerzas internas, esto quiere decir
las fuerzas elásticas.
6. Si el sistema es indeformable, cuerpo
rígido, el trabajo realizado por las fuerzas
internas es igual a cero.
I Winl = 0 ...(2)
Luego, reemplazando (2) en (1):
6x1 = 2 m-(v f “ v o) - O )
IW
7. El teorema de la energía cinética para un
cuerpo rígido, se puede enunciar del si­
guiente modo:
"El trabajo realizado por la fuerza resul­
tante de un sistema de fuerzas externas
que actúan sobre un cuerpo, es igual a la
variación de la energía cinética que ex­
perimenta el cuerpo"
^(resultante) =1 . m. (vv*) „.(4)
8. La energía cinética de un sistema me­
cánico depende del sistema de referen­
cia que se elija
*
*
#
*
*
*
*
*
♦
*
#
*
*
*
<
5
*
*
*
*
*
*
*
*
#
#
*
*
*
«
X
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
ENERGIA POTENCIAL
CONCEPTO. Se llama, energta poten­
cial, a la parte de la energía de un sistema
mecánico que sólo depende de su configu­
ración, es decir, de la posición mutua de
todas las partículas (puntos materiales) del
sistema y de sus posiciones en el CAMPO
de potencial externo (gravitatorio, eléctrico,
magnético).
Formas de energía potencial:
1 Energía potencial gravitatoria.
2. Energía potencial elástica.
3. Energía potencial de interacción
gravitatoria.
4. Energía potencial eléctrica.
"Energía potencial de interacción gravita­
toria, entre dos cuerpos”
Energía potencial gravitatoria (Ep)
CONCEPTO. Es una magnitud física es­
calar. Se define como la capacidad que tiene
un punto material para realizar trabajo me­
cánico en virtud a su posición dentro del
campo gravitatorio homogéneo "g”, respec­
to de un sistema de referencia.

263. +Eo f- 4-
I
4
9 1
M » t ~ -
_____ I______, 2 .
i
i
!
I
-Ep 4~
-4 t -
1. Su valor es igual al producto de la masa
del cuerpo "m" por la intensidad del
campo gravitatorio "g", por la altura "h",
respecto del sistema de referencia o
Linea de referencia, donde convencio­
nalmente la energía potencial es cero.
Ep = 0
Luego:
rEp = m . g . h
+H
m
3
Q
ÜTiT
Z
-y
Z
Z
l
2. La energía potencial gravitatoria será po­
sitiva cuando el cuerpo o punto material
se encuentra arriba respecto del nivel de
referencia.
3. La energía potencial, será cero, cuando
el cuerpo se encuentra sobre el nivel de
referencia (L.R)
*
*
i
fy
*
*
*
*
*
&
*
*
*
*n
*
♦
*
*
*
*
*
»
#
*
*
#
*
#
*
*
*
*
*
$
*
fc
*
*
*
*
?
*
*
*
*
*
*
*
*
*
*
s
is
*
*
*
*
$
*
*
*
$
S
s
*
*
*
*
*
*
*
#
*
*
*
*
*
*
♦
4. La energía potencial será negativa
cuando el cuerpo se encuentra abajo del
nivel de referencia.
5. La línea de referencia se traza en forma
arbitraria, siempre perpendicular a las
líneas de fuerza del campo gravitatorio.
PRINCIPIO DE CONSERVACION DE LA
ENERGIA MECANICA
"Si la única fuerza que realiza trabajo
sobre un cuerpo o sistema de cuerpos, es su
peso, entonces, la energía mecánica del sis­
tema se conserva en el tiempo"
| EM (inicial) = EM (final) ||
Ejemplo
1. La figura muestra un péndulo, os­
cilando en un plano vertical.
2. Las fuerzas que actúan sobre la ma­
sa pendular es su peso (m , g) y la
tensión en la cuerda T “.
3. La tensión “T“ es una fuerza que en
todo instante es perpendicular al
movimiento, el vector velocidad
tangencial. Por consiguiente la ten­
sión en la cuerda no realiza trabajo.
4. Luego, la única fuerza que realiza
trabajo es el peso del cuerpo, enton­
ces, la energía mecánica del cuerpo
se conserva en el tiempo

264. TEOREMA DEL TRABAJO Y LA
ENERGIA MECANICA
El trabajo realizado por fuerzas diferen­
tes al peso y la fuerza elástica sobre un
cuerpo o sistema, es igual a la variación
de ia energía mecánica
ZW(sin considerar el peso) = EM(final)
- EM(inicial)
La figura muestra un bloque de masa “m*
que resbala sobre un plano inclinado ru­
goso.
2, Las fuerzas que actúan sobre el bloque
son el peso "m . g", la reacción normal al
plano "N” y la fuerza de rozamiento
opuesto al movimiento del bloque T .
3. La reacción normal “N" no realiza trabajo
sobre el bloque, por ser perpendicular al
movimiento
4. La fuerza de rozamiento T realiza trabajo
negativo, por ser opuesto al movimiento
5. La única fuerza diferente al peso que
realiza trabajo sobre el bloque es la fuer­
za de rozamiento.
Luego:
W1= EM(final) - EM(inicial)
6. El trabajo realizado por la fuerza de roza­
miento es igual a variación de la energía
mecánica.
ENERGIA POTENCIAL ELASTICA
CONCEPTO. Es aquella magnitud tísica
escalar que nos expresa aquella energía los
cuerpos elásticos cuando se les deforma
parcialmente al estirarse o comprimirse
longitudinalmente
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
4
>
*
*
*
*
♦
*
*
s
js
*
*
*
*
*
*
*
*
*
n
*
*
*
*
*
*
*
*
*
«i
*
*
s¡*
m
La Energía Potencial Elástica, depende
de la posición (deformación parcial) y de la
interacción de las fuerzas potenciales inter­
nas (fuerza de elasticidad) que dificultan su
deformación.
ELEMENTOS
—
»
1. Elongación (X).
Es el vector posición, indica la posición
del extremo del resorte respecto a la posi­
ción de equilibrio.
(III)
¡ac
P.E
2. Fuerza Deformadora (F).
Es aquella fuerza externa aplicada al re­
sorte, que lo deforma parcialmente a un
cuerpo elástico, su módulo es directa­
mente proporcional a la deformación.
LEY HOOKE
"Si la deformación del resorte es en una
sola dimensión, la fuerza deformadora es
directamente proporciona! a la deforma­
ción del resorte”
F = k . x
k : es la constante de elasticidad oel
resorte.
3. Constante de Elasticidad (k).
La constante de elasticidad del resorte,
caracteriza sus propiedades elásticas.
Su valor depende del material del resorte
y de la forma del resorte.

265. , F 2F 3F .. . . N
k = —= — = — Unidades: --
x 2x 3x m
4. Gráfica : Fuerza externa versus elon­
gación
La energía acumulada por el resorte es
igual al trabajo realizado por la fuerza
externa sobre el resorte.
E p = Area del Triángulo
c E 1 c
E P = - . x . F
pero, la ley de Hooke
Reemplazando (2) en (1)
F s k . x ... (2)
E p = 1 x .( k x)
*
$
*
*
*
*
*
*
*
$
*
*
*
*
i
*
$
*
&
$
#
*
*
♦
*
❖
*
$
*
*
E 1 o
E P = j . K . X 2
P.E
-*------- - I
i F
iVW
S----- -
Ep=r¿ K X
"La energía potencial elástica acu­
mulada por el resorte, es directa­
mente proporcional al cuadrado de
la deformación del resorte".
Cj
”
_______
PROBLEMAS RESUELTOS
PROBLEMA N9 01
Desde el piso se lanza una pelota ver­
ticalmente hacia arriba con una velocidad
“v0", después de chocar cuatro veces con
el piso alcanza una altura máxima de 20
cm. Si en cada choque la pelota pierde la
mitad de la energía que lleva, determinar
"Vo".
SOLUCION
La energía inicial de la pelota es:
1 2
EM = - m v c
Si en cada choque pierde la mitad de la
energía que lleva, después de cuatro
choques su energía mecánica será:
* PROBLEMA Ne 02
1
*
*
*
*
*
#
#
*
*
*
*
$
*
#
*
*
*
*
*
*
*
*
Un móvil de masa "m“ se muevé den­
tro de un aro situado en un plano vertical.
En el punto más alto "A" su velocidad es
de 4 m/s y en el punto más bajo ”B" es de
6 m/s. Si se desprecia la fricción entre la
pista circular y el cuerpo, calcular el radio
del aro.
g = 10 m/s2.

266. Principio de conservación de la energía
mecánica,
EM (A) = EM (B)
1 2
2
En el S.I.:
mg(2R) + - m v A = - m v B
10(2R) + |(1 6 ) = 1(36)
R = 0,5 m
PROBLEMA N903
A una partícula que tiene una energía
cinética inicial de 40J en la posición x = 0,
se le aplica una fuerza resultante que va­
ría como muestra la figura. Sabiendo que
su energía cinética es igual a 400 J en la
posición x = 6 m, calcular la fuerza má­
xima aplicada a la partícula.
SOLUCION.
Del Teorema de la Energía Cinética
"El trabajo realizado por todas las fuer­
zas, es igual a la variación de la Energía
Cinética",
Wrieto = Ek (f) —Ek (i)
*
*
m
*
s¡#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
$
<
N
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
i
*
PROBLEMA Ns 04
Una esfera de peso 20 N se abandona
en "A", sabiendo que no hay rozamiento,
determinar la reacción normal sobre la
esfera cuando pasa por la posición B-
g = 10 m/s2
SOLUCION:
Principio de conservación de la energía
mecánica, entre los puntos A y B.
EM (A) = EM (B) '
mg (2R) = | m v2
v B = 4 g R ....(1)
Dinámica circular en “B"
■(6) Fmáx = 400 J - 40 J
Fmáx = 120 N
En toda gráfica F - x, el área bajo la
curva, es igual al trabajo realizado sobre
la partícula.
*
*
*
*
*
*
fc = tn . ac

267. Fe —m . Be
Reemplazando (1) en (2)
N = 5 mg
J£t
$ (N - mg Cos 60 ) = m
N = 100 newtons
PROBLEMA NB05
Una partícula de masa m = 2 kg es
abandonada en "A". Calcular la reacción
normal cuando pasa por la posición "C",
sobre la superficie de curvatura “2R“.
No hay rozamiento, g = 10 m/s2
SOLUCION.
Principio de conservación de la energía
mecánica
EM (A) = £M (C)
1 2
mg (4R) = mg (R) + - m T
v c = 6g R -...(1)
Dinámica circular en “C"
♦
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
#
*
*
*
*
(2 R)
Reemplazando (1) en (2):
N = |m g (3)
l N = 70 newtons
PROBLEMA NB06
En ia figura se abandona un cubito de
hielo en la posición "A", luego se desliza
sin rozamiento, abandona la rampa en
dirección horizontal, describiendo un mo­
vimiento parabólico. Calcular el despla­
zamiento horizontal "x“ que experimenta
el hielo, donde : H = 4m
h = 2m
SOLUCION:
Principio de conservación de la energía
mecánica, entre los puntos A y B.
EM (A) = EM (B)
mg H = mg h + 1 m v2
v B = 2g(H - h) ... (1)
En el tramo B - C:
En la vertical; eje y.
h = voy . t + | g . t2
h = 0 + 1 . q. t2
.... (2)

268. En el eje horizontal. M.R.U.
x = vb . t .... (3)
Reemplazando (1) y (2) en (3):
Del dato:
x = 4 m
PROBLEMA N®07
Una cadena uniforme de longitud "L",
se abandona sobre una superficie hori­
zontal perfectamente lisa, como indica la
figura. Calcular la velocidad de la cadena
en el instante que el último eslabón se
desprende de la superficie horizontal.
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
&
(L2 - x 2)
1
!
>
L ' g
* La energía potencial gravitatoria es ne­
gativa, cuando al centro de masa (G) se
encuentra debajo de la línea de refe­
rencia (L.R.).
PROBLEMA N®08
Una esferita de masa "m" se deja en
libertad en la posición "A". Hallar la dis­
tancia "d", si el coeficiente de rozamiento
entre B y C es 0,5 (cinético). La tubería es
lisa.
SOLUCION:
El peso de cada parte de la cadena ho­
mogénea es «rectamente proporcional a
la longitud.
W = k x ! . O
Principio de conservación
de la energía mecánica.
EM(¡) = EM(f)
*
é
SOLUCION
La energía mecánica se conserva entre
los puntos A y B.
£M(A) = EM(B) = mgh ..,.(1)
El trabajo realizado por la fuerza de
rozamiento entre B y C, es igual a la
variación de la energía mecánica.
W1= EM(C) - EM(B)
’^ l . v 2
g *
*
- |j (mg)d = - mg h

269. Reemplazando:
d = 2m
PROBLEMA N® 09
La figura muestra un proyectil que se
mueve horizontalmente con la velocidad
"v”y una energía cinética igual a 600 J. El
proyectil atravieza un bloque de madera
de espesor d = 19 cm, de tal modo que la
velocidad del proyectil cuando sale es
"0, 9v". Calcular la fuerza de oposición
promedio que ejerce la madera al paso del
proyectil.
SOLUCION:
Del teorema del trabajo y la energía me­
cánica: El trabajo realizado por fuerzas
diferentes al peso, es igual a la variación
de la energía mecánica del proyectil.
!------------------------------------------------I-
1
¿-----------------------------------------------*
WF = | m ^ v F-v ,]....(1 )
Pero, del dato del problema:
& 4
* ¿ m v2 = 600 J
$ 2
$
J Reemplazando en (1)
*
*
*
*
- F . d. = - | m ( 0 , 19 v2)
F (0,19m) = (0,19) (600 J)
F = 600 N
PROBLEMA Nfi 10
Desprecie la pérdida de energía por roza-
* En el sistema mecánico mostrado, ha­
* llar la mínima velocidad “v0" que debe
* tener el carrito en la posición "A" de modo
* que pueda rizar el rizo completamente.
* _
* miento.
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
+
*
♦
*
*
*
1
»
*N
*
*
*
*
*
*
* SOLUCION:
jjl
* Cuando el carrito pasa por el límite supe­
* rior de su trayectoria, la reacción normal
* de la superficie sobre las ruedas es igual
* a cero, N = 0, de la condición del proble­
* ma, su energía cinética debe ser mínima.
*
De la segunda ley de Newton, en la
* posición "B". Dinámica circular.

270. I F (radiales) = m . ac , entonces:
v2
m • g = m . —
Luego:
v2 = g . R
-.(1 )
.... (2)
Por principio de conservaron de la ener­
gía mecánica.
Ep (A )+ E k(A) = Ep (B) + Ek (B)
1 ? 1 p
0 + — m . vr0 = m . g . (4R)+ —. m . r
.... (3)
Reemplazando (2) en (3)'
l . v 20 = 4 g . R + l . g . R
Despejando tenemos que:
v0 = 3 . Vg. R
PROBLEMA N® 11
La figura (1) muestra un péndulo de
masa "m”y longitud “L", que se abandona
en la posición “A", de tal modo que la
cuerda forma un ángulo " 6" respecto a la
vertical. Hallar la tensión “T" en la cuerda
cuando el péndulo pasa por su posición
de equilibrio, esto quiere decir "Cuando
adquiere su máxima velocidad”.
Por principiode conservación de la ener­
gía mecánica, entre A y B.
Ep(A) + Ek(A) = Ep(B) + Ek(B)
m .g h + 0 = 0 + “ . m . v 2
Luego: ^ ^ . g . h ....(1)
Cálculo de la altura *h‘,en la figura (2).
h = L(1 - Cos 0) ....(2)
En p
8", de la segunda ley de Newton en
dinámica circular.
X F (radiases) = m . ac : entonces:
.... (3)
Reemplazando (1) en (3):
t v 2
T - mg = m . —
t 2 . q . h
T - m.g = m . — “ —
Reemplazando (2) en (4):
T = m.g ( 3 - 2 Cos 6)
CASOS PARTICULARES
1) Cuando 6 = 90°, entonces:
Cos 0 = 0 , en (5):
T = 3 m .g
2) Cuando G= 60°, entonces.
Cos G= —, en (5):
T = 2 m , g
.... (4)
- - (5)

271. La figura (1) muestra un péndulo de
masa "m“ y longitud ”L". Determinar la
mínima velocidad "v0“que se debe aplicar
al cuerpo en su posición de equilibrio, tal
que, puede describir por lo menos una
vuelta en el plano vertical.
r —
/
t
i
i
! °
i
V
«
— ' A
N
/
1
/
L.R
V ... J
v0 = n
í5 . g . L
“Velocidad mínima en la posición de equi­
librio"
SOLUCION:
Analizando al cuerpo en la posición
indicada por la figura (2):
De la segunda ley de Newton, en
dinámica circular.
£ F (radiales) = m.ac. entonces
v2
(mg + T) = m. — ....(1)
Pero de la condición del problema el
cuerpo pasa con su mínima energía ciné­
tica, esto quiere decir que la tensión T * en la
cuerda debe ser mínima en valor, por con­
siguiente,
T = 0 ....(2)
Reemplazando (2) en (1):
v = g. L .... (3)
m .q
PROBLEMA N®13
En la figura (1), se suelta el rodillo
(cilindro) de masa "M” unido a un resorte,
desde una posición donde el resorte'de
constante de elasticidad “k" no está de­
formado (x = 0) y el cilindro rueda sin
resbalar sobre el plano inclinado. Hallar
la máxima deformación del resorte. El
plano forma un ángulo " 6 " respecto a ia
horizontal.
Sugerencia: La tuerza de rozamiento por
rodadura NO realiza trabajo
sobre el rodillo.
Por principio de conservación de la ener -
gía mecánica.
Ep (1) + Ek(1) = Ep (2) + Ek (2)
0 + | m . v 2o = m.g.(2L) + | m . v 2 ... (4)
Reemplazando (3) en (4):
| . v c = 2 g . L . + | (g.L)
*
¥
*
*
*
*
*
$
SOLUCION:
Cuando el resorte alcanza la máxima de­
formación (en la zona elastica), la veloci­
dad del rodillo es igual a cero, en ese
instante.
De la figura (2);
x = deformación máxima del resorte.
h = x . S e n 6 -— (1)

272. Por principio de conservación de la ener­
gía mecánica. Debe tenerse en cuenta
que el rodillo no resbala, por lo tanto, no
hay fuerza de rozamiento por desliza­
miento.
Ep (1) + Ek(1) = Ep (2) + Ek (2)
m.g.h. + 0 = — k . x2 + 0 .... (2)
Reemplazando (1) en (2):
m
Luego
1 2
m g . x . Sen G= —. k . x
X
(m
axim
o)=
2m . g .Sen 6
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
.R *
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
$
*
*
♦
PROBLEMA N9 14
Una bola colgada de un hilo, se ba­
lancea en el plano vertical de modo que
su aceleración en las posiciones superior
e inferior (límite) son de iguales módulos.
Encontrar el ángulo" 6 ” de inclinación en
$
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
«
*
*
*
*
#
*
*
i*
T
T
i
!
t
-A —
Jmg
De la condición del problema, la veloci­
dad en la posición "A" es igual a cero.
Por principio de conservación de la ener­
gía mecánica.
Ep(1)+ Ek(1) = Ep(2) + Ek(2).... (1)
donde:
vA=0, h = L.(1-CosG) .. .(2)
En(1): mgh + 0 = 0 + l . m . v 2e -.(3)
Reemplazando (2) en (3):
Vg = 2 g.L.(1- Cos G) ....(4)
La aceleración total en “A" es puramente
tangencial, no tiene la componente cen­
trípeta (vA = 0)
—
£F(Tangen) m . g . Sen 6
m
= g . Sen 6
m
.... (5)
La aceleración total en "B“ es puramente
centrípeta, no tiene la componente tan­
gencial, todas las fuerzas son radiales
IF (radiales) v2
aB = ----------- - = - . . . . (6)
Reemplazando (4) en (6):
2 g.L.(1- Cos 6)
aB =2.g (1 -C o s 6 )
....(7)
De la condición, igualamos las ecuacio­
nes (5) y (7)

273. Sen G= 2 - 2 Cos 0 , entonces:
Sen G+2 Cos 6 = 2 .... (8)
Resolviendo la ecuación (8)
6 = 53®
PROBLEMA N9 15
La figura muestra un resorte AB de
constante de elasticidad K = 4 N / m y está
unido a un collar en "B”de 99 kg de masa,
el cual se mueve libremente a lo largo de
la varilla horizontal La longitud natural
del resorte es 5m (X = 0). Si el collar se
deja en libertad desde el reposo en la
posición mostrada en la figura, determi­
nar la velocidad máxima que alcanza el
collar.
r
C B
------ --------1
7m
A
V J
SOLUCION
Cálculo de la deformación del resorte en
las posiciones inicial (B) y final (c).
x 0 = lo n g itu d n a tu ra l d e l re s o rte = 5 m
x b = d e fo rm a c ió n in ic ia l = 2 0 m
x c = d e fo rm a c ió n fin a l = 2 m
Consideramos el Sistema (masa + re­
sorte):
La energía cinética del collar será má­
xima, cuando la energía potencial elás­
tica sea mínima, por consiguiente pasa
por su posición de equilibrio en “C".
Principio de Conservación de la Energía
Mecánica entre B y C.
Tomando como línea de referencia a la
varilla:
Ek(B) + EP(B) = Ek(C) + EP(C)
Reemplazando:
V = 4 m/s
PROBLEMA N9 16
Un carrito de masa “m" se abandona
en la posición (A). Determinar la altura
mínima "H", tal que el móvil puede pasar
por la posición 1
1
B“. Desprecie el roza­
miento Radio del rizo “R".
SOLUCION
Analizando las fuerzas que actúan sobre
el móvil, en "B”

274. Cuando el móvil pasa con su mínima
velocidad en “B", la reacción normal so­
bre las llantas tiende a cero.
N = 0
Dinámica circular:
fe = m . ac
V2
mg = m . - -
,2
V = g . R .... (1)
Principio de conservación de la Energía
Mecánica.
EM (A) = EM(B)
Ep (A) + Ek(A) = EP(B) + Ek(B)
mg H + 0 = mg(2R) t ^ m V 2
de (1): mg H = mg (2R) + ■- m V2
Luego:
H = (2,5) R
PROBLEMA N® 17
En la figura mostrada se abandona un
bloque de masa 1 Kg en la posición (A)
desplazándose luego por acción de su
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
#
*
*
m
*
*
*
#
*
«
r
«
*
*
*
*
*
*
El trabajo realizado por la fuerza de roza­
miento, es igual a la variación de la ener­
gía mecánica que experimenta el bloque:
Wf= EM(B) - EM(A)
wf = EP(B) + Ek(B) - Ep(A) - Ek(A)
Wf =mg (0,4) t ^ m V 2 - mg(1,2) - 0
Wf = mg (-0,8) +1 m V2
Reemplazando:
W* = -3,5J
El signo (-), se debe a que la fuerza de
rozamiento se opone al movimiento del
bloque.
PROBLEMA NB18
Un bloque parte de "A" sin velocidad
inicial y se desliza por el camino mos­
trado. ¿Qué distancia "d" recorre en la
parte plana, si sólo existe rozamiento en
la parte horizontal?. El coeficiente de ro­
zamiento cinético es 0,5:
' p
Considere: g =10 m/s

275. Principio de la Energía Mecánica:
EM(A) =EM(B) = mg H ....(1)
Teorema del trabajo y la Energía
Mecánica:
El trabajo realizado por la tuerza de
rozamiento es igual a la variación de la
energía mecánica entre B y C.
Wf =EM (C) - EM (B) ....(2)
mg
Reemplazando en (2):
- fk d = 0 - m g h
- u . (mg) d = - mg H
Reemplazando datos:
d = 5 m
PROBLEMA Ns 19
Un bloque parte de "A " sin velocidad
inicial y se desliza por el camino mostrado
en la figura (R = 1 m). Hasta que altura (B)
sube el bloque, si sólo hay rozamiento en
la parte plana. El coeficiente de rozamien­
to cinético es 0,4.
(A)
(B)
SOLUCION:
Teorema del trabajo y la Energía Me­
cánica
El trabajo realizado por la fuerza de roza­
miento es igual a la variación de la ener­
gía mecánica, que experimenta el blo­
que:
f -- ■
■
■ ■ ■.........
mg
n ■ fk
(A)#---------------------------- L
V - . .. -
ím
------------------------ « IB J
_ J
Wf = EM (B) - EM (A)
Wf = EP(B) + Ek(B) - Ep (A) - Ek(A)
Wf = mg h + (0) - mg R - (0)
-fk d = - mg (R - h)
u (mg) d = mg (R - h)
Luego:
h = R - u d
h = 1 —(0,4) (2)
h = 0,2m
*
#
♦
*
*
*
*
*
*
*
fy
*
+
*
fy
fy
*
*
*
*
#
#
fy
*
fy
*
*
*
*
m
*
*
*
*
*
fy
*
*
*
*
m
*
*
*
*
fy
*
*
*
*
*
*
*
#
♦
*
*
*
*
*
«
#
*
*
*
*
*
*
*
*
*
fy
fy
fy
*
*

276. PROBLEMA N® 20 *
•
Un canal se compone de dos cuadrantes *
con centros Oí y O
2 respectivamente, de ra- #
dios de curvatura igualesa "R". Se abandona £
una esferita en la posición " A" a una altura *
h= R/5 de la horizontal que pasa porel punto J
de inflexión de la trayectoria curvilínea.
Despreciando todo tipo de rozamien- |
to, determinar en qué posición del según- *
do tramo, definido por el ángulo "e", la *
1) Analizando a la esferita en la posi­
ción (B) en que abandona la super­
ficie, si deja de hacer contacto, en­
tonces la reacción normal es igual a
cero, N = 0 ...(1)
2) De la segunda Ley de Newton (Di­
námica circular) en "B".
F (radiales) = m ac, entonces
2
mg. Cos 0 = m .V B
R
Luego:
V b= R . g . Cos 6 ...(2)
3) Por principio de conservación de la
energía mecánica entre los puntos
A y B, respecto a la línea de refe­
rencia ( L . R ).
Ep(A) + E«(A) = Ep(B) + Ek(B)
m.g(h+y)+0 =0+|.m . V * ...(3)
4) De la tigura (2) se deduce que
y = R - R . Cos G ...(4)
Reemplazando (2) y (4) en (3):
m.g | y + R - R Cos G
m (R g . Cos G)
0 4
—- Cos G - Cos 6
o 2
Cos 0 = 1
5
Luego:
ir = 3 7 °
PROBLEMA Ne 21
La figura (1) muestra una estructura en
forma de "T" de dimensiones "L“ y de
peso despreciable en sus extremos se
encuentran fijos dos esferas de pesos
“mg“y "6mg". Al romperse el hilo, ¿Cuál
es la máxima energía cinética que adquie­
re el sistema?. La estructura puede girar
libremente alrededor de la rótula, "0".

277. Hilo
X
V.
SOLUCION:
1) Por principio de conservación de la
energía mecánica.
Ep(1) + Ek(1) = Ep(2)+Ek(2)...(1)
2) Tomamos como línea de referencia
la horizontal que pasa por la rótula.
En (1):
-6mg.L + 0 = -mg(2L Cos G)
-6mg(Sen 0 + Cos 0). L + Ek (2).
Ek(2) = Energía cinética del sistema
en la posición (2)
Ek(2)= m.g.L(2Cos0 + 6SenG + 6Cos
0 - 6 )
Ek(2) = 2m.g.L(3Sen 9 + 4Cos G- 3)
(3)
3) Analizando la ecuación (3). La ener
gía cinética será máxima, cuando:
M = 3 Sen G+ 4 Cos 0 . . . (4)
De la propiedad trigonométrica:
i *
*
' *
* ¡i*
4i
*
*
*
*
*
*
*
*
*
*
*
*
*
>
)*
*
*
*
*
*
*
*
*
*
3Sen 0 + 4Cos G< y¡32+ 42
Luego El valor máximo de "M” es 5:
M (máximo) = 5 .... (5)
Reemplazando (5) en (3):
Ek(2)=2 m.g.L. ( 5 -3 ) = 4m.g.L
.... (6)
Ek(2) = 4. m. g. L
4) De otro modo. La ecuación (4) mul­
tiplicamos por "5" y dividimos entre
"5", hacemos este artificio para ob­
tener una suma de ángulo.
M = 5 ^ | s e n G + | c o s G j =
5(Cos 53°. Sen 0 +Sen53°.Cos 0)
M = 5 . Sen (0+53°) ....(7)
M será máximo en valor, cuando:
Sen (0 + 53°) = 1
Luego: M (máximo) = 5 y
O+ 53° = 90°
G= 37°
Ges el ángulo que define la posición
de la estructura cuando la energía
cinética del sistema es máximo.
5) Otro criterio para resolver este pro­
blema es cuando un cuerpo o sis­
tema de cuerpos es dejado en liber­
tad, adquiere su máxima energía ci­
nética (velocidad máxima) cuando
pasa por su posición de equilibrio,
esto quiere decir que su energía po­
tencial es mínima en ese instante.
Luego: G=375,define la posición
de equilibrio del
sistema.
Nota : Revisar el prob. en el capítulo de
Estática

278. *
«
*
*
fc
fc
«
*
fc
*
fc
*
PROBLEMA N9 22
La figura (1) muestra un sistema me*
cársico en equilibrio y el resorte de cons­
tante de elasticidad k = 20 N/m, con su
longitud natural de 5m, unido en sus ex­
tremos a dos esferas de masas, m = 2 kg.
SI ia cuerda se corta en el punto "A",
determinar ia máxima deformación del re­
sorte. La longitud de la cuerda es L = 5m.
g = 10m/s2
* v_
*
*
fc
fc
*
fc
fc
fc
*
*
#
*
fc
«
fc
*
*
fc
fc
f-Mr L.R
fc
fc
fc
fc
1) De la figura (2), la deformación
resorte: ~ = 5 . (1 - Sen 0) .... (1)
2) Cuando el resorte alcanza la má­
xima deformación "X”, la energía
cinética del sistema es igual a cero,
esto quiere decir que las masas tie­
nen velocidad igual a cero
3) Por principio de conservación de la
energfa mecánica
Ep(A) + Ek(A) = Ep(B) + Ek(B)
2 mg.(5Cos 6) +0 =—.k. x2 +0
10 m.g.Cos 6 =— . k. x2 .... (2)
4) Reemplazando (1) en (2):
10 m . g . Cos G= ^ k 100.
2
(1 - Sen 6)2 ....(3)
Pero: m = 2 kg., K = 20 N/m ,
g = 10 m/s2
5) Reemplazando en (3). tenemos:
Cos G= 5 (1 - Sen 6)2 .... (4)
6) Resolviendo la ecuación tenemos:
0 = 37° ....(5)
Reemplazando (5) en (1):

279. x (máximo) = 4 m
PROBLEMA N« 23
Un bloque de masa 15 kg está so­
metido a la acción de una sola fuerza en
dirección horizontal y su módulo varíe
con la posición "x" tal como Indica el
gráfico. Si el bloque parte del reposo
(V = 0) en la posición x = 0, ¿Cuál será su
velocidad en x = 25 m?
*
*
*
*
*
*
*
*
*
«
*
*
*
#
■
#
*
*
*
*
*
*i
*
m
*
*
*
*
4
*
*
1) Teorema de la Energía cinética "El
trabajo neto es igual a la variación
de su energía cinética"
VW (5+21°> (25) = | (15) (25) J
2) W
total= rT(v<
=
“vo)
Pero V0 = 0
1 1 2
^ x 15x25 = ir . 15 x V Í
2 2 F
V f = 5 m/s
Luego:
PROBLEMA N224
Sabiendo que el sistema mostrado en
la figura se cumple que: M = 2 m. Hallar
el máximo valor de " G ”, que define la
posición desde donde se debe soltar ”m",
con la condición de que el bloque "M" no
se despegue del piso.
SOLUCION:
<
ü
*
*
*
1) El bloque deiará de hacer contacto
con el piso (Normal = 0), cuando la
tensión en la cuerda es igual al peso
del bloque, T = Mg .. (1 )
2) La tensión máxima en la cuerda se
obtiene cuando "m" pasa por la posi­
ción más baja de la trayectoria.

280. *
. / t e
L .-''
A
7 ~
I (l-Cos6) X
J _________
— - g *
T=Mg
V
mg
3) Cálculo de la velocidad “v“.
Ep{A) + Ek(A) = Ep(B) + Ek(B)
1 2
mghA + 0 = 0 + —m . V B
V j = 2g.L(1 - C o s e ) ...(2)
4) Dinámica circular en "B ”
Fcp = m. ac
2
Mg - mg = m
g (M-m) = m . 2g (1 - Cos 6)
g . m = 2 mg . (1 - Cos 6)
Cos 6 =
1 = 2 - 2 Cos e
1
e = 60°
PROBLEMA Ne 25
Un bloque que parte del reposo en A
resbala por una rampa y pierde entre A y
B el 10% de su energía mecánica, por
efecto del rozamiento. Si en el punto de
máxima altura su velocidad es vx= 6 m/s.
Calcular la altura máxima “H".
&
*
*
*
*
*
*
*
*
*
*
*
*
*
*
if-
*
*
*
*
*
*
*
*
*
*
*
£
*
*
*
*
*
*
*
*
«If
*
<
¥
*
*
SOLUCION:
90% EM(A) = EM(C)
O
0.9 mgh = mgH + —m. v x
0,9 x 10 m/s2 x 10m = 10H+1(62)
90= 10H + 18
H = 7,2m
PROBLEMA Ne 26
Un péndulo formado por una esferita
de peso 8N y una cuerda de longitud "L“
de peso despreciable, se abandona
cuando el hilo forma un ángulo de 60°
con la vertical.
El clavo colocado horizontalmente en
"A" obliga al péndulo a desviarse, como
muestra la figura, determinar la tensión en
la cuerda cuando forma nuevamente 60°
con la vertical.

281. “
' i
i
•
SOLUCION:
1) Por P.C.E.M.:
EM (A) = EM (B)
L L 1 2
mg ^ = m9 4 + 2 m
2) Dinámica circular en "B"
c y2
Fc = m. ac = m —
T 1 flL
T - m g -
~2
t 3 _ 3 ...
T = - m g = - W
T = 12 N
Un bloque de masa m = 4kg se aban­
dona sobre un plano inclinado 30° res­
pecto a la horizontal perfectamente liso.
En la parte inferior del plano se en­
cuentra un resorte fijo de constante
elástica K = 2 000 N/m. El bloque se
detiene luego de recorrer una distancia de
2m. Hallar la máxima deformación del
resorte.
g =10 m/s2
SOLUCION:
Principio de conservación de la energía
mecánica.
EM (A) = EM (B)
mgh = ^ K. x2
En el S.l :
(4) (10) (1)= 1 (2 000) x2
x = 0,2m

282. La figura muestra un resorte CA de
constante de elasticidad K = 81 N/m y está
unido en A a un collarín de masa m = 0,75
kg el cual se mueve libremente a lo largo
de una varilla horizontal. La longitud
natural del resorte es 1o = 1,0 m. Si el
collarín se deja en libertad desde el re­
poso en la posición mostrada en la figura,
determinar la velocidad que alcanza el
collar en la posición B.
B A
*
*
*
*
#
#
*
*
*
*
*
0,9m
SOLUCION:
1) Longitud natural = 10 = 1m
x a = 1 , 0 m
X B = 0,5m
2) Principio de conservación de la
energía mecánica.
EM(A) = EM(B)
0,9m 1,6m
PROBLEMA N* 29
El móvil que muestra la figura está
inicialmente en reposo y contiene en su
interior un bloque de masa ’ m" unido a
un resorte no deformado (x = 0), de cons­
tante de elasticidad "k". Si de pronto el
móvil adquiere una aceleración constante
“a", hallar la máxima deformación que
experimenta el resorte. El coeficiente de
rozamiento cinético entre el bloque y la
plataforma es " u ".
1, 2 1 , 2 1 2
2 k x A= 2 k ' x B+ 2 v B
2 81 N/m
v B ='
Hm
Vb = 9 m/s
SOLUCION:
1) Elegimos un sistema de referencia
No inercial, sobre la plataforma, pa­
ra t = 0, la veloctdac! inicial es cero
y la deformación x = 0.

283. 2) Las fuerzas externas para nuestro
observador es: F, = -m.a. peso,
fuerza elástica, fuerza de rozamien­
to.
*
3) Teorema del Trabajo y !a energía
mecánica
W(Fuerzas NO conservativas) =
EM (final) - EM(inicial)
WF'- W ,r = Ep (Q) + Ek(Q) -
EP (P)-E k(P )
1 2
m .a.x-u.N .x = - k .x - 0 ,
Además: N = m.g
(ma - u. m.g) x = ~ . k . x2
2m . .
X = _K“ (a “ u - 9)
PROBLEMA Ns 30
Un cuerpo de masa m = 1 kg., se mueve
en el plano x - y, según las graficas (x - 1)
e (Vy - 1). Calcule la Fuerza resultante que
debe estar aplicada sobre esta masa du­
rante su movimiento.
Para t = 5 segundos
«
i»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
m
*

284. El movimiento en el eje x es con
velocidad constante, por con­
siguiente la aceleración en este eje
es cero.
a* = 0 F* = 0
2) El movimiento en el eje Y es retar­
dado uniformemente.
p
ay = -1 m/s
*
*
*
#
*
*
*
*
*
*
*
*
2da Ley de Newton
Fy = m ay
Fy = 1 kg . (-1 m/s2) o-1 N
Para : t = 5 segundos
F (t = 5) = (O; —
1) N
9

285. CANTIDAD DE MOVIMIENTO
CONCEPTO.
Es una magnitud física vectorial, que sir­
ve para expresar ia medida del movimiento
mecánico de traslación de los cuerpos o par­
tículas. La cantidad de movimiento o mo-
mentum lineal se determina mediante el pro­
ducto de la masa del cuerpo por su velocidad
instantánea, por consiguiente el momentum
y la velocidad tienen la misma dirección y
sentido.
- = ^ P V -
P = m . V
Se mide en: N.s.
IMPULSO
Es aquella magnitud física vectorial que
nos expresa la acción casi instantánea que
realiza una fuerza externa sobre un cuerpo;
modificándole su momentum lineal. Se de­
fine como el producto de la fuerza resultante,
por el intervalo de tiempo relativamente pe­
queño. El impulso y la fuerza tienen la misma
dirección y sentido.
I = F r . At
♦
*
&
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
Ü
En la figura mostrada el cuerpo de masa
"m" de forma esférica viene con una veloci­
dad "V i” y luego de la interacción rebota con
una velocidad “V2“,
De la 2da. Ley de Newton
—
> —
>
F r = m . a
F r = m .
(V2 - V 1)
A t
F r At = m V 2 —m V i
—
> —
> —
>
I = P 2 - P i
I = AP
Se mide en : N. s
“El impulso, es igual a la variación del
momentum lineal".

286. Todo cuerpo modificará definitivamente
su cantidad de movimiento, cuando sobre él
se manifiesta una fuerza resultante que pue­
de actuar en un intervalo de tiempo. Cuando
el intervalo de tiempo es relativamente pe­
queño casi instantáneo, se dice que el cuer­
po ha.recibido un impulso y cuando la fuerza
actúa durante un intervalo de tiempo consi­
derable, entonces la fuerza estará realizando
un ! abajo sobre el cuerpo modificando su
en írgía cinética
SISTEMA FISICO
Es aquel conjunto de partículas o cuer­
pos considerados en estudio, elegidos en
forma arbitraria. La figura muestra un sis­
tema físico Si, limitando por una línea curva
cerrada. Las demás partículas pertenecen
al sistema S2.
€>
mc
FUERZA EXTERNA
Es aquella fuerza que actúa sobre el sis­
tema, debido a la interacción de un compo­
nente del sistema con partículas externa al
sistema. En la figura, F43 es una fuerza
externa al sistema físico Si.
FUERZA INTERNA
Es aquella fuerza debido a la interacción
de las partículas considerados dentro del
sistema físico. En la figura las masas mi; m2
y ms pertenecen al sistema Si, la interacción
entre ellas constituyen las fuerzas internas al
sistema. La sumatoria de las fuerzas inter­
nas siempre es igual a cero
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*1
*
♦
*
*
*
¡i
*
*
*
*
*
*
*
*
*
*
♦
*
*
«
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
£F(j¡itemas) = 0
SISTEMA AISLADO (S.A.)
Es aquel sistema físico, cuya resultante
de fuerzas externas es igual a cero.
X
F(extem
as)=0
Principio de Conservación del Momen-
tum Lineal
Es una Ley Universal de gran trascen­
dencia y aplicación en ia mecánica. Se pue­
de expresar de los siguientes modos:
I) Si el impulso sobre una partícula o siste­
ma físico (sistema de partículas) es igual
a cero, la cantidad de movimiento se
conserva en el tiempo.
I = F r . A t
I = A P = (P2 - P i )
-(1)
.... (2)
Si la fuerza resultante es igual a cero,
entonces el impulso es también igual a
cero.
De (1) y (2):
—
>
F r = 0 - >
Luego:
I = 0
Pin
icia
l—
P
fin
al
II) En todo sistema físico aislado, la canti­
dad de movimiento se conserva en el
tiempo.
(INICIAL)

287. .«<o—
"3
«f O -
V
-------------------------- 'Ü _______
(FINAL)
E
P
inicial—E
Plinal
La cantidad de movimiento es una mag­
nitud física vectorial, por consiguiente po­
demos escribir en función de dos com­
ponentes rectangulares.
E
P
irticial(x
)= E
Pfinal(x
)
£Pin
icia
l(y
)—ZPfin
a
l(y
)
En el movimiento parabólico, se conser­
va la cantidad de movimiento de la par­
tícula en el eje (x), la fuerza resultante en
el eje "x" es igual a cero. En cambio en
el eje "y" la fuerza resultante es igual al
peso “mg", no existe conservación del
momentum lineal en el eje “y*.
G
Vc.M. =
mi.Vi + m2-V2 + m3.V3
mi + m2 + m3
*
*
*
*
o
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
*
*
*
*
*
*
*
*
e
*
*
*
*
*
*
*
*
*
*
»
*
*
*
*
VELOCIDAD DEL CENTRO DE MASA
Consideramos un sistema físico com­
puesto de partículas de masas m i, m2, m3 ...,
y velocidades Vi, V2, ..V3, respecto a un
sistema inercial de referencia.
El centro de masa (C.M.) es aquel punto
donde se considera concentrada la masa del
sistema y donde actúa la fuerza resultante.
La velocidad del C.M., se define del si­
guiente modo:
*
*
*
*
*
*
♦
*
*
*
*
*
*
#
*
*
*
*
ii
«fO-
SISTEMA REAL
• O -
C.M
C.M
(mj * + m^)
SISTEMA EQUIVALENTE
Sea M la masa del sistema físico:
M = mi + rr»
2 + ms
La cantidad de movimiento del sistema
será:
Psistema = M . Vcm
Sí el sistema físico está aislado (S.A.)
sabemos por principio de conservación del
momentum, que "P‘ permanece constante
en el tiempo. Por consiguiente.
“El centro de masa de un sistema aislado
se mueve con velocidad constante (M.R.U.)
respecto a un sistema de referencia inercial"
Teorema de la Cantidad de Movimiento
Consideramos un sistema físico de 3 par­
tículas, de masas mi, rri2 y m3, que se mue­
ven con velocidades Vi, V2 y V3 respecto de
un sistema de referencia inercial

288. *
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Psist= m. V i + rr«2.V2 + m3.V3 ....(1)
Realizemos el siguiente artificio:
0 = (mi+m2)V3 - miV3 - m2V3. . .(2)
Sumando las Ec. (1) y (2):
— > —> —> —» —>
Psist ~ m i(Vi - V3) + m2(V2 - V3)
—
>
+ (mi + m2 + m3)Vs
Velocidad relativa:
V i - V3 = V 13

289. PROBLEMAS RESUELTOS Y PROPUESTOS DE :
CANTIDAD DE MOVIMIENTOS
Psist = rni.Via + IT12. V 23 + M.V3
Generalizando, para un sistema de "n"
partículas.
—
» n- 1 > I
Psist = 2 . ITI¡ ■V,n + M Vn 1
I
M = mi + m2 + . . . +mn
La cantidad de movimiento del sistema,
es igual al momentum de (n - 1 ) partículas
respecto de n-ésimo cuerpo, más la masa del
sistema por la velocidad de la partícula n-
ésima.
PROBLEMA Ns 01
Según Albert Einstein la equivalencia
entre la energía “E” y la masa “m" de una
partícula es : E = me2 donde "C ” es la
velocidad de la luz. Un fotón tiene una
energía E = h. f, donde “h" es la constante
de Planck y "f" la frecuencia de la luz.
Determinar el momentum del fotón.
SOLUCION:
E! fotón se mueve con una velocidad
igual a "C".
Donde: me2 = E = h f'
W V 1-
m = h f/C2 ...(1)
El momentum lineal del fotón:
*
*
*
*
*
*
*
*
*
*
*■
*
*
*
*
*
*
*
m
*
*
*
*
*
♦
*
*
*
*
*
*
*
p = m C
Reemplazando (1) en (2):
P = -
h f
PROBLEMA Ns 02
Un hombre de masa “m" se mueve
sobre una tabla de masa M (M = 4m).
Sabiendo que la tabla puede moverse li­
bremente sin rozamiento sobre el plano
horizontal, determinar el desplazamiento
del hombre respecto de la tierra cuando
se mueve de extremo a extremo de la
tabla de longitud 5 metros.
SOLUCION:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Consideramos el sistema (Tabla + hom­
bre).
Conservación del momentum lineal
P(inicial) = F
*(final)
0 = mVn - M V t
M Vt = m Vh ....(1)

290. Donde "V" es la velocidad media que se
define como la relación del desplaza­
miento entre el tiempo (t)
En (1):
árn x (5 - x)
4 m . y = m — j—
x = 1,0 m
El hombre se desplaza respecto de la
tierra, 4m.
La tabla retrocede respecto del piso x,
x = 1,0 m
PROBLEMA Ns 03
Un satélite se mueve "horizontalmen­
te" a una velocidad de 8 km/s con res­
pecto a ia tierra. Dejamos caer vertical­
mente una carga de 50 kg lanzándola hori­
zontalmente del satélite. Calcular la velo­
cidad del satélite después del lanzamien­
to de la carga, si la masa total (incluyendo
la carga) es de 450 kg.
¿Cuál es la velocidad de la carga, con
respecto a ta tierra inmediatamente des­
pués del lanzamiento?
SOLUCION:
8Km/s
450Kg
(ANTES)
‘JüOKg
f ' F V i .
Respecto de un observador ubicado en
la tierra
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
4
>
*
*
*
*
*
*
*
*
ü
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
K
>
*
*
*
*
*
*
*
*
*
4
>
+
*
*
*
*
Conservación del momentum lineal:
—
» —
*
Px(an
tes) = Px(después)
M Vi = m V + (M - m)U
450 (8) = 50(0) + (400)U
U = 9 km/s
La velocidad de la carga, respecto de la
tierra, inmediatamente despues del lan­
zamiento es igual a cero
PROBLEMA Nfi 04
En la proa y en la popa de un bote de
masa M = 70 kg, están sentados a una
distancia L = 8m una de otra dos personas
A (80 kg) y B (50 kg) como indica la figura.
Despreciando la resistencia del agua, de­
terminar en que sentido y distancia se
desplazará el bote si las personas se cam­
bian de asiento.
SOLUCION:
%
D
á
( l-x ;
4 :’f
(L+X.)
Consideramos el sistem (A+B+ bote):
Conservación del momentum lineal:
P(in
icia
l)—
P(fin
a
l)
0 = M Vb + rriA-VA - ms-Ve
_ x (L + x) ( L - x )
0 =M ^ m A . v t ’ - rriB
(rriA - me). L
x=---------- 1
----
(itia + rriB + M)
Reemplazando datos

291. x = 1,2m
El bote se desplaza hacia la derecha,
debido a que la masa de A es mayor que
B.
Si rrA = rnB —
> x = 0
Si, mA < mB el bote se desplaza hacia la
izquierda.
PROBLEMA N« 05
Un hombre de masa "m" está parado
sobre un carrito de masa ”M" (M = 9 m)
que se mueve con una velocidad V = 15
m/s. SI ei hombre comienza a moverse
con una velocidad u = 5 m/s, respecto dei
carrito en la misma dirección y sentido,
hallarla pueva velocidad del carro que se
mueve libre de rozamiento.
(ANTES)
Li¡£* m
M V
n i
.....
DESPUES) H r r
'«fQ
SOLUCION:
Conservación del Momentum Lineal:
—
> —
>
P(antes) = P(después)
(M + m) V = m(U + u) + M U
Reemplazando datos:
10 m(15) = m(U + 5) + 9m U
150 = U + 5 + 9U
Luego.
U = 14,5 m/s
*
*
*
*
*
*
Un motociclista de masa total "m'' se
encuentra inicialmente en reposo sobre
una tabla áspera de masa "M" (M = 9 m) y
se encuentra apoyado sobre una superfi­
cie horizontal perfectamente lisa. Si el
motociclista comienza a moverse y el ve­
locímetro de éste marca 20 km/h, hrllar la
velocidad de la tabla respecto de la tierra
SOLUCION:
*
*
*
*
*
#
*
*
*
*
*
J¡5
*
*
*
*
*
*
*
O
s
*
*
*
#s
*
*
*
*
*
*
%
4»
*
*
>
1
9
$
*
*
*
*
*
*
El velocímetro marca la velocidad rela­
tiva del motociclista respecto de la tabla.
Teorema de la cantidad de Movimiento.
P (inicial) = P
(fin
al)
0 = mi.Vi/2 + (mi + rr>2) V2
0 = m. Vif2 + (m + M)(—
U)
m
U =
(m + M)
. V1/2
Del dato
U = 2 km/h
El momentum lineal del sistema físico
(m + M) se conserva en el tiempo
PROBLEMA N907
El sistema mostrado se deja en liber­
tad a partir del reposo de la posición
mostrada en la figura. Sabiendo que no
existe rozamiento, hallar el desplazamien­
to que experimenta el carro de masa “M",
hasta el instante en que ia barra AB uni­
forme y homogénea de longitud "L" haga
un ángulo de 37° con la horizontal. La
masa de la barra homogénea es “m“.
donde: M = 4 m

292. X = -
Consideremos el sistema físico (m + M)
conservación del momentum en el eje x
aplicando el Teorema de la Cantidad de
movimiento (Velocidad relativa).
U : Velocidad del carro de masa M.
(m + M )' 10
x : desplazamiento horizontal del carro.
PROBLEMA Nfi 08
La figura AB es una rampa de lan­
zamiento de cohetes, inclinada en un
ángulo de 45° respecto a la horizontal. El
sistema está inicialmente en reposo y el
carro de masa "M" puede moverse libre­
mente sobre una carrilera sin fricción.
Hallar la velocidad con que el cohete de
masa "m " (M = 3 m) abandona la plata­
forma, respecto de un observador fijo en
la tierra sabiendo además que la veloci­
dad del carro después del lanzamiento es
160 m/s.
lücm1
—
» —
»
P
x(in
icial) = P
x(fin
al)
0 = m i.V i/2 - (mi + rri2) U
n m (10CIT1> r-nn^X
0 = m .--------------(5m) j
Diagrama de velocidades del cohete, que
tiene una velocidad "V" cuando aban­
dona la rampa, respecto de la tierra.
x = 2 cm
El centro de masa "G” de la barra homo­
génea experimenta un desplazamiento
de 10 cm. respecto del carro, en el eje "x".
En general se cumple que:
*
¡t*
*
*
*
*>
*
f i r ^
V s e n a ,
7 *
V A SS' A n / M
i
V V C O S u >
Consideremos el sistema físico (carro +
cohete).
Conservación del momentum lineal en el
eje x:

293. Px
(in
icia
l) —
Px
(fin
a
i)
O = m (V cos a) - M U
0 = m (V cos a) - (3m) U
V Cos a = 3 U ....(1)
Del diagrama de velocidades:
T0 45° = „ ^ S e n ° , , 1
V Cos a + U
V. Sen a = V. Cos a + U .... (2)
Reemplazando (1) en (2):
V . Sen a = 4 U .... (3)
Dividiendo (3): (1)
4 ~
T g a = | -> a = 53
Reemplazando en (3)
V = 800 m/s
PROBLEMA NB09
Un automóvil de masa "m" se encuen­
tra inicialmente en reposo sobre un plano
inclinado áspero de masa M(7 M = 9 m)
que hace un ángulo de 37° con la horizon­
tal y se encuentra apoyado sobre una
superficie horizontal perfectamente lisa.
Si el automóvil comienza a subir sobre el
plano inclinado sin resbalar, y el velo­
címetro de este marca 20 km/h, hallar la
velocidad del plano inclinado respecto de
la tierra.
SOLUCION:
Consideremos al sistema físico (auto +
plano móvil).
Conservación del momentum lineal en el
eje x.
*
*
*
*
*
*
*
*
O
í
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
P
x(in
icial) =P
x(fin
al)
Teorema del Momen*un Lineal (Veloci­
dad relativa).
0 = m i.V i/2 + (mi + m2)V2
0 = m(20 Cos 37°)+(m + M)(-U)
m
U =-
(M + m)
Reemplazando datos:
. (20 Cos 37°)
U = 7 km/h
PROBLEMA Ne 10
Una esfera de masa m = 1,0 kg se
abandona en la parte superior de un blo­
que de masa M = 2,0 kg que se encuentra
en reposo, como indica la figura. Despre­
ciando toda forma de rozamiento, hallar la
velocidad de la esfera cuando abandona
la superficie cilindrica de radio de cur­
vatura.
R = 0,3 m.
g = 10 m/s'
,2

294. Px
(in
icia
l)—
Px
(fin
a
l)
O= m V - mU
U - S - V
u=lv --- (1)
Conservación de la energía mecánica:
EM (inicial) — EM (final)
mg R r - i m ^ + k - U 2
Reemplazando:
V = 2,0 m/s
PROBLEMA Ns 11
Un carrito de masa "m" se mueve hori­
zontalmente con una velocidad V = 5,0
m/s y hace contacto con la superficie
superior de otro carro de masa "M“ (M
= 4m) inicialmente en reposo. Despre­
ciando toda forma de rozamiento de­
terminar la altura máxima que alcanza
el carrito sobre ”M''.
p
g = 10 m/s
*
*
♦
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
5
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Cuando "m" alcanza su altura máxima
"H", la velocidad relativa de "m" respecto
de ”M“ es igual a cero, por consiguiente
el sistema (m + M) se mueve con una
velocidad común “U" respecto de la tie­
rra, sólo un instante. Conservación del
momentum lineal, en el eje x.
—
» —>
Px
Q
n
icia
l)= P
x
(fm
a
O
m V = (m + M) .U
Reemplazando:
U = 1,0 m/s ....(1)
Conservación de la energía mecánica
E
M
(ín
icial) - E
M
(iin
al)
| m V2 = 1 (m + M) U2 + mgh
Reemplazando datos:
H = 1,0m
PROBLEMA NE12
Un carro de masa "M" puede moverse
sin fricción sobre un plano horizontal. En
el techo del carro fue colgado una esfera
de masa "m" (M = 9m) unido a una cuerda
de longitud 1,0 m. En el momento inicial
el carro y la esfera estaban en reposo, y la
cuerda fue inclinada un ángulo de 60° con
respecto a la vertical. Luego es soltado la
esfera, ¿Cuál será la velocidad del carro
en el instante, cuando la cuerda está en
posicion vertical? g = 10 m/s2

295. SOLUCION:
Consideremos el sistema (M + m)
Conservación del momentum lineal en el
ejex:
—
> —
»
P
x(in
icial) —
P
x(fm
al)
0 = m V - M U
tJ
V
-A
- t r
Principio de conservación de la energía
mecánica
E
M
(in
icial) —
E
M
(fjn
al)
mgh = 1 M U2 + ~ m V2 .... (2)
Reemplazando (1) en (2)
u
i 2 m 2 .g.h
M (M + m)
U = — m/s
*
*
PROBLEMA Ns 13
Un cuerpo esférico de masa "m", que
se mueva horizontalmente con una velo­
cidad V0 = 6 m/s hace contacto con la
superficie superior de un carro de masa
M(M = 5 m) inicialmente en reposo. Si no
existe rozamiento. Hallar la velocidad de
“m" cuando sale por la parte superior de
la superficie cilindrica de radio R = 1,1 m.
g = 10 m/s2
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
$
*
*
Consideremos nuestro sistema físico
(M + m)
Conservación del momentum lineal en el
eje x :
Px
(in
icia
l) =Px
(tin
a
i)
m V0 = (m +M) U
m(6) = (6m) U

296. "U" es la componente de la velocidad "V"
en el eje x, en el instante que abandona
”m" a la superficie.
Conservación de la energía mecanica.
E
M
(in
cial) = E
M
(fin
al)
1 2 1 9 1 9
- m V 0 = - M U ‘ +—m V“ +mg R
Reemplazando datos:
^m(36) =l(5rr}flJ+ ¿ m V z+mac)a,1)
V = 3 m/s
PROBLEMA N9 14
La figura muestra dos bloques A y B
de masa 1 kg y 2 kg» respectivamente. Si
se obliga a los bloques a aproximarse
comprimiendo el resorte y luego se libera
el sistema del reposo, se observa que
adquiere "B" una velocidad máxima de 0,5
m/s. Suponiendo que la masa del resorte
es despreciable y que se desprecia la fric­
ción, ¿cuál fue la energía potencial al­
macenada originalmente en el resorte?
1
- W M - H D *»— —
•i»»*?,-
SOLUCION:
Consideremos el sistema (A+resorle +B)
Conservación del momentum lineal
~
¡l
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
3¡f
*
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
%
*
P(in
icia
l) = P(fin
a
l)
0 - me Vb - mA Va
Reemplazando:
V a = 1,0 m/s
Conservación de la energía mecánica
E
M
(fjn
al) = E
M
(in
ical)
itia.V A+ 1 mB .VV 8+ 1 k . x2 = Ep
S i: VA y VB es máximo , entonces la
deformación en el resorte es nulo (x = 0).
La energía cinética es máxima
Reemplazando los datos:
Ep = 0,75 J
PROBLEMA NB15
Una pelota de masa m = 0,5 kg, inflada
con cierto gas, se encuentra inicialmente
en reposo. Un niño le aplica una patada
cuya fuerza varía en el tiem po como
muestra la gráfica. Si después la pelota
se mueve con una velocidad V = 20 m/s,
determinar la fuerza máxima aplicada al
cuerpo.
SOLUCION:
El impulso es iguai al arpa r ajo ia curva

297. La fuerza aplicada será máxima en el
insiante t = 0,4 s.
| También el impulso es igual a la variación
* del momentum:
*
I = m(VF- V0)
Pero : V0 = 0 Vf = 20 m/s
*
Reemplazando: I =10 N.S. ... (2)
$
J De{1)y (2)
*
*
*
*
*
*
*
*
*
*
*
*
Fmáx = 25 N

298. r
A1STM O V IL VE VAPOR, QUE SE ATR IB U YE A H EW C N .

299. [C O LISIO NES O CHOQUES
J
CONCEPTO
Son aquellas interacciones mutuas vio­
lentas que alteran el movimiento de los cuer­
pos o partículas, produciendo un intercambio
de cantidad de movimiento y energía en un
tiempo relativamente pequeño.
Durante el choque las fuerzas internas
generadas son muy grandes comparada con
las fuerzas externas (despreciable). Por con­
siguiente el momentum se conserva durante
el choque.
[P A.C = P D.C
“El momentum instante antes del choque,
es igual al momentun instante después de
choque".
(ANTES)
»T v2
• o — — - * — ©»•
~.v. ■j'a.'v-~
».vav- l; —
,'C T w r-r ws
(DURANTE)
R ju ü u u , p
_____
r , - - k- ' /.rií^r s ¡ '»
1*!L.
(DESPUES)
J
««
“Durante el choque, la fuerza resultante
sobre el sistema físico (2 partículas) es
igual a cero"
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
■
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
5)5
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
"Durante el choque se tiene en conside­
ración solamente las fuerzas de Acción y
Reacción”.
Clasificación de los choques, según su
línea de acción.
1) Choque Frontal
Son aquellos que se caracterizan porque
antes y después de producido el choque,
los cuerpos de desplazan a lo largo de la
misma linea de acción. Estos choques
se denominan también unidimenciona-
les, como muestra la figura anterior.
2) Choque Oblicuo o Excéntrico
Son aquellos a través de los cuales se
transfiere cantidad de movimiento lineal
e inclusive se transmite momentum an­
gular (L), puesto que las líneas de acción
de los cuerpos antes y despues del cho­
que son diferentes. Estos choques se
denominan también bidimensionales
. (x e y).
Este caso es frecuente en los juegos de
billar. Por comodidad tendremos en con­
sideración solamente el movimiento de
traslación, despreciando el movimiento
de rotacion de las bolas de billar.
I) Antes del choque.
II) Después del choque:

300. * En la mesa del billar, V2 = O
Del principio de conservación del Mo­
mentum Lineal:
P inicial
(mi Vi + rri2 V2)
(Tga
P
iníc.jl—
P
fin
al
_ V-R. Alejamiento
~ V.R. Acercamiento
Clasificación de los choques, según la
disipación de la energía.
* 1)
*
*
*
*
*
*
*
Choque perfectamente elástico
(e= 1)
Es una colision ideal, durante la cual los
cuerpos o partículas no experimentan
ninguna deformación permanente, ni
tampoco liberan energía (calor). Por lo
consiguiente la energía cinética se con­
serva durante el choque.
E
k(antes)=E
k(después)
| 2) Choque Inelástico ( 0 ( e (1)
*
*
*
*
*
*
*
*
*
*
<
s
>
♦
*
*
*
*
*
$
*
i*
m
*
*
*
*
*
*
%
*
*
Es aquella colisión, durante la interacción
se libera energía en forma de calor o por
deformación de los cuerpos Por consi­
guiente la energía cinética final es menor
que la inicial.
Ek (antes) > Ek (después)
3) Choque perfectamente Inelástico
( e = o)
Es aquella colisión, durante su realiza­
ción se libera energía en forma de calor,
deformándose permanentemente los
cuerpos, tal que después del choque los
cuerpos avanzan juntos con la misma
velocidad La energía cinética que se
pierde se gasta en la deformación de los
cuerpos.
Coeficiente de Restitución (e)
Es aquel factor adimensional que nos
define la relación entre la velocidad relativa
de alojamiento después del choque y la
velocidad relativa de acercamiento antes del
choque,
0 < e < 1
*
% o -
t ml
*
*
*
*
*
*
*
*
*
*
<
t¡
*
#
0
*
*
*
►
(n^mig)
Principio de conservación del momentum
lineal.
P (antes)= P (después)
m i.Vi + m2-V2 = (mi + nri2).U

301. Gráfica Fuerza versus tiempo (F - 1)
Cuando una pelota choca contra el piso,
durante la interacción !a pelota se deforma,
entonces la fuerza de reacción normal (fuer­
za externa) es variable en el tiempo. Con­
siguiendo en la gráfica F - 1una curva.
El área bajo la curva es igual al impulso
o vai ¡ación del momentum lineal, en un inter­
valo de tiempo.
t(s)
I = AP = área
Ley de Reflexión en los Choques
Una partícula incide sobre una superficie
rugosa" u " formando un ángulo" a " respecto
de la normal y rebota formando un ángulo
“ p E l coeficiente de restitución " e " entre
la partícula y la superficie es:
/
e =
T g a - u
T g p + u
*
*
*
*
*
*
*
*
Demostración
Consideremos que la partícula incide con
una velocidad "V" y se refleja con una
velocidad" U “.
*
*
*
* .
*
*
*
*
*
* VCosa
<8s
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
4
>
*
*
*
*
*
¡ft
*
*
*
*
*
*
*
*
*
*
*
UCosB
VS e n a
El impulso en cada eje, es igual a la
variación del momentum lineal:
I = F r . At = m(Vf - V¡)
El eje "x", actúa la fuerza de rozamiento
" f *: f = u.N
-u N = m(U Sen p - V Sen a ) .... (1)
En el eje “y”,actúa la reacción normal ”N",
el peso es despreciable comparado con
la fuerza de reacción.
N = m(U Cos P+ V Cos a) .... (2)
Dividiendo las Ec. (1) y (2):
U Sen 0 - V Sen a
U Cos 0 + V Cos a
.... (3)
Definición del coeficimente de Restitu­
ción.
V.R. Alojamiento
~
~V.R. Acercamiento
La velocidad de la superficie (Tierra), an­
tes y después del choque es igual a cero
e =
U Cos P
V Cos a

302. U = e V
Cos a
Cos p
Reemplazando (4) en (3):
e Tg p - Tg a
..(4)
-u =
e +1
Despejando “e"
CASOS PARTICULARES
I) Una partícula incide sobre una superficie
perfectamente lisa, formando un ángulo
" a " respecto de la normal y rebota for­
mando un ángulo" B E l coeficiente de
restitución entre la partícula y la superfi­
cie es:
Sabiendo que;
0 < e < 1 a < p
II) Para un choque perfectamente elástico
(e = 1),el ángulo de incidencia y el ángulo
de reflexión son iguales.
Sí
III) Cuando una partícula choca perpendicu­
larmente con una superficie fija (Tierra),
su velocidad de incidencia "V” y su velo­
cidad de reflexión "U“ se relacionan del
siguiente modo:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
AU
1 U = e . V ]¡
e < 1
Si el choque es perfectamente elástico
(e = 1), las velocidades de incidencia y
reflexión son iguales.
IV) Cuando una partícula es abandonada
desde una altura 'H“ y choca con una
superficie horizontal la altura máxima que
alcanza después del primer rebote será:
e <1
En general, la altura máxima después de
n-ésimo rebote será:
hn = e2n . H
n= 1; 2; 3; 4;

303. PROBLEMAS RESUELTOS DE
CHOQUES
PROBLEMA Ne01
Una pelota pequeña de 0,5 kg. se mue­
ve con una velocidad de 20 m/s horizon­
talmente, impacta con una pared vertical
y luego rebota. Si el coeficiente de resti­
tución es 0.8. Calcular el impulso que le
da la pared a la pelota.
SOLUCION-
(D
_
_ _
*
*
i ) .
(II)
eV
El impulso es igual a variación del mo­
mentum lineal,
—
> —
» -» -»
I = AP = m ( V F- V 0) ... (1)
V0 = + 20 m/s
Vf = - eV = —16 m/s
Reemplazando en (1)
l= 0,5 kg (-1 6 - 2 0 ) m/s
l = -18N.s
( - ) : Sentido a la izquierda.
PROBLEMA N902
Se proyecta una partícula con un án­
gulo de incidencia de 45° sobre una su­
perficie horizontal cuyo coeficiente de
fricción es u = 2/9.
Calcular la medida del ángulo " 6 " de
rebote, si el coeficiente de restitución del
choque ese = 0,8.
*
*
*
*
*
*
*
*
*
.*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
♦
&
*
*
*
*
*
*
*
$
*
*
*
♦
*
*
*
$
♦
*
*
*
*
*
SOLUCION:
Ley de Reflexión para choques:
e = I9L5L1Ü
Tg p + u
Reemplazando los datos:
Tg 45° - 2 /9
0,8 =■
Tg 0 + 2 /9
Resolviendo:
T g 0 = §
0 = 37
PROBLEMA Ns 03
Sobre un plano inclinado 0 = 60° con
la horizontal se dispara un proyectil hori­
zontalmente, rebotando verticalmente.
Sabiendo que no existe rozamiento, de­
terminar el coeficiente de restitución "e"
entre la esferita y el plano inclinado fijo a
la tierra.

304. e = -
Ley de Reflexión para choques:
Tg a
Tg P
donde: a = (90° - 0) y
Reemplazando en (1):
e = Cotg2 0
(1)
p = e
1
I I I .
PROBLEMA Ne04
Una partícula es lanzada contra una
superficie horizontal con un ángulo " 0 "
respecto de la vertical.
El coeficiente de restitución para el
choque es e = 1 /2 y el coeficiente de fric­
ción estática entre la partícula y la super­
ficie es u = 0,5.
¿Para qué ángulo de incidencia “ 0" el
rebote será vertical?.
SOLUCION:
............ ........... ' I
Ley de Reflexión para choques:
e = 5 ^ u
Tgp + u
En este caso : a = 6 y p = 0o
Reemplazando en (1):
Tg0 = u(e + 1)
Tge = !
0 = 37°
*
*
*
*
*
«
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
<
jí
*
*
*
*
*
*
*
*
*
«
tí
m
*
*
*
*
*
*
*
Oe
*
*
*
*
*
*
*
*
*
*
*
*
Oe
«
fe
*
5
t»
*
*
*
<
K
Dos cuerpos cilindricos de masas A
(12 kg) y B (2 kg) se desplazan con velo­
cidades de Vi = 4m/s y V2 = 6 m/s respec­
tivamente en sentidos opuestos, sobre un
eje horizontal que no ofrece rozamiento.
Después del choque el cuerpo de mayor
masa mantiene el mismo sentido con una
velocidad Ui = 2 m/s. Determinar el coe­
ficiente de restitución y la energía calo­
rífica desprendida.
SOLUCION:
Conservación del momentum lineal (eje x):
P ¡(x) = P f(x)
M Vi - mV2 = m Ui + m U2
(12) 4 -(6 ) 2 =(12) 2+(2) U2
U2 = 6 m/s .... (1)
Coeficiente de Restitución (e)
V.R. Alejamiento
“ V.R Acercamiento
U2 - U 1 6 - 2
e —
V2 + V1 6 + 4
e = 0,4
Conservación de la energía.
Ek (inicial) = Ek (linal) + Q
1 2 1 2 1 2 1 2
- M V , + - m V 2= - M U , ^ m U í + Q
Reemplazando:
Q = 72 J

305. Un caro de masa M = 10 kg se desplaza
por inercia a razón de V = 6 m/s. Desde
una altura h = 1 ,0 m se abandona una
esfera de masa m = 2 kg., como muestra
la figura. Calcular la energía calorífica
desprendida en el choque, si la esfera se
adhiere al carro. No hay rozamiento en el
plano. g = 1 0 m/s2
Conservación del momentum lineal en el
eje x.
P¡(x) =Pf(x)
M V = (M + m) U
Reemplazando los datos:
U = 5 m/s ....(1)
Conservación de la energía en todas sus
formas:
E (antes)= E (después)
mgh+ ~ . M V2 = ~ (m +M) Ua+Q
Reemplazando los datos:
Q + 50 J
PROBLEMA NB07
Una esfera de masa "m" se lanza hori­
zontalmente con una velocidad V = 5 m/s
y choca elásticamente (e = 1 ) con una
cuña de masa M(M = 5m), rebotando ver­
ticalmente. Calcular la altura máxima que
alcanza la esterilla después del choque.
No hay rozamiento. La cuña se encuentra
en reposo antes del choque.
*
*
*
*
*
*
*
*
*
S
*
*
t=
*
*
*
*
*
*
5
?
$
*
*
S
*
*■
sü
Sü
*
S
Ü
*
*
Slí
Sí!
S
K
*
*
*
*
Consen/ación del Momentum lineal (eje x)
—
> —
>
Pi(x) =Pf(x)
- m V = - M U
Reemplazando datos:
U = 1 m/s .... (1)
Conservación de la energía mecánica:
~ m V2 = ^ M U 2 +mgh
Reemplazando :
h = 1,0 m
PROBLEMA Ne 08
Un bloquecito de masa "m" se desliza
partiendo del reposo por un tobogán com­
pletamente liso que termina horizontal­
mente, de tal manera que el bloquecito
impacta sobre el péndulo de masa "M" al
que queda adherido, elevándose los dos
hasta una altura "h“ máxima. Hallar "h"
L : longitud de la cuerda

306. SOLUCION:
Cálculo de velocidad de "m" cuando im­
parta con "M".
Conservación de la Energía Mecánica,
instante antes del choque.
EM (A) = EM (B)
m gL = | m V2
V2 = 2 g L ....(1)
Choque inelástico (e = 0)
P (antes) = P (después)
m V = (m + M) U
m
(m + M)
. V .... (2)
Conservación de la energía mecánica,
después del choque.
1
EM(B) = EM(C)
(m + M) U = (m + M) g . h
- U2 = g - h
Reemplazando (1) y (2) en (3)
.... (3)
PROBLEMA Ne 09
Un bloque ”A" de masa 2 kg. se desliza
sobre una superficie horizontal sin roza­
miento con una velocidad de 1 0 m/s direc­
tamente y frente a él se mueve un bloque
”B" de masa 5 kg. con una velocidad de 3
m/s, en la misma dirección y sentido. Si
un resorte de masa despreciable y coefi­
ciente de elasticidad K = 1 120 N/m va fijo
en la parte posterior de "B", como indica
la figura. Hallar la máxima deformación
del resorte cuando chocan los bloques.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
tu
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
’ - D w r f n
';*Pi,ur«nuj.ir yrre
rrrñs^
SOLUCION.
La máxima deformación en el resorte se
produce cuando ambos cuerpos se des­
plazan con la misma velocidad,esto quie­
re decir que la velocidad relativa de acer­
camiento entre A y B es igual a cero.
_______
Conservación del momentum Lineal:
—
>
P (inicial) - P (final)
itia Va + itib .Vb = (mía + me) V
Reemplazando:
V = 5 m/s ....
Conservación de la energía mecanica
E
M
(jn
icial) —
E
m
(final)
2 -| 2
mA • V A+ —ms V B =
|(mA+m e) V2 + | k . x2
Reemplazando:
x = 0,25 m
PROBLEMA Ns 10
Un proyectil de masa m = 200 g, se
desplaza a una velocidad V = 75 m/s. ex­
plotando luego en dos fragmentos A (50g)
y B (150g), respectivamente. Sabiendo
que inmediatamente después de la ex­
plosión los fragmentos se mueven en las
direcciones mostradas en la figura, deter­
minar la velocidad de A y B.

307. ,i(3 —
SOLUCION:
Conservación del Momentum Lineal, ins
tante antes e instante después de la ex­
plosión.
P y(antes)—
Py(después)
0 = itia.Va Cos 53° - meVe-Cos 37°
Reemplazando:
VA = 4 Vb -..(1)
En el eje "x"
Px(antes)= Px(despues)
mV = mA-VA-Sen 53°+mB.VB.Sen37°
Reemplazando:
1 500 = 4 Va + 9 Vb .... (2)
Resolviendo (1) y (2):
Va = 240 m/s
Vb = 60 m/s
$
*
♦
*
*r
*
♦
*
*
*
*
*
s
>
*
*
*
*
*
Un cuerpo esférico de masa m = 0,5 kg.
se mueve horizontalmente con una velo­
cidad V0= 9 m/s y se hace contacto con la
superficie de un carro de masa M = 4,0 kg.,
inicialmente en reposo. En el carro se
encuentra instalado un resorte de
m asa d e sp re cia b le y co n sta n te
elésti- ca = 400 N/m. Despreciando toda
fo rm a de rozam iento, d ete rm ina r la
máxima deformación en el resorte.
*
*
*
*
*
*
S
*
*
*
*
*
s
S
*
#
*
$
*
*
*
*
*
*
$
*
*
«
fe
#
*
*
*
*
si#
si»
SOLUCION:
La deformación en el resorte será má­
xima, cuando la velocidad relativa "m"
respecto del carro "M" es igual a cero.
Por consiguiente el sistema (m + M) mar­
cha con una velocidad común igual a “U“,
sólo un instante.
Conservación del momentum lineal:
F
3
(in
icia
l) —
P(fin
a
l)
m Vo = (m + M) U
Reemplazando:
U = 1,0 m/s ....(1)
Conservación de la energía mecánica:
E
M
(m
icial) = E
M
(fin
al)
1 * 1 5 1 9
~ m V 0 = - ( m + M)U + - kx
Reemplazando datos
x = 0,3 m
x : maxtma deformación en el resorte.

308. Un péndulo formado por una esferita
de masa "m" e hilo de longitud L = 2,0 m,
se desvía un ángulo 9 = 60° respecto de la
vertical y se suelta sin velocidad inicial.
La esferita choca con un bloque de masa
M(M = 2 m) con coeficiente de restitución
e = 1/2. Determinar el espacio recorrido
por el bloque sobre el plano horizontal
hasta detenerse, si el coeficiente de roza­
miento cinético es (15.
SOLUCION:
Cálculo de la velocidad de "m" instante
antes del choque.
mg h = ~ m V2
V2 =gL ...(1)
Conservación del momemtum, instante
antes e instantes después del choque.
v=o
P(antes) =P (después)
m V = M U - m Ui
U i = - V + 2 U ....(2)
Coeficiente de restitución (e):
U + U i i
2
e =-
V = 2 U + 2 Ui ....(3)
Reemplazando (2) en (3):
.... (4)
*
*
3
¡
S
*
*
*
*
*
*
M
Después del choque:
Teorema del Trabajo y la Energía Me­
cánica.
Wf = EM(o = EM(¡)
- f.d = E
k
(f)- E
k(¡)
- u (Mg) d = 0 - ^ M U2
d - i ^
2 ug
Reemplazando (4) en (5)
(5)
Del dato
d = 0,5 m
PROBLEMA Ns13
Un bloque de masa "M" se encuentra
asociado a un carrito de masa "Mo" me­
diante un resorte ingrávido de constante
elástica k = 2 0 0 0 0 N/m, inicialmente en
reposo. Se dispara horizontalmente una
bala de masa “m" con velocidad "V"
(mV = 300 N.s) si después del choque la
bala queda incrustada en el bloque de
masa “M“ (M = 8 m), hallar la máxima de­
formación del resorte. Desprecie toda for­
ma de rozamiento.
Considere : M0 = 9m
m
V '
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
Choque del proyectil con el bloque de
masa “M".
V=0
M
* (m+M)
(Antes) (Después)

309. P(antes) = P(después)
m V = (m + m) Vi
Vi =
m
(M + m)
V .... (1)
La máxima deformación del resorte se
establece cuando el conjunto tiene la
misma velocidad, esto quiere decir que la
velocidad de "M" respecto del carrito es
igual a cero.
(M + m)
” 1
i!
:-v w v w m -
Mo
H -
w . ISl
u =- .... (2)
+ | k x 2
Reemplazando (1) y (2) en (3)
.... (3)
x = m V I ^ ----------
y(m+m+M
0)(M+m)k
x : deformación máxima en el resorte.
*
*
*
*
*
*
&
#
jfc
*
*
*
*
*
*
*
*
*
*
. *
*
*
*
*
*
*
*
*
La cantidad de movimiento se conserva
en el tiempo, entonces el momentum del
proyectil antes del impacto es igual al
momentum del sistema cuando la defor­
mación es máxima.
P(in
icia
l) =P(fin
a
l)
m V = (M + m + M0)U
m V
(M + m + Mo)
Conservación de la energía mecánica,
después del choque entre m y M
EM (1) = EM (2)
| (m+M) V * = | (m+M+ Mc) U2
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
En la figura mostrada se tiene una cu­
ña de masa "M" inicialmente en reposo.
Si se lanza horizontalmente una esferita
de masa “m", determinar el ángulo ” 6 ” de
tal manera que después del choque elás­
tico (e = 1 ), la esferita rebota vertical­
mente. Desprecie el rozamiento.
M m
16 - 7
*
*
*
*
« o -
ffl
© /
i
I /
------ 0 / ^
A B
U ^
f e - :
. ■ . rrr» rn
SOLUCION:
Considerando “U" la velocidad de la cuña
"M" después del choque.
P(x)(antes) = Px(después)
mV = M U
v J u
m
(1)
Considerando "Uy“ la velocidad de ”m"
después del choque.
Conservación de la energía cinética, en
el choque elástico
_ 2 mV2 = ^ MLj2 + | rn U »
Reemplazando (1) en (2):
(2)
r M _ ,
m
M u * .... ( 3 ,
m
Definición del coeficiente de restitución
(e), para choques frontales o perpendicu­
lares, luego hay la necesidad de descom­
poner las velocidades y tomaremos como
referencia la dirección perpendicular a la
cuña.

310. V.R. Alejamiento
V.R. Acercamiento
Ui . Cos 6 + U Sen 0
e = ------------------------------ = 1
v . Sen 6
Despejando:
Ta e = Í T u " - (4)
$
*
*
*
*
*
&
* Del dato
*
*
*
•
J
S
*
*
*
*
*
♦
*
*
*
*
*
*
#
T
9e=|
0 =53°

311. CONCEPTO.
Es una parle de ia mecánica de fluidos
(líquidos y gases) que tiene la finalidad de
analizar el comportamiento y efectos físicos
que originan los fluidos en el estado de re­
poso.
La Estática de Fluidos consta de las si­
guientes partes.
I) Hidrostática: Estudia a los líquidos en
reposo relativo.
II) Neumostática: Estudia a los gases en
reposo relativo.
DENSIDAD (D).
D =
m
(1)
.... (2)
.... (3)
Unidades: g/cm3 , kg/m3
De la Ec. (1): m = D.v
El peso de una sustancia es:
W = m . g
Reemplazando (2) en (3)
~W = D - G . v i
W: peso D: densidad
v: volumen g: aceleración de la
*
*
ft
ft
Para una sustancia molecularmente ho­
mogénea, su densidad nos expresa la masa
de la sustancia contenida en la unidad de
volumen.
gravedad
*
*
ft
*
*
*
*
*
*
ft
*
ft
*
ft
*
ft
ft
ft
ft
*
ft
*
*
ft
ft
ft
ft
ft
*
ft
ft
ft
ft
ft
ft
*
*
ft
*
ft
ft
Es una magnitud física Tensional, que
expresa la distribución normal de una fuerza
sobre una superficie. La magnitud Tensorial
implica que la presión tiene múltiples puntos
de aplicación y manifestación normal sobre
las superficies, que establece la diferencia
con la magnitud vectorial.
La magnitud de la presión se define como
la fuerza perpendicular que actúa por cada
unidad de área.
Presión =
Fuerza Normal
área
Unidades:
1 pascal =
m

312. La figura (1) muestra una pirámide de
peso 400 N, de base cuadrado cuyo lado
mide 2 m.
La figura (2) muestra la presión "P" que
ejerce la pirámide sobre la superficie horizon­
tal.
ü
„2
p F 400N 100.
A 4 m m
La presión "P" también se puede definir
como la distribución de la fuerza por cada
unidad de área
"La pirámide ejerce sobre la base una
fuerza de 100 N por cada m2.
PRINCIPIO DE PASCAL
"Todo fluido transmite la presión que so­
bre él es ejercida en toda dirección, sentido
y con la misma intensidad"
GAS
i 1
" 0
• P
e
• F i q . ( l )
• ■
V
0
F
• •
'*‘
S
• 0
•
• •
F i g . ( 2 )
1) La figura (1) muestra un recipiente cilin­
dro conteniendo un cierto "gas", tapado
por un émbolo de área "A", en equilibrio.
2) Al émbolo se le ejerce una fuerza "F”,
figura (2), de tal modo que el gas se
comprime, disminuyendo su volumen.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Si la presión inicial que ejerce el gas
sobre la pared del recipiente era "P",
figura (1), ahora la presión se incrementa
en (F/A), figura (2). ■
P
in
icial+ A—
P
fin
al
"Si se aplica una presión a un fluido, la
presión se transmite a través de todo el
fluido, en toda dirección y sentido y con la
misma intensidad"
PRENSA HIDRAULICA
Es una máquina simple que tiene por
objeto multiplicar la fuerza que se le comu­
nica y muy usual para levantar cargas pe­
sadas.
Esta máquina tiene como principio de
funcionamiento el Principio de Pascal. Físi­
camente una prensa hidráulica está consti­
tuida por dos cilindros y dos pistones y ém­
bolos deslizantes de diferente diámetro, en
uno de los cuales se coloca la carga que se
desea elevar y en el otro (el de menor diá­
metro) se le aplica la fuerza correspondiente.
F,
1
C IT E _________ _______
¡
J
'i
En la prensa hidráulica mostrada, apli­
camos en el émbolo menor una fuerza Fi la
cual transmite al líquido una presión "Pi" y
ahora el líquido le comunica al otro pistón la
presión "P2” que según el Principio de Pas­
cal.

313. f l = f z
Ai A2
de donde:
A2 > Ai F2 > F1
PROBLEMA Nfi 01
En la figura mostrada se tiene una
prensa hidráulica cuyos émbolos tienen
un área Ai y A2 (A2 = 20Ai). Determinar
la magnitud de la fuerza "F" que se debe
aplicar a la palanca, para mantener en
equilibrio el bloque "Q" de peso 3 000 N.
Desprecie el peso de los émbolos y de la
palanca.
*
*
*
*
o
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
t:
30
EM 0 = 0
F (30) = F,(10)
Luego:
F = 50 N
PRESION HIDROSTATICA
CONCEPTO.
Es la presión que soporta todo cuerpo
sumergido en forma parcial o total en un
Pero:
F 2 = i a T
3 000 = 20 F1
F1 = 150 N
*
*
*
*
*
*
*

314. *
*
*
aire
figura (2) %
1) La figura (1), muestra un recipiente de
forma cilindrica conteniendo cierto líqui­
do.
2) El líquido adopta la forma del recipiente
que lo contiene, debido a la acción del
campo gravitatorio o debido a su peso,
figura (1).
3) En ausencia del campo gravitatorio (sin
peso) adoptará como forma natural la
esférica, esto quiere decir que el líquido
no se derrama.
4) La presión "P" que ejerce el líquido sobre
el fondo del recipiente se debe al peso del
líquido, figura (2).
Presión^
Fuerza W Peso del líquido
área ~A~área de !a base
r _W D g. v
A A
Pero: v = A. h
Reemplazando en (1)
p _ D. g. A. h
J
T
O
.
“La presión hidrostática es igual al pro­
ducto de la densidad del líquido “D”; la acele­
ración de la gravedad (g) y la profundidad (h)“
PROBLEMA N502
En la figura mostrada, determinar la
presión hidrostática en el punto "A". La
densidad de los líquidos no miscibles
son:
Di = 800 kg/m3 , D¿ = 1 000 kg/m3
g = 1 0 m/s‘
£
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
n
*
*
*
«
¡t
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
X
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
> í l ) .
A . —
0 , 8 m
SOLUCION:
Presión hidrostática debido a varios líqui­
dos:
Pa = Di. g. hi + Ü2. g. h2
En el S.I.:
Pa = 800 x 10 x 0,5 + 1 000 x 10 x 0,8
Pa = 12 000 pascal
Pa = 12 k Pa
PRINCIPIO FUNDAMENTAL DE LA
HIDROSTATICA
"La diferencia de presiones hidrostáticas
entre dos puntos situados en un mismo líqui­
do en reposo relativo es igual al producto del
peso específico del liquido por la altura entre
dichos
*
1Tquido
h ___ Isóbara_[_l^
Isóbara (2)
Fig.(I)

315. 1) En la figura (1), calculamos las presiones
liidrostáticas en los puntos 1 y 2 .
P2 = D (Líquido), g. hg ......(I)
Pi = D (Líquido), g. hi .... (II)
Restando las ecuaciones (I) —(II)
(P2 —P1) = D (Líquido), g. (h2 - hi)
De la figura (1):
P2 - P1 = D (Liquido), g. H
2) Por consiguiente, todos los puntos si­
tuados en un mismo líquido en reposo
relativo y a un mismo nivel o profundidad
soportan la misma presión.
3) La Isóbara, es la línea o plano formado
por puntos que soportan la misma pre­
sión, figura(1 ).
PROBLEMA Nfi 03
Un tubo en "U" contiene mercurio
(D = 13,6 g/cm3). ¿Qué altura de agua se
debe verter en una rama para que el mer­
curio se eleve en la otra rama 5 mm?
SOLUCION:
'H2o
_
_ /
■ _ v
Hq
Principio fundamental de la Hidrostática.
P1 = P2
PaTM + Dh¿0 g.h= DHg.g.(H)+PATM
Dh2
0. h = DHg. H
h = £ * H
Dh?
0
*
*
*
$
*
♦
*
ta
*
*
(K
*
*
*
*
*
*
*
*
f¡>
*
$
*
*
♦
*
m
*
*
*
*
*
*
*
*
*
s
N
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
m
h = 136 mm
PROBLEMA N®04
En un tubo en “U" de ramas verticales
y de igual sección se vierten tres líquidos
(1); (2) y (3) obteniéndose el equilibrio en
la forma mostrada. Hallar la altura ”h".
Di = 3 000 kg/m3 D3 = 4 000 kg/m
D2 = 5 000 kg/m3
3
SOLUCION:
Principio fundamental de la hidrostática
Pa = P b
Di. g. hi + D2. g. h2 = D3. g. h3
Reemplazando en el S.I.:
Di. hi + D2. h2 = D3. h3
3000 (0,3) + 5000 (h - 0,3) = 4000 (h)
h = 0,6 m
PRINCIPIO DE ARQUIMEDES
Todo cuerpo sumergido en forma parcial
o total en un líquido en reposo relativo, está
sometido a la acción de una fuerza perpen­
dicular a la superficie libre del liquido o per­
pendicular a las isóbaras, hacia arriba debido
a la presión que ejerce el liquido sobre el
cuerpo denominado fuerza de Empuje.
“El empuje es la fuerza resultante de
todas las fuerzas que aplica el líquido sobre
el cuerpo, debido a la presión hidrostática'

316. El valor del empuje es igual al peso del
volumen del líquido desalojado por el cuerpo.
Pero el volumen del líquido desalojado es
igual al volumen sumergido del cuerpo.
Empuje = D (Liq). g. Volumen sumergido
Ñ " i l
i
1
1
i
t
1
t
y 0
& f '
X
*
V] P2 y
F í g . ( i )
/
/
1) Consideramos un cuerpo cilindrico de al­
tura H = h2 - hi y de área de ia base "A",
como indica la figura
2) En la figura (1) se muestra el diagrama
de presiones que actúa sobre el cilindro,
debido al líquido que lo rodea.
m
*
*
*
♦
Si»
*
*
*
#
*
*
m
&
m
*
*
*
£
*
*
*
*
*
$
#
*
*
*
*
*
#
*
*
*
*
*
*
♦
*
*
#
*
*
*
#
*
*
*
m
*
*
*
*
#
3) De observarse que la presión hidrostática
aumenta con la profundidad. Además en
el perímetro de la base del cilindro la
presión actúa en toda dirección y sentido
pero con la misma intensidad.
4) Las presiones que actúan en la superficie
lateral del cilindro se eliminan, razón por
la cual la fuerza resultante es igual a cero
en la horizontal.
5) Las presiones Pi y P2 son de magnitud
diferente, debido a las alturas hi y h2,
respectivamente
6) Sabemos que:
Fuerza = Presión x Area
Luego: F2 = P2 -A ....(1)
F1 = P1 . A .... (2)
7) El empuje se define como la fuerza resul­
tante que actúa sobre el cuerpo, debido
a la presión que ejerce el líquido sobre el
cuerpo
Empuje = F2 - F1 .... (3)
Reemplazando (1) y (2) en (3)
E = P2. A - P i . A
E = (P2 - P i ).A (4)
Por el principio fundamental de la
Hidrostática, en (4)
E = D (líq). g (h2 - hi). A
Pero: Volumen sumergido =
(h2 - h i) . A
Luego: ^
| Empuje = D (líq). g. V(sumergido) |
PRESION ATMOSFERICA
Es la presión que ejerce el aíre sobre los
cuerpos, debido a la acción del campo gravi­
tatorio. El aire que rodea a la Tierra esta
compuesto con mayor porcentaje por Nitró-
geno(78%) y oxígeno(21 %).
La densidad del aire varía con la altura,
por consiguiente con la intensidad del campo
gravitatorio. Ahora bien, la presión del gas

317. es proporcional a la densidad del gas, enton­
ces, la presión atmosférica es máxima en el
nivel del mar y es mínimo e igual a cero en el
límite de la atmósfera.
EXPERIMENTO DE TORRICELLI
a i r e
a
=rr.;
O
O
0
- 'i
lOOcm
—
.—
I
—
.0
0
Hg
Fit)-(l) Fig.l2)
( Vacfo
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
£
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1) La figura (1) muestra una probeta de 100
cm. de longitud.
2) La probeta se llena con mercurio(Hg),
figura (2).
3) La probeta se invierte tal que el mercurio
(Hg) se derrama sobre un recipiente, co­
mo muestra la figura (3). .
4) En la figura (3) se observa que no todo el
mercurio baja de la probeta debido a la
5)
presión atmosférica que actúa sobre la
superficie libre del mercurio.
Por el principio fundamental de la hidros­
tática, los puntos (1) y (2) se encuentran
en un mismo líquido (Hg) y el mismo
nivel, por lo tanto
Pi = Pa
Patm = 76 cm Hg
“La presión atmosférica es equivalente, a
la presión que ejerce una columna de
mercurio (Hg) de 76 cm de altura”.
En el S.l.
Patm = D Hg • g ■h
Patm = 1 3 600 & (9,8) ^ . (0,76m)
m s
| Patm = 1.1 x 10a pascal | l (.■
Si la experiencia de 1orricelli, se realiza
con agua ( H20 ) en lugar de Hg.,
la columna de agua sería de una altura
h = 10,33 m aproximadamente
P a t m = 10 33 m H2O
Al conjunto mostrado en la figura (3)se le
denomina Barómetro, sirve para medir la
presión atmosférica.
MANOMETRO
Es aquel dispositivo que se utiliza para
medir la presión de un gas encerrado en un
recipiente.
La presión manométrica de un gas es
igual a la presión hidrostática, es decir a la
columna del líquido en el tubo abierto
F i q . ( l )
*
ft

318. La presión absoluta del gas, es mayor
que, la presión atmosférica.
Pi =P2
Pgas=Patm +D. g. H - .(1 )
pa t m |
La presión absoluta del gas, es menor
que la presión atmosférica.
Del principio fundamental de la Hidros­
tática.
P3=P4
Pgas + D g. h. = Patm
Pgas = Patm - D. g. h .... (2)
PRINCIPIO DE ARQUIMEDES EN LOS
GASES
Todo cuerpo sumergido en forma parcial
o total en un gas, experimenta la acción de
una fuerza vertical con sentido hacia arriba,
denominada "Empuje”, cuyo valor es igual al
producto de la Densidad del gas que rodea
al cuerpo, aceleración de la gravedad y el
volumen sumergido.
f " " I
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
#
*
*
*
■
x
*
*
*
*
*
*
*
*
*
*
*
*
*
H
e
*
*
*
*
*
$
*
*
*ic
rEmpuje = D
gas. g . Vs
PROBLEMA N° 5
Un hombre cuyo volumen es 80 litros,
sube a una balanza y observa que la aguja
indica una lectura de 800N. Sabiendo que
la densidad del aire es 1 ,2 kg/m3, determi­
nar el peso rfcal del hombre.
g = 1 0 m/s2
SOLUCION:
La balanza nos indica la reacción normal
entre los pies del hombre y la plataforma
de la balanza.
XFy = 0
E = 1,2 kg/m3 (10m/s2) (80 x 10“3m3)
E = 0,96 N
Reemplazando en (1)
W = 0,96 N + 800 N
W = 800, 96 N
PROBLEMA N° 6
En el espacio vacío de un tubo baro­
métrico que marcaba 75 cm. de Hg., figura
(1 ), se introduce un poco de gas y enton­
ces el instrumento indica 72 cm. de Hg.,
figura (2 ).
¿Cuál es la presión absoluta del gas?

319. Fig.O)
SOLUCION:
1) De la figura (1), se deduce que la
presión atmosférica es 75 cm de
Hg., en el lugar donde se realiza la
experiencia.
P (atmosférica)=75 cm H g ....(1)
2) En la figura (2), por el principio fun­
damental de la hidrostatica
Pi = P 2
P atm = 7 2 c m H g + P gas .—(2)
Reemplazando (1) en (2):
75 cm Hg = 72 cm Hg + P gas
P gas = 3 cm Hg
P absolutagas = 3cmHg = 30mm Hg
PROBLEMA N° 7
La figura (1) muestra un tubo de vidrio
de un metro de largo (1 m) abierto por uno
*
i*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
#
*
*
de sus extremos. Se introduce en forma
invertida en un recipiente que contiene
mercurio. Calcular a que profundidad se
encuentra el extremo cerrado del tubo,
figura (2 ), sabiendo que el volumen del
aire se reduce a la mitad.
' F 1 g . l l ) _
AIRE
•
o
•
V
J
: v
lm
Fig-(2)
SOLUCION:
1) Cálculo de la presión absoluta del
aire comprimido, en la figura (2).
2) Por el principio fundamental de la
hidrostática.
P1 = P2
P (aire) = (H + 50) cmHg + Patm
P (aire) = (H + 50)cmHg + 76 cm Hg
P (aire) = (H + 126) cmHg .. (1)
3) Como la temperatura es constante,
aplicamos la ley de Boyle-Mariotte.
P¡. Vi = Pf . Vf .... (2)
4) De la figura (1):
Pi (aire) = 76 cm Hg -(3)

320. Vi = v y V, = | |
*
Reemplazando en (2): *
76 cm Hg.V = (H +126)cm Hg. *
*
Luego: {
H = 26 cm. *
*
PROBLEMA N° 8 J
Una burbuja de aire asciende desde el *
fondo de un lago aumentando 6 veces su £
volumen inicial. ¿Cuál es la profundidad *
del lago? *
Presión atmosférica =10,33 m H2O ®
*
SOLUCION: %
*

321. PROBLEMAS RESUELTOS DE :
HIDROSTATICA
PROBLEMA Nfi 01
En el barómetro mostrado, determinar
la presión absoluta del gas. Densidad del
mercurio = 13 600 kg/m , Presión atmos­
férica = 76 cmHg
g = 1 0 m/s2
Principio fundamental de la hidrostática
Pi = P2
Pgas = 24 cm Hg + Patm
Pgas = 100 cm Hg
En el S.I.:
Pgas= Ü
H
g- g. h
Pgas=13 600-^. 10 ™ (1m)
rrr
Pgas= 136000 Pa
*
*
«r
*
¡«
>
*
s
#
*
Ü
*
*
*
*
*
*
*
*
$
$
*
üjS
s
N
s
fc
*
sfs
*>
#
*
s
í*
PROBLEMA N« 02
Un cuerpo pesa 100 N en el aire, 90 N
en el agua y 80 N en un liquido "x". Deter­
minar la densidad del líquido x.
Consideremos su peso real en el aire,
igual a 100 N.
El dinamómetro "D" nos indica el peso
aparente. La diferencia entre el peso real
y el peso aparente es igual al empuje que
ejerce el líquido sobre el cuerpo
Ehso = Dh2
c g • V = 10 N
Ex = Dx . g. V = 20 N
Dividiendo las Ecuaciones:
dx = 2Dh n
Dx = 2 000 kg/m
PROBLEMA Ns03
Un bloque está sumergido parcial­
mente en el agua, sabiendo que el volu­
men no sumergido es el 2 0 % de su volu­
men total, determinar la densidad del
cuerpo.
Densidad del agua = 1 000 kg/m
SOLUCION:
*
*
*
*
*
$
*
*
*
*
*
*
*
%
Vs : Volumen sumergido
V Volumen tota!
Z F y = 0
W = E
Dcg V = DLiq g. V
Vs
De= ■Duq

322. Porcentaje de volumen sumergido-
% V S= 100%
Reemplazando los datos:
De —0,8 Dl_iq
Dc = 800 kg/m
PROBLEMA Ns04
La figura muestra a un bloque de volu­
men 2 0 0 0 cm3 sumergido en agua total­
mente unido a una cuerda vertical que se
encuentra atado en el fondo del recipien­
te. Si la masa del bloque es igual a 700
gramos, determinar la tensión en la cuer­
da AB.
g = 10 m/s2
SOLUCION:
Cálculo de la densidad del bloque:
D = ^ =
m 700 g
v ” 2000 cm3 ~
0,350 g/cm
En el S .l.: D = 350 kg/m
Realizamos el D.C.L del bloque:
1
IF y = 0
T = E —W
*
*
*
i
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
H
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
T = Diiq.g . V —Dc. g.V
T = g V (Di¡q - Dc)
T =10 m/s2.2 x 10'3m3.650kg/m3
T = 13 N
PROBLEMA N5 05
La figura muestra dos líquidos (1) y (2)
no miscibles contenidos en un recipiente.
Determinar la densidad del cuerpo, sa­
biendo que el 1 0 % de su volumen esta
sumergido en el líquido (1). Las densi­
dades de los líquidos son:
Di = 1 000 kg/m3 , = 3 000 kg/m3
SOLUCION:
Cuando un cuerpo está sumergido en
varios líquidos, cada líquido ejerce? un
empuje independiente sobre el cuerpo.
D.C.L. del cuerpo
EFy = 0 *
W = Ei + E 2 .... (1)
V : volumen del cuerpo
Vi =0,1 V y V2 = 0,9V
Reemplazando en (1)
De g. V = Di . g. Vi + D2. g. V2
Dc = (0,1) Di + (0,9)D2
Dc = 2 800 kg/m

323. La figura muestra dos esferas (1) y (2)
de volúmenes iguales y densidades 900
kg/m3 y 1 700 kg/m3, respectivamente:
Flotando en el interior de un líquido, uni­
dos mediante una cuerda de peso despre­
ciable. Determinar la densidad del líquido
que establece el equilibrio de los cuerpos.
SOLUCION:
Consideremos nuestro sistema físico
(1 +cuerda +2).
El empuje sobre las esferas (1) y (2)
tienen el mismo módulo, por tener igual
volumen.
XFy = 0
2 E = W i + W2
2. Diiq. g. V = Di. g. V + D2. g. V
„ Di + D2
D|¡q = ---- - ----
Reemplazando:
Düq = 1 300 kg/m
PROBLEMA N9 07
La figura muestra un tubo en "U" con­
teniendo dos líquidos A y B no misibles.
Hallar ia densidad de los líquidos sabi­
endo que:
*
*
*
«
*
>
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
¥
*
*
*
*
*
*
*
*
*
$
*
#
$
*
*
*
*
*
*
*
SOLUCION:
Principio fundamental de la Hidrostática
"Dos puntos que se encuentran en un
mismo líquido y a su mismo nivel, sopor­
tan igual presión"
Px =Py
Patm + DA.g.hi = DB.g.h2 + Patm
Da
A hi
Db
Reemplazando:
^ 0.3 cm ^
Da = ----- . Db
0,5 cm
Da = | . D b
O
Reemplazando en la condición inicial:
Da +Db = 1 600 kg/m3
Da = 600 kg/m
DB= 1 000 kg/m3
PROBLEMA N9 08
Un tubo en "U" cilindricos de 4 cm2 y
2 0 cm2 de sección transversal, como
muestra la figura, contiene mercurio a un
mismo nivel. Por el tubo de mayor sec­
ción se vierte lentamente 816 gramos de
H2O.
Determinar la altura que sube el nivel
del mercurio en el otro tubo:
DHg = 13,6 g/cm3

324. SOLUCION:
Cálculo de la altura de la columna de
agua:
m
D = - m = D V
816 g = 1 g/cm3. (20 cm2).h
h = 4 0 ,8 c m — (1)
Del principio de conservación de la masa
(Hg), el volumen desplazado en el tubo
de mayor sección es igual al volumen que
ocupa en el tubo de menor sección. El
mercurio en el tubo de mayor sección
desciende "x“ y en el tubo de menor sec­
ción sube "5x".
Principio fundamental de la hidrostática
Pi =P2
ÜHg.g .(6x) = DH20 .g.h
ÜHg (6x) = DH
2o h
13,6 g/cm3. (6x) = 1 g/cm3 (40,8 cm)
x = 0,5 cm
*
*
*
*
*
*
♦
*
Un bloque de masa "m “ y densidad 500
kg/m3es abandonado sobre el plano incli­
nado. Despreciando toda forma de roza­
miento. Determinar la aceleración del
bloque. 0 = 30°
Realizamos el D.C.L. del bloque:
El mercurio sube en el tubo de menor
sección "5x", por consiguiente : 2,5 cm.
*
*
*
*
$
*
*
*
#
*
*
*
♦
*
♦
*
*
*
S
lí
*
Slí
*
*
*
*
*
*
*
*
*
Slí
*
*
*
*
*
s
u
*
$
*
2da Ley de Newton
F r (// al plano) = m a
(E - W) Sen 0 = — . a
9
. g . Sen 0
L- 1 j. g . Sen 0
Reemplazando datos:
a = 5 m/s

325. Considerando que no hay resistencia
del agua debido a la viscocidad, una es­
fera de volumen 0,006 m3 se lanza del
punto “A" con una velocidad de 3 m/s.
¿Al cabo de qué tiempo vueíve a pasar por
el punto de partida, sobre el plano incli­
nado, La masa de la esfera es 5 kg.
g =10 m/s2
AIRE
AGUA
SOLUCION:
Cálculo de la densidad de la esfera:
Dc =™ = | . 1° 3 kg/m3
Del problema anterior, ia aceleración de
la esfera se determina del siguiente mo­
do:
a =
f Düq
1- 1 1 g. Sen 0
Reemplazando en el S.l. :
a =
a = 1 m/s
De la ecuación cinemática:
Vf = V0 - a t
cuando se detiene instantáneamente,
para regresar, VF = 0
t =3 s
0 = 3 —(1) t ->
Luego el cuerpo regresa al punto “A”
luego de 6 segundos.
PROBLEMA Nfi 11
La figura muestra dos bloques (1) y (2)
de pesos 40 N y 30 N respectivamente,
*
*
#
*
*
*
*
*
*
♦
*
&
*
#
¡¥
*
*
*
*
*
*
*
*
*
*
*
#
cuyos volúmenes son iguales. Despre­
ciando toda forma de rozamiento, hallar el
volumen de los bloques, para establecer
el equilibrio.
g = 10 m/s2
SOLUCION-
El empuje “E” sobre cada bloque tiene
igual módulo, por tener igual volumen.
D.C.L. del bloque (1):
XFy = 0
T = E - W i
D.C.L. del bloque (2):
T + W i = e
.... (1)
I F (// plano) = 0

326. T = (E - W2) Cos 60° ....(2)
Igualando las Ec. (1) y (2):
( E - W i ) = ( E - W 2) . |
Del dato:
E = 50 N
Duq. g, V = 50 N
1 000 kg/m3 . 10m/s2 V = 50 N
V = 5 10-3 m3
W
AIRE
0
O
í
> ' .
V 9
O ";T| }
¡
1 o c 9
°í ¿ 3
.
.
. t• «
.
-á g ü a '
X
- - A
- y -
E -
A : área de la cara del cubo
D,C L. (corcho cúbico)
IFy= 0
E = W
DLíq - g Vs = Dc g . V
Vs=^ V - (1)
A(10-x) = ~ A . (10)
x = 7,5 cm
*
*
*
*
*
*
#
>
*
La figura muestra dos bloques (1) y (2)
de pesos 10 N y 40 N respectivamente y
volúmenes iguales, en equilibrio. Despre­
cie toda forma de rozamiento.
Determinar el volumen de cada blo­
que.
g = 1 0 m/s2
PROBLEMA N® 12
Un corcho cúbico de arista 10 cm., con
o ’
densidad 0,25 g/cm flota en el agua.
¿Qué altura del bloque queda por encima
de la superficie del agua?
SOLUCION:
D.C.L del bloque (1):
*
#
I F (// plano) = 0
T = (E —W i) Cos 60°
D.C.L. del bloque (2):
/

327. Igualando las Ec. (1) y (2):
(E - W i) ~ = W2 —E
Reemplazando
E = 20 N
D u q . g . V = 20 N
1 000 kg/m3 . 10 m/s2 . V = 20 N
V = 2 . 10-3 m3
V = 2 litros
PROBLEMA N5 14
Un tubo en "U" de sección transversal
constante que contiene un líquido, es
acelerado hacia la derecha con una acele­
ración constante "a", como indica la figu­
ra. ¿Cuál es la diferencia de alturas "h“
entre las columnas de líquido de las ra­
mas verticales?
SOLUCION:
Consideremos como nuestro sistema fí­
sico el tubo horizontal de sección "S".
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
»
O
*
*
*
*
*
*
*
*
*
*
*
<
t>
#
*
*
*
*
*
m
*
*
*
*
*
*
Si F = P.S
F1 = D. g. hi(5)
F2 = D. g. h2(5)
2da' Ley de Newton : Fr = m.a
(Ft - F2) = m . a
S.D.g (hi - h2) = D. (SL). a
hi - h2 = —L
9
'-H
r±
Luego:
CONSECUENCIA
Un recipiente que contiene un cierto líqui­
do, acelera horizontalmente. Debido a la
inercia, la superficie libre del líquido se
inclina un ángulo "6" respecto de la hori­
zontal.
De la fórmula anterior

328. Pero:
h
3 = L ' 9'
= Tg0
a = g . Tg 0
"El ángulo de inclinación " 0 * es direc­
tamente proporcional a la magnitud de la
aceleración"
PROBLEMA N® 15
La figura muestra un ascensor que
sube verticalmente con aceleración con­
stante "a" en su interior lleva un líquido
de densidad "D" en reposo respecto a las
paredes dei ascensor. Hallar la diferencia
de presiones entre los puntos A y B sepa­
rados una distancia "h".
SOLUCION:
Tomaremos como muestra (sistema físi­
co) un "tubito” imaginario del líquido, de
altura "h" y sección “S", entre los puntos
A y B.
lí
2da Ley de Newton
(F2 - Fi - mg) = m a
(F2 - F i ) = m(a + g) Fz
Pb(S) —Pa(S) = Duq - (S.h) (a + g)
m
g
*
*
*
*
*
*
*
s
ü
$
*
*
*
*
*
*
*
*
*
$
*
*
*
<
*
>
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
i *
Í4
*
*
*
Pb - Pa = Düg • (g + a ). h
CONSECUENCIA
En la figura mostrada, un bloque se en­
cuentra parcialmente sumergido.
La presión hidrostática a la profundi­
dad "h" será:
P = Duq . (g + a ). h
II) La fuerza resultante (EMPUJE) que
ejerce el líquido sobre el cuerpo
sumergido parcialmente, será:
E = P.A
E = Duq (g + a), h . (A)
A: área de la base del cuerpo
A.h volumen sumergido (Vs)
E - D|_¡q . (g + a). Vs
“La magnitud del empuje es proporcional
al módulo de la gravedad efectiva".
Este resultado es compatible con el Prin­
cipio de equivalencia, base de la Teoría
de la Relatividad.
PROBLEMA Ns 16
En la figura mostrada el ascensor está
inicialmente en reposo y en su interior
contiene agua, sobre el cual flota un blo­
que de madera. Cuando el ascensor sube
con aceleración “a". ¿Aumentará el volu­
men sumergido en agua?
*
*
*
*
*
¡»
*

329. SOLUCION:
Cuando el ascensor está en reposo, el
peso del cuerpo es igual al empuje Con­
sideremos el volumen sumergido Vv
V : volumen total del cuerpo.
E = W
Duq- g . Vi = Dc. g . V
V1 = Í ? £' V
Duq
(1)
Realizamos el D.C.L. del bloque, cuando
el ascensor sube con aceleración. Con­
sideremos el volumen sumergido V2.
E ’ = Empuje = Duq . (g + a ) . V2
2da Ley de Newton
(E ’ - mg) = m.a
E ’ = m(g + a)
Del problema anterior, sabemos que:
Duq . (g + a) V2 = Dc . V. (g + a)
Dc
V2 = “ -V
oL
íq
.... (2)
De las Ec. (1) y (2):
Vi = V 2
*
d
»
<
*
*
*
*
*
*
*
*
*
d*
*
d
»
d
)
*
*
«
ü
*
*
*
*
*
*
*
"El volumen sumergido permanece
constante, independiente de la acelera­
ción del sistema'1
PROBLEMA Ns17
Un cisterna de largo "L" y una altura
"h“ está llena hasta el máximo de un lí­
quido de densidad “D” y se mueve con
una aceleración "a” en la dirección hori­
zontal. Determinar la diferencia de pre­
siones entre los puntos A y B.
*
*
d
»
d
>
*
d
»
*
dí
df
*
*
*
*
*
d
s
*
*
*■
*
d
>
d
*
*
d
*
*
x ■
------ ^ — ^ u a
n v ' N . ■. N " B ■
y v ^
■ ' . ' v x
v ' N v n
' O* VS N S v
SOLUCION:
Consideremos nuestro sistema físico, el
“tubito" BC de sección "S".
Si, F = P.S
F2 = PB . S
F3 = Pc . S
IF y = 0
(F3 —F2) = W
(Pc- P b)S = D. g. (S.h)
Pc - Pb = D. g. h ....(1)
Consideremos nuestro sistema físico, el
"tubito" AC de sección "S".
2da Ley de Newton
Fr = m . a
( F i - F 3) = D V a
(PA - Pc)S = D.(SL). a
Pa ~ Pc = D.L.a
Sumando las Ec. (1) y (2):
.... (2)
Pa —Pb = D(g.h + a.L)
La diferencia de presiones entre A y B se
incrementa debido a la inercia.
Si a = 0, el móvil está en reposo o se
mueve con velocidad constante, enton­
ces:

330. Pa - Pb = Dg.h
PROBLEMA N® 18
La figura muestra un globo esferico
inflado con Helio de densidad 0,1 kg/m y
volumen 1 ,0 m3 , está unido por una cuer­
da de peso despreciable a un bloque de
densidad 1 1 0 0 kg/m3 y volumen 0,006 nv
sumergido totalmente en agua. Sabiendo
que el bloque se encuentra en equilibrio,
determinar el peso del material que está
fabricado el globo. No hay rozamiento.
Densidad del aire = 1,2 kg/m3
g = 1 0 m/s2
AIRE
ÍGÜA
SOLUCION:
Realizamos el D.C.L. del bloque:
£ F (// plano) = 0
T = (W2 - E2) Cos 60° ....(a)
Realizamos el D.C.L. del globo:
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*h
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
4
=
*
*
(K
*
#
*
*
*
¡fe
*
*
*
*
Ei empuje sobre el globo, debido al
aire que lo rodea.
Wi : peso del gas Helio
x ■ peso del material que está fabri­
cado el globo.
£ Fy = 0
T + Wt + x = Ei ...(P)
Reemplazando ( a ) en ( p)
x = ( E i —Wi) —-g(W2 - E 2)
En el S.L:
gVg
x = g.Vi(Da - DHe) - s y ~ (De- DHío)
x = 10 (1) (1,1) - ^ 6.10’3 . (100)
x = 8 N
PROBLEMA Nfi 19
Despreciando el espesor de ias pare­
des del recipiente cilindrico de radio
0,5 m. ¿Cuál será el peso de dicho recipi­
ente, si se encuentra en flotación en el
agua?
g = 1 0 m/s2
V
O 0 ' O
AIRE
0 ,6 m
O O
O ■ — 0 ,4 m ~ ~
AGUA - o —- Ii —
- - -
-----------
------------

331. SOLUCION:
Cálculo de la presión manométrica del
aire comprimido.
Principio fundamental de la hidrostática
Pi = P2
Paire = D. g. h
Paire = 100 —
% . 1 0 —
^ (0,4 m)
m s
Paire = 4 000 N/m¿ -(1)
Realizamos el D.C.L. del recipiente.
Despreciamos el volumen de las pare­
des, por consiguiente el empuje es nulo.
*
*
*
*
*
*
*
n
>
*
*
*
*
*
*
*
*
o
»
*
*
*
*
del aire comprimido.
I F y = 0
W = Faire — Paire S
W = (Paire) . 7
1 R 2
Reemplazando (1) en (2):
N 1 p
W = 4000 —
m2 4
....(2)
W = 3 141,6 N
PROBLEMA N®20
La figura muestra un globo esférico
inflado con Helio de densidad 0,1 kg/m3 y
*
*
o
*
*
<
*
*
*
*
*
*
*
*
*
*>
*
*
*
volumen 1 m ,y está unido por una cuerda
de peso despreciable a un bloque de den­
sidad 1 100 kg/m3 y volumen 0,005 m3
sumergido totalmente en agua. Sabiendo
que el bloque se encuentra en equilibrio,
determinar el peso del material que está
fabricado el globo.
Densidad del aire = 1,2 kg/rr.3
g = 1 0 m/s2
SOLUCION:
IF y = 0
Ei + E2 —W 1 —W 2 —x = 0
x = E1 + E2 —W 1 —W2
En el S.I.:
x = ( E , - W i ) + (E2- W 2)
X =gVi(Daire—
DH
e) + gV2(Dagua—
De)
Reemplazando datos:
x = 10 (1) (1,1) + 10 x 5.10'3(—
100)
x = 6 N
PROBLEMA Nfi 21
Un cilindro sellado que está comple­
tamente lleno de un líquido de densidad
”D", gira alrededor de un eje con una
velocidad angular “W". Hallar la diferen­
cia de presiones entre los puntos A y B,
sabiendo que la recta que contiene a es­
tos puntos es una recta radial y horizontal
(considerar al líquido en reposo con res­
pecto al cilindro).

332. Elegimos como nuestro sistema físico el
tubito de líquido AB de sección "S".
R+r
M r . :
r-j
| E
t í
4
R
Dinámica circular
Fc = m ac
(Fi - F2) = m , W2 Rg
Pero: Fi = PA(s) y F2 = PB(S)
Reemplazando:
(Pa - Pb) S = D V. W2 . Rg
(Pa- Pb) S = D. (R - r)S. W'
Luego;
2 + r)
2
P A - P B = ^ ( R 2 - r 2)
PROBLEMA Ne 22
En el sistema mostrado, cuando el as­
censor baja a velocidad constante el em­
*
$
&
#
*
*
$
+
*
si»
*
♦
*
«
ü
«
*
*
¡s
*
*
*
*
*
*
*
#
*
«
!>
*
*
*
*
#
«i
♦
sfc
♦
♦
*
*
*
*
%
*
*
•*
*
*
*
*
*
*
*
#
*
*
*
*
#
*
#
>
*
puje que actúa sobre el cuerpo parcial­
mente sumergido es E = 20 newtons. De­
terminar la magnitud del empuje, cuando
el sistema baja con una aceleración de
a = 5 m/s¿
SOLUCION:
La magnitud del empuje depende de la
"gravedad local” que afecta al fluido que
lo rodea.
E = ÜLiq V , (g ± a)
(+): cuando sube con “a"
( - ) cuando baja con "a"
Cuando el sistema baja con velocidad
constante (a = 0).
E = Duq V . g
20 N = 1‘000 kg/m3 (V). 10 m/s2
V = 2 .10~3 m3
cuando el sistema baja con aceleración
constante "a”.
Ei = 1000 kg/m3.(2.10'3m3). (10-5) rtVs2
Ei = 10 N
PROBLEMA Nfi 23
La figura muestra un recipiente cer­
rado, en su interior contiene un cierto gas
de densidad 10 kg/m3. La esfera de volu­
men 0,005 m3 y densidad 250 kg/m3, se
encuentra suspendido en el techo. Hallar
la tensión en la cuerda AB.

333. A
SOLUCION:
Realizamos el D.C.L. de la esfera.
I F y = 0
T + E = W
T = W —E
T - g. V (De — Dgas)
En el S.L:
T = 10m/s2.5x10'3m3 (240 kg/m3)
T = 12 N
PROBLEMA Ns24
La figura (1) muestra un recipiente que
contiene agua, la balanza indica un peso
de 25 newtons. En la figura (2) el bloque
atado por una cuerda se sumerge hasta la
mitad si el empuje que actúa sobre el
bloque es E = 5 newtons, hallar la lectura
de la balanza en ia figura (2 ).
ifí
| SOLUCION:
$ De la figura (1), se deduce que el peso
* total (agua + recipiente) es igual a W =
£ 25 N.
íK
* Realizamos el D.C.L. (bloque) y el dia-
| grama del cuerpo libre del (recipiente +
* agua).
*
* El empuje (E) es una fuerza de acción.
La reacción actúa sobre el bloque y la
J acción sobre el sistema físico (agua +
* recipiente).
4*

334. D.C.L del sistema físico, (agua + recipi­
ente), actúan las fuerzas peso total (W),
Empuje (E) y la normal (N).
I Fy = 0 ..... lera, condición de
Equilibrio.
N = W + empuje
Luego: N =25 newtons + 5 newtons
N = 30 newtons.
La lectura en la balanza es igual a la
reacción normal.
PROBLEMA Ns 25
La figura muestra una esfera de volu­
men 2 litros y densidad 400 kg/m sumer­
gido totalmente en el agua por acción de
la cuerda AB.
Determinar la tensión en la cuerda.
Dagua = "
10 0 0 kg/m3
g = 1 0 m/s‘
SOLUCION:
Diagrama del cuerpo libre de la esfera:
IFv= 0
T + W = E
T = E - W .... (1)
Reemplazando en (1)
T = Di_.g.v - Dc.g.v
T = g.v (Dl - Dc)
*
«
*
*
*
*
*
«i
»
*
*
*
*
#
S
jS
*
*
*
*
*
»
m
*
*
*
N
*
*
*
En el S .l.:
T = 10 % . 2 x 10-3 m3. (600 kg/m3)
T = 12N
PROBLEMA Ne26
Un oso polar de peso 2 500 N se en­
cuentra parado sobre un bloque de hielo
(densidad 900 kg/m3) flotando en el agua.
Determinar el mínimo volumen del bloque
de hielo, tal que, el oso no se hunda.
g = 1 0 m/s2
SOLUCION:
D.C.L. del bloque de hielo
*
*
*
*
*
»
*
*
*
*
*
*
#
*
#
*
*
*
*
*
*
*
m
*
*
ZFy = 0 -> E = WA + Woso
E - W h = W o s o
D l g v - DH. g. V = WO
S
o
g . v (Dl - Dh) = Woso
Reemplazando datos en el S.l.:
10 v (100) = 2 500
v = 2,5 m
PROBLEMA N®27
Dos esferas de pesos 10 N y 40 N, y de
igual volumen flotan en el interior de un
líquido unidos por una cuerda de peso
despreciable, en la forma que muestra la
figura. Hallar la tensión en la cuerda.

335. SOLUCION:
D C.L esfera (1)
IF y = 0
E = W i,+ T .....(1)
El empuje "E" sobre los cuerpos son igua­
les, dado que los volúmenes son ¡guales.
D.C.L. esfera (2)
£ F y = 0
W2 = T + E .... (2)
Sumando las Ecuaciones (1) y (2).
Wg = W i + 2 T
W2 - Wi
2
Reemplazando los datos:
T = 15 N
PROBLEMA N®28
La figura muestra una esfera flotando
entre dos líquidos no miscibles (1 ) y (2 ).
Si el 50% de su volumen está sumergido
en el líquido (2 ), determinar la densidad de
la esfera.
*
*
*
*
*
*
*
*
*
*
$
*
*
s
te
*
*
s
í?
#
*
*
*
*
#
*
♦
*
*
*
*
#
*
*
*
*
*
*
*
*
*
#
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
SOLUCION
Cuando un cuerpo está sumergido en
varios líquidos cada líquido ejerce un em­
puje independiente.
D.C L.(Esfera)
En el S I :
V V
Dc g . v = D i . g . - + D 2. g. —
Dc =
Di + D2
Reemplazando los datos:
Dc = 700 kg/m
PROBLEMA Ne29
La figura muestra dos bloques (1) y (2)
de volúmenes iguales y de pesos 10 N y
40 N respectivamente. Despreciando to­
da forma de rozamiento, determinar el vo­
lumen de cada bloque, sabiendo que el
sistema se encuentra en equilibrio.
g = 1 0 m/s2

336. SOLUCION:
D.C.L bloque (1)
IFy= 0
T = E = W i
T = (E —10) ...(1)
I F (// plano) = 0
T = (W2 - E) Cos 60°
*
*
*
*
m
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Los bloques (1) y (2) tienen igual volu­
men, por consiguiente los empujes serán
iguales.
D.C.L bloque (2)
T = (40 —E ) . ¿
Igualando las Ec. (1) y (2)
(E = 10) = (40 —E) |
E = 20 N .... (3)
Pero en el S.L.
E = Duq . g . V
20 N = 103 kg/m3 . 10 m/s2. V
V = 2 x 10~3m3
V = 2 litros
PROBLEMA Ns30
La figura muestra dos bloques (1) y (2)
de igual volumen y pesos 10 N y 40 N
respectivamente. Despreciando toda for­
ma de rozamiento, hallar el volumen de
cada bloque, para el equilibrio.
Dagua = 1 0 0 0 kg/m3
g = 1 0 m/s2
*
*
*
1) D.C.L bloque (1):

337. Z F (// plano) = 0
T = (E - 10) CosG -■(1)
La resultante vertical entre el empuje "E"
y el peso = 10 N, tiene sentido hacia
arriba.
Sí los bloques (1) y (2) tienen igual
volumen, entonces los empujes también
son iguales.
2) D.C.L. bloque (2)
*
*
*
*
*
*
*
*
$
$
*
*
*
*
*
*
*
*
*
*
*
*
s
is
*
$
*
*
*
*
I F (// plano) = 0
T = (40 - E) Cos 6 ....(2)
La resultante vertical entre el empuje “E"
y el peso W2 = 40 N, tiene sentido hacia
abajo.
Igualando (1) y (2)
(E - 10) Cos 6 = (40 - E) Cos 6
E = 25 N

339. ‘
f i P
i
MOVIMIENTO ARMONICO
SIMPLE a
CO
N
CEPTO
SPR
E
V
IO
S:
Elongación (X)
Es una magnitud vectorial, indica la posi­
ción de la partícula "m" en cada instante de
tiempo T respecto de la posición de equili­
brio, (PE).
P.E. '
■
/W M íW W '.vM f-TOW AW - m
1 ........
Amplitud (A)
Es la máxima elongación alcanzada por
la partícula en movimientos. La partícula
inicia su movimientos, (t = 0) cuando X = A,
mediante Ley
[ x (t) = A Cos (wt)
$
*
*
*
*
*
*
*
*
*
*
m
+
*
*
+
*
*
*
*
*
*
*
*
*
FUERZA RECUPERADORA (F)
Es aquella fuerza interna que manifiestan
los cuerpos elásticos al se' estirados o com­
primidos, actuando sobre la partícula *m“
haciendo que recupere su posición de equili­
brio. La fuerza recuperadora es la tensión o
compresión de los resortes, se representa
por un vector F que actúa sobre la partícula
indicado siempre la posición de equilibrio.
Ley de Hooke:
F = —K .X
K : constante de rigidez del resorte
(N/m).
CO
N
CEPTOD
E
LM.A.S.
Es aquel movimiento oscilatorio y pe­
riódico, realizado en línea recta ocasionado
por una fuerza recuperadora y descrito ma­
temáticamente mediante funciones seno y
coseno.
R
E
LA
C
IO
NE
N
TREE
LM
.A.S. YE
LM
.C
.U
.
Sí una partícula se desplaza con un mo­
vimiento circular uniforme (M.C.U.), sus pro­
yecciones sobre su diámetro cumplen con
los requisitos del M A.S. Observe atenta­
mente las proyecciones y compárelas con el
M.A.S. realizado por "m".
$
*
$
#
$
*
❖
*
*
*
*
r
k /
Á B
______ 1 (•={)
V .
X
/ 1
/ »
/ »
/ i
/ i
f i
i
a _ b _
->

340. Es la proyección del radío "A" sobre el eje
horizontal.
El ángulo “ 0 ”, es el desplazamiento
angular que experimenta la partícula en M
C. U ., 6 = co.t
X (t) = A . Cos 6
X (t) = A . Cos (m.t) (1)
VELOCIDAD INSTANTANEA
Es la proyección de la velocidad tangen­
cial sobre el eje horizontal La velocidad "V"
en el M.C.U. es V = coA.
V (t) = V . Sen 6
V (t) = ü)A. Sen (cot) ... (2)
ACELERACION INSTANTANEA
Es la proyección de la aceleración cen­
trípeta sobre el eje horizontal La acelera­
ción centrípeta en el M. C. ü . , es o2 A
a (t) = ac . Cos G
a (t) = tú2 . A . Cos (<ot) .... (3)
*
*
*
*
*
*
*
*
+
m
*
*
*
*
*
*
*■
*
*
♦
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
Reemplazando (1) en (3):
a (t) = co2 . X .... (4)
PERIODO DE LA PARTICULA "nV7
Analizando la partícula de masa ”m" diná­
micamente, realizamos el diagrama del cuer­
po libre en cierto instante “t".
F
Segunda Ley de Newton:
F r = m.a
K . X = m(cu2.X)
K = m . co'
.2
ü>
- ñ (5)
Reemplazando en (5): co=
ENERGIA TOTAL DEL SISTEMA
La partícula de masa “ m" inicia su mo­
vimiento en el instantet=0,cuando laelon-
gación es igual a la amplitud (x = A) La
fuerza recuperadora F que actúa sobre la
partícula “m varía con la distancia como
muestra la figura

341. La energía total del sistema masa-re­
sorte, es igual al área bajo la recta.
ETotai = Area A
ETotai = | A (KA)
ETotai = 7, K A
Si 0 X A, la energía total del sistema es
la suma de dos términos que corresponden
a la energía cinética y la energía potencial
elástica.
ETotai = Ec + Ep
1 KA2 = 1 mV2 + 1 KX2
2 2 2
Donde V es la velocidad de la partícula
"m" en el instante “t" que se encuentra a la
distancia X de la posición de equilibrio.
ASOCIACION DE RESORTES
Los resortes unidos a masas se pueden
conectar a ella, de dos formas básicas, en
serie y en paralelo. El conjunto de resortes
es factiole de ser sustituido por un solo re­
sorte equivalente y cuya constante de rigidez
se denomina constante equivalente (Ke)
ASOCIACION EN SERIE
Puede apreciarse en el gráfico adjunto
que la tensión que soportan los resortes son
iguales (T = KX).
Luego:
T = K1X1 = K2X2 = K3X3 = KeXe .... (1)
*
*
$
*
*
4»
♦
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
i
<
¥
*
*
*
*
*
*
*
*
*
*
El desplazamiento X e equivalente es
igual a la suma de los desplazamientos de
los resortes.
Xe = X1 + X2 + X3 .... (2)
Reemplazando (1) en (2):
CASO PARTICULAR
Asociación de los resortes en serie:
Ke =
K1 . K¿
K1 + K2
ASOCIACION EN PARALELO
**1
m -''
-«•¡i.:»-
|
.v.-v.v.
•
i *•
. -
■■
■
■■ -.
.
.
- %-
En el caso de la deformación X es igual
en todos los resortes. La tensión equivalente
(Te) será:
Te = T i + T 2 + T3 ....(1)
La tensión en cada resorte es:
Ti =Ki K ; T2 =K2 X ; T3 =K3X
Reemplazando en (1):
P j ^ K i ^ K ^ K s J j
* Como regla práctica, haremos ana­
logía con la asociación de conden­
sadores.

342. PENDULO SIMPLE
CONCEPTO:
Es aquel sistema constituido por una ma­
sa "m" de pequeñas dimensiones suspen­
dida de un hilo inextensible y peso despre­
ciable, que puede oscilar alrededor de su
posición de equilibrio, con un movimiento
que es aproximadamente un M A S .
-Para determinar la causa de las oscilacio­
nes, realizamos el diagrama del cuerpo libre
de la masa pendular "m". Identificando, la
fuerza recuperadora en una componente del
peso mg tangente a la circunférencia.
F = m. g Sen © .... (1)
De la segunda Ley de Newton:
F = m. a .... (2)
Reemplazando (1 ) en (2):
m, g. Sen 6 =m. w2. x ... (3)
Para amplitudes pequeñas se cumple (0
er» radianes) .
Sen 0 s 0
x = 0. L = Sen 0. L
Reemplazando (4) en (3):
g. Sen 0 = co2. (Sen 0. L)
.... (4)
4n
9 =
r- 2nñ
El período de un péndulo fue descubierto
por Gaiileo en 1 583.
PERIODO DEL PENDULO SIMPLE EN
UN SISTEMA ACELERADO:
Si L es la longitud del péndulo, se de­
muestra que en el caso de oscilaciones de
pequeña amplitud su período T será dado por
Ja fórmula:
El período del péndulo simple es:
- Directamente proporcional a la raíz cuad­
rada de su longitud.
- Inversamente proporcional a la raíz cua­
drada de la aceleración de la gravedad
efectiva gef.
- Independiente de la masa del péndulo
- Independiente de la amplitud.
Él período de un péndulo, en el interior
de un ascensor que se mueve con acele­
ración a.

343. * Si el ascensor sube a (+): t
* Si el ascensor baja a (-): i
¿Qué ocurrirá con ei péndulo cuando el
ascensor baja con aceleración a = g?
El periodo se hace infinito. El péndulo
ilegará a Su estado de imponderabilidad, es
decir el péndulo queda inmovilizado con re-
| lación al ascensor, cuando éste se encuentre
* en su posición extrema. Pero si el ascensor
J adquiere a = g hacia abajo cuando el péndulo
* no está en su extremo, entonces ia bolita
J girará uniformemente unido al hilo en el plano
i vertical y con la velocidad que tenía en el
J instante en que el ascensor adquiere a = g.
*
*
*
*

344. >ii» a
PF
9. MOVIMIENTO ARMONICO SIM­
PLE Y PÉNDULO SIMPLE
PROBLEMA Ns 01
Un cuerpo cuelga del extremo de un
resorte y oscila verticalmente con el pe­
ríodo de 2 segundos. Al aumentar la ma­
sa del cuerpo en 1 ,0kg, el nuevo período
es de 3 segundos.
¿Cuál es el valor de la masa inicial?
SOLUCION:
El período de oscilación es directamente
proporcional a la raíz cuadrada de la ma­
sa.
1er. Caso:
T A 2 m
T , = 4 *
2do. Caso:
k
(1)
.... (2)
*
&
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
i»
*
*
m
*
S
jf
*
*
*
*
*
*
S
¡
6
*
%
s
¡»
*
*
*
*
*
*
*
T , m
(m + 0,5) 9
Resolviendo:
m = 0,4kg
PROBLEMA Nfi 02
Un cuerpo cuelga del extremo de un
resorte y oscila verticalmente con el pe­
ríodo de 2 segundos. Al aumentar la ma­
sa del cuerpo ¿Cuál es el valor de la masa
inicial?.
d) 4 kg
a) 1,0kg
O g k g
e) gkg
PROBLEMA N903
Una caja de masa M está sobre una
mesa horizontal. El coeficiente de roza­
miento entre la caja y la mesa es igual a
14. Dentro de la caja descansa un cuerpo
de masa m que puede moverse sin roza­
miento sobre el fondo de la caja. Este
cuerpo está sujeto a la pared por medio
de un resorte cuya rigidez es K. ¿Con qué
amplitud de las oscilaciones del cuerpo
comenzará la caja a moverse sobre la
mesa?.

345. SOLUCION
La fuerza F máxima que aplica el resorte
sobre la caja será:
F = K . A ..(1)
Cuando el resorte está pronto a mover­
se:
SF* = 0
F = fs(máx)
F = n . N;
Pero- N = (m + M) g
K A = p . . (M + m) g
*
*
*
e
*
*
*
*
*
#
*
*
*
*
*
*
*
*
m
*
#
*
*
#
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
♦
*
♦
*
*
*
«
*
*
*
é
#
*
*
*
*
*
*
#
*
*
*
*
*
*
*
m
*
#
*
#
*
Una caja de masa M = 9 kg. está sobre
una mesa horizontal. De la caja, por medio
de un resorte de rigidez K = 500N/m, está
suspendida un bloque de masa m = 1
kg. ¿Con qué amplitud de las oscilaciones
del bloque "m" empezará la caja a saltar
sobre la mesa? g "= 1 0 m/s2
al 0,1m b) 0,2m c) 0,3m
d) 0,4m e) N.A.
PROBLEMA N° 05
En los sistemas armónicos (A) y (B)
mostrados determinar la razón de los pe­
riodos:
(B>
I b
(A)
= 7
SOLUCION:
Período de oscilación del sistema’
T = 2n

346. Cálculo de la constante de rigidez equiva­
lente: (analogía con la Asociación de
Condensadores)
A : Asociación en paralelo:
Ka = 2K ....(1)
B Asociación en serie:
K b = 2
.... (2)
Relación entre los períodos de A y B
.... (3)
IZ
t b V k
b _
K a
Reemplazando (1) y (2) en (3):
PROBLEMA Ne06
La figura muestra una instalación de
un sistema de resortes donde la constan­
te de rigidez es K = 400N/m. Determinar
el período de oscilación de la plataforma
de masa m = 11 kg.
a) 3,1416 s
c) 0,31416 s
e) N.A.
b) 6,2832 s
d) 0,62832 s
*
*
m
*
*
*
*
#
*•
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
$
*
*
*
*
<
*
*
*
*
*
*
*
*
#
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
&
*
#
*
Un sistema masa-resorte oscila libre­
mente en un plano horizontal sin fricción.
Si la energía del sistema es 40 joules,
calcular la energía cinética del bloque de
masa "m" cuando la elongación es la mi­
tad de amplitud A.
r
A/2
r 1 i
; -a ^ m w ,
v v w m .sJ
P.E
SOLUCION.
La energía total del sistema se expresa
del siguiente modo:
| KA2 = Ep + Ek = 40J
2 K- A2 = 2 K’ X* + Ek
Para nuestro caso: X = A/2
Reemplazando en (2):
3
(1)
.... (2)
Ek = - ... (3)
Reemplazando (1) en (3):
Ek = 30 J
PROBLEMA Nfi 08
Si el sistema formado por un bloque
de 3,0kg y un resorte de constante elás­
tica K = 300 N/m se deja en libelad de
movimiento siendo X0 = 2 ,0 m, determinar
la máxima velocidad que adquiere el blo­
que. No hay rozamiento

347. H
-----WvVAWV'.'VWAMV----- H
a) 10m/s b) 15m/s
c) 20m/s d) 25m/s
e) Ninguna
PROBLEMA N2 09
El período de vibración del sistema
mostrado es 0,3 segundos; si se saca el
bloque A el nuevo período es 0,6 segun­
dos. Sabiendo que la masa del bloque A
es 22,5kg, determinar la masa del bloque
B. No hay rozamiento.
SOLUCION:
El período de oscilación depende úni­
camente de la masa del sistema. La
constante de rigidez depende del mate­
rial y de la forma del resorte.
$
*
$
♦
*
$
*
*
*
*
*
*
*
*
*
*
❖
♦
*
a
fe
*
K
2do. Caso:
-r y
, mB
-“ ¡T
.... (2)
(mA+ mB)
2 :
T ,
me • I - < 3>
Reemplazando; rrtA = 22,5kg, en (3):
me = 18 kg
PROBLEMA N®10
El bloque mostrado de masa M = 1,0 Kg
oscila tal que su amplitud es A = 30 cm en
el instante en que M pasa por su posición
de equilibrio es impactada verticalmente
por una masa m = 3,0kg, el cual se adhiere
a M. Calcular la amplitud del sistema de
masas.
*
*
*
*
*
*
d) 25cm e) Ninguna
PROBLEMA Ne 11
Las masas de la figura se deslizan
sobre una mesa que no ofrece rozamien­
to. El resorte está unido al bloque de
masa "m". Si ahora los bloques m y M
son empujadas hacia la izquierda de ma­
nera que el resorte se deforma 60cm por
comprensión. ¿Cuál será la amplitud de
oscilación de m, después que las masa se
liberan?

348. . , m 4
donde: — = —
M 5 #
*
PROBLEMA Nfi 12
Una bala de masa m = 0,2kg es dis-
EM (1) = EM (2)
¿ k . X 2 = | ( m + M)V2
k X2 = (m + M) V2 .... (1)
Principio de conservación de la Energía
Mecánica:
EM (2) = EM (3)
| (m + M)V2 = 1 MV2 + | K. A2
$
$
*
$
$
*
m
*
*
*
*
$
*
*
a) 0,05m b) 0,15m
c) 0,20m d) 0,25m
e) N.A,
PROBLEMA N2 13
Un péndulo oscila en un plano vertical
con el período de 2,0 segundos. Al au­
mentar la longitud de la cuerda en 25cm.,
el nuevo período es 3,0 segundos. ¿Cuál
es la longitud inicial de la cuerda?
SOLUCION:
k A2 = m V2
Dividiendo (1) r (2)
x2 m + M
a 2_ m
m
(
2)
Vm+ M
Reemplazando.
A = 40cm

349. El período de oscilación es directamente
proporcional a ia raíz cuadrada de longi
tud de la cuerda.
2n
£
Relación entre los períodos:
j2 _ L1
T’ = L2
1 2
Reemplazamos datos en (1):
4 = L
9 L + 25
Resolviendo:
L = 20 cm.
PROBLEMA N° 14
Un péndulo oscila en un plano vertical
con el período de 3,0 sagundo. Al aumentar
la longitud de la cuerda en 70 cm., el nuevo
período es 4,0 segundos. ¿Cual es la longi­
tud inicial de la cuerda?
a) 90cm
d) 60cm
PROBLEMA N” 15
b) 80cm c) 70cm
e) Ninguna
Un péndulo de longitud 5m que oscila
en un plano vertical, sa encuentra sus­
pendido en el techo de un carro. Si el móvil
acelera horizontalmente con a = 10, de­
terminar el período de oscilación, g =
10m/s2
SOLUCION
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
ti
*
*
*
*
*
*
*
$
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
+
♦
*
*
*
*
*
*
*
*
*
*
*
El período de oscilación es directamente
proporcional a la raíz cuadrada de la Ion
gitud de la cuerda e inversamente pro­
porcional a la raíz cuadrada de la
gravedad efectiva.
£
T = 2n
Calcular la gravedad efectiva:
Q
ef = +a2
g8f = 20m/s2
Reemplazando datos en (1):
(11
T - 2t
i
T = n segundos
PROBLEMA N° 16
Un péndulo de longitud 3,0m que oscila
en un plano vertical, se encuentra sus­
pendido en el techo de un ascensor. Si
el ascensor sube con aceleración cons­
o
tante a = 2,2m/s , determinar el período
de oscilación.
a) /es b) 2.ns c) 37ts
d) 47ts e) Ninguna
PROBLEMA N° 17
Si el punto "P” de la cuerda inextensible
que se encuentra en la figura, se desplaza
verticalmente hacia abajo una distancia de

350. tancia de 8cm. Hallar las elongaciones de
cada uno de los resortes sabiendo que:
Ki = 4.k2 . La masa de la polea móvil es
despreciable.
SOLUCION:
Diagrama del cuerpo libre, de la polea
móvil
De la condición de equilibrio:
ki.xi = 2 .k2.X2 ....(1)
De la condición ki = 4.k2
Reemplazando en (1):
x2 = 2 . xi .... (2)
Analizando cinemáticamente a la polea
móvil
Reemplazando (2) en (3):
*
,f¡
*
*
*
*
*
*
*
a
a
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
i
*
*
*
*
*
*
#
*
*
*
*
*
*
xi = 2 cm
X2 = 4 cm
PROBLEMA Ne 18
Si el punto P de la cuerda inextensible
que se muestra en la figura, se desplaza
verticalmente hacia abajo una distancia
d = 12 cm. Hallar ias elongaciones de
cada uno de los resortes, sabiendo que:
ki = 2.k2. La masa de las poleas móviles
son despreciables.
a) xi = 4 cm ; X2 = 2 cm
b) xi = 2 cm ; x2 = 4 cm
c) xi = 2 cm ; x2 = 2 cm
d) xi = 4 cm ; x2 = 4 cm
e) Ninguna.

351. Una caja de masa M está sobre una
masa horizontal. De la caja, por medio de
un resorte de rigidez K, está suspendido
un bloque de masa m. ¿Con qué amplitud
de las oscilaciones del bloque, la caja
empezará a saltar sobre la mesa?
SOLUCION:
Deformación del resorte, cuando el blo­
que está en resorte:
k . x0 = m . g
Xo = mg/k (1)
Analizando a la caja, determinamos la
deformación del resorte cuando la reac­
ción normal es igual a cero,N=0.
I F y = 0
k . x = M . g
x = Mg/k .... (2)
S
Ü
S
ü
S
ü
S
ü
*
*
Sü
sü
S
Ü
*
*
*
*
S
ü
Sü
*
S
ü
*
*
*
*
S
Ü
*
*
S
ü
S
ü
«
ü
*
sü
sü
#
*
*
S
ü
Sü
#
*
S
ü
Sü
S
ü
S
ü
sü
*
«
ü
*
Sü
S
Ü
S
Ü
*
*
*
Sü
*
*
S
ü
Sü
*
*
*
S
ü
*
*
*
*
*
*
-A
X = A-X„
Luego: x = A - x0
—
> A = x - x0
Reemplazando (1) y (2) en (3):
(3)
PROBLEMA Ns20
Una caja de masa M = 9kg está sobre
una mesa horizontal. El coeficiente de
rozamiento entre la caja y la mesa es igual
a Ms = 0,4. Dentro de la caja descansa un
bloque de masa m = 1 kg que puede mo­
verse sin rozamiento en el interior de la
caja. Este bloque está sujeto a la pared
por medio de un resorte cuya rigidez es
k = 200N/m. ¿Con qué amplitud de las
oscilaciones del bloque comenzará la ca­
ja a moverse sobre la mesa? g = 1 0 m/s
TV-Tam.;/1
:.i . iflwra. aí
a) 0,1m
d) 0,4m
b) 0,2m
e) N.A,
c) 0,3m

352. GRAVITACION UNIVERSAL
%
Las fuerzas entre el sol y los planetas o
entre la tierra y los cuerpos próximos a su
superficie son simplemente manifestaciones
de una propiedad intrínseca de la materia,
descubierta en 1 666 por I. Newton con el
objeto de explicar el movimiento planetario
La partícula elemental que genera el campo
gravitatorio se denomina “gravitón".
LEY DE^GaAVITACIONUNiVERSAL
"Dos partículas materiales cualesquiera
se atraen con una fuerza de magnitud direc­
tamente proporcional al producto de las ma­
sas e inversamente proporcional al cuadra­
do de la distancia que las separa".
*
*
*
*
*
*
*
*
*
*
*
S
f<
*
*
*
*
*
*
*
*
*
*
*
#
*
*
CAMPO GRAVITATORIO
Es aquella región del espacio que rodea
a una masa "M" creadora del campo, lugar
en el cual deja sentir su efecto (atracción)
sobre otras partículas. El campo gravitatorio
se comporta como un agente transmisor de
fuerzas gravitatorias
El campo gravitatorio se puede repre­
sentar mediante líneas de fuerzas (lineas
geométricas) ingresando a la masa "M "
creadora del campo. Se traza una línea de
fuerza de modo que en cada punto la direc­
ción del campo es tangente a la linea que
pasa por el punto.
n>¡ *
*
*
*
G: constante de gravitación universal, lla­
mada constante de Cavendish.
G = 6,67 10
1 N m¿
kg2
Debido a¡ pequeño valor de "G", la fuerza
de gravitación sólo es sensible cuando se
trata de masas muy grandes o de distancias
muy pequeñas
*
*
*
su
¡S
í
*
*
4
s
*
*
*
*
#
*
*
Representación gráfica del campo gravita-
torio de una masa puntual o esférica.
Intensidad del Campo Gravitatorio (g)
Es una magnitud física vectorial se define
como la relación de la fuerza resultante por
cada unidad de masa, en un punto del cam­
po. El vector intensidad del campo tiene la
misma dirección y sentido que la fuerza re­
sultante gravitatoria

353. .... (1)
UNIDADES:
N m
k g ’ s 2
Ley de Gravitación Universal;
M . m0
F = G . - (2)
Reemplazando (2) en (1):
M . m0
g = -
rrio
.... (3)
Laintensidaddelcampogravitatorioen
unpuntodelcampoesdirectamentepropor-
cional a la masa creadora del campo 'M" e
inversamente proporcional al cuadrado de la
distancia.
A la intensidad del campo gravitatorio se
le denomina también aceleración de la gra­
vedad.
ACELERACION DE LA GRAVEDAD EN LA
SUPERFICIE DE UN PLANETA:
Consideremos un planeta de masa "M" y
radio de curvatura "R“. La intensidad del
campo gravitatorio en la superficie, se ob­
tiene de la ecuación (3), cuando la distancia
"d" es igual al radio "R".
*
*
*
*
*
Slí
*
*
*
*
*
*
*
*
.... (4)
La intensidad del campo gravitatorio
(aceleración de la gravedad) en la superficie
del planeta es directamente proporcional a la
masa creadora de campo "M" e inversamen­
te proporcional al cuadrado del radio “R" de
curvatura.
VARIACION DE LA ACELERACION DE
GRAVEDAD CON LA ALTURA:
Consideremos un planeta de masa "M” y
radio de curvatura "R La intensidad del
campo gravitatorio a una altura ”h” sobre la
superficie del planeta, se obtiene de la fór­
mula (3), haciendo: d = R + h.
Combinando la ecuación (4) y (5):
*
*
*
*
*
g= gs-
R
R + h

354. gs : aceleración de la gravedad en la super­
ficie del planeta.
INTENSIDAD DEL CAMPO GRAVITATO-
RIO EN EL INTERIOR DE UN CASCARON
ESFERICO.
Cualquier partícula abandonada en el in­
terior de un cascarón esférico, permanece en
equilibrio, por consiguiente la fuerza resul­
tante gravitatoria que actúa sobre la partícula
es igual a cero. Luego, la intensidad del
campo gravitatorio (aceleración de la gra­
vedad) en el interior del cascarón es igual a
cero.
"La partícula de masa "m" se encuentra
en equilibrio en el interior del cascarón”
ENERGIA POTENCIAL DE INTERAC­
CION GRAVITATORIA:
La energía potencial gravitatoria (Ep) en­
tre dos partículas de masas "M" y "m", se
define como el trabajo realizado por un
agente externo para trasladar una de las par­
tículas desde el infinito, lentamente, hasta un
punto del campo generado por la otra par­
tícula
*
*
*
*
*
*
*
*
K
*
*
*
*
*
O
*
*
«t
*
*
*
*
*
*
*
*
*
*
*
#
*
•fr
*
*
w
m
*
*
#
*
*
m
*
0
*
*
*
*
*
'•
*
*
*
*
*
*
$
*
*
*
#
♦
*
*
4)
*
*
*
*
r
En =
—
G. M. m
En el movimiento cuasiestático (equili­
brio) de la partícula "m“, la fuerza externa
(igual a la fuerza de atracción en módulo)
realiza un trabajo negativo (opuesto al mo­
vimiento), por esta razón la energía potencial
de interacción gravitatoria tiene signo nega­
tivo siempre.
'LEYES DEL MOVIMIENTO PLANETARIO:
Los astrómonos griegos y egipcios estu­
diaron el movimiento de los planetas y el sol
con respecto a la tierra, utilizando a esta
última como sistema de referencia. La con­
secuencia fue que obtuvieron resultados
muy complejos que dificultarán describir
leyes generales.
A principios de siglo XVI, el astrónomo
polaco Nicolás Copérnico sugirió que po­
drían obtenerse si se referían los movimien­
tos de los planetas y la tierra con respecto al
sol, o sea si se usaba el sol como sistema
solar, es formado por la estrella solar, es
formado por la estrella llamada sol y los
planetas mercurio. Venus, Tierra, Marte, Jú­
piter, Saturno, Urano, Neptuno y Plutón, que
giran alrededor del sol describiendo órbita
elípticas.
LEYES DE KEPLER:
Como consecuencia de la hipótesis de
Copérnico y las observaciones astronómicas
de Tycho Brahe y otros: el astrónomo J
Kepler, natural de Praga, formuló, un siglo
después, las leyes del movimiento plane­
tario. que son las siguientes:
I- Los planetas describen órbitas elípticas
ocupando el sol uno de los focos.
II- La recta que une un planeta con el sol
(radio vector) describe áreas iguales en
tiempos iguales.
III- Los cuadrados de los períodos de revolu­
ción son proporcionales a los cubos de
sus distancias medias al sol.

355. *
*
La elipse, es una curva muy parecida a 2
un óvalo cuyas propiedades se estudian en *
cursos avanzados de matemáticas. Posee *
un centro C y dos focos F y F, en uno de los *
cuales se supone situado el sol. El círculo es *
un caso particular de la elipse que se pre- *
senta cuando los dos focos coinciden con el *
centro C. En lo sucesivo y para mayor sen- *
cillez supondremos siempre que la órbita es *
un círculo. *
*
*
*
*
*
«
l*
*
*
*
*
«
l»
*
i
*ts
*
*
*
*
*
*
*
Para aclarar la segunda ley supongamos
al planeta en A y que al cabo de un tiempo
dado, un mes por ejemplo, se encuentra en
B. El área descrita por una recta imaginaria
que lo une al sol, o radio vector, es el sector
AFB. Si ahora volvemos a observar al
planeta durante el mismo tiempo, un mes, a
partir de cualquier otra posición C compro­
baremos que el área descrita CFD es igual a
la de AFB Es decir, las áreas descritas «¿
n
tiempos iguales son iguales.
Usando razonamientos matemáticos
algo complejos, puede demostrarse que esta
ley es equivalente a afirmar que la fuerza
ejercida sobre cada planeta es central y
dirigida siempre hacia el sol.
T ^ K R ^ j

356. PROBLEMAS RESUELTOS DE
GRAVITACION
PROBLEMA N901
Dos planetas de masa M ¡ y M? giran
alrededor de una estrella ” E , en órbitas
circulares de radios Ri y Ra respectiva­
mente. Si» R2 = 3 .R1 y el período del pla­
neta Mi es de 100 días. Hallar el período
del planeta M¿.
Analizando el planeta Ms:
Dinámica circular, para Mi:
Fc = m.ac
G. M Mi 2 n
--------5- - = M i. a) . R1
R,
G.M =
A if
2
T,
J s
3
R ,
R s
= Constante
AnalizandoelplanetaM?:
I i T ,
3 “ 3
R , R ,
"Ley de Periodos''
.(1)
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
¥
*
♦
*
*
*
*
*
$
¡#
*
♦
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
¥
*
*
*
Reemplazando en (1): R2 = 3. Ri
27 (100)2 = T j
T2 = 519 días
PROBLEMA N9 02
Dos planetas de masa Mi y M; giran
alrededor de una estrella "E", en órbitas
circulares de radios R¡ y R2 respectiva­
mente si R2 = 4Ri y el período del planeta
Mi es de Ti = 200 días. Hallar el período
del planeta M2.
a) 50 días b) 100 días
c) 400 días d) 800 días
e) 1 600 días
PROBLEMA N903
Un planeta de masa "M" tiene una luna
de masa "m “, que gira alrededor, del pla­
neta en órbita circular con radio “d" me­
dido desde los centros geométricos de
los cuerpos esféricos. Determinar a qué
distancia del planeta, entre M y m, se
encuentra la zona de ingravidez, es decir
la aceleración de la gravedad es nulo.
SOLUCION
(d-x)
" o
-O— r -
Si la aceleración de la gravedad en el
punto "A* es nulo, entonces la fuerza
resultante sobre cada unidad de masa
‘m0‘' es igual a cero

357. -» Fr = Fl
G Mm0 G mm0
x2 (d - x ) 2
M m
x2 (d - x f
d
+
l
<
m
n
PROBLEMA Ns 04
Un planeta de masa "M" tiene una luna
de masa m, (M = 16m), que gira alrededor
del planeta en órbita circular con un radio
de 50 000 km medido desde los centros
geométricos de los cuerpos esféricos.
Determinar a qué distancia del planeta,
entre el planeta y la luna, se encuentra la
zona de ingravidez, es decir la aceleración
de la gravedad es nulo.
a) 10 000 km b) 20 000 km
c) 30 000 km d) 40 000 km
e) Es físicamente imposible
PROBLEMA Ne05
Determinar la intensidad del campo
gravitatorio, en un planeta cuya densidad
promedio es el doble de la densidad pro­
medio terrestre y cuya radio es la cuarta
parte del radio terrestre.
SOLUCION:
Cálculo de la intensidad del campo gravi­
tatorio en la superficie.
En la tierra:
gT = G
En el otro planeta:
M t
9
R t
....(1)
*
♦
*
*
<
0
*
*
*
*
*
*
*
%
*
*
«ls
*
*
*
*
*
*
m
*
*
m
*
$
#
4
=
*
*
*
*
*
*
M r R t ,
gp = ---------~ 9T (3)
M t • R P
4 Tí i
Pero: M = D. V = D . R
O
Reemplazando en (3):
9p =
D p . R p
Dt - r t
9t - • <
4)
Reemplazando datos en (4)'
1
9p - 2 ■ 9t
o
gP= 4,9 m/s
PROBLEMA Nfi 06
¿Cuánto pesará un cuerpo de masa
1kg (peso en la Tierra: 9,8N) en un planeta
cuya densidad promedio es el triple de la
densidad promedio terrestre y cuyo radio
es la mitad del radio de la Tierra?.
a) 4,9N b) 0.98N
c) 14.7N d) 19.6N
e) 980N
PROBLEMA N9 07
La figura muestra tres masas iguales
a "m " colocados en los vértices de un
triángulo de lados 3L; 4L y 5L. Hallar la
energía potencial gravitatoria del sistema
de tres cuerpos aislados de otros cuer­
pos.
gp = G . ^ ....(2)
R d

358. SOLUCION:
Ep(sistema) =Ep (1-1}+Ep (1-3) +Ep(2-3)
-G mm G. mm G. mm
Ep(sistema)~
Ec
-P(sístema) —
PROBLEMA N®08
L 5L
47 G. m.m
60
4L
L
La figura muestra tres masas iguales
a "m” colocados en los vértices de un
triángulo equilátero de lado "L“. Hallar la
energía potencial de interacción gravita­
toria deí sistema de tres cuerpos. Ver
gráfico.
m
ft
Y
id d --------------- --------------------(¡k m
a) -G m 2/L b) -2Gm 2/L
c) -3Gm 2/L d) -6Gm2/L
e) Ninguna
PROBLEMA N9 09
Hallarla mínimavelocidad "Vo"con quese
debe lanzar un cuerpode masa "m" y radiode
B l co
¡
i
i
¡
*
«
*
*
*
>
*
*
*
*
*
*
*
*
*
*
*
*
é:
*
♦
*
*
*
*
*
*
*
*
*
*
#
*
*
#
*
»
*
■
w
»
*
*
#
*
*
♦
*
*
*
*
*
*
*
*
#
*
*
m
*
*
♦
curvatura "R", tal que no regrese ”m" al
planeta.
SOLUCION:
La energía potencial de interacción,
gravitatoria entre M y m e s igual a cero,
cuando la distancia de separación es
muy grande (infinito).
Principio de conservación de la energía:
EM(ínicial) = EM(final)
EP(A) + Ek(A) = Ep(B) + Ek(B)
-G . mM 1 o
— f 2 m o
Si, V0 es mínimo, entonces la velocidad
en (B) es igual a cero.
2 GM
R
PROBLEMA N910
Un cuerpo de masa "m" se abandona
desde una altura igual al radio (h = R)
respecto de la superficie del planeta de
radio "R” y masa "M". Calcular la veloci­
dad del cuerpo "m" cuando choca con la
superficie.
G: constante de gravitación.
9 m
a)
GM
R
2 R
e) Ninguna
d ) J ™
3R

359. Dos estrellas de masas M 1 y M2 , tienen
cada una satélites de masas mi y rm, que
giran alrededor de ellas con el mismo
radio orbital R. El período de mi es el
triple del satélite m^. ¿Cuál es la relación
entre las masas de las estrellas?
SOLUCION:
Analizando la estrella En
/
>
'Ú t
|R /
/
/
Dinámica circular, para "m i”:
Fc =m.ac
G. M i.m i _ 2 „
------- ------ = mi. .R
.. 4 n 2 R2 „
M i . T , = — — = Constan.
Analizando la estrella E2:
Mi .T * = M 2 T*
Pero: T i = 3 . T2
Reemplazando en (1):
(1)
M2 = 9 . Mi
*
*
*
*
$
*
*
$
*
*
*
#
*
#
*
*
*
*
*
PROBLEMA Ns 12
Dos estrellas de masa Mi y M2 ; tiene
cada una satélite de masas mi y m2, que
giran alrededor de ellas con el mismo
radio orbital R. El período de mi es el
doble del satélite m2- ¿Cuál es la relación
entre las masas de las estrellas?
a) M2 = 8 Mi
c) M2 = 4 Mi
e) M2 = M 1
PROBLEMA N9 13
b) M2 = G . Mi
d) M2 = 2 Mi
La figura muestra un planeta de masa
“M'', creadora del campo gravitatorio. De­
terminar el trabajo realizado por un agen­
te extremo, para trasladar una masa "m“
desde la posición A hasta la posición B,
siguiendo la trayectoria mostrada.
*
*
*
*
*
*
$
*
*
*
$
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Cálculo del potencial gravitatorio, en los
puntos A y B
M
a
M
b
VA= - G .
VB= - G .
El trabajo realizado por un agente ex­
terno, contra el campo gravitatorio crea­
do por M, será:
WA _»b = m . (VB- VA)
Wa -»B = m
G. M GM
b + a
WA -> B = G.m.M
PROBLEMA N®14
a b j
La figura muestra un planeta de masa
"M" y radio de curvatura "R”. Un cuerpo
de masa "m" se traslada desde la posición
A(0 ; a) hasta la posición B (0 ; b) a velo­
cidad constante. Calcular el trabajo reali­
zado por la fuerza externa sobre el cuerpo
n m ii
m .

360. ... . .
y
B i (0;b)
A >(0;a)
( W _ *
i _ ^
g y (R;0)
a) G.M.m (a + b) / (a . b)
b) G.M.m (a - b) / (a . b)
c) G M.m (b - a) / (a . b)
d) G.M.m/R
e) G.M.m.R / (a . b)
PROBLEMA N® 15
En la configuración mostrada, deter­
minar una relación entre las masas pun­
tuales mi y rri2 , de tal modo que la
intensidad del campo gravitatorio en el
H^nto A sea horizontal.
*
*
>
t>
*
*
*
*
*
*
*
*
*
*
*
*
*
•H
*
*
>
)
>
Ífí
❖
*
*
*
4
¡¡
sh
+
*
❖
*
*
*
*
*
*
*
*
*
4
*
$
♦
4»
♦
*
*
*
*
*
4
*
4
»
4
*
4
»
*
Llevamos una masa de prueba "m0" al
punto A para determinar la dirección y
sentido de la intensidad de campo gene­
rado por cada masa.
De la condición del problema, la intensi­
dad resultante es horizontal
"Lgy —0
>
<
¡>
g2 = gi . Cos60°
G rri2 _ G.mt 1
mt = 8 m2
PROBLEMA N9 16
En la configuración mostrada, deter­
minar la intensidad del campo gravitato­
rio en el punto "A", los tres cuerpos pun­
tuales tienen masa ”m" cada uno.
A
L y '
i l 30l A _____
30° >s
---------- / ---------i - *

361. c) 4 Gm/L2 d) 3 Gm/L2
e) Ninguna
PROBLEMA Ns 17
Dos masas puntuales "m" y "M" aisla­
das de otros cuerpos, separados inicial­
mente una distancia "d" son lanzadas en
sentidos opuestos con igual velocidad en
módulo "V”. Determinar la máxima dis­
tancia de separación que alcanzan los
cuerpos:
SOLUCION:
Cuando los cuerpos alcanzan la máxima
distancia de alejamiento, tienen veloci­
dades iguales a "U“ (sentidos iguales).
Principio de conservación del momento
lineal:
P (in
icia
l) =P
(fm
al)
MV - mv = (m + m) U
( M - m ) V
U = -
(M + m)
.... (1)
Principio de conservación de la Energía
Mecánica.
E
M
(in
icial)= E
M
(ñ
n
al)
«f
*
*
s
f
c
i
*
#
*
*
$
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
♦
#
*
*
*
¡4
!
*
*
*
*
*
O
í
*
*
*
*
*
*
*
*
#
*
*
1 w
2 1•i i2 G. m
M
—
m
V +—
M
V - —-—
2 2 d
1 / ...... 2 G. m
M
^ ( m + M )U - — x—
C
V
I
>
CJ
-1
X —
d G (m+M)
PROBLEMA N®18
Dos cuerpos esféricos de masas M y
m (M = 2m), aisladas de otros cuerpos, se
abandonan cuando la distancia de sepa­
ración es "D". Debido a la fuerza de atrac­
ción gravitatoria los cuerpos se acercan
entre sí, entonces hallar la velocidad del
cuerpo de masa M cuando la distancia de
separación sea ia mitad (D/2).
a)
O,
lóni
3D
<2Grn
' 3D
e) Faltan datos
b)
d)
i2GM
3D
Gm
D~
PROBLEMA Ne 19
Encontrar el radio de órbita circular en
el plano ecuatorial, de un satélite similar
a la luna que permanece sobre el mismo
punto sobre la tierra todo el tiempo. Don­
de "R" radio de la tierra, "T" período de
rotación de la tierra y “g0" gravedad sobre
la superficie.

362. del satélite:
GM
g = 5~
X
.... (1)
Aceleración de ¡a gravedad en la superfi­
cie de la tierra-
n GM ,o
"r^” ■ <2)
De las ecuaciones (1) y (2):
g = g o . ^ ....(3)
Dinámica circular, en la órbita del satélite:
o
F = m . to .x
4 n2
m.g = m . — 5- . x
T2
.... (4)
x =
IR 2 .T 2
4 n
■So
*
m
*
*
m
*
*
$
*
*
*
*
*
*
*
*
O
s
#
#
*
*
♦
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
«
*
De la condición, el satélite y la tierra
tienen igual período.
Reemplazando (3) en (4):
PROBLEMA Nfi 20
Un satélite artificial de la tierra desde
el Ecuador y se mueve por una órbita
circular en el plano de éste en el sentido
de la rotación de la tierra. El radio de la
órbita del satélite R = 3.Rt , siendo el radio
de la tierra Rr = 6 400 km. ¿Al cabo de
cuánto tiempo pasará por primera vez el
satélite sobre el punto de lanzamiento?
G = 6,67.10 N.m2/kg2
a) T = 10,5 h b) T = 12,5 h
c) T = 14,5 h d) T = 16,5 h
e) T = 18,5 h
PROBLEMA Nfi 21
Determinar la velocidad inicial v0 con
que se debe lanzar verticalmente un cuer­
po, desde la superficie de un planeta de
masa M para que alcance una altura má­
xima igual al radio R del planeta.
1/2
1/2
a) (GM/R)
c) (GM/2R)
e) Ninguna
PROBLEMA Nfi 22
b) (2GM/R)
d) (Gm/3R)
1/2
1/2
Un planeta de masa M genera a su al­
rededor un campo gravitatorio. Determinar
el trabajo realizado por un agente externo
para trasladar un satélite de masa m desde
la posición A hasta la posición B, siguiendo
la trayectoria mostrada en la figura.
*
*
$
#
*
*
*
*
«
>
*
*
*
c) -G M m/2a d) +GM m/a
e) Ninguna
PROBLEMA Ne 23
La figura muestra tres cuerpos ais­
lados de masas m; 2m; 3 m colocados en
los vértices de un triángulo equilátero de
lado L. Hallar la energía potencial de in­
teracción gravitatorio del cisterna:

363. c) -1 3Gm /L d) -1 6Gm /L
e) Ninguna
PROBLEMA N« 24
Se coloca dos satélites A y B de igua­
les masas que orbitan circularmente la
tierra. El satélite A está situado a una
altura 3R y B está a 5R sobre la superficie
terrestre (R: radio de la Tierra). Hallar la
relación de energías cinéticas del satélite
B respecto de A (B/A):
b )'
e) Ninguna
c ) f
PROBLEMA Ns 25
Calcular la aceleración centrípeta con
que se mueve un satélite artificial de la
Tierra, por una órbita circular que se en­
cuentra a un tercio del radío terrestre so­
bre la superficie de la Tierra.
g : aceleración de la gravedad en la
superficie terrestre.
a)3g
d) g/8
PROBLEMA Ns 26
b) 4g
e) Ninguna
c)9g/16
Se lanzan dos satélites alrededor de la
Tierra, uno de ellos (A) se ve fijo y el otro
(B) se observa que da dos vueltas por día.
Se puede afirmar:
*
*
*
$
♦
*
*
$
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
#
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
#
*
*
#
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
a) El satélite A está a mayor altura que
B.
b) El satélite & está a mayor altura que
A.
c) El satélite A tiene mayor masa que
B.
d) El satélite B tiene mayor masa que
A.
e) Ninguna anterior es correcta.
PROBLEM A Ne 27
Entre las masas de la Tierra y la Luna
existe la relación 81:1
La distancia entre los centros de am­
bos astros es de 385 400km. ¿Dónde se
halla el centro de gravedad del sistema?
a) A 4 700 km de la Luna.
b) A 8 100 km de la Tierra
c) A 300 000 km de la Tierra.
d) A 4 700 km de la Tierra.
e) Ninguna anterior.
PROBLEMA Nfi 28
La figura muestra un plano tangente a
un planeta de masa "M" y radio de cur­
vatura "R". Sobre el plano se mueve un
carro de masa "m " debido a la acción del
campo gravitatorio. Determinar la acele­
ración de carro en cada instante de tiem­
po definido por la posición “x“.
a)
G M . x
(x2 + R2)3/2
b)
G M . x
(x2 + R2)1/2
G. M. m. x
c)V + R2)3/2
e) Faltan datos
d)
G M. m. x

365. C
A
P
ÍT
U
L
OII
TEMPERATURA
t i
CONCEPTO:
Es una magnitud física escalar, mide el
grado de agitamiento molecular de una sus­
tancia. La temperatura caracteriza el grado
de calentamiento de un cuerpo
En los cuerpos sólidos, la energía ciné­
tica de vibración es directamente proporcio­
nal a la temperatura, absoluta de la sustan­
cia.
En el caso de un gas ideal (moléculas
monoatómicas), la energía cinética promedio
de cada molécula es directamente propor­
cional a la temperatura absoluta
T : temperatura absoluta (Kelvin)
CERO ABSOLSUTO DE TEMPERATURA:
Es aquella temperatura, al cual la energía
cinética promedio de cada molécula es igual
a cero, por consiguiente la presión del gas
perfecto tiende a cero, manteniendo el vo­
lumen constante, o el volumen del gas tiende
a cero si la presión permanece constante.
m
*
*
#
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
$
*
*
*
*
*
*
*
*
*
O
í
*
ESCALA ABSOLUTA DE TEMPERA­
TURAS:
El científico inglés W. Kelvin introdujo la
escala absoluta de temperaturas.
La temperatura CERO de la escala abso­
luta (también llamada escala de Kelvin) co­
rresponde al cero absoluto.
La unidad de temperatura de la escala
Kelvin, es igual a un grado de la escala
centígrada.
La unidad de temperatura absoluta en el
S I. se denomina Kelvin y se designa por K.
RELACION ENTRE LA ESCALA ABSO­
LUTA Y LA ESCALA CENTIGRADA
La temperatura de congelación del agua,
a presión atmosférica norma!, es 0°C y la
temperatura de ebullición 100°C.
ESCALA
KELVIN
naic
W K
ESCALA
CENTIGRADA
100°C
2*3 t
Una variación AT de la temperatura ab­
soluta es igual a una variación At por la es­
cala centígrada: AT = At, relación de las
escalas Kelvin y centígrada
I K = C + 273

366. CONCEPTO:
Es aquel fenómeno físico que consiste en
el aumento en sus dimensiones que experi­
mentan ciertos cuerpos como resultado del
ai ciento de su temperatura. Si la tempera­
tura de un cuerpo disminuye ésta tenderá a
contraerse.
Cuando calentamos un cuerpo (Aumento
de su temperatura) las moléculas de la sub­
stancia aumentan su energía cinética (vi­
bración, rotación, traslación) por consiguien­
te las moléculas necesitan mayor espacio
para moverse, entonces decimos que el
cuerpo se ha dilatado
Podemos simular a las moléculas como
si fueran esferas unidas medíante resortes,
que cuando es calentado vibran con mayor
amplitud esto quiere decir que los resortes se
estiran, por lo tanto necesitan mayor espacio
para moverse
*
$
*
«
*
•
*
*
*
*
*
*
*
*
*
*
s
»
$
*
*
$
*
*
*
*
*
*
J
j*
*
*
*
*
$
#
En toda dilatación la masa del cuerpo se
mantiene constante.
DILATACION LINEAL
Es el aumento longitudinal que experi­
mentan los cuerpos lineales al incremen­
tarse su temperatura. Experimentalmente
se demuestra que el incremento de su longi­
tud es directamente proporcional a su longi­
tud inicial y al incremento de su temperatura
‘ A L = a .Lo . A t
* Lf - Lo = a L0 . A t
* Lf = Lo . (1 + a . t)
a : coeficiente de dilatación lineal de­
pende de las propiedades térmicas
del material.
1 oL
[ a ] = °C ~1 , °K_I
DILATACION SUPERFICIAL
Es el aumento de superficie o área que
experimentan aquellos cuerpos (placas,
planchas, láminas) en los que se consideran
dos de sus dimensiones como los princi­
pales, debido al incremento de su tempera­
tura. Experimentalmente se demuestra que
el incremento de área es directamente pro­
porcional al área inicial (Ao) y al incremento
de temperatura ( AT).
*
*
*
*
*
Si*
*
*
<te
*
♦
*
*
*
*
*
*
$
* A A = P . A0 . A T
* Af —Ao = p . Ao .A F
* AF = A0 (1 + P . A T )
P: coeficiente de dilatación superficial,
depende de las propiedades térmi­
cas del material
[ p ] = °C_1 , °K_1
Además.

367. Consiste en el aumento en su volumen
que experimentan los cuerpos debido al in­
cremento de la temperatura aquellos cuer­
pos en que se consideran sus tres dimen­
siones como los principales Experimental­
mente se demuestra que el incremento en su
volumen es directamente proporcional a su
volumen inicial y al incremento de la tem­
peratura
* V = y . Vo . A T
*V f - V 0 = y .V 0 . AT
* Vf = V0 . (1 + y . AT)
coeficiente de dilatación volumétri­
co, depende de las propiedades tér­
micas del material
Además:
[ Y] - °C-1 , °KT1
Y = 3 . a
Do =
m
Vo
.... (1)
Densidad final a la temperatura
“T + A T":
m
*
*
*
íji
#
m
*
*
*
*
*
*
*
*
*
*
$
*
*
*
m
$
m
fle
«
s
*
VARIACION DE LA DENSIDAD CON LA
TEMPERATURA
Un incremento en la temperatura de un
cuerpo, consigue un incremento de su vo­
lumen, por consiguiente su densidad dis­
minuye.
Densidad inicial a la temperatura T ":
Vf Voí1 + y -T)
La densidad final, Df es menor que la
densidad inicial D0.
CALORIMETRIA
CONCEPTO:
Es una rama de la física molecular que
estudia las medidas de la cantidad de calor
que intercambian dos o más sustancias que
están a diferentes temperaturas, y así mismo
analiza las transformaciones que experimen­
tan dichas sustancias al recibir o perder ener­
gía calorífica.
CALOR
Es una forma de energía, debido al mo­
vimiento de las moléculas
El calor es una energía en tránsito (de
frontera a frontera) que intercambian los
cuerpos debido exclusivamente a la diferen­
cia de temperaturas entre los cuerpos
*
#
*
*
$
*
*
*
*
*
A : cuerpo caliente
B : cuerpo frío
Q : cantidad de calor
Cantidad de calor (Q):
Es la medida de energía en forma de
calor, que ingresa o sale de un cuerpo. El
calor es un flujo energetico que fluye espon­
táneamente desde el cuerpo de mayor hacia
el cuerpo de menor temperatura

368. UNIDADES DEL CALOR:
CALORIA (es!)
Es la cantidad de calor que se debe en­
tregar o sustraer a un gramo (1g) masa de
agua para que su temperatura aumente o
disminuye en AT =1°C estrictamente de
14,5°C a 15,5°C.
KILOCALORIA (Kcal)
Es ia cantidad de calor que se debe en­
tregar o sustraer a un kilogramo (1kg) masa
de agua para que su temperatura aumente o
disminuya en A T = 1°C, estrictamente de
14,5°C a 15,5°C.
1 Kcal = 1 000 cal
1 cal = 4,2 J
CAPACIDAD CALORIFICA (C)
Es la cantidad de calor que se debe en­
tregar o sustraer a una sustancia, tal que, su
temperatura aumente o disminuya en un gra­
do centígrado {1°C) o su equivalente
Unidades:
cal J
°C ’ °C
CALOR ESPECIFICO (C.e)
Es la cantidad de calor que se le debe
entregar o sustraer a cada unidad de masa
de una sustancia, tai que su temperatura
aumente o disminuya en una unidad. Tam­
bién se le define como la capacidad calorífica
por cada unidad de masa de una sustancia.
Unidades:
cal J
g. °C Kg. °C
CALOR SENSIBLE (Q)
Es aquella cantidad de energía interna
que transitoriamente cede o recibe un cuerpo
o sustancia a través de sus fronteras debido
a una diferencia de temperaturas entre él y
el cuerpo o medio que le rodea El calor
sensible es la cantidad de calor que el cuerpo
utiliza íntegramente para aumentar o dis­
minuir su energía interna, esto quiere decir,
para aumentar o disminuir su temperatura.
Q = m . Ce . A t
Q : cantidad de calor ganado o perdido por el
cuerpo,
m : masa del cuerpo o sustancia
Cexalor específico del cuerpo o sustancia.
AT : variación de la temperatura.
EQUILIBRIO TERMICO O LEY CERO DE
LA TERMODINAMICA
Cuando en un recipiente cerrado y ais­
lado térmicamente son introducidos dos
cuerpos uno caliente y el otro frío, se es­
tablece un flujo de calor entre los cuerpos, de
manera que disminuye la temperatura del
cuerpo caliente debido a que pierde calor y
el otro aumenta su temperatura debido a que
gana calor.
El flujo de calor entre los cuerpos cesará
cuando los cuerpos alcanzan temperaturas
iguales, entonces se dice que han alcanzado
el “Equilibrio Térmico", definiéndose el equili­
brio térmico como aquel estado en el cual no
existe flujo de calor
Del principio de conservación de la ener­
gía, se cumple que el calor ganado por el
cuerpo frió es igual al calor perdido por el
cuerpo caliente.
*
*
*
*
$
*
&
m
*
*
#
*■
*
*
*
*
*
*
s
H
*
*
$
*
*
*
*
*
*
*
*
*
*
>
»
>
#
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*■
*
*
*
*
*
*
¡ü
*
*
*
| Q (ganado) = —Q (perdido^

369. CALORIMETRO DE MEZCLA
Es aquel recipiente cerrado y aislado tér­
micamente que se utiliza para determinar el
calor específico de los cuerpos (líquido, só­
lido, gas)
H20.-£
Temperatura
. Aislante
Térmico
EQUIVALENTE EN AGUA DE UN CA­
LORIMETRO
Es aquella cantidad de agua que es ca­
paz de absorver o disipar la misma cantidad
de calor, que un calorímetro, experimentan­
do el mismo cambio de temperatura.
Q(agua) = Q(calorimetro)
mH20 Ce (H2Q). AT = mcal.Cecal. A T
Pero:
Ce(H2
0) = 1,0
cal
g°c
H2O = rrtcai - Cecal
*
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
*
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
fr
Si el calorímetro tiene capacidad despre­
ciable, entonces el calorímetro no gana ni
pierde calor.
El equivalente en agua se expresa en
gramos»
CALOR ESPECIFICO DEL AGUA (H2O)
cal J
Ce (H20 )= 1,0
g°c
cal
•= 4200
kg°C
Ce(hielo) = 0,5 = 2 100
g. c
Ce(vapor)=0,5 — - = 2 100
kg°C
J
g°c kg.°C
CAMBIO DE FASE
Es aquella transformación fisica que ex­
perimenta una sustancia pura al recibir cierta
cantidad de calor cuando está saturada. En
consecuencia durante el cambio de fase la
sustancia experimenta un reordenamiento
molecular, adoptando nuevas propiedades
físicas y perdiendo otras manteniendo la pre­
sión y temperatura constante. La sustancia
puede encontrarse en su fase, sólido, líquido
y gaseoso
SUSTANCIA PURA
Es aquella sustancia que presenta una
composición química homogénea y que es
capaz de reaccionar (no experimenta diso­
ciación atómica), sin embargo su estructura
molecular puede experimentar cambios.
Ejemplo El agua (H2O), el aire, el ni­
trógeno, el oxígeno, etc.

370. Es aquella manifestación física que pre­
senta una sustancia pura y que está definida
por los parámetros termodinámicos:
Presión (P), volumen (V), temperatura (T),
densidad (D).
Estado = f (P ; V ; T ; D)
El agua no disuelve la grasa a 10°C, en
la misma fase líquida a 60°C logra disolver la
grasa, por consiguiente la sustancia tiene
diferentes propiedades a diferentes estados
termodinámicos.
FASE TERMODINAMICA
Es aquella situación de homogeneidad
física, configuración molecular, que presenta
una sustancia pura a determinadas condicio­
nes de presión y temperatura. La sustancia
puede incrementar su temperatura sin modi­
ficar la configuración de su estructura mo­
lecular
Una sustancia pura posee tres termo­
dinámicas: solido, líquido, gas (vapor).
CONDICIONES DE SATURACION
Se denomina asi a los valores de presión
y temperatura que se mantienen constante
durante el cambio de fase. Si en un cambio
de fase la temperatura de saturación también
constante, su respectiva presión de satu­
ración también permanece constante.
El decir, según si ¡a sustancia para cada
presión de. saturación existe un solo valor de
su temperatura de saturación.
Por ejemplo si la presión es 1,1 105Pa, el
agua no puede hervir a 95°C, ni 105°C, le
corresponde una temperatura de ebullición
de 100°C.
Análogamente, si el agua hierve a 100°C,
la presión no puede ser 104Pa, ni 106 Pa,
pues le corresponde la presión normal
(1.1.105 Pa).
*
&
&
&
*
*
*
*
*
&
*
&
&
&
&
&
*
&
&
$
&
&
*
#
&
$
&
&
*
&
*
*
m
*
&
*
&
*
&
#
$
*
*
*
#
&
4
&
#
*
*
$
*
*
GRAFICA PRESION - TEMPERATURA DE
SATURACION (para el H20 )
P ÍN /m 1)
611,3
V A P O R
Sublimación
273.01 T (° K )
PUNTO TRIPLE (A)
Es aquel valor de la temperatura y pre­
sión de saturación, para el cual la sustancia
se encuentra en las tres fases (sólido, líqui­
do, vapor), por consiguiente las tres fases
coexiste simultáneamente.
Para el agua : T = 0,01 °C
P = 611,3 N/m2
SUBLIMACION:
Es aquel proceso de cambio de fase,
cuando la sustancia pasa de la fase sólido a
la fase vapor, sin pasar por la fase líquida.
Esta generalmente ocurre en algunas sus­
tancias llamada "volátiles"
Para el agua (de hielo a vapor) ocurre a
bajas presiones, debajo del punto triple “A".
CALOR LATENTE (L)
Es aquella cantidad de calor necesaria y
suficiente que se debe entregar o sustraer a
una unidad de masa de una sustancia satu­
rada, para que ésta pueda cambiar de fase.
Unidades: — , ~
g kg

371. Cantidad de calor “latente" entregado a la
sustancia para el cambio de fase:
Q = rn . L
Calor latente para el agua a la presión
atmosfera normal.
* Fusión - solidificación:
T = 0°C
*
*
&
*
$
*
*
*
*
$
L = 80 — = 340 ^
9 Kg
Vaporización - condensación:
T = 100°C
L = 540 — = 2 300 S
K '
g Kg

372. c PROBLEMAS RESUELTOS DE
CALOR
PROBLEMA Ne01
Un termómetro con escala arbitraria,
tiene como punto de fusión del hielo -40°
y como punto de ebullición del agua 160°,
cuando en este termómetro se lee 20°,
¿cuánto vale la temperatura en la escala
centígrada?
SOLUCION:
E b u llic ió n .
160
Z0
C o n g e l a c i ó n ________
-40
N °C ^
100
1 0
De la relación de Thales
160 + 40 100
20 + 40
T = 30°C
*
#
#
*
$
#
1
*
A
*
*
*
*
#
*
PROBLEMA Ne02
¿A qué temperatura las lecturas de un
termómetro Fahrenheit y Centígrado son
iguales?
a) +40°C b) -40°C
c) —
20°C d) +20°C
e) Ninguna
PROBLEMA N®03
Se tiene un termómetro mal calibrado
señala +1° a la temperatura de congela­
ción del agua y 99° a la temperatura de
ebullición del agua con el termómetro mal
calibrado se mide la temperatura de cierta
sustancia dando como lectura 25°, ¿cuál
es la verdadera temperatura en °C de ta
sustancia?
SOLUCION:
De la relación de Thales
2 5 -1 T - 0
9 9 -1 ~ 1 0 0 -0
24
98 :
T
100
T = 24,49 °C
*
*
*
*
*
*
PROBLEMA Nfi 04
¿A qué temperatura las lecturas de un
termómetro Fahrenheit y Centígrado son
iguales, pero de signos contrarios?
a )-1 1 ,4°C b)-22,4°C
c) -6,8°C d) —
40°C
e) Ninguna

373. En ia figura mostrada, en cuántos °C
se debe incrementar la temperatura de las
barras A y B para que sus extremos se
junten. Las barras están empotradas o
paredes impermeables al calor y además:
aA = 15 x 10^°C_1
aB = 1 x 10‘ O
Ü
C
1
60cm 6cm 30cm
SOLUCION:
De la condición del problema:
^L(A) + AL(B) = ®cm
a A. L,. AT + ag.L^. AT = 6cm
(15 x 10^)(60)AT+(10_3)(30) AT = 6
Despejando
AT =50 °C
*
*
*
*
*
*
*
PROBLEMA NB06
Dos barras de longitudes Lt y son
de materiales diferentes sus coeficientes
de dilatación térmica son respectivamen­
te:
a1= 3 x 1 0 _€oC y ccj =6 x 10~* cC_1
¿Cuáles son los valores de Li y L2 para
que su diferencia de longitudes sea igual
a 9cm a cualquier temperatura?
a) L1 = 18cm y L2 = 9cm
b) Lt = 10cm y L2 = 19cm
c) L1 = 20cm y L¿= 11cm
d) L1 = 20cm y L2 = 29cm
e) Ninguna
Determinar las longitudes de dos vari­
llas a la temperatura del ambiente de coe­
ficientes de dilatación lineal
ai = 18 x 10‘6 °C_1y a2 = 12X 10-6 °C -1
De tal modo que la diferencia de sus
longitudes sea igual a 5cm, a cualquier
temperatura.
SOLUCION:
*
*
#
*
$
*
*
*
*
#
*
*
*
*
*
*
*
*
*
#
*
De la condición:
b - a = 5cm ....(1)
La variación de la longitud por cada uni­
dad de temperatura, para cada varilla
debe tener el mismo valor.
a v a. AT = a2.b. AT --.(2)
Reemplazando datos en (2):
3a = 2b .... (3)
Resolviendo las ecuaciones (1) y (3):
a = 10 cm
b =15 cm
PROBLEMA NB08
Una varilla de cierto metal de 50 cm de
longitud es calentada de 0°C a 100°C ob­
servándose que su longitud, aumenta en
0,075cm. Otra varilla de la misma longi­
tud que la anterior pero de un material
diferente es calentado desde 0°C a 100°C
observándose que su longitud aumenta
en 0,045cm. Tomando un trazo de cada
varilla se forma una varilla de 50cm de
longitud, la cual es calentado desde 0°C
hasta 100°C aumentado su longitud en
0,057cm. Determinar la longitud de cada
trozo tomado a 0°C.

374. a) 25 y 25cm b) 20 y 30cm
c)35y15cm d)40y10cm
e) 45 y 5cm
PROBLEMA Ns 09
Se tiene una lámina metálica de coefi­
ciente de dilatación superficial 2,02 x 10~*.
1/ C, al cual se le ha sustraído un círculo
de radio 1 cm. Se pretende hacer pasar
por el orificio una esfera de radio 1,02cm,
¿en cuánto se debe incrementar la tem­
peratura de la lámina metálica, tal que, la
esfera pueda pasar por el orificio?
SOLUCION
Experimentalmente se demuestra que el
espacio vacio, el orificio, se dilata como
si fuera del mismo material de la lámina
metálica.
a = radio del orificio a la temperatura T0,
inicial = 1,0cm.
b = radio del orificio a la temperatura Tf,
final = 1,02cm.
*
§
«
s
#
*
*
#
m
é
#
4
*
*
*
*
*
#
*
*
*
*
*
#
*
*
#
*
*
#
*
*
*
*
*
?
s
>
*
*
#
*
*
*
*
*
*
*
*
*
#
*
*
*
<
*
#
*
#
*
*
*
#
*
*
#
*
*
P = coeficiente de dilatación superficial
del metal = 2,02 x lO ^ .I^ C .
La variación superficial del orificio, es di­
rectamente proporcional al área inicial y
al cambio de temperatura (TF- T0)
A área = p A(inicial). A T
n (b2 - a2) = p. k. a,: AT
(b + a ).(b -a ) = p .a 2 AT ...(1)
Reemplazando datos en (1):
A T = 200°C
PROBLEMA Ns 10
Se tiene un círculo metálico de coefi­
ciente de dilatación superficial, 2,01 x 10'
■ O *
Si el radio del círculo es 1,0 cm, ¿En
cuánto se debe incrementar la tempera­
tura, tal que, el radio del círculo sea 1,01
cm?.
a) 100°C
c) 150°C
e) Ninguna
PROBLEMA Ne 11
b) 120°C
d) 200°C
Un frasco de vidrio de capacidad
1 010cm3, contiene 1 OOOcm3 de m ercurio
(Hg) cuyo coeficiente de dilatación cúbica
es 18,2.1o-5 °C ' a la temperatura de 0°C.
Se calienta el sistema hasta alcanzar una
temperatura de 100°C, observándose que
el frasco de vidrio se encuentra comple­
tamente lleno de mercurio. Calcular el
coeficiente de dilatación cúbica del vidrio.
SOLUCION:

375. La variación del volumen del mercurio es
igual a la variación del volumen del vidrio
(frasco), más, 10cm3,
AV(Hg) = AV(vidrio) + 1Ocm3
y (Hg) -V0(Hg) AT = Y(v) VD(V). AT + 10m3
Reemplazando datos en (1):
Y(vidrio) =8,11 . 10~5 °C~1
PROBLEMA Nfi 12
Un frasco de vidrio de capacidad 1 000
cm a 0°C se llena completamente con y
mercurio a ésta temperatura. Se calienta
el sistema hasta 100°C y se nota que se
derrama 15,2cm‘ del fluido (Hg). Si el
coeficiente de dilatación volumétrica del
mercurio es 18,2.10'5 °C 1, determinar el
coeficiente de dilatación lineal del vidrio.
b) 2 . 1o~5 ° c r'
d) 1cr4°c_1
d 0 =
m
Vo
Densidad final:
Dp = t?- =:
.... (1)
m
Vf Vo (1 +Y-AT)
Reemplazando (1) en (2):
D
f^ V
(1 + Y-AT)
Reemplazando datos en (3):
... (2)
.... (3)
&
*
$
$
4
»
*
*
*
$
*
*
*
❖
*
*
*
&
a) 3. 10_5oC~1
c) 10"5oC“ 1
e) Ninguna
PROBLEMA N» 13
La densidad de cierto material a 0°C es
de 28g/cm . Si su coeficiente de dilata­
ción lineal es de 0,45 °C ~ ¿Cuál es la
densidad de ese material a 20 °C?
SOLUCION:
Densidad inicial:
La densidad de cierto material es
4,0g/cm3 a la temperatura a 0°C. Si la
densidad disminuye a la mitad cuando la
temperatura es 100°C, determinar el coe­
ficiente de dilatación volumétrico, de la
sustancia.
b) 2 . 1CT3oC- 1
dj 10“ 2oC~1
*
&
*
$
$
*
*
*
*
*
*
*
*
*
❖
*
*
*
*
*
*
*
*
*
*
*
❖
*
*
*
$
M
í
#
*
*
*
*
a) 3 .1 0”3 ° C 1
c) 10“ 3°C~1
e) Ninguna
PROBLEMA Ne 15
La figura muestra un bloque de hielo
sumergido parcialmente en agua. Si el
recipiente se encuentra completamente
lleno con agua, cuando el hielo se derrite,
¿cuánto (en kg) de agua se derrama?
SOLUCION:
1) D.C.L.(bloque de hielo):

376. V = Vi + V2 Volumen total
Vi : Volumen no sumergido
V2 ’ volumen sumergido
2) IF y = 0 (condición equilibrio)
E = W
DH50 g-Va = ÜH.g V
Dh2
o V2 = Dh.V .... (1)
3) Consideremos, V', el volumen que
ocupa el bloque de hielo cuando se
derrite Principio de conservación
de la masa, cuando el bloque de
hielo se derrite
m(hielo) = m(agua)
Dh.V = Dh.V ' . (2)
Comparando las ecuaciones (1) y (2):
V = V 2
"El nivel de agua se mantiene inalterable,
el agua no se derrama"
PROBLEMA Nfi 16
La figura muestra un bloque de hielo
sum ergido parcialm ente en m ercurio
(Hg). Si el recipiente se encuentra com­
pletamente lleno de Hg, cuando el hielo se
derrite se puede afirmar que:
a) El nivel del mercurio desciende o
baja,
b) El nivel del mercurio se mantiene
inalterable.
c) Se derrama aproximadamente el
10% de la masa del agua
*
*
*
*
*
*
íjs
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
d) Se derrama aproximadamente el
50% de la masa del agua.
e) Se derrama aproximadamente el
92% de la masa del agua
PROBLEMA Nfi 17
Determinar la altura de una catarata,
sabiendo que la diferencia de tempera­
turas entre las aguas de arriba y las de
abajo es 1,0°C. Calor específico de agua
= 4 200 J/kg °C. g = 10 N/kg.
SOLUCION
Principio de conservación de la Energía:
EM = Q(calor)
m.g.h = m.Ce. A T
g.h = Ce. AT ....(1)
Reemplazando datos en (1) en el sistema
Internacional:
1 0 ~ h = 4 200 —
kg kg°C
. (1,0 °C)
h = 420 m
PROBLEMA N£ 18
James P. Joule, durante su luna de
miel en Suiza, midió la diferencia de tem­
peratura entre las aguas de arriba y las
aguas de abajo de una catarata de 50
metros de altura. Estimar aproximada­
mente dicha diferencia.
Calor específico del agua
J
= 4 200
kg°C
a) Cero
c) 0,12°C
e) 2,4°C
PROBLEMA Nfi 19
b) 0,24°C
d) 1,2°C
A 10kg de un líquido "x" cuya tempera­
tura es 50°C, se le agrega 1,0 kg de hielo
a -50°C. Si la mezcla líquida que resulta
tiene una temperatura de 30°C. ¿Cuál es
el calor específico de "x"? Calor espe­
cífico del hielo = 0,5 K cr l/’C Calor latente
de fusión del hielo = 80 K al/Kg.

377. Qa = m.Ce(H20) AT = 30kcal
Q4 —m.Ce(x). AT
Principio de conservación de la Energía-
Q1 + Q2 + Qa = Q4
135kcal = 10kg, Ce(x). (20°C)
Ce(x) = 0,675 kcal/kg°C
PROBLEMA Nfi 20
Se tiene un calorímetro ideal, que no
gana ni pierde calor, en el cual se intro­
duce 1kg de hielo a la temperatura de
-20Ü
C y se vierte 1kg de agua a la tempera­
tura de +20°C. Hallar la cantidad de hielo
que queda en el recipiente cuando se al­
canza la temperatura de equilibrio.
a) 675g
d) 975g
PROBLEMA Ne 21
b) 775g c) 875g
e) No tiene solución
física.
Un calorímetro contiene 50 gramos de
agua en su fase líquido a C'C Se intro­
duce en el calorímetro 50 gramos de hielo
a -30°C. Determinar la cantidad de agua
que se solidifica cuando se alcanza la
temperatura de equilibrio, sabiendo que
el calorímetro no gana ni pierde calor.
SOLUCION;
Analizando se deduce que la tempera­
tura final de equilibrio es 0°C. sea, "x" la
cantidad de agua que se solidifica.
Q1: calor ganado por el hielo
Q2: calor perdido por el agua, para soli­
dificar "x" gramos.
(X
*
*
m
*
*
«i
*
*
*
m
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
Principio de conservación de la energía
Qi = Q2
mH.Cei-:. AT = x.Cl
50g. 0,5 Cal (30°C) = x.80 —
g.°C 9
x = 9,365 gramos
Estado final de Equilibrio Térmico:
Temperatura = 0°C
Masa de hielo = 59,375 gramos
Masa de agua = 40,625 gramos
PROBLEMA N922
Un calorímetro de equivalencia en H20
de 40 gramos contiene 100g de hielo a la
temperatura de -20°C. Determinar la can­
tidad de agua que a 80°C se debe vertir en
el calorímetro para obtener una tempera­
tura, final de equilibrio igual a 40°C.
a) 185g b) 195g
d) 385g e) 485g
PROBLEMA Ns 23
c) 285g
Se tiene un calorímetro ideal, que no
gana ni pierde calor, en el cual se intro­
duce 800 gramos de hielo a la temperatura
de~20°C y se vierte agua fría (fase líquida)
a la temperatura de 0°C una cantidad de
800 gramos. Hallar la cantidad de hielo
que queda en el recipiente cuando se al­
canza la temperatura de equilibrio.

378. c
, . ,
-20°C 0°c
Qi Calor ganado por el hielo
Q2: Calor perdido por “X" gramos de
agua.
Principio de conservación de la energía:
Q 1 = Q 2
rriH-Ce(H). AT = X(9). Cl(s)
800g. 0,5 ^ (20°C) = X(g). 80 ^
g C 9
X = 100g
X : cantidad de agua que se solidifica.
Estado final de equilibrio térmico:
Temperatura = 0°C
Masa de agua = 700g
Masa de hielo = 900g
PROBLEMA NB24
Un calorímetro de cobre de calor espe­
cífico 0,09 Cal/gr°C de 200gr masa, con­
tiene 100gr de agua a 20 C de tempe­
ratura. En estas condiciones se introdu­
ce un trozo de 1kg de cierto metal a la
temperatura de 70 <
5
C. Determinar el calor
específico del metal, si la temperatura fi­
nal de equilibrio fue de 50°C.
a)0,017Cal/gr°C b) 0,0017Cal/gr°C
c) 0,177Cal/gr°C d) 1,77Cal/gr°C
e) Ninguna
PROBLEMA Ne25
Se tiene un calorímetro de equivalente
en agua despreciable, en el cual se intro­
duce un bloque de hielo de masa 400
gramos a la temperatura de 0°C y se vierte
$
*
$
#
*
*
«
5
*
*
#
*
♦
♦
£
$
H
A
♦
s
f
?
*
*
*
*
s
k
$
*
*
*
*
*
*
♦
♦
*
*
&
*
*
*
*
*
*
*
*
*
$
*
*
agua caliente en una cantidad de 400 gra­
mos a 50°C. Hallar la cantidad de agua en
su fase líquida que queda en el recipiente
cuando logra alcanzar la temperatura de
equilibrio.
SOLUCION:
r
V
N
q2
0°C 50°C
L . J
Qt * calor ganado por "x" gramos de hie­
lo.
Q2 : calor perdido por el agua.
Principio de conservación de la Energía:
Q 1 = Q 2
X(g)-C L(f) = mH20.Ce(H20). At
X(g). 80 ~ = 400g . 1 ,0 ^ (50°C)
X = 250 gramos
X : cantidad de hielo que se derrite.
Estado final de equilibrio térmico:
Temperatura =0°c
Masa de agua = 650g
Masa de hielo = 150g

379. CONCEPTO:
Es la ciencia que tiene como objeto el
estudio de la transformación de la energía
calorífica en trabajo mecánico.
PRELIMINARES:
SISTEMA AISLADO:
Es aquella región del espacio que se aisla
en forma real o imaginaria, con el fin de
estudiar lo que ocurre dentro de ella. En este
caso particular nuestro sistema aislado será
el gas ideal contenido en el recipiente, cuyo
volumen es variable
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
La masa del sistema aislado se mantiene
constante en el tiempo.
SUSTANCIA DE TRABAJO:
Es aquel fluido (gas ideal) empleado co­
mo intermediario para la transformación de
la energía calorífica en trabajo mecánico. La
sustancia de trabajo forma parte del sistema
termodinámico aislado.
GAS IDEAL:
Es aquel cuyas moléculas no interac-
cionan entre sí a distancia y tienen dimensio­
nes propias infinitamente pequeñas. Al cho­
car entre sí y con las paredes del recipiente,
las moléculas del gas perfecto se comportan
como esfera perfectamente elástica.
El hidrógeno, helio, oxígeno y nitrógeno
pueden considerarse gases perfectos a las
densidades correspondientes a las condicio­
nes normales.
ESTADO TERMODINAMICO
Es una característica del sistema aislado.
El estado termodinámico de un sistema que­
da determinado mediante las coordenadas .
presión (P), volumen (V) y temperatura(T).
*
*
*
*
*
*
*
#
*
*
*
EQUILIBRIO TERMODINAMICO:
Se dice que una sustancia (gas ideal)
esta en equilibrio termodinámico cuando sus
variables termodinámicas (P; V, T) permane­
cen constantes en el tiempo, es decir cuando
su estado no varía. Implica el equilibrio Me­
cánico; Térmico y Químico.

380. 1) Equilibrio mecánico : no debe haber
ninguna fuerza desequilibrada en el sis­
tema aislado.
2) Equilibrio térm ico: Todos los puntos del
sistema deben estar a una misma tem­
peratura y a su vez ser igual a la tempera­
tura del medio ambiente. No debe haber
f ujo de calor (Q =0)
3) Equilibrio químico : La sustancia (gas
ideal) no debe experimentar reacciones
químicas.
ECUACION DE ESTADO TERMODI-
NAMICO:
Relaciona los parámetros: presión (P) vo­
lumen (V) y temperatura(T), de un gas ideal
en estado de equilibrio termodinámico
rP.V = n.R.T
P : presión (N/m = pascal)
o
V : volumen (m )
n : cantidad de sustancia (mol)
R : constante universal de los gases
T : temperatura absoluta (°K)
J
mol. °K
En todo sistema aislado (masa constan­
te) se cumple la siguiente relación de
estados termodinámicos (1); (2); (3);
—¡(n)
P.V—n.R = constante
Pi - Vi P2 ■Va
Ti T¡>
Pn-Vn
Tn '
PROCESO TERMODINAMICO :
Si cualquiera de los parámetros P; V; T
de un sistema varía, se produce una varia­
ción del estado termodinámico del sistema
que se llama proceso termodinámico.
Un proceso termodinámico se dice que
se desarrolla en equilibrio (proceso cuasi-
estático) si el sistema recorre con una lenti­
*
*
*
*
#
*
*
♦
*
*
#
*
*
*
#
#
*
*
*
*
*
m
#
*
#
*
m
*
*
*
#
Ü
f
m
#
*
*
*
*
*
#
#
*
*
#
*
#
#
*
*
*
*
*
*
*
#
*
*
*
*
#
&
i
#
*
#
#
■
#
*
#
$
#
tud infinita una serie continua de estados
termodinámicos en equilibrio infinitamente
próximos.
La figura representa un proceso termo-
dinámico en equilibrio, pasando del estado
(1) al estado (2)
ENERGIA INTERNA (U)
La energía interna de una sustancia se
define como la sumatoria de todas las formas
de energía asociadas a las moléculas que la
constituyen. En el caso de un gas ideal
(moléculas monoatómicas), la energía inter­
na es igual a la sumatoria de la energía
cinética promedio de cada molécula.
Energía cinética de una molécula, de un
gas ideal .
T : temperatura absoluta
K : constante de Boltzmann
K - — - - 8-3 1J/m o, °K
No 6,023. 1023 1/m ol
K = 1,38. 10_23J/°K
No . número de Avogadro
“La energía interna de un gas ideal, de­
pende exclusivamente de la temperatura ab­
soluta"
R = K.No

381. Energía interna de un sistema aislado de
un gas ideal, formado por “n* moles.
En todo proceso termodinámico la varia­
ción de la energía interna, no depende de los
estados intermedios, solamente de los esta­
dos inicial y final.
c AU = U2- Ü
1
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
#
*
*
*
*
fc
s
i?
*
"La variación de la energía interna, es
independiente del camino seguido durante el
proceso termodinámico”
TRABAJO (W)
Cuando el sistema evoluciona de un es­
tado termodinámico (1), hasta un estado final
(2), el trabajo realizado por el sistema no
depende sólo de los estados inicial y final,
sino también de los estados intermedios, es
decir, de la trayectoria.
El trabajo realizado por et sistema, es
numéricamente igual al área bajo la curva en
el diagrama P - V.
rWi 2 = Area
Cuando el gas se expande (el volumen
aumenta) el trabajo realizado es positivo. Si
el gas se comprime (el volumen disminuye)
el trabajo realizado por el sistema es nega­
tivo.
PRIMERA LEY DE LA
TERMODINAMICA
Del principio de conservación de la ener­
gía se cumple que:
"En todo proceso termodinámico se cum­
ple que la cantidad de calor entregado o
sustraído a un sistema, es igual al trabajo
realizado por o sobre el sistema, más el
cambio de la energía interna experimentado
por el sistema".
*
*
*
*
*
*
*
*
*
#
*
*
*
*
#
*
*
Q (+). calor entregado al sistema
Q (-): calor liberado por el sistema
W (+): trabajo realizado por el
sistema
W (-): trabajo realizado sobre el
sistema
A U : variación de la energía interna
A U (+): aumenta la temperatura del
sistema
A U(—
): disminuye la temperatura del
sistema.

382. CAPACIDAD CALORIFICA MOLAR DE UN
GAS IDEAL:
La temperatura de un gas puede elevarse
bajo condiciones muy diferentes, mante­
niendo la presión constante o manteniendo
el volumen constante. En cada caso la can­
tidad de calor por cada Mol necesaria para
ek var en un grado la temperatura del gas
será diferente.
(JAS
o a s
O
H
II
a
Qp
A Presión
(mstante
A Volumen
Constante
FK» I
CAPACIDAD CALORIFICA MOLAR A
VOLUMEN CONSTANTE (C v):
Se define como la cantidad del calor por
cada mol de sustancia para elevar la tempera­
tura en un grado, sin que varíe su volumen.
Cv =
Q
n. AT
UNIDADES:
cal
m o l. °K mol°C
Cantidad de calor entregado al sistema:
1 Q = n.Cy. AT ....(1)
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
«ir
*
*
&
*
*
*
*
m
♦
*
*
*
*
* r
*
*
*
*
*
*
*
*
*
Primera ley de la termodinámica
Q = W + AU .... (2)
El trabajo realizado en un proceso a
volumen constante es igual a cero, W = 0.
Reemplazando (1) en (2):
n.Cv- AT = 0 + AU
(3)
CAPACIDAD CALORIFICA MOLAR A
PRESION CONSTANTE (C p) :
Se define como la cantidad de calor, por
cada mol de sustancia, necesaria para elevar
la temperatura en un grado, sin que varíe la
presión.
Cn —'
Q
n . AT
Cantidad de calor entregado al sistema:
♦ i i i—
► v
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
.... (4)
Primera ley de la termodinámica
Q = W + AU .... (5)
Reemplazando (3) y (4) en (5)
n.Cp. AT = P. AV + n. Cv- AT
N.Cp. AT = n.R. AT + nCv AT
| Cp —Cy ~ R
RELACION DE MAYER
Cp > Cv
R = 8,314- '
R = 2 -
m ol °K
cal
moL °K

383. Cp
Cv
= Y
1) Para gases monoatómicos'
Helio, Neón, Argón, Criptón, Xenón
Cp = § R
y= :
y
5
Cv = | R
2) Para gases diatómicos:
Hidrógeno, Nitrógeno. Oxígeno, monó-
xido de carbono (CO).
Cp = |R y
7
y =-5
Cv = § R
3) Para gases poliatómicos
Cloruro de hidrógeno HCI , agua (vapor
H20), anhídrido carbónico (C02), Etilio
(C2H4) Metano (CH4), Amoniado (NH3)
Cp = | r
Y=
y
4
Cv = § R
MASA MOLECULAR (M) DE ALGUNAS
SUSTANCIAS:
Cálculo de la cantidad de sustancia (n):
m
n = M
m : masa de la sustancia gaseosa
M : masa molecular de la sustancia.
PROCESOS TERMODINAMICOS:
1) PROCESO ISOBARICO (P = cons­
tante)
Es aquel proceso termodinámico reali­
zado por el sistema (gas ideal), evolu­
cionando de un estado (1) hasta un esta-
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
do (2), manteniendo constante la presión,
para lo cual recibe o iibera calor. Durante
el proceso realiza t abajo y modifica su
energía interna, por consiguiente varía la
temperatura.
Cantidad de calor entregado
Q = n. Cp. AT
Trabajo realizado por el sistema:
W = F.d = (P. A.) d
W =P.(Ad) = P(V2 - V i)
W = P AV
Variación de la energía Interna: Primera
ley de la Termodinámica
Q = W + AU
A U = Q —W
A U = n.Cp. A T -P AV
Ley de Charles (P = constante)
Y i
Ti
V2
T2
- Diagrama P - V :
(
> 4
v
*-

384. Wi _» 2 = Area bajo la recta
Pi = P2 = P
Wi ., 2 = P- AV l|
PROCESO ISOCORO (V = constante)
Es aquel proceso termodinámico, en el
cual el sistema evoluciona del estado (1) al
estado (2), manteniendo el volumen cons­
tante. En este proceso el sistema no realiza
trabajo, el calor entregado sirve para incre­
mentar la energía interna.
Cantidad de calor entregado:
Q = n.Cv- AT
Trabajo realizado por el sistema:
W = F.d
pero: d = 0
W = 0
Variación de la energía Interna:
Primera Ley de la Termodinámica
Q = W + AU
AU = Q - W
AU = n. Cv. AT
"Todo el calor sirve para incrementar su
energía interna''
Ley de Gay - Lusacc (V = constante)
Vi = V 2
f l = f2
T, T2
*
*
*
*
*
*
*
*
*
*
«
X
*
*
*
<
*
>
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
i*
*
*
*
*
*
*
*
*
*
*
*
<
0
*
*
*
*
*
*
*
*
*
*
+
*
*
*
*
*
*
*
*
Wi 2 = Area = 0
PROCESO ISOTERMICO (T = constante)
Es aquel proceso termodinámico, en el
cual el sistema evoluciona del estado (1) al
estado (2), manteniendo la temperatura
constante. Todo el calor entregado al
sistema se transforma en trabajo.
La energía Interna depende sólo de la
temperatura.
S i: T = constante = Ti = T2
U1 = U 2
Calor entregado al sistema.,
Q = n.R.T.Li
V1
v
Trabajo realizado por el sistema:
Primera Ley de la Termodinámica
Q = W + AU
W = Q - AU
'V 2I
W = n. R. T. Ln
Vi
Ley de Boyle - Mariotte
P1.V1 = P2 V2
Diagrama P - V :
W1 _* 2 = Area
W i -» 2 = n. R. T. Ln
V2
Vi

385. Es aquel proceso termodinámico, duran­
te el cual no existe transferencia de calor, se
aprovecha la energía interna de la sustancia
(gas ideal) para realizar trabajo.
Calor entregado: Q = 0
Trabajo realizado por el sistema.
W =
P 2 . V 2 - P 1 . V i
1 - y
Cr
Cv
W = - n . Cv. (T2 - T 1)
Variación de la energía Interna:
Primera Ley de la Termodinámica
Q = W + AU
*
*
#
*
*
*
#
$
*
*
*
*
H
a
*
<
Ü
sü
*
#
#
*
*
AU = Q - W ; pero : Q = 0
AU = —
W
Ecuación general de los gases:
P i . V i P2 V2
T i T2
Además:
P i • V j = P 2 V |
*
#
*
#
*
#
*
*
*
*
$
*
*
m
*
*
*
*
La adiabática tiene mayor pendiente ab­
soluta que la isoterma.
Isoterma :
Adiabática :
Isóbara :
P V1= constante
P. V7= constante
P. Vo = constante
C p
T = c ; >1

386. PROBLEMAS RESUELTOS DE
TERMODINAMICA 3
PROBLEMA Ns 01
Una botella contiene hidrógeno (gas)
a la presión de 8,31 x 106 Pa y una tem­
peratura de 127°C. Determinar la densi­
dad del gas.
masa atómica (H) = 0,001 kg
SOLUCION
La ecuación de estado de un gas ideal:
R T
P . V = — .
M
P.M = ™ R . T
P.M = D . R T
D : densidad del gas (H2)
Reemplazando en (1), en el S.I.:
D =
8.31x106 Pa . 2x10 kg/m ol
8,31 J/(m ol K). 400K
D = 5 kg/m
PROBLEMA N®02
a) T = 250 K
c) T = 750 K
e) Ninguna.
PROBLEMA N®03
bJT = 500 K
d) T = 100 K
*
$
#
É
*
*
*
*
*
*
*
*
*
La figura representa en el diagrama,
P -V el ciclo experimentando por un gas
ideal. La energía interna en A es de 10J y
en B es 15J.
V í m 2)
Preguntas y Respuestas:
a) ¿Cuál es el trabajo efectuado por el gas
de A a B?
Proceso Isobárico (A -» B)
Wa -» B = P . (VB - VA)
WA -
WA
B = 2 0 ‘ í (2m3)
m
B = 40 J .... (1)
Una botella contiene hidrógeno (H2) a $
la presión 831 x 104 Pa, cuya densidad es •
4kg/m3. Determinar la temperatura del J
gas.
masa atómica (H) = 0,001 kg s
i?
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
b) ¿Cuál es el calor suministrado al gas de
A aB ?
lera. Ley delaTermodinámica
Q = W + AU
Qa -* B = Wa —
>B + (Ub - Ua)
Qa —
»B = 40J + (15 -1 0 ) J
QA —
»B = 45J ....(2)
c) ¿Cuál es el trabajo realizado por el gas
d eC aA ?
W = Area bafo la recta CÁ
(B+ b). h
WC A = - -
Wc -> A = -
WC A = - 30 J
(20 + 10) x (2)

387. d) ¿Cuál es el trabajo efectuado por el gas
en este ciclo?
Wneto = Area encerrado por la curva.
Wneto = Area AABC
Wneto = + g b h
Wneto = ^ (2m3) (10 N/m2}
Wneto = + 10 J ....(4)
e) St el gas recibe 45J de calor de B a C,
¿cuál eslaenergíainternaen C?
a) 15 J
d) 80 J
b) 45 J c) 60 J
e)Ninguna
f) ¿Cuál es el calor suministrado al gas de
a?
a) -15 J b) —
30 J c )-6 0 J
d )-8 0 J e)Nlnguna
PROBLEMA N« 04
Un sistema pasa del estado x al estado
Y siguiendo la trayectoria XAY cuando
recibe 100J y realiza un trabajo de 40J.
Preguntas y Respuestas:
a) ¿Cuál es la variación de la energía in­
terna entre los estados X e Y?
lera. Ley de la Termodinámica:
(X —
>B Y)
Qxay = Wxay + AUxy
100J = 40J + DUXY
*
*
$
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
#
#
*
#
*
*
*
*
*
#
m
*
*
*
*
#
b) ¿Qué cantidad de calor recibe o libera, si
el sistema a lo largo de la trayectoria XBY
realiza un trabajo de 80J? v
lera. Ley de la Termodinámica
(X -» B -» Y)
Qxby = Wxby+ AUxy
Qxby = 80J + 60J
Qxby = + 140 J .... (2)
c) Si el sistema recibe una cantidad de calor
de 70 J a lo largo de la trayectoria XCY.
¿Qué trabajo es realizado por o sobre el
sistema?
a )-1 0 J b) +10 J c) -20 J
d) +20 J e) Ninguna
PROBLEMA Nfi 05
En el diagrama Presión (P), versus,
volumen (V). se muestra un ciclo termo-
dinámico, en el cual el gas ideal evolu­
ciona por los estados 1 -» 2 -»3 -> 1 Hallar
el trabajo realizado por el gas en este
ciclo.
Ver gráfico:
*
*
*
*
#
*
*
*
*
*
El trabajo realizado por el gas es numéri­
camente igual al área encerrada por la
curva en el diagrama P - V Si el sentido
del ciclo es antihorario el trabajo tiene
signo negativo (-), si el sentido del ciclo
es horario el signo del trabajo será posi­
tivo (+).
v

388. W = - ^ ( V 3 - V 2) (P1 - P 2)
El signo (-) significa que se realiza tra­
bajo sobre el sistema termodinámico
PROBLEMA N® 06
En el diagrama P - V, se muestra un
ciclo termodinámico, en el cual el gas
ideal evoluciona por los estados A-> B —
>
C-» A. Hallar el trabajo realizado por el gas
en este ciclo.
Ver gráfico:
d) 40 kJ
PROBLEMA N® 07
e) Ninguna
W = P (V 2 - V i )
W = 104 - ^ ( 8 -
m
W = 60 KJ
2) m
$
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
=
1
»
*
Un sistema termodinámico evoluciona
desde un estado (1), Pi = 10 KN/m2, Vi =
2m3; hasta un estado (2); V2 = 8m , iso-
báricamente. Si recibe una cantidad de
calor Q = 100 KJ. Hallar el cambio de
energía interna del sistema.
SOLUCION:
Cálculo del trabajo realizado por el siste­
ma, a presión constante.
Primera Ley de Termodinámica:
Q = W + AU .... (2)
Reemplazando (1) en (2):
100 KJ = 60 KJ + AU
A U = 40 J
PROBLEMA Nfi 08
Un sistema termodinámico evoluciona
(Jesde un estado (1) Pi = 2 0 0 K P a;
Vi = 5m3, hasta un estado (2) V2 = 8m
isobáricamente. Recibe una cantidad de
calor Q = 500 KJ. Hallar el cambio de
energía interna del sistema.
a) + 100 KJ b) - 100 KJ
c) + 200 KJ d) - 200KJ
e) Ninguna
PROBLEMA N®09
En el sistema termodinámico mostra­
do se produce un proceso isotérmico (T =
constante). El pistón desciende 0,5m.
Hallar el calor disipado al medio ambi­
ente. El bloque tiene una masa M - 400
Kg y desprecie el peso del pistón.
g = 10 N/Kg
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
En todo proceso termodinámico a tem­
peratura constante, la energía interna "U"
se mantiene coreante
AU = 0 .... (1)
Cálculo del trabajo realizado sobre el sis­
tema:
W = F. d = (Mg) d
W = (4 000 N)(0,5m)

389. W = 2,0 KJ .... (2)
Primera Ley de la Termodinámica:
Q = W + AU .... (3)
Reemplazando (1) y (2) en (3):
Luego:
Q = -2,0 KJ
PROBLEMA Ne 10
En el sistema termodinámico mostra­
do se produce un proceso isotérmico, (T
=Cte). El pistón desciende 20cm. Hallar el
calor disipado al medio ambiente. Despre­
cie el peso del pistón.
g = 10 N/kg ; M =4 kg
d) 80J e) Ninguna
PROBLEMA N° 11
Un sistema termodinácorealiza un
proceso ¡socoro (V =constante) obtenien­
do calor de una resistencia eléctrica R =20
ohmios, por el cual circula una corriente
i =10 ampere, durante 1,0 minuto. Hallar la
variación de la energía interna del sis­
tema.
SOLUCION
En todo proceso termodinámico a volu­
men constante, el trabajo realizado por el
sistema es igual a cero:
W = 0 .... (1)
Cálculo del calor entregado al sistema.
Ley de Joule - Lenz:
AU =120 KJ
PROBLEMA Ne 12
Un sistema termodinámico realiza un
proceso isócono (V = constante) obten­
iendo caior de una resistencia eléctrica
R = 6 ohmios, sometido a una diferencia
de potencial igual a 200 voltios, durante
1,0 minuto. Hallar la variación de la ener­
gía interna.
%
Se puede enunciar de las siguientes for­
mas:
- "Es imposible construir una máquina tér­
mica capaz de convertir todo el calor que
se le entrega en trabajo'.
- "Ningún cuerpo frió entrega calor en for­
ma expontánea a un cuerpo caliente,
existiendo la posibilidad que lo haga en
forma forzada pero invirtiendo trabajo".
- "Es imposible reducir la temperatura de
un sistema al cero absoluto (0°K), en un
número finito de operaciones.
CONCEPTOS PREVIOS:
FOCO TERMICO
Es aquel sistema de masa inmensamen­
te grande al cual se le puede sustraer o
entregar calor, sin que su temperatura ex­
perimente cambios notables (por lo general
se busca mantener constante).
% Q =¡2 . R . t
*
#
*
$
ít*
*
*
Q =(100) (20) (60)
Q =120 KJ .... (2)
Primera Ley de la Termodinámica:
Q = W + AU .... (3)
J Reemplazando (1) y (2) en (3):
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
—m
iw
iniiwmm— bmm
SEGUNDA LE Y DE LA
TERM ODINÁM ICA

390. FUENTE (Foco caliente)
Es aquel foco térmico que transfiere calor
a la sustancia de trabajo. Ejemplo: genera­
dores de vapor, calderos, hornos.
SUMIDERO (Foco frío)
Es aquel foco térmico en el cual se des­
foga ei calor previamente utilizado, normal­
mente recepciona calor. Su temperatura
siempre es menor que la temperatura de la
fuente
Ejemplo: Los condensadores,
radiadores.
MAQUINA TERMICA
Es aquel dispositivo que para su ope­
ración continua requiere de una fuente y un
sumidero. La maquina térmica es aquel dis­
positivo mecánico que se encarga de trans­
formar la energía calorífica que se le
transfiere, en energía mecánica.
Ejemplo: Los motores de combustión in­
terna (petróleo y gasolina), las turbinas de
vapor
REPRESENTACION DE UNA MAQUINA
TERMICA
W
Conservación de la energía:
Qt = W + Q2
W = Qi - Q2
Relación de Kelvin:
Ti Qi
t 2 q 2 |
m
*
*
*
*
*
*
4
*
*
*
*
*
*
*
*
*
*
*
*■
*
*
*
*
$
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
¥
*
EFICIENCIA DE UNA MAQUINA TER­
MICA:
Eslarelaciónentreeltrabajonetoentre-
gado por la máquina, entre el calor invertido
para su funcionamiento, proveniente del foco
caliente.
W Qi - Q2
n —
MAQUINA REFRIGERADORA:
Es aquel dispositivo que transfiere calor
del foco frío hacia el foco caliente, prescindi­
endo para ello de un trabajo adiciona!. Su
objetivo es extraer ''Q2“ de un ambiente frío
definido.
W: trabajo entregado a la maquina re­
frigerante
W = Qi - Q2
Si el objetivo es expulsar calor o entregar
calor al foco caliente, se le denominará
bomba de calor o máquina calefactora. Su
objetivo es expulsar “Qi" a un ambiente ca­
liente definido.

391. CICLO TERMODINAMICO:
Es aquel proceso termodinámico, en
donde el sistema retorna a su estado inicial
por un camino diferente. En todo ciclo ter­
modinámico la variación de la energía interna
es igual a cero.
Wneto = Qi - Q2 |
*
*
0
í*
«tí
*
$
*
*
!fs
*
*
*
*
*
El trabajo neto realizado por el sistema,
durante el ciclo es igual al área encerrada por
las curvas, en el diagrama P - V.
Q i(+ ): Cantidad de calor entregado
al sistema
Q2( - ) : Cantidad de calor liberado por
el sistema.
CICLO HORARIO Y ANTIHORARIO:
En un proceso termodinámico, cuando el
sistema se expande (el volumen aumenta) el
trabajo realizado es positivo, si el volumen se
comprime (el volumen disminuye) el trabajo
realizado es negativo).
Sí el ciclo termodinámico tiene sentido
horario, el trabajo neto realizado es positivo.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
m
*
*
*
*
*
*
0
0
Si el ciclo termodinámico tiene sentido
antihorario, el trabajo neto realizado es ne­
gativo.
CICLO DE CARNOT
Fue dése, iio por el Ing. francés Sadi Car-
not, en 1 824
El ciclo de Carnot, es aquel mediante el
cual una máquina térmica logra obtener la
máxima eficiencia posible. El ciclo está
constituido por dos procesos isotérmicos y
dos procesos adiabáticos
1 Expansión Isotérmica (A —
»B): el sistema
(gas) recibe una cantidad de calor Q1 y
se expande a una temperatura constante
Ti.
2) Expansión Adiabática (B —
> C): el gas
sigue expandiéndose, pero sin ingreso ni
salida de calor, de modo que su tempera­
tura disminuye hasta T2.
3) Comprensión Isotérmica (C —
» D): el gas
es comprimido, manteniendo su tempe­
ratura constante T2, de modo que expul­
san una cantidad de calor Q2
4) Comprensión Adiabática (D —
» A): fina­
liza la compresión de manera que du­
rante el proceso no entra ni sale calor,
hasta alcanzar la temperatura Ti.
EFICIENCIA DEL CICLO DE CARNOT
La eficiencia depende sólo de las tem­
peraturas absolutas de los focos frió y ca­
liente.
n = 1 -
T2

392. ENTROPIA (S)
Una propiedad de importancia en ter­
modinámica es la entropía. Si un cuerpo o
sustancia absorve la cantidad de calor Q
manteniéndose a la temperatura T, experi­
menta, un aumento de entropía.
AS =
Q
*
*
*
*
1
*
♦
*
*
«
*
$
Dem odoquelavariacióndeentropíade
un cuerpo se mide por la relación entre el
calor absorvido(o desprende).
Laentropíaes una medídadel estado de
desorden de las moléculas de un cuerpo, o
medida del estado de agitación de las mo­
léculas.
Cuanto mayorseaeldesordenmolecu-
lar, mayor es la entropía del cuerpo. Así,
una sustancia en estado sólido, cuyas mo­
léculas están relativamente ordenadas, tiene
menos entropía que en estado gaseoso,
cuando sus moléculas están muy desorde­
nadas.
Una consecuencia del segundo principio
de la termodinámica es que: la entropía de
un sistema aislado, como el universo, no
puede disminuir y portanto, solo son posibles
aquellos procesos en los que la entropía
aumenta o permanece igual, o sea:
AS >0
Consideremos, por ejemplo, el caso de
dos cuerpos a temperaturas Ti y T2, con
Ti > T2.
Sabemos que si juntamos, hay una trans­
ferencia de calor Q del primero al segundo
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
La entropía del cuerpo caliente, que pier­
de calor, sufre un cambio, -Q íT r y la del
cuerpo frío, que gana calor, un cambio +Q/T2.
El cambio total de entropía del sistema
es:
A Q Q Q
a s = o o
Ti . T2

393. Ál
c PROBLEMAS RESUELTOS DE
SEGUNDA LEY DE LA TERMODINAMICA
PROBLEMA Ns01
Un motor de Carnot recibe 10 000J de
un foco caliente a 727°C, uno realiza un
trabajo y cede una cierta cantidad de ener­
gía a un foco a 27°C.
n = 1 -
300 °K
1000°K
*
*
*
Preguntas y Respuestas:
a) ¿Cuál es el rendimiento térmico de este
motor?
n = 0,7
n = 70%
b) ¿Qué cantidad de calor es cedido al foco
frío?
Relación de Kelvin:
Q2 Qi
t 2 ~ t ,
*
*
i
&
*
*
*
*
*
*
*
*
*
*
fr
*
*
*
*
*
*
*
*
*
*
#
s
*
*
*
*
<
T
>
*
«
5
*
*
*
*
*
*
*
*
*
*
*
*
Q2 = ^ . Q i
Ti
q2=J00^K <10000J)
1000 K
Q2= 3 000 J
c) ¿Cuál es el trabajo neto realizado?
W
neto_ Ql ~Q
?
n_ Qi " Qi
W
peto=m , Qi
W
neto=(0.7) (10 000 J)
W
neto = 7000 J
PROBLEMA Ne 02
La eficiencia de un motor de Carnot es
de 40%. estando su foco frío a 27°C, ¿en
cuántos grados centígrados hay que au­
mentar la temperatura, de su foco calien­
te, para que su eficiencia aumente al 50%.
a)60°C
d)120°C
PROBLEMA N903
b)80°C c)100°C
e) Ninguna
Un motor que sigue el ciclo de Carnot,
funciona, cuyo foco caliente se encuentra
a 400 K toma 100 KJ por ciclo y cede 80
KJ al foco frío.
a) ¿Cuál es la temperatura del foco frío?
b) ¿Cuál será el rendimiento térmico del
ciclo?

394. a) De la relación de Kelvin:
T i _ Q i
T2 Q2
400 °K _ 100 KJ
T2 80 KJ
T2 = 320 °K
b) Rendimiento o eficiencia:
n 1 02
n = 1 _ o ;
n = 1 —
80 KJ
100 KJ
n = 0,2
n = 20%
PROBLEMA N®04
Si la eficiencia de una máquina térmica
que funciona siguiendo un ciclo de Car­
not es del 49%, la fuente que entrega calor
se encuentra a 527°C y proporciona
500KJ a la máquina. Hallar el trabajo rea­
lizado por la máquina en cada ciclo.
a) 125 KJ
c) 325 KJ
e) Ninguna
b )225 KJ
d) 425 KJ
*
*
*
*
*
*
*
*
*
*
*
*
*
Una máquina refrigerante de Carnot
toma energía calorífica del foco frío a
300°K, la cantidad de 1 200J y lo cede al
foco caliente a una temperatura de 400°K.
a) ¿Cuánto de calor cede al foco caliente?
b) ¿Qué trabajo se entrega a la máquina?
*
*
*
*
*
*
*
*
*
*
*
V
+
*
*
*
*
#
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
SOLUCION:
a) Relación de Kelvin:
I i = Q l
T2 Q2
400 °K _ Q1 _
300°K 1200 J
Qi = 1 600 J
Conservación de la Energía:
Q2 + W = Q1
W = Qi - Q2
W = 1 600 J - 1 200 J
b)
W = 400J
PROBLEMA Ne 06
¿Qué cantidad de calor extrae un re­
frigerador reversible de un sistema que
está a -13°C, si lo expulsa al medio am­
biente que está a 27°C, invirtiendo un tra­
bajo de 50KJ?

395. c) 325KJ d) 425KJ
e) Ninguna
PROBLEMA N= 07
Una máquina de Carnot funciona entre
las temperaturas del foco caliente y el
foco frío. Su hermano propone mejorar el
rendimiento que se obtiene del siguiente
modo: la máquima sigue el ciclo de Car­
not y funciona en dos etapas. En la lera.
Etapa recibe una cantidad de calor Qi a la
temperatura constante Ti, realizando un
trabajo Wi y expulsando una cantidad de
calor Q2 a la temperatura constante T2.
El calor expulsado en la primera etapa
es recibido en la 2da. Etapa, en la cual
realiza un trabajo W2 y expulsa una can­
tidad de calor Q3 a la temperatura cons­
tante T3 .
Después de analizar ei proceso cícli­
co, determinar ia eficiencia.
SOLUCION:
Por la definición, la eficiencia de ia
máquina e s :
W1 + W 2
n = ■
Q i
.... 0 )
Trabajo realizado por etapas:
W 1 = Q 1 - Q 2
W2 = Q2 —Q3
*
*
*
*
*
#
*
*
*
*
*
*
•u
*
#
*
*
*
*
*
*
*
n =
Q1
Q1 - Q 3
n = ..“ o T
Relación de Kelvin
Q l _ I i
Os T3
Reemplazando en (2):
n = ■
T 1 - T 3
PROBLEMA Ne08
En el esquema, A y B son dos máqui­
nas térmicas reversibles. Si la eficiencia
de A es el doble que de B. Determinar la
temperatura "Tx".
Veigráfico:
0
♦
$
*
#
*
*
*
*
*
*
*
#
*
a) 1 125 °K
c) 1 250 °K
e)Ninguna.
b) 1 200 °K
d) 1 300 °K

396. INTRODUCCION A LA
ELECTRICIDAD
Es parte de la física, que estudia los
fenómenos producidos por las cargas eléc­
tricas, para su mejor estudio se divide en
electrostática y electrodinámica.
CARGA ELECTRICA
La carga eléctrica es una propiedad fun­
damental de la materia (como la masa). En­
tre partículas que manifiestan esta propiedad
existen fuerzas de atracción y repulsión, lla­
madas fuerzas eléctricas. La existencia de
dos clases de fuerzas eléctricas se explica
por la existencia de dos tipos de carga eléc­
trica se llaman positiva y negativa. Dos cuer­
pos con carga eléctrica del mismo signo se
repelen es decir ejercen entre sí fuerzas de
repulsión y dos cuerpos con carga eléctrica
de signos diferentes ejercen fuerzas de
atracción entre sí
La materia está constituida por unidades
pequeñas llamadas moléculas y las molécu­
las constituidas por átomos, los cuales a su
vez están formados por "neutrones'' que no
tienen carga electrica; protones y electrones,
que tiene carga eléctrica igual en magnitud
pero de signos diferentes: positiva y negativa
respectivamente.
La carga eléctrica de un cuerpo macros­
cópico está dada por la diferencia entre el
número de protones y electrones que existen
en él. Un cuerpo es eléctricamente neutro si
el número de protones es igual al número de
electrones; cargado positivamente, si tiene
exceso de protones cargado con carga eléc­
trica "negativa” si tiene exceso de electrones.
«
s
>
*
*
*
*
*
m
*
♦
*
*
*
%
m
*
*
0
*
*
*
*
*
*
$
*
*
*
*
*
*
*
«
i»
*
*
*
*
*
*
íjs
*
*
*
*
*
*
*
*
$
*
*
*
«S
s
*
S
ü
*
*
*
*
*
La conservación de la carga electrica es
un principio fundamental de la física: si un
cuerpo pierde cierta cantidad de carga eléc­
trica otro cuerpo la adquiere. Es decir: “La
carga no se crea ni se destruye".
CARGA ELEMENTAL (e).
Existe una carga mínima, denominada
elemental, que poseen partículas elemen­
tales como los electrones y protones.
Las cargas de las partículas elementales
sólo se diferencian por sus signos. Separar
parte de la carga, por ejemplo del electrón,
es imposible.
e = 1,6 . 1CT19coulomb
partícula Masa carga
Electrón me=9,1091 x ICT^kg -e
protón mP
=1,6725 x 10~27kg +e
neutrón mn= 1,6748 x10~27kg 0
CUANTIZACION DE LA CARGA:
Todo cuerpo, molécula o átomo puede
ganar o perder un número entero de elec­
trones, entonces, la carga de todo sistema de
cuerpos es múltiplo de la carga elemental.
q = n e
n = número entero positivo o negativo
e = carga elemental
q = carga del cuerpo o sistemas de
cuerpos.
LEY DE CONSERVACION DE LA CARGA
ELECTRICA.
La suma algebraica de las cargas eléctri­
cas de los cuerpos o partículas que forman
un sistema eléctricamente aislado no varía
cualesquiera que sean los procesos que ocu­
rran en dicho sistema.
Iq (iniciales) = Zq (finales)
En el sistema considerado pueden for­
marse nuevas partículas con carga eléctrica,
por ejemplo, electrones debido al fenómeno
de ionización de los átomos o moléculas; en
iones, a causa del fenómeno de la diso­
ciación electrolítica, etc. Pero si el sistema

397. está eléctricamente aislado, la suma alge­
braica de las cargas de todas las partículas
nuevas surgidas en dicho sistema será siem­
pre igual a cero. La ley de conservación de
la carga eléctrica es una de las leyes de
conservación fundamentales, lo mismo que
las leyes de conservación del impulso (can­
tidad de movimiento) y de la energía. Se dice
que un sistema de cargas eléctricas, es eléc­
tricamente aislado cuando sobre el sistema
elegido no ingresan ni salen cargas, y ade­
más no interactúan con cuerpos cargados
que se encuentran fuera del sistema elegido.
Aislante eléctrico
FENOMENOS DE ELECTRIZACION:
Es aquel fenómeno por el cual los cuer­
pos pueden cargarse positivamente o nega­
tivamente por defecto o exceso de elec­
trones. Las formas de electrización son los
siguientes:
1) POR FROTAMIENTO O FRICCION:
Cuando dos cuerpos eléctricamente neu­
tros se ponen en contacto, resultando
del frotamiento o fricción, las cargas
pasan de un cuerpo a otro. En cada uno
de ellos se altera la igualdad de la suma
de las cargas positivas y negativas y los
cuerpos se cargan con electricidades de
diferente signo.
Después:
Por ejemplo, la frotación de una varilla de
vidrio con un paño de seda, el vidrio
resulta cargado positivamente y el paño
de seda cargado negativamente
2) POR CONTACTO: Cuando dos cuerpos
conductores se ponen en contacto (por lo
menos uno de ellos cargado) se es­
tablece una transferencia de cargas entre
los cuerpos debido a la diferencia de
potencial entre las superficies de ambos
cuerpos conductores, el flujo de cargas
cesa cuando las superficies de ambos
cuerpos tienen el mismo potencial eléc­
trico. Para el caso de dos esferas con­
ductoras la cantidad de carga acumulada
por cada esfera, despues del contacto es
directamente proporcional ai cuadrado
de sus radios geométricos, su de­
mostración se verá en los capítulos pos­
teriores.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
s
k
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
¡¡
*
*
*
*
*
*
*
*
*
*
*
*
*
=
t=
*
*

398. *
*
o
»
*
*
*
*
*
*
*
*
*
*
♦
*
$
*
*
*
*
*
I
*
♦
*
*
*
a
La figura (1) muestra dos cuerpos esféri­
cos conductores de radios a y b La
esfera de radio “a“ se encuentra cargado
con magnitud "Q" y la esfera de radio "b”
se encuentra descargada (carga neta
igual a cero), todo este conjunto consti­
tuye un sistema aislado eléctricamente.
Luego ias esferas se ponen en contacto,
donde se establece la transferencia de
cargas, como muestra la figura (2).
Nuestro objetivo es hallar la carga final,
después del contacto de la esfera de
radio "b", como muestra la figura (3).
Del principio de conservación de las car­
gas eléctricas, en un sistema aislado.
£q (iniciales) = Zq (finales)
Q = Q' + q
Luego: Q’ = (Q -q ) ....(1)
La carga acumulada por cada esfera,
después del contacto, es directamente
proporcional al cuadrado de sus radios
geométricos.
q=V Q
‘ ....(2)
a
Reemplazando (1) en (2) tenemos
a =
(a2 + b2)
.Q
3) POR INDUCCION: En este caso la pre­
sencia de la carga puntuaL"Q" cerca de
una esfera de radio “R" descargada
(Qi = 0), origina en la esfera una dis­
tribución de cargas de tal forma que en
una parte del cuerpo surge un exceso de
cargas con signo negativo y en la otra
parte un exceso de cargas positivas, es
decir la esfera se ha polarizado (tiene un
polo negativo y otro positivo).

399. Si se desea cargar la esfera en forma
definitiva (con carga neta) se debe man­
tener fijo la posición del cuerpo inductor
"Q“ y se debe conectar a "tierra" la parte
positiva de la esfera como muestra la
figura (2).
La "Tierra" es considerada un gigantesco
conductor negativo (-) un mar de elec­
trones, cuyo potencial eléctrico es igual a
cero. Capaz de entregar o recibir elec­
trones a través de su superficie. En la
figura (2), al cerrar la llave “k", la Tierra
se pone en contacto con electricidad po­
sitiva entregando de esta manera los
electrones necesarios hasta neutralizar
dicha zcm , luego ya no subirán más
electrones. Después de abrir la llave k la
esfera quedará cargada con una magni­
tud "q" pero de signo opuesto al cuerpo
inductor, como muestra la figura 3. Se
demuestra que la magnitud "q" es:
q ~ S . Q
Si se desea cargar la esfera de radio "R*
con signo positivo, es obvio que la carga
puntual inductora de'rerá ser negativa.
4) POR EFECTO FOTOELECTRICO: Se
produce cuando luz de alta frecuencia
(luz ultravioleta), incide sobre ciertos
metales como zinc (Zc). La superficie
metálica emite electrones de los átomos
que se encuentran en la superficie, de­
bido a ia energía entregada por la luz de
alta frecuencia.
La emisión de estas partículas por la
acción de la luz ultravioleta se denomina
' efecto fotoeléctrico'' y los electrones irra­
diados por la placa metálica recibe el
nombre de "fotoeléctrico" y no se diferen­
cian de los electrones comunes.
Por consiguiente la placa metálica, de
zinc, se carga eléctricamente con signo
positivo.
*
*

401. DPI
ELECTR O STA TIC A
Se llama electrostática a la parte de la
teoría de la electricidad en que se estudia la
interacción y las propiedades de los sistemas
de cargas eléctricas en reposo respecto de
un sistema de referencia elegido.
1. LEY CUALITATIVA: Enunciado por
primera vez por el físico norteamericano
Benjamín Franklin (1 706 - 1 790).
"Las cargas del mismo signo se repelen
y cargas eléctricas de signos diferentes
se atraen1
'.
LEY CUANTITATIVA: Fue enunciado
por primera vez por el físico francés Car­
los Augustín de Coulomb (1 736 -1 806).
“La fuerza de interacción en el vacío de
dos cuerpos puntuales en reposo car­
gados es directamente proporcional al
producto de los módulos de las cargas e
*
*
*
ü
«
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
=
»
*
*
*
♦
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
inversamente proporcional al cuadrado
de la distancia entre ellas".
Cargas puntuales en el VACIO.
i
-O
i
qi - q2
d'
|2
UNIDADES
q F d K
Coulomb Newton metro 9.10» N '" 2
c 2
CONSTANTE ELECTRICA (ep):
El coeficiente "K" en el sistema interna­
cional (S.I..) se puede escribir en la forma:
K = -—-— = 9.109
4 tco
La magnitud eo (e es una letra griega que
se lee "épsilon" se denomina constante elec­
trica. Su valor es
1
Eo= . u
4 ti K
Equivalencia:
= 8,85.10
-12 _C1_
N. m2
1|.iC = 1 micro coulomb = 10 C

402. ACLARACIONES SOBRE LA LEY DE
COULOMB
1. Observese que se cumple la tercera ley
de Newton, "Principio de la igualdad de la
acción y reacción".
2. Por cargas puntuales entendemos cuer­
pos cargados cuyas dimensiones son pe­
queñas en comparación con la distancia
que los separa.
LEY DE COULOMB
PROBLEMA N®01
En la figura, la esfera A y el péndulo
poseen cargas de igual magnitud y de
signos contrarios. Sabiendo que B está
en equilibrio y que su masa tiene un valor
de 10 gramos.
Determine la magnitud de la carga en
SOLUCION; Calculo de la fuerza
eléctrica:
F = K t o9^gf
9 x 10'
F = 1Q11 x q 2
D.C.L. de la esfera : "B"
... (1)
«i*
*
*
F = m g .... (2)
Reemplazando (1) en (2)
1011qz = 10_2(10)
Luego.
q = 10^C
PROBLEMA N* 02
La figura muestra do* esterillas de
igual tamaño cargadas con magnitud
q" y »3 q., reSpectivamente. Despreciando
las fuerzas de fricción, hallar el peso del
bloque “W", tal que el sistema se encuen­
tre en equilibrio, q = 10pC
*
♦
*
*
*
*
#
*
#
*
*
#
*
*
*
*
*
*
#
*
*
*
*
*
SOLUCION:
1) Hallaremos primeramente la fuerza
de atracción eléctrica entre los cuer­
pos cargados eléctricamente; de la
ley de Coulomb.
F = K . a i ^
F = 30 N

403. 2) Como no existe rozamiento, la ten­
sión en la cuerda no vertical es igual
a la fuerza electrica "F". Haciendo
el D.C.L. del nudo y aplicando la
primera condición de equilibrio
tenemos que:
IF y = 0
W = 2F. Sen 53°
W = 2 30N . i
5
W = 48 N
PROBLEMA N®03
La figura muestra dos esferas idénti­
cas de peso 10N y carga q = 20|iC, cada
uno. Determinar la tensión en las cuerdas
(1)V(2).
tensión en la cuerda (1) En este dia­
grama las fuerzas eléctricas se anulan
Realizamos el D.C.L. del sistema forma­
do por las dos cargas, para determinar la
Cálculo de la fuerza eléctrica de repul­
sión.
F = K . S ^ = 40N
G
Realizamos el D.C.L. de la esfera inferior.
IF y = 0
T2 = W + F
Reemplazando:
T2 = 10 + 40
Luego: Tg = 50 N
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
■
»
*
PROBLEMA N* 04
La figura muestra dos esferas car­
gadas con igual magnitud pero signos
diferentes (q = 20uc), peso 20N cada uno
y separados a una distancia de 30 cm.
Determinar la tensión en la cuerda (1).
Cálculo de la fuerza eléctrica

404. F = K . a f = 9 x 1 0 9 ^ ^ >
cr 9 x 1 o
F = 40 N ....(1)
Realizamos el D.C.L. de la esfera (+q):
T. Cos 60° = (F + W) .... (2)
Reemplazando en (2):
2
v /
= (40 + 20)
Luego: T = 120 N
PROBLEMA Ne 05
La figura muestra tres esferillas A, B y
C cargada. Qa = 40^C; Qb = 90(iC. Deter­
minar el valor de la carga que debe tener
la esferilia ”C“ y la distancia "x“ con la
condición de que las esferillas B y C estén
cada una en equilibrio. La superficie es
aislante y lisa.
*
*
*
*
*
$
*
*
*
s
t=
*
*
*
*
*
*
*
%
*
*
*
»
*
*
*
*
*
*
*
*
*
*
m
«
i»
$
*
*
*
♦
*
1) Analizando primeramente el estado
de equilibrio de la esterilla "C" ha­
ciendo el D.C.L y aplicando la pri­
mera condición de equilibrio
X Fx = 0
Fac - Fbc
K (40|i) Qc _ K (90u) Qc
x2 (10 —x)2
x = 0,04 m
2) Analizaremos a continuación de la es­
fera ”B". Haciendo el D.C.L. y apli­
cando la primera condición de equili­
brio, tenemos que
XFx = 0
Fc b = Fa b
K (90i,) Qc _ K (40[i) (90¡i)
(0,06)2 (0,1)2
Luego: Qc = 14,4|iC
Pero el signo de "Oc" es negativo, enton­
ces:
Qc = —
144 10~7 C
PROBLEMA Nfi 06
La figura muestra una barra homogé­
nea y uniforme en equilibrio. Cada esfera
tiene un peso de 5N y cargadas con mag-

405. nitud q = 20¡jC, pero signos diferentes.
Hallar el peso de la barra.
■
2
tx
j-n
M
6
k
’grt^',a
L
>
v
>
,it,vaxv
© T
t m r
0,3r
SOLUCION: Realizamos el D.C.L. de la
esfera "+q”
ZFy = 0
T + 5N = F
T + 5N =K.
—
K
Reemplazando datos:
T + 5N = 40N
V 5N
T = 35N .... (1)
Realizamos el D.C.L. de la barra:
ÍT
1
K ETT
(2)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ZFy = 0 -> W = 2T
Reemplazando (1) en (2)
W = 70 N
PROBLEMA Ne 07
La figura muestra dos esferitas car­
gadas con magnitud "q" y “3q" res­
pectivamente. La esferilla móvil de masa
m = 90g y carga eléctrica "q" se encuen­
tra en equilibrio en la posición mostrada.
La esferilla de carga ”3q” se encuentra
fijo, si el radio del casquete, dieléctrico y
liso, es R = 10cm. Hallar "q". g = 10m/s
1) Analizaremos ese estado de equili­
brio de la esfera cargada con magni­
tud "q”. Haciendo el D.C.L y apli­
cando las condiciones de equilibrio:
* IF y = 0
N. Sen 30°= mg. Cos 30° ...(1)
* ZFx = 0
N.Cos30°=F+mg. Sen30° (2)
*
*
*
*
*
*
*
*
*
*
*
tg 30° = m9 Cos3Q°-
F + mg. Sen 30°
Despejando F = m ,g
3) De la ley de Coulomb:
K- (q) (3q) m n
n ? ~ 9
(2R Cos 3 0 °r
-- (3)

406. Reemplazando datos en el S I.
Luego: q = 10_6C
PROBLEMA N* 08
En el sistema mostrado las barras son
ingrávidas. Determinar la tensión en la
cuerda horizontal AB para que el sistema
se encuentre en equilibrio en la posición
mostrada si se sabe que las esferas mos­
tradas de igual peso y carga (q = 150uC),
pueden moverse a io largo de las barras
mostradas (L = 50 cm)
Hallaremos primeramente la fuerza de
repulsión entre las esferas cargadas
eléctricamente.
Sabemos:
F = K
<n 02
d2
F = K . i
F = 450N
Hallaremos a continuación ei peso de la
esfera cargada. Haciendo D.C.L. de la
esfera y aplicando la primera condición
de equilibrio tenemos:
EFx = 0
F Cos 60° = W Sen 60°
Hallaremos finalmente, la tensión en la
cuerda horizontal. Haciendo D.C.L. del
sistema ‘ barra + esfera" y aplicando la
segunda condición de equilibrio tene­
mos:
*
*
IMo=0
T. (2L Sen 60°) = F. L Sen 60°
+ W LC os60°
Despejando:
T = 300 N
PROBLEMA N®09
Cuatro cargas puntuales de valor "q"
cada uno están situados en los vértices
de un cuadrado. ¿Cuál será la carga “Q"
de signo contrario que es necesario colo­
car en el centro del cuadrado tal que, el
sistema se encuentre en equilibrio.
SOLUCION:
1) Si el sistema está en equilibrio, enton­
ces cada carga debe estar en equili-

407. 2) IF y =0 —
»F5 . Sen4£Í>=F2. Sen 4 Í+ F3
Luego:
2.K.q.Q ^ _ k q.q J K + k W -
L£ 2 " 2L2
Reduciendo: Q. V2~= q.
T +1
q = 5 [1 + 2 V2 ]
PROBLEMA Nfi 10
En los vértices de un triángulo
equilátero de lado 0,3m se han colocado
tres cargas eléctricas de magnitud: +Q; +
2Q; -3Q; donde: Q = 10j C Determinar la
fuerza resultante que actúa sobre la carga
“-t-Q". Considere sólo fuerzas eléctricas.
*
*
*
#
«
♦
*
*
*
*
*
*
*
*
*
*
*
*
#
♦
#
*
*
*
*
*
*
#
*
brío, luego; analizarnos la carga (4), J
donde: *
F3 = ^ ....(1) ¡
L *
F5 = K . 3^ = 2 K ay ....(2) *
L_ L m
o ♦
* *
F2 = K .a:- | .... (3)
2L *
*
Cálculo de las fuerzas F1 y F2 :
Q(2Q)
F1 = K . = 20 N
L2
Q(3Q)
F2 = K " = 30 N
L2
Cálculo de la fuerza resultante:
Fp = F^ + Fg+ 2Fi F2. Cos 120°
Reemplazando: Fr = 10V7 N
PROBLEMA N® 11
En ios vértices de un cuadrado se han
colocado cuatro cargas eléctricas, como
muestra la figura. Si "Q” se encuentra en
equilibrio, determinar la relación entre las
cargas: Las cargas "-q “ se encuen­
tran fijos al plano.
SOLUCION:
Graficando las fuerzas eléctricas, sobre
la carga “Q“.

408. K .
XF = O
Fi = F . -JZ
0 - 0 _ (< Q q
(L V2T
<2
Q
= 2 ^2
PROBLEMA N« 12
En los vertices de un exágono regular
se colocan cargas eléctricas iguales de
valor "+q”.
¿Oué carga habrá que colocar en el
centro del exágono, para que todo este
sistema de cargas permanezca en equili-
b io.
SOLUCION:
*
*
%
*
*
♦
*
*
*
*
*
*■
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
#
♦
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
1) Para el equilibrio de ias seis(6) cargas
de magnitud ”q' el signo de la carga
"Q” colocada en el centro debe ser
negativo.
Por simetría del esquema, es sufi­
ciente analizar el equilibrio de una
sola de estas cargas, no importa cual
sea. Escojamos por ejemplo la carga
situada en el vértice “6"
F,=FsJ y í ;
(a/3) 3a
F3 = J S Í , Í ¿ ; F 7= S 4 f l
(2a)2 4a a2
2) De la condición de equilibrio:
IF x = 0
F3 + 2Fi.Cos60° + 2F2 Cos30° = F7
ü_<¿+ 2 1 +
4a4 ' a2 ‘ 2
2 — = K
3a2 ' 2 a2
Q = 1,83 . q
PROBLEMA N® 13
Un estudiante realiza un experimento
para medir la carga eléctrica de cuatro
cuerpos. Los siguientes son sus resul­
tados experimentales.
Qt = 2,4- 10~19C ; Q2 = 11,2 10~iaC
04 = 8,0. 10-19C
Q3 = 8,8 . 10_19C ;
¿Cuales de estos resultados no son
correctos?
Carga elemental = 1,6 10-19 C = e
SOLUCION
1) Del principio de cuantizacion de la
carga, sabemos, que toda carga eléc­
trica de un cuerpo o partícula es múlti­
plo entero de la carga eierr.antal o sea
de la carga de un «lebrón. Es decir:

409. Q=n.e n =— ,n =0;1,2;3;4;...
e
Haciendo las divisiones respectivas:
Para Q i:
Qi 2 ,4 .10 19,
e 1 , 6 . 10-19 C
Para Q2:
Ü2 11,2 . 10 19C
= 1,5
n e 1 ,6 . 10~19C
= 7
Para Q3:
Q3 8 ,8 . 10~19C
e 1,6.10 -19,
Para Q4:
Q4 8, 0 . 10~19 C
n = — = -
e 1 ,6 .1 0,-19 ,
= 5,5
= 5
2) Los valores de “n" para Q1 y Q3 son
incorrectos, por consiguiente Q4 y Q2
son correctos.
CONCEPTO.
El campo eléctrico, es un campo de fuer­
zas, una de las fuerzas de la materia que
estudia la física a la par que la sustancia. La
peculiaridad más importante de los campos
de fuerzas en ia que con su ayuda se efec­
túan las interacciones de diversos tipos. Así,
el campo de gravitación efectúa la interac­
ción gravitaloria de las masas que se en­
cuentran en él. Todos los campos poseen
propiedades muy importantes que caracteri­
zan su materialidad, en primer lugar la ener­
gía. Entre el campo y la sustancia no existen
límites infranqueables, se pueden transfor­
mar el uno en la otra y viceversa.
El campo físico no puede determinarse
como el espacio en que actúan ciertas fuer­
zas. El espacio, lo mismo que el tiempo, es
una forma de existencia de la materia. Del
hecho de que los campos existan en el espa-
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
#
$
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*■
*
*
*
*
#
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
♦
*
ció no se deduce, ni mucho menos que el
campo pueda identificarse con el espacio, ya
que una forma de existencia de la materia no
puede confundirse con la materia misma.
La interacción coulombiana entre las
partículas o cuerpos eléctricamente car­
gados y en reposo, se efectúa por medio del
CAMPO ELECTROSTATICO que ellos
crean. El campo electrostático es el campo
invariable con el campo eléctrico estacio­
nario, creado por las cargas eléctricas en
reposo. Este campo es una de las formas del
campo electromagnético, el cual efectúa la
interacción entre las partículas (o cuerpos)
eléctricamente cargados que se mueven, en
el caso general, de un modo arbitrario con
respecto al sistema de referencia elegido.
La propiedad característica de un campo
eléctrico arbitrario, que lo distingue de otros
campos físicos, es la de actuar tanto sobre
las cargas eléctricas (partículas y cuerpos
con cargas), en movimiento, como sobre las
que están en reposo.
Para caracterizar cuantitativamente la
fuerza con que actúa el campo eléctrico so­
bre las partículas y cuerpos cargados sirve
al vector, intensidad del campo eléctrico "E".
INTENSIDAD DEL CAMPO
—
»
ELECTRICO (E):
Es una magnitud física vectorial, que
sirve para describir el campo eléctrico. Su
valor se define como la fuerza resultante que
actúa por cada unidad de carga positiva en
un punto del campo.
E =
qo
.... (1)
■vS iM i
+ C
J.
Se representa por un vector que tiene la
misma dirección y sentido que la fuerza eléc­
trica resultante.

410. Para detectar el campo se utiliza una
carga puntual "qo” de prueba Esta carga de
prueba, es tan pequeña, que su presencia no
provoca una redistribución en el espacio de
las cargas que crean el campo que se inves­
tiga En otras palabras, la carga de prueba
"qo" no distorciona el campo que se estudia
con su ayuda.
En la figura, tenemos una carga creadora
del campo “Q” y una carga de prueba puntual
positivo "qo”.
De la ley de Coulomb:
F = K
Q- qo
.... (2)
Reemplazando (2) en (1):
Q.qo
K.
E = -
qo
Luego:
Fórmula práctica esca­
la r lo se considera el
signo de la carga crea­
dora.
Unidades de la intensidad del campo
eléctrico:
N V
C ' m
De la fórmula (1), la fuerza eléctrica F que
actúa sobre una carga "q" en un punto del
campo será:
F = q E .... (3)
PRINCIPIO DE SUPERPOSICION DE
LOS CAMPOS:
Si en un punto dado del espacio varias
partículas cargadas crean campos eléctricos
cuyas intensidades sean:
E 1 . E 2 . E 3 .... E n, etc
La intensidad resultante sera la suma
vectorial de las intensidades parciales
—
>
E r = E i + E2 + E3 + .... + E n
*
*
«
*
4.
*
*
*
*
*
*
*
*
*
&
m
*
♦
*
*
#
*
$
*
<
5
«
*
*
*
m
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
$
*
*
*
*
*
*
♦
*
Ejemplo:
La figura muestra dos partículas puntua­
les q^+J y q2(-) cargados eléctricamen­
te. La intensidad del campo creado por
cada carga en un punto A son:
E 1 y E 2
La intensidad resultante en el punto “A"
será:
E r = E 1 + E2..(vectorialmente)
ErW e * + Eg + 2. Ei . E2 . C o s 7 ....
(escalarmente)
6 es el ángulo formado por los vectores
E, y Ez.
LINEAS DE FUERZA DE UN CAMPO
ELECTRICO.
Las líneas de fuerza representan gráfi­
camente a un campo eléctrico. Fueron
ideadas por un físico inglés Michael Faraday
(1 791 - 1 867). Convencionalmente las
líneas de fuerza salen de las cargas positivas
e ingresan a las cargas negativas.
Las líneas de fuerza son líneas con­
tinuas, no se cortan entre sí, debido a la
unicidad del campo en un punto. La intensi­
dad de! campo en un punto se representa por
un vector tangente a la línea de fuerza.

411. La densidad de líneas de fuerza es mayor
en las proximidades de los cuerpos car­
gados, donde la intensidad del campo tam­
bién es mayor
Interacción entre dos cargas de igua!
magnitud.
Las líneas de fuerza no son idénticas a
las trayectorias que siguen en el campo elec­
trostático las partículas ligeras cargadas. En
cada punto de la trayectoria de una partícula
la velocidad tiene una dirección tangente a la
curva. Según la tangente de una línea de
fuerza está dirigida la fuerza que actúa sobre
la partícula cargada y, por consiguiente, la
aceleración.
/ 'N
*
*
*
*
*
<
*
¡
*
*
*
*
*
*
*
*
*
*
*
*
s
jt
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*■
*
*
*
*
*
*
*
*
*
*
s
(s
*
*
*
*
*
*
*
CAMPO ELECTRICO HOMOGENEO O
UNIFORME
Un campo eléctrico cuya intensidad es
igual en todos los puntos del espacio se llama
campo homogéneo o uniforme Las líneas
de fuerza son paralelas.
q E
Figura (1)
qE
<5>
D
2)
3)
Fipura (2 )
La figura (1) muestra la acción del campo
E sobre una carga eléctrica positiva (+).
La fuerza sobre la carga tiene la misma
dirección y sentido del campo,
La figura (2) muestra la acción del campo
E sobre una carga eléctrica (-). La fuerza
sobre la carga tiene la misma dirección,
pero sentido opuesto al campo.
La fuerza F que actúa por parte del campo
electrico sobre una carga arbitraria “q“ si­
tuada en un punto dado del campo es:
F = q -E
Donde E es la intensidad del campo, en
el punto en que se encuentra la carga “q",
distorsionado por esta carga, es decir, difer­
ente del campo que existía antes de intro­
ducir en él la carga "q”.
TRAY£CTORIí

412. 1 CA
CAMPO ELECTRICO
PROBLEMA Ne 01
En el triángulo rectángulo mostrado en la
figura, determinar ei valor de la intensidad de
campo en el punto medio M de la hipotenusa.
- • q
l -
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
2q | , ------------------------------J
SOLUCION:
Graficandolosvectoresintensidadesdecampo
en el punto M, generados porcada una de las
cargas. Esfác¡l comprobar que:
Ea = Eb
Por tanto el vector intensidad de campo
resultante es el generado sólo por la
carga que está en C. Según esto:
E = Ec -> E = K -
( L /'Í2 f
E =
PROBLEMA Ne02
En los vértices de un triángulo rectán­
gulo se han colocado dos cargas eléctri­
cas de magnitud:
Q i= -125 .1 0-8C y Q2=+27 .1 0-8C
Separados una distancia de 0,4 m
como muestra la figura. Determinar la
intensidad del campo eléctrico resultante
en el vértice "A".
*
*
*
*
*
Llevamos una carga de prueba ”+q0" al
vértice “A” para determinar la dirección y
sentido del campo eléctrico.

413. Ei = K. = 9 . 109 125 10_8
Ei = 4 5 KN/C
E2 = 27 KN/C
25. 10~2
.... (2)
Cálculo de ¡a resultante, mediante el
método del paralelogramo.
E „ = E , = E 2+ 2E1 . E2 . Cos 127°
Reemplazando datos:
Er = 36 KN/C
PROBLEMA N903
En los vértices de un cuadrado se han
colocado cuatro cargas puntuales de
magnitud Q; 2Q; 3Q y 4Q. Si, la carga "Q"
genera un campo cuya intensidad en el
centro del cuadrado es: 25 2 N/C, deter­
minar la intensidad de campo resultante
en el centro del cuadrado:
SOLUCION:
Las cargas equidistan del centro, por
consiguiente la intensidad del campo se­
rá directamente proporcional a la magni­
tud de cada carga. Sea, E = 25 V2 N/C,
la intensidad del campo generado por
„Q..
Cálculo de la resultante de la intensidad
de campo, en el centro del cuadrado
*
*
*
a¡
#
*
#
*
*
*
*
%
*
*
*
*
*
*
*
Reemplazando la magnitud de "E" en (1):
E r = 100 N/C
PROBLEMA N®04
En la figura, determinar el valor de la
carga que se debe colocar en ia posición
“B" para que e la intensidad del campo en
el punto "C" sea horizontal, sabiendo que
la carga en la posición “A" es de magnitud
QA = 64(i,C.
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
1) De la geometría elemental se de­
duce un triángulo ABC de lados: 7d
15d y 2 Od, respectivamente.
2) Es fácil deducir que la carga en "B”,
que cumple con la condición debe
ser de signo negativo.
Grafícando los vectores parciales
intensidades de campo en el punto
C. deducimos que se debe cumplir
que:
ZEv = 0

414. Ea. Sen 37° = Eb- Sen 53°
K ——K ■
^
(20 d)
27
iz 5 (15 d)2 5
Qb = • Qa -» Qb = 27jiC
Pero el signo de la esfera en “B“ es
negativo.
QB = —
27|iC
PROBLEMA Ne 05
Los puntos A, B, C y D determinan un
cuadrado.
Tres cargas son colocadas como se
muestra en la figura en los vértices A, C y
D.
Q A= 10 C y QD = 28C.
Calcular la magnitud y signo de la car­
ga “Qc" que se debe colocar en el vértice
"C", tal que, ia intensidad del campo eléc­
trico E en el vértice “B", sea horizontal.
*
*
&
*
*
*
4
>
*
*
*
*
*
*
*
*
*
*
«
<
*
#
0
<
¥
<
¥
*
*'
*
$
*
*
*
W
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
♦
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
♦
*
#
*
#
1) Analizamos las intensidades de
campo parciales en el punto "B"
graficando la intensidad creada por
“Qd“ observamos que tiene una
componente vertical hacia arriba, de
aquí deducimos que el signo "Qc"
debe ser negativo, tal que la intensi­
dad sea vertical hacia abajo, de la
condición del problema.
1EV= 0
K. Qd V2
k. Qc
L2 (V 2 .L )2 2
Qc = . Qd
4

415. Qc = -7 V2 C
2) En la solución del problema no ana­
lizamos la intensidad de la carga
"Qa", debido a su dirección horizon­
tal
PROBLEMA N®06
La esfera mostrada tiene un peso
W = 20N y carga eléctrica q = 10C. Hallar
la intensidad del campo eléctrico homo­
géneo "E", sabiendo que a¡ soltar el cuer­
po, éste inicia un movimiento horizontal
hacia la derecha.
SOLUCION:
1) Sabiendo que al soltar el cuerpo (ve­
locidad inicial nula) inicia su movi­
miento horizontalmente hacia la de­
recha esto significa que la fuerza
resultante es hacia la derecha.
r
y i
q.E.Sen53°
E.q
A * 3*
- 1 . . . 1
r q.ECos53°
V J
*
*
*
4
»
*
*
*
*
m
m
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
♦
*
*
*
&
#
*
*
$
*
*
$
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
4
*
*
*
*
*
*
*
$
2) EFy^.entonces q.E.Sen 53° =W
10C. E - i = 20N
5
E = 2,5 N/C
Luego:
PROBLEMA N9 07
Si se abandona la esfera mostrada de
masa m = 10 kg y carga eléctrica
q = 5.^3 C. Determinar la aceleración sa­
biendo que el campo eléctrico es homo­
géneo de intensidad E =20 N/C. Con­
sidere el campo gravitatorio de intensidad
g =10 m/s .
f A
A —
E
w
m,q
^ ____
SOLUCION:
1) Sobre la esfera actúan su peso y la
fuerza eléctrica.
2 ) Cálculo de la fuerza resultante: "F r "
F r = V(m.g)2+(qE)2 .... (1)
Fr 'V(rrT.g)2+ (q.E)2
a m m
4) Reemplazando datos en (2):
v10000 + 30000

416. a = 20 m/s
PROBLEMA Ne08
Determinar la intensidad de campo E
mínimo posible, del campo electrostático
homogéneo mostrado en la figura, con la
condición que el sistema conserve su es­
tado de equilibrio la esfera y el bloque
tienen igual peso, W = 40N y
carga q = 20uC, coeficiente de roza­
miento estático: 0,75 entre el bloque y la
superficie hor,zonta!.
Analizando el estado de equilibrio de la
esfera cargada con signo positivo.
Haciendo D.C.L. y aplicando las condi­
ciones de equilibrio tenemos:
XFy = 0
T = W + F
I
t = w + K ^ Ü
d2
Reemplazando datos:
T = 130 N ... (1)
Analizando el estado de equilibrio del
bloque "W". Haciendo el D.C.L. y apli­
cando las condiciones de equilibrio.
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
T= q.E + |i.W T
«=o—
qE = T - nW
Reemplazando datos:
7 líN
E = 5 MN/C
PROBLEMA Ne09
Una esferita de peso 4 x 10_3N y carga
eléctrica q = ~1üuC, unida a un hilo de
seda se encuentra suspendido de un pun­
to fijo, dentro de un campo eléctrico ho­
mogéneo. Sabiendo que la esferita se
encuentra en equilibrio, determinar “ E".
m
*
*
*
m
*
*
*
*
*
*
SOLUCION:
Realizamos el D.C.L. de la esfera de
peso W y de carga "q”.
De la condición de equilibrio la suma de
las tres fuerzas es igual a cero: del trián­
gulo de fuerzas tenemos
tg 37° = ~ => F = | W

417. qE = f W E =
3 W
4 q
Reemplazando datos
3 4 .1 0-3 N
E = -
10“5 C
E = 300 N/C
PROBLEMA Ng10
¿Con qué aceleración constante se
desplaza el móvil, para que la esfera de
masa m = 0,1 kg y carga q = -20pC se
encuentre en equilibrio respecto del ca­
rro. El hilo de seda forma un ángulo de
45° respecto de la vertical. El campo ho­
mogéneo en el interior tiene una intensi­
dad E = 30KN/C. 6 = 45°
Realizamos el D.C.L. de la esfera "q“
IF y = 0
T.cos G= mg . . . (1)
Fr = m.a.
(T Sen 6 - F) = m.a.
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
T Sen 6 = F + ma . . . (2)
Dividiendo: (2) (1)
T „ F + m a , . _ _
Tg 0 = ----------, donde : F = qE
mg
a = g. Tg 6 -
S LÉ
m
(3)
Reemplazando datos en (3):
a = 3,8 m/s
PROBLEMA Ne 11
La figura muestra un ascensor que
sube con aceleración constante "a". En
el techo del ascensor se encuentra sus­
pendido una esferita de masa "m" y carga
"q" mediante un hilo de seda sabiendo
que dentro del ascensor existe un campo
eléctrico homogéneo "E" hallar el ángulo
* 6 “ que forma el hilo con la vertical.
*
#
*
*
*
*
*
1) Realizamos el diagrama del cuerpo
libre de la esferita respecto de un
observador ubicado en el piso del
ascensor, sistema de referencia NO
inercial

418. Para nuestro observador la esferita
estará en reposo relativo.
LF = 0
*
*
*
*
Luego se construye el triángulo de
fuerzas:
Tg 6 = — q E -
m . (g + a)
0 = are Tg J L § _
m . íg + a)
PROBLEMA NB12
Un péndulo de masa "m“, carga eléc­
trica "q” longitud. "L", se utiliza para me­
dir la intensidad del campo eléctrico ho­
mogéneo por comparación. Cuando el
sistema se coloca en un campo de inten­
sidad Ei = 80N/C el hilo de seda forma un
ángulo de 45° respecto de la vertical.
Cuando el sistema se lleva a otro campo
homogéneo el hilo experimenta una des­
viación angular de respecto de la ver­
tical. Hallar la intensidad E¿ de este úl­
timo campo homogéneo.
*
*
*
*
*
*
*
*
#
*
*
*
*
*
#
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
SOLUCION:
1) D.C.L. (esfera), en el primer campo
eléctrico, Ei.
* Del triángulo de fuerzas.
2) D.C.L. (esfera) en el segundo
campo eléctrico, E2.
* Del triangulo de fuerzas
T937° = S# • { P)

419. 3 q E2 c 3 p
— = ------■=- —
>C2 = ~
7• El
4 q . Ei 4
, E 2 = 6 o £
PROBLEMA N9 13
Un péndulo de longitud "L" masa "m ”
y carga eléctrica "q" se mueve en un plano
vertical con velocidad angular constante
” “ sabiendo que el campo eléctrico "E“
es homogéneo, calcular la diferencia en­
tre la tensión máxima y la tensión mínima
en el hilo de seda. Considere el campo
gravitatorio "g ”.
L
/
*n
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
SOLUCION:
1) La tensión máxima se consigue cuando
el cuerpo pasa por la posición más baja
de su trayectoria y la tensión mínima en
el punto mas alto de la trayectoria circu­
lar. .
qE * ^
2) Dinámica circular en "A".
IF (radiales) = m.ac
Tmáx - q.e - m.g = m.m2.L . . . (a)
3) Dinámica circular en "B“:
Tmin+q.E+m.g = m.w2 L .. ((3)
4) Igualando. ( a ) y ( P ):
Tmáx —q E —m.g = Tm¡n + q E + m.g
Tmáx —Tmin = 2(m.g + q.E)
PROBLEMA 14
En un campo electrostático uniform e
de intensidad E = 5.10a N/C y cuyas líneas
' de fuerza están digiridss horizontalmente
hacia la derecha en un plano vertical, ata­
da aw n hilo de longitud L = 0,5 m una
esferita de masa m = 0,5 kg y carga eléc­
trica q = 6jíC gira con velocidad angular
constante w = 6 rad/s.
Hallar la tensión MAXIMA en el hilo de
seda.
Considere el campo gravitatorio:
(g = 10 m/s2).
*
*
#
*
*
*
*
*
*
*
1) Cálculo de la gravedad efectiva:
F
(resu
ltan
te)
3= =Q
ef
masa
I
f 2 +
s i.
m

420. 2) La tensión en el hilo será máxima,
cuando la esferita para por la posi­
ción más baja respecto del "campo
efectivo", por consiguiente la ten­
sión “T“ y el peso efectivo son co­
rneales.
3) Dinámica circular:
£F(racJ) = m.ac
p
T - m . gef = m . tú L . . . (2)
Reemplazando (1) en (2):
T = m . get + m - co2.L .. (3)
Datos en (3), tenemos:
Tm
axim
a—11 N
PROBLEMA N® 15
Una esferita de masa “ m" y carga eléc­
trica "-q " se lanza verticalmente hacia
arriba dentro de un campo homogéneo
eléctrico de intensidad “E" representado
mediante líneas de fuerzas verticales ha­
cia arriba. Determinar la velocidad “Vo"
de lanzamiento tal que, la esferita alcanza
una altura máxima “d". Desprecie el cam­
po gravitatorio.
*
*
*
*
<
¥
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
s
js
*
*
*
*
*
*
*
*
sis
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
i*
#
*
*
*
*
*
*
*
*
*
SOLUCION:
1) Cálculo de la aceleración, mediante
la segunda ley de Newton
a = < f H ) ..(1)
2) Del movimiento vertical:
V F
V= V ov “ 2 -ad
0 = V c - 2ad ..(2 )
Reemplazando (1) en (2):
VD= m
Luego:
q.E .d
m
VF=0©-

421. CONCEPTO.
Es una magnitud física escalar, se define
como la capacidad que tiene un cuerpo car­
gado "q" para realizar trabajo en virtud a su
posición dentro del campo homogéneo la
energía potencial es igual al producto de la
fuerza eléctrica por la distancia a la línea de
referencia, osea a una superficie equipoten­
cial.
V(mayor)
E - 0
P
+ d
Linea de
referencia
V(menor)
- d
( 3 )
• -
q
(2 )
q
( i)
q
Ep = Trabajo realizado por el
campo sobre la carga “q"
E p = F d
Pero:
F = q . E
Luego: Ep = q . E . d
1)
.... (2)
■(3)
En principio la línea de referencia es
una superficie equipotencial donde
arbitrariamente la energía potencial
de cualquier carga es igual a cero.
De otro modo el potencial de refer­
encia es igual a cero.
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
#
*
*
tjt
*
*
*
*
*
*
m
m
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ik
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
2) La fórmuia de la energía potencial
eléctrica tiene la misma forma de la
energía potencial gravitatoria
Ep (eléctrica) = q. E. d
Ep (gravitatoria) = m. g. h
Donde, d y h mide paralelamente a
las líneas de fuerza del cam ->o ho­
mogéneo.
3) La energía potencial puede ser po­
sitiva o negativa, dependiendo de la
posición de la carga, respecto de la
línea de referencia. Se debe tener
en consideración que el sentido de
las líneas de fuerza está dirigida de
mayor a menor potencial eléctrico.
Además en la fórmula (3) se reem­
plaza el signo de la carga ’q" colo­
cada en el campo.
Ep (T) = q. E. d
Ep (2) = 0
Ep (3) = q. E (-d)
UNIDADES EN EL S.l.
Ep q E d
Joules Coulomb
N V
C ° m
metro
ENERGIA POTENCIAL ELECTRICA
PROBLEMA Ne 01
En la posición A mostrada en ia figura
se abandona un bloque de 1 kg. de masa
y 2C de carga el cual se mueve sobre la
superficie cilindrica, lisa y no conductora
de radio de curvatura R = 1m. Sabiendo
que la intensidad del campo uniforme es
E = 10 N/C, calcular la máxima fuerza de
reacción sobre el bloque.
(g = 10 m/s ).

422. SOLUCION:
Como sobre el bloque sólo actúan fuer­
zas conservativas, su energía mecánica
se conservará en el tiempo, es decir:
EMa = EMb
1 O
mgR + EqR = —mV
mV
= 2(mg + Eq) ...,(1) *
Fcp=
mV¿
N o -E q -m g (2)
No = 90 N
R u H R
Reemplazando (1) en (2) y despejando:
No = 3 (Eq + mg)
PROBLEMA Ne 02 -
La figura muestra un péndulo de longi­
tud L = 0,5 m de masa m = 0,05 kg y carga
q = 50GjjC, se abandona en la posición
"A". El campo eléctrico de intensidad
E = 600 N/C es uniforme, representado
mediante líneas de fuerzas verticales.
C alcular la m áxim a velocidad que
adquiere "m". Considere : g = 10 m/s
*
*
*
♦
*
*
si*
*
*
#
m
*
m
m
#
*
*
$
4!
a
s
#
#
*
m
íni.q
SOLUCION:
1) Sobre el cuerpo esférico actúan dos
fuerzas constantes : el peso "m.g" y
la fuerza eléctrica “q.E" y la tensión
"T“ que es una fuerza variable.
2) La energía potencial del cuerpo será
debido al campo gravitatorio y al
campo eléctrico.
3) La esterilla alcanza su máxima velo­
cidad cuando pasa por su trayecto­
ria más baja esto quiere decir cuan­
do la energía cinética será máxima.
4) Principio de conservación de la
energía mecánica

423. E f (A) + Ek(A) = Ep(B) + Ek(B)
1 2
mgh+ qEh + 0 = 0 + —.m .V B
Pero: h = L
L u e g o :V = ^ 2 L ^ g + 5
mEj
Reemplazando:
V(maxima) —4 m/S
PROBLEMA Ns03
En la figura mostrada se abandona un
bloque de masa "m" y carga "q" en la
posición “A" dentro de un campo homo­
géneo eléctrico de intensidad E = 10 N/C.
Sabiendo que el bloque llega a la posición
“B“ con una velocidad de 8 m/s. Hallar el
trabajo realizado por la fuerza de roza­
miento sobre el bloque, donde : m = 1kg,
q = 5|iC y h = 1 m. Desprecie el campo
gravitatorio. g = 0
En principio la energía potencial se pue­
de presentar como energía potencial gra­
vitatoria, elástica y eléctrica.
Teorema del trabajo y la energía me­
cánica "El trabajo realizado por fuerzas
diferentes a las fuerzas conservativas es
igual a la variación de la energía me­
cánica".
W,r = Ek(B) + EP(B) - Ek(A) - EP(A)
W,r = 1 m.V2 + 0 - 0 - q. E. h
2
W,r ,1.kg. 64 ” —5C. 1 0 ~ . 1m
2 s* U
W<
r= 32 J - 50 J = —
18 J
Luego
Wfr = —
18 J
El trabajo realizado por la fuerza de roza­
miento (fuerza no consecutiva) es igual al
18 Joules.
Se dice que la fuerza es consecutiva
cuando el trabajo realizado por dicha
fuerza es independiente del camino o
trayectoria seguida, esto quiere decir que
sólo se necesita conocer el estado inicial
y final del cuerpo.
Si el trabajo realizado por la fuerza de­
pende del camino que sigue, entonces la
fuerza se denomina NO conservativa,
ejemplo : La fuerza de rozamiento.
PROBLEMA Ns04
Una esferita de masa "m" y carga “q"
puede girar en el plano vertical suspen­
dida de un hilo de longitud "L”, gira al­
rededor de una carga inmóvil, igual a la
carga de la esferita , donde " a “ es el
ángulo que forma la dirección del hilo con
la vertical. Encontrar la velocidad angular
con la cual ¡a esierita gira uniformemente.

424. 1)
2)
En principio, la esferita se mueve
por una trayectoria que es parte de
una superficie equipotencial es­
férica.
Haciendo el D.C.L. de la esferita
respecto de un observador en la
Tierra.
3)
* F (radicales) = m . ac
T sen a - F = m.tú . R
T . sen a =F+m. co2 R ... (1)
* Fy = 0
T.cosa = m.g .... (2)
Dividiendo las ecuaciones: (1) (2)
tg a =
F + m. 10 . R
co2 =
m g
g- tg a F
R m R (3)
Pero de la ley de Coulomb:
F =
R,2
Además: R = L.sen a
Reemplazando (4) en (3):
- (4)
C0=
g k.q.q
L.Cosa m lA se n a
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
Una esferita de masa "m" y carga "q"
puede girar en un plano vertical suspen­
dida de un hilo de seda de longitud "L”.
En el centro de giro se encuentra una
segunda esferita, cuya carga es igual en
valor y en signo a la carga de la esferita
que gira. ¿Cuál es la velocidad horizontal
MINIMA que hay que comunicarle a la
esferita en su posición más baja para que
pueda realizar una vuelta completa?
SOLUCION:
1) En principio la esferita se mueve en
una superficie equipotencial eléctri­
ca se mantiene constante en el tiem­
po.
2) La esferita se mueve en un campo
(gravitatorio) conservatorio, enton­
ces la energía mecánica se con­
serva en el tiempo.
EM (A) = EM (B)
Ek(A) + EP(A) = Ek(B) + EP
(B)
+ mg (2L) + — -9^-9-

425. Dinámica circular en "B"
F (radicales) = m.ac
(mg + T - F) = m , —
donde-
F = k (2)
De la condición del problema (V0 y
V son mínimos) !a tensión en la
cuerda tiende a cero, (T -> 0).
Luego; en (2):
V = g. L - k-q-q
m. L
(3)
Reemplazando (3) en (1):
PROBLEMA Ne 06
La figura muestra un péndulo de masa
"m'“, longitud "L" y carga eléctrica "+q“,
dentro de un campo (homogéneo) eléc­
trico “ E" representado mediante lineas de
fuerzas verticales. Hallar la mínima velo­
cidad V0 que se le debe comunicar en su
posición más baja, tal que, pueda des­
cribir por lo menos una vuelta en un piano
vertical. Considere el campo gravitatorio
“g".
< i ! 1
E
/
"■ 'x
i
/
*
*
■
*
*
$
*
*
*
*
Dinámica circular, en el punto más
alto. La tensión mínima en "B" debe
tender a cero (T -» 0), de la con­
dición del problema.
F (raaicales) = m. ac
V 2
(qE + mg) = m. — ....(1)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
2) Principio de conservación de la
energía mecánica
EM (A) = EM (B)
Ep (A) + Ek(A) = EP(B) + Ek(B)
1 2 1 5
¿ m V 0=(qE+m g)(2 L)^m V 2 .... (2)
Reemplazando (1) en (2), tenemos
|m V 0=(qE+mg)(2L)+|(qE+mg)L

426. En el sistema mecánico mostrado, el
carrito en la posición "A", tiene masa "m"
y carga eléctrica “+q". Sabiendo que el
campo eléctrico "E" es homogéneo, cal­
cular la mínima altura “Ho" desde el cual
se debe abandonar el carrito, tal que, pue­
da dar una vuelta completa sobre el rizo
de radio de curvatura “R". Los rieles por
donde se desliza el carrito es liso y no
conductor de las cargas eléctricas. Con­
sidere el campo gravitatorio “g".
SOLUCION
1) Para que el carrito pueda dar una
vuelta con su mínima energía
mecánica, la reacción normal en la
parte más alta del rizo, punto “B”,
debe tender a cero (N -» 0).
2) Dinamica circular en “B”:
*
*
*
*
*
*
*
*
m
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ije
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
3) Como los campos “g” y "E" son con­
servativos, aplicamos la conser­
vación de la energía mecánica entre
A y B
EM (A) = EM (B)
Ep(A) + Ek(A) = Ep(B) + E«(B)
(mg+qE) H0+ 0 = (mg + qE) (2R)
1
.... (2)
Reemplazando (1) en (2), tenemos:
(mg+q.E) (H0- 2R) = ~ (mg + qE) R
Luego:
“su valor no depende de la inten­
sidad de los campos g y E".
PROBLEMA N®08
En la figura mostrada se abandona
una esferilla de masa "m" y carga q en la
posición "A" más alto de la superficie
cilindrica de radio de curvatura "R ' sa­
biendo que el campo eléctrico "E!‘ es ho­
mogéneo. Hallar la posición definida por
el ángulo 6 donde el cuerpo abandona la
superficie. Desprecie el rozam iento.
Considere el campo gravitatorio "g".
1) El campo gravitatorio y eléctrico son
conservativos, esto quiere decir que
el trabajo realizado por “m.g“ y “q.E"
no depende del camino seguido por
el cuerpo.
F (radicales) = m.ac
2

427. 2) Principio de conservación de la
energía mecánica.
EP(A) + Ek(A) = EP(B) + Ek(B)
1 2
mgh + q. E. h+0 = 0 + ^ m, V „
Luego:
m. V E =2h(m g + q E ).... (1)
Dinámica circular en "B"
F (radicales) = m.a
2
V >
3
(mg + q.E) cos 6 - N = m. —
H
pero cuando la esfera abandona la
superficie: N = 0
Entonces:
2
R(mg + qE)cos 6 =m. V B ... (2)
Además : h = R(1 - cos G) ... (3)
Igualando (1) y (2):
2R(1-cos 6)(mg+qE) = R(mg + qE)CosG
6 = are Cos (2/3)
*
S
jí
*
* CONCEPTO.
*
a
»
*
*
*
*
m
&
#
♦
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
#
*
*
*
*
*
*
*
*
n
*
*
*
*
«
K
*
*
*
*
#
*
*
*
*
*
Es una magnitud física escalar. Se de­
fine como el trabajo realizado por un agente
externo contra el campo eléctrico, por cada
unidad de carga positiva, para trasladar a
velocidad constante desde el infinito hasta
una cierta posición dentro del campo. Sea,
“O" la carga creadora del campo eléctrico.
INICIAL
Q3 — —
mov
Fex
FINAL
Q (j------ • q
qO -
Potencial Eléctrico =
carga
VA = -
W„ >A
q
.... (1)
Pero el trabajo realizado es:
W,
Reemplazando (2) en (1):
VA =
i/ Q
d
.... (3)
Fórmula (3) para determinar el potencial
eléctrico en el punto "A", donde se reemplaza
el signo de la carga creadora “Q“.
El potencial electricosemideen Voltios
(V), en honor al científico italiano Alejandro
Volta (1 7 4 5 -1 827)
1 voltio
1 coulomb C s¿

428. Una carga eléctrica colocada en un cam­
po eléctrico tiene energía potencial debido a
su interacción con el campo. El potencial
eléctrico en un punto se define como la ener­
gía potencial debido a su interacción con el
campo. El potencial eléctrico en un punto se
defi 13 como la energía potencial por unidad
de carga colocada en dicho punto.
Potencial = Energía potencial
carga
V = -^E
Ep =q.V
1 joule = 1 coulomb x voltio
POTENCIAL ELECTRICO EN UN PUNTO
“A” DEBIDO A UN SISTEMA DE CARGAS
PUNTUALES.
El potencial eléctrico resultante en el pun­
to "A" es igual a la suma de potenciales
parciales, como sabemos, considerando el
signo de las cargas puntuales
2
| VA= Vi + V2+ V3 + ......+ Vn ||
DIFERENCIA DE POTENCIAL (Vab)
CONCEPTO. Es una magnitud física esca­
lar. Su valor se define como el trabajo reali­
zado por un agente externo sobre cada uni­
dad de carga para trasladar a velocidad
constante desde un punto inicial A a otro final
B dentro del campo eléctrico.
*
*
*
*
*
*
. • qn
*
*
*
«
¡*
#
*
*
*
*
*
*
*
*
*
*
*
*■
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
#
*
*
*
*
Vba = Vb - Va =
trabajo realizado de ''A'1 hacia "B"
carga en movimiento
1)
2)
3)
.... (1)
La diferencia de potencial también suele
llamarse TENSION.
El sentido de las líneas de fuerza es tal
que se dirigen de mayor a menor poten­
cial.
El trabajo por un agente externo (F ext)
para trasladar “q" de un punto inicial "A”
hacia el punto final “B" es igual al pro­
ducto de la magnitud de la carga por la
diferencia de potencial entre dichos pun­
tos.
Wa -* b = q. (Vb - Va) (2)
4) En la fórmula anterior, se debe entender
como el trabajo realizado por un agente
externo al campo (fuerza eléctrica).
También se debe recordar que se reem­
plazará el signo de la carga en movi­
miento. Además la diferencia de poten­
cial es el final “B“ menos el inicial "A". El
trabajo realizado por la fuerza externa
puede ser positivo o negativo.
1

429. 5) El trabajo A B es positivo, la fuerza ex­
terna tiene igual sentido del movimiento.
Si el trabajo es negativo, entonces el
sentido de la fuerza es opuesto al mo­
vimiento.
6) El trabajo realizado por un agente ex­
terno (fuerza externa) sobre la carga ”q"
desde A B dentro del campo es inde­
pendiente del camino o trayectoria que se
sigue. Sólo depende del potencial inicial
y final.
SUPERFICIES EQUIPOTENCIALES
CONCEPTO. Se denomina así a aquel lugar
geométrico constituidos por puntos de igual
potencial eléctrico. Las superficies equipo­
tenciales son perpendiculares a las líneas de
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
slí
s
lí
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ü
-
*
*
*
*
*
*
*
1) El trabajo realizado para trasladar una
carga, del punto A hasta el punto B que
pertenecen a la misma superficie equipo­
tencial, es igual a cero.
2) En el caso del campo homogéneo las
líneas de fuerza son paralelas por con­
siguiente las superficies equipotenciales
también son paralelos representados por
líneas punteadas.
• A
------------ b ---------------------------------
I
I
V(mayor) V(menor)
La intensidad del campo eléctrico está
dirigida en el sentido en que disminuye el
potencial eléctrico.
Va > Vb
RELACION ENTRE LA INTENSIDAD DEL
CAMPO ELECTRICO HOMOGENEO E Y
LA DIFERENCIA DE POTENCIAL "V ‘
1) Para nuestra demostración llevamos una
carga "q“ desde el punto “A" hasta el

430. punto "B" a la velocidad constante, por
consiguiente realizamos un trabajo con­
tra el campo.
LFy = 0
Fexi = q . E .... (i)
¿
2)
( i)
qE
B
- f -
2) El trabajo realizado por la fuerza externa
será:
WFex = F ex. f .... (ii)
3) Reemplazando (i) en (ii):
WFex = q.E.d .... (iii)
4) Por otro lado sabemos que el trabajo
realizado sobre la carga por la variación
del potencial.
WFex = q. (Vb - V a) .... (iv)
5) Igualando las ecuaciones (iii) y (iv):
| (Vb - V a) = E. d |
d = distancia de separación entre las
superficies equipotenciales.
POTENCIAL ELECTRICO
PROBLEMA Nfi 01
La carga 0 = 2.10 3C, que muestra la
figura, genera un campo en el espacio que
lo rodea. Determinar el trabajo que debe
realizar un agente externo para mover una
carga de prueba qD= 4pC, desde el punto
A hasta el punto B.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Hallando los potenciales en los puntos A
y B generada por la carga "Q"
V = K . §
d
Va = 9.109. 2' 1
2°— = 9 . 106
Va = 9 ■10 voltios
n6 ,
— (1)
VB= 18. 10° voltios ....(2)
Trabajo realizado sobre la carga "qo":
Wa -» b = qo (Vb - Va)
WA -» b = 4 . lO ^ C ía 106 V)
Luego:
Wa - » b = + 36 J
PROBLEMA N202
En los vértices de un triángulo equi­
látero se han colocado tres cargas eléctri­
cas puntuales de magnitud: Q ; -2Q ; 30.
Sabiendo que la carga "Q" genera un po­
tencial de 10 voltios en el baricentro de
triángulo, determinar el potencial eléctri­
co resultante en el baricentro.
SOLUCION:
f.-ZQ
/ 1
i

431. Las cargas equidistan del punto "G" por
consiguiente el potencial eléctrico gene­
rado por cada carga es proporcional a la
magnitud de la carga. El signo de la
carga y del potencial generado son igua­
les.
+ Q : potencial eléctrico : + 10V
-2 Q : potencial eléctrico : -20V
+3Q : potencial eléctrico: +30V
Potencial eléctrico resultante en el punto
“G”.
Vg = Vi + V2 + V3
Vg = 10V - 20V + 30V
Vq = 20 voltios
PROBLEMA NB03
Tres cargas puntuales de magnitud:
Q1 = 40 (iC, Q2 = -50 |iC y Q3 = 30 han
sido colocados en tres vértices de un rec­
tángulo cuyos lados miden 30 cm y 40 cm
como se muestra en la figura.
Determinar el trabajo realizado por un
agente externo para trasladar una carga
q0 = -2 |ic desde el punto A hasta B.
1) Cálculo del potencial en el punto
"A": Va = Via + V2a + V 3A
V a " K di + d2 + d2
Luego:
V a = 72. 1 0 4 V
2) Cálculo del potencial en el punto "B“
Vb = Vib + V2B + V3B
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
^ Ql 02 ° 3
Vb = k
Luego:
VB = 9 0 . 104 V
3) Cálculo del trabajo realizado por el
agente externo sobre la carga “ qo".
W A - B = q o ( V B - V A)
WA-» b =-2.1O^C. 18.104V
WA-)B = -0,36 J
PROBLEMA N204
Determinar el trabajo que debe hacer
un agente externo para mover una carga
de prueba qD = 10 C, desde el punto M
hasta el punto A.
qi = 40. 10~9C y q2 = -30 . 10-9 C
íjí
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Cálculo del potencial eléctrico en el punto
"A" generado por las cargas q, y q2.
Va = Vai + Va2
V A = 9 10 9 4 0 ^ 0 1 _ 9109 3 0 Í 0 1
o 6
VA =0
Cálculodelpotencialeléctricoenelpunto
M:
V m = V m i + V M 2
V m = 9 - 1 0 9 .4 0 ^ 0 9 - 9 - 1 0 9. 3 a ^ ° 9
V m = 18 voltios .... (2)

432. Trabajo para mover la carga "qo"
Wm -> a = qo (Va —Vm)
Wm ->a=1 O
-9 c(0 -18)V = - 1,8x10-8 J
PROBLEMA Ne 05
La figura muestra una pirámide de al­
tura 24m y base cuadrada cuya diagonal
mide 14m. En los vértices del cuadrado
se han colocado cuatro cargas puntuales,
Q = 25C, idénticas.
Determinar la energía potencial eléc­
trica de la carga q =2«C, ubicada en el
vértice "A" de la pirámide.
Cálculo del potencial eléctrico en el punto
“A”. Las cargas ”Q“ equidistan del punto
A, donde . d = 25m.
V a = V i + M
z + V3 + V 4
Va = 4 K ° = 4.9.109-(^ }
d 25
VA = 36. 109 voltios .... (1)
Cálculo de la energía potencial de la
carga “q", ubicado en el punto A
Ep = q Va
Ep = (2 . l O ^ C ) ^ . 109V
Ep = 72 K J
PROBLEMA N2 06
Calcular ia diferencia de potencial
(Va - Vb) entre los puntos A y B del campo
eléctrico homogéneo de intensidad E =4 N/C
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
En principio las líneas de fuerza está
dirigida en el sentido en que disminuye el
potencial eléctrico. Por consiguiente el
potencial en "A" es menor que el poten­
cial en "B“.
Luego: - (V a - Vb) = E.d .. .por cortesía
N
-(Va - Vb) = 4 ^ . 2 m = 8 voltios
Va - Vb = -8 voltios
PROBLEMA Ns 07
Calcular la diferencia de potencial
(Vi - V2) entre los puntos 1 y 2 del
campo eléctrico homogéneo de intensi­
dad E = 9N/C.

433. Las líneas de fuerza se dirigen de mayor
a menor potencial eléctrico. Por con­
siguiente el potencial en "1 " es menor que
el potencial en el punto "2 ”, entonces: (V,
- V2) es negativo.
Luego: - ( Va - Vb) = E.d
- ( V i- V 2) = 9 ^.3 m = 27 voltios
V i- V 2 = -27 voltios
PROBLEMA NB08
La figura muestra un campo homo­
géneo de intensidad E = 10N/C, repre­
sentado mediante lineas de fuerza hori­
zontales hacia la derecha.
Determinar la diferencia de potencial
eléctrico ( V b - V a ) entre los puntos B y A.
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
La diferencia de potencial entre dos pun­
tos es igual al producto de la intensidad
del campo "E" por la distancia "d" entre
las superficies equipotenciales, que son
perpendiculares a las lineas de fuerza.
a
>
B
- P -
i-*-
Las líneas de fuerza tiene el sentido de
mayor potencial a menor potencial eléc­
trico, entonces:
Va> Vb
En ( 1 ) : - (VB - VA) = E . d
(VB- VA) = - 1 0 ~ . 0,4m
( V b - V a ) ) - 4 voltios.
EQUILIBRIO ELECTROSTATICO
*
*
*
*
*
*
De mecánica sabemos que los cuerpos
se desplazan de mayor a menor potencial
gravitatorio. Si abandonamos una esfera pe­
queña sobre unasuperficie cilindrica, el cuer­
po se moverá tendiendo a alcanzar su estado
de menor energía potencial.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

434. FlG « j
El líquido contenido en un recipiente (tu­
bo en "U") como muestra la figura (b), al abrir
la llave E se desplazará debido al campo
gravitatorio, de mayor a menor potencial- El
flujo calorífico se propaga de mayor a menor
potencial. El flujo calorífico se propaga de
mayor a menor temperatura, del cuerpo ca­
liente hacia el cuerpo frío, dicho flujo cesa
cuando los cuerpos alcanzan igual tempera­
tura, entonces se dice que el conjunto ha
alcanzado el equilibrio térmico. Del mismo
modo en electricidad las cargas eléctricas se
desplazan de mayor a menor potencial eléc-
La figura muestra dos esferas conduc­
toras aisladas, de radios de curvatura "r“ y
“R", se encuentran cargadas con magnitud
“+q" y “+Q" respectivamente. Determinar la
carga final que tendrá cada esfera tiempo
después de cerrar la llave “S", siendo conec­
tado mediante un alambre conductor. Con­
sideremos que inicíalmente el potencial en el
punto A es mayor que B (Va > Vb).
Debido a la diferencia de potencial entre
los puntos A y B se establece un flujo de
cargas eléctricas (convercionalmente positi­
vas) de mayor a menor potencial. El flujo de
cargas cesa cuando los puntos A y B alcan­
zan igual potencial eléctrico.
Sea q’ y Q’ las cargas que al final ad­
quieren las esferas de radios r y R, respecti­
vamente.
El flujo de cargas cesa cuando:
VA’ = VB’
-0 1 —,k._5C
k . ^- + k
r (d + r) (d + r)
l. Q’
+ k -
q Q’
r (d + r) R (d + R)
.... (1)
*
m
*
*
*
*
*
*
*
*
S
í
*
#
*
*
*
*
*
*
*
*
*
#
*
5
)!
*
*
*
*
*
*
#
*
*
#
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
A
*
Del principio de conservación de las car­
gas eléctricas, se cumple que:
carga inicial = carga final
q + Q = q' + Q’ .... (2)
CASOS PARTICULARES
I) Si los cuerpos esféricos están separados
una distancia muy giande, entonces:
(d + r) ~ (d + R)
(3)
"La carga almacenada por cada esfera es
directamente proporcional al radio de
curvatura".
II) Si los cuerpos esféricos son puestos en
contacto, entonces d - 0 .Reemplazando
en la ecuación (1 ):
.... (4)
"La carga almacenada por cada esfera es
directamente proporcional al cuadrado
del radio de la curvatura".
III) Cuando dos cuerpos esféricos de igual
radio de curvatura son puestos en con­
tacto, las cargas eléctricas se reparten
equitativamente________________
S i: R = r ■ q’ = Q’
■(q + Q)
POTENCIAL ELECTRICO DE UNA ES­
FERA CONDUCTORA
1 ) Consideramos una esfera de radio "R" y
carga “q“.
2) En todo cuerpo conductor de las cargas
se distribuyen superficialmente bus­
cando las zonas de mayor convexidad
(las puntas). En este caso la distribución
de cargas es uniforme.
3) Cuando analizamos el potencial externo
al cuerpo esférico (R < d) consideramos
a la carga concentrada en el centro de la
esfera.

435. 4) El potencial fuera del cuerpo esférico es
inversamente a la distancia.
5) El potencial dentro de la esfera es cons­
tante e igual al potencial en la superficie.
*
*
*
S
tc
5) La intensidad del campo en el interior de
la esfera es NULO.
6) Cálculo del potencial fuera de la esfera:
- ■ ( 1)
V = K §
_______d
7) Cálculo del potencial en la superficie de
la esfera.
Si, d = R, entonces..
v - K . a .... (2)
CAMPO ELECTRICO DE UNA ESFERA
CONDUCTORA
1) Consideramos una esfera de radio “R" y
carga "q".
2) Como sabemos las cargas se encuentran
uniformemente distribuidas en la superfi­
cie de la esfera
3) Cuando analizamos ei potencial y el
campo eléctrico fuera de la esfera consi­
deramos a la carga "q" concentrada en el
centro de la esfera
4) La intensidad del campo fuera de la es­
fera es inversamente proporcional al cua­
drado de la distancia.
i
*
*
*
*
*
$
$
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
$
*
*
#
*
*
CLASIFICACION ELECTRICA DE LOS
CUERPOS
1) CONDUCTORES.
Son aquellas sustancias que ofrecen una
relativa facilidad al desplazamiento de las
cargas eléctricas a través de su masa.
Estrictamente son aquellos cuerpos que
poseen cargas eléctricas libres a aquellos
electrones que no se encuentran ligados al
núcleo del átomo.
Cuando un cuerpo conductor aislado es
cargado se cumple que dicha carga al cabo
de un tiempo relativamente corto queda al­
macenada en la superficie externa del con­
ductor y en reposo alcanzando mayor con­
centración en las zonas de mayor convexi­
dad (poder de las puntas), cumpliéndose que
en condiciones finales el campo eléctrico
dentro de! conductor es nulo y su potencial
eléctrico es constante
Ejemplo: los metales.

436. Poder de las puntas
2) NO CONDUCTORES, AISLADOS
Son aquellas sustancias que ofrecen una
gran dificultad al desplazamiento de las car­
gas eléctricas a través de la masa. Son
estrictamente aquellos cuerpos que no
poseen electrones libres, de tal manera que
cuando un dieléctrico es cargado la carga se
distribuye volumétricamente.
Ejemplo : vidrio, seda papel
caucho, madera seca.
3) SEMICONDUCTORES.
Comprenden la clase de sólidos cuyas
propiedades eléctricas son intermedias entre
los buenos conductores metálicos y los bue­
nos aisladores, son de interés teórico con
siderable y también práctico porque forman
la base de una amplia variedad de disposi­
tivos usados en los circuitos electrónicos:
diodos, transistores, fotoceldas y detec
tores de partículas. La conductividad de
estos materiales se incrementa fuerte­
mente con la temperatura.
EQUILIBRIO ELECTROSTATICO
PROBLEMA NB01
Se tiene "n + 1 " esferas conductoras
de igual radio de curvatura, de los cuales
una sola esfera tiene carga y ésta es de q
= 128|iC. Si ésta se pone en contacto con
la segunda esfera hasta alcanzar el equili­
brio eléctrico, luego con la tercera, repi­
tiéndose el proceso con las otras esferas
restantes. Hallar el número de esferas, si
después del últim o contacto la carga de la
esfera inicial es 2pC.
*
*
*
sü
*
*
*
$
sü
#
*
*
*
*
*
*
*
*
*
*
$
s
u
sü
#
*
*
*
*
*
*
$
*
*
*
*
*
*
<
¥
*
*
•ü
*
*
*
*
*
*
*
*
*
*
sü
*
sü
*
*
*
■
ü
*
sü
*
*
*
*
H
*
*
*
sü
*
$
*
«
ü
*
s
ü
*
Cuando dos esferas de igual tamaño se
ponen en contacto, éstas se reparten las
cargas equitativamente.
Carga de la esfera inicial: q
Despues del 1e r. contacto : q/2
Despues del 2da. contacto : q/4
Despues del 3 e r. contacto : q/S
Despues del n-ésimo contacto:
2pC
J L
2n
Reemplazando el dato:
128 = 2n+1
Luego: (n + 1) = 7
PROBLEMA Ne02
Dos esferas conductoras de radios de
curvatura “ r" y "R” (R = 2r), se encuentran
cargados con magnitud : q = +16pC y
Q = -4pC, alejados entre sí a una distancia
infinitamente grande. Determinar la car­
ga final que tendrá cada esfera tiempo
después que les conecte mediante un
alambre conductor.
SOLUCION-
AI cerrar la llave "S" se establece un flujo
de cargas eléctricas (convencionalmente
positivas) de mayor a menor potencial.
El flujo de cargas eléctricas cesa cuando
Jos potenciales eléctricos en A y B alcan­
zan igual valor. Inicialmente VA VB
w »
#
■ i q’ kO’
V a = V b - » k .-a - = — ■
r h
i _q:
r R
3 i = q :
r 2 r

437. Principio de conservación de las cargas
eléctricas:
q +Q = q’ + Q’
16^C - 4|iC = q’ + 2q’
Luego. q’ = 4|uC
Q’ = 8nC
PROBLEMA Nfi 03
Una esfera conductora de radio de cur­
vatura r = 3cm y cargada con magnitud
q = 250|iC, se ponen en contacto con otra
esfera conductora de radio de curvatura
R = 4cm, descargada (Q = 0), Después de
separar las esferas, hallar la carga en
cada esfera.
SOLUCION:
Cuando ponemos en contacto las esferas
se establece un flujo de cargas eléctricas,
de tal modo que las cargas se reparten
directamente proporcional al cuadrado
de sus radios de curvatura.
R
SL= Q I
9 16
Principio de conservación de las cargas
eléctricas.
q + Q = q’ + Q’
250|iC + 0 = ~ Q ’ + Q
1 b
Resolviendo: Q’ =160nC
q’ = 90 ^C
*
*
¡fc
*
#
*
*
*
*
*
*
*
«
i»
*
*
*
*
*
*
<
!í
*
*
*
*
*
*
*
*
3
»
i»
*
*
*
*
*
*
*
#
*
*
*
♦
*
*
*
*
*
*
#
*
S
¡*
*
*
*
*
*
*
$
Dos gotas de agua esféricas de radios
de curvatura Ri = 1,0mm y R2 = 3^7 mm y
cargados con magnitud: qi = 20¡.iC y q2 =
70(iC.
Luego se juntan las gotas para form ar
otra gota también esférica. Determinar el
potencial eléctrico de la nueva gota con­
siderándola como una esfera conductora.
SOLUCION:
R, R. R
Q,m
Principio de conservación de la masa:
mi + rri2 = m .... (1)
D. Vi + D V2 = D.V
4n _ 3 4ti _ 3 4rc _3
3 1 + 3 R 2 _ 3 -R
R*+ r ’ = R3
Réemplazando : R = 2mm
( .
Principio de conservación de las cargas
eléctricas:
qi + q2 = Q .... (2)
Reemplazando : Q = - 50 C
Cálculo del potencial eléctrico, de la
nueva gota:
VE = k . £ = 9 10V <
5 ^
2. 10,-3
VE = -225 MV
PROBLEMA NB05
Dos esferas conductoras de radios de
curvatura r = 1,0m y R = 2,0m, se en­
cuentran cargados con magnitud: q =

438. 60 C y Q = -3 0 C, respectivamente. Deter­
minar la diferencia de potencial entre ios
puntos A y B sabiendo que la distancia de
separación entre A y B es d = 4,0m.
VA = 495 KV .... (1)
VA- VB = 522 KV
*
*
$
*
*
*
«
ü
*
*
*
m
SOLUCION:
Para un análisis exterior se considera
que toda la carga de un cuerpo esférico
se encuentra concentrado en el centro de
curvatura.
Cálculo del potencial eléctrico en el punto
“A".
W . a KQ
'"' = k
vA, a l 09<“ J
1 6
Cálculo del potencial eléctrico en el punto
"B”:
V b = k . + k —
p—
R (d+r)
(-30.10-*) „ « ( 6 0 . 1 0 - 6 )
V b = 9 . 1 0 ------------------ + 9 . 1 0 a
2 5
VB = —
27 KV ....(2)
Diferencia de potencial entre A y B:
(VA- VB) =495KV +27KV
La figura muestra dos cascarones es­
féricos concéntricos de radios de cur­
vatura a = 4cm, b = 6cm. El cascarón de
radio "a" tiene una carga uniforme magni­
tud q = 25 C. Hallar la magnitud "Q" de
la carga del cascarón de radio "b", tal que
la intensidad de campo en los puntos:
A = (3 ; 4) y B = (6 ; 8) sean iguales en
magnitud, dirección y sentido.
*
*
*
$
*
*
#
*
0
»
$
s
N
#
*
*
#
*
*
*
*
1 . En principio, la intensidad del campo
en el interior de un cascarón conduc­
tor es igual a cero debido a su carga
uniforme y la superficie. Por con­
siguiente la intensidad del campo en
el punto A = (3 ; 4) se debe úni­
camente a la carga “q"
EA= k- Ea = 9.109 2 5 -10“
25.10“
= 9 . 10
N
2. El punto B = (6 ; 8) se encuentra
externo a la superficie de radio b, por
consiguiente el campo se debe a la
suma de cargas: "q + Q"
E b = k .
(q + Q )
D2
De la condición del problema :

439. Ea = Eb
Reemplazando en (1):
k i = k ( a i | ) .
<r D
Del dato tenemos:
q (q+Q)
25x C
25 x 1CT4 m2
(25|iC + Q)
10 0 x 10^ m2
Luego. Q = +75 ^iC
PROBLEMA N8 07
La figura muestra tres cascarones es­
féricos de radios de curvatura a, b y c,
cargados eléctricamente con magnitud
Qa, Qb y Qc respectivamente. Hallar
los potenciales eléctricos en los puntos:
1, 2, 3 y 4. La posición del punto 4 está
definida por el radio "d".
SOLUCION:
1
*
*
*
*
*
*
*
m
*
*
Debemos recordar antes, que el po­
tencial eléctrico en el interior del
cuerpo conductor esférico es cons­
tante e igual al potencial en la super­
ficie. Para efectos externos (fuera
de la superficie) se puede consi­
derar que toda la carga (carga neta)
del cuerpo esférico está concentra­
do en su centro geométrico.
2. Cálculo de los potenciales .
En el punto "1“ :
Vi = k
En el punto "2"
V2 = k.
Qa Qb Qc
a ' b c
(Qa + Qb) Qc
b + c
En el punto “3'':
i Qa + Qb + Qc
En el punto "4” :
V4
, [Q a + Qb +
L «
Q c
í PROBLEMA N®08
La figura muestra tres cuerpos esféri­
cos de radios de curvatura a, b y c, car­
gadas con magnitud Qa, Qb y Qc res­
pectivamente. El cascarón de radio "C" y
ia esfera de radio "b “ son concéntricos y
aislados. Hallar la carga final, tiempo des­
pués, que se pone en contacto la esfera
de radio “a” con el cascarón de radio “c".
*
*t*
1. Analizamos el caso general, cuando
los cuerpos están separados a una
distancia finita “d". Sí cerramos el
circuito medíante la llave "S", se es­
tablece un flujo de cargas eléctricas
(convencionalmente positivas) de
mayor a menor potencia!. El flujo de
cargas cesa cuando los potenciales
de los puntos 1 y 2 se hacen ¡guales.

440. kQ’A k_(Q_B + Q ’c)
(d + c)
kCte
c c
kQ’A
(a + d)
kQ’c
+ -------+
despejando:
Q'a _ (Qb + Q’c)
a (a + d) c (d + c)
... (1)
2. Analizando la ecuación (1). Si la
distancia "d' es muy grande (d —
»<*>)
entonces: (a + d) = (d + c), entonces
se deduce que:
Q’a (Qb + Q'c)
'2 ~ „2 .... (2)
Para nuestro caso particular; los
cuerpos están en contacto, enton­
ces: d= 0. Reemplazando en (1):
Q’a (Qb + Q’c)
a2 ' c2
.... (2)
Porprincipiodeconservacióndelas
cargaseléctricas:
q final =q final
Qa +Qb +Qc =Q’a +Q’b +Q’c
Luego
Q’c = Qa + Qc - Q’a .... (3)
Reemplazando (3) en (2). tenemos
que:
D
«
*
*
*
*
Q’a= . [Qa + Qb + Qc]
Reemplazando en (3), tenemos:
C2. (Qa+Qc) a2 Qb
Q’c = -
(a2 + c2)
PROBLEMA N9 09
La figura muestra tres cuerpos de ra­
dios de curvatura a = 3cm, b = 4cm y R.R.
La esfera de radio R y carga Q = 25uC, se
encuentra dentro del cascarón de radio
"b", aislados eléctricamente ambos cuer­
pos. Los cuerpos de radios a y b no
tiene carga eléctrica. Sabiendo que la es­
fera de radio "a” se pone en contacto con
el cascarón de radio "b “ y tiempo después
se separa. Hallar la carga final de los
cuerpos A y B.
*
«
le
*
*
*
*
*
*■
*
*
*
*
*
*
*
1. Cuando ponemos en contacto los
cuerpos de radios a y b, se esta­
blece un flujo de cargas eléctricas a
través del punto de contacto, de ma­
yor a menor potencial El flujo de
cargas (positivas) cesa cuando los
potencíales de los cuerpos en con­
tacto se hacen iguales. En éstas
condiciones las cargas eléctricas se
reparten directamente proporcional
al cuadrado de los radios de cur­
vatura, teniendo en cuenta que los
cuerpos de radios b y R forman un
solo cuerpo, se cumple que
Q’a (O + Q’b)

441. 2. Por principio de conservación de las
cargas eléctricas en un sistema ais­
lado.
Zq iniciales = Zq finales
Q = Q’a + Q’b + Q
Luego: Q’a = -Q ’b -..(2)
Reemplazando (2) en (1)
Q’a -
(a2+a2)
Q y Q’b=
-a
2,^2
a +b
.Q
Reemplazando valores:
Q'a = +9p.C y Q’b = -9|aC
PROBLEMA NB10
La figura muestra tres cascarones es­
féricos de radios de curvatura a = 10 cm,
b = 20cm, c = 30cm, inicialmente el cas­
carón de radio “a" no tiene carga (Qa = 0)
y los cascarones de radios b y c
se encuentran cargados con magnitud
Qb = 40¡.iC y Qc = 30|iC. Las esferas de
radios a y b están conectadas por medio
de un alambre aislado que pasa a través
de un agujero en el cascarón de radio “c".
Considerando que la distancia de sepa­
ración es muy grande entre las esferas de
radios a y b hallar la carga final en el
cascarón de radio “a" cuando se cierra el
interruptor “S".
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
a
jí
*
*
*
*
*
*
O
s
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
tí
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
Al conectar el alambre conductor, cerra­
mos la llave "S", se establece un flujo de
cargas eléctricas (convensionalmente
positivas) de mayor a menor potencial
eléctrico. El flujo de cargas cesa cuando
los potenciales eléctricos en los puntos 1
y 2 alcanzan igual valor.
Vi = V 2
kQa = k^b + ka
a b e
Q’a Qb Qc ...
= — + — .... (1)
a b e
Por principio de conservación de las car­
gas eléctricas:
Zq iniciales = Zq finales
Qb+ Qc = Q’a+ Q’b+Qc
Luego Q’b= Qb- Q'a —■(2)
Reemplazando (2) en (1), tenemos:
Qa ^ Qb-Qa _Qc
a ~ b + c
Q’a=
(a+b)
Qb+ ■Qc
c
Reemplazando los datos en (3):
Q’a = 20 |iC
PROBLEMA Ne 11
En el centro "0" de una capa esférica
co nd ucto ra sin carga, que tie ne un
pequeño orificio, se encuentra una carga
puntual "q “. Los radios interno y externo
de la capa son iguales a "a" y "b", respec­
tivamente.
¿Qué trabajo se debe realizar contra
las fuerzas eléctricas para desplazar len­
tamente la carga "q ” a través del orificio,
desde el punto 0 hacia el infinito?
2

442. *
*
*
*
*
«
ti
SOLUCION:
1. La capa esférica se polariza, de modo
que en la superficie de radio "a" se
induce una carga "-q" y en la superfi­
cie de radio "b" se induce una carga
"+q''; la carga neta de la capa es igual
a cero, por consiguiente la capa es­
férica genera un potencial eléctrico en
el punto "O".
Vo = k fc 9 í+ k £ a í
a b
V0 = -
4nE0
.... (I)
2. El trabajo realizado por un agente
externo contra las fuerzas eléctricas
es igual al producto de la carga "+q"
que se traslada por la diferencia de
potencial entre el punto inicial (0) y
el punto final ( ) . Pero en el infi­
nito el potencial eléctrico es igual a
cero entonces:
W0 -»« =q(Vc —Vo)=-q . V0 ....(II)
Reemplazando (I) en (II), tenemos:
*
*
*
<
je
*
*
*
*
*
*
*
*
*
*
*
*
«
t=
*
*
<
#
*
*
#
*
*
*
*
*
*
*
*
«
i»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
tí
*
*
stf
«
t=
*
*
Se tiene un anillo de radio "R" cargado
con magnitud "+q" uniformemente dis­
tribuido en el anillo. Sabiendo que el anillo
se encuentra en el plano x - y con centro
en el origen de coordenadas, hallar el po­
tencial eléctrico en un punto de eje del
anillo P(0; 0; d) y en el centro (0; 0; 0)
SOLUCION:
1 Cada diferencial de carga Aqi ; Aq2¡
Aq3;..., Aqn, del anillo genera un po­
tencial en el punto P. La distancia
entre el punto P y cada diferencial de
carga es constante igual a :
2. El potencial en el punto "P" será:
VP =K.
A q i A qj Aq_
3 Aqn
D D D D
K
VP= - [A q, + Aq 2 + Aq 3 +...+ Aq n]
Pero:
q =Aq1 +Aq2 +Aq3 + ... + Aqn
Luego: VP= ^ ....(2)
Reemplazando (1) en (2) tenemos

443. Vn - K-q
rR2 +d2
.... (3)
De la ecuación (3), el potencial eléctrico
en “O" el origen , cuando d=Q
Entonces
v „ = k a
PROBLEMA Ns 13
Un anillo conductor de 3 m de radío
tiene una carga de 3 x 10~2C uniforme­
mente distribuida. Si desde un punto de
su eje de simetría a una distancia de 4m
de su centro "0“ se coloca un cuerpo de
0,2 kg de masa y -10~5C de carga eléc­
trica, hallar su velocidad cuando pase por
el punto "0". Desprecie la acción de la
gravedad sobre el cuerpo.
VB = ^ => Vb = 90 x 106V
H
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
SOLUCION:
Hallaremos primeramente los potencia­
les eléctricos en los puntos A y 0 del
espacio generado por la carga distribuida
del anillo.
Hallaremos a continuación la Energía Po­
tencial Eléctrica que tiene la carga móvil
q cuando pasa por estos puntos.
EP elecv = VAq —
* —EP electa -540 J
EP electe —VBq —
>= EP electe- 900 J
Finalmente, como sobre la carga móvil
sólo actúa una fuerza electrostática, que
una fuerza conservativa se conservara
su energía mecánica, es decir:
EMa =EM0 => EP electa =EP electo+EK0
- 540 = 900 + ~ (0,2) V2
V = 60 m/s
« / ^
B— l
I * ENERG IA PO TEN CIAL OE
IN TER A C C IO N ELECTRICA
*
*
*
*
*
*
*
*
*
*
*
CONCEPTO.
Es la capacidad que tiene un sistema de
cargas puntuales para realizar trabajo en
virtud a su configuración.
La energía potencial de interacción eléc­
trica entre dos cargas se define como el
trabajo realizado por un agente externo so­
bre "q“ en contra de las fuerzas eléctricas
para trasladar desde el infinito hasta una
cierta distancia de separación, a velocidad
constante.
Configuración inicial.
---------—
Configuración final.

444. Eí trabajo realizado para acercar una dis­
tancia "d" las cargas, es directamente pro­
porcional al producto de las cargas e inver­
samente proporcional a la distancia de sepa­
ración final.
EP = W
Ep = k . ... (1 )
EF k . W 2+ k , » t k . W
d i2 día d23
• q,
2 Para un sistema de cuatro cuerpos n =4
*
*
«
n
*
*
#
«
¡*
*
*
*
*
*
*
*
E p = k M + k ® + kM +
d i2 di3 d u
k.% C £ + k . % S i+ k . M
d23 d24 d34
*
*
*
m
*
#
*
Como el trabajo realizado puede ser po­
sitivo o negativo, en la fórmula (1) se reem­
plazará el signo de las cargas, por consi­
guiente la energía potencia! de interacción
puede ser positivo o negativo.
ENERGIA POTENCIAL DE INTERAC­
CION ELECTRICA DE UN SISTEMA DE
PARTICULAS CARGADAS.
La energía potencial de un sistema de “n“
partículas es igual a la suma de energía
potecial “n“ partículas combinados de dos en
dos , donde se reemplazará el signo de las
cargas.
1. Para un sistema de tres cuerpos,n =3. J
#
*
*
*
*
*
*
*
*
*
*
*
*
a
t»
*
*
*
*
*
*
*
*
*
PROBLEMA NQ01
Se tiene dos cargas eléctricas puntua­
les de magnitud 20 y 50 microcolumb,
separados una distancia de 5 cm. Hallar la
energía de interacción eléctrica entre las
cargas.
SOLUCION:
1. La energía de interacción entre dos
cuerpos está determinada por la si­
guiente fórmula.
Ep = k
Qi-q2
I
U -
2. Reemplazando valores en la fórmula
EP= 9 .10'
N.m
20 x 10~6 C- 50 x 10~6 C
0,05 m
EP = 180 J
PROBLEMA Ne02
Determinar la energía de interacción
del sistema de cargas puntuales, situadas
en los vértices de un triángulo equilátero
de lado L

445. SOLUCION:
1 La energía potencial de interacción
eléctrica del sistema, es igual al tra­
bajo realizado por un agente externo
para llevar desde el infinito hasta los
vértices del triángulo las cargas: + q ;
+ 2q; -3q.
Su valor se determina mediante la
fórmula (1 ), donde se considera el
signo de las cargas.
d l2 = dl3 = d23 = L
(2) * + 2 q
Ep =k
q,q:
(3)
-3q
d ,
<12 '-‘ 13 VJ 23
Reemplazando valores y signos en (1):
„2
. [ 2 - 3 - 6 ]
EP = ^ _
PROBLEMA Ns 03
En el sistema mostrado, la energía de
interacción de las cargas puntuales, si­
tuadas en los vértices del cuadrado de
lado "L" es igual a :
>+ q
*
*
*
*
*
*
*
*
*
N
e
*
N
<
*
*
*
*
N
*
*
*
*
*
*
*
*
*
*
*
N
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
N
»
N
s
*
*
*
*
*
*
*
*
¥
*
*
N
?
N
i
*
*
*
*
*
*
s
ü
*
*
*
*
*
*
*
N
»
N
f
*
1. La energía potencial de interacción
eléctrica del sistema, es igual a! tra­
bajo realizado por un agente externo
para llevar desde el infinito hasta los
vértices del cuadrado las cargas eléc­
tricas. Su valor se determina medi­
ante la fórmula (1), donde se con­
sidera el signo de las cargas, además
las distancias de separación son
d i2 = d i3 = d24 = d34 = L
dt4 = d23 = L . 2
( l)
+ q
I '
I
i
i
í
L !
i
i
I
(2 )
(3)# 1
-q
pn _ u q iq 2 x q i-q 3 . q ^ q ^ «
tp - K , + . + , +
d i2 d i3 di4
q2-q3 q2-q4 + q3-q4
d23 d24 d24 (1 )
2. Reemplazando valores y signos en
(1 ):
L
Ep =
Luego:
Ep = -^2
- n - q

446. CAPACIDAD ELECTRICA
CONCEPTO.
Es una magnitud física escalar que nos
expresa la cantidad de carga “q“ que se debe
entregar o sustraer a un cuerpo conductor,
par» modificar en una unidad el potencial
eléc'rico en su superficie.
q : carga elétrica
V : potencial en la superficie
La capacidad eléctrica se mide en Fara­
dios (F), en honor físico inglés Michael Fara-
day (1 791 - 1 867)
1 faradio =
1 coulomb
voltio
1 micro faradio = 1|iF = 10 6 faradios
1 pico faradio = 1pF = 10-12 faradios
Si en un cuerpo conductor aislado
aumenta la cantidad de carga consumida al
mismo, las cargas se distribuyen por la su­
perficie del conductor con distinta densidad
superficial. El cáracter de la distribución de
las cargas depende solamente de la forma
del conductor y no de la cantidad de carga
que hay en él. Cada nueva porción de cargas
se distribuye por la superficie del conductor
de una manera semejante al anterior.
La capacidad eléctrica de un conduc­
tor aislado es numéricamente igual ‘a la
carga eléctrica que hay que comunicarle
a éste para que su potencial varíe en una
unidad. C = q/V
La capacidad eléctrica de un conductor
aislado eléctricamente depende de su forma
y dimensiones. Para los conductores geo­
métricamente semejantes, las capacidades
son proporcionales a sus dimensiones linea­
les.
*
*
*
*
*
*
w
*
*
*
*
m
*
*
*
*
*
*
*
♦
*
*
*
*
#
*
*
*
*
#
*
*
*
*
*
*
$
*
*
*
*
x»
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
f — -----
J “
C 4 C 4
V 1 2C
□ o r
i—•’
i K------------»-l
V ........ J
La figura muestra tres cuerpos conduc­
tores aislados de lados 1cm, 2cm y 4cm
respectivamente, por consiguiente sus ca­
pacidades eléctricas serán : C, 2C y 4C
Las cargas eléctricas en el cuerpo con­
ductor se distribuye de tal modo que el po­
tencial eléctrico en cualquier punto del cuer­
po sea de la misma magnitud. Las cargas
alcanzan mayor concentración en las zonas
de mayor convexidad o en las puntas del
cuerpo.
CAPACIDAD ELECTRICA DE UNA
ESFERA CONDUCTORA
El potencial eléctrico en la superficie de
la esfera de radio "R“ es:
V = k R
.... (1 )
De la definición de capacidad eléctrica.
C =
_ S
v
...(2 )
Reemplazando (1) en (2);
“La capacidad eléctrica de un cuerpo es­
férico es directamente proporcional al radio
de la curvatura.

447. La capacidad de un cuerpo conductor
aislado depende también de las propiedades
dieléctricas del medio que lo rodea, para un
medio isótropo y homogéneo, la capacidad
del cuerpo conductor es directamente pro­
porcional la capacidad del cuerpo conductor
es directamente proporcional a la permitivi-
dad eléctrica “ £ * del medio.
PROBLEMA Ns 01
Dos cuerpos conductores de capaci­
dad eléctrica Ci = 40mF y C2 = 20(iF
se encuentran cargados con magnitud
Q=30[iC y q = 0, respectivamente. Los
cuerpos están conectados por medio de
un alambre. Considerando que la distan­
cia de separación es muy grande entre los
cuerpos, hallar la carga final en cada cuer­
po cuando se cierra el interruptor "S"
SOLUCION:
Cuando cerramos la llave "S", se es­
tablece un flujo de cargas eléctricas (con­
vencionalmente positivas) de mayor a
menor potencial electrico. El flujo de car­
gas cesa cuando los potenciales eléctri­
cos en los puntos A y B alcanzan igual
valor:
Va = Vb
.O _J[_
C1 C2
Reemplazando datos:
Q’ = 2q' ....(1)
Conservación de las cargas eléctricas:
#
*
*
*
*
*
*
4
»
❖
*
*
*
*
4i
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
q' = 10(í C
Q’ = 20pC
PROBLEMA Ns02
Se tiene 8 gotitas esféricas de mercu­
rio, iguales, de capacidad eléctrica 3 F
cada uno. ¿Cuál será la capacidad de la
gota grande que se obtiene como resul­
tado de la unión de estas gotitas?
SOLUCION:
Sea "m” la masa de cada gotita y ”M" la
masa de la gota grande.
Principio de conservación de la masa
M = 8 m ....(1)
Sea “a" el radio de cada gotita y b el radio
de la gota grande en (1 ):
_ 471 o 4ix 3
D T b =8 D' T a
b = 2a ....(2 )
Capacidad de cada gotita:
C , = ^ = 3pF ....(3)
Capacidad de la gota grande:
C - E - f - 2 C ,
C = 2 (3[iF)
C = 6|iF

448. 1 Si en las proximidades de un cuerpo con­
ductor "A" hay otros conductores, su ca­
pacidad eléctrica es mayor que la del
mismo conductor aislado. Esto explica
porque cuando al conductor A se le
comunica una carga "q”, los conductores
que lo rodean se cargan por Inducción
con la particularidad de que las cargas
más próximas a la carga inductora "q“
serán las de signo contrario. Estas car­
gas, debilitando el campo creado por la
carga "q“ hacen que disminuya el poten­
cial del conductor y que aumente su ca­
pacidad. C = qA/
En un sistema de dos conductores próxi­
mos entre sí con carga “q” iguales en
valor absoluto pero de signos opuestos,
surge una diferencia de potencial (Vi -
Va) proporcional a “q".
Vi - V2 = ~ q
En la que "C" es la capacidad mútua de
los conductores.
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
M
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
j|e
♦
*
*
*
*
*
3.
“La capacidad mutua “C" de dos conduc­
tores es numéricamente igual a la carga
que hay que trasladar de un conductor a
otro para que la diferencia de potencial
entre ellos varíe en una unidad"
La capacidad mutua ”C“ de dos conduc­
tores depende de sus formas, dimensio­
nes y disposición mutua
C también depende de las propiedades
dieléctricas del medio que lo rodea los
conductores. Si el medio es isótropo y
homogéneo, C es directamente propor­
cional a la permitividad eléctrica "E“ del
medio.
Cuando uno de los conductores se aleja
hacia el infinito, la diferencia de potencial
(V, —
V2)entreellosaumentaysu capacidad
mutua disminuye y tiende a la capacidad del
conductor aislado que queda
4. Un sistema de dos conductores con cargas
iguales en valor absoluto pero de signos
diferentes, se llama CONDENSADOR si la
forma y la disposición de los conductores
asegura la concentración de¡ campo elec­
trostático que crean estos conductores en
una región limitada del espacio. Los con­
ductores reciben en este caso el nombre de
ARMADURAS DEL CONDENSADOR. La
capacidad del condensador es la capacidad
mútua de sus armaduras. Según la forma
de las armaduras el condensador puede
denominarse; Planos esféricos, cilindri­
cos.

449. CONCEPTO,
Es aquel dispositivo formado por dos pla­
cas conductoras paralelas, con igual magni­
tud de carga pero signos diferentes. La dis­
tancia de separación entre las placas debe
ser relativamente menor comparado con las
dimensiones de la placa con el fin de ob­
tener un campo homogéneo entre las placas.
Se entiende por carga de un condensa­
dor al valor absoluto de la carga Iql de una
de las armaduras.
La capacidad eléctrica de un condensa­
dor es directamente proporcional al área de
las placas e inversamente proporcional a la
distancia de separación entre ellas.
C = £° - t í
C = Capacidad (F)
p
A = Area (m )
d = Distancia (m)
Eo= Constante eléctrica
La diferencia de potencial entre las ar­
maduras de un condensador plano es
igual al producto de ¡a intensidad del
campo eléctrico entre las placas, por la
distancia de separación entre las placas
1 V = E . d í
2 .
V = E
La energía almacenada por un conden­
sador es igual al semi-producto de la
capacidad del condensador, por el cua­
drado de la diferencia de potencial entre
las armaduras del condensador.
.... (1)
Pero: V = y en (1), entonces:
.... (2)
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
#
*
*
*
*
m
$
•
*
*
*
*
♦
*
*
*
*
t
*
*
*
*
También: V = ^ en (1), entonces:
c
.... (3)
3 La capacidad de un condensador plano
form ado por dos placas m etálicas
paralelas, lleno de una sustancia dieléc­
trica de permitividad "e" está expresada
por la fórmula:
C = £ . Eo ^ (en el S.l.)
En general se puede expresar:
C =
e A
4n k d
Para el aire y vacío £ = 1
-q
BATERÍA
CONDENSADOR PLANO
PROBLEMA Ne 01
La diferencia de potencial, entre las
armaduras de un condensador que se en­
cuentran separadas 0,1 m, es igual a 3 000
voltios. Una esferita de masa 3,0 gramos
y carga "-q use encuentra sujeto a una de
las placas mediante un hilo de seda.
Hallar "q". g = 10 N/kg.
a
d

450. Realizamos el D.C.L. de la esfera car­
gada.
De la condición de equilibrio, la fuerza
resultante es igual a cero Del triángulo
de fuerzas.
q E = m . g ....(1)
Cálculo de la intensidad del campo ho­
mogéneo:
V = E d
E = 3 . 10 N/C
Reemplazando datos en (1 ):
q = 1,0|iC
PROBLEMA N®02
En un condensador de placas planas
paralelas, en el vacío, se dispara un elec­
trón de la placa positiva hacia la negativa.
Si la diferencia de potencial entre las pla­
cas es de 100 V y la separación entre ellas
es 1 cm, ¿cuál debe ser su energía
cinética inicial para que el electrón ape­
nas llegue a la placa negativa?
Carga elemental: e = 1,6 . 10- '9 C
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
«
N
♦
*
2 .
Cuando se trabaja a nivel de partícu­
las elementales se desprecia la ac­
ción del campo gravitatorio.
Como la única fuerza que actúa sobre
el electrón es la fuerza eléctrica "eE",
que es una fuerza conservativa, en­
tonces se conservará la energía me­
cánica en el tiempo.
EM(A) = EM(B)
Ep(A) + Ek(A) = Ep(B + Ek(B)
Tomando como línea de referencia la
placa positiva.
0 + Ek(A) = -{-e)E d +0
La energía potencial en el punto B es
negativa
Luego
Ek (A) = e . E . d = e . AV
3. Reemplazando valores:
Ek(A) = 1,6. 10_19C . 100V
.-. Ek(A) = 1,6 10'17J
4. Debemos recordar que la diferencia
de potencial entre las placas de un
condensador e s :
AV= E . d = 100 V
PROBLEMA N®03
La diferencia de potencial entre las
placas de un condensador es 240 KV.
Determinar el trabajo realizado por un
agente externo para trasladar una
carga q = 50 C, desde el punto A hasta la
posición B.
i

451. SOLUCION
Diferencia de potencial entre las placas
del condensador, es igual al producto de
la intensidad del campo homogéneo “E"
por la distancia entre las placas.
AV = E . di
240 KV = E (3d)
E . d = 80 KV .... (1)
Diferencia de potencial entre los puntos
A yB - VB>VA
(VB - VA) = E . d = 80 KV
Trabajo realizado para trasladar la carga
“q":
WA_>B = q( VB - Va )
Reemplazando datos en (2):
W a -> b = 50 . 10^ C (80 000 V)
Wa _>b =+ 4J
PROBLEMA Ne 04
Una partícula penetra en un condensa­
dor plano paralelamente a sus láminas
con una velocidad igual a: V0 = 1 OOOm/s.
La partícula tiene una masa m = 10-®kg
y carga eléctrica q = 200 C. Hallar el
ángulo "a" que forma la velocidad de la
partícula cuando sale del condensador,
respecto de la horizontal; sabiendo que
la intensidad del campo eléctrico es
E = 1 000N/C, además: L = 0,05m. Despre­
cie el campo gravitatorio.
SOLUCION:
1. En el eje X, la fuerza resultante es
igual a cero, sobre la partícula, en­
tonces se cumple el M.R.U..
*■
*
*
*
*
*
*
*
*
*
*
<
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
«
i!
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
4
>
*
*
*
n
a
*
*
2 .
e = Vx t
L = V0T => t = ~~ .. (1)
V o
Cálculo de la Aceleración en el eje
Y, de la segunda Ley de Newton
F (resultante) qE
a = ------------------- =
masa m
qE
=> ay = —
y IT)
.... (2)
3. Cálculo de la Velocidad Final en el
eje Y : Vpy =Voy +ay . t .... (3)
Reemplazando (1) y (2) en (3):
/ _ q- E. L
y ~ ~mV0
(4)
. VFyr qEL
x m.V o
jalk.
m V ,
a = 45°
a = are tg
De los datos:
PROBLEMA Ne 05
Una esferita de masa “m" y de carga
"+q" está suspendida de un hilo delgado
de longitud “L", dentro de un condensa­
dor plano de láminas horizontales. La in­
tensidad del campo del condensador es
igual a "E", las líneas de fuerza están
dirigidas hacia abajo. Se pide encontrar el
período de oscilaciones de este péndulo.
+q

452. El período de un péndulo depende
de la longitud del hilo y de la "gra­
vedad efectiva" del campo donde se
encuentra oscilando.
T = 2 k
Jé - ( 1)
2. La esferita se mueve por acción de
dos fuerzas "m . g" y “qE" cons­
tantes en módulo, dirección y sen­
tido por consiguiente se puede de­
terminar un campo de fuerzas equi­
valente al sistema. Cálculo de la
gravedad efectiva.
2da. Ley de Newton :
F (resultante) mq + qE
gef=— --------------. (2)
masa m
3. Reemplazando (2) en (1);
T = 2 k . _
+ 9 Í
m
PROBLEMA Ns 06
Dentro de un condensador plano cuyo
campo tiene una intensidad igual a "E"
gira uniformemente una esferita de masa
"m" y carga eléctrica ,,+q", suspendida de
un hilo de longitud "L". El ángulo de incli­
nación del hilo respecto a la vertical es
igual a "a". Hallar la velocidad angular de
la esferita.
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
w
*
*
*>
*
*
*
*
*
*
*
*
*
$
*
%
*
*
*
*
SOLUCION:
1 En principio la esferita se mueve en
una superficie equipotencial eléctri
ca y gravitatoria, Jescribiendo una
trayectoria circular.
2. Haciendo D.C.L. de la esferita y apli­
cando las leyes de Newton.
H-(radicales) = m ac
p
T . sen a = m . co . R
Pero: R =L . sen a
.... (1 )
en (1)
T = m . a» . L .... (2)
* XFy = 0
T cos a = m. g + qE .... (3)
mor. L. cos a = mg + q E
Despejando tenemos:
(0 =

453. Una esferita de masa "m" y de carga
"q" está suspendida de un hilo delgado de
longitud "L", dentro de un condensador
plano de láminas verticales, la intensidad
del campo del condensador es igual a "E“,
las líneas de fuerza están dirigidas hacia
la derecha. Se pide encontrar el período
de las oscilaciones de este péndulo.
SOLUCION:
1 . El período de un péndulo depende de
la longitud del hilo y de la gravedad
efectiva del campo donde se encuen­
tra oscilando.
T = 2 n
Si
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
$
*
*
#
*
*
*
*
*
*
*
*
*
*
*
+
*
*
<
(•
*
*
2. La esferita se mueve por acción de
dos fuerzas "m .g” y "q . E" constantes
en módulo, dirección y sentido por
consiguiente se puede determinar un
campo de fuerzas equivalente al
sistema. La "Gravedad efec tiva" es
la suma vectorial de la aceleración de
la gravedad terrestre y la aceleración
del campo electrostático y su direc­
ción coincide con la del hilo en la
posición de equilibrio.
F (resultante)
Qef =
masa
= Vg2+ (q E/m )z .... (2)
Reemplazando (2) en (1), tenemos:
T =2n
(qE / m)
PROBLEMA Ns 08
En una de las placas de un condensa­
dor plano de capacidad “C“ hay una carga
"+qMy en la otra, una carga "+4q“.
Hallar la diferencia de potencial entre
las placas del condensador.
SOLUCION:
1. Añadamos a cada placa la carga
q’ = -5q/2 (semisuma de las cargas
de las placas tomada con signo con­
trario). Entonces el condensador re­
sultará cargado "normalmente" y las
cargas de las placas serán ±3q/2. La
diferencia de potencial entre las pla­
cas será:
v carga 3q
~
~capacidad ~
~2C
2. Pero los campos de las cargas “± 3q/2"
de las placas dentro del condensador se
compensan uno a otro. Por consiguien­
te, las cargas que hemos añadido no
cambian el campo entre las placas ni la
diferencia de potencia! en el condensa­
dor
+4q -3 q /2 +3q/2
* I
*
#
* 1
*
*
E 2 1 E
Sistema Real Sistema Equivalente

454. En un condensador plano una arma­
dura tiene carga Qi = +70 C y la otra, la
carga 02 = +10 C. Dentro del condensa­
dor, y paralela a las armaduras se coloca
una placa metálica sin carga. ¿Qué mag­
nitud de carga se inducirá en las superfi­
cies izquierda y derecha de la placa?
1 . En principio le daremos la forma natu­
ral a un condensador, mediante el
siguiente artificio; a cada placa le aña­
dimos la carga q' = (Qi + Q2)/2 (se­
misuma de las cargas de las placas
tomadas con signo contrario). Enton­
ces el condensador resultará cargado
con la siguiente magnitud:
„ (Qi - Q2) .
Q = — -------y signos diferentes:
Luego:
Q = 30jjC
+ Q - Q +Q -Q
.................. ■
—o o— - f t
- -
E _ +
" —
i
Sistema Equivalente -C
1
Metal polarizado'
*
*
*
*
*
*
*
0
*
*
*
*
*
*
*
*
%
*
m
*
*
m
*
#
*
*
*
*
*
*
*
*
♦
ü
*
*
*
«I
*
*
&
*
*
*
*
*
*
<
0
*
*
*
*
2 Cuando colocamos el metal entre las
placas del condensador, la placa me- J
tálica se polariza, por consiguiente.
*
PROBLEMA Ne 10
De la placa positiva de un condensa­
dor plano, cuyas placas están sometidas
a una diferencia de potencial "V" se lanza
una partícula de masa ”m" y carga eléc­
trica “-q“, en la dirección y sentido del
campo. Determinar la mínima velocidad
"Uo" con que se debe lanzar la partícula
para que con las justas llegue a la otra
placa. Desprecie la fuerza gravitatoria.
SOLUCION:
1. Tomando como referencia la placa
positiva, la energía potencial electrica
de la partícula en A es cero:
Er(A) = 0
La energía potencial en el punto B es
negativo.
Ep (B )= —
(-q ).E .d
Ep (B) = q. E . d ...,(1)
2 Como la única fuerza que actúa so­
bre la partícula es la fuerza elec­
trostática, que es una fuerza con­
secutiva, se conservará su energía
mecánica es decir:
EM (A) = EM (B)
Ep(A) + Ek(A) = Ep(B) + Ek(B)
0 + ~ mU o = q. E. d + 0
Luego:
v ° = j
2(E.d).q
m

455. Pero por otro lado sabemos que:
V = E . d ....(3)
Reemplazando (3) en (2):
U 0 =^
2. V.q
m 1
ASOCIACION DE CONDENSA­
DORES
CAPACIDAD EQUIVALENTE (Ceq).
Se denomina así a aquel único conden­
sador capaz de reemplazar a un conjunto de
condensadores, acumulando la misma can­
tidad de energía que el conjunto de conden­
sadores.
El condensador equivalente debe encon­
trarse sometido a la misma diferencia de
potencial "V" que los dos puntos que limitan
al conjunto de condensadores reemplaza­
dos.
1. EN SERIE. Cuando dos o más conden­
sadores están instalados en serie, todos
ellos acumulan la misma cantidad de car­
ga independiente de sus capacidades.
C, C, c , Qg
*?] [i
0
— (v)—
♦
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Sistema Equivalente
La carga en cada condensador es el
mismo, q - Constante
Todos los condensadores almace­
nan la misma carga.
La energía que entrega la Fuente
(Pila o batería) es igual a la suma de
energía acumuladas por cada con­
densador.
V = - 9 - V i= - 9 -
Ce ’ Ci '
V3 = ^ -
C3
iv) Reemplazando (2) en (1) •
_ 9 _ _ _ 9 _ + -S - + -SL
Ce C1 C2 C3
Luego:
J _____1_ J _ _1_
Ce C1 + C2 + C3
EL PARALELO. Cuando dos o más conden­
sadores están instalados en paralelo, todos
ellos están sometidos a la misma diferencia
de potencial "V" o tensión, por consiguiente
la carga acumulada por cada condensador
es directamente proporcional a su capaci­
dad.
- I b
■ ® _ j
*
*
*
*
*
i) La diferencia de potencial entre las ar­
maduras es una constante, inclusive del
capacitor equivalente.
V = constante
ii) Por principio de conservación de las car­
gas eléctricas, la carga que entrega la
fuente (pila o batería) es acumulada por
los condensadores.
q = q i + q 2 + q3 .... (1 )
iii) Pero:
q = V . Ceq ' qi = V . C r

456. V Ceq = V Ci + V . C2 + V . C3
Luego.
Ceq = C1 + C2 + C3
CASOS PARTICULARES
1, Dos condensadores instalados en serie:
Hh
ct
- II-
Ceq —
C1 .C 2
C1+C2
2. Cuando "n" condensadores iguales a “C"
están instaladas en serie, la capacidad
equivalente será:
C
eq —n
ASOCIACION DE CONDENSADORES
PROBLEMA NB01
La capacidad equivalente entre los
puntos X e Y es 14|iF. Calcular la capaci­
dad equivalente entre los puntos Y e Z.
x
Capacidad equivalente entre los puntos
X e Y :
Cxy = C + 2|iF = 14^0
C = 12|iF
*
*
*
si»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Capacidad equivalente entre los puntos
Y e Z :
PROBLEMA Ns 02
Determinar la capacidad equivalente
de los condensadores idénticos de ca­
pacidad "C“ cada uno, entre los puntos 1
y 2.
c c
i! II
c
II -
1
I I 11
SOLUCION;
1 . Todos los puntos de un alambre
conductor poseen el mismo poten­
cial eléctrico.
I
c
r II
c
IL , - ft
2 2
1 i
ir
1
i
2 . Se puede observar que la diferencia
potencial entre las placas del con­
densador es constante, esto quiere
decir que están instalados en
paralelo.
SOLUCION:

457. PROBLEMA Ns 03
Determinar la capacidad entre los pun­
tos A y B de un circuito ilimitado formado
por la sucesión de una cadena de conden­
sadores idénticos de capacidad "C" cada
uno.
. .. oo
SOLUCION:
1.
*
*
*
*
*
#
*
$
*
*
*
*
>
1
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
S
fc
*
*
*
*
«
*
*
*
*
Ceq = ^ ( ^ - 1 )
PROBLEMA N904
Determinar la capacidad equivalente,
de los condensadores idénticos de ca­
pacidad "C" cada uno, entre los puntos 1
y 2.
c c
II 11
c
Jl_
c c
ti I
I
1
1
1 11 II'
SOLUCION:
1. Todos los puntos de un alambre
conductor poseen el mismo poten­
cial eléctrico.
£
1 1
C 3 C
1 2
C
- H I -
C 3 C
-II-
2 2

458. Un condensador de placas paralelas
de capacidad 6|iF es cargado con 12 |iF,
Este condensador se conecta a un con­
densador de capacidad 2|iF descargado,
como indica la figura. La carga que al final
adquiere el condensador de 2|.iF será:
SOLUCION:
Al cerrar los interruptores, se establece
un flujo de cargas eléctricas entre las
armaduras de los condensadores, de­
bido a la diferencia de potencial. El flujo
de cargas cesa cuando las armaduras
alcanzan igual potencial eléctrico Por
consiguiente los condensadores están
sometidos a la misma diferencia de po­
tencial ”V". Entonces las cargas almace­
nadas por cada condensador serán di­
rectamente proporcional a sus capaci­
dades.
Principio de Conservación de las cargas
eléctricas:
q (inicial) = q (final)
12pC = q + 3q
Carga almacenada por el capacitor 2|iF:
q = 3^C
*
*
*
*
<
t=
*
*
*
*
*
*
$
*
&
*
*
#
*
$
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*¡
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Hallar la diferencia de potencial entre
los puntos 1 y 2 del circuito, si la f.e.m,
es £ = 110V.
C C
-oí
----------!!-------- — ii—
r z :2C : z2C
-o?
SOLUCION:
La diferencia de potencial entre 1 y
2 es:
a)
¿ 2C
2
- ( 1 )
b)
2C
3
Los condensadores en serie, acu­
mulan igual cantidad de carga. Los
condensadores en paralelo, acumu­
lan cargas cuya magnitud es direc­
tamente proporcional a sus capa­
cidades.
c)

459. La capacidad equivalente es:
8
11
Luego:
e =
^eq
110 V .- iS L .
i T c
„ § = 2 0 V .... (2)
d)
Reemplazando (2) en (1):
V i2 = 10 V
PROBLEMA Ne 07
Hallar la capacidad del sistema de con­
densadores idénticos entre los puntos 1
y 2. Las cuatro láminas son idénticas de
área "A” y separadas la misma distancia
“d
*
*
*
*
*
>
)5
*
$
*
*
*
*
*
$
*
*
*
*
$
*
*
*
*
*
*
*
*
&
#
*
*
*
*
*
*
*
*
SOLUCION:
Analizando la diferencia de potencial en­
tre las placas 3
Con cuatro láminas se puede formar tres
(3) capacitores.
La capacidad equivalente:
C
Ceq — + C
Luego: Ceq — 0 C
PROBLEMA NB08
Cuatro placas metálicas iguales se en­
cuentran en el aire a distancias iguales
"d" una de otra. El área de las placas
extremas están unidas entre sí y las de en
medio, conectadas a una batería de f.e.m
"V“. La distancia "d" entre las placas es
pequeña en comparación con las dimen­
siones de éstas. Hallar las cargas en cada
placa, si:
C = £o ^ „
SOLUCION:
1. El condensador complejo que se for­
ma, puede reemplazarse por un equi­
valente de tres condensadores de
igual capacidad "C": El condensador
I (placas 2 y 1), el condensador II
(placas 3 y 2) y el condensador I y III
están acoplados en SERIE: las pla­
cas 1 y 4 tienen potenciales iguales
(ya que están unidas por un conduc­
tor), y el condensador II está acoplado
en paralelo a este par.

460. 2 . Los condensadores I y III acoplados
en serle, acumulan igual cantidad
de carga "q El condensador II acu­
mula una cantidad "2q“ debido a la
mayor diferencia de potencial. En el
condensador II
V . C = (2q)
Luego:
V.C . . .
q = i r " " (tx)
Carga en la placa # 1
qi = -q = -V . C/2
Carga en la placa # 2:
q2 = en total = + q + 2q = 3q = 3v 0 2
Carga en la placa # 3:
q3 =-q -2q = -3q =3V. C/2
Carga en la placa # 4
q4 = +q = V , C/2
Dede observarse que las placas # 1
y # 4 solamente se polarizan.
PROBLEMA Ne09
Hallar la capacidad del sistema de con­
densadores idénticos entre los puntos 1
y 2. Las cuatro láminas son idénticas de
área "A" y separadas. Además:
*
#
*
#
*
*
*
*
«i
#
*
*
*
*
#
♦
<
&
0
1
*
*
*
*
*
m
*
*
#
*
#
*
*
*
*
s
¡>
♦
$
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
1. Analizando la diferencia de poten­
cial entre las placas:
=
1
2 Con cuatro láminas se puede formar
tres (3) condensadores
2C C
1o--------------11------^ --------¡|---------o 2
Luego la capacidad equivalente:
1 1 1
Ceq 2C C
PROBLEMA Ne 10
Cuatro placas metálicas iguales se en­
cuentran en el aire a distancias iguales
"d" una de otra. El área de cada una de las
placas es igual a "A". Las placas 1 y 3
están unidos por un alambre conductor
que no ofrece resistencia y las placas 2 y
4 están conectadas a una batería de f.e.m
“V". La distancia "d“ entre las placas es
pequeña en comparación con las dimen­
siones de éstas. Hallar la carga en las
A
placas, sabiendo q u e: c = E o .~

461. 1. El condensador complejo que se for­
ma se puede reemplazar por un equi­
valente formado por tres condensa­
dores de igual capacidad "C" el con­
densador I (Placas 2 y 3), el conden­
sador II (placas 1 y 2) y el conden­
sador III (placas3y 4). Los condensa­
dores I y II están acoplados en pa­
ralelo. las placas 1 y 3 tienen po­
tenciales iguales (ya que están uni­
dos por un conductor) y la placa "2 ”
es común; el condensador III está
acoplado en serie con este par
2 La capacidad equivalente será:
2
Ceq = g C y q(totai) = 2q
Pero : q (total) —V . Ceq
2
Luego 2q = V , —C
O
q = 3 ■V - C .... (a)
3, Cálculo de la carga en cada placa
Placa "1" qt = -q = -V C/3
Placa "2" :q2 =q+q=2q=2V.C/3
Placa "3": q3=-q+2q=q=V.C/3
Placa "4” . q4 = - 2q = -2VC/3
NOTA: Las placas 1 y 3 se polarizan.
* PROBLEMA Ne11
#
Cinco placas metálicas iguales se en-
$ cuentran en el aire a distancias iguales
£ “d” una de otra. El área de cada placa es
igual a "A ”, Las placas 1; 3 y 5 están
unidas por medio de un alambre al polo
negativo de una batería y las placas 2 y 4
al polo positivo. La f.e.m de la batería es
"V", además la distancia "d" entre las pla­
cas es pequeña en comparación con las
dimensiones de éstas. Hallar las cargas
en cada placa, sabiendo que:
*
*
4
*
&
*
*
*
¡
S
a
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
#
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
<
¥
*
$
*
c = £o
a
1, El condensador complejo que se for­
ma se puede reemplazar por un equi­
valente formado por cuatro conden­
sadores de igual capacidad "C“: El
condensador l (placas 1 y 2) el con­
densador Ii (placas 3 y 2), el conden­
sador III (placas 5 y 4), el conden­
sador IV (placas 5 y 4).
Las placas 2 y 4 tienen potenciales
iguales, del mismo modo la placa 1 ,3
y 5 tienen igual potencial por con­
siguiente los cuatro condensadores
están instalados en paralelo.

462. 2. En cada condensador se cumple
que
q = V .C (1)
3. Cálculo de la carga en cada placa
Placa “1" :qi = -q = -VC
Placa "2" iq2 =q+q=2q =2V. C
Placa "3" q3= -q -q = -2q=-2V.C
Placa ”4" :q4 = q+q=2q= 2V C
Placa "5” :qs = -q = -V . C
PROBLEMA Nfi 12
Un condensador de capacidad Ci =
3¡iF se conecta, por medio del conmu­
tador K, primero con una batería de f.e.m
£ = 7V y después con un condensador sin
carga de capacidad Cz = 6¡iF. Hallar la
carga final acumulada por cada conden­
sador.
f r
=FC„
SOLUCION.
Primer Caso: C-| instalado con la batería
£ = 7V. Cálculo de la carga acumulada.
q = £ - Ci
q = 7V . 3p.F
q = 21|iF .... (1) 7v_j¡_
Segundo Caso: C, instalado con el con­
densador C2. La carga "q” se reparte
directamente proporcional a las capaci­
dades C, y C2, debido a que la diferencia
de potencial entre las placas es el mismo
para ambos capacitores.
*n
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Sí
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
Ca C?
=> q2 =2qi .... (2)
Tercer Caso: Por principio de conser­
vación de las cargas eléctricas.
q = qi + q2
21¡iC = qi + 2qi
Luego:
qi = 7(ic
q2 = 14|iC
PROBLEMA Ne 13
Entre las placas de un condensador
plano de área "A" y distancia de sepa­
ración "a” entre las placas, existe un perfil
metálico de altura "b" cuyas bases tienen
igual área que las placas del condensa­
dor, dicho perfil se desplaza verticalmen­
te sin ponerse en contacto con ninguna
de las placas. Determinar la capacidad
equivalente del sistema así formado.
/ /

463. El sistema equivalente es igual a la aso­
ciación de dos condensadores instalados
en serie. El perfil metálico se polariza tal
que, en su interior el potencial eléctrico
es constante y el campo eléctrico es nulo.
a .
u
T I '
t!
n
ro
Ceq —
C1 , c 2
C 1+C2
donde:
c1=eo -
x + y = (a - b)
Reemplazando en (1):
A
c 2 = e o .^
Ceq —£0 .
(x+y)
Luego:
PROBLEMA N9 14
La figura muestra un cuadrado con
sus diagonales, en cada lado se encuen­
tra instalado un condensador de capaci­
dad equivalente del conjunto, entre los
*
#
*
$
#
#
$
$
*
*
*
*
*
*
*
*
¡S
e
#
*
*
*
*
*
*
*
*
*
*
»
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
♦
*
#
*
*
*
S
fs
#
1. Hay que encontrar los puntos de
igual potencial eléctrico. En el caso
dado es fácil observar que el
esquema posee un eje o plano de
simetría. En la figura se representa
por medio de una línea punteada,
figura (a).
2. Claramente que todos los puntos,
que descansan sobre el eje de si­
metría, deben tener el mismo poten­
cial, igual a la semisuma de los po­
tenciales de los puntos 1 y 2.
Vn - Vp = Vo :
V 1+V2
3. De esta manera, los potenciales de
los puntos N, P, Q son iguales. De
acuerdo a ia regla establecida, es­
tos tres puntos se pueden unir en
uno solo y, como resultado de esto
la combinación de resistencias con­
sidera entre 1 y 2 se descompone
en dos sectores en serie uno de los
cuales se indica en la figura (b).
2C

464. Cálculo de la capacidad equiva­
lente.
15, 15 r
—
Luego:
C —— C
^eq d ’
PROBLEMA Ne 15
La figura muestra un exágono regular
junto con sus diagonales, en cada seg­
mento se instala un condensador de ca­
pacidad igual a "C".
El exágono se conecta a un circuito
entre los puntos 1 y 2 como se indica en
la figura. Encontrar la capacidad equiva­
lente al sistema.
SOLUCION:
1.
2.
En el caso dado es fácil observar
que el esquema posee un eje de
simetría. En la figura se representa
por medio de una línea punteada.
Según el criterio de simetría todos
los puntos contenidos en el eje o
plano de simetría se encuentran a
igual potencial eléctrico. Por con­
siguiente los puntos M i, M2 y M3
tiene igual potencia e igual a la semi­
suma de los potenciales de los pun­
tos 1 y 2.
De acuerdo a la regla establecida
estos tres puntos, Mi, M2 y M3 se
pueden unir en uno solo llamado
punto "M", como resultado de esto
la asociación de condensadores
considerando se descompone en
*
*
*
*
*
*
*
*
*
*
*
*
*
<
¥
*
*
*
*
m
*
*
*
*
<
t=
*
*
«
t>
*
*
*
*
*
*
*
*
*
*
<
¥
<
t¡
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
dos sectores unidos en serie uno de
los cuales se indica en la figura (a).
3. Cálculo de la capacidad equivalente
entre los puntos 1 y 2.
V
PROBLEMA N916
Doce (12) condensadores iguales de
capacidad “C" cada uno se encuentran
instalados en cada arista del cubo. Hallar
la capacidad equivalente del conjunto en­
tre los puntos 1 y 2.

465. SOLUCION:
Criterio de la Simetría. "Todos los puntos
del plano de simetría se encuentran a
igual potencial eléctrico1
'
Por consiguiente los condensadores en­
tre los puntos "3" no almacenan carga, no
funcionan, por lo tanto, al suprimir no se
altera el conjunto de capacitores.
*
*
*
*
*
*
m
*
*
*
*
O
s
«
ft
*
*
*
*
*
$
*
*
*
$
*
$
*
*
*
*
#
*
t¡
0!
4
3
Ceq — . C
PROBLEMA Ne17
Doce (12) condensadores ¡guales de
capacidad "C" constituyen un armazón en
forma de cubo. Hallar la capacidad equi­
valente del conjunto entre los puntos 1 y
2.
SOLUCION:
1 “Todos los puntos del plano de
SIMETRIA se encuentran a igual po­
tencial eléctrico”
2. Los puntos que descansan sobre el pla­
no se simetria; 1, 2, 3, 4, 5 y 6; deben
tener el mismo potencial igual a la semi­
suma de los puntos x e y,
3. De acuerdo a la regla establecida
estos seis puntos, se pueden unir en
uno solo como resultado de esto la
asociación de condensadores se
descompone en dos sectores unidos
en serie uno de los cuales se indica
en la figura (b)
1 O-
8C/3
— lt—
8C/3
-o 2

466. 12C/5 12C/5
— II—
Luego:
TEOREMA DE LA TRAYECTORIA
*
*
«Is
$
*
*
*
*
*
*
*
*
*
4
)
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
Consiste en el desplazamiento imagina­
rio de una carga de prueba convencional­
mente positivo a través del tramo de un cir­
cuito eléctrico.
La carga de prueba al atravesar el con­
densador "Ci" pierde energía esto significa
que se desplaza de mayor a menor potencial.
Cuando la carga de prueba atraviesa la ba­
tería gana energía “+E“ cuando se desplaza
del polo negativo al polo positivo, en caso
opuesto perderá ,,-E Cuando pasa a través
del capacitor "C2" la carga de prueba vuelve
a perder energía.
La caída de potencial a través del con­
densador es igual a: q/c.
Respecto al circuito mostrado en la
figura; salimos del punto "1 " y llevamos la
carga "q" hasta el punto 4
*
*
*
*
V i - -9- + e - 7|- = V4
C1 C2
EFECTO PUENTE
Cuatro capacitores están dispuestos co­
mo muestra la figura. Se aplica una diferen­
cia de potencial "V" entre los terminales A y
B y se conecta un electrómetro "G“ entre los
puntos X e Y para determinar la diferencia de
potencial entre ellos. El electrómetro marca
CERO sí:
C 1. C4 = C2 C3
Vx = Vy
Desplazamiento

467. Esta es una disposición en puente que
permite determinar la capacitancia de una
capacitor en función de un capacitor patrón
y del cociente entre dos capacitancias.
PROBLEMA N2 01
Cinco capacitores están dispuestos
como muestra la figura (1 ), todos ellos
tienen igual capacidad ”C". Hallar la capa­
cidad equivalente entre los puntos A y B.
SOLUCION:
Del ''Efecto puente", los potenciales en
los puntos X e Y son iguales, por con­
siguiente el condensador en la diagonal
no acumula carga, o sea no funciona,
entonces si retiramos este condensador
el sistema no se altera, teniendo su equi­
valente en la figura (2)
De la figura (2), podemos deducir fácil­
mente la capacidad equivalente
Ceq —C
PROBLEMA Ne 02
La figura muestra un tramo de un cir­
cuito. Si la diferencia de potencial entre
los puntos A y B es (Va - Vb) = 20 Voltios,
determinar la carga acumulada en cada
condensador de capacidad C y 2C.
*
*
m
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
#
*
*
♦
*
*
«
fc
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«i
*
#
s
H
#
*
*
*
*
*
*
*
*
A
O-
C
-JH
2C
—ib
B
-o
SOLUCION: .
Aplicando el teorema de la trayectoria; lle­
vamos una carga de prueba desde A ¡.asta
B Cuando la carga de prueba atravieza el
condeosador de la placa positiva a la placa
negativa de un condensador disminuye su
potencial e n : ^
Va - + 40V - - Vb
3(í 6|¿
(VA - V B) + 40V + -a-
2 |i
Despejando tenemos:
q = 120¡i C
Ambos condensadores almacenan igual
cantidad de carga, están instalados en
serie.
PROBLEMA Nfi 03
En el circuito eléctrico mostrado ha­
llar la carga acumulada por el capaci­
tor C = 2,0|jF, sabiendo que la diferencia
de potencial eléctrico entre los puntos 1 y
2 es:
Vi - V2 = 30 V
20V C 15V
lo---------o}----- -------II------ ------ lj------— o2
SOLUCION: Teorema de la Trayectoria

468. (Vi - V 2) + 3 5 = ^
Reemplazando:
q = 130 nC
PROBLEMA Ne04
En el circuito eléctrico mostrado, hal­
lar la carga acumulada por cada conden­
sador, sabiendo que la diferencia de
potencial entre los puntos 1 y 2 es:
V i - V 2 = 4 0 V
r
4|iF
ii
50V
ni
2pF
......I
I ..
■
N
^ 2
ii
_ J
SOLUCION:
Teorema de la Trayectoria (1 2)
Los condensadores acumulan igual mag­
nitud de carga "q".
V i - - 9 - + 5 0 - ^ - = V2
4p 2n
(V, - V2) + 50 = ^9
4|i
Reemplazando:
q = 1 20n C
r
0 4
f 5Ü
V 2 uF
II o
V
I ....... U
-Q
II °
+q - q
*
*
#
S
fe
»
«f
*
*
*
*
*
*
*
*
*
*
En 1 848 el físico alemán Gustavo Ro­
berto Kirchhoff va a establecer reglas gene­
rales para el cálculo de circuitos eléctricos
complejos que determinan íntegramente su
estado eléctrico, aportando de esta manera
leyes de gran trascendencia en la electrici­
dad Analizamos a continuación para el caso
de los condensadores
1o LEY DE NUDOS
*
*
*
*
$
de cargas eléctricas En la figura (I)
se muestra un sistema de conden­
sadores sin carga, esto significa que
la carga neta en el nudo es cero
(eléctricamente neutro)

469. 2. Cuando se establece una diferencia
de poteocial entre los puntos 1 , 2 y
3 se consigue un estado de polari­
zación entre las placas del conden­
sador. Pero, por principio de con­
servación de las cargas eléctricas
las carga neta en el nudo debe ser
nula, entonces:
-qi + q2 + q3 = 0
Por principio de conservación de las
cargas eléctricas:
"La carga neta en el nudo es cero”
2o LEY DE VOLTAJES
1
A ol i i
i
( 1 +q
-q +q
II n
1 "
-q
-q
i
[
+q
11 u
1
2 .
3.
4
E1 **2
En todo circuito simple, los capaci­
tores acumulan igual cantidad de
carga, independientemente de sus
capacidades
Tomando como referencia el punto
A llevamos la carga de prueba "q”
en sentido horario. Si la carga de
prueba imaginariamente pasa de la
placa positiva a la negativa de un
condensador pierde su energía o
potencial eléctrico en :
- q/C(Joules/Coulomb)
En el caso que la carga de prueba
pasa imaginariamente de la placa
negativa a la placa positiva su po­
S.
C
tencial se incrementa en :
Teorema de la trayectoria: Circuito
cerrado.
VA+ei - c V £2- c V e3" á = VA
£
1- + £ 2 - - E3 — ■= 0
L»3
“La suma de caídas de potencial a
lo largo de cualquier camino cerrado
en una red es nula”
*
*
*
*
♦
*
*
*
*
♦
♦
+
o
»
*
#
*
*
*
*
*
*
*
#
#
*
*
*
*
*
*
9
¡5
*
*
*
*
#
*
*
*
S
§
¡
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
OTRO MODO :
£ i + £ 2 - £ 3 = ^ + ^ + ^
"Suma algebraica de f.e.m es igual
a la suma de caídas de potencial en
los condensadores”
££ = X
i = 1
i
C¡
5. La ecuación anterior se justifica por
el principio de conservación de la
energía:
La energía entregada por la f.e.m es
almacenada por los capacitores
Energía
Entregada
PROBLEMA N2 01
Energía
Almacenada
En el circuito eléctrico mostrado de­
terminar la carga acumulada por cada
condensador. c
Ci = 2(iF
C2 = 4 F
1. Aplicamos el Teorema de la trayec­
toria al circuito simple, llevamos la
carga de prueba “q“ siguiendo un
camino cerrado: 1—
>2—
>3—
>4—
>1.
35V'
+q -q
-q +q
5V

470. 2. V i - - 9 - —
£2—-9- + £i = Vi
C1 O2
Luego:
£1 -£ 2 = ^ - + ^ ? -
C1 C2
Reemplazando
3 5 V - 5 V = -3- + -9-
2|i 4|i
La carga acumulada:
q = 40|i.C
PROBLEMA N802
En el circuito eléctrico mostraod, ha­
llar la carga acumulada por cada conden­
sador de capacidad "C".
9, _ •a
1
c
1
,
c
L.....•
II ■ IV
E1 = 15 V
E2 = 10V C = 20^ F
E3 = 7 V
SOLUCION:
1. En todo circuito simple, los capaci­
tores acumulan igual canlidad de
carga independientemente de sus
capacidades eléctricas.
15V
20yc 1QV
- i —
-q +q
H h —
+q -q
-íh
-q +q
20p 7? ZOu
2. La carga de prueba ’q" se lleva de
mayor a menor potencial.
I £ = X
i = 1
i
Ci
*
*
*
*
*
*
*
*
*
■*
*
*
*
*
*
*
#
*
*
*
*
*
*
$
*
+
#
*
#
*
*
*
#
%
%
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
Tomando como referencia el punto
"A" del circuito, llevamos la carga de
prueba en sentido horario.
£ i + £2 = g + ^ + §
150V+ 1 0 V -7 V = 3
20p
La carga acumulada será:
q = 120|¿ C
PROBLEMA Ne03
¿Qué cantidad de carga pasará por el
"G’', galvanómetro después de cerrar el
interruptor K en el circuito representado
en la figura la fuerza electromotriz en la
batería es : e = 8V, y la capacidad de cada
condensador, igual a C + 5|aF?
SOLUCION:
1 Antes de cerrar el interruptor K, los
condensadores están conectados
en serie, la carga total de la placas
derechas de los condensadores era
nula. La carga en cada placa es "q".
De la 2da. ley d Kirchhoff:
q q 2q - e.C
e = c +c = c :,uego;q=^ "
=> q = 20pC.

471. 2.
3.
Después de cerrar el interruptor, el
condensador inferior está descar­
gado, los puntos A y B se encuen­
tran a igual potencial, y el superior
se carga con magnitud Q siendo
positiva en la placa de la derecha.
La carga que pasa por el galvanó­
metro e s :
G = (Q —q) + q = Q ....(1)
De la 2da. Ley de Kirchhoff.
Q
C
£ =
C . £ = O = 40(iC .... (2)
La carga que pasa por el galvanó­
metro hacia las placas derechas de
los condensadores es igual a :
Q = 40|jC
PROBLEMA Nfi 04
¿Qué carga pasará por el galvanó­
metro después de cerrar el interruptor K
en el circuito representado en ia figura?
Ci = 3|iF ; C2 = 6nF ; £ = 5V
SOLUCION:
1. Antes de cerrar el interructor K los
condensadores Ci y C2 estaban
aclopados en serie y conectados a
la batería como muestra la figura
(1). Sus cargas eran iguales a:
*
*
*
*
*
*
*
£ = ^ + 0.
C1 CZ
Q = e
Luego: Q = 10|i C
C1.C2
(C i+C2)
.... (1)
En la placa derecha del condensa­
dor C1 y en la placa superior del
condensador C2, las cargas tenían
signos distintos; la carga total de
estas placas era nula.
*
*
&
*
#
*
m
*
*
*
*
2. Despues de cerrar el interruptor K,
la diferencia de potencial entre las
placas del condensador C1 y las
cargas en ellas, se anularon y las
placas del condensador C2 adqui­
rieron las cargas ± q ; en el conden­
sador C2:
Va =£ =v¿L
Cg
q2 = £ . C2
Luego: q = 30|i C ... (2)

472. La placa superior de C2 se carga
positivamente. De este modo, la
carga total de la placa derecha del
condensador C1 y la placa superior
del condensador C2 se hizo igual a
,,+q“. Esta carga pasó por el gal­
vanómetro al cerrar el interruptor K.
PROBLEMA Ne 05
En el circuito mostrado, hallar la dife­
rencia de potencial entre los puntos A
y B.
Ci = 1|iF , C2 = 2|iF
e,=10V , £2 = 20 V
C3 = 3(iF
— II— .— r ---------- 1
!-------------
C1
c2
el
*C3
e2
--------------o!-------------- ------------ O
I------------
SOLUCION:
1 Asumimos arbitrariamente las car­
gas qi, q2 , q3 en las placas.
Por principio de conservación de las
cargas eléctricas, en el nudo "A".
q i + q 2 + q3 = 0 (1)
-----------1|------------- ------------IH ----------
*>3
C3T
-«3
el e2
----------- jl------------- ,----------- .1
------------ -
2. Teorema de ta trayectoria en la ma­
lla: MBAOM
Vm + £1 + pr- - = Vm
C3 C1
*
*
*
*
*
*
*
*
¡í-
*
*
0
$
#
*
*
*
*
*
*
*
*
*>
0
*
*
*
*
*
*
*
0
*
*
*
0
*
*
*
*
*
0
0
0
*
*
*
0
0
#
*
*
0
*
*
*
0
0
0
0
0
3. Teorema de la trayectoria en la
malla. bNPAb
q2=
%
- E .... (3)
4. Reemplazando (2) y (3) en (1).
%
ei ^ í+/- -Qa- ®2-Ca+%-0
'-'3 °2
(E-). C2 - Ej. C-j)
q3= C1+ C2 + C3_
V a - V R =
(£
2 C 2 —E|. C ^)
C i+ O2 ^ Cg
Reemplazando datos tenemos:
q3 = 15¡
_
l
C
q2 = 30|iC
q, = 15|iC
El signo (-) de q2 significa que la
placa del condensador "C2" del lado
izquierdo tiene carga con signo (-) y
el de la derecha positivo (+) por con­
siguiente opuesto al considerado
inicialmente
L u e g o :
Va - V b = + 5V
PROBLEMA N9 06
Determinar la carga acumulada por ca­
da capacitor C1 = 10¡iF, C2 = 20(jF, C3 =
30}.iF en el circuito mostrado, sabiendo
que los potenciales eléctricos en los pun­
tos t, 2 y 3 son iguales a. Vi = 10V ;
V2 = 7V ; V3 = 8V

473. *
*
*
*>
*
*
*
*
Sí
*
*
*
*
*
*
*
*
*
#
*
SOLUCION:
1. Teorema de la trayectoria (1 ó 2)
C
?
1 q2
Qi ^2
l O V - ^ - —r - = 7V
10|¿ 20(i
Luego: 2q,+ q2 = 60nC ... (1)
2 Teorema de la Trayectoría- (1 ó 3)
V ,- — - — = Vo
1 Ct C3 3
^1 ^3
10V- 7 7 T - ^ r = 8V
10(i 30n
Luego: 3q, + q3 = 60|iC ... (2)
3. Ley de Nudos:
- q i + q 2 + q3 = 0 ...(3)
4 Resolviendo las ecuaciones (1), (2)
y (3):
q1= 20|iC
q2= 20|iC
q3 = 0
*
*
*
*
$
*
S
Í
*
Sis
#
*
*
*
s
ie
*
*
*
*
*
*
*
*
*
Sí
*
*
*
*
*
*
m
*
*
*
#
#

474. LEY DE COULOM B EN UN
M EDIO DIELECTRICO
Fue enunciado por primera vez por el
físico francés Carlos Agustín de Coulomb
(1 7 3 6 -1 806) -
"La fuerza de atracción o repulsión eléc­
trica que experimentan dos cargas eléctricas
puntuales es directamente proporcional al
producto de sus cargas e inversamente pro­
porcional al cuadrado de la distancia que los
separa"
También se puede escribir así:
£: Constante dieléctrica del medio
e > 1
La fuerza "F" es menor en un medio
dieléctrico comparado con el medio aire o
vacío. En el vacío. 6 = 1
INTENSIDAD DEL CAMPO ELECTRICO
EN UN MEDIO DIELECTRICO:
*
#
■
*
*
*
*
*
*
*
*
*
$
#
*
s
u
*
*
*
*
*
*
*
*
m
♦
*
*
*
$
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
♦
*
♦
*
*
*
1
4.
5.
6.
La intensidad del campo eléctrico se
define como la razón de ia fuerza
eléctrica por cada unidad de carga
eléctrica positiva.
.... (a)
2. Ley de Coulomb:
F = K , a Q
.... (P)
3. Reemplazando ( p ) en ( a ):
E =
o .
£ d2
La PERMITIVIDAD “e" de un medio
es la magnitud fisica que indica
cuantas veces es menor la intensi­
dad E del campo eléctrico dentro del
dieléctrico homogéneo, que la inten­
sidad E0 del campo en el vacío.
El potencial eléctrico en un punto
debido a una carga puntual en un
medio dieléctrico será:
V K 0 1
e
“Se considera el signo de la carga"
La energía de interacción electros­
tática de dos cargas puntuales en un
medio dieléctrico tendrá la siguiente
forma:
Ep = -
K
- ^
e d

475. Todos los tipos de condensadores se
caracterizan por su tensión disruptiva o ten­
sión de perforación “Vo" que es la diferencia
de potencial entre las armaduras con la cual
se produce una descarga eléctrica (rayo) a
través de la capa de dieléctrico del conden­
sador La magnitud de la tensión disruptiva
depende de las propiedades del dieléctrico,
de su espesor y de la forma de las arma­
duras.
Rigidez Eléctrica (Dieléctrica)
Es la mínima intensidad del campo eléc­
trico "Eo" para ia cual comienza la ruptura del
dieléctrico, valores de la rigidez eléctrica de­
penden de la temperatura, humedad, del
espesor del dieléctrico y para la tensión ai-
terna la rigidez eléctrica es menor que para
la tensión alterna la rigidez eléctrica es
menor que para la tensión continua.
CO NDENSADORES CON
DIELECTRICO *
b )'•
t -
@ 0 0 0 0
0 0 0 0 0
0 0 0 0 0
1 . Se denomina DIELECTRICO a toda
aquella sustancia que ofrece una gran
dificultad al desplazamiento de las car­
gas eléctricas a través de su masa. Es­
trictamente vienen a ser toda sustancia,
que no poseen cargas eléctricas libres,
de tal manera que cuando un dieléctrico
es instalado entre las placas de un con­
densador los valores de la capacidad,
intensidad de campo y diferencia de po­
tencial son alterados.
2. Todo dieléctrico es identificado por un
número que es característica de cada
material, denominado constante dieléc­
trica "e".
$
*
*
*
*
#
*
*
*
*
*
*
*
$
*
*
*
*
*
*
$
*
#
#
#
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
#
*
%
*
*
*
*
*
SUSTANCIA
C o n s t a n t e
dieléctrica “£'
A¡¡re(a 0°C y 760rnm/Hg) 1,000 594
Ebonita 2 ,7 -2 ,9
Cuarzo 4,5
Vidrio 5 - 1 0
Alcohol etílico 27
Agua (pura) 81
3. La relación entre un condensador sin die­
léctrico (vacío) entre sus placas de ca­
pacidad “Co" y la de un condensador con
dieiéctrico de constante "e” y capacidad
"C", es:
C = £ . C0 |
Pero
O
o
II
f
5
a
i
>
Reemplazando (2) en (1):
C = E . E o . £ |
Donde:
(1)
(2)
£ ■Constante eléctrica = 8,85.10
... (3)
,-12_F
m
£ . Constante dieléctrica o permitividad,
sin unidades dimensionales.
A . área (m2)
d : distancia (m)
4. La figura anterior muestra dos con­
densadores de igual forma geo­
métrica instalados en paralelo, uno
sin dieléctrico y el otro con dieléctrico.
La relación con las cargas almace­
nadas en sus placas será:

476. q : carga con dieléctrico
q0: carga sin dieléctrico
PRUEBA:
i) Sabemos que:
£ = (a)
¡0
iii)
V = constante
Carga almacenada:
q = V C ...(P )
qo = V . Co .. - (y)
(P): ( Y ) , d e ( a ) :
qo '--o
q = £ qo
5 . Cuando colocamos un dieléctrico entre
las placas de un condensador que ge­
nera un campo eléctrico de intensidad E0,
el dieléctrico se polariza generando un
campo de menor intensidad opuesto al
campo externo. Por consiguiente el cam­
po resultante entre las placas del conden­
sador será:
n
^(Resultante) ~ ^ 0
■ ■
E E0
Ed|
V J
Donde:
E0 : intensidad sin dieléctrico
Ed : intensidad inducida.
Conclusión, si introducimos un dieléctrico
entre las placas de un condensador, su
capacidad eléctrica aumenta y la intensi­
dad del campo eléctrico entre las placas
disminuye.
*
*
*
*
*
m
*
m
*
*
*
*
s
ü
*
*
*
4
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
s
jt
*
*
*
#
*
*
*
*
*
*
*
#
*
*
*
7. Cuando dos condensadores de igual for­
ma geométrica, uno con dieléctrico y el
otro sin dieléctrico, instalados en serie se
cumple:
i) Almacenan igual cantidad de carga:
q
q = constante y £ = —
Uo
ii) q = C0 . Vo = C . V
_V _ C o _ l
V0 C e
Luego:
V =
V0
e
-> V0 > V
iii) Pero: V = E . d
Reemplazando en (A):
Eo d
£ >1
■- - (A)
E. d =
Luego:
Eo
e
£ > 1 => E <E 0

477. CONDENSADOR CON DIELECTRICO
PROBLEMA Ns 01
Un condensador de aire de capacidad
Co = 8{.iF se llena de un dieléctrico de
permitividad £ = 5. ¿Qué capacidad debe
tener el condensador que hay que conec­
tar en serie con el dado, para que el sis­
tema formado por ellos vuelva a tener la
capacidad C0 ?
SOLUCION:
1. Cuando el capacitar "Co", se llena
con el líquido dieléctrico ”£” su ca­
pacidad aum enta, teniendo el
siguiente valor:
C i= £ . Co .. . (1 )
2. De la condición del problema la ca­
pacidad equivalente al sistema es
n f ii
'-'O
Ceq —
C 0.C i
(C0+C1)
— Co
- -0
m
c i
CNJ
u
J
Despejando: C? = 9 °~^1 .. (2)
(C 0+ C i)
Reemplazando (1) en (2):
e
C2 = .C o
( e - D
De los datos en (3):
. . . (3)
C ¿ —10|j.F
PROBLEMA NB02
Determinar la capacidad equivalente
al sistema mostrado en el sistema de uni­
dades M.K.S.C., siendo ei y £2las constan­
tes dieléctricas instalados hasta la mitad
en el condensador plano de área "A" y
distancia "d “ de separación entre las pla­
cas.
$
*
*
*
*
*
$
*
*
■
#
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
$
*
*
*
#
*
*
¡S
í
*
*
*
*
*
*
*
*
«
F
*
é
0
*
m
*
#
*
#
*
*
*
„ 2eo . ei . e? A
(->eq - • .
(E |+E2) d
El sistema equivalente es igual a la aso­
ciación de dos condensadores en serie,
siendo la distancia de separación entre
las placas "d/2“. En el sistema real se
puede observar que en cada dieléctrico
el campo eléctrico "resultante parcial” es
diferente.
Luego:
1 1 1
Ceq C i C 2
„ C1.C2 , 4
Calculo de C1:
c, =
PA
=> C
1X
^ £, .Eo.^p ..(P)
Cálculo de Ci:
c 2 = £2 k £0 • ^^2
2A
=* C2 = £2 . £ o — ...(y )
Reemplazando (P) y (y) en (a).
2A 2A
El. Eo . £2 Eo j
^ d d
'-'eq = —
2A
(E1+ £2). Eo-—j~
SOLUCION

478. Determinar la capacidad equivalente
al sistema mostrado en el sistema de uni­
dades M.K.S.C., siendo ei y £2 las constan­
tes dieléctricas, de los dieléctricos ins­
talados hasta la mitad en el condensador
plano de área "A” y distancia de sepa­
ra1
:!ón entre las placas “d".
_ i
r-Vs.
SOLUCION:
A/2
El sistema equivalente es igual a la aso­
ciación de dos condensadores en para­
lelo. siendo el área de las placas 'A/2”.
En el sistema real se puede observar que
la diferencia de potencial es el mismo
para ambos dieléctricos.
Luego:
Ceq =: Ci + C2
Cálculo de C1:
A /2
. . . (a)
Ci —£1 + £0
C1 =£1 . £0
Cálculo de C2:
C2 = £2 +£o
d
_A
2d
A /2
d
■■ (P)
=
=
> C2 = £2 . £0 ■— - . . (Y)
Reemplazando (b) y (y) en (a):
A A
Ceq = £1 £0 - + £2 - £0
#
*
*
*
i
*
#
*
*
*
*
#
#
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
»
*
$
*
*
*
*
<
K
*
*
#
*
*
*
$
*
♦
Ceq =
(ei+£2) epA
2 ' d
PROBLEMA Nfi 04
Parte del espacio entre las armaduras
de un condensador plano está Heno de
dieléctrico con constante dieléctrica ,'£“I
como muestra la figura. El área de las
placas del condensador es "A". Determi­
nar la capacidad del condensador así for­
mado.
Sistana Real
El sistema equivalente es igual a la aso­
ciación de dos condensadores en pa­
ralelo. siendo el área de las placías'4A / y
“A2"
. (b-a) . a
A i - — A y A2=- , A
Luego:
Ceq —C i + C2
Cálculo de C1:
C , = £ o . f
(1)
. . . (2)
=> C1 = £ 0 .
Cálculo deC2:
A. (b-a)
d.b
■O)
C2= £ . £0 -

479. C 2 = £ . £,
A.a
° d.b
(4)
Reemplazando (3) y (4) en (2):
PROBLEMA Ne05
Dos esferitas de masas "m", radios,
cargas “q" iguales y de densidad “pe" que
penden de un mismo punto y de hilos de
igual longitud se sumergen en un dieléc­
trico líquido, cuya permeabilidad eléctrica
es igual a “e“ y su densidad " p l " . Sabi­
endo que los hilos forman un ángulo "
theta " respecto de la vertical y las esferi­
tas están separadas una distancia "d",
hallar la magnitud de las cargas.
F =
_
e d2
, T = tensión.
s*
*
*
*
*
5
Ü
*
*
*
*
*
*
*
*
*
*
SOLUCION:
1. Realizamos el diagrama del cuerpo
libre de la esferita de la izquierda,
donde:
E = empuje = g . pl . V
W = peso = g . pc . V
*
*
*
*
*
*
*
*
*
*
<
¥
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
2. De la primera condición de equili­
brio:
ZFX= 0 =* T Sen 0 = F . . . (1)
IF y = 0 => TCose + E ? W
i
=> ECos e= W-jE .. .(2)
Dividiendo las ecuacionps;(1): (2):
T9e = ^ - K j 2 1
W -E Ed2 gV(pc-pL)
Pero: P c = -
m
V =
m
Pc
T g e = ^ ¿
pc
e . d m 9 (Pc-PL)
Despejando:
q
2=f d2 (mg)!1
-^] Tg6
K pc
PROBLEMA Ne 06
La figura muestra dos condensadores
de igual forma geométrica instalados en
serie, sometidos a una diferencia de po­
tencias entre los puntos 1 y 2. dos esteri­
llas cargadas con igual magnitud "q", de
igual radio y peso, suspendidos de hilos
de seda de igual longitud, se encuentran
entre las placas del capacitor.

480. El primer condensador no tiene dieléc­
trico (VACIO) y el segundo contiene entre
sus placas un dieléctrico líquido de per-
mitividad ”e", y densidad "D“. ¿Cuál debe
ser la densidad “d" del material de las
esferilias para que los ángulos de des­
viación de los hilos en el vacío y en el
dieléctrico sean iguales?
SOLUCION:
Realizamos el D.C.L. (esfera) en el vacío:
ZF = 0
Tg 6 =
q-E0
W
.(a)
ZF = 0
J3l_
W - D . g . V
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Realizamos el D.C.L. (esfera) en el
dieléctrico:
Eo
E :
Eo
E
W
W - D . g
_d_
d - D
— , donde: W = d. g. V
■(O
La intensidad E0 y E se relaciona del
siguiente modo:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
El condensador esférico consta de dos
armaduras metálicas concéntricas cuyos ra­
dios son, respectivamente, iguales a Ri y R2.
Los cuerpos conductores esféricos están
cargados con igual magnitud "q“ pero de
signos diferentes El campo de una esfera
cargada superficialmente solo existe fuera
de la esfera. Por esto, en la región entre las
armaduras, el campo electrostático está
creado únicamente por la carga de la ar­
madura interior de radio R1, y fuera del con­
densador, los campos de las armaduras de
radios R1 y R2, con cargas de signos distin­
tos, se destruyen mutuamente.
Por definición de condensadores:
C = — 9—
(V1-V 2)
Ver gráfico:

481. *
#
«
if
*
*
*
*
♦
♦
*
*
*
*
*
#
*
*
*
*
*
«
is
41
Pero sabemos que el potencial en super­
ficies esféricas, están definidas así:
Para "I":
v , = K R ; * k T ^ = k -q
J _____l
Rl R2
...(2)
Para "2":
V2 = K ^ * K t j S > = 0 . . . ( 3 )
Reemplazando (2) y (3) en (1)
q 1 R1 R2
C =
K (R2 - R 1)
Sis
#
*
*
*
*
*
*
*
*
sis
m
*
*
*
í PROBLEMA N®01
En el sistema internacional-
r a „ r R l - R 2
C —4 ti £0 • 771 _ 7
(R2 - R1)
Considerando un material dieléctrico de
permitividad V entre las placas del conden­
sador esférico, la fórmula tendrá la siguiente
forma:
C = 4 n e o e . - ^ (en el S.l.)
(R2 - R 1)
CONDENSADOR CIUNDRICO
Está constituido por dos cilindros metáli­
cos huecos y coaxiales de altura ’h“ y radios
R1 y R2. Los cuerpos conductores cilindricos
tienen igual magnitud de carga "q" pero con
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*§s
*
#
*
*
*
*
s
§
>
«
0
*
*
*
*
*
*
Un condensador complejo está hecho
de tres cascarones esféricos de radios de
curvatura a, b y c. Los cascarones inferior
(a) y exterior (c) son conectados mediante
un alambre aislado el cual pasa a través
de un agujero en el cascarón de radio “ b".
Los tres cuerpos esféricos son concéntri­
cos y conductores (a < b < b). Calcular la
capacidad equivalente del sistema entre
los puntos 2 y 3.
signos diferentes. La fórmula de la capacidad
del condensador cilindrico tiene la forma:
C =
2K
En el sistema Internacional (S.I.):

482. El condensador complejo se puede
reemplazar por un condensador
equivalente, formado por dos con­
densadores C¡ y C¿ instalados en
paralelo. Los cascarones esféricos
de radios a y c tienen igual potencial
eléctrico.
2. El capacitor "1" (cascarones a y b),
el capacitor "2" (cascarones b y c).
Ceq = C i + C 2
Ceq = 4ji£o
a. b b. c
(b-a) T (c-b)
3. En la figura puede observarse que
la diferencia de potencial entre los
puntos 1 y 3 es igual a la diferencia
de potencial entre los puntos 2 y 3,
por consiguiente, los capacitores C1
y C2 están sometidos a la misma
diferencia de potencial.
PROBLEMA Ne 02
Si un condensador esférico de aire
(entre las placas) se conecta con una
fuente de alta tensión, dicho condensador
se perfora (rayo) cuando la diferencia de
potencial V0 = 40KV. Determinar la ri­
gidez eléctrica del aire en las condiciones
del experimento. El radio de la armadura
interna del condensador es r = 3cm y el
de la armadura externa, R = 9cm.
Observación: Se llama rigidez eléctrica
a la intensidad “Eo" del campo eléctrico con
la cual se produce la perforación del dieléc­
trico.
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
$
%
+
*
m
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
#
*
*
#
*
♦
♦
*
$
*
*
*
*
1. Si el condensador esférico tiene una
carga "Q” en cada placa, pero sig­
nos diferentes, el potencial de la ar­
madura interior será:
M 1 r o - g
V1 = — ! t-
4jie0 r r
Q ( R - r )
4ji£o R. r
. . . ( D
El potencial es rnáximo en la armadura
2. El potencial de la armadura exterior
es nulo. Por consiguiente, para la
capacidad del condensador esférico
se obtiene:
C = 4n£o
P r
(R . 0
La mtensidad del campo es máxima
cerca de la superficie de la ar­
madura interior del condensador:
Eo =
1
4rt£o
Q
r2
. . (2)
La diferencia de potencial entre las
armaduras será:
Vi - V2 = Vi - 0 = Vi
Del dato:
Vi = Vo 40 KV

483. e- v- ¡ b5t 7 - ,3>
Reemplazando datos:
Eo = 40KV ^ - = 2 0 ^ = 2 0 0 ^
6.3 cm m
PROBLEMA Ne03
La armadura interna de un conden­
sador esférico, de aire, cuyo radio es
r = 2cm, está rodeada de una capa esférica
de dieléctrico de permitividad e = 2. El
radio exterior de la capa dieléctrica es de
R = 4cm. ¿Qué carga máxima puede co­
municarse a este condensador? La rigi­
dez eléctrica del aire, igual a la de! dieléc­
trico, es:
E0 = 90
KV
cm
SOLUCION
1. La intensidad del campo eléctrico es
máxima cerca de la superficie de la
armadura interior del condensador:
E0= -
1
4JI£o
Q
r2
- . ( 1 )
2. Cálculo del potencial en la superficie
de la armadura interior:
1 Q . (-Q )
r R
4tco
Q ( R - r )
4k£o R . r
.... (2)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
(R - r ) . r
V1 = Eo . ¡r
4.
El potencial en la superficie de la
armadura exterior es cero
V2 = 0 .... (4)
La capacidad del condensadc es:
C = 4 £ £o -
(R .r)
De la definición de capacidad:
Q
C =
Tvi-víl
Luego:
Q =C.(Vi - V2) =4ti£o e
R. r
(R-r)
(R - r)
rE 0
Q = 4 JtEo - £ ■E0 . r2
Reemplazando datos:
9.10
2 .
9 0 0 0 .4 . 10
Q =8 . 10-7 C=0,8|iC
* PROBLEMA N9 04
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
El radío de la armadura externa de un
condensador esférico de aire (entre las
armaduras) es R = 4cm y el de la armadura
interna "r“ se elige de manera que el con­
densador no se perfore (rayo) con la di­
ferencia de la potencial máxima V0. La
rigidez eléctrica det aire es:
E0 = 3 .10
V
cm
Observa ción:Sellam arigidez eléctrica
alaintensidad,'Eo" delcam poeléctricocon
lacual seproduce laperforación del dieléc­
trico.
SOLUCION:
1. El condensador esférico tiene igual
magnitud de carga “G" en sus ar­
maduras pero son signos diferen­
tes. El potencial en la armadura ex­
terior es igual a cero.

484. 4TCo
Q (-Q)
r R
e s :
Vi =
4nEo
Q (- Q;
r R 4jt£o R • r
La diferencia de potencial entre las
armaduras será:
V i- V2 = V =
Q ( R - r )
4neo R - r
La intensidad de campo eléctrico es
máxima cerca de la superficie de la
armadura interior del condensador:
Eo =
1 O
4n:eo ' r2
.... (2)
Reemplazando (2) en (1):
( R - r )
Vi = E0 . — - 1 . r .... (3)
Completando cuadrados:
Vi=
R‘
I - ¡'“I
.21
.... (4)
El potencial " V r será máximo
cuando:
- f . 0 r = -
R
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
¡i»
*
*
*
*
«
5
*
*
*
*
*
*
*
*
*
*
V0 = E o . ^ = 3 . 1 0 4— ,1 c m
4 cm
Vo = 3 . 104 V
2

485. Se llama "Electrodinámica" a la parte fun­
damental de la teoría de la electricidad en
que se estudian los fenómenos y los
procesos relacionados con el movimiento de
las cargas eléctricas o de ios cuerpos macro­
scópicos cargados. El concepto más impor­
tante de la electrodinámica es el de corriente
eléctrica
CORñ'ENTE ELECTRICA
Se da el nombre de "Corriente eléctrica"
a todo movimiento ordenado de las cargas
eléctricas. A la corriente eléctrica que surge
en los medios conductores como resultado
del movimiento ordenado de las cargas libres
bajo la acción de un campo eléctrico, creado
en estos medios, se denomina "Corriente de
Conducción".
Movimiento ordenado de electrones
libres de un conductormetálico.
V a > V b
Son ejemplos de corrientes de conduc­
ción la corriente en los metales y semicon­
ductores debido al movimiento ordenado de
los electrones “libre" y la corriente en los
electrolitos, que consiste en el desplaza­
miento ordenado de los iones de signo con­
trario, los iones negativos se dirigen al ánodo
y los iones negativos hacia el cátodo.
M
ovim
iento■
y
ítc
n
n
c
lod
ctonta
CORRIENTE DE CONVECCION;
Es el movimiento ordenado, en el espa ­
cio de cuerpos macroscópicos cargados.
Un ejemplo de este tipo de corriente es la
*
ti«
m
*
*
*
*
*
*
*
*
s
t¡
*
*
*
*
*
si»
i*!
*
*
#
*
*
*
*
*
*
m
*
*
*
*
$
*
*
♦
*
*
Sjí
*
*
*
*
*
*
*
*
a
s
*
*
*
*
m
*
$
*
*
*
*
O
s
*
*
*
*
corriente aebiao al movimiento de la tierra,
que tiene exceso de carga negativa, por su
órbita. Un caso especial de corriente es la
del desplazamiento a la cual no es aprecia-
ble la definición de comente eléctrica dada
anteriormente.
Movimiento ordenado de cargas
eléctricas positivas
Va > Vb
Por consiguiente, cuando los portadores
de carga se desplazan en un medio estático
se dice que estamos frente a una corriente
de convección. Este es el caso de cuerpos
cargados electrostáticamente que se les ha­
ce girar sobre sí y es el caso de las corrien­
tes atmosféricas que se producen en las
tormentas.
Las condiciones necesarias para que
surja y exista corriente eléctrica en un medio
conductor es:
a) Que en el medio dado "Portadores de
carga'1 libres, es decir, partículas car­
gadas que pueden desplazarse por el
ordenamiento. Estas partículas, en los
metales semi-conductores son los elec­
trones de conducción, en los conductores
líquidos (electrolitos), los iones positjvos
y negativos, y en los gases, los iones y
electrones con cargas de signos con­
trarios
b) Que en el medio dado exista un campo
externo, E, cuya energía se invierta en
trasladar ordenadamente las cargas
eléctricas. Para mantener la corriente
eléctrica, la energía del campo eléctrico
debe reponerse continuamente, o sea,
es necesaria una FUERTE DE ENERGIA
ELECTRICA - un dispositivo en el cual
se transforme una forma cualquiera de
energía en energía del campo eléctrico.
Se considera que el sentido de la co­
rriente eléctrica es el del movimiento or­
denado de las cargas eléctricas positi­
vas. Pero en realidad, en los conductores

486. metálicos la corriente la crea el movi­
miento ordenado de los electrones que
se desplazan en sentido contrario al de la
corriente.
En principió, el sentido de las líneas de
fuerza del campo electríco E se dirige de
mayor a menor potencial, del mismo modo
las cargas eléctricas libres positivas se des­
plazan de mayor a menor potencial eléctrico.
En el caso del conductor metálico los elec­
trones se desplazan de menor a mayor po­
tencial eléctrico, esto significa que se mue­
ven en sentido opuesto al campo eléctrico.
Si el campo eléctrico que actúa sobre las
cargas eléctricas libres se mantiene cons­
tante en módulo y dirección se obtiene una
corriente continua (C.C). Si el campo eléc­
trico se mantiene constante en dirección y
módulo variable y si el campo eléctrico cam­
bia enintensidad y dirección se obtendrá una
corriente alterna (C.A).
C. C : Corriente debido a las pifas y
batérías
C. A : Corriente debido a las hidroeléc­
tricas (de uso doméstico)
Convencionalmente en el desarrollo del
capítulo consideraremos cargas eléctricas li­
bres a las cargas positivas, esto significa que
el flujo de cargas eléctricas será de mayor a
menor potencial eléctrico, por consiguiente el
sentido de la intensidad de corriente será de
mayor a menor potencial.
Además en los fenómenos y leyes que
estudiaremos vamos a considerar que la
comente eléctriica es contíinua.
1. INTENSIDAD DE LA CORRIENTE
ELECTRICAfri. Es aquella magnitud es­
calar que nos expresa la cantidad de
carga neta que en la unidad de tiempo
atravieza la sección recta de un conduc­
tor. La corriente eléctrica se dice que es
continua.
(C.C) si su intensidad y sentido no varían
con el tiempo:
. 1 Coulomb
1 ampere = ~ -------- r
1 segundo
La intensidad de corriente se mide en
ampere (A) en honor al físico francés
Andrés María Ampere (1 775 - 1 836).
2. RESISTENCIA ELECTRICA (R). Es la
dificultad que ofrece un cuerpo conductor
al desplazamiento de las cargas eléctri­
cas a través de su masa.
Notación :«
—
i >
_» •—
pwvwvh—
•
La resistencia eléctrica de un conduc­
tor se mide en Ohm (Í2) en honor al
físico Alemán Jorge Simón Ohm (1
787 - 1 854)
LEY DE POULLIET.
"La resistencia eléctrica que ofrece un
conductor al paso de la corriente eléctrica
es directamente proporcional a la longi­
tud del conductor "L" e inversamente pro­
porcional al área "A" de la sección recta”
p : resistividad eléctrica
[p ] = í i m
3. RESISTENCIA ELECTRICA (p). Llama­
da también resistencia específica de un
conductor, es aquella que nos expresa la
capacidad de formar dentro de una sus­
tancia una corriente eléctrica bajo la ac­
ción de un campo eléctrico La resisti­
vidad caracteriza las propiedades eléctri­
cas de los conductores.
*
#
*
*
*
0
*
♦
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
«
Ü
#
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
$
*

487. RESISTIVIDAD DE ALGUNOS CONDUC­
TORES A 20 C DE TEMPERATURA
CONDUCTOR p(Q •m)
Placa 1,6 10"8
Cobre 1.8 10~8
Aluminio 2,7 10-8
Tungsteno 5,6 10-8
Plomo 2,1 10~7
Constatan (Aleación Ni
4 5 10-7
y Cu)
Carbón 3,7 10“7
Agua de mar 2,0 10_1
Germanio 5,0 10_1
Oxido de oobre (CuO) 1,0 103
Agua destilada 5,0 103
Agua químicamente pura 106
De la tabla se puede deducir que el mejor
conductor metálico es la plata (Ag)
4. CONDUCTIVIDAD (C). Se define como
la inversa de la resistividad. El término
conductividad se usa para describir el
grado de eficiencia con que un material
permite el flujo de corriente a través de su
masa. Los conductores que mejor con­
ducen la corriente son los de plata, cobre,
oro, aluminio, tungsteno, zinc, latón, plati­
no, hierro, niquel, estaño, acero, plomo,...
La plata (Ag) tiene la conductancia o con­
ductividad más elevada (bajísima resis­
tencia), no obstante se emplea los con­
ductores de cobre debido a su abundan­
cia y bajo costo.
LEY DE OHM
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
m
*
*
*
s
N
*
En todo conductor metálico se cumple
que la diferencia de potencial V existente
entre los puntos 1 y 2 que limitan la resisten­
cia R es directamente proporcional a la inten­
sidad de corrienteV 'q u e la atravieza.
A : Amperímetro
V : Voltímetro
V
R
* V = ¿. R
. R = -M_
*
Gráfica • V - ¿
Todos los conductores o resistencia que
cumplen con la ley de Ohm se denominan
conductores ohmicos y se caracterizan por
mantener su resistencia R constante, inde­
pendiente de la tensión V aplicada.
*
*
s
ü
*
#
*
#
*
*
*
*
*
*
*
ASOCIACION DE RESISTENCIAS
Resistencia equivalente (Req).
Es aquella única resistencia capaz de
reemplazar a un conjunto de resistencia limi­
tado por dos puntos, disipando la misma
cantidad de energía que el conjunto reem­
plazado.
A) En serie. Por todas ellas circula la misma
intensidad de corriente independiente­
mente del valor de cada resistencia

488. Sistema Real:
R
,
i Corriente convencional de +a -
Sistema Equivalente:
R.»
1. Del principio de conservación de las
cargas eléctricas.
i = constante
2. Del principio de conservación de la
energía:
V = V i+ V 2 + V3 ...(1 )
3. De la ley de Ohm: V = i . Req
Vi = i Ri ; ¡2 - i . R2
V3 = i R3
Reemplazando e n (1 ):
i . Req = t . Ri + i . R2 + i . R3
j
~^Req^Ri^R^^R^j
B) En Paralelo: Todas las resistencias
están sometidas a la misma diferencia de
potencia. La corriente "i" que llega al nudo
se reparte inversamente proporcional a la
magnitud de la resistencia correspon­
diente.
Sistema Real:
*
*
*
*
*
*
*
&
*
*
*
«
f¡
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
sfs
*
*
*
*
*
*
<
t
*
S
í
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s*
*
*
*
*
*
Sistema Equivalente:
K,
1.
2.
3.
Tensión eléctrica constante. Igual
en cada rama: Vi = V2 = V3
Del principio de conservación de las
cargas eléctricas.
i = ii + i2 + i3
De la ley de Ohm i -
V
.... (1)
n =
Ri
1
2=
V
Req
V
R2
i3 =
R3
Reemplazando en (1):
V V V V.
Req Ri R g+ R3
_ l__________V ± _1_
Req R1 + R2 + R3
CASOS PARTICULARES
1) Dos resistencias instaladas en paralelo:
2) Cuando "n" resistencias iguales a”R''
están instaladas en paralelo, la resisten­
cia equivalente será:
Req = 3
n

489. PROBLEMA N®01
Se tiene un alambre conductor de alea­
c io n e s m uy e s p e c ia le s lla m a d o
"NICHRON" em pleado para artefactos
c a le fa c to re s , su re s is tiv id a d es:
1,1í2.mm2/m, si su sección transversal es
de 0,5 mm2 y tiene una longitud de 10 m.
Calcular la resistencia eléctrica del con­
ductor en Ohmios.
SOLUCION:
De la ley de Poulliet
R = p t
Reemplazando datos en (1):
-•(1 )
R = 1,1
Luego:
C
2 .m nr 10m
m 0,5mm
R = 22Í2
s
t=
*
*
*
PROBLEMA Ne 02
La resistencia equivalente entre A y B
es 5 Ohm. Calcular la resistencia equiva­
lente entre A y C.
A
Req R 10 5
Resolviendo : R = 10£í
2. Resistencia equivalente entre los
puntos A y C.
11 _
1
_
R eq- 6 + 14 -
PROBLEMA Ne03
En el circuito eléctrico mostrado hallar
la resistencia equivalente entre los pun­
tos A y B.
*
$
*
*
*
*
*
*
*
♦
1 En principio, consideramos que to­
dos los alambres de conección tie­
nen resistencia eléctrica despre­
ciable. Entonces todos los puntos
de un mismo alambre de conección
constituyen una “Línea equipoten­
cial", es decir el potencial es el mis­
mo en todos estos puntos.
6 « 20 30 8
A
i ---------------i
B
SOLUCION:
1 Resistencia equivalente entre los
puntos A y B.

490. 2. Uniendo los puntos de igual poten­
cial eléctrico Entre los puntos A y B:
1 1 1
Req 6 2 3
Luego: Req =
PROBLEMA NB04
Determinar la resistencia equivalente
entre los puntos 1 y 2, sabiendo que el
valor de cada resistencia es "R“.
R R R R R
1 2
SOLUCION.
1. Puesto que en el problema dado las
resistencias de los alambres son
iguales a cero, entonces todos los
puntos de un alambre conductor
ideal poseen un potencial eléctrico
constante.
2. Haciendo coincidir los puntos de
igual potencial eléctrico.
R R
-
o /
O
l íO
o
5 y
I 2
R
J
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ste
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Finalmente:
PROBLEMA N« 05
Determinar la resistencia equivalente
entre los puntos A y B de un circuito
ilimitado formado por la sucesión de una
cadena de resistencias idénticas de mag­
nitud R cada uno.
SOLUCION:
Si a la cadena ilimitada de resistencias el
valor del conjunto no se altera
Es igual a la resistencia
eq i,1siente: Req

491. Req - R . Req - R = O
Resolviendo la ecuación de segundo
grado
Req = R .
Á
z
X ¡ * U & u ?
K
. 2 .
2 ¿3?
1 , 2 1* 1 —
o-----------
2 3 4
*
*
*
*
*
$
*
*
*
*
*
*
8
»
#
»
*
«
5
*
*
PROBLEMA Ne06
Hallar la resistencia equivalente entre
A y B (todas las resistencias se miden en
ohmios)
SOLUCION:
Reduciendo el conjunto de resistencias
iguales, en la vertical, instalados en
paralelo
Cálculo de la resistencia equivalente.
1 1 2 3 4 5 6
---- —
—4
-—4
-—4-—4
-
--- 4
-
-
- 4-
Req 1 ^ 2 ^ l í 16 32
Resolviendo: Req = j
PROBLEMA N®07
La figura muestra un cuadrado con
sus diagonales, en cada lado se encuen­
tra instalado una resistencia de magnitud
”R”. Hallar la resistencia equivalente del
conjunto, sabiendo que la corriente ingre­
sa por el vértice "1" y sale por el vértice
«
i2"
*
*
*
*
*
*
*
*
*
*
*
*
*
*
N
*
*
*
*
*
*
*
*
*
*
*
*
*
1. Hay que encontrar los puntos de
igual potencial eléctrico. En el caso
dado es fácil observar que el es­
quema posee un eje de SIMETRIA.
En la figura se representa por medio
de un línea punteada, figura (a).

492. Claramente que todos los puntos
que descansan sobre el eje de si­
metría, deben tener el mismo poten­
cial, igual a la semisuma de los po­
tenciales de los puntos 1 y 2.
V a = V b = V e =
V1+V2
4.
i *
—
a ----
15
Luego: Req = ?5 R
*
*
*
«
i*
De esta manera, los potenciales de
los puntos A, B y C son iguales de
acuerdo a la regla establecida, es­
tos tres puntos se pueden unir en
uno solo y, como resultado de esto,
la combinación de resistencias con­
siderada se descompone en dos
sectores unidos en serie uno de los
cuales se indica en la figura (b).
R
2
Cálculo de la resistencia equiva­
lente.
4 „
PROBLEMA N9 08
Un exágono regular junto con sus dia­
gonales está hecho de alambres. La resis­
tencia de cada alambre es igual a “R“. El
exágono se conecta a un circuito entre los
puntos 1 y 2 como indica la figura. Encon­
trar la resistencia total del exágono.
*
*
*
*
*
♦
*
*
*
*
*
*
*
#
*
*
*
«
S
*
*
S
lí
*
*
*
*
*
*
*
#
*
*
*
*
*
*
1. Criterio de simetría: "Todos los pun­
tos del plano de simetría se encuen­
tran a igual potencial eléctrico". En
la figura (a) se representa por medio
de una línea punteada.
2. Los puntos Mi, M2 y'M3 que descan­
san sobre el plano de simetría de­
ben tener el mismo potencial eléc­
trico e igual a la semisuma de los
potenciales en los puntos 1 y 2.
De acuerdo a la regla establecida
estos tres puntos: Mi, M2 y M3 se
pueden unir en uno solo, como re­
sultado de esto la asociación de re­
sistencias considerada se descom­
pone en dos sectores unidos en se­
rie uno de los cuales se indica en la
figura (a).

493. 4 Cálculo de la resistencia equiva­
lente:
ilR /4 0 11R/40
1 O -----O ------•------ C3------o 2
Req=l¿ R
PROBLEMA Ns09
Doce alambres iguales de resistencias
"R" cada uno constituyen un armazón en
forma de cubo. Hallar la resistencia
equivalente del conjunto, sabiendo que la
corriente ingresa por el vértice "1" y el
vértice "2"
1. Se puede observar en la figura (a)
que los puntos Bi y B2 se encuen­
tran a igual potencial eléctrico, de­
bido a la simetría del esquema; en­
tonces : B1 = B2 = B
Del mismo modo los puntos Ai y A2
se encuentran a igual potencial de­
bido a la simetría del esquema, en­
tonces:
*
*
*
*
«
t=
*
=
!*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
3. De acuerdo a la regla establecida
los puntos Ai y A2, se pueden unir
en uno solo llamado punto A. Del
mismo modo los puntos Bi y B2 se
pueden unir en uno solo llamado
punto B.
1 ’ 2
R
2
i
R
..A__.
A R
Por consiguiente, la asociación de
resistencias adopta la forma indi­
cada en la figura (b).
Cálculo de la resistencia equiva­
lente:
Req = 1 2 ’ R
*'

494. Doce (12) alambres ¡guales de resis­
tencia "R" constituyen un armazón en for­
ma de cubo. Hallar la resistencia equi­
valente del conjunto sabiendo que la co­
rriente ingresa por el vértice A y sale por
el vértice B.
SOLUCION
1. Criterio de Simetría: "Todos los pun­
tos del plano de simetría se encuen­
tran a igual potencial eléctrico"
Todos los puntos que descansan so­
bre el plano de SIMETRIA, Mi, M2,
M 3, M4, M 5 y Me, deben tener el
m ism o p o te n cia l, igual a la
semisuma de los potenciales de los
puntos A y B.
B
De acuerdo a la regla establecida
estos seis puntos: Mi, M2, . . . . ,Ms,
Me; se pueden unir en uno solo co­
mo resultado de esto la asociación
de resistencias considerada se des­
compone en dos sectores unidos en
serie uno de los cuales se indica en
la figura (b).
*
*
♦
*
*
*
#
*
*
*
*
*
*
*
*
*
*
i
*
*
*
*
*
%
*
*
*
*
*
*
H
*
*
¥
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
#
*
*
*
*
*
*
*
*
*
*
*
$
*
Cálculo de la resistencia equiva­
lente:
5R/12 M 5R/12
O
------- C
U
-------• -C3--------O
B
PROBLEMA Nfi 11
Doce (12) alambres iguales de resis­
tencia “R" constituyen un armazón en for­
ma de cubo. Hallar la resistencia equi­
valente del conjunto sabiendo que la co­
rriente ingresa por el vértice A y sale por el
vértice B
SOLUCION
1. Criterio de simetría: "Todos los pun­
tos del plano de simetría se encuen­
tran a igual potencial eléctrico"

495. Por consiguiente las resistencias
entre los puntos "M“ no funcionan
Reduciendo tenemos:
3. Cálculo de la resistencia equiva­
lente:
3R/8 3R/8
M G
Luego: Req = | R
FUENTES DE ENERGIA
ELECTRICA
Se denomina así a todo aquel dispositivo
que se emplea para convertir alguna forma
de energía (térmica, química, mecánica, nu­
clear) en energía eléctrica libres para des­
plazarse a lo largo de un tramo del circuito
eléctrico. Toda fuente de energía eléctrica
(corriente continua), tiene dos zonas bien
definidas denominados bornes o polos, lla­
mándose polo positivo (+) al que se encuen­
tra a mayor potencial y polo negativo (-) al
que se encuentra a menor potencial.
En las pilas voltaicas o acumuladas du­
rante la transformación de energía ocurren
ciertas reacciones químicas, la corriente
eléctrica se debe al movimiento ordenado de
los iones positivos y negativos en ia solución
iónica.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
é
*
*
*
m
*
#
*
*
*
*
*
*
s
tí
*
*
*
*
*
*
*
REPRESENTACION DE LAS FUENTES
DE TENSION
1. Pila Ideal: Tiene resistencia interna
idealmente nula (T = 0)
4 r Vb a =£
2. Pila Real: Tiene resistencia interna di­
ferente de cero ( r * 0)
Cálculo de la diferencia de potencial en­
tre los puntos A y B debido al paso de la
corriente V .
Vba = £ —¿. r
3. Generador de Tensión:
— 8
Vb - Va = Vba = £
FUERZA ELECTROMOTRIZ [f.e.m], (£)
CONCEPTO.
Es una magnitud física escalar, su valor
se define como el trabajo realizado por la
fuente de energía (pila, batería, generado­
res) sobre cada unidad carga libre positiva
para trasladar desde el borde negativo (-)
hacia el borne positivo (+), en este caso la
unidad carga gana o recibe una energía ,,+e“.
Cuando la unidad de carga libre positiva (+)
se desplaza desde el borne positivo (+) hacia
el borne negativo (-) pierde una energía igual
a "-e”.
o

496. Si el desplazamiento de la carga libre “q"
positiva es de A hacia B, gana una ener­
gía igual a: ”+e"
2.
Si el desplazamiento de la carga libre "q“
positivo es de B hacia A, pierde una ener­
gía igual a: "-e“.
Luego:
P Trabajo Wa
~ Carga ~
B
(1)
q
£ : Voltios, Wa -> b : Joules
q Coulomb
El trabajo realizado por la pila o batería
sobre las cargas será igual a
Wa -> b = £ - q
PILA O BATERIA
.... (2)
La pila se puede simular como un obrero
que lleva las cargas eléctricas libres positi­
vas de menor a mayor potencial eléctrico. La
fuerza electromotriz (f.e.m) será proporcio­
nal a la altura que eleva las cargas libres q
el obrero-pila.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Slí
*
*
*
*
*
*
*
*
CONCEPTO.
Es una magnitud física escalar, se define
como la rapidez con que se realiza trabajo.
En este caso la fuente de energía realiza el
trabajo sobre las cargas eléctricas libres po­
sitivas para llevar del polo negativo hasta el
polo positivo.
c
5
11
A 1+ B
i ,
P = ^ S . . . . ( 3 >
Reemplazando (2) en (3):
P = £
Potencia entregada por la fuente de ener­
gía
1 watt = 1 voltio . ampere
La potencia eléctrica se mide en "watt",
en honor al físico inglés JAMES WATT, in­
ventor de la máquina de vapor
POTENCIA CONSUMIDA POR UNA RE­
SISTENCIA AL PASO DE LA CORRIENTE
ELECTRICA.
a) De la Ley de Ohm, la corriente eléctrica
V atravieza la resistencia ”R‘ debido a
una diferencia de potencial entre los pun­
tos A y B. Luego.
i , R
Al----------* = » ---- ----- IB
Va - Vb =
Wa->b
Wa -í b = (Va —Vb) . q
Entonces : Wa -> b = V . q
W
.... (4)
Trabajo realizado por el cam­
po eléctrico en el conductor
sobre la carga libre "q" para
llevar desde A hacia B.

497. b) La potencia consumida por la resistencia
será:
Wa - * b _ M _ v 3
r C - t - t - v . t
1
Luego: Pc = V . 1
En (5):
, V
Pc = v . R = d
H
.... (5)
.... (6)
Potencia consumida por la resistencia
“R" al paso de la corriente V .
LEY DE JOULE - LENZ
Por principio de conservación de la ener­
gía, la potencia consumida por la resis­
tencia al paso de la corriente, la resis­
tencia lo libera al medio ambiente en for­
ma de energía calorífica.
2. Luego:
_ W _ trabajo consumido
C~ t ~ tiempo
W = Energía liberada =Q = Pc.t
Q = Pc t .... (7)
"La cantidad de calor liberada por una
resistencia "R" debido al paso de la cor­
riente es igual al producto de la potencia
consumida por el intervalo de tiempo, de
funcionamiento"
Reemplazando (6) en (7), tenemos:
- -2 V
Q = V . í A = r R .t = -~ -.t
_____________________ H___
En ésta fórmula la cantidad de calor "Q”
se mide en Joules
Equivalencia:
1 Joule = 0,24 calorías
A ésta misma conclusión, sobre la base
de experimento llegaron independiente­
mente, el uno del otro el científico inglés
James P Joule y el ruso Emilio Lenz. Por
esta causa, el principio enunciado más
arriba, lleva el nombre de Ley de Joule -
Lenz.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Ü
í
s
j*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
fe
*
*
*
*
*
INSTRUMENTOS PARA MEDICIONES
ELECTRICAS
Amperímetro.
Es aquel instrumento que sirve para
medir la corriente eléctrica en un tramo del
circuito. El amperímetro A se conecta siem­
pre en serie con los elementos en donde se
desea conocer la corriente V . Este instru­
mento posee una resistencia interna Y ' muy
pequeña expresada en miliohmios (míi).
REPRESENTACION:
AMPERIMETRO IDEAL (r = 0)
Los amperímetros tienen dos bornes o
polos bien definidos, positivo y negativo res­
pectivamente.
Voltímetro.
Es aquel instrumento que sirve para me­
dir los voltajes o tensiones que se producen
en el tramo del circuito eléctrico.
El voltímetro se instala siempre en para­
lelo entre los puntos del elemento en donde
se desea medir la tensión. Este instrumento
posee una resistencia interna “r" relativa­
mente grande expresada en kilohmios (kQ).
REPRESENTACION:
De la Ley de Ohm.
V = ¿o. r
V : Tensión indicada por el voltímetro,
r : resistencia interna

498. Voltímetro Ideal.
Tiene resistencia interna infinitivamente
grande (—
» « ), por consiguiente su lectura
será exacta. A través del voltímetro no pasa
corriente.
POTENCIA ELECTRICA
l=j
-<£>-
= (1 + a At)
Ro: Resistencia inicial
A t: Variación de la temperatura
R : Resistencia final.
* PROBLEMA N®01
Galvanómetro (G).
Es aquel instrumento sensible a corrien­
tes pequeñísimas.
DILATACION LINEAL DE LOS
CONDUCTORES
Todo coductor que transporta energía
eléctrica experimenta una evaluación de su
temperatura lo cual le produce el fenómeno
térmico de dilatación longitudinal, conside­
rando conductores muy delgados
Inicial:
Lo, Ro. To
Fina!:
L, R.T
1. De la Ley de Poulliet:
para To: R o^p ....... (1)
ParaT R = p . ~ ....(2)
2. Además, dilatación:
L = L0 (1+ a . At) ...,(3)
a : coeficiente de dilatación lineal
(C~1 , °K~1)
3. Considerando que la sección transversal
'A" y la resistividad "p" se mantiene cons­
tante (1), (2) y (3):
_R = _L R
Ro Lo
*
*
*
*
*
*
*
0
*
*
$
*
*
*
m
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
El bobinado de un motor eléctrico es
de alambre de cobre, si su resistencia
antes de empezar a trabajar es de Ro= 80£i
y después de trabajar At = 6h continuas su
resistencia es de 120Q. Determinar el in­
cremento de temperatura en el bobinado.
Coeficiente de dilatación lineal del co­
bre: 4 . 1 0
-3 o«-1
SOLUCION:
Debido al incremento de temperatura, el
alambre de cobre experimenta una di­
latación longitudinal, por consiguiente la
resistencia aumenta.
Luego:
R = R0 . (1 + o. At)
Reemplazando datos en la formula ante­
rior.
120Í2 = 80S1.(1 + 4 . 1CT3 . At)
At = 125 C
S
jí
*
*
*
*
*■
*
*
*
*
*
*
*
PROBLEMA N» 02
Un foco tiene las siguientes caracte­
rísticas: 100 watts y 200 voltios. Determi­
nar el valor de la resistencia de protección
que debe instalarse en serie con el foco,
cuando al conjunto se le aplica una ten­
sión de 220 V.
* Suponer que la resistencia dei foco
es constante.
SOLUCION-
1 Si ia diferencia de potencial entre los
extremos del conjunto es 220 V, en­
tonces el foco debe consumir 200 V
y la resistencia de protección 20 V.
A o- i§L -o C

499. 2. Calculo de la corriente que atra-
vieza al foco y la resistencia de pro­
tección.
De la característica del foco:
P =V ./ => 100W = 200tV x i
/= 0,5 ampere ..(1)
Aplicando la Ley de OHM a la resistencia
de protección:
r = 7 -
R =
20V
0,5A
Luego- R = 40Í2
PROBLEMA Nfi 03
Por una resistencia de 4 ohm ios atra-
vieza una corriente de intensidad 5 am­
pere. Determinar la cantidad de calor disi­
pado por la resistencia en un intervalo de
1 minuto
SOLUCION:
De la Ley Joule Lenz:
Q = /2. R . t ....(S.l.)
Q = (5Af . (4Q) (60s)
Q = 6 000 J
Q = 6 KJ
PROBLEMA Ne 04
Cuando la intensidad de corriente "I"
atravieza una resistencia eléctrica "R “ és­
ta disipa una potencia de 80 watt. Si la
corriente disminuye en un 50%, determi­
nar la potencia disipada por la resistencia.
SOLUCION.
1. Potencia disipada por una resisten­
cia:
P, = |2 . R = 80 watt ....(1)
2. Cuando la corriente disminuye:
l¿ I2. R
p2 = T R = „
4 4
.... (2)
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
♦
♦
*
*
m
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
P2 = 20 watt
PROBLEMA NG05
Se tiene una lámpara que tiene las
siguientes características V = 120 voltios
y P = 40 watts, ¿qué resistencia comple­
mentaria hay que conectar en serie c v> la
lámpara, para que su funcionamiento sea
normal cuando la red tiene una tensión de
220 V?.
SOLUCION:
Sabemos que:
P = V . i
40 W = (120V). /
-.(1)
La lámpara funciona normalmente con
una corriente de intensidad "i".
L = á = @ .
M
120V 100V
Aplicando la Ley de Ohm a la resistencia
de Protección
Vmb =/■ R
(100V) = (1 /3 A). R
Luego:
R = 300Q
PROBLEMA Nfi 06
Determinar la potencia que entrega la
batería de fuerza electrom otriz "e” y resis­
tencia interna ”r“ en el circuito mostrado.

500. Calculo de la intensidad de corriente
aplicando la segunda iey de Kirchhoff;
I£ = T i. R
8 =/(r + R)
/=
e
(r+ R )
Cálculo de la potencia entregada por la
f.e.m:
P =¿D ¡^/2 . r i V ...(2)
Reemplazando (1) en (2):
P =
e2 . R
(r+ R )2
PROBLEMA Ns 07
Determinar el valor de la potencia eléc­
trica que se entrega o absorve en cada
una de las fuentes eléctricas reales en el
circuito que se muestra.
40 n
7(1
50V
• in
SOLUCION.
Cálculo déla intensidad decorriente 7"
aplicandolasegundaLeydeKirchhoff:
2£ = /. R
(200 - 50) V =/. (40+7+1+2) í l
i - 3,0 A ...(1)
Cálculo de la potencia entregada por la
fuente de 200 V.
Pi = / . £ —Z2. r
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Pt = 582 W
Cálculo de la potencia que absorve la
fuente de 50 V.
P2 = - /. e - / '2. r
P2 = -(3)(50)-(9)(1)
P2 = -159W
PROBLEMA Ns 08
En la figura, si la resistencia R = 1,0 Q
puede disipar hasta una potencia máxima
de 9,0 w a tts sin ca le ntarse e xcesi­
vamente. Hallar la potencia máxima que
puede disipar el siguiente circuito:
Analizando la resistencia " R d e la con­
dición del problema.
”2
P(máx) =1 (máx) • R
9 = /2 (1)
/= 3,0 A .... (1)
Analizando el circuito mostrado en la
figura:
Cálculo de la potencia máxima que disipa
el circuito:

501. P = 13,5 W
PROBLEMA N9 09
Un hornillo eléctrico tiene tres seccio­
nes de igual resistencia. Si las tres seccio­
nes están conectadas en paralelo, el agua
de una tetera hierve a los 6 minutos.
¿En cuánto tiempo hervirá una canti­
dad igual de agua en la tetera para las
diferentes conecciones en las secciones
del hornillo eléctrico indicadas en la
figura a, b y c.
a)
b )
c)
R
—
C3—
R
R
—
o —
— o ----- #-----en----- -
R
---- ---------ca--------------
SOLUCION;
1.
2.
Primero encontramos la resistencia
equivalente del hornillo eléctrico pa­
ra cada variante de las conexiones,
llamando "R" a la resistencia de una
sección equivalente R0 es igual a
R/3.
En los casos a, b y c respectiva­
mente, tendremos:
3 2
Ra = 3.R
R b 4 R
3. En los tres casos: a, b y c el agua en
la tetera necesita igual cantidad de
calor “Q" para hervir el flujo de calor
en cada hornillo a, b y c son diferen­
tes. Representamos por to, ta, tb y
tc los tiempos necesarios para ca­
lentar el agua de la tetera en cada
uno de los casos considerados.
S
ü
*
*
*
*
*
#
*
#
*
¡S
í
*
*
#
*
*
*
*
*
*
*
*
*
*
*
a
jí
*
*
*
#
*
#
*
*
*
*
*
«
*
*
*
#
*
#
*
*
*
*
*
*
*
*
m
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
«
*
4. De la ley Joule - Lenz:en este caso:
V = constante
V2 V2 V2
Q = Ro ' *° = Ra *a = Rb' ^
/2
tb = - • tc - .(2 )
5. Reemplazando (1) en (2) y simplifi­
cando:
3. t ° = | = f .tb= f .tc ...(3)
De aquí obtenemos fácilmente los
valores de las magnitudes que bus­
camos:
ta = 9 to = 54 min
tb =
9
2
to —27 min
tc = 2 to —12 min
PROBLEMA Ne 10
En el circuito eléctrico mostrado, la
f.e.m e= 30 V y todas las resistencias son
iguales a R = 2Q. Hallar la potencia entre­
gada por la f.e.m al circuito.
SOLUCION:
1 En el eléctrico se produce un corto
circuito debido al alambre conductor
conectado en diagonal. Los alam­
bres en la conexión tienen resisten­
cia nula por consiguiente el poten­
cial en el alambre es constante.

502. 2 Reduciendo el sistema, hallamos la
resistencia equivalente.
lR/2
Req = — R = 3 fi
3. Cálculo de la potencia entregada la
f.e.m de la fuente.
I
1
J3R/2
P = ^ = 9 0 0 W
R 3
Luego:
Potencia = 300 W
PROBLEMA Ns 11
Once foquitos de navidad se conectan
en serie a un tomacorriente doméstico,
220 voltios, entonces cada uno disipa 16
watts. Luego se conectan en paralelo ei
mismo tomacorriente y se observa que se
queman. Se compran luego otros once
foquitos iguales y se les vuelve a conectar
pero protegido cada uno con una resisten­
cia "r”. Si brillan ahora como los foquitos
originales ¿cuánto vale cada resistencia
de protección?
&
S
i*
*
*
*
*
*
*
*
*
*
#
*
*
*
♦
*
*
*
*
*
*
$
*
*
*
#
*
*
*
*
#
*
*
*
*
*
#
*
*
*
*
*
*
*
*
fiü
s
is
sie
*
*
*
*
*t*
*
s¡«
#
*
*
*
*
«
t*
*
*
*
m
*
*
*
s
fc
*
*
*
*
*
*
SOLUCION:
Cuando los once foquitos se conectan en
serie, cada uno están sometidos a una
tensión 220V/11 = 20 voltios.
La potencia disipada será:
P = V./ => 16W = 20V . i => / =0,8A
La corriente que circula por cada resis­
tencia es: /= 0,8A
Cálculo de la resistencia de cada foquito.
De la Ley de Ohm:
V = /. R => 20V = 0,8A R
=> R = 25Q
El foquito y la resistencia de protección
están conectados en serie y el conjunto
sometido a una tensión de 220V.
De la condición (en paralelo) para que los
foquitos brillen como antes deben disipar
la misma potencia, esto quiere decir que
el foquito debe estar sometido a una ten­
sión de 20V y por él debe circular una
corriente i = 0,8A.
Entonces la resistencia de protección
debe estar sometido a una tensión de
200V y atravezado por una corriente
i =0,8A DE la ley de Ohm.
V0 = / . r =» 200V = 0 ,8 A r
Resistencia de protección:
r = 250Q

503. h
TEOREMA DE LA TRAYECTORIA
1. Consiste en el desplazamiento imagina­
rio de una carga de prueba convencional
positivo a través del tramo de un circuito
eléctrico.
2. En principio la intensidad de corriente
eléctrica se desplaza de mayor a me­
nor potencial por consiguiente si la carga
de prueba q atravieza una resistencia, en
el mismo sentido de la corriente, pierde
una energía igual a: ”-/R " Cuando la
carga de prueba atravieza la resistencia
en sentido opuesto a la corriente gana
una energía igual a :"+ IR”.
R
Desplazamientode "q" Desplazamientode "q"
Cuando la carga de prueba atravieza la
f.e.m desde el polo negativo hacia el polo
positivo, gana una energía igual a "+e“,
cuando lo hace desde el polo positivo
hacia el polo negativo pierde una energía
igual a:
*
3
¡
S
*
ü
s
*
*
*
*
*
*
#
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
+
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
S
lí
J
*
¡
Respecto del circuito mostrado inicial­
mente, llevamos una carga de prueba en
el sentido de la corriente 7 " saliendo del
punto 1—
>2 —
>3 —
>4:
Teorema de la trayectoria
V i -/ . Ri + £ - / . R 2 = V 4
PROBLEMA Ne01
A un cierto circuito se tiene la sección
AB, mostrada en la figura. Sabiendo que
la diferencia de potencial entre A y B es
12V (Va - Vb = 12V). Determinar la inten­
sidad de corriente que circula por la sec­
ción AB.
r — .
8
V
I * 5 , -
A
l *
B
J
SOLUCION:
Teorema de la trayectoria:
VA - / (20) + 8V -/(3Q ) = VB
(VA - VB) + 8V = (5 ÍÍ)./'
Del dato: 12V + 8V = (5Q)/
Resolviendo.
i - 4 ampere
PROBLEMA N902
En cierto circuito eléctrico se tiene la
sección AB, mostrada en la figura. Sa­
biendo que la diferencia de potencial en­
tre A y B es 36 voltios (Va - Vb = 36V),
determinar la f.e.m, “e", además la inten­
sidad de corriente que circula por la sec­
ción AB es igual a 5 amperes.

504. SOLUCION:
Teorema de la trayectoria.
VA- 4 /+ £ - & '= VB
(Va - Vb) + £ = 1 0 /
Del dato: 36V + £ = 50V
Luego:
£ = 14 voltios
PROBLEMA Ne03
En cierto circuito se tiene la sección
AB, mostrada en la figura. La f.e.m de la
fuente e-, = 20V, e2 = 30V y la resistencia
del tramo R = 5 ohmios. Sabiendo que la
diferencia de potencial entre A y B es 10V
(Va - Vb = 10V). Hallar la tensión en los
extremos de la resistencia "R”.
-Df
B
SOLUCION:
1. En el tramo del circuito AB la co­
rriente que circula es único.
■
■
■ '
20
- 50 • 3
■
V
A
V
í ____ “
L
B
J
2. Del teorema de la trayectoria:
A -» 1 —
> 2 —
>B
Va + 20V -5T+ 30V = Vb
Luego: (Va - VB) + 50V = 5/
/= 12 A ....(a)
3. De la ley de Ohm:
V , - V 2 = 5 ./(P )
Reemplazando (a) en (P):
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
■
*
*
*
*
*
*
En cierto circuito se tiene la sección
AB, mostrada en la figura. La f.e.m de la
fuente es e = 10V y las resistencias
Ri = 1.0Q, Rz = 2,0Q sabiendo que la
diferencia de potencial entre A y B es de
50V, hallar la intensidad de corriente que
circula por las resistencias.
ni *2
— ni----------- < = > ------- o
B
"1
SOLUCION:
Aplicando el Teorema de la Trayectoria:
in
10V
ni
2J1
A Dl
r— B
i. 1 J
Va -(1 ,0 )/+ 10 -(2 ,0 )/= Vb
(Va - V b)+ 10 = 3 . /
Del dato : Va - Vb
Reemplazando:
/= 20,0 A
V12 = 60V
En 1 848, el físico alemán Gustavo Ro­
berto Kirchhoff va ha establecer reglas gene­
rales para el cálculo de circuitos eléctricos
complejos que determinan íntegramente su
estado eléctrico, aportando de ésta manera
dos leyes de gran trascendencia en la elec­
tricidad. Analizamos a continuación para el
caso de las resistencias eléctricas.
1o LEY DE NUDOS O DE CORRIENTE
Está basada en el principio de conser­
vación de las cargas eléctricas y establece
que la suma de corriente que ingresan a un
nudo cualesquiera de un circuito, es igual a
la suma de corrientes qu-» salen de dicho
nudo.

505. "La carga neta en un MUDO es igual a
CERO"
Del circuito mostrado:
i 1 = /*2 + /3
Luego:
/i -/2 - / 3 = 0
~l|<ngresan) —H(salen) = 0
Se llama NUDO de un circuito bifurcado
el punto en que hay más de dos direcciones
posibles de la corriente. En un nudo con­
curren más de dos conductores.
Primera Ley de Kirchhoff (reglas de los
nudos): la suma algebraica de las corrientes
convergentes en un nudo es igual a cero
k n
I
k 1
Ik= 0
donde n es el número de conductores
que convergen en el nudo, e lk, la intensi
dad de corriente convergente en el nudo.
Se consideran positivas las corrientes que
ingresan al nudo, y negativas las que salen
del mismo.
2° LEY DE MALLAS O DE VOLTAJES
*
*
*
♦
*
*
♦
*
*
*
*
*
*
*
$
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
!*
*
*
*
*
*
*
♦
*
*
<
¡s
*
*
*
*
*
*
*
*
♦
*
*
1 En el circuito simple mostrado tomando
como referencia el punto A llevamos la
carga de prueba q en sentido horario en
el mismo sentido de la intensidad de la
corsiente.
2. Del teorema de la trayectoria;
Circuito cerrado.
VA + S1-/.R 1 +£2 -/.R 2 -63 -/R 3 = Va
£1 - / . Ri + £2 -/R 2 - £3 - / R3 = o
"La suma de caídas de potencial a lo
largo de cualquier camino cerrado en
una red es nula”
3. Otro modo:
£1 + £2 +
. £3 = i. Ri + / R2 + / R3
"La suma algebraica de f e.m es igual a
la suma de caídas de potencial en las
resistencias".
n2 : número de f.e.m.
CIRCUITO COMPLEJO
Segunda Ley de Kirchhoff: en cualquier
contorno cerrado elegido arbitrariamente
en un circuito bifurcado, la suma algebraica
de los productos de las intensidades de
corriente lk por las resistencias Rk de las
partes correspondientes de este contorno
o malla, es igual a la suma algebraica de
las f.e.m aplicadas al mismo.

506. Donde, n i, es el número de comente en
la malla elegida arbitrariamente y ri2 el
número de f.e.m en la malla.
Para aplicar la segunda Ley de Kirch
hoff, se elige un sentido determinado de
recorrido sobre la malla (en el sentido de
las agujas del reloj o en el contrario).
Las corrientes que coincidan con este
sentido de recorrido se consideran positi
vas si "crean" corrientes dirigidas en el
mismo sentido que el recorrido del con­
torno.
Orden del Cálculo de un circuito Bifurcado
de Corriente continua:
a) Se eligen arbitrariamente los sentidos
de las corrientes en todas las placas del
circuito.
b) Para los "m ” nudos del circuito, se
escriben "m - 1“ ecuaciones indepen­
dientes según la primera ley de Kirch
hoff
ó Se escogen los contornos (o mallas)
cerrados arbitrarios y después de elegir
los sentidos de los recorridos se escribe
el sistema de ecuaciones de la segunda
ley de Kirchhoff. En un circuito bifur­
cado que conste de "p" partes, (ramas)
entre nudos vecinos y de "m" nudos, el
número de ecuaciones independientes
de la segunda ley de Kirchhoff será:
" p - m + 1 Al hacerlas, los contornos
se eligen de tal manera, que cada nuevo
contorno tenga por lo menos una parte
del circuito que no esté en los contornos
ya considerados.
Ejemplo: En el circuito anterior mos­
trado, m = 2 y p = 3 esto
significa que tenemos 2
nudos y 3 mallas.
*
*
*
«
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
♦
*
*
*
*
*
*
♦
♦
*
*
<
S
*
*
♦
*
♦
*
*
*
*
*
*
*
*
*
♦
♦
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
#
♦
*
LEYES DE KIRCHHOFF
PROBLEMA N° 01
Calcular "R" si la intensidad de la co­
rriente en el circuito es 300 miliampere.
SOLUCION:
2da. Ley de Kirchhoff; para el circuito
simple (una sola comente)
- £ = i . Req
(8V - 5V) = / . (R + 4U)
3V = 3 x 10_1A . (R + 40)
Luego"
R = 6 0
PROBLEMA N° 02
En el circuito eléctrico mostrado, hallar
la intensidad de corriente "I" que circula
por la resistencia de 2 Ohmios.
5UV
2fi
— ---------
I
3fi
* 10V
----- — n
SOLUCION:
1 Las resistencias de 30 y 612, están
instalados en paralel' por consi
guíente se p n ’ri rt-f iplazar por
su equivalen!!.

507. 10V
2. 2da. Ley de Kirchhoff; para el cir
cuito simple:
le = I . Req
(50V - 10V) = I (2U + 2Í2)
Luego:
I = 10 ampere
PROBLEMA N° 03
Para determinar la fuerza electromotriz
Y la resistencia interna de una pila, se
conecta en serie con un amperímetro y una
resistencia variable. Cuando la corriente es
de 1,0 ampere, la resistencia exterior es
1,55 Ohm y cuando la corriente es de 0,5
ampere, dicha resistencia es de 3,35 Ohm
¿Cuánto valen las características de la pila
mencionada?
SOLUCION:
1 En el circuito simple, aplicamos la
2da. Ley de Kirchhoff
? -< * > -
£ = / . (r + R) (1)
Usando dos veces la fórmula (1)
para los dos casos:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
■
S
f
*
*
*
#
*
*
*
*
*
*
$
*
$
*
$
*
*
*
*
*
*
*
*
*
*
*
♦
*
♦
*
*
*
*
#
*
*
♦
*
#
*
*
#
>
*
*
*
<
¡*
*
*
«
a
*
<
¡
>
*
*
*
*
*
*
£ = 1 . (r + 1,55)
2do. Caso-
£ = 0,5 (r + 3,35)
Resolviendo (2) y (3):
(3)
£ = 1,8 vollios
r = 0,25 Ohm
PROBLEMA N° 04
Las corrientes en ampere, que pasan
por las resistencias de 1,0 Ohm y 3,0 Ohm
son:
SOLUCION
Aplicando la 2da ley de Kirchhoff a
cada malla
3Í2
Malla izquierda ■l£ I/. R
(16 + 4)V = /i (4 + 1) í i
í = 4 A

508. Malla derecha: l£ = - / . R
(4 + 2)V = / 2(3Q)
¡ l = 2 A
PROBLEMA N° 05
Fn un circuito eléctrico mostrado, ha­
llar ias lecturas en los amperímetros idea­
les A i, A2 y A 3.
SOLUCION:
1 lera Ley de Kirchhoff en el nudo
"M ”
/, - l 2 + ... (1 )
2. 2da Ley de Kirchhoff (malla iz­
quierda)
16V = 2/, + 2 / 3 ... (2)
3, 2da. Ley de Kirchhoff (malla dere­
cha)
-2V = 2 / 2 - 2 / 3 .... (3)
Ordenando las ecuaciones (1), (2)
y (3)
1 ./2 - 1- / 3 = 0 ... (a)
1 /, + 0. / 2 + 1. i 3 = 8 ... (|M
0. /, + 1. / 2 - 1. / 3 = -1 (y)
i _ - 1 ■i 2 -/ 3 ' 3¡4)
A A
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
1 -1 -1
= 1 0 1
0 1 -1
0 -1 1
Ni = 8 0 1
-1 1 -1
1 0 -1
'2 = 1 8 1
0 -1 -1
1 -1 0
3 = 1 0 8
0 1 -1
-15
-6
= - 9
Reemplazando
/'i = 5A ¡2 = 2A , h - 3A
PROBLEMA N° 06
En el circuito eléctrico m ostrado,
cuando la llave ” S” se encuentra en la
posición (1) el amperímetro ideal K indica
una lectura de 2,0 ampere. Hallar la lectura
en el amperímetro cuando la llave S pasa a
la posición (2). Desprecie las resistencias
de las fuentes de energía.
Cuando la llave S están en la posición
(1), funciona sólo la f.e.m ”e" Apli­
cando la segunda ley de Kirchhoff.
l e = ii R
£ = i r
e = (2,0A) (5Í2)

509. Cuando la llave S está en la posición
(2 ), funciona las dos fuentes de energía.
Aplicando la segunda ley de Kirchhoff
l e = 1. i R
2 6 + 8 = / 2(R)
Reemplazando (1) en (2):
30V = / 2(5Í¿)
(2)
¡2 — 6,0 A
PROBLEMA N® 07
En el circuito eléctrico mostrado A i, A2,
A 3 son amperímetros ideales que indican
las siguientes lecturas h , I?, I3 respecti­
vamente, debido a la diferencia de poten­
cial que se establece entre los puntos x e
V
Si se cumple la siguiente relación:
lt _ l2 I3
a _ b c
Hallar ; a, b y c.
SOLUCION:
1 Debido a la simetría del esquema,
se puede observar que por la resis­
tencia "2R" circula una corriente
" ll" y por la resistencia "R" circula
una comente "I3"
4
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
<
1
?
*
*
*
♦
*
#
*
*
<
8
>
*
*
*
%
•
*
*
*
*
*
*
»
*
*
*
*
*
*
*
*
*
*
De la ley de ohm, analizarnos la
diferencia de potencial entre los
puntos X y M o P e V:
I,. (2R) = l3. R
I3
2
(a)
El amperímetro "A 2" indicaré:
l2 = h + la - (PJ
Reemplazando (a) en (P):
l2 = h + 2 li => l2 = 3 li
•2
I1 =
Igualando (a) y (y) tenemos que.
Luego
I3
2
Identificando términos tenemos:
a = 1 : b = 3 ; c = 2
PROBLEMA N° 08
Un circuito eléctrico, formado por las
resistencias 5£2, 3Í2 y R, está conectado a
dos fuentes de f.e.m : £i = 3V y £ 2 = 5V,
¿Para qué valor de "R” la corriente a
través de la resistencia 5U será nula?
3

510. SOLUCION:
1. 2da Ley de Kirchhoff, en la malla
pabdp
3V = a , + 3 (/, + /2)
Luego:
/ 3 - 8 /i
/z = 3
5í)
. . (a)
5V
2. En la segunda Ley de Kirchhoff, si
el desplazamiento de la carga de
prueba en opuesto al desplaza
miento de la corriente, entonces la
caída de potencial será negativo.
Malla : pabcqdp :
3V - 5v = 5/i - R . Í 2 <
P
>
Reemplazando (a) en (|í) y despe­
jando :
h =
6 - 3R
15 + 8R
Entonces, ¡1 = 0 será cierto
cuando: 6 - 3R = 0
R = 20
Hallar la corriente que pasa por el
puente ab en el circuito representado en la
figura. Las resistencias del puente, de los
conductores de alimentación y la interna de
la batería se desprecian. r = 1Í2
£ = 7V
SOLUCION:
1. Cálculo de la resistencia equivalen­
te:
D r 2 7
Req = 2 3 r =6 r
de la ley de ohm:
6 = I. Req = I g r
Luego:
I = . (1)
1ab,
Cuando dos resistencias están co
nectadas en serie la corriente que
llega a ellos se reparte inversa
mente proporcional a la magnitud
de las resistencias
v y

511. 1 , I
2 - Ub + -3
Luego : lab — . . (2)
reemplazando (1) en (2):
lab = f r
de los datos
lab = 1 A
PROBLEMA N° 10
En el circuito eléctrico mostrado hallar
la lectura en el amperímetro A ideal. Las
resistencias internas de las baterías se
desprecian.
c _R P e
SOLUCION:
1. El amperímetro marcará la intensi­
dad "I4 " considerado en el gráfico
Nudo b : I = h + I2 - - • («I
Nudo g : I = I3 + I4 . . (P)
Luego U — lí + I2 - la . . . (I)
2, De la segunda ley de Kirchhoff en :
Malla a —
> b —
» f —
► g -» h —
»a
48 - 28 = h R => lí = ~ . . . (II)
Malla: a —
>b—
►
c—
>d —
>f —
>g —
»h ->a
4E - e - 26 = I2 R
e
<2 = (III)
*
*
*
♦
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
#
♦
*
*
*
*
*
*
*
*
*
♦
♦
*
#
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
3c
26 +8 = I3 . R ■
-=
>
3. Reemplazando (II), (III) y (IV) en (I):
la = r
- . . (IV)
2 e c 3e n
'♦ = R + R ' R = °
la lectura en el amperímetro
es nulo.
I4 = 0
PROBLEMA N° 11
En el circuito eléctrico mostrado en la
figura donde R = 10Q, la capacidad del
cordensador C = 5nF, se pide encontrar
la carga "q" en las armaduras del capacitor,
si la f.e.m de la fuente de energía es
igual a r.= 1Q1V y su resistencia in­
ternar — 0,1íi.
De la 2da. Ley de Kirchhoff:
8 = (R + r) í
101V = (10.1Ü)/
í = 10 A . . (1)
101V
ion

512. V ab = ¡ ■R
V Ab = 100V
Cálculo de la carga acumulada en el
condensador
q = VAB . C
q = 500 (.1 C
PROBLEMA N° 12
Hallar la diferencia de potencial (Va - Vb)
entre las armaduras A y B del condensador
"C" del esquema, si la f. e . m de las
fuentes valen: 8i = 4 .0 V; £2 = 1.0V y
las resistencias: Ri = 10 ohm ; R2 =
20 ohm; R3 = 30 ohm, las resistencias
internas de las fuentes son despreciables.
1. A través del condensador no hay
flujo de cargas eléctricas, por con-
2 lera. Ley de Kirchhoff; nudo "M"
/ = / l * ¡2 . . (1)
1.0V = 20 . / 1 + 30 /
Luego;
/ i = (1 -3 0 0 /20 .(2)
4. Malla ; FGBMAQPF ;
4.0V +1.0V = 1 0 ./? + 3CV
Luego ; ¡2 - 15 - 30i) /10 . . . (3)
5 Reemplazando (2) y (3) en (1)
_ 1-30/ 5 -3 0 /
1 ~ 20 + 10
/ = 0,1 A
de (2) y (3) / j = -0,1 A
¡2 = 0.2A
El signo (-) indica que el sentido de
la corriente n es opuesto al indi
cado en el dibujo, por consiguiente
el sentido correcto es; M —
> P
6. Teorema de la trayectoria:
B —
> M -> A
VB - 10 ¡2 + 1,0V = VA
VA - VB = -1.0V
PROBLEMA N° 13
En el esquema la f.e.m de las fuentes
Ei = 1,0V ; 82 = 2.5V y las resisten­
cias; Ri = 10 ohm; R2 = 20 ohm. Las
resistencias internas de las fuentes son
despreciables. Calcular la diferencia de po­
tencial (Va - Vb) entre las armaduras A y
B condensador ”C".

513. 1 A través del condensador no hay
flujo de cargas eléctricas (I = 0), no
pasa corriente.
2. Malla: MPBQTSiv’ : 2da. Ley de
Kirchhoff:
(2,5-1 )=20. /+ 10. i
/ = ¿ A = 0,05 A --(1 )
3. Teorema de la Trayectoria:
A -» S -> M -> B
VA - 1,0+2,5-20 /= Vb ... (2)
Reemplazando (1) en (2).
(VA- Vb) = -0,5 V
PROBLEMA Ne 14
Determinar la diferencia de potencial y
la carga acumulada en el condensador
C = 5|iF. Los valores de las resistencias
se indica en la figura. Desprecie las
resistencias internas de las baterías de
f.e.m: e = 6V. ¿Qué signo tendrá la carga
en la armadura del condensador acoplada
a las resistencias?
*
*
*
*
$
*
*
*
$
*
*
*
*
*
*
*
*
*
*
i#
*
*
*
*
*
*
*
*
*
*
<
¥
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
SOLUCION.
1 Cálculo de la intensidad de corriente
en el circuito. 2da. Ley de Kirchhoff:
2E - £ =/. (2P+ P)
/ =
e
3R
....(1)
Por el tramo : a -> b -» k: no circula
corriente, debido al condensador
2. Teorema de la trayectoria:
a -» x -» z'-> k -»b :
Va - / . R - £ - £ = Vb
Va- V b = 2£+ /R ....(2)
Reemplazando (1) en (2):
(Va —Vb) = —
De los datos
(V a -V b) = 14V
=> Va > Vb : por consiguiente, el po­
tencial en la armadura del con­
densador unida a las resistencias
es más elevado que el potencial
de ia armadura unida con la
batería, es decir ésta armadura
está cargada positivamente.
3. La carga acumulada en cada placa
será:

514. a = 70(iG
PROBLEMA N® 15
Determinar la carga en cada conden­
sador C, 2C y 3C en el circuito repre­
sentado en la figura. Despréciese la resis­
tencia interna de la batería. Considere:
C = 1¡jF ; e = 9V
SOLUCION:
1. Aplicando la 2da. Ley de Kirchhoff en
el circuito:
e =i(R+2R) / —
3R
... (a)
2. Ley de Nudos, en "e“:
qi + q2 = q3 .... (P)
3. Teorema de la trayectoria: a ->e -»b
w | § + f c | ! W . n = §
q2= 2 q i+ - E . C ...(I)
4. Teoremadelatrayectoria.b-»e-»d
i 91 ^ q3 ; 2
1
x
1~~C 3C = = 3
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
¡ü
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
qi = | e . c
Délos datos:
.... (III)
qi = 2|iC
q2 = 10|aC
q3 = 12[iC
PROBLEMA N® 16
Determinar la carga que pasa por el
interruptor K, cuando se cierra, en el cir­
cuito representado en la figura. C = 1 (if,
£= 6V .
Despréciese la resistencia interna de
la batería.
q3 = 2 £ . C -3 q i .... (II)
*
*
*
*
*
*
1. Antes de cerrar el interruptor K la
carga total de la placa inferior del con­
densador C y la placa izquierda del
condensador 2C era igual a cero.

515. 2. Después de cerrar el interruptor K
se establece un reordenamiento de
cargas en los condensadores, como
puede apreciarse en la figura. La
resistencia “R“ entre los puntos a y
d no funcionan en el tiempo, se
comporta como un conductor ideal,
en un intervalo de tiempo pequeño
se produce una descarga eléctrica a
través de ésta resistencia cuando se
cierra K.
3 Aplicando la 2da. Ley de Kirchhoff al
circuito: £ = ¡(R + 2R + 3R)
4. Teorema de la trayectoria:m—
»a->d
| r = / (2R + 3R) = 5r R .... (2)
Reemplazando (1) en (2):
qi = | £ . C .... (a)
5. Teorema de la trayectoria: b —
»a -»d
^2
2C
= ' ( 3R) = 3/ R .... (3)
Reemplazando (1) en (3):
q2 = £. C ... (P)
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
Del principio de conservación de las
cargas deducimos, que por el inte­
rruptor K pasa una cantidad de car­
ga'
q = qi +q2 = — £ . C
De los datos:
qi=5nC , q2=6nC
PROBLEMA Ns 17
1 = 1 l
Determinar la corriente que fluye por
cada resistencia: Ri = 10Í2, R2 = 20f2y
Rs = 30£2. del tramo del circuito, si los
potenciales en los puntos 1, 2 y 3 son:
Vi = 10V ; V2 = 6V ; V3 = 5V
*
*
*
*
*
*
*
*
*
*
*
1.
2.
De la primera Ley de Kirchhoff:
Ley de Nudos . en "O”
, 1 = , 2 + i 3 .... (a)
Teorema de la trayectoria :
1 -» 0 -> 2
Vi = 10/' i - 20/ 2 = V2
<2 = 0,2 - 0 , 5 m - . (P)

516. 3. Teorema de la trayectoria:
1 -> 0 -> 3
V-| —10. 1 ~ 30 . t 3 = V3
i 3 = (1 - 2/ 1)/6 .... (y)
Reemplazando (p) y (y) en (a ):
i 1 = 0 , 2 A ; t2 = 0,1 A; / 3 = 0,1A
PROBLEMA N®18
En el circuito eléctrico mostrado, la
fuerza electromotriz £ = 22,1 V tiene una
resistencia interna r = 1 ohm, además R =
10 ohm. Calcular la diferencia de lecturas
en el voltímetro ideal de resistencia in­
terna infinitamente grande y el voltímetro
real de la figura.
-o>A«-c
SOLUCION
1 En el 1er caso: Rv = 00
2da. Ley de Kirchhoff:
£ -< . ir +n ....(a)
De la ley de Ohm.
V a b = V, =,;. R .... (p)
Reemplazando (a) en (P):
Vi = £ . - =>
(R+r)
Vi = 20,09 voltios
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*¡*
*
*
*
S
Ü
#
*
*
*
r
r
R, Rv
(R+Rv)
2da. Ley de Kirchnoff:
R .R v
£ = I . r + -
(R + Rv)
De la Ley de Ohm :
.... (y)
Vab = V2 - I .
..R Rv
(R + Rv)
.... (6)
Reemplazando (y) en (0):
V2 = £ . R R v
[r. R + R. Rv + r. Rv]
Reemplazando valores:
V2 = 20voltios
3. Luego la diferencia de lecturas:
AV = V1 - V2= 0,09 voltios
PROBLEMA Ne19
En el circuito eléctrico mostrado, ha­
llar las lecturas en los amperímetros igua­
les A i, A2 y A3.

517. 18V
SOLUCION:
1. Corriente de mallas (malla izquier­
da) suponemos que: lí I2
16V = 2li + 2 (li - l 2) ....(1)
2. Corriente de mallas (malla derecha)
—
2V = 2 I2 —2(li —I2) ....(2)
3. Ordenando las ecuaciones (1) y (2)
2 . I 1 - I . I2 = 8 .... (a)
-1 . h + 2 . 1
2 = -1 -...(P)
... (3)
A =
Ai =
A2 =
2 -1
- 1 2
8 -1
-1 2
2 8
-1 -1
= 4 -1 = 3
= 16-1 =15
= - 1+8 = 6
Reemplazando en (3):
h = 5A ; l2 = 2A
I3 = Ii — 12 = 3A
Luego:
LEY DE CONSERVACION
DE LA ENERGIA
Elegimos arbitrariamente un condensa­
dor o sistema de condensadores como nues­
tro “Sistema Físico" en estudio el cual al­
macena energía debido al campo eléctrico
entre sus placas. La energía electrostática
inicial "W r del campo eléctrico varía si el
interruptor K cambia eléctricas en las placas
del condensador. En nuestro caso particular,
las baterías y pilas realizan trabajo sobre
nuestro sistema físico. Cuando el interruptor
K cambia de posición, de 1 a 2 o viceversa,
en el condensador se establece un reorde­
namiento de cargas, si las cargas positivas
pasan del polo positivo hacia el polo negativo
de la pila,entonces dicha pila realiza un tra­
bajo negativo sobre el sistema, en caso po­
sitivo. El trabajo realizado por el conjunto de
pilas debido al desplazamiento de cargas
sobre el sistema de condensadores se pue­
de invertir en aumentar la energía del sis­
tema y/o disipar a través de la resistencia "R"
en forma de calor al medio ambiente. Sea,
W2 la energía final del conjunto de conden­
sadores, entonces, del principio de conser­
vación de la energía:
"El trabajo realizado por el conjunto de
pilas (f.e.m) es igual a la variación de la
energía del conjunto de condensadores, más
la cantidad de calor disipado al medio am­
biente".
Wbaterías = AW + Q
Wbaterías = W2 - W 1 + Q

518. ¿Qué cantidad de calor se desprende
en la resistencia R cuando el conmutador
K se pasa de la posición "1" a la posición
"2"? C = 100uF, e = 100 V la resistencia
interna de las baterías se deprecian.
¿SOLUCION:
1, Cuando el conmutador K está en la
posición "1", la energía almacenada
por el condensador es;
W i = | c . e 2
Del dato:
W i =0,5 J ...(a)
2.
3.
Cuando el conmutador K está en la
posición "2", la energía almacenada
por el condensador es :
W2 = | . C(% )2= ^ C£2
=> W2 = 12,5 J .... (p)
La carga acumulada por el conden­
sador es directamente proporcional
a la diferencia de potencial aplicada
en el condensador.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
s
t¡
*
*
*
*
*
*
9
¡f
*
*
*
*
*
*
*
*
s
is
*
*
*
s
N
*
4.
En el primer caso (K:1) la carga acu­
mulada es igual a : q = C . £ + 0,01 C
En el segundo caso (K:2) la carga
acumulada por el condensador es
5q = 0.05C. Entonces cuando el
conmutador K pasa de la posición
”1" a la posición “2", por la resisten­
cia R atravieza una cantidad de
carga igual a “+4q'‘, luego el trabajo
realizado por la batería será positivo
dado que las cargas se desplazan
desde el polo negativo hacia el polo
positivo.
Wbateria =(4q )(4£) + (4q)£ = 20q.£
Reemplazando datos:
Wbateria = 20 C .£2 = 20 J ... (y)
Del principio de conservación de la
energía:
“El trabajo realizado por la batería,
es igual a la variación de la energía
del condensador ”C" más la canti­
dad de calor disipado1
'
Wbateria = (W2 - W i )+Q ...,(8)
Reemplazando (a), (P) y (y) en (5)
l Q = 8J
PROBLEMA N902
¿Qué cantidad de calor se desprende
a través de la resistencia R, cuando el
conmutador K se pasa de la posición ”1”
a la posición "2"?.
La resistencia interna de las baterías
se desprecian. £ = 10 V, C = 2|iF,

519. SOLUCION
1 Cuando K está en la posición ” 1", la
energía almacenada por el conden­
sador es igual a :
Wi = ^ C. (4£)2 = 8CE2
=> W i = 1 600(iJ .... (a)
2. Cuando K está en la posición "2" la
energía almacenada por el conden­
sador es igual a :
w 2 = | c . e 2
W2 +100nJ .... (p)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
4.
5.
=» q =C.£ => q = 20|iC ...(1)
Cuando el conmutador K se pasa de
la posición "1" a la posición “2" se
experimenta un reordenamiento de
cargas en las placas del condensa­
dor, entonces por la resistencia R
atravieza una cantidad de carga
igual a ”+3q". Luego, la batería rea­
liza un trabajo negativo, debido a
que las cargas se desplazan del
polo positivo al polo negativo
Wbatería = -(3 q ). £ = -3q . £
=* Wpila = -600|iJ .... (y)
Del principio de conservación de la
energía: el trabajo realizado por la
batería, es igual a la variación de la
energía del condensador, más la
cantidad de calor disipado:
Wpila = (W2 - W i)+ Q ...(2)
Reemplazando (a), (p) y (y) en (2),
tenerrtos:
-600uJ = —
1 500uJ + Q

520. Cuando el conmutador K pasa a la
posición "1", el condensador C al­
macena una carga “q", la armadura
derecha se carga positivamente.
2da. Ley de Kirchhoff:
2E - £ = 5 =>
c
q = E . C
Del dato tenemos:
q = 50|uC
-(1 )
*
*
*
*
*
*
*
2 Cuando el conmutador K pasa a la
posición "2" el condensador C al­
macena igual cantidad de carga que
en el caso anterior- q = e. C pero la
armadura derecha se carga negati­
vamente Por consiguiente, cuando
el conmutador K se pasa de la posi­
ción 1 a la posición 2 por la resisten­
cia “FT atravieza una cantidad de
carga igual a: “+2q''
3. La energía almacenada por el con­
densador, cuando el conmutador K
está en la posición 1 y en la posición
2 son iguales:
*
*
*
*
sin
*
$
*
*
*
*
*
*
#
*
Wi = W2 = A C £2 = 2 50|iJ ..(2)
4. Cuando las cargas “+2q" atraviezan
la resistencia, la f.e.m, realiza un
trabajo positivo sobre las cargas
igual a:
Wp¡ia = E (2q) = 2q£ = 2CE2
=> Wp¡ia = 1 OOOuJ ....(3)
5. Por el principio de conservación de
la energía se cumple que:
"El trabajo realizado por la f.e.m es
igual a la variación de la energía del
sistema (circuito eléctrico), más el
calor disipado"
Wp,ia = (W2 - W i) + Q (4)
Reemplazando (2) y (3) en (4):
1 000|j.J = (250|iJ - 250pJ) +Q
Luego; el calor disipado a través de
la resistencia R es:
Q = 10J|iJ
PROBLEMA Ns04
Entre las armaduras de un condensa­
dor plano se encuentra una lámina dieléc­
trica (e =3) que llena todo el espacio del
condensador. El capacitor está acoplado
a través de una resistencia "R" a una
batería de f.e.m V = 100 voltios. La lámina
se saca rápidamente, de manera que la
carga en el condensador no tiene tiempo
de variar. ¿Qué energía, en forma de calor,
se desprenderá después de esto en el
circuito. La capacidad del condensador
sin el dieléctrico es Co = 100:iF.

521. SOLUCION:
1 La carga acumulada por el conden­
sador con el dieléctrico es:
q =£ . C0.V. Luego q = 30 000|iC,
esta misma carga, por condición del
problema, se conserva en el ins­
tante inicial en el condensador al
quitar el dieléctrico, en este preciso
instante la energía eri el condensa­
dor es:
Wi .1 i
' 2 Co
Luego. Wi = 4,5 J .... (a)
R
2. Instantes después se produce un
reordenamiento de cargas en el
condensador, ahora sin dieléctrico.
Al final la carga en el condensador
es:
qo =Co V => q0 =10 000|iC ..(1)
En estas condiciones la energía al­
macenada será:
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
t*
*
*
*
*
*
*
*
*
3.
W2 = 0,5J .... ((3)
Eri este proceso a través de la resis­
tencia R atravieza una cantidad de
carga igual a:
(q - qo) =(£ - 1)qo = 20 OOOiaC ,.(2)
Entonces, las cargas +(q q0) se
desplazan del polo positivo al polo
negativo de la f.e.m, por con­
siguiente la batería realiza un tra­
bajo negativo.
Wbateria = —
(q —qo) ■V
Wbateria ——
2J ■(Y
)
4. Del principio de conservación de la
energía:
"El trabajo realizado por la batería
es igual a la variación de la energía
del condensador, más la cantidad
de calor disipado”
Wbateria = W2 - Wi + Q .... (3)
Reemplazando (a), (|3), (y) en (3)
tenemos:
-2 J = 0,5 J - 4,5 J + Q
Q = 2J
PROBLEMA N®05
¿Qué cantidad de calor se desprende
en la resistencia R una vez que se cierra
el interruptor K?. La resistencia interna de
la batería se desprecia, e = 10V ; C = 3[iF.

522. Cuando el interruptor K está abierto
los condensadores de capacidad C
y 2C se encuentran instalados en
serie, y la carga acumulada en cada
placa es q1
2da. Ley de Kirchhoff:
£ = q , = § c . e
De los datos tenemos:
qi = 20|iC ....(1)
*
*
*
*
*
*
«is
*
*
*
*
*
*
*
densadores será:
Wt = —. Ceq £2
Wi =- § C U * W i=
2.
=> W i = 100|iJ ....(a)
Después de cerrar K, el condensa­
dor C se carga hasta la tensión su
carga en cada placa es q2 ; de la
2da. Ley de Kirchhoff
£ =C => Q
2 =C.£ => c¡2= 30(íc ...(2)
La energía almacenada será:
3. Cuando se cierra el interruptor K se
origina un reordenamiento de cargas
en los capacitores, entonces, por la
resistencia atravieza una cantidad de
carga iguala (q2- q1) debe observarse
que el condensador "2C" queda des­
cargado, entonces, el trabajo reali­
zado por la batería será:
Wbatería = (q2 - q i) . E ... (3)
Reemplazando (1) y (2) en (3):
Wbatería = 100|iJ .... (y)
4 Del principio de conservación de la
energía, el trabajo realizado per la
batería (f.e.m) es igual a la variación
de la energía del sistema, más el
calor disipado.
Wbatería = (W2 - W i) + Q (*)
Reemplazando (a),(p) y (y) en (*)
tenemos;
100|í J = 50|iJ + Q
PROBLEMA N®06
En el circuito electrico mostrado las
dos llaves K funcionan simultáneamente.
¿Qué cantidad de calor se desprende en
la resistencia R cuando los conmutadores
K se pasan de la posicion 1 a la posición
2?.
C = 2 |jF ; £ = 2V. La resistencia interna
de las baterías se desprecian.
*
í *
*
*
*
#
*
*
*
*
*
*
*
%
*
*
*
R
1 2
>
“ c u
= 5t
~
1 ?
.
"
°k ►

523. Cuando las llaves están en la posi­
ción "1", la energía almacenada por
el condensador es igual a:
W i— .c.e2=> Wi :4jjJ ..(a)
2. Cuando las llaves están en la posi­
ción "2", la energía almacenada por
el condensador es ¡gual a
W2= C (5£)2 =* W2 . C . e2
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Wbater¡a = 20C. £2 = 160|iJ ...(y)
Del principio de conservación de la
energía: el trabajo realizado por la
batería, es igual a la variación de la
energía del sistema (condensador
"C"), más el calor disipado.
Wbateria = (W2 -W ,) + 0 ,..(3)
Reemplazando (a), (P) y (y) en (3)
a la diferencia de potencial aplicada
al condensador Para K en 1 enton­
ces q = C e .... (1)
Para K en "2" la carga acumulada
es: 5C£. Por consiguiente cuando
las llaves pasan de la posición "1" a
la posición “2'', por la resistencia R
atravieza una cantidad de carga
igual a ”+4q". Luego, el trabajo reali­
zado por la batería de f.e.m "5£"
será:
*
*
*
*
*
*
*
«
o
*
*
ü
*
#
*
*
*
*
2.
2da. Ley de Kirchhoff:
£ £ = £ / . R
12V =/-| . (4 + 2)
/ j = 2 ampere
En un segundo caso cerramos la llave
“S", entonces la resistencia de 2 í i no
funciona, la diferencia de potencial entre
sus extremos se hace tgual a cero, a éste
fenómeno se denomina “Corto circuito"

524. Por consiguiente la lectura en el amperí­
metro "K" se modifica, ahora indicará "i2".
2da. Ley de Kirchhoff:
££ = £ /'. R
12V = /2 . (4Q)
4 = 3 ampere
Podemos justificar que no pasa corriente
(i = 0) por la resistencia de “2 fi“, apli­
cando la ley de Ohm.
AV = / x R = 0
La diferencia de potencial entre sus ex­
tremos es igual a cero.
Pero: R * 0 i = 0
PUENTE DE WHEATSTONE
El circuito mostrado en la figura se llama
“Puente de Wheatstone". Se usa para medir
resistencias. Cuando la corriente a través del
galvanómetro "G" es cero (de modo que los
puntos x e y están al mismo potencial)
Se cumple que:
R i . R4 = R2 . R3
Vx = Vy => Ig = 0
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Esta es una disposición en puente, que
permite determinar la resistencia de uno en
función de una resistencia patrón y del co­
ciente de dos resistencias.
R1- ■R3
PROBLEMA Ns01
Cinco resistencias están dispuestas
como muestra la figura (1), todos ellos
tienen igual magnitud “R“. Hallar la resis­
tencia equivalente entre los puntos A y B.
SOLUCION:
1 Del "efecto puente", los potenciales
en los puntos x é y son iguales, por
consiguiente por la resistencia en la
diagonal no pasa corriente (I = 0), o
sea no funciona, entonces si retira­
mos ésta resistencia "R" el sistema
no se altera, teniendo su equiva­
lente en la figura (2).

525. f ig ( 2 )
fácilmente la resistencia equiva­
lente.
Req = R
PROBLEMA Ns 02
La fuente de energía "£" tiene resisten­
cia interna despreciable. Calcular "R" sa­
biendo que, cuando el interruptor "S”está
abierto, el amperímetro ideal "K" indica
una lectura 3 ampere y cuándo "S" está
cerrado indica 8 ampere.
-WMW-
R
+ ¡E-
o-
-WiV-
3a
*
*
*
í*r
*
*
*
*
*
*
*
*
*
*
%
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
1. Cuando “S” está abierto, ¡as resis­
tencias están conectadas en serie.
2da. Ley de Kirchhoff
£ = i i . Ri
£ = (3A). (R+3Q) ....(1)
2 Cuando “S" está cerrado, se pro­
duce "Corto circuito", por con­
siguiente la resistencia “R" no
funciona.
£ = *' 2 - R2
£ =(8A). (3Q) = 24 voltios
Reemplazando en (1):
24 = 3 (R + 3)
Luego:
R = 5Q
PROBLEMA Ns03
En el circuito eléctrico mostrado, de­
terminar la resistencia equivalente entre
los puntos A y B.
SOLUCION
1. Todos los puntos de un mismo
alambre de conección constituyen
una "Línea equipotencial".

526. 3fi
JWMr
Ifi
H f------ W -
i 3n
ífi
-w v - -OB
in l3n
A A
ii
A
2. Uniendo los puntos de igual poten­
cia) eléctrico
*
*
*
*
*
*
*
*
*
*
3. Identificando el "Efecto Puente1
' la
resistencia que se encuentra entre
los puntos M y N, no funciona, en­
tonces puede ser retirado sin alterar
al sistema.
M
1 _ 1 1 . 1
_
Req " 6 + 2 + 3
Req = 1fl
PROBLEMA N904
Se tiene una rejilla de alambre ilimi­
tada con celdas cuadradas. La resistencia
entre los nodos contiguos de cada con­
ductor es igual a R0- Determinar la resis­
tencia equivalente entre los puntos A y B
de ésta rejilla.
Sugerencia: Hacer uso de los prin­
cipios de simetría y superposición.
*
*
♦
A • B
SOLUCION:
1. Conectamos mentalmente a los
puntos A y B una fuente de tensión
V
Entonces: V=l.Req = l0 Ro — (o.)
Donde:
I es la corriente en los cables
de alimentación
lo : es la corriente en el conduc­
tor AB.
I
4

527. i
4
B
lo
A B
3. Análogamente, si la corriente “1
“ in­
gresara a la rejilla desde el infinito y
"saliera" desde el punto ”B", por el
conductor AB pasaría también la
corriente ”1/4",
Superponiendo éstas dos solucio­
nes, obtendremos lo = 1/2.
Reemplazando en (a):
I. Req = lo • Ro = Ro
Luego:
o R°
Req = —
I: Saliendo por “B"
La corriente "lo" puede ser repre­
sentada como la superposición de
dos corrientes. Si la corriente I fluye
ra hacía el punto A y se extendiera
por la rejilla hacia el infinito, a través
del conductor AB, por simetría,
pasaría una corriente "1/4'’.
*
*
*
*
PROBLEMA Ne 05
En el circuito eléctrico mostrado, de­
terminar la resistencia equivalente entre
los puntos A y B.
Donde : R = 3Q ; r = 1Q
1. Para resolver este problema, apli­
caremos el criterio de superposición
de corrientes como muestran las
figuras
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
* __
* o
* -
S A
#
*
#
*
*
*
*
*
2. Ley de Ohm en (d):
^ab = Oí + *2) -
3. 2da. Ley de Kirchhoff;
en la malla AXYQPA
lí . r +(h —l2)R —1
2 R = 0
(c)
.... (P)
I,
' 1
- W -
r
-m b -
--------•m ­
r r
<I,-I2>
R
-------- W t-
I, I,
2 ‘ 2
4. Teorema de la trayectoria:
A —
> X —
> Y —
» Z —
»B

528. (d) (li+ I2)
-j» ; -
A Req B
Vab = h. r+ R . I2 ....(y)
Reemplazando (p) en (y):
Vab = _|i ... (6)
5. Reemplazando (6) y (p) en (a);
( 3 L ± R )_ í3 R + jí.Req
*
$
*
*
*
*
*
f
*
*
*
*
*
f
R
3 V *
/ 5
4 7 l
V ...
1c | I J
En un circuito complejo, no siempre los
elementos resistivos se conectan en serie y
en paralelo. En muchos circuitos pueden ha­
llarse grupos de tres resistencias, que de­
finen un triángulo o una estrella por con­
siguiente se tiene que efectuar la respectiva
transformación del triángulo a estrella o vice­
versa, para simplificar y poder hallar la resis­
tencia equivalente
A) TRANSFORMACION DE TRIANGULO
A ESTRELLA
La sustitución del triángulo de resisten­
cias una estrella equivalente se realiza con
la condición de que ésta sustitución no cam­
bie los potenciales eléctricos de los puntos
A, B y C, que son los vértices del triangulo y
de la estrella equivalente, como muestra la
figura. Sí mismo, se considera que la parte
del circuito no transformada, su régimen de
trabajo no se altera (no cambia la corriente,
tensiones y potencias)
*
*
*
*
m
*
5*
*
Datos: Ri, R2, R3
Incógnitas: Ra, Rb, Rc
1. Los circuitos mostrados permanecen
equivalentes para todos los regímenes
de trabajo, a continuación para la de­
mostración utilizaremos el criterio de su­
perposición de corrientes:
PRIMERO: Consideramos. Ia = 0
En el triángulo resistivo: le = Ib
y en la estrella "Ra" no funciona
Entonces. R2y R3queda en paralelo con
R1t luego:
Rcb =
(R2 + R3) Ri
.... (a)
Ri + R2 + R3
En la estrella resistiva: IC = IB
La resistencia equivalente será'
Rcb = Rc + Rb — (p)

529. .... (I)
n n Ri (R2 + R3)
Rb + Re = -------¡r-----—
R1 + R2 + R3
2. SEGUNDO: Consideramos : Ib = 0
En el triángulo resistivo: lc = lA y en la
estrella RB no funciona.
Entonces : R, y R3 queda en paralelo
con R2, luego:
Rca =
R2 (R1 + R3)
.... (y)
R1 + R2 + R3
En la estrella resistiva : IC = IA
La resistencia equivalente será :
Rca = Re + Ra (8)
Igualando () y ( 5 ):
R2 (R1 + R3)
Ra + Re = - ....(II)
R i + R 2 + R 3
3. TERCERO : Consideramos: le = 0
En el triángulo resistivo: lB = - lA y en la
estrella "Re” no funciona
Entonces: Rt y R2 queda en paralelo con
R3, luego:
Rab =
R3 (Ri + R2)
.... (0)
R1 + R2 + R3
En la estrella resistiva:
Ib = - Ia
La resistencia equivalente será:
Rab = Ra + Rb —• (<
!>
)
Igualando (0) y (0):
R3 (R1 + R2)
Ra +Rb =
R t + R2 + R3
.... (III)
Resolviendo las ecuaciones (I), (II) y (III)
obtendremos:
Ra =
R b ~
R2 • R3
R1 + R2 + R3
R1 . R3
R1 + R2 + R3
*
*
*
*
o
»
*
!*
>
*
0
*
#
*
*
#
$
*
*
*
*
*
0
*
#
0¡
*
*
m
*
o
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
D
é
*
*
*
R1 • R2
Ri + R2 + R3
B) TRANSFORMACION DE ESTRELLA A
TRIANGULO
La sustitución de la estrella de resisten­
cias por un triángulo equivalente se realiza
con la condición de que esta sustitución no
cambie los potencíale eléctrico de los puntos
A, B y C, que son los vértices de la estrella y
del triángulo equivalente, como muestra la
figura.
Así mismo se considera que parte del
circuito no transformada, su régimen de tra­
bajo no se altera (no cambia la corriente,
tensiones y potencias)

530. Incógnitas: Ra, Rb, Rc
Análogamente al caso anterior haciendo:
Ia =0, luego Ib =0 y finalmente: le = 0, se
demuestra que:
Ra -
Rb =
RC =
R1. R2 + Ri. R3 + R2- R3
' Ri
Ri. R2 + Ri- R3 + R2- R3
R¡ '
Ri- R2 + Ri. R3 + R2. R3
R¡
PROBLEMA N° 01
En el circuito eléctrico mostrado, de­
terminar la resistencia equivalente entre
los puntos A y B.
3íi 1Í2
------— ------ w w ------
b fi
■
— v m ------- ■
----- ----------
B
in 3fi
SOLUCION:
En principio en el circuito dado no se
produce el efecto puente, entonces
para deducir tenemos que realizar
una transformación triángulo de re­
sistencias a una estrella.
Los puntos, P, Q y B son los vértices
del triángulo inicial como puede ob­
servarse en la figura.
*
*
*
*
«
N
*
*
*
*
0 96 3 126
q = 70 + 7 = ~7CT
Luego:
Req = 1,8 í i

531. PROBLEMA Nfi 01
La figura muestra dos cuerpos esféri­
cos de pesos iguales a 20N y cargados
con igual magnitud q = 10mC, pero con
signos diferentes. Si la distancia de se­
paración es d = 0,1 m. Determinar la ten­
sión en las cuerdas (1) y (2).
SOLUCION: .
La fuerza de atracción "F" entre las car­
gas eléctricas será:
10 10
•F = k. = 9.109 . - ^ - 5- = 9QN
d2 10 *
D.C.L. (esfera con carga positiva):
IF y = 0
Ti = F + W
Ri = 90N + 20N
Ti =110N
* •
D.C.L. (esfera con carga negativa)
IF y = 0 __________
T2 +W = F
T2 = F - W
T2 = 90N - 20N
T2 70N
-q
*
*
*
$
*
*
*
*
*
*
*
*
*
*
La figura muestra un sistema mecá­
nico en equilibrio, donde cada esferita
tiene un peso de 10N y carga de magnitud
q = 10~5 C. Sabiendo que la polea móvil
tiene el peso de 30N determinar el peso
del bloque "W".
a) 20N
d) 25N
b) 40N
e) N.A.
c) 50N
* PROBLEMA Nfi 03
*
*
*
*
S
fS
*
*
*
*
*
*
$
*
*
♦
*
*
*
*
*
*
*
s
jí
*
*
*
*
*
*
*
*
*
*
*
*
La figura muestra dos cargas puntua­
les de magnitudes iguales q = 10-4 C
pero de signos diferentes y pesos despre­
ciables, separados una distancia d = 1m.
Sabiendo que existe rozamiento entre el
bloque de peso “P" y la superficie hori­
zontal (is = 0,5, determinar el peso del
bloque, si está pronto a moverse.

532. De la condición de equilibrio, es fácil de­
ducir que la tensión en el hilo es igual a
la fuerza de atracción entre las cargas sin
peso.
T = K ^ r = 9 x 10!
10'
1
= 90N
Diagrama del cuerpo libre, del bloque.
IF y = 0
Nt = P ....(1)
ZFx = 0
fs(máx) = T
Reemplazando en (2): 0,5P = 90N
Luego:
P = 180N
PROBLEMA Ne 04
La figura muestra dos cargas puntuales
de magnitudes ¡guales q = 2,10 C, pero
signos diferentes y pesos 5N cada uno,
separados una distancia de 0,3 m, además,
la polea móvil pesa 15N, determinar el peso
del bloque "W ". sabiendo que está pronto
a moverse. Existe rozamiento sólo entre el
bloque y el piso horizontal, n* = 0,2.
a) 450N
d) 900N
b) 150N
e) N.A.
c) 650N
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
s
k
*
*
*
*
*
*
*
*
*
s
i»
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Dos cargas puntuales de magnitud
Qi =-16¡iC y Q2 = -9|iC, están separados
una distancia d = 0,7m. ¿A que distancia
"x" a partir de la carga Q i, cualquier carga
positiva o negativa se encontrará en equi­
librio?.
Q1 * 'A •Q c
SOLUCION:
Llevamos una carga de Prueba ',+q" al
punto A, el cual por condición del pro­
blema debe estar en equilibrio
y 1
©~
(1 )
+q
—e —
A:
O
i(2)
( d - x )
EFx
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
Entonces: Fi = F2 .... (1)
F1 . fuerza que ejerce Q1 sobre "q".
F2 : fuerza que ejerce Q2 sobre !'q“.
Reemplazando en (1):
3.Q2
K . a f U k .
xr (d-x)
, [0 2
1—x = ——.■
>
i Q
i
Luego
d
,+
I q T
Qi

533. PROBLEMA Ns 06
Dos cargas puntuales de magnitud
"Q" y "4Q", respectivamente, están sepa­
rados una distancia de 0,9m. ¿A qué dis­
tancia a partir de la carga "Q", una partí­
cula de carga 26uC se encontrará en equi­
librio?
a)0,1m b) 0,2m c) 0,3m
d) 0,5m e) N.A
PROBLEMA N®07
Dos cargas puntuales de magnitud
Qi = 32 x 10-10C y Q2 = 16 x 10~10C,
están separados una distancia igual a
0,6m. Determinar la intensidad del campo
resultante en el centro del segmento que
une la posición de las cargas.
1
O
-Q
0, 6m
SOLUCION:
Llevamos una carga de prueba "+q0" al
punto medio del segmento que une la
presión de las cargas
'1
O - -
Ej +q„ E2
---------9--------*«
*
*
s
j¡>
*
*
*
*
*
*
*
*
*
*
#
*
%
*
*
*
*
*
«
•
*
*
*
*
#
*
*
*
*
#
iii
*
(1) (2 )
Ei: Intensidad de campo generado por
la carga - Q i, ubicado en el punto
(1).
Ez: Intensidad de campo generado por
la carga -Q 2, ubicado en el punto
(2).
r K Q i _ K.Q 2 _
Ei = — 5- y E2 = — 3 — - (1)
En (1), no se reemplaza el signo de las
cargas, sólo del módulo, el signo ha sido
utilizado para determinar el sentido de la
intensidad dei campo “E".
Cálculo de la intensidad resultante:
E = E2- E1 .... (2)
En (2), consideramos positivo (+; a la
derecha y negativo hacia la izquierda (-).
Reemplazando (1) en (2).
r K ,_ 9 x 109
E = -^ (Q 2 -Q i )=--------— 7
d 9 x 1 0
.(16. 10~10)
E = -160N/C
El signo (-) significa que el sentido es
hacia la izquierda
PROBLEMA Ne08
Dos cargas puntuales de magnitudes
Q1 = 18p.C y Q2 = 32|jC. Se encuentran
separadas una distancia de 1,4m, como
muestra la figura. Determinar la intensi­
dad de campo resultante en el punto M.
m
*
*
*
*
*
*
*
*
*
*
*
*
a)Cero
d) 30 N/C
PROBLEMA Ne09
b)10N/C
e) Ninguna
c)20N/C
En el triángulo rectángulo isósceles
mostrado en la figura, determinar el valor
de la intensidad del campo resultante en
el punto medio "M" de la hipotenusa.

534. ♦ -q
I S
I
l yM
T _ q
SOLUCION.
Llevamos una carga de prueba “+q0“,
para determinar los vectores intensida­
des de campo en el punto "M", generado
por cada una de las cargas.
- q
(2 )
-q
E i: Intensidad generado por la carga
“-q" ubicado en el vértice (1)
E2: Intensidad generado por la carga
“-q* ubicado en el vértice (2).
E3: Intensidad generado por la carga
"+2q” ubicado en el vértice (3).
Es fácil comprobar que:
Ei = E 2
Por lo tanto, el vector de campo resul­
tante es el generado sólo por la carga
ubicado en el vértice (3).
K(2q)
Lf
2
*
*
*
«
s
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
■
*
#
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
Reemplazando datos:
E = 576 N/C
PROBLEMA N2 10
En los vértices de un cuadrado se han
colocado cuatro cargas puntuales como
indica la figura. Si, la carga "Q" genera un
campo cuya intensidad en el centro del
cuadrado es 25 ^2 N/C, determinar la in­
tensidad de campo resultante en el centro
del cuadrado.
2Q
a) 25 N/C b) 50 N/C
c) 100 N/C d) 150 N/C
e) Ninguna
PROBLEMA N» 11
En los vértices de un triángulo equi­
látero de lado d = 0,3m, se han colocado
dos cargas puntuales de magnitudes igua­
les a Q = 16 x 10-10C como muestra la
figura. Hallar la magnitud de la intensidad
del campo resultante en el tercer vértice
iion
‘ O ) N
/
/
/

535. Llevamos una carga de prueba "+q0" al
vértice (3), para determinar la dirección y
sentido de la intensidad de campo gene­
rado por cada carga.
( i) (?)
Ei: Intensidad de campo generado por
la carga ubicado en el vértice (1).
E2: Intensidad de campo generado por
la carga ubicado en el vértice (2).
Ei = E2 = k .
Q
.... (I)
... (III)
Reemplazando datos en (111):
E = 9. 10;
,9 16 x 10
9 x 10
,-io
,-2
■.V3
Luego
N
:276-8 c
PROBLEMA N*12
En los vértices de un triángulo rectán­
gulo se han colocado dos cargas eléctri­
cas de magnitud
Q1 = +125 x 10~®C y
Q2 = -27 x 10~8C,
como muestra la figura.
Determinar la intensidad de campo
eléctrico resultante en el vértice A.
*
*
*
*
*
*
*
Cálculo de la resultante, mediante la ley
del paralelogramo
E2=E^ + E2 +2 E1.E2.C0S 60° .... (II)
Reemplazando (I) en (II):
E = K .. V3
#
■
*
*
*
*
*
#
♦
*
*
*
#
*
*
*
*
*
*
c) 54 KN/C d) 63 KN/C
e) 18 N/C
PROBLEMA N®13
En los vértices de un triángulo rectán­
gulo isósceles se han colocado dos car­
gas puntuales de magnitudes Q = 32pC y
"-q". Determinar la magnitud de la carga
"q" tal que la intensidad de campo "E" sea
horizontal en el vértice (3).
/
/
/
/
»
( i )
SOLUCION:
+Q _ [¿ - q
(2 )
Llevamos una carga de prueba “+q0“ al
vértice (3), para determinar la dirección y
sentido de la intensidad generado por
cada carga.

536. Ei Intensidad de campo generado por
la carga "Q" ubicado en la posición
(1).
E2: Intensidad de campo generado por
¡a carga "-q" ubicado en la posición
(2).
De la condición del problema, la in­
tensidad resultante es horizontal,
entonces:
IE y = 0
E2 = Et . Cos 45°
K _g__K - 5 - ^
K- l 2~ K 2 l 2 ' 2
q = f . V 2
Reemplazando el dato, tenemos:
q =8 n
/2^|jC
(2)
' T
30®
a) 8(ac
c) 32jxC
e) Ninguna
E
(3 )
b) 16|iC
d) 64nC
*
*
*
*
*
*
*
*■
Una esferita de masa "m” y carga "q"
está suspendida de un hilo de seda del­
gado, dentro de un campo eléctrico ho­
mogéneo de intensidad ”E" las líneas de
fuerza están dirigidas hacia abajo. Se pide
determinar la tensión en el hilo.
"El signo de la carga es negativo"
PROBLEMA Ne 14
En los vertices de un triángulo rectán­
gulo se han colocado dos cargas puntu­
ales de magnitudes:
Q = +64nC y “-q" (signo negativo).
Determinar la magnitud "q", tal que la
resultante de la intensidad de campo "E"
sea vertical en el vértice (3).
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
&
*
*
*
*
#
*
SOLUCION:
Realizamos el diagrama del cuerpo libre
de la esfera. Sobre la esferita actúan su
peso W =m.g., la fuerza eléctrica F =q.E
y la tensión en la cuerda.
De la condición de equilibrio.
IF y = 0
T —q .E —m .g = 0
Luego.
qE
m
g
T = (mg + qE)
PROBLEMA Ne 16
Una esferita de peso 4N y carga
esferita
q = - 4 x 1CT5C está sujeto mediante un hilo
de seda, dentro de un campo eléctrico
homogéneo de intensidad E = 300 KN/C,
las líneas de fuerza están dirigidas hacia
abajo. Se pide determinar !a tensión en el
hilo

537. -q
a) 4N
d)9N
PROBLEMA Ne 17
b) 16N
e) Ninguna
c) 8N
Una esferita de peso 32 x 10 N y carga
16 x 10~*C está suspendida de un hilo de
seda, dentro de un campo eléctrico ho­
mogéneo de intensidad "E" como mues­
tra la figura. Sabiendo que el hilo forma un
ángulo de 45° con la vertical, determinar
iip ii
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
SOLUCION:
1. D.C.L. de la esferita de peso W y
carga "q".
De la condición de equilibrio, la su­
ma de las tres fuerzas es igual a
cero.
Del triángulo de fuerzas:
Tq 45° = — =
9 W W
Luego:
E W 32 x 1(T6 N
" q ~ l e x i o ^ c
E = 200
N
C
PROBLEMA Ne 18
Una esferita dejpeso 4 x 10 4N y carga
eléctrica q = -10 C, unida a un hilo de
seda se encuentra suspendido de un pun­
to fijo, dentro de un campo homogéneo de
intensidad "E". Sabiendo que la esferita
se encuentra en equilibrio, determinar
ii gii
a) 100 N/C
c) 300 N/C
e) Ninguna
PROBLEMA Ns 19
b) 200 N/C
d) 400 N/C
Una esferita de masa "m" y carga "q“
se lanza horizontalmente con velocidad
inicial V0, dentro de un campo homogé­
neo eléctrico de intensidad E, represen­
tado mediante líneas de fuerza verticales
hacia abajo. Hallar la aceleración de la
esferita.
v

538. Realizamos el D.C.L. de la esferita, sobre
el actúa su peso "m g." y la fuerza eléc­
trica “q.E“.
De la 2da Ley de Newton:
Fr mg+qE
0 - -
m m
mg
Luego: qE
a = g + SLÍ
m
*
*
*
*
*
*
*
*
*
*
*
*
*
"La trayectoria que describe la esfenta es
una parábola"
PROBLEMA N®20
Una esferita de masa m = 0,001 kg y
carga q = 10~5C se lanza con una veloci­
dad inicial V0 = 20 m/s formando un án­
gulo de 30°, respecto de la horizontal,
dentro de un campo homogéneo de inten­
sidad E = 1 500 N/C, representado me­
diante lineas de fuerza hacia abajo. Deter­
minar la altura máxima alcanzada por la
esferita.
g = 10m/s2
PROBLEMA N* 21
Se considera una circunferencia de ra­
dio "R", cargada uniformemente con den­
sidad lineal "D". Calcular el potencial en
el centro de curvatura.
D _ carga total q
~ longitud " 2n. R
*
*
*
*
$
*
*
é
*
*
*
*
*
Todos los puntos de la circunferencia, de
cada diferencial, de carga, equidista del
centro “0“. El potencial eléctrico es una
magnitud física escalar:
V(centro) = p (carga total)
Vo = £ . (2n. R D)

539. PROBLEMA Ne22
Se considera una semicircunferencia
*
■
ü
f
de radio "R", cargada uniformemente con J
densidad lineal "D". Calcular el potencial •«
en el centro de curvatura. *
,-1
P Caiga total q
~ longitud “ n.R
*
#
*
*
3.10
=12. 106V
El trabajo realizado por un agente ex­
terno, contra ei campo eléctrico creado
por "Q”será-
Wa -> b = q ■(Vb - Va)
Wa -» b = 6 . lO ^C . 3 . 106V
WA -^b = 18J
c) K.D.íi d) 2tc K.D
e) Ninguna
PROBLEMA N®23
En el vértice de un rectángulo se en­
cuentra una carga Q = 4.10~4C. Determinar
el trabajo realizado por un agente externo,
para trasladar una carga q = 6¡iC desde la
#
$
*
*
*
*
*
*
"El trabajo realizado contra un campo
conservativo (campo eléctrico) es inde­
pendiente del camino que se sigue Sólo
interesa el potencial inicial y final"
PROBLEMA N®24
En el vértice de un cuadrado de lado
1,2m se encuentra una carga puntual
Q = -8 x 1 0 "4C.
Determinar el trabajo realizado por un
agente externo para trasladar una carga
de prueba.
q = 1,6 x 1 0 SC, desde la posición A
hasta la posición B siguiendo la trayecto­
ria indicada en la figura.
SOLUCION:
Cálculo del potencial en los puntos A y B
Va - K . ^ 9 . 10a
4.10~
4,10,-1
*
*
sií
*
*
*
#
#
*
*
*
*
*
PROBLEMA NB25
La figura muestra un campo eléctrico
homogéneo de intensidad E = 10N/C re­
presentado mediante líneas de fuerza ver­
ticales hacia arriba.
Determinar la diferencia de potencial
eléctrico entre los puntos A y B (V a - Vb).

540. N
0,3m
0,4m
hacia la derecha. Determinar el trabajo
realizado por un agente externo para tras­
ladar una carga de prueba q = 50|iC, desde
la posición A hasta la posición B siguien­
do como trayectoria la hipotenusa del
triángulo rectángulo.
SOLUCION
r
La diferencia de potencial entre dos su- J
perficies equipotenciales, es igual al pro- é
ducto de la intensidad del campo "E" por J
la distancia "d“ entre las superficies que #
son perpendiculares a las líneas de ®
fuerza: #
(VA—Vb) = E . d ....(1) ?
0,3ni
b___ B
0,4ra
r
i
i
r
"'
►
«
¡
F
t
~
iJ
d
_.
1
C
O
1
1
*
*
Las líneas de fuerza tienen el sentido, de
mayor potencial a menor potencial eléc­
trico, entonces:
Va < VB
En (1):
- (VA- VB) = E. d.
(VA - VB) = - 10 ~ . 0,3 m.
(Va - Vb) = -3 voltios
PROBLEMA N9 26
La figura muestra un campo eléctrico
homogeneo de intensidad, E = 500 KN/C,
representado mediante líneas de fuerza
a) CERO b) -10 J
c)+10J d )-1J
e) Ninguna
PROBLEMA Ns 27
La diferencia de potencial entre los
puntos A y B es 6 voltios. Entonces la
diferencia de potencial entre las placas
del condensador es:
*
*
d • B
' ! |
d !
i ! d
A i
i
V
. . . - í
SOLUCION:
Entre las placas del condensador se es­
tablece un campo homogéneo eléctrico
"E", entonces:
(Va - VB) =E . d = 6 voltios .... (1)
La diferencia de potencial entre las pla­
cas del condensador será:
V = E(3d) = 3E . d
Reemplazando (1) en (2):
.... (2)
E

541. La diferencia de potencial entre las
placas de un condensador es 240 KV.
Determinar el trabajo realizado por un
agente externo para trasladar una
carga q =5 x 10“5C. desde el punto A hasta
la posición B, siguiendo la trayectoria
mostrada.
r
/ i
1 1
b) -8 J
e) Ninguna
c) +4 J
a) -4 J
d) +40 J
PROBLEMA N9 29
Determinar la diferencia de potencial
entre las placas de un condensador que
se encuentran separadas 50mm; entre las
cuales está suspendida una pequeña es­
fera de masa 0,2 gramos con carga.
*
*
¿
t
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
s
t*
*
*
*
*
*
*
q = +5 . 10~®C.
g = 10 m/s
De la condición
de equilibrio, la
fuerza resultan­
te es igual a ce­
ro,criterio del po­
lígono cerrado:
F
Tg37° =
mg
F = - . m . g .
/
y m
g
¿ r
V
F
/
F = ^ 2. 10“
4
kg. 10m/s =15. 1 0^ N
*
*
*
*
*
*
*
s
f*
*
*
*
*
*
S
f»
*
Reemplazando en la ecuación (1)
15x10’4N = 5 x 1 0 “eC E
E = 3 0 x 1 03 N/C ....(2)
E : intensidad del campo eléctrico ho­
mogéneo.
La diferencia de potencial entre las pla­
cas del condensador:
V = E d
V = 30 . 10'
3 N
50 x 10“3 m
V = 1 500 voltios
PROBLEMA N®30
La diferencia de potencial, entre las
armaduras de un condensador que se en­
cuentran separadas 0,1m, es igual a 3 000
voltios. Una esferita de masa 3 gramos y
carga "-q" se encuentra sujeto a una de
las placas mediante un hilo de seda. Ha­
llar "q". g = 10m/s
SOLUCION:
D.C.L. de la esfera cargas (+q):
La fuerza eléctrica "F* es igual a-
F = q .E ....(1)
F

542. a) 1|iC b) 2(iC
d) 4nC e) Ninguna
PROBLEMA N* 31
Se tiene 8 gotitas esféricas de mercu­
rio, '.guales.se cargan hasta alcanzar un
miumo potencial igual a 10 voltios. ¿Cuál
serfi el potencial de la gota grande que se
obtiene como resultado de la unión de
éstas gotitas?
SOLUCION:
Consideramos cada gotita de masa "m",
carga “q“ y radio de curvatura "a". Por
consiguiente la gota resultante tendrá
una carga neta igual a ’8q*.
Por principiode conservaciónde la masa:
masa resultante = 8 . masa de c/gota
D. Vol (grande) = 8 x D. Vol (gota)
f . b ’ - f . a ’ .e
Luego: b = 2a.
El potencial de la gota grande será:
..(1)
El potencial de la gota pequeña es:
.... (2)
Reemplazando (2) en (1):
V = K < M = K .!Í9 >
b a
V(gotagrande) = 40 voltios
Se tiene 27 gotitas esféricas de mercu­
rio, iguales, se cargan hasta alcanzar un
mismo potencial igual a 5 voltios, ¿Cuál
será el potencial de la gota grande que se
obtiene como resultado de la unión de
éstas gotitas?.
a) 20 V b) 40 V c)45V
d) 135 V e) N.A.
PROBLEMA Ne 33
Un condensador de placas paralelas
de IfoF de capacidad es cargado con
8 x10 C. Este condensador se conecta a
un condensador de 3jiF descargado, se­
gún la figura. La carga que al final ad­
quiere el condensador de 3|¿F será:
■
3i)F
SOLUCION:
Al cerrar los interruptores, los condensa­
dores quedarán instalados en paralelo,
es decir estarán sometidos a la misma
diferencia de potencial "V", por consi­
guiente las cargas almacenadas por ca­
da condensador serán directamente pro­
porcional a sus capacidades.
$
*
*
*
*
♦
*

543. Por principio de conservación de las car­
gas eléctricas:
Zq (inicial) = Xq (final)
8 x lO ^C = | + q
Luego:
q = 6 . ICT^C
PROBLEMA Nc 34
Un condensador de placas paralelas
de capacidad 6|¿F es cargado con 12^0.
Este condensador se conecta a un con­
densador de capacidad 2iF descargado,
como indica la figura. La carga que al final
se adquiere el condensador de 2nF será:
2W
F
*
*
*
*
*
*
a) 3nC b) 4iC c) 6|iC
d)8nC e) N A.
PROBLEMA N® 35
En el circuito electrónico mostrado,
determinar la carga acumulada por el ca­
pacitor 3(.iF.
2l
.F
Cuando dos o más condensadores están
instalados en paralelo, las cargas acumu­
ladas son directamente proporcionales a
sus capacidades.
2wF
Hí—
2q
-íl-
3viF
H h -
4uF
Cuando dos o más condensadores están
instalados en serie, todos los condensa­
dores almacenan igual cantidad de carga
independientemente de sus capacida­
des:
*
a
*
#
*
#
«i
*
*
*
*
*
*
*
6pF
—fl—
3pF
-II—
2wF
-II-
3q 3q B 3q B
Analizando el condensador equivalente.
^TOTAL = V AB •^eq
3q = 30V . 2[iF
q = 20]iC
La carga acumulada por el capacitor 3|iF
es "3q", o sea: 60(iC.
í PROBLEMA Ns36
*
m
*
En el circuito eléctrico mostrado, de­
terminar la carga acumulada por el ca­
pacitor C = 1|iF.
C
6v
jF
5uF
H i -
4V
- .1+
*
*
*
*
a) 1pC
d)4nC
b) 2|iC
e) Ninguna
c) 3p.C

544. En el circuito eléctrico mostrado está
alimentado por una f.e.m. de voltios. De­
terminar la carga acumulada por el con­
densador de capacidad de 6^F.
3»F
SOLUCION:
1.
*
*
*
*
*
*
*
*
#
$
*
*
*
*
*
*
*
*
*
Los condensadores de capacidad
3(iF y 6 F están instalados en serie,
por consiguiente almacenan igual
cantidad de carga "q"
El circuito eléctrico mostrado es ali­
mentado por una f.e.m. de 5 voltios. De­
terminar la carga acumulada en cada pla­
ca del condensador de capacidad ^2^lF.
10 UF 40,, F
-----------II-------------------------------II- —
II
— .
IZuF
------------------------ --------- 1|-------
5 V
a) 20iC
d) 80|iC
PROBLEMA N®39
b)40|iC
e) Ninguna
c) 60(J.c
En el circuito eléctrico mostrado, de­
terminar la carga acumulada por cada
condensador. Los alambres tienen resis­
tencia despreciable.
2. Las cargas almacenadas por dos o
más condensadores instalados en
paralelo son directamente propor­
cionales a sus capacidades
8 yF 10 yF
---------- II---------- ------ " ------
4q 5q
q
II
2yV
3. Analizando el condensador equiva­
lente:
qTOTAL = Vab ■
Ceq
5q = 10V . 10nF
#
*
*
*
*
B *
*
*
*
*
m
*
♦
#
q = 20|aC
La carga acumulada por el capacitor
6p.F es: q = 20pC
luF 2wF
i i .............. n 3V|F
--------- ni
i i i i
* A
»
m
*
*
*
*
*
*
*
10V
SOLUCION:
1. Todos los puntos de un conductor
tienen igual potencial eléctrico
luF B 2UF
1
» II
3uF
11
II
— A B-—
.. A

545. Uniendo los puntos de igual poten­
cial eléctrico
luF
*
*
#
*
$
j
§
?
*
6uF
Hl-
6q
Analizando el condensador equiva­
lente
qTOTAL = V a b Ceq
6q = 10V . (6nF)
B|
#
*
*
*
*
*
*
s
*
$
#
q = 10|iC
La carga acumulada por los conden­
sadores es: 10nC ; 20nC y 30|iC.
PROBLEMA Na40
En el circuito eléctrico mostrado de­
terminar la carga acumulada por cada pla­
ca del condensador de capacidad 6|iF.
a) 10|iC
d) 40|iC
b) 20(iC
e) Ninguna
*
*
*
*
m
*
*
*
*
*
*
En el circuito eléctrico mostrado, to­
dos los condensadoras tienen igual ca­
pacidad C = 20¡iF y la f.e.m. es igual a
E = 6V.
Hallar la carga acumulada en cada pla­
ca del condensador que se encuentra en­
tre los puntos A y B.
*
*
*
c) 30(iC I
H
f
SOLUCION
Los alambres de conexión constituyen
superficies equipotenciales, es decsr to­
dos los puntos de un mismo alambre
tienen el mismo potencial eléctrico.
El punto "A" tiene el mismo potencial del
borne negativo y el punto "B“ tiene igual
potencial que el borne positivo de la
f.e.m.
Vb - Va = E = 6 voltios .... (1)
Analizando el capacitor “C” ubicado entre
los puntos A y B
q = (Vb - Va) . c
q = 6 v . 20nF
.... (2)
q = 120 n coulomb
q : carga acumulada en cada placa del
condensador.

546. ELECTRODINAMICA
PROBLEMA NB01
En el circuito eiectrico mostrado todas
las resistencias son iguales a "R“. Si la
llave "S" está abierta, la resistencia equi­
valente entre los puntos A y B es igual 11
Ohmios. Determinarla resistencia equiva­
lente entre A y B cuando "S" está cerrado.
SOLUCION:
Cuando la llave ”S” está abierta, las tres
resistencias de la derecha están ins­
taladas en serie.
Req = R + + R
4R
11
Req = — R = 11
4
Luego: R = 4Í2 (1)
Cuando la llave "S" está cerrada, se pro­
duce "corto circuito” para dos resisten­
cias del extremo superior derecho.
R e q = R + | + R = | R
de (1): Req=10Q
PROBLEMA Ne02
En el circuito mostrado todas las re­
sistencias son iguales a R. Si la llave "S"
está abierta, la resistencia equivalente en­
tre los puntos X e Y es igual a 13 ohmios.
Determinar la resistencia equivalente en­
tre X e Y cuando "S" está cerrado.
*
*
*
#
*
#
*
*
*
#
*
*
#
*
*
A
*
*
*
•o
#
*
*
*
*
*
*
*
*
*
*
*
*
«X
*
*
*
*
*
*
*
*
*
d
*
a) 1311 b) 15íí
c) 26Í1 d) 39íl
PROBLEMA Nfi 03
En el circuito eléctrico mostrado todas
las resistencias son iguales a "R”. Si la
llave "S" está abierta, la resistencia equi­
valente entre los puntos A y B es igual a
9 ohmios. Determinar la resistencia equi­
valente, cuando “S" está cerrado, entre A
VB-
SOLUCION:
Cálculo de la resistencia equivalente en­
tre A y B, cuando la llave "S“ está abierta.
Req= R+f + R=^T
Del dato:
Luego: R = 4ú
Cuando la llave “S" está cerrado, se pro­
duce “corto circuito'' para cuatro resisten­
cias, por consiguiente el sistema se re­
duce a:

547. Req = 2R
de(1):
Req = 8 íi
PROBLEMA Ne 04
En el circuito eléctrico mostrado, si las
llaves Si y S2 están abiertas, la resistencia
equivalente entre los puntos A y B es igual
a 33 ohmios. Determinar la resistencia
equivalente entre A y B cuando las llaves
Si y S¿ están cerradas.
s,
2R 6R
. . - ^
3R
a) 1Q b) 2 íi
c) 3 íl d) 4Í2
PROBLEMA Ne 05
Un conductor delgado de 20cm de
largo está sometido por sus extremos a
una diferencia de potencial de 40 voltios,
¿Qué diferencia de potencial existe entre
dos puntos M y N del alambre separados
una distancia de 5 cm?
SOLUCION.
De la Ley de Poulliet, la resistencia de los
segmentos AB y MR de un mismo alam­
bre, son directamente proporcionales a
sus longitudes y la corriente que circula
por ellos es la misma.
M, iN
*
*
*
*
*
*
#
4t
*
*
#
*
*
*
*
*
*
*
st¡
*
B l
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
&
*
*
*
*
#
*
*
h
Ley de Ohm
Vab Vmm
5cm
I =
V m n = V ab
Vmn = 40V
Luego:
Rab Rmn
Rmn
Rab
5 cm
= constante
20 cm
Vmn = 10 voltios
PROBLEMA NB06
Si un alambre uniforme de 20cm. de
longitud y de elevada resistencia se co­
necta a una batería de 30 voltios.
¿Cuál es la diferencia de potencial en­
tre los puntos M y N que distan respecti­
vamente, 3cm y 15cm de un extremo?.
a) 10V b) 12V
c) 15V d) 18V
PROBLEMA Nfi 07
En el circuito eléctrico mostrado, la
f.e.m. tiene resistencia interna desprecia­
ble. Hallar la intensidad de corriente "I"
que atraviesa la resistencia de 3 ohmios,
ubicada entre los puntos A y B.
ft

548. Todos ¡os puntos de un mismo alambre
de conexión forman una línea equipoten­
cial. Por consiguiente la diferencia de po­
te n cia l entre los e xtrem os de la
resistencia "3£2“ es:
(V b - V a ) = 1 2 v o ltio s - (1)
Aplicando ia ley de Ohm a la resistencia:
(VB- VA) = I . R
Reemplazando 12V = I . (3Q)
Luego:
I = 4 ampere
PROBLEMA N808
En el circuito eléctrico mostrado, la
f.e.m. tiene resistencia interna desprecia­
ble. Determinar la lectura en el amperí­
metro ideal "K".
2£
}
4« |
3«
70
15V
5n
a) 1 A b) 2 A
c ) 3 A d) 4 A
PROBLEMA N809
En un cable de transm isión de energía
eléctrica existe una caída de potencial
igual 12,5 voltios al paso de una corriente
de intensidad 3 0 0 ampere. ¿En qué canti­
dad de calor se ha disipado la energía
perdida durante 1 minuto?
SOLUCION:
De la Ley de Joule - Lenz
Q = V . i . t ....(S.l.)
Q = (12,5) (300) (60)
*
*
*
*
*
*
m
»
*
#
*
m
#
*
*
*
«
*
#
*
«
ta
*
*
*
*
*
*
*
$
*
*
*
*
*
*
«
*
*
*
#
#
*
*
*
*
*
*
*
K
*
*
*
Q = 5 4 Kcal (2)
PROBLEMA Nfi 10
Por una resistencia de cobre de 20
ohmios pasa una corriente de intensidad
5 ampere. Determinar la cantidad de calor
disipado en 30 segundos.
a) 10 KJ b) 12 KJ
c) 15 KJ d) 20 KJ
PROBLEMA N9 11
Calcular el costo de funcionamiento
de una lámpara que durante 24 horas está
conectada a una línea de 100 voltios y
absorve una corriente de un ampere. Sa­
biendo que el precio de cada kilowatt-
hora es 0,02 dólar ($).
SOLUCION:
Cálculode lapotenciaeléctricade lalámpara
p = V . i = 100x1 =100 watt
P = 0,1 KW ....(1)
La energía consumida:
W = P . t = (0,1 KW) (24h)
W = 2,4 KW-h
Costo: (2,4) (0,02 dólar)
PROBLEMA N« 12
Calcular el costo de funcionamiento
de una refrigeradora que durante 24 horas
está conectada a una línea (tomacorrien-
te) de 220 voltios y absorve una corriente
de intensidad 0,5 ampere. El costo de
cada kilowatt-hora es 100 soles (S/..)
a) s/.132
c ) s/.264
b) s/.200
d) s/.300
PROBLEMA NB13
En el circuito eléctrico mostrada las
resistencias x = 10Q, y = 30Q, z = 60í¿,
disipan las siguientes potencias: 90W,
120W, y 60W respectivamente. Si la f.e.m.
de la fuente de energía es t = 90v, hallar
la intensidad "i" de entrega la
fuente "e" al circuito.

549. SOLUCION:
La potencia eléctrica es una magnitud
física escalar, por consiguiente la poten­
cia que entrega la fuente de energía, es
igual a la suma aritmética de las poten­
cias parciales disipadas por cada resis­
tencia.
Pn
eta=P(x)+P(y)+P(z)
P
neta= 90W + 120 W + 60W
Pneta = 270 W
Cálculo de la corriente “i" entregada por
la f.e m.
Pneta = i2 . Req
Pero: Req = x +
.... (1)
(y+z)
= 10 + 20
=300
En (1) 270W = i2 . (300)
i = 3,0 A
*
*
*
*
*
*
*
*
»
m
*
*
*
&
m
*
*
*
*
m
*
Otro modo:
Pneta=£ . i
270W = 90V . i
i = 3,0 A
PROBLEMA N® 14
Cuando en una casa se tiene funcio­
nando una tostadora de 1 200W, un foco
de 120 W y una placa de 600W, el fusible
se "quema" tan pronto como se enciende
otro foco de potencia 60W ¿Cuál es apro­
ximadamente el amperaje del fusible de la
línea?.
Considere que la tensión (d.d.p) en los
tomacorrientes es de 220 voltios.
c) 9,0 A d) 9,8 A
PROBLEMA N® 15
Se tiene dos cocinas eléctricas (1) y (2)
cuyas resistencias se encuentran insta­
lados como indica la figura, en serie y en
paralelo respectivamente. Ambas coci­
nas se conectan a una fuente de 220 vol­
tios. Si la cocina (1) hace hervir el agua en
9 min. ¿En cuánto tiempo hará hervir la
misma cantidad de agua la cocina (2)?
*
#
♦
m
m
m
*
m
m
*
*
*
*
*
*
*
*
*
m
*
*
*
*
m
m
*
*
*
#
*
*
*
*
*
*
Primero encontramos la resistencia equi­
valente del hornillo eléctrico para cada
variante de las conexiones.
Ri = 3R y F¡2 = .... (1)
En los dos casos, el agua en la tetera
necesita igual cantidad de calor para
hervir.
De la Ley Joule - Lenz:
Qi = Q2
V2 V2
F V tl = R Í t2
.... (2)
Reemplazamos (1) en (2):
t 2 = !
Luego:
t2 = 1 min.

550. Se tiene dos cocinas eléctricas (1) y (2)
de resistencias instaladas como indica la
figura. Ambas cocinas se conectan aúna
fuente de 220 voltios. Si la cocina (1) hace
hervir el agua, en 18 minutos. ¿En cuánto
tiempo hará hervir la misma cantidad de
agua la cocina (2)?
#
#
*
K
¡
*
*
a) 1 min.
c) 4 min.
PROBLEMA Ns 17
b) 2 min.
d) 8 min.
Se tiene un hornillo de resisten­
cia R=50, por el cual circula una com ente
de 10 ampere. ¿En cuánto tiempo se po­
drá calentar 240cm3 de agua de 20°C
hasta 70°C? ■
SOLUCION:
■1. En 240cm3 de agua se tiene una
masa de 240 gramos. La cantidad
de calor para incrementar la tem­
peratura en 50°C, será:
Q = m . C e . Al .... (c.g.s.)
Q = 240g. 1 — . 50°C
g°c
Q = 12 000 calorías x
1J
0,24 Ca!
Q = 5 x 104 J ....(1)
El calor absorbido por el agua es
igual al calor disipado por la resis­
tencia, de la ley de Joule - Lenz.
Tenemos:
Q = r . R . t ... (S.l.)
t = 100 segundos
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
PROBLEMA Ns 18
Se tiene un hornillo de resistencia
R = 200, conectado a una fuente de ener­
gía igual a 100 voltios. Si la masa de un
bloque de hielo es 240 gramos, inicial­
mente a 0°C. ¿En cuánto tiempo se podrá
obtener 240 gramos de agua a 100°C?
1J = 0,24 cal
a) 2 min. b) 3 min.
c) 4 min. d) 6 min.
PROBLEMA N9 19
En la figura se muestra una batería de
120v de f.e.m., cuya resistencia interna es
r = 100. Sabiendo que "R" es la resisten­
cia del calentador y el amperímetro "K"
indica 2 ampere.
¿Cuánto tiempo tarda en hervir 0,24
litros de agua en el calentador, siendo la
temperatura inicial a 10°C?. El rendimien­
to del calentador es 100%.
#
*
#
*
*
*
m
*
#r
*
*
*
SOLUCION:
Cálculo de la resistencia “R" del calen­
tador. 2da. Ley de Kirchhoff:
I£ = i . Req
120 = i . (r + R)

551. Cantidad de calor para incrementar la
temperatura en 90°C.
Q = m . C e . At . . . (c.g.s.)
Q = 240 g x 1 x 90°C
9- C
Q = 21 600 cal = 21 !0;0 J
0,24
Q = 90 KJ.
Cantidad de calor disipado por el calen­
tador, es igual al calor ganado por el agua
para hervir.
De la Ley Joule - Lenz
Q = r x R x t , (S.l.)
90 . 10 = 4 x 50 x t
Luego: t = 450 segundos
t = 7,5 min
PROBLEMA N920
Resolver el problema anterior consi­
derando que el rendimiento del calenta­
dor es el 75%.
a) 10 min. b) 12 min.
c) 15 min. d) 18 min.
PROBLEMA N921
Una batería tiene una fuerza electro­
motriz (f.e.m.) de 6 voltios y resistencia
interior de 0,6 ohm. y proporciona una
corriente de 0,5 ampere. El voltaje (d.d.p.)
entre los bornes a y b es:
- -
6
h , »
V
¿ ~
V
1+
J
SOLUCION:
Teorema de la trayectoria:
Vb + 6V —i. r = Va
*
*
$
*
m
s
ü
*
m
*
(Va - Vb) = 5,7 voltios
PROBLEMA Ne22
Una batería de resistencia interna
r = 0,4Q ; proporciona una corriente de
intensidad 5 ampere. Si la diferencia de
potencial entre los bornes "a" y "b “ es 10
voltios (Va - Vb = 10V), determinar la
f.e.m. "e".
r
fa 1
r
D * 1 ■ - - - f
V
+
y
a) 11 V b) 12 V c) 13 V
d )1 4 V e) Ninguna
PROBLEMA Ne23
En cierto circuito se tiene la sección
AB, mostrada en la figura. Sabiendo que
la diferencia de potencial entre los puntos
A y B es de 10 voltios
(Va > VB)
Hallar la tensión en los extremos de la
resistencia R = 5 ohm y la corriente que
circula por él.
SOLUCION:
La corriente "i" circula en el sentido de
m ayor (A) a m enor (B) potencial.
Teorema de la trayectoria:
Va +20 - i . R + 30 = VB
(Va - Vb) + 50 = i x R
Del dato:

552. Entonces:
1 = 12 ampere - ( 1 )
Aplicando la ley de Ohm, a la resistencia
R:
V = I. R
V = (12A). (50)
V = 60 voltios (2)
PROBLEMA N*24
En cierto circuito se tiene la sección
AB, mostrada en la figura. El amperímetro
ideal "K" indica una lectura de 5 ampere.
Determinar la diferencia de potencial en­
tre los puntos A y B, (Va - Vb). Considere:
VA > Vb
a) 25 V
c) 15 V
b) 20 V
d) CERO
PROBLEMA N° 25
En cierto circuito se tiene la sección
AB, mostrada en la figura. Sabiendo que
la diferencia de potencial entre los puntos
A y B es 20 voltios (Va - Vb = 20V), deter­
minar la potencia disipada por la resisten­
cia R = 60.
18V
■ J -
ev
H-
SOLUCION:
La corriente “I" circula en el sentido de
mayor (A) a menor (B) potencial eléctrico.
Teorema de la trayectoria:
Va + 1 8 V -I. R -8 V = Vb
(VA- V B) + 10V = ¡LR
♦
*
*
*
#
m
m
*
*
«
¡¡
*
*
*
*
*
*
*
m
<
¡
e
*
*
4»
*
*
*
*
*
*
*
*
*
#
»
*
*
*
s
H
*
*
S
ü
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
#
%
*
*
*
*
*
Del dato: 2 0 + 1 0 = 1 . (6)
Luego: I = 5 ampere ... (1)
Cálculo de la potencia eléctrica
P = I2 . R = 25A2 . (60)
P = 150 watt
PROBLEMA N» 26
En cierto circuito se tiene la sección
AB, mostrada en la figura. La corriente
que circula por el tramo AB es igual a 6
ampere además se sabe que:
(Va - Vb) = 10 voltios.
Determinar la potencia disipada por la
resistencia "R “
2 4 V 4V
I I
0
I I
a) 180 W b) 160 W
c) 140 W d) 120 W
PROBLEMA Ne27
La figura muestra un tramo de un cir­
cuito eléctrico. Si, por la resistencia de
"3R" atraviesa una corriente de intensi­
dad 2 ampere, determinar la potencia disi­
pada por la resistencia de magnitud 100.
SOLUCION:
Las resistencia: 2R, 6R y 3R se encuen­
tran instaladas en paralelo, por con­
siguiente la comente "I" que ingresa por
el borne “A" se reparte inversamente pro­
porcional a la magnitud de cada resisten­
cia.

553. ( V a - Ve) =i i(3R) =i2. (6R) =/3. (2R)
Resolviendo:
h = 2 ampere (dato)
iz = 1 ampere
/3 = 3 ampere
lera Ley de Kirchhoff (Ley de nudos).
I = i 1 + í 2 + í 3
1=
=6 ampere
La potencia disipada por la resistencia de
10íiserá:
I2 . R
P = 36 x 10 watt
P = 360 W
PROBLEMA H- 28
La figura muestra un tramo de un cir­
cuito eléctrico. Si el amperímetro ideal
"K" indica una lectura de 10 ampere, de­
terminar la potencia disipada por la resis­
tencia de magnitud 2 ohmios.
♦
*
*
*
*
#
*
*
w
*
*
*
*
*
*
*
*
*
#
*
$
*
*
m
*
*
m
*
*
*
*
*
*
*
*
*
*
#
m
*
*
*
*
b) 1 038 W
d) 1 058 W
En el circuito eléctrico mostrado, hallar
intensidad de corriente que fluye por a
resistencia d ” 7W ", sabiendo que el am­
perímetro ideal ” K“ indica una lectura de 6
ampere.
SOLUCION:
Las resistencias de 2£i y 4 íi están conec­
tadas en paralelo por consiguiente las
corrientes que circulan por ellas son 6A y
3A respectivamente. Entonces de la 1ra.
Ley de Kirchhoff por la resistencia de 1í2
circula una corriente de 9A.
V m - 9 x 1 - 3 x 4 = V n
V m - V n = 21 v o lt io s - (1)
Ley de Ohm, entre los extremos de la
resistencia de 7Í2:
( V m - V n ) = / x R
21V = I x 7Q
Luego
I = 3 ampere
PROBLEMA N®30
En el circuito eléctrico mostrado, el
amperímetro ideal “K" indica una lectura
de 1 ampere. Determinar la potencia disi­
pada por la resistencia de magnitud 5
ohmios.

554. a) 57,8 W
c) 62,8 W
PROBLEMA N» 31
La caída de tensión en la resistencia
"3R" es 15 voltios. Determinar la caída de
tensión en la resistencia "6R“.
SOLUCION:
Las resistencias R y 3R están instaladas
en paralelo, por consiguiente las corrien­
tes que circulan por ellas serán 31 e I
respectivamente. Por lo tanto, a través de
ia resistencia "6R" circulará una corriente
igual a la suma ' 41
Vba = i • r
15V = I . (3R)
5V = I. R
Aplicando la ley de Ohm a la resistencia
"6R"
Vcb = i r
Vcb =(4I).(6R) = 24 . 1. R
Reemplazando de (1) tenemos:
V c b = 24(5V) = 120 voltios.
De ia condición del problema; y la ley de
Ohm; Resistencia n
3R"
*
*
*
*
«
x
*
S
M
*
+
*
*
*
*
*
*
«
H
*
*
*
*
*
*
*
*
*
*
*
*
m
«
¡
»
m
*
*
*
*
*
#
*
*
»
*
*
*
*
♦
*
*
*
*
*
*
PROBLEMA N9 32 •
La caída de tensión en la resistencia
"R “ es 0,5 voltios. Determinar la caída de
tensión en la resistencia "8R".
8R
2R
5
i
- l
a) 2 V b) 3 V
c) 4 V d) 6 V
PROBLEMA N®33
En el circuito mostrado, determinar la
lectura en el amperímetro ideal “k". Las
resistencias internas de las fuentes de
energfa son despreciables.

555. De la segunda ley de Kirchhoff, su­
ma algebraica de las f.e.m. (s), el
signo de la f.e.m. se consigue del
siguiente modo: Si la corriente se
desplaza del borne negativo (-) al
borne positivo (+), gana un potencial
"+e' en caso contrario pierde "-e".
12V 4V
Para un circuito simple (una sola corrien­
te) se cumple que:
I£ = / Req
(12 - 4 —2)V = /. (2 + 3 + 1)Í2
6V = / . (60)
Luego:
i - 1,0 ampere
PROBLEMA N®34
En el circuito eléctrico mostrado en el
amperímetro ideal "K" indica una lectura
de 0,8 ampere. Determinar la fuerza elec­
tromotriz V , de resistencia interna des­
preciable.
r 6V
2fí I
*
*
&
í
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
«
t*
*
*
*
*
$
*
*
*
*
$
*
*
*
*
*
*
*
s¡*
*
*
*
*
.m
*
*
*
m
*
*
*
*
«
¡*
*
*
*
En el circuito eléctrico mostrado, ha­
llar la magnitud de la f.e.m. V , sabiendo
que el amperímetro ideal "K “ indica una
lectura de 2 ampere.
Desprecie la resistencia interna de la
fuente de energía.
SOLUCION:
Las resistencias de 3Í2 y Gil están ins­
taladas en paralelo, por consiguiente las
corrientes que atraviesan sobre ellos son
inversamente proporcionales a sus resis­
tencias.
81
--------
r *
«! ■
¿
2 6
fi
(VA - V B) = / 1 . ( 6 í l ) = / 2 (3Q)
Resolviendo.
í = 2 ampere (dato)
i 2= 4 ampere
2da. Ley de Kirchhoff, en la malla
&BCDA:
= I¿ . r
Existe una sola f.e.m

556. De la primera ley de Kirchhoff (nudo B)
I = it + i2 = 6 ampere
Reemplazando en (1):
£ = 60 V
PROBLEMA N* 36
En el circuito eléctrico mostrado, el
amperímetro ideal "k" indica una lectura
de 5 ampere. Determinar la f.e.m., ”e".
Desprecie la resistencia interna de las
fuentes de energía.
a) 10 V
c) 30 V
PROBLEMA Ne 37
b) 20 V
d) 40 V
En el circ u ito e lé ctrico m ostrado,
cuando la llave "S" se encuentra en la
posición (1) el amperímetro ideal “K" in­
dica una lectura de 0,4 ampere y cuando
se encuentra en la posición (2) indica 1,8
ampere. Hallar la f.e.m., "e". Las resisten­
cias internas de las fuentes de energía
son despreciables
*
*
*
*
*
*
*
*
m
*
*
*
*
4
*
*
*
*
*
*
*
*
*
*
m
*
*
%
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*>
*
*
<
*
*
0
*
*
*
*
*
*
*
*
*
*
*
*
«i
*
*
*
*
*
SOLUCION:
Cuando la llave "S" está en la posición
(1), tenemos un circuito simple:
2da. Ley de Kirchhoff.
! £ = ! / . R
4V = (0,4 A ). R
Luego:
R =10Q ....(1)
Cuando la llave “S" esta en la posición
(2), tenemos un circuito simple con dos
fuentes de energía.
2da_ Ley de Kirchhoff:
(£ + 4V) = (1,8 A)(10íí)
Resolviendo:
£ = 14V
PROBLEMA N938
En el circ u ito eléctrico m ostrado,
cuando la llave "S" se encuentra en la
posición (1) el amperímetro ideal "K" in­
dica una lectura en el am perím etro
cuando la llave “S" pasa a la posición (2).
Desprecie las resistencias internas de las
fuentes de energía.
5n
c) 5 A d) 6 A
PROBLEMA N®39
La fuente de energía es de 12 voltios y
la resistencia interna despreciable. Calcu­
lar "R2" sabiendo que, cuando la llave "S"
está abierta el amperímetro ideal "K " in­
dica una lectura de 2 ampere y cuando "S”
está cerrado indica 3 ampere.

557. SOLUCION'
Cuando "S“ está cerrado se produce un
"corto circuito”, es decir R2 no funciona,
la d.d.p. entre sus extremos es igual a
cero.
2da. Ley de Krrcchofí:
1£ = /i . Ri
12V = 3 A Ri
Ri = 4 Í2
Cuando “S“ está abierto, R, y R2 están
instalados en serie.
2d&. Ley de Kirchhoff:
ZE = /2(Ri + R2)
12V = 2 A . (4£í + R2)
R2 = 2í í
PROBLEMA N940
En el c irc u ito e lé ctrico m ostrado,
cuando la llave "S" está cerrado el am­
perímetro ideal "K" indica una lectura de
6 ampere. Determinar la potencia disipada
por la resistencia de 8fí, cuando la llave
"S" está abierta.
*
#
*
«
fc
m
*
«
fc
*
*
0
*
*
*
*
#
*
8fi
PROBLEMA N« 41
La fuente de energía “£" tiene resisten­
cia interna despreciable. Calcular “ R" si
cuando la llave "S“ está abierta el am­
perímetro ideal “K" indica una lectura de
5 ampere y cuando "S" está cerrado in­
dica 15 ampere.
*
*
*
*
*
<
fc
*
*
*
*
*
#
*
*
*
*
s
fc
«
fc
*
*
*
*
s
fc
■
fc
#
*
«
fc
«
fc
<
fc
«
fc
m
«
fc
•i»
«
fc
•fc
SOLUCION:
Cuando "S“ está abierto, R no funciona.
2da. Ley de Kirchhoff.
£ = /i . R1
£ = 5A . 6Í1 = 30 voltios
£ = 30V ,...(1)
Cuando “S” está cerrado, las resistencias
están conectadas asociados en paraleio.
2da. Ley de Kirchhoff:
£ =¡2 Req
De (1): 30 = (15).
Resolviendo:
6 R
(6+R )
R = 3Q

558. L
MAGNETISMO
CONCEPTO.
Es parte de ía física, estudia las pro­
piedades de los imanes.
IMANES
Son cuerpos que gozan de dos propie­
dades importantes:
1o Atraen el hierro
2o Se orientan en una determinada direc­
ción en el espacio.
CLASES DE IMANES:
a) Naturales.
Son los minerales de hierro que se cono­
cen con el nombre de MAGNETITA (fesO/j).
b) Artificiales.
Son los más importantes, están constitui­
dos de acero y se pueden obtener por dife­
rente métodos, por ejemplo: por frotamiento,
por inducción, y mediante co- rrientes eléctri­
cas (electroimanes).
HISTORIA DEL MAGNETISMO NATURAL
El magnetismo o piedra imán era cono­
cida por los griegos hace ya muchos siglos
Según una leyenda, un pastor llamado Mag-
nes, fue el primero en encontrar ese mineral
con su cayado de hierro. Otra leyenda dice
que la palabra magnetita viene de Magnesia,
una región de Asia Menor, donde se encon­
traron grandes reservas de este minera!. En
el año 2 700 A.C. los chinos se servían de
toscas brújulas construidas con grandes pie­
dras alargadas de piedra imán que, libre­
mente suspendidas señalaban aproximada­
mente al norte y al sur geográfico. Hacia el
año 1 200 D.C. se empezaron a usar agujas
de acero para la navegación.
Willian Gilbert, en 1 600, escribió un libro
titulado "El Imán", en el que describe a la
Tierra como un gran imán, y lo prueba apo­
yándose en la atracción que ejerce sobre la
aguja de las brújulas. Mientras tanto, la teoría
del magnetismo evolucionó, dejó de ser un
*
*
*
»
*
#
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
«
le
*
*
*
■*
#
*
*»
%
+
«i
*
*
*
♦
*
*
•H
*
*
*
*
*
*
*
milagro y empezó a especularse sobre la
constitución y estructura interna de los ima­
nes Los imanes artificiales permanentes se
desarrollaron lentamente, desde el simple
tipo de acero al carbono, hasta el mucho más
potente de acero al tungsteno (1 900), y los
hoy utilizados (aleaciones de aluminio, ní­
quel, cobalto y hierro) producidos por primera
vez en 1940.
Los imanes de FERRITA (ferroganéti-
cos), no aparecieron hasta 1 950; a éstos se
les conoce también con el nombre de imanes
de cerámica y no tienen hierro sin combinar;
están compuestos de óxido bárico-férrico
(Ba Fei20i9).
Materiales Magnéticos y no Magnéticos
Lleva los polos, de un imán en "U" (imán
de herradura) frente a diversos materiales,
como cobre, latón, aluminio, cristal, cartón,
hierro y acero. Solamente los dos últimos
serán atraídos mientras que los restantes no
lo serán por ser no-magnéticos El hierro y el
acero (este último es una aleación de hierro
y carbón) son fuertemente magnéticos. Tam­
bién lo son el níquel y el cobalto, aunque te
resultarán más difíciles de conseguir.
Hoy sabemos que los átomos de una
sustancia magnética son ellos mismos pe­
queños imanes. (La causa de este magne­
tismo de los átomos, según veremos más
tarde, es una corriente eléctrica que circula
por cada uno de ellos). Los átomos de un
material no-magnético no poseen esta pro­
piedad.
La figura representa, en forma imagi­
naria, el interior de una sustancia magne­
tizable, en (a) desimantada y en (b) en forma
imantada. De ello se deduce que un imán es
un material magnético con sus átomos iman­
tados, o colocados en un cierto orden. Cuan­
do se pierde esta ordenación, el material
magnético deja de ser un imán.

559. a) Estructura de una sustancia magnética
cuando no está imantada.
N
b) Cuando la
imantada.
*
*
sustancia magnética esta $
Puedes comprobar lo dicho, anterior­
mente, del siguiente modo; imanta un alfiler
de acero frotándolo varias veces contra el
polo de un imán permanente siempre en una
sola dirección. Con ello se habrá producido
un alineamiento u ordenación de los imanes
elementales, y el alfiler se convierte en un
imán y atrae pequeñas partículas de hierro
por un extremo. Caliente el alfiler magneti­
zado o imantado en una llama de gas y verás
como de esa manera has conseguido que
disminuyera en ella la fuerza de imantación.
El imán resultante es mucho más débil, he­
cho que puedes explicar como consecuencia
del desorden de los imanes moleculares por
efecto de la llama.
♦
*
*
#
*
*
*
*
*
O
í
*
*
*
*
*
*
*
♦
*
*
*
*
* ■
m
*
*
*
a
*
*
1o Cuando se golpea repentinamente pro­
vocándole un desordenamiento molecu­
lar.
2o Cuando es calentado hasta alcanzar una
temperatura característica conocida con
el nombre de temperatura de CURIE.
Hierro ............... 750°C
Níquel ............... 350°C
Cobalto ............... 1 100°C
Ferrita ........... 218°C
Polos de un imán.
Se llama polos magnéticos o polos del
imán a las zonas donde se concentran los
efectos magnéticos externos del imán. Si se
suspende el imán de manera que puede
oscilar libremente, adoptará siempre la mis­
ma posición coincidiendo su eje meridiano
geográfico.
El polo que se orienta hacia el norte geo­
gráfico se llama polo norte magnético (N), y
el otro se llama polo sur magnético (S). A la
parte intermedia de le llama zona neutra.
La concentración de éstos polos en el
imán recto se hallan a una distancia de los
extremos igual a 1/12 de la longitud de¡ imán
¡
s - f f l m m . ú
- i d
Inseparabilidad de los polos:
En la figura anterior, las cabezas de las
pequeñas flechas están en los polos norte
(N) de los imanes atómicos. EL CALOR per­
turba su orientación.
Pérdida de las Propiedades Magnéticas
Un imán puede perder sus propiedades
magnéticas debido fundamentalmente a dos
razones:
*
*
*
$
#
*
*
*
*
*
*
Los polos de un imán son inseparables,
es decir si cortamos un imán en dos partes,
cada una de las porciones obtenidas consti­
tuyen un nuevo imán con sus respectivos
polos norte y sur.
Se puede seguir dividiendo un imán has­
ta llegar a las moléculas. La molécula con
polaridad magnética, se llama imán molecu­
lar.

560. LEYES DEL MAGNETISMO
Ley Cualitativa.
"Los polos magnéticos externos, del
mismo nombre se repelan y los de nombre
diferente se atraen''
Ley Cuantitativa.
“Las fuerzas desarrolladas entre polos
magnéticos son directamente proporciona­
les al producto de las intensidades de los
polos magnéticos e inversamente proporcio­
nales al cuadrado de ia distancia que los
separa”
donde:
p = K mg
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
K= H
o = i0-7 N
4 n a 2
La magnitud [Lo(n es una letra griega que
se lee 'MU”).
Se denomina constante magnética, su
valor es:
|io = 4n . K = 4n . 10‘
- 7 N . Wb
A.m
|io = 12,6. 10”7 — ó 4
m A£
Unidad de la Intensidad de Polo Magnético
Amper x metro (A.m):
m :
K
Fuerza de atracción o repulsión
magnética.
Intensidad de los polos magnéticos
o llamada masa magnética.
Distancia de separación entre polos
magnéticos externos.
Constante, su valor depende del sis­
tema de unidades.
Permeabilidad magnética, no tiene
unidades, su valor depende del me­
dio donde están situados los polos
magnéticos.
Unidades:
m F d K
S.l. A.m Newton m 1 0 - 4
A"
Constante magnética (no)
El coeficiente "K" en el sistema interna­
cional (S.l.) puede escribir, en la forma:
*
*
*
*
*
*
*
#
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
En el Sistema Internacional (S .l) se de­
fine como la masa magnética que ac­
tuando sobre otra igual en el vacio y a un
metro de distancia se repelen con una
fuerza de 10 ?N
La permeabilidad magnética en el vacío
es igual a la unidad (n = 1) y que en el aire
posee aproximadamente el mismo valor.
[masa magnética] = [A.m]
CAMPO MAGNETICO
CONCEPTO.
Es propiedad de la materia como con­
secuencia de las cargas eléctricas en mo­
vimiento. El campo magnético es el lugar
geométrico donde el imán deja sentir sus
efectos magnéticos sobre otro cuerpo que
tiene masa magnética o sobre cargas eléctri­
cas en movimiento (corriente eléctrica).
LINEAS DE FUERZA.
Son aquellas líneas geométricas que sir­
ven para representar gráficamente el campo
magnético. En el caso particular de un imán
las líneas de fuerza salen del polo norte (N)
e ingresan al polo sur (S), convensional-
mente.
F
ci

561. INTENSIDAD DEL CAMPO
- >
MAGNETICO (H)
CONCEPTO.
Es una magnitud física vectorial que sirve
para describir el campo magnético. Su valor
se define como la fuerza resultante mag­
nética que actúa por cada unidad de masa
magnética en un punto del campo magné­
tico.
La masa magnético Norte de prueba “mo"
es tan pequeña que no altera o distorsiona el
campo magnético en estudio.
El vector intensidad del campo magné­
tico tiene la misma dirección y sentido de la
fuerza resultante magnética.
fy
*
fy
m
fy
&
fy
fy
*
fy
fy
fy
*
*
fy
*
*
fy
*
*
fy
fy
fy
*
*
*
*
fy
fy
S
is
❖
*
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
fy
H = ■
m0
Donde:
M : Masa magnética Norte o Sur, crea­
dora del campo magnético en estu­
dio.
m0 : Masa magnética Norte, detectora
del campo magnético en estudio.
De la Ley Cuantitativa:
P _ K M. m0
.... (2)
Reemplazando (2) en (1) tenemos:
K M. m0
Luego:
mo
H =
K M
H d?
L ~ (3 )
La fórmula (3) expresa la intensidad del
campo magnético en función de la masa
magnética "M" creadora del campo magné­
tico.
M H d K
S.l A.m
Amper
metro
m io -7 4
A2
R epresentación de la Intensidad del
campo magnético:
La tangente geométricamente a una lí­
nea de fuerza magnética tiene la misma di­
rección del vector intensidad del campo
magnético en ese punto y además es único,
por consiguiente, las líneas de fuerza no se
cortan.

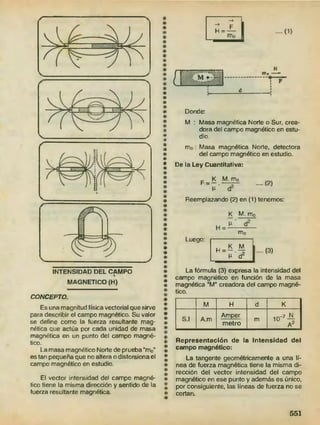
562. Hi: debido al polo Norte.
H2; debido al polo Sur
m0: masa magnética Norte de prueba.
H = H1 + H2
En el caso de un imán sus masas mag­
néticas norte y sur son iguales
M
n
orte—
M
sur=M
Par de fuerzas o cupla sobre un imán
recto en un campo magnético externo se
origina una fuerza sobre el polo norte y otra
sobre el polo sur, de igual magnitud y de
sentidos opuestos, tendiendo a alinearse con
el campo magnético uniforme externo, for­
mando una Cupla cuyo valor es igual al pro­
ducto de una de las fuerzas por la distancia
perpendicular entre las fuerzas.
Unidades
d F C
MKS mt. Newton Newton-mt
c.g.s cm. dina dina-cm
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
#
*
♦
*
*
♦
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
¡9
*
*
*
♦
*
*
♦
♦
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
1. De la definición de la intensidad del
campo magnético:
H =
M
F = M . H .... (2)
2. Reemplazando en la ecuación (1)
L = M .H d .S e n 0 .... (3)
3. Se debe observar que si 9 = 0 ° entonces
la cupla es nula
4. Analizando dimensionalmente la ecua­
ción (3), en el Sistema Internacional:
[C] = [M ]. [d] [H ]. [Sen 0 ]
N.m = A.m . m . — 1
m
1N = A .... (4)
FLUJO MAGNETICO ($)
Se define como el producto de la intensi­
dad del campo magnético H por la superficie
A perpendicular a las líneas de fuerza del
campo.
<
j>= H.A
<
¡>= número de lineas de fuerza
Si la superficie es inclinada con respecto
a las líneas de fuerza, entonces:

563. Unidades:
♦ H A
Weber ampere / metro m2
En el Sistema Internacional (S.l.) el flujo
magnético se mide en WEBER
La unidad llamada weber en honor al
físico alemán Wilhelm E Weber (1 804 -
1 891). Se abrevia Wb.
Inducción Magnética (6).
Es aquel vector que se emplea para
escribir el campo magnético. También se le
denomina densidad del flujo magnético. Su
valor se define como el número de líneas de
fuerza que perpendicularmente atraviesa la
unidad de área de una superficie situada en
el campo magnético
$
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
#
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
#
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Unidades- .
A B
S.l Weber
2
m .™
> . 1 Weber
1Tesla = -------5—
m
La unidad llamada tesla es en honor al
ingeniero norteamericano nacido en Yu-
goeslavia, Nicholas Tesla (1 856-1 94.1). Se
abrevia T
Conclusión:
1. El número de líneas de fuerza que
atravieza perpendicularmente la unidad
de área de una superficie situado en el
campo magnético será directamente pro­
porcional a la intensidad del campo mag­
nético, es decir que en el lugar donde las
líneas de fuerza se encuentran más jun­
tas la intensidad del campo será mayor y
en el lugar donde se encuentran más
separadas la intensidad del campo será
menor.
2. La inducción magnética es una magnitud
física vectorial Se representa del
siguiente modc
3. ¿En qué zona la intensidad del campo es
menor?, en la figura mostrada.
Si, 0 = O entonces las lineas de fuerza
son perpendiculares a la superficie

564. "La intensidad en la zona (a) es menor
que la intensidad del campo magnético en la
zona (b)“
PERMEABILIDAD MAGNETICA (|i)
Es una magnitud adimensional, su valor
indica el comportamiento que experimenta
una sustancia cuando se encuentra situado
dentro de un campo magnético externo. La
permeabilidad magnética indica si la sustan­
cia concentra, dispersa o simplemente no
altera el campo magnético (las líneas de
fuerza) Su valor se derine como el cociente
de la inducción magnética entre la intensidad
del campo magnético en el vacío.
B
M~ M
qH
Luego:
B = nnoH I (S.l.)
"El vector inducción magnética, tiene la
misma dirección y sentido de la intensidad
de) campo magnético"
Unidades.
Donde:
¡lo: Es una constante magnética, di­
mensional.
¡ i: Es una magnitud adimensional que
caracteriza las propiedades magné­
ticas del medio, denominada “per­
meabilidad magnética relativa del
medio". La permeabilidad V no de­
pende del sistema de unidades que
se eligen y para el vacío es igual a
la unidad
Al producto “nno" se le da a veces el
nombre de "permeabilidad Magné­
tica absoluta del medio".
* 1. Sustancia paramagnética (|i> 1):
4
*
* Son aquellas sustancias que al encon-
* trarse dentro de un campo magnético con-
| centran las líneas de fuerza débilmente o
* simplemente no lo alteran. Estas sustancias
* tienen permeabilidad magnética constante y
* ligeramente mayor o igual a la unidad.
J Ejemplo: El aluminio, el platino, el oxí-
* geno, el aire, el vacío,..
*
♦
*
*
*
+
<
¥
* 2. Sustancias diamagnéticas (|i < 1):
*
* Son aquellas sustancias que al encon-
* trarse en un campo magnético externo dis-
| persan a las líneas de fuerza, magnetizán-
i dose en sentido opuesto al campo magnético
* inductor. Estas sustancias tienen permeabili-
* dad magnética constante y menor que la
* unidad.
*
| Ejemplo: El antimonio, el bismuto, el
*
*
* 3. Sustancia ferromagnéticas (|j > 1)
| Son aquellas sustancias que al encon-
* trarse en un campo magnético externo con-
J centran a las líneas de fuerza, magnetizán-
* dose en favor al campo magnético inductor.
* Estas sustancias tienen permeabilidad mag-
* nética variable y mucho mayor que la unidad.
J Ejemplo:EI hierro,el níquel,el cobalto,...
fio H B
SI
m-7 Weber Ampere
Tesla
Ampere-metro metro

565. PROTECCION CONTRA EL
MAGNETISMO
Las materias no magnéticas, esto es, no
¡mantables, tales como el vidrio, el cobre o la
madera dejan pasar a través de ellas, con
mayor o menor facilidad las líneas de fuerza
de un imán, mientras que otros, materiales o
sustancias magnéticas, tales como el hierro
o el acero, se emplean como barreras para
impedir la penetración de las líneas de fuerza
de los campos magnéticos en un recinto
determinado.
Muchas veces se hace necesario hacer
esto último, por ejemplo, para proteger cier­
tos instrumentos muy sensibles o delicados
o desviar de ellos las líneas de fuerzas
magnéticas. El empleo del hierro o el acero
para lograr estos fines se funda en el hecho
de que las sustancias magnéticas como las
dos mencionadas, ofrecen a las líneas de
fuerza magnéticas un paso más fácil a través
de su masa que el que ofrece el aire, lo cual
facilita la concentración o canalización de
aquellas líneas. Bastará, pues, disponer al­
rededor del cuerpo o aparato que deseas
proteger, sustancias buenas conductoras de
las líneas magnéticas.
Con frecuencia, en numerosos aparatos
de medición y en los circuitos de los radios
receptores, las bobinas o carteles están dis­
puestos dentro de envolturas de hierro o
acero, que actúan como cortacircuitos, e in­
terfieren el paso de las líneas de fuerza de
campos magnéticos exteriores.
El hecho mil veces comprobado de que
una aguja imantada se oriente siempre en un
mismo sentido y hacia un determinado punto
de la Tierra, nos demuestra que nuestro pla­
neta esta rodeado por un campo magnético
como sí existiera un gigantesco imán que
pasara por su centro. Uno de los polos de
este imán, el llamado polo Norte magnético,
está localizado cerca del polo sur geográfico
(del agua dista actualmente unos 2 240km)
y el otro polo, el llamado polo Sur magnético,
está localizado en la zona del polo norte
geográfico (del cual dista también unos 2 240
Km).
La distancia que si un imán puede girar
libremente, su polo Norte se orienta y mira
siempre hacia lo que se ha designado como
polo Norte magnético. Pero también sabe­
mos que polos de nombre o signo contrarios
se atraen por consiguiente, el denominado
polo Norte magnético de la Tierra es real­
mente el polo Sur magnético. Asimismo el
denominado polo Sur magnético de la Tierra,
es realmente el polo Norte magnético
William Gilbert, médico de la reina Isabel I
de Inglaterra, sentó hacia el año 1 600 el prin­
cipio de que la Tierra era un imán. Para de­
mostrarlo tomó un imán natural, un trozo re­
dondo de magnetita, que representaba la Tie­
rra, e hizo girar a su alrededor una brujula; ésta
se conjugó exactamente del mismo modo que
lo hace una brújula cuando se traslada de un
extremo a otro de la Tierra
*
*
*
#
*
*
*
0
0
*
#
*
*
*
*
*
*
*
#
*
*
*
*
#
*
*
*
*
*
ü
s
*
*
#
*
*
*
*
*
*
m
*
+
*
*
*
*
*
ü
*
*
*
$
*
*
♦
*
«
¡í
*
#
*
*
*
*
*
*
#
*
#
*
*
*
<
Ü
Objetó protegido contra las lineas
de fuerza de un campo magnético.
Hierro dulce de elevada
permeabilidad magnética
7

566. MAGNETISMO
PROBLEMA N® 01
Un imán barra de 5N de peso, y masa
magnética en cada polo Igual a 2(A.m) se
encuentra dentro de un campo magné­
tico uniforme externo de intensidad
H = 0,5 (A/m), como indica la figura sabien­
do que el imán está atado exactamente en
sus polos calcular la tensión en los hilos
que los sostienen.
H
SOLUCION:
GTi u 2
1 De la primera condición de equili­
brio:
XFy=0 =» T, + T2 = W
Tt + T 2 = 5N ...(1)
2. De la 2da. condición de equilibrio:
LMa =0
k,W ..F ..Tz
M , + M . = M .
A A A
♦
*
+
♦
*
*
*
*
*
*
*
*
*
*
*
0
*
*
*
%
*
*
*
&
*
*
*
*
*
*u
«t
*
*
*
*
*
*
*
*
*
*
S
U
♦
*
*
*
*
*
«
K
*
*
*
*
*
«
i*
*
*
*
*
*
*
*
*
*
*
#
*
*
<
S
«i
=> W + 2F = 2 . T2 .... (2)
3. Calculo de la fuerza magnética:
F = m .H
=> F = (2 A.m) (0,5 A/m)
F = 1 N .... (3)
Reemplazando (3) en (2):
5N + 2N = 2 . T2
T2 = 3,5 N
En (1):
Ti = 1,5 N
PROBLEMA N®02
La figura muestra un imán recto de
48cm de longitud, con masa magnética en
cada polo igual a 625 (A.m). Calcular la
intensidad del campo magnético en el
punto “P".
Considere: Tg74° = 24/7
SOLUCION:
1. Analizamos el sistema equivalen­
te La distancia entre los polos
magnéticos es 5L/6 (L es la longitud
del imán recto).
2. Cálculo de la intensidad de campo
magnético producido por cada polo
magnético.

567. Donde-
m =625 (A.m), K - 10~7 N/A2
d =0,25 m , en el vacío: n =1
m0= masa magnética Norte de
prueba.
Reemplazando datos en (1) tene­
mos:
Hi = H2 = 10_i (A/m) .... (2)
3. Cálculo de la intensidad del campo
magnético resultante: de la Ley del
paralelogramo:
H 2= H ^ + H | + 2 .H i H 2.C o s (7 4 °) ..(3)
Reemplazando (2 ) en (3) tenemos:
H = 16.10 (A/m)
PROBLEMA Ne03
La figura muestra un imán recto en
equilibrio. El imán se encuentra atado me­
diante una cuerda AB desde uno de sus
polos magnéticos. La intensidad de cada
polo del imán es igual a 3 A.m y su peso
W = 24N, El sistema se encuentra dentro
de un campo magnético externo, unifor­
me y horizontal de intensidad H = 4 (A/m).
Hallar los ángulos a y 6 que definen la
posición de equilibrio.
*
*
*
*
*
*
*
*
#
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
#
*
*
*
*
*
*
$
*
*
•j?
*
*
1
2.
Del D.C.L. del imán y aplicando la
lera, condición de equilibrio se de­
duce que el ángulo " a “ es igual a
cero:
=j
> a = 0
D C.L. del imán considerado que el
ángulo "a" es igual a cero. Aplicando
la 2da. condición de equilibrio res­
pecto del punto “A".
IM a = 0
M , —M . = 0
A A
W — . Sen 9 = F.L.Cos 0
Tan 0 = VV
....(1)
3. Pero: F = m.H
=> F =(3A.m)(4A/m) =12N ..(2)
Reemplazando (2) en (1):
_. 2 (12N) ,
= “1>4Ñ~ =

568. PROBLEMA Ns 04
Un imán barra se utiliza para medir la
intensidad de un campo magnético uni­
forme. Cuando el imán atado por una
cuerda desde uno de sus polos se coloca
dentro de un campo cuya intensidad es de
Ht =80 A/m, se observa que la barra forma
un ángulo de 45° con respecto a la verti­
cal.
Si el sistema se traslada ahora a otro
campo magnético la barra forma un án­
gulo de 37^ con respecto a la vertical.
Hallar la intensidad de este últim o campo
magnético.
*
*
*
*
*
*
«
*
*
m
#
#
m
<S*
*
*
«
t*
$
*
*
*
*
♦
*
*
*
*
*
*
f
*
*
«
*
*
*
*
*
*
#
*
*
*
#
*
tu
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
»
*
*
♦
0
*
*
*
*
«
a
*
#
*
«
1. D.C.L (Sistema # 1)
2da. Condición de Equilibrio.
IM A = 0 => = M *1
A A
W.aSen45° = Fi.2a.Cos45°
W = 2Fi ....(1)
Pero: F, = m.Hi .... (2)
Reemplazando (2) en (1):
W = 2.mHi ... (3)
2. D.C.L (Sistema # 2)
2da. Condición de Equilibrio.
.,W ..Fg
8 = B
IM b = 0
o o
W.a.Sen37° = F2.2a.Cos37°

569. Pero:
F2 = m.Hz .... (5)
Reemplazando (3) y (5) en (4):
2mHi = 2.HZ
H2 = ^ . H i
H2 = 60 A/m
PROBLEMA N805
Hallar la intensidad del campo magné­
tico creado por un imán recto en los pun­
tos de la circunferencia mostrada. La
distancia de separación entre los polos
magnéticos es "2a", las masas magnéti­
cas de los polos Norte y Sur son iguales
a "m". El valor de la intensidad magnética
debe estar expresada en función del án­
gulo “0", donde:
SOLUCION:
0 °< 6 <360°
Analizando el sistema equivalente mos­
trado en la figura donde:
6 = 2 a ....(1)
Polo Norte = + m
Polo Sur = - m
Masa magnética de prueba = + m0
H2 = H1 = H 2 " (2)
*
«
H
*
*
*
*
*
*
*
*
*
&
*
$
*
*
*
*
*
%
fr
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
4
*
*
*
*
*
*
*
*
*
1
?
*
*
*
fr
*
*
*
*
*
*
*
*
fr
*
*
Además:
H2 = *
m
Reemplazando (3) en (2):
k'Z ~,2
I j2_ K .m
V . 4 2.a4'
1 1
■
+ •
Cos4cc Sen4a
--(4 )
PROBLEMA N9 06
La figura muestra un imán recto de
30cm de longitud sobre un plano horizon­
tal liso, la masa magnética en cada polo
magnético del imán es igual a 50 (A.m).
Sabiendo que el imán se encuentra dentro
de un campo magnético uniforme externo
de intensidad igual a 25 (A/m), calcular la
cupla aplicada sobre el imán en el instante
que el imán forma un ángulo de 53° con
las líneas de fuerza magnética.

570. r .... -
*
•
'A
. F
/ J
s
&
r
— -e
»
/ / 7
/ / / H
/ /y
--o-
-rj '-q
/ r r
-
*
■ (y •
F “
V J
1 Calculo de la distancia de separa­
ción entre los polos magnéticos del
imán:
d = | L | . (30cm) = 25cm
D 6
2. Calculo de la fuerza magnética apli
cada en cada polo magnético del
imán:
F = M.H
=> F = (50) A.m) (25 A/m)
Luego:
F = 1 250 N
3. Par de Fuerzas o Cupla sobre el
imán:
C = F . d . Sen53°
C = 1 250N . 0.25cm . ~
5
Luego:
C = 250 N.m
*
*
*
*
*
*
*
*
*
*
*
*
S í
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
CONCEPTO.
Es parte de la física que estudia las re­
laciones entre la corriente eléctrica y los
campos magnéticos. El magnetismo es una
manifestación de las cargas eléctricas en
movimiento.
I PARTE:
CAMPO MAGNETICO CREADO POR UNA
CORRIENTE ELECTRICA
Efecto Oersted:
La experiencia fundamental fue realizada
en 1 820 por el físico danés Hans C. Oersted
(1 7 7 0 -1 851).
"Si una aguja magnética se dispone para­
lelamente a un conductor, al hacer pasar una
comente “/" la aguja magnética gira tendi­
endo a disponerse perpendicularmente a la
corriente”
S: abierto
“Toda corriente eléctrica crea a su alrede­
dor un campo magnético''
Ladirección y sentidodelcarnpomagnético,
igual que la dirección que toma la aguja, de­
pende del sentido de la corriente

571. / i
/ r ®
— ¡i—
S
:cerra
d
o
V
PARTE: 1.1
1. Campo magnético creado
corriente rectilínea:
por una
El campo creado por una corriente rec­
tilínea está representada por líneas de fuer­
zas circulares perpendiculares al conductor
y con su centro sobre el mismo.
El sentido de las líneas de fuerza, y por
tanto el campo magnético, puede determi­
narse mediante ia regla de la manoderecha.
Regla m .d .:
Se toma el conductor con la mano dere­
cha de modo que el pulgar indique el sentido
de la corriente eléctrica, el sentido de las
líneas de tuerza estarán indicados por los
demás dedos.
Ley de: BIOT - SAVART
' La intensidad del campo magnético "H"
creado por una corriente rectilínea V inde­
finida (conductor muy largo), en un punto a
la intensidad de la corriente e inversamente
proporcional a la distancia"
*
*
*
%
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
%
*
*
<
¥
s
jc
*
♦
*
*
*
*
*
*
$
*
S
¡
>
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
(S.l.)
H i r
ampere
metro
ampere fpetro
Relación entre la inducción magnética y
la intensidad de campo
B = nnoH (S.l.)
H
-'
Ho:
permeabilidad magnética del me­
dio, no tiene unidades y su valor no
depende del sistema de unidades,
para el aire o vacio es igual a la
unidad.
Es una constante magnética dimen­
sional y se utiliza solamente en el
sistema internacional
M
O H B
S.l. Jrvin-7 Weber ampere
Tesla
‘HtXI U
ampere.m metro
Nota En los casos posteriores, vamos a
considerar p = 1, osea en el aire o
vacío se hará el estudio de los cam­
pos magnéticos.
Donde K es constante de proporcionalidad
cuyo valor depende del sistema de unidades.

572. CONDUCTOR RECTILINEO
PROBLEMA Ns 01
La figura muestra dos conductores (1)
y (2) rectilíneos e infinitamente largas con
comente I y 2L
La distancia entre ellos es de 6cm.
Encontrar la distancia a partir del conduc­
tor (1) donde el campo magnético es nulo.
21
<1*
SOLUCION-
(2)
2. Luego: H ( = H2 ..(1)
(1)-
-00
6cm
(2 )
*
#
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
4
>
*
*
*
*
*
*
*
*
1 Del gráfico, para que la intensidad
del campo magnético sea nulo las
intensidades H1 y H2 deben ser
iguales en modulo y dirección.
3 De la Ley de Biot - Savart H1 = H2.
K . —= K . 7 ~ r-
x (x+6)
1
X
Por lo tanto:
2
x+6
x = 6 c m
a la izquierda del conductor (1).
PROBLEMA NB02
La figura muestra dos conductores
rectilíneos infinitamente largos por los
cuales circula corrientes, r= 2 amper, tal
como se muestra. Los corrientes i y 2¿
respectivos tienen sentidos contrarios.
Determinar la inducción magnética en el
punto M equidistante de los conductores
sabiendo que la distancia de separación
entre ellos es 20cms.
*
<
¥
$
*
*
*
*
*
*
*
*
*
«
*
*
*
*
(¡5
1.
2.
3.
En el punto M existe una superposi­
ción de campos magnéticos crea­
dos por las corrientes 2¿- é ¿ res­
pectivamente.
Luego: B = B1 + B2
B1 : creado por V
B2 : creado por "2¿‘
Reemplazando en (1):
- (1)
B =
Uo
2 n r
S.l

573. B =
3(.toi 3x4n x 1 0 x 2 Weber
2 7tr 2n xO,1 m
B = 12 x 10 Teslas.
PROBLEMA Ns 03
En la figura se representa las seccio­
nes de dos conductores (1) y (2) rectilí­
neos uniformemente largos por las cuales
fluye corrientes eléctricas iguales a 30
amperios. Determinar la inducción mag­
nética en el punto M.
AH
/
lOcm /
/
lOcm
v
i © ------ ----------------- ------- ® *■
Sale 10c«i Entra
(1)____________________ (2)
SOLUCION
2.
En la grafica, Ci línea de fuerza
creada por el conductor (1), C2 línea
de fuerza creada por el conductor
(2), B1 y B2 son tangentes en M a C1
y C2 respectivamente
Aplicando la Ley de paralelogramo,
para la suma vectorial
*
*
*
sfs
*
*
*
%
*
*
*
*
*
*
k-
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
a
i*
*
*
B2=B^ + B^+2Bi B2 .Cos120° ...(1)
3 Pero. Bi=B2 = Ho ~
z
— (S.l.)
2itr
Donde: Bi=B2=4rc x 10
30
2ic x(0,1)
B1 = B2 = 6 x 10
.5 Weber
m
Reemplazando en (1):
B = 6 x 10 Teslas
PROBLEMA N®04
En la figura se tiene (3) tres sec­
ciones de conductores rectilíneos infini­
tamente largos recorridos por corrientes
11 = I2 = 1/2 I3. Hallar un punto sobre AC,
tal que la inducción magnética originada
por las corrientes sea cero, se sabe que:
AB = BC = 5cm.
SOLUCION:
1. Suponiendo que en el punto P la
inducción magnética resultante es
cero.
(5-x)
*
*
*
*
*
*
*
*
Ba vector hacia abajo (-), creado por
h.
Bb: vector hacia arriba (+). creado por
I2.
Be: vector hacia abajo (-), creado por
I3
:

574. 2. Luego: Bp =“Ba + Bb - Be = 0
de la condición de! proble­
ma.
=* Bb = Ba + Be .... (1)
3. Reemplazando valores en (1).
P0 I2_____Mo-li ¡Job
2tc. (5-x) 2k (x) + 2k (10-x)
I2 _ ji + b
5 - x _ x ' (1 0 -x )
de la condición: h = I2 = ~ I3
1 1 2
5 - x " x ’ (1 0 -x )
Resolviendo la ecuación tenemos
una única solución:
x = 3,3cm
Entonces la inducción magnética es
cero a 3,3cm (derecha) del punto A.
PROBLEMA N905
Por dos conductores perpendiculares
circulan corrientes ¿1 = Sampere y ¡r¿= 25
ampere, respectivamente. Determinar la
inducción magnética en el punto P (0,2 ;
0,2) en metros. Los conductores son infi­
nitamente largos.
SOLUCION:
1. En la figura:
B1: inducción magnética creado por
"¿1" representado por un vector
entrando al plano horizontal i (-).
B2‘ Inducción magnética creado por
"¿2" representado por un vector
saliendo del plano horizontal t (+).
2 Inducción magnética en el punto P:
♦
*
*
*
*
*
*
*
*
♦
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
$
*
*
*
*
*
* LEY GENERAL DE
* BIOT - SAVART
* ------- --------- -- ,
*
“La intensidad del campo magnético “H”
h creado por un segmento de conductor que
| lleva una corriente V , en un punto a la dis-
* tancia ”r“ es directamente proporcional a la
* intensidad de la corriente e inversamente
* proporcional a la distancia".
*
*
*
*
*
*
*
*
m
*
$
*
*
*
*
«
¡*
*
B = 2 x 10 5Teslas
B = - (1)
hacia hacia
arriba abajo
3 Reemplazando en (1), para el (S.l.)
Del dato:
4 x 10~7
Luego:

575. H = K (Sen a + Sen p)
Donde K es un coeficiente de proporcio­
nalidad cuyo valor depende del sistema de
unidades empleado.
(S.l.) i H = -— (Sen ct+ Sen p)
4ji r
1. Si hacemos a = 90° y p = 90°, tenemos
el caso del conductor infinitamente largo.
2. Entonces: Sen a = Sen p = 1
Reemplazando en las fórmulas tenemoo
(S.l.) u 1 *
Análogamente para la inducción mag­
nética
Un segmento de conductor MR conduce
una corriente eléctrica V .
La inducción magnética en un punto a
una distancia "r" del conductor es:
B = r ^ (Sen a +Sen P)
— , ■ ■
(S.l.)
1. Si hacemos a = 0 y p = 90°, tenemos el
caso de la corriente conducido por una
semirecta
*
♦
fr
fr
*
*
fr
fr
*
fr
fr
*
fr
$
*
*
*
fr
*
*
*
#
*
*
*
*
*
«
fr
fr
•
*
*
fr
«l
*
*
*
O
*
fr
fr
fr
*
fr
fr
*
*
*
e
*
*
*
*
*
*
*
*
fr
fr
fr
*
fr
fr
fr
*
*
*
fr
fr
por lo tanto la inducción magnética en el
extremo del conductor a una distancia V .
B =
Hob
_
4rt r
(S.l.)
2. Si hacemos a = 90° y P = 90°, entonces
tenemos el caso de la corriente V con­
ducido por un conductor infinitamente
largo.
Sen a = 1 y Sen p = 1
por lo tanto la inducción magnética a una
distancia "r" del conductor será:
B = ~ (S.L)
2k r ' '
Aplicaciones de la Ley de Biot-Savart
Teorema 1
La semirecta (conductor eléctrico que se
extiende hasta el infinito) conduce una co­
rriente eléctrica V ". La inducción magnética
producido a una distancia Y del extremo es:
B =
M
o ±_
4 n r
(S.L)
Teorema 2
Un conductor eléctrico de longitud infinito
conduce una corriente eléctrica V . La induc­
ción magnética producida a una distancia V
del conductor es

576. B_üs. _
é_ (s.l.)
2 n r ' '
Teorema 3
La intensidad del campo magnético so­
bre el eje de simetría a una distancia V de
un segmento de un conductor eléctrico que
conduce una comente V es igual a:
H -— . — Sen a (S.l.)
2 7t r '
Del mismo modo ia inducción magnética
en ese punto, se representa por un vector
que tiene la misma dirección y sentido a H, y
de magnitud:
B = . — . Sen a
2 n r
Ahora bien, si a = 90°, entonces se trata
de un conductor infinitamente largo.
*
«
e
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
La intensidad del campo magnético en el
centro de una figura geométrica regular de
"n" lados y apotema T . donde el conductor
lleva una corriente eléctrica V es igual a:
H = L
2 n
n . Sen .
r | n j
.... (1)

577. La inducción magnética en ese punto, se
representa por un vector que la misma direc­
ción y sentido de H, y de npagñitud:
B = . n . Sen
2 n r
(S .l.)... (2)
Teorema 5
La intensidad del campo magnético en el
centro de una figura geométrica regular de
“n" lados, donde la corriente "1“ ingresa por
un vértice y sale por cualquier otro vértice, es
igual a cero.
Hcentro —0
a) Triángulo equilátero:
b) Cuadrado:
*
*
*
*
*
*
*
*
%
*
*
*
8
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* -
*
*
*
*
*
*
*
Teorema 6
La intensidad dei campo magnético H en
el centro de una espira circular, donde la
corriente “I" ingresa por un punto del conduc­
tor y sale por cualquier otro punto, es igual a
cero.
Hcentro = 0
f t
Espira Circular
Ahora bien si “n" el número de lados
tiende al infinito (n —
><
*>
)entonces el polígono
regular tiende íi una circunferencia de radio
»p
íi
1. Tomando como premisa, el límite trigo­
nométrico:
.. Sen x .
Iim -------- = 1
! 2. Entonces llevando el límite la ecuación
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
H = iím
— >o
n
i
2r
Sen
(
s
) ©
y
3. Finalmente obtenemos, H para una cir­
cunferencia de radio "r"

578. Esta ultima relación es la fórmula de la
intensidad del campo magnético en el centro
de una espira circular.
La inducción magnética en el centro se
representa por un vector que tiene la misma
dirección y sentido de H, y de magnitud:
o Mo f
~ 2 '~ r
SEGMENTO CONDUCTOR
PROBLEMA NB01
Un conductor eléctrico que lleva una
corriente eléctrica V tiene la forma de un
triángulo equilátero de apotema “a". De­
terminar la intensidad del campo mag­
nético en el centro P.
*
*
*
*
*
*
*
*
*
*
*
*1
=
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
$
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
Stf
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
1 De la fórmula para polígonos regu­
lares
Hp = - — . n . Sen
2xt a I n
.... (1)
t¡
2. Para este caso particular:
n = número de lados = 3
3. Reemplazando en ia fórmula (1):
~ — , 3 x Sen 60°
2n a
Hp =
3 V3 ¿
Hp = ~ 4 íta ~ <
SX)
Se representa por un vector sabien­
do el punto P (.).
4. A nálogam ente la inducción
magnética.
Bp = H
c>Hp
Bp =
3 VSfip ¿
4n a
(S I)
PROBLEMA NB02
Hallar la inducción magnética en el
centro de una espira cuadrada cuyos la­
dos miden 1mt., sabiendo que por ella
circula una corriente de 10 amper.
Ver figura:

579. 1. De ia fórmula para polígonos regu­
lares; en el punto P:
BP= . n . Sen
f t
~ -(1)
27t a
2. Para este caso particular:
n = números de lados = 4
í * 45o
n 4
3. Reemplazando en la ecuación (1):
Bp = x 4 . Sen 45°
2n a
Bp = ^2 en (S.L) .... (2)
Tt3
Se representa por un vector salien­
do (.) del punto P
4. Reemplazando valores en (2):
(io = 4 x 1 0 -7 , 10 amperios
a = 0,5 metros
Luego
Bp = 8 ^2 x 10-6 Teslas
5 La intensidad del campo magnético
en el punto P, se puede deducir de
la ecuación (2):
en el S.l.
1
»
*
*
%
*
tk
*
s
fí
*
*
*
*
$
*
*
*
íj>
♦
*
*
*
*
*
*
*
*
*
*
#
*
*
PROBLEMA NB03
Hallar la inducción magnética en el
centro de una espira exagonai regular de
apotema “a" y por ella circula una co-
De la fórmula para polígonos regu­
lares:
Bp = -. n . Sen!—
2n a I n
.... (1)
2. Para este caso particular:
n = numero de lados = 6
h b 30°
n 6
3. Reemplazando en la fórmula (1):
BP = x 6 x Sen 30°
71
Bp =
2n a
(S.l.)
4.
Se representa por un vector salien­
do en el punto P (.).
Del mismo modo el vector intensi­
dad del campo magnético se repre­
senta por vector (.) en el punto P de
magnitud'
H p =
3 ¿
2na
(S.l.)
i PROBLEMA NB04
$
*
*
*
*
*
La figura muestra conductores infini­
tamente largos formando un ángulo recto.
Al punto o nudo P llega una corriente "2¿“
y se ramifica en partes iguales. Determi­
nar la intensidad del campo magnético en
el punto M, a la distancia "r" del punto P.

580. SOLUCION:
1.
2.
En el circuito mostrado el conductor
F ü no produce campo magnético en
el punto M, porque dicho punto se
encuentra en su linea de acción.
Por consiguiente producen campo
magnético solamente los conduc­
tores AP y PB.
Aplicando la Ley de Biot-Savart; pa­
ra el punto M
H = Hap + Hpb
H = —
**471
2¿_ J
r 4n
t/
r
H = -
4jt
3 £
r
, para el S.l.
3. Debemos recordar que la intensidad
de campo magnético creado en un
punto por una semirecta de corrien
te es la mitad de la intensidad crea
do por un conductor infinitamente
largo.
PROBLEMA Ne05
Una espira rectangular de lados a y b
conduce una corriente eléctricaV ", deter­
minar la inducción magnética en el centro
"o" de la espira.
y * B .
SOLUCION:
1 El campo magnético en el centro es
igual a la superposición de campos
creados por los cuatro lados.
B = 2(Ba + Bb) ....(1)
$
*
*
*
■
*
#
&
*
*
*
*
*
*
*
*
*
*
i
*
*
*
m
*
*
*
o
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
#
*
*
*
*
Ba = campo creado pór el conduc­
tor de lado a.
Bb = Campo creado por el conduc­
tor ile lado bf.
Ba+Bb=~~ . — Sen cx+-^ . L Sen p
2n y 271 x ’
Ba +Bb = . ¿
271
■
Sena Senft¡
y + x
De la figura en los triángulos rectángulos:
Ba+Bb—
Mo is
271
Pero: x . y =
y x " + x Vx2+ y2
ab
x + y2 ^
Va2+:b2
3. Finalmente reemplazando en la
ecuación (1):
jj0 8 i Va^+~b£
ab
Se representa por un vector sa­
liendo (-)delcentrodelaespira.
i PROBLEMA Nfi 06
*
*
*
*
*
&
*
*
*
*
6
»
S
jí
*
*
*
#
*
*
*
Un conductor infinitamente largo está
doblado formando un ángulo recto y con­
duce una corriente eléctrica" i". Determi­
nar la inducción magnética en el punto P
(a; b; o)

581. 1. En el punto P, hay superposición de
los campos creado por cada semi-
recta x e y:
Bp = Bx +By ....(1)
2. Aplicando el teorema:
B* = (Sen 90° + Sen B)
47TD
Bx = ít ~ 11 +
4nb (a2 + b2)1/z
....(2)
3. Análogamente en el eje y:
By = (Sen 90° + Sen a)
4na
Mo ¿
By ’ 4;ta | 1 + (g2+ b2)1/2
n M
e (/ ¡ i / 2 , l21/2
Bp = ----(a + b + (a + b ) )
4nab
o»
*
*
*
$
*
*
*
CAMPO MAGNETICO
CREADO POR UNA
CORRIENTE CIRCULAR
2. Campo magnético creado por una co­
rriente circular:
Toda corriente eléctrica que c irc u í por
una espira origina campos magnéticos, co­
mo iníSica el gráfico.
*
*
*
*
*
*
*
*
*
*
Las líneas de fuerza que representan el
campo magnético de una corriente circular
son cerradas pero no son circulares teniendo
el aspecto indicado en la figura.
Como puede observarse el campo mag­
nético creado por una corriente circular es
muy parecido o semejante al de un imán
recto colocado en el centro y con su línea
N - S en la dirección.
Reemplazando (2) y (3) en (1) #
tenemos: 1
*
*
*

582. De las líneas de fuerza, de modo que
podemos hablar de los polos magnéticos
de una espira.
"Campo magnético creado por un con­
junto de espiras circulares paralelas por las
cuales circula la misma corriente, unidad en
serie, cuyo eje es común”.
Campo magnético en el eje de simetría de
una espira circular:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
$
#
*
*
í
*
*
*
*
*
*
*
*
#
*
*
*
<
*
*
La intensidad del campo magnético
creado por la corriente 7 " en el punto P:
(S.l)
El punto P se encuentra en el eje de
simetría a una altura "h* del centro de la
espira.
La intensidad del campo magnético H se
representa por un vector colineal al eje de
simetría, el sentido depende del giro (horario
o antihorario) de la corriente eléctrica
Para el circuito mostrado en la figura, si
el giro de la corriente, es antihorario el vector
H es hacia arriba y si el giro es horario ei
sentido de H es hacia abajo, lo cual se puede
verificar mediante la regla de mano derecha.
CONDUCTOR CIRCULAR
PROBLEMA 1
La figura muestra dos espiras circu­
lares de radios iguales a 25 cm, están
situados sobre dos planos mutuamente
perpendiculares, ta que sus centros coinci­
den. Si las corrientes que circulan por cada
espira es Igual a v2 amperios, determinar
la intensidad del campo magnético en el
centro de estas dos espiras.
SOLUCION:
1. En el gráfico. La espira que se en­
cuentra en el plano x - y crea un
campo magnético cuya intensidad
de campo esta representado, en el
centro, por un vector en el eje "+z".
Análogamente la intensidad de
campo al centro, creado por la
espira situado en el plano x - z, está
representado por un vector en ei eje
"-y".
*
*
*
*
*
*
#
*
*
*
»
*
*
*
*
*

583. El módulo de las intensidades par­
ciales son iguales a H. La intensidad
resultante será:
Hp = H2 + H2
Pero:
H = 2 “ T e ne' ( S I)
3 Reemplazando en (1);
h r = 4
2 0,25 m
Hr = 4,0 A/m
PROBLEMA 2
Un conductor de longitud infinito con­
duce una corriente eléctrica 'V que viene
desde el infinito describe una circunferen­
cia de radio "r" y luego sigue la misma
dirección rectilínea, determinar la intensi­
dad del campo magnético en el centro de
la espira circular.
SOLUCION:
1 Un sistema equivalente al círculo
mostrado será igual a la intensidad
de campo magnético creado por la
corriente rectilínea de longitud infi­
nita, más, el campo magnético crea­
do por la espira circular sola, todo
ello por el principio de superposición
de campos.
*
*
*
S
Í?
*
*
H r = H f e .. (1) *
*
«
u
*
$
*
*
s
*í
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*■
*
*
*
*
*
*
*
*
*
*
*
*
*
3. Luego, podremos escribir la siguien­
te relación, para la intensidad en el
punto P.
H = Hreclilinea+ Hcircular
H = -i- , en el S.l
2m 2r ’
4. Finalmente:
Se representa por un vector en­
trando (x) el punto P, determinado
por la regla de la mano derecha.
PROBLEMA 3
La figura muestra dos espiras de radio
"a“ y “b" respectivamente colocados hori­
zontalmente frente p o r las que circula co­
rriente h e ¡2.
¿En qué relación deben estar las co­
rrientes, para que la intensidad del campo
magnético en el punto A sea cero?
2. Sistema equivalente:

584. 1. En el punto A existe una superposi­
ción de campos magnéticos crea­
dos por las corrientes lt e I2-
Hi: Intensidad de campo creado
por h.
H2: Intensidad de campo creado
por I2.
2. De la condición del problema:
Hi + H2 —0
Luego: H1 = H2 .... (1)
De la fórmula : (S.l)
h a2 I2 b2
2 ’ (a2+b2)3/2 2 ' (b2+a2)3/2
Finalmente:
*
*
*
#
*
*
*
*
*
*
*
CAMPO MAGNETICO CREADO
POR UN ARCO CONDUCTOR
DE CORRIENTE ELECTRICA
1. La intensidad del campo magnético
«I-I" creado por un ARCO conductor
que lleva una de corriente eléctrica
V , en el centro de curvatura "O" es
directamente proporcional a la in­
tensidad de la corriente e inversa­
mente proporcional al radio de cur­
vatura “R".
*
*
*
*
ü
>
*
*
*
*
2. Módulo:
Su valor en el sistema internacional (S I)
de unidades, es:
H - 4 n ‘ R
Para: 0 < 8 < 2 71
Donde:
0 = Angulo central, medido en radia­
nes.
R = Radio de curvatura, medido en me­
tros.
1= Intensidad de corriente eléctrica,
medido en ampere.
+
*
H R
Sistema
Internacional
amper©
metro
ampere metro

585. 3. Dirección:
El vector ■
■
itérisidad de campo magnético
l_l es perpendicular al plano donde se
encuentra contenido el arco conductor.
4. Sentido:
Se determina aplicando la regla de la
mano derecha- los dedos tienen el sen­
tido de la corriente V y el pulgar indica e!
sentido del vector, "H", intensidad de
campo magnético.
5. Análogamente, la inducción magnética "B"
creado por una corriente eléctrica V que
circula por un conductor curvilíneo de
radio de curvatura “R”, en el centro de
curvatura es igual a:
B =no ■H ...(1)
s
u
*
&
*
*
*
*
*
*
*
*
S.l
ampere
R metro
H
ampere
metro
4nx10~7 Weber
ampere x metro
B Tesla
ARCO Y SEGMENTO CONDUCTO?!
PROBLEMA 1
Determinar la intensidad del campo
magnético en el punto "o “ del circuito
mostrado en la figura que lleva una co­
rriente V , si se conocen los radios de
curvatura “a'' y "b".
Unidades en el sistema internacional
(S.l)
*
*
*
*
*
te:

586. PROBLEMA 2
Por un conductor delgado doblado se­
gún muestra ta figura fluye una corriente
eléctrica de i n t e n s i d a d e l radio de cur­
vatura es "a” de la parte curvilínea. Deter­
minar la intensidad del campo magnético
en el origen de coordenadas.
*
*
*
*
*
Pero:
SOLUCION:
La intensidad del campo magnético en el
punto "o” es igual a la suma del campo
creado por el segmento de conductor,
más, el campo creado por el arco conduc­
tor.
H = H arco (a) + H (segmento AB)
r= a-
42
.... (2)
*
*
>
1
=
*
*
*
*
*
*
*
*
*
PROBLEMA 3
Determinar la intensidad del campo
magnético en el punto “o" en el circuito
mostrado en la figura (1), considere cono­
cidos la intensidad de corriente el
radio "a" y el lado "b".

587. Reemplazando en (1):
SOLUCION:
1. En el punto “o", los segmentos con­
ductores que llevan corriente en di­
rección radial no producen campo
magnético.
2. La intensidad del campo magnético
"H“ en el punto "o” es igual a la suma
del campo creado por los segmen­
tos de conductor de longitud "b",
más, el conductor curvilíneo de ra­
dio de curvatura “a”.
Pero:
Se representa por un vector entrando al
papel por el punto "o".
PROBLEMA 4
Determinar la intensidad del campo
magnético en el punto "o “ en el circuito
mostrado en la figura (1), considere cono­
cidos la intensidad de corriente y los
radios de curvatura “a" y “b”,
H = JL +2. - L . — Sen 45°..(1)
4n a 4it b '
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
c
*
*
*
*
#
*
*
*
*
$
$
#
*
♦
*
*
*
*
*
*
♦
♦
*
*
*
+
*
*
SOLUCION:
1. El segmento de conductor que lleva
corriente en dirección radial no pro­
duce campo magnético en el punto
"o".
2. La intensidad del campo magnético
en el punto "o” es igual a la suma del
campo magnético creado por las
semirectas de conductor, más, el
campo creado por los conductores
curvilíneos
—
> —
* —
> —
»
H = H 1+ H 2+ H 3+ H 4..
. (1)

588. 4jta 4nb 8a 8b
„.(2)
Hi: Campo creado por la semirecta
de conductor (i¿)
H21 Campo creado por la semirecta
de conductor (17)
H3‘ Campo creado por el arco de con­
ductor de radio de curvatura "a"
H4: Campo creado por el arco de con­
ductor de radio de curvatura “b”.
Luego:
H = (1 i V l J_
a r b )|8 ' 4n
Serepresentaporunvectorsalíen-
dodelpapelporelpunto'V
PROBLEMA 5
En el circuito mostrado circula una
corriente eléctrica de intensidad V deter­
minar la intensidad del campo magnético
en el punto "o", considere conocido el
radio de curvatura “a" y los segmentos de
longitud "2a".
Sugerencia: Tang
SOLUCION:
— 1= -
( 2 r *
1 La intensidad del campo magnético
en el punto “o" es igual a la super­
posición de campos de
#
*
#
*
*
*
*
*
*
+
*
*
*
#
s
*
*
*
*
*
íf¡
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
+
*
#
*
*
*
*
*
*
*
*
*
*
*
♦
i
*
¡k
*
*
«
e
*
*
*
*
*
*
*
2. H =H arco (a) - H (segmento BC)
- 2 . H (segmento AB)
H ~ 2.Sen
4n a 4n 2a
[53^
2
- 2 . — . — .Sen
4n a 2
3. Luego:
VF 4Vüf
7£ —--- ---- 1
—
5 5
H - 7 - “ .[íi- V 5 ]
4jt a
S I
Se representa por un vector sa­
liendo del papel por el punto “o".
B
PROBLEMA 6
En el circuito mostrado circula una
corriente eléctrica de intensidad " l" deter­
minar la intensidad del campo magnético
en el punto "o", considere conocido los
radios de curvatura “a" y "b", los conduc­
tores en dirección de los ejes X e Y son
infinitamente largos.

589. SOLUCION:
1. El conductor que lleva corriente, en
dirección del eje X, también el seg­
mento de conductor en dirección ra­
dial, no produce campo magnético
en el punto "o".
H = H arco (a) + H arco (b) + H
(segmentos en eje Y).
u (n/2) (n/2) j _ j _
n — . ■ I . • i ■ _
- -
4 a 4 b 4ji a
. Sen 90° , en el S.l.
Luego:
*
9
?
«i
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
4
=
*
*
*
*
*
*
*
*
*
*
*
*
«
i*
*
s
is
*
*
*
*
#
*
Se representa por un vector salien­
do del papel por el punto “o”.
PROBLEMA 7
En el circuito eléctrico mostrado cir­
cula corriente eléctrica de intensidad
determinar la intensidad del campo mag­
nético en el punto "o", considere conoci­
dos los radios de curvatura a, b y c.
SOLUCION:
1. En el punto ''o”, los segmentos con­
ductores que llevan corriente en di­
rección radial no producen campo
magnético.
2. H = H arco(a) +H arco (b)+H arco (c)
71/2
47t
Luego:
H = ^ —
v ^ n /2
a 47r
i/ Tí §/
b "* 4tt ’ c
Se representa por un vector salien­
do del papel por el punto "o",
PROBLEMA 8
Err el circuito eléctrico mostrado circula
una corriente eléctrica de intensidad V de­
terminar la intensidad del campo magnético
en el punto “o", considere conocidos los ra­
dios de curvatura a y b, además la distancia
"c".
:

590. SOLUCION
1. En el punto "o", los segmentos con­
ductores que llevan corriente en la
dirección radial no producen campo
magnético.
—
> —
> —
> —
>
H= H arco (a) + H arco (b) + H
segmento de longitud (2c)
Luego-
Se representa por un vector sa­
liendo del papel por el punto "o”.
PROBLEMA 9
*
*
*
*
*
*
#
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
m
(n/2)
4n ' b
Pero: r = f (2)
Reemplazando (2) en (1):
Se representa por un vector entran­
do al papel por el punto "o".
| PROBLEMA 10
*
*
*
*
*
*
*
*
*
*
*
Por un conductor delgado doblado se­
gún muestra la figura (1) fluye una co­
rriente V . El radio de curvatura es "R" de
parte curvilínea y el ángulo central es
Hallar la intensidad del campo magnético
en el centro de curvatura "o".
1. En el punto "o", los segmentos con­
ductores que llevan corriente en di­
rección radial no producen campo
magnético.
—
> -»
2- H = 3 . H (segmento de longitud "a”)
+ H (arco conductor)
H= 3 . . - j- (Sen 45° + Sen 45°)
4n 4 '
*
*
*
En el circuito mostrado circula una
corriente eléctrica de intensidad, V , de­
terminar la intensidad del campo magnético
en el punto “o", considere conocido el radio
de curvatura “b" y los segmentos de longitud
“a
SOLUCION:

591. a - ■
tf
(1)
*
*
*
*
2. La intensidad del campo magnético
en el centro de curvatura "o” es igual
a la suma de campo creado por el
segmento AB, más, el campo
creado por el arco conductor.
—
* -» —
¥
H = H(segmento) + H(arco) ...(1)
En el S.l:
Pero: a = R . Cos a
En (2):
H' ¿ - n ' <e+2TanÍÍ|
De (1):
... O)
AC C IO N DE UN CAMPO
MAGNETICO SOBRE UNA
CORRIENTE ELECTRICA
1. Acción de un campo magnético sobre
una comente eléctrica:
La fuerza con que el campo magnético
externo actúa sobre los conductores con co­
rriente que se encuentra en él, se conoce con
el nombre de “Fuerza de Ampere".
LEY DE AMPERE
"La fuerza ”F que actúa sobre el ele­
mento de longitud m
l " de un conductor con
corriente“/ “situado en un campo magnético
uniforme, es directamente proporcional a la
intensidad de la corriente que pasa por el
conductor y el producto del elemento de lon­
gitud "l" por la inducción magnética "B" por la
función Sen 0
*
o
*
*
«
«
*
*
*
*
*
*
*
«
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Veamos el gráfico:
a) Módulo:
| F =¿ . I . B Sen 0 | d ) (S O
Unidades:
F t' i B
N ampere m
Weber ,
2 - Testa
m
b) Dirección:
La fuerza que un campo magnético ejer­
ce sobre un elemento de conductor que lleva
una corriente es perpendicular al plano de­
terminado por el campo magnético y la co­
mente.

592. c) Sentido:
Se determina aplicando la regla de la
mano derecha. Los dedos se hacen girar del
sentido de la corriente hacia el sentido del
campo magnético a través del menor ángulo
"0“, e! pulgar indica el sentido de la fuerza.
Torque sobre un espira rectangular de­
bido a un campo magnético externo:
Ver la figura (1)
1. Una espira rectangular de lado a y b lleva
una corriente V se encuentra en un cam­
po magnético externo
AB = CB = a
BC = AD = b
y
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*-
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
**!
*
*
*
*
*
3. Observamos la espira de planta: osea
desde arriba:
2. Las fuerzas que actúan sobre los lados
BC y AD son iguales en magnitud y direc­
ción pero sentidos opuestos, la suma es
nula: ______________
Fi + F2 =0 I
Las fuerzas que actúan sobre los lados
AB y DC son de igual magnitud, paralelas
y sentidos opuestos, produciendo un tor­
que sobre la espira. La magnitud del tor­
que o cupla sera.
C = F . d
C = i a B Sen 90° x b Sen 0
C = ¿a . B , b Sen 0
C = i B a b Sen 0 (SI)
Donde "0" es el ángulo que forma los
lados AD y BC con el campo magnético
o líneas de fuerza.
4. También se debe observar que los lados
AB y CD son perpendiculares a las líneas
de fuerza del campo magnético, por lo
tanto:
F = ¿ a . B Sen 90°

593. PROBLEMA 1
En el esquema mostrado, la corriente
que circula por el conductor es 2,0 am­
pere y está sometido a la acción de un
campo cuya inducción magnética es
B = 50 tesla. Hallar la fuerza magnética
neta que actúa sobre el conductor.
AC = 0,3 m
SOLUCION
CD = 0,4 m
,
A
c " ..... ,_E 0
F2
V J
Fuerza de Ampere:
F = i/. L . B. Sen 6
Fi =(2)(0,3)(50)(1) = 30N
*
*
*
♦
«
•
*
*
*
*
*
*
*
*
*
*
*
*
F2 = (2)(0,4)(50)(1) = 40N
Cálculo de la fuerza resultante:
Fr
2 2
+ F ,
Fr = 50N
* PROBLEMA 2
En el esquema mostrado la corriente
que pasa por el conductor es 5 amperes,
y está sometido a la acción de un campo
cuya inducción magnética es 0,5 Wb/m¿.
Hallar la fuerza magnética neta que actúa
sobre el conductor.
S
U
*
*
*
*
*
*
*
*
*
*
*
*
1. ARST es isósceles =» K5 =5T=2m
2 Además: Fi = F2 = F = i i B . Sen 0
(S.l)
F=5 x 2 x 0,5xSen 90°=5N ..(1)

594. Fr = V f * + f ' + 2Fi F2 Cos 74°
Ley de paralelogramo
Fr = V52+ 52+ 2 x 52 x 7/25 = 64
Fr = 8N
PROBLEMA 3
Una varilla de 60 cm. de longitud y
peso 24 x 10 N está suspendida por un
par de resortes flexibles como muestra la
figura. El sistema está dentro de un cam­
po magnético (.) saliendo. ¿Cuál es la
intensidad y dirección de la corriente, tal
que, la elongación en el resorte se du­
plique? B = 0,4 Weber/mt2
*
♦
*
<
5
*
#
*
*
*
*
*
*
4»
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
4
9
$
*
*
*
*
F = Peso
¿ ¿B Sen 6 = W
¿(0,6m)(0,4Wh/m )Sen 90°= 24.10“ ' N
¿ = 10 ampere = 1m A
La corriente de i = 1m A se des­
plaza de izquierda a derecha.
PROBLEMA 4
Un circuito rectangular ABCD cuyos
lados tienen longitud a y b, se encuentra
en un cam^o magnético homogéneo, de
inducción g y puede girar en tom o al eje
YY’, como indica la figura. En el circuito
pasa una corriente constante V . Determi­
nar el trabajo realizado por el campo mag­
nético, al girar el circuito 180°, si, ini-
ciaimente, el plano del circuito era per­
pendicular al campo magnético que esta
saliendo (.) del plano vertical.
2

595. Las fuerzas que actúan sobre los
lados BC y AD son perpendiculares
al desplazamiento de estos lados,
por eso ellas no realizan trabajo.
Las fuerzas que actúan sobre los
lados AB y CD son constantes, for­
man un ángulo recto con la dirección
del campo.
F = ¿ aB , Sen 90°
F = ¿-.aB .... (1)
4. El trabajo que buscamos será igual
al doble del producto de la fuerza F
por el desplazamiento de los lados
AB o CD en dirección de la fuerza.
Al girar el circuito 180° este des­
plazamiento es igual a "b".
W = 2F . d = 2¿aB x b
Luego:
Acción y reacción entre dos corrientes
eléctricas:
La interacción entre dos conductores que
llevan corriente se debe a que uno de ellos
un campo extemo sobre el otro y del mismo
modo el segundo conductor crea un campo
extemo sobre el primero.
*
*
*
*
*
¡
S
*
$
m
#
«i
*
*
*
*
4
»
*
*
*
*
*
*
♦
*
*
#
m
*
*
*
*
*
*
#
#
*
*
*
*
*
*
*
*
•»
*
♦
*
*
*
*
v
*
*
*
$
*
*
#
*
*
*
*
*
*
*
*
+
*
*
*
*
*
*
*
♦
*
*
1. La corriente I2 crea un campo
magnético sobre Ii
2n r
2. La fuerza F21 que ejerce el campo
magnético B2 sobre la corriente h es
igual:______________________
[~F21 = h i B2 . Sen 8 S.l |
0 - menor ángulo desde h hacia B2.
1 longitud del conductor que lleva a
h.
3. Reemplazando:
F21 = lí .1 — . Sen 90°
2itr
F21 Mo . .
T =5 i ' hl2 . .. (2)
Fuerza por cada unidad de longitud
sobre el conductor que lleva a h-
S I
4. Por consiguiente las fuerza F21 y F12
son fuerzas de acción y reacción.

596. 7,
La corriente h crea un campo mag­
nético sobre te­
-
2tí r
F12 es la fuerza que ejerce el campo
magnético B1 sobre la corriente I2,
cuya magnitud es igual:
¡ F12 = l2 . 1B1 . Sen 6 |
6 :menor ángulo desde I2 hacia Bi.
I longitud del conductor que lleva a I2.
Reemplazando:
F12 = I2 • í . . Sen 90°
2nr
.... (2)
Fuerzaporcadaunidaddelongitud
sobreelconductorquelleva8 i¿.
F12 = ■
“ . Il l2
2nr
TEOREMA
Un conductor de longitud infinito que lleva
una corriente eléctrica "í" ejerce una fuerza
magnética, sobre un segmento de conductor
de longitud "i" que lleva una corriente''^2','de
magnitud:
F = - £ - lh
2nr
S.l
$
*
s
is
$
*
•»
*
*
*
*
*
*
*
#
*
#
*
*
*
*
4
?
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
s
t»
*
*
*
*
+
*
*
*
*
*■
*
*
*
*
i
■
*
*
*
*
•fs
*
*
*
*
*
*
*
*
*
Unidades-
F Mo r l í/
N . A^./W eber
4nx10 — ------
A.m
m m ampere
"Los conductores en que las corrientes h
e I2 tienen el mismo sentido se atraen, y los
conductores en que las corrientes tienen
sentidos opuestos, se repelen entre sí".
I l ( , -
1I. I.,
F r
1
A T R A C C IÓ N REPULSIÓN
El descubrimiento de este importante fe­
nómeno se debe a 'Andrés María Ampere en
1 820. Los resultados de Ampere se puede
resumir en la siguiente Ley:
"Dos corrientes paralelas del mismo sen­
tido se atraen, pero si son de sentidos con­
trarios se repelen"
c Ho . .
F = —
— . h . I2
2rcr
(S.l)
Unidades:
F Ho r I
newton . .- -7 Weber
4n x 10 — ------
A.m
m ampere
m fitro
Físico francés (Andrés María Am­
pere)

597. La figura muestra tres conductores
(1); (2); (3) infinitamente largo, que llevan
corrientes I; 21 y 31 respectivamente. De­
terminar la fuerza resultante por cada uni­
dad de longitud, que actúa sobre el con­
ductor (3).
SOLUCION
Diagrama de Fuerzas:
F13 : (1) sobre (3)
F13: (2) sobre (3)
r ■
, 3 1
v
J
_ J
* c ^ i
p 1 2 _
2nr
Fl3 =
F23 =
Ho I
2k (2a)
H
e (2_J
)
2 ' (a)
Cálculo de la fuerza resultante:
■
(3
1
)
(31)
F r = F 23- F 13
F r = (9-ñ
4ita
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
<
¥
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
*
*
*
*
*
*
*
*
*
*
Determinar la fuerza con que actúa un
conductor recto, infinitamente largo, so­
bre un circuito en forma rectangular, si­
tuado en el plano del conductor. Se sabe
que por el conductor pasa una corriente
"I" y por el circuito pasa V . Los lados del
circuito SD y B ü tienen longitud "a“ y
paralelas al conductor. La distancia fintre
AD y el conductor es "x“.
La longitud de los lados es AB = DC =
h, las direcciones de las corrientes se
indican en la figura por medio de flechas.
SOLUCION:
1. Diagrama de fuerzas sobre la es­
pira, debido al campo magnético
creado por la corriente "I".
2. Las fuerzas que actúan sobre los
lados AB y DC son iguales en mag­
nitud y dirección pero de sentidos
opuestos, la suma es nula.

598. Fi es la fuerza con que actúa la
corriente I sobre AD es:
Fi =
Uo
2rtX
F2 es la fuerza con que actúa la
corriente I sobre BC es.
F2 =
Ho
2n (x + h)
a . Ii
3. Las fuerzas Fi y ¥2 están dirigidas a
lo largo de una recta en sentidos
opuestos siendo F1 > F2 Por lo tan­
to, el circuito se atraerá ai conductor
rectilíneo con una fuerza:
F r =Fi.F2= — . a . I
2n 4 1- - y
[x x + hj
en el S.l
¡J
FUERZA DE LORENTZ
]
3. Movimiento de las partículas cargadas en
los campos eléctricos y magnéticos:
3.1.
3.2.
El campo magnético actúa no sólo
sobre los conductores con corriente,
sino también sobre las partículas
aisladas con carga eléctrica que se
mueven en él.
La fuerza magnética "F" que actúa
sobre la carga eléctrica "q" que se
mueve en el campo magnético con
la velocidad "V", se llama Tuerza de
Lorentz".
_ ^= q ^ v ^ E ^ S e i^e J | .. . (1)
3.3. El módulo, de ia fuerza magnética,
expresada en (1 ), tiene las siguien­
tes unidades en el sistema interna­
cional.
F q V B
Newton Coulomb
m
s
Weber _ .
----- 5—= Testa
m
*
*
*
o
♦
*
*
*
*
*
*
xt
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
«
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
♦
*
♦
■
*
$
La dirección; de la fuerza magné­
tica sobre la carga eléctrica positiva
"q" es perpendicular al plano deter­
minado por el campo magnético y la
velocidad de la carga eléctrica.
3.5 Ei sentido, de la fuerza magnética
se determina aplicando la regla de
la mano derecha. Los dedos se ha­
cen girar del sentido de la velocidad
hacia el sentido del campo mag­
nético a través del menor ángulo "6”,
el pulgar indica el sentido de la fuer­
za magnética.
3.6. Si la carga eléctrica en movimiento
tiene carga negativa q“ se pro
cede del mismo modo, pero la fuer
za magnética tendrá sentido opues
to.
3.7 La fuerza de Lorentz está siempre
dirigida perpendicularmente a la ve­
locidad de traslación de la partícula
cargada y le comunica a esta una
aceleración normal o centrípeta.
Como no hace que varíe el módulo
de la velocidad, sino que solo cam­
bia su dirección, la fuerza de Lorentz

599. no realiza trabajo y la energía ci­
nética de la partícula cargada, no
varía, al moverse en un campo mag­
nético
3.8. En la figura (3), el campo magnético
se representa mediante líneas de
fuerza entrando perpendicularmen­
te al papel, representado por (x).
PROBLEMA 1
La fuerza (1), muestra un péndulo de
longitud "L", masa “m" y carga “q", que
se abandona en la posición indicada. El
campo magnético el indicado mediante
puntos (.). Hallar la tensión en. la cuerda
cuando pasa la masa pendular por su
posición más baja, como muestra la fi­
gura (2). Considere conocidos: m, h, h, L,
q* B,
*
*
*
*
*
*
*
*
*
«
*
*
m
*
*
*
*
*
*
a
*
*
*
*
*
*
*
*
*
*
*
*
*
0
é
*
*
*
*
*
*
«
*
*
*
*
O
*
*
4
*
«
*
»
$
*
*
+
*
*
*
*
*
*
*
*
*
*
*
*
*■
*
*
SOLUCION:
1.
2.
3
La fuerza magnética F” es perpen­
dicular al movimiento, es colineal
con la tensión en la cuerda en todo
instante, no realiza trabajo mecá­
nico
La fuerza "F" que actúa sobre la
carga eléctrica "q" en movimiento es
debido al campo magnético externo
“B".
F = q V B . Sen 90° ..
r ........ 1
1
A
f
Ji l _ ^ v
M ,1*8
■
S
4.
Por principio de conservación de la
energía mecánica de la figura (2).
EM (1) = EM (2)
Luego:
mgh = 1 m . V2 = 2gh .(2)
V Velocidad de la partícula cuando
pasa por su posición más baja.
Dinámica circular, en la posición (2).
El D.C.L del péndulo muestra la fi­
gura (3).
XF (radianes) = m . ac
T - m g - F = m . — .... (3)
5 Reemplazando (1) y (2) en (3):
T - mg - g. v. B = m . ^ .... (3)
Finalmente:
T = mg + q. B. !2gh + 2mg —

600. La figura muestra un péndulo de longi­
tud “L", masa "m “ y carga ,‘+q,,. se aban­
dona en la posición indicada. El campo
magnético "B " está representado por lí­
neas de fuerza saliendo del papel (.) indi­
cado mediante puntos. El campo eléctrico
"E" está representado por líneas de fuerza
verticales hacia abajo. Hallar la tensión en
la cuerda la masa pendular pasa por su
posición más baja, sabiendo que en ese
instante su velocidad máxima es “V”.
0 ):
E
! B
SOLUCION:
La fuerza magnética "Fm“ es perpendicu­
lar al movimiento, colineal con la tensión
en la cuerda en todo instante, por con­
siguiente no realiza trabajo mecánico.
Fm = q . V . B . Sen 90° ....(1)
Diagrama de cuerpo libre, en la posición
más baja.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
«
fc
*
*
*
*
*
*
El peso "mg" y la fuerza eléctrica:
Fe = q . E, realiza trabajo mecánico.
Dinámica circular:
Fc = m . ac
V2
(T - mg - Fm- Fe) = m . — ....(2)
Principio de conservación de la energía
mecánica:
EM (1) = EM (2)
Ep (1) + Ek (1) = Ep(2) + Ek(2)
mgL + qEL + 0 = 0 + ^ m V2
m.V2 =2mgL + 2qEL .... (3)
Reemplazando (1) y (3) en (2):
T - mg - qVB - qE =2mg + 2qE
.-. T = 3mg+q. V. B+3q. E
CAMPO MAGNETICO
CREADO POR UNA CARGA
ELECTRICA EN MOVIMIENTO
4. Campo magnético creado por una car­
ga eléctrica en movimiento:
1. Una carga eléctrica "q" moviéndose
en un medio homogéneo iluminado
con la velocidad V, crea un campo
magnético cuya inducción B, se cal­
cula por la fórmula.
S.l
2.

601. La dirección y sentido del campo
—
»
magnético B se determina aplican­
do la regla de la mano derecha:
Los dedos se hacen girar del sentido
de la velocidad hacia el sentido del
—
>
vector posición (r), el pulgar indica
el sentido del vector inducción mag­
nético.
Se considera en la fórmula el signo
de la carga
4.
En este caso la carga (-q) crea un
campo magnético entrando, opues­
to cuando la carga es (+q)
Debe observarse que la posición del
campo magnético calculado esta
determinado por el vector posición
—
>
(0­
5. Carga eléctrica positiva. Inducción
en el punto A
Ver gráfico.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Una carga eléctrica (+q) se desplaza en
un plano horizontal con una velocidad angu­
lar "co" describiendo una circunferencia de
radio “r".
Determinar el vector inducción magné­
tica en el centro de la circunferencia.
q = 5 x 10-4 coulomb
co= 20 rad/s
r = 10 cm
*
#
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
«i
♦
*
*
*
*
*
*
#
m
*
*
*
*
*
*
*
B = ~ - Xa y . Sene
4n f-
Pero: V = co. r
6 = 90°
2. Reemplazando en la fórmula.
Mo qwr
4n r2
B = Vo qp
4tc r
0 4n x 10~7 5 x 1 0-4 x 20
B = — --------x -
4n 0,1
B = 10“
i Weber
m
3 La inducción en el centro de la
circunferencia gpunto "O" es igual
a 10“® Teslas.

602. CAMPO MAGNETICO
CREADO POR UN SOLENOIDE
3. Campo magnético creado por un so-
lenoide:
Solenoide es una bobina cilindrica de
gran número de espiras de conductor que
forman una "línea helicoidal".
Si las espiras se tocan o están muy cerca
unas de otras, el solenoide se considera
como un sistema de corrientes circulares del
mismo radio, unidas en serie, cuyo eje es
común.
Cuando por el conductor pasa una co­
rriente V el solenoide crea un campo mag­
nético
Las líneas de fuerza que representan el
campo magnético se obtienen combinando
las líneas de fuerza de las distintas espiras
como indica la figura (b).
Para determinar el sentido de las líneas
de fuerza puede emplearse la regla de la
mano derecha.
Regla de la mano derecha
“Se agarra el solenoide con la mano dere­
cha de modo que los dedos indiquen el sen­
tido de la corriente en las espiras, entonces
el pulgar indica el sentido del campo en el
interior del solenoide, osea, el polo Norte".
i|
*
♦
*
*
*
*
#
*
#
«
1
*
*
*
*
*
*
*
*
*
*
#
♦
*
*
*
*
*
#
*
*
#
#
*
*
*
*
*
*
*
#
*
*
♦
*
*
*
*
*
*
♦
*
#
*
*
*
♦
*
*
*
*
*
*
*
*
♦
*
*
#
Comparando la figura (b) se observa que
exteriormente el campo magnético de un so­
lenoide es idéntico al de un imán recto que
coincide con su eje y cuya línea S-N está en
el sentido de las líneas de fuerza interiores.
El polo norte N de un solenoide, es el
extremo donde salen las líneas de fuerza y
el polo sur S es el extremo por donde entran
Si miramos el solenoide por los extremos,
el polo norte N de un solenoide está en el
extremo en el cual se ve la corriente en el
sentido contrario a las agujas del reloj y el
polo sur S en el extremo en el que se ve la
corriente en el sentido que las agujas del
reloj, ver figura (b).
La intensidad del campo magnético en un
punto arbitrario A que se encuentra en el eje
será:
(S.l)

603. Donde:
N : Número de espiras circulares
L : Longitud del solenoide
R Radio de la bobina cilindrica.
n = — ; es el numero de espiras por
unidad de longitud.
Solenoide muy largos con respecto al ra­
dio:
1. Si (L > R), la intensidad del campo mag­
nético, en el interior del solenoide, en el
centro de su eje es igual
a = p = 90°
=> Sen a = Sen P = 1
Reemplazando en la ecuación anterior:
(5.1)
El vector inducción magnético será:
(5.1)
La intensidad del campo magnético en el
centro A de un solenoide largo
_a ja «
»
K
K
«
X
K
K
X
>
tí
3 sntwvwi
a
K
)l'l>
l>
.X
*K
X
V
X
K
rffliX
V
X
*X
X
líV
x
K
K
X
K
I
,>
X
X
»
X
K
>
’
............. .....V
X
K
X
X
K
K
X
,
..»
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
»
X
X
X
*
X
X
X
X
X
j(
_..X
X
J
(X
X
^
X
X
X
X
X
X
X
X
^
X
X
X
X
X
X
X
X
X
<
“-,'
•^WJSiBtietOTWtJWSOT-
Para solenoides muy largos, con respec­
to al radio, aproximadamente:
a = 90°
De la figura debe observarse que cuando
L es muy grande respecto al radio R del
solenoide el ángulo a tiende a 90°.
*
S
jí
<
#
*
#
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
•
J
e
*
*
*
*
*
*
*
*
Si introducimos un núcleo de hierro dulce
en un solenoide, su campo magnético se
reformará extraordinariamente, n de hie­
rro es cientos de veces superior al del
aire. Este dispositivo recibe el nombre de
ELECTROIMAN, muy usado en teléfo­
nos, altavoces, timbres, motores y gene­
radores eléctricos Cuando se interrumpe
la corriente cesa el magnetismo, por esto
no puede colocarse un núcleo de acero,
puesto que conservará el magnetismo
permanente.
2. La intensidad H del campo magnético en
un solenoide suficientemente largo, en
los puntos de su eje que coinciden con
los extremos es igual a la mitad de la
intensidad en el centro.
Si, a =0° y P =90° el punto A se
encuentra en el extremo izquierdo, reem­
plazando en la fórmula:
Sen a = 0 , Sen p = 1
(S I)

604. CAMPO MAGNETICO
PRODUCIDO POR UN TOROIDE
6. Campo magnético producido por un
TOROIDE:
r-l toroide es una bobina anular cuyas
=spiras van arrolladas sobre un núcleo en
forma de toro. El campo magnético de un
toroide está íntegramente localizado
dentro de su volumen.
Las características del campo magnético
del toroide se calculan por las fórmulas
siguientes:
“Intensidad del campo magnético H, en el
interior del toro".
H=f
2 n R
(S.l)
Donde-
N : Número de espiras del toroide con
corriente V
R : Radio de cierta circunferencia traza­
da dentro del toro.
La intensidad H del campo magnético en
la línea axial del toroide son:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
H - L N
n = — . — . i
2k r
Donde.
r : Es el radio promedio.
(SI)
Ri + R2
Siendo Ri y R2, respectivamente,
radio interno y externo del toro.
Numero de espiras por unidad de
longitud de la línea axial del toroide.
n =
N
2k r
Por lo tanto la intensidad del campo
magnético en la línea axial será:
i i (S.l)
La inducción magnética en la línea axial
será:
| B = [i.|i0 n . i (S.l)
PROBLEMA:
Un toroide se enrolla uniformemente y
tiene N vueltas de alambre por los que circula
una corriente V . El radio interior del toroide
es "a" y el exterior es "b". Hallar la relación
b/a que permitirá que la intensidad del campo
magnético H, en la toroide, no varíe en más
de un 25%.
SOLUCION:
1. De la fórmula general:
H ~ ! N •
H ~ 2 k - R - '
Donde: a < R < b
en (S.l)

605. 3. Error relativo: — — — < 25%
Ha
Reemplazando:
N ¿
f 1 11
2n a b
*--------
N l
2tí ' a
Por lo tanto:
INDUCCION
ELECTROMAGNETICA
CONCEPTO:
Es el fenómeno que consiste en la induc­
ción de corriente eléctrica en un conductor
por acción de un campo magnético externo
variable.
EFECTO FARADAY
"Cuando varia el flujo de inducción a tra­
vés del área del circuito, se induce en el
circuito (espira) una f.e.m que tiende a pro­
ducir una corriente eléctrica".
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Si!
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
s
ü
*
*
*
*
*
*
*
*
*
*
a
je
*
S
is
*
*
*
S
K
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1. Este fenómeno de inducción electromag­
nética descubierto en 1831 independien­
temente por Miguel Faraday, el nortea­
mericano José Henry y el ruso H. Lenz,
aunque Faraday fue el primero en publi­
car sus observaciones.
2. La f.e.m producida se llama fuerza elec­
tromotriz de inducción (f.e.m.i),
3. Debe observarse que la (f.e.m.i) existe
solamente mientras el flujo de inducción
está variando, anulándose tan pronto ce­
sa la variación del flujo magnético.
4.
E = f.e m.i
A
<
¡>= Variación del flujo
At = intervalo de tiempo.
El signo menos de la Ley de inducción
magnética está de acuerdo con la Ley de
Lenz: en toda variación del flujo mag­
nético a través de la superficie limitada
por un contorno cerrado (espira), en este
último surge una corriente de inducción
cuya dirección es tal, que su propio cam­
po magnético se opone a que varíe el
flujo magnético que produce la corriente
de inducción.
5. Para determinar completamente el fenó­
meno de la inducción electromagnética

606. es necesario conocer no sólo la magnitud
de la f.e.m.i, sino además el sentido en
que tiende a producir la corriente. Este
sentido está dado por la Ley de Lenz.
LEY DE LENZ
'El sentido de la corriente producido por
la f e.m.i es tal que el campo que ella crea
tiende a compensar la variación del flujo a
través del circuito".
La corriente inducida, tiene un sentido, de
tal modo que el campo magnético creado por
él se opone al aumento o disminución del
flujo magnético externo. A este fenómeno se
denomina "inercia electromagnética".
1. Si el flu jo m agnético externo está
aumentando:
La figura (1), muestra una esfera circular
atravesado por el flujo magnético externo
hacia arriba.
Si el flujo esta aumentando, el sentido de
la corriente inducida {#) producida por la
f.e.m.i, tiene sentido HORARIO, porque
así esta corriente producida crea un flujo
magnético hacia abajo, indicado por lí­
neas discontinuas, que tiende a compen­
sar el aumento del flujo magnético ex­
terno.
m
*
<
)
<
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
»
*
*
*
*
*
*
*
*
$
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
<
¥
*
*
*
*
*
*
*
*
*
«
*
«
fs
*
*
*
*
#
*
«
*
*
*
*
s
ü
Si el flujo magnético externo está dis­
minuyendo:
La figura (2), muestra una espira circular
atravesado por el flujo magnético externo
hacia arriba.
Si el flujo está disminuyendo, el sen­
tido de la corriente inducida pro­
ducida por la f.e.m.i, tiene sentido AN­
TIHORARIO, porque así esta co­
rriente producida crea un flujo magné­
tico hacia arriba, indicado por líneas
discontinuas, que tiende a compensar
la disminución del flujo maqnético ex­
terno
Aunque la Ley de Lenz es suficiente para
determinar el sentido de la corriente in­
ducida, se dan también algunas reglas
prácticas.
1. Regla de la mano derecha:
Sí se agarra al conductor (espira)
con la mano derecha de modo que
los dedos indiquen el sentido del
flujo magnético externo, el sentido
de la corriente inducida es el indi-

607. cado por el pulgar si el flujo dis­
minuye, es el contrario si el flujo
magnético, externo aumenta.
2. Como ejemplos de aplicación de
las reglas anteriores el alumno
verificará el sentido de la co­
rriente inducida en los casos
indicados.
3. En la figura (3) el polo norte de
un imán se aleja con una veloci­
dad “V* de la espira circular, el
número de líneas de fuerza mag­
nética que atraviesa la espira dis­
minuye, por consiguiente la co­
rriente inducida V tiene sentido
HORARIO.
*
#
*
*
*
*
*
*
*
*
*
a»
#
*
*
*
*
*
m
*
*
*
*
«
*
*
*
*
*
*
*
*
IMAGENES ELECTROSTATICAS
I. Carga puntual y esfera conductora:
Se tiene una esfera conductora de radio
"R" conectado a Tierra. A una distancia
"d“ de su centro (R d) se coloca una carga
puntual “q Hallar la posición de la carga
imágen su magnitud y ¡a fuerza eléctrica
resultante que actúa sobre la carga pun­
tual “q“.
SOLUCION:
La presencia de la carga puntual
"+q" origina una distribución de car­
gas en el cuerpo esférico, cargán­
dose el cuerpo con una carga neta
"q“ cuyas cargas se encuentran dis­
tribuidas en la superficie heterogé­
neamente, el sistema equivalente
será "imaginar" a la carga “q"' en un
punto del eje x debido a la simetría,
como muestra la figura siguiente. A
este modo de cargar el cuerpo es­
férico se denomina: método de in­
ducción.
Si "q" no estuviera en el eje x, se
tendría componerte tangencial del
campo eléctrico E en los punto A y
B, La carga imagen q’ está ubicada
en la posición (x ;0).

608. Luego el sistema se reduce a dos
cargas puntuales q y q’
2. Para hallar el valor de ''q’“ y su posi­
ción Y , tengamos presente que el
potencial eléctrico en los puntos A y
B es igual a cero, debido a la cone­
xión de la esfera a Tierra.
VA =
1
47t£o
j L
(d - R) (R - x)
= 0
. (R -x )
q (d —R)
Vb =
4nf<, (d + R) (R + x)
..(1)
= 0
, (R + x)
q _ _ ~
—~ . q
q (d + R)
.... (2)
Igualando las ecuaciones (1) y (2):
(R - x) (R + x)
(d - R) ~ (d + R)
Resolviendo tenemos:
X =
Reemplazando (3) en (1):
, R
q = - - . q
De la Ley de Coulomb:
F = k , - a J l
(d - x)2
(3)
.... (4)
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
s
is
*
s
H
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
S
O
*
*
*
Reemplazando (3) y (4) en (5):
_2
F = k . 4 ^
(d2 - R2)2
PLACA CONDUCTORA
ti) Placa conductora infinita y carga pun­
tual:
Se tiene una placa conductora infinita
conductora conectada a Tierra y a una
distancia “d” se coloca a una carga pun­
tual “q".
Hallar la fuerza eléctrica resultante que
ejerce “q" sobre la placa conductora infi­
nita.
“La superficie de ia esfera de radio
R se comporta como una superficie
equipotencial, por consiguiente las
líneas de fuerza intersectan perpen­
dicularmente a la superficie"

609. 1 La "Tierra" y la placa conductora
infinita forman un solo “gran conduc­
tor” neutro. Al colocar la carga “q"
cerca del plano las libres de este
"gran conductor" se redistribuyen
quedando el plano cargado con
carga de signo contrario a la carga
inductora "q". Las líneas de fuerza
del campo eléctrico salen de la car­
ga puntual “q" y terminan en el plano
conductor infinito (si q, es positivo).
El plano conductor se comporta co­
mo una superficie equipotencial, de­
bido a la simetría de la líneas de
fuerza podemos "IMAGINAR" que
las líneas de fuerza convergen en
un punto donde se encuentra la car­
ga imagen:
q’=-q
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
2.
paración entre la carga puntual “q" y
la carga imagen -,q’" es igual a: (2d).
Luego el sistema inicial se reduce a
la interacción de dos cargas pun­
tuales q y q’:
De la Ley de Coulomb; la fuerza F,
que la carga "q" ejerce sobre la pla­
ca es del mismo valor pero de sen­
tido contrario a la fuerza que la Pla­
ca (o la carga imagen q’). ejerce
sobre la carga "q":
F = k
(2d)2
_k g!
3.
F =
En la región (X < 0), detrás del plano
infinito, no hay líneas de fuerza
(E=0) y el potencial eléctrico es
cero, como también lo es en la su­
perficie del plano:
V(X=o) = 0
El criterio de carga imagen es un
sistema equivalente, o artificio
“físico".
III) Carga puntual y dos semiplanos infini­
tos:
Se tiene una armadura de dos semipla­
nos conductores infinitos que se intersec-
tan formando un ángulo recto. La arma-

610. dura se encuentra conectada a Tierra. Si
colocamos una carga puntual "q“ en la
posición (a. b; o), hallar la posición de las
cargas imagen.
SOLUCION:
1
2.
La armadura a Tierra puede ser
reemplazada por tres cargas ima­
gen:
qi = - q , posición: (-a; -b, o)
q2= + q , posición: (-a; -b; o)
q3= - q , posición: (a; -b; o)
La carga puntual "q” y las cargas
imagen qi, q2 y qa se encuentran
contenidos en la misma circun­
ferencia, con centro en el vértice de
la armadura, punto "O”.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
&
*
*
4»
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
«fr
*
$
4¡
3. La 'Tierra" y los dos semiplanos in­
finitos forman un solo "gran conduc­
tor" neutro, al colocar la carga pun­
tual "q" cerca de los semiplanos las
cargas libres de este “gran conduc­
tor” se redistribuyen quedando la
armadura cargada.
Realmente las cargas se encuen­
tran en los semiplanos, el criterio de
las cargas imagen es un sistema
equivalente de la distribución real de
las cargas. Sí la armadura no estaría
conectado a Tierra la distribución de
cargas sigue siendo el mismo, dado
que la carga excedente se distri­
buye en el infinito.
Carga puntual entre dos planos conduc­
tores:
La presencia de una carga puntual entre
dos planos conductores que forman un án­
gulo “a" entre sí origina una redistribución de
las cargas eléctricas libres en los planos
conductores, el cual se puede reemplazar
por un sistema equivalente, es decir por las
"cargas imagen".
Si 360%/a es un número entero, enton­
ces el número de cargas imagen.
a a
n = 3; 4; 5; 6; .........
Número de cargas imagen=n - 1
I) Si a = 120°
n = 3
Cuando la carga puntual se en­
cuentra a igual distancia de los
planos conductores, “n" es el nú­
mero de lados del polígono regu­
lar en cuyos vértices se encuen­
tran ubicados la carga puntual y las
“cargas imagen" En este caso
tenemos un triángulo equilátero.

611. #
*
2. Si, a = 72°
n = 5
La carga puntual y las cargas ima­
gen se encuentran ubicadas en los
vértices de un pentágono regular.
3. Si, a = 60°
n = 6
La carga puntual y las cargas ima­
gen se encuentran ubicadas en los
vértices de un exágono regular.
*
*
*
*
S
fs
*
*
*
*
*
*
*
*
PROBLEMA 1
Sobre un plano conductor ilimitado
conectado a Tierra cuelga, de un re­
sorte aislante de rigidez ko = 1 000 N/m,
una pequeña bola. Una vez que la bola
se cargó, ésta descendió X =1 cm, y la
distancia hasta el plano conductor lle­
gó a ser igual a d =3 cm. Determinar la
carga de la bola.
SOLUCION:
1. El resorte incrementa su defor­
mación en "X" debido a la fuerza
de atracción entre la carga de la
bola y su carga imagen. La carga
de la bola y la carga imagen tie­
nen igual magnitud de carga pero
signos opuestos, equidistantes,
del plano ilimitado. Por consi­
guiente:
Ko.AX = Feléct
*
*
*
*
*
*
*
*
*
*
*
*
Ko.AX = k .
- k -9 1
|2
4d‘
Despejando:
...o )

612. +q <
P la n o
1 C o n d u c to r
k
d
■a*-
- q <
V
1
5 . . . .
m agen
d
y
2. Reemplazando datos en (1):
q = 2 . 3 . 10 m .
' 103 . 20“2
9 . ;10
C
m
q = 2nC
PROBLEMA 2
Las cargas puntuales "q" y "+q" se
sitúan a la distancia x = 60 cm una de la
otra y a unas distancias idénticas y = 30
cm de un mismo lado de un plano conduc­
tor ilimitado. Sabiendo que la magnitud
q = y¡5 nc, hallar la intensidad del campo
eléctrico resultante en el punto medio del
segmento que determinan las posiciones
de las cargas “q" y "+q'
SOLUCION
(1)
q * ~
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
*
*
*
2.
La placa conductora infinita es un
gran conductor neutro, al colocar las
cargas puntuales q y +q cerca del
plano las cargas libres de este "gran
conductor” se redistribuyen quedan­
do el plano cargado con carga de
signo opuesto igual a "-2q", repre­
sentado por las cargas imagen. Del
principio de conservación de las car­
gas, el complemento de la carga en
el plano "+2q” se distribuye en el
infinito, por consiguiente se despre­
cia su influencia sobre las cargas
puntuales q y +q
Llevamos una carga de prueba “qo"
en el punto medio del segmento que
determinan las posiciones de las
cargas q y +q. Calculo de las inten­
sidades de campo eléctrico:
Ea = E4 =
E1 = E2 y
k.q _ kg
(a'f5): 5a2
Se puede observar que E1 y E2 se
destruyen, por consiguiente la inten­
sidad resultante será:
= Eg + E^+2E3.E4.Cos53° .(2)
Reemplazando (1) en (2):
Er =
4V5 kq
25
... (3)
Reemplazando valores en (3) tene­
mos:
E r = 8.104N/C
PROBLEMA 3
En el espacio tridimensional, en plano
X-Z se encuentra contenido una lamina
conductora infinita, conectada a Tierra.
En la posición A (2; 2; 0) se encuentra una
carga puntual q -40mC. ¿Qué trabajo se
necesita realizar contra las fuerzas eléc­
tricas para llevar lentamente esta carga a
la posición B(5; 5, 0)cm.?

613. El trabajo realzado por un agente
externo para trasladar la carga pun­
tual ' q" es igual al productor de la
carga en movimiento, por la diferen­
cia de potencial entre la posición B
y la posición A
WA -» b = q • (VB- VA) ... (1)
-K
J
.•
B(5,5;o)
+ q » *(2»
2,o)
Reemplazando (2) en (1) tenemos:
40 . 10-6 C . (5. •
WA b = 216 J
Wa -> b = 40 . lO ^ C .ÍS M . 106V)
*
«
i!
*
*
*
*
*
*
«i*
*
*
i*
*
*
*
*
*
*
%
*
*
*
*
*
$
-c ia .A 'tZ ^ io )
B ( 5 ; - 5 ; 0 )
-q
Imagen
2 Ubicamos nuestro sistema de refe­
rencia sobre la carga imagen "-q".
La carga imagen genera un poten­
cial eléctrico sobre la carga “+q" en
las posiciones A y B.
VA = K = —9 . 106 V
dA
VB =K ~ = - 3. 6.1 06V ...(2)
dB
PROBLEMA 4
A la distancia d = 30 cm de un plano
conductor ilimitado, conectado a Tierra,
se encuentra una carga puntual q =20jxC.
¿Qué trabajo se necesita realizar contra
las fuerzas eléctricas para separar len­
tamente esta carga a una gran distancia
del plano?.
SOLUCION:
*
*
*
*
*
*
tk
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«lf
*
*
*
s
ü
*
*
d
Plano ■ 1
d J
1.
2.
Imagen
El trabajo realizado por un agente
externo para trasladar la carga pun­
tual "q“ es igual al producto de la
carga en movimiento por la diferen­
cia de potencial entre la posición
final y la posición inicial)
WA -» b = q • (Vb - VA) .-(1 )
Ubicamos nuestro sistema de refe­
rencia sobre la carga imagen °-q".
La carga imagen genera un poten­
cial eléctrico sobre la carga "+q’' en
el punto A:
_ M^q) _ _ luj
(2d) _ 2d
VA - — (2)
La velocidad de alejamiento entre la
carga puntual ”q“ y la carga imagen
"-q" es lento (tiende a cero) de la
condición del problema, por consi­
guiente nuestro sistema de referen­
cia en “-q" es inercial.
Cuando la distancia de separación
es muy grande (d _
►■») el potencial
generado por la carga imagen sobre
"q" es CERO:
VB= 0 .... (3)
Reemplazando (2) y (3) en (1) te­
nemos.
Wa -¡B = q
2d
VVA ->~ 2d - (4)
Reemplazando datos en (4):
WA -
9. 109. 400. 10 12
=6J

614. Entres dos semiplanos conductores
mutuamente perpendiculares se encuen­
tra una carga puntual "q", distante, “d" de
éstos. Hallar el módulo del vector fuerza
que actúa sobre la carga puntual "q". La
posición de la carga "q" en coordenadas
cartesianas será (d; d; 0).
*
*
*
*
#
*
#
#
¡§
*
*
*
#
■
#
*
1. En este caso los semiplanos no
están conectados a "Tierra", pero la
distribución de cargas sigue siem­
pre el mismo; debido a la carga ¡n-
ductora "q La figura anterior
muestra la posición de las cargas
imagen, el cual es nuestro sistema
equivalente.
2. Cálculo de las fuerzas que actúan
sobre la carga inductora ''+q"

615. E N E R G IA
E LE C TR O S TA TIC A ” U " 'a
CONCEPTO:
La energía de un cuerpo conductor ais­
lado con carga ”q ' es igual al trabajo reali­
zado por un agente externo para cargar el
cuerpo trasladando las cargas dq desde el
infinito.
Para comunicar una carga eléctrica a un
conductor hay que realizar un trabajo en
vencer las fuerzas repulsivas de Coulomb
entre las cargas de igual signo. El trabajo se
gasta en aumentar la energía eléctrica del
cuerpo cargado. El trabajo que realizan las
fuerzas externas, al trasladar la carga "dq"
desde el infinito al conductor aislado es.
2 C
Demostración:
1. Sabemos que:
dWA -> b = dq (Vb - Va)
Pero “A" está en el infinito.
Entonces, Va = 0 =>
Donde "B” está en el cuerpo conductor
1
Además; V = — dW«
Integrando, tenemos:
B= § .d q
#
+
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
m
*
*
*
#
*
*
*
X
*
*
dq
W - _ B= 2 C
De la definición:
U = W„ 1 a:
’ B= 2 ' C
Para el caso particular de una esfera
conductora aislada de radio R su capaci­
dad eléctrica es: C = R/K entonces su
energía electrostática será igual a:
PROBLEMA
Un sistema se compone de dos cas­
carones metálicos concéntricos delga
dos de radios "a" y ”b" con cargas q y O
correspondientes.
Hallar la energía propia de cada uno de
los cascarones Ui y U •
.la energía de inte­
racción entre estas U12 y la energía total
eléctrica U del sistema.
*
*
¡a
*
*
*
*
m
*
*
*
*
&
1. La energía electrostática de todo
cuerpo cargado es:
u = ! ¿
2 C
Para el caso de un cuerpo esférico
k i
2 R
.... (1)
2. Para efectos externos al cascarón
de radio “a" se puede considerar

616. que toda la carga está concentrada en el
centro de curvatura, entonces el sistema
se reduce a la interacción de una carga
puntual “q“ con el cascarón de radio "b"
cargado con magnitud "Q".
Q=AQi +AQ2+AQ3+ ... +AQn
U12 :Energía de interacción elec­
trostática.
U12: ^ [AQi + AQ2+ AQ3+
D
+AQn]
U12= k ^ .... (2)
- ! • a b b
V(tierra) —
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
La energía eléctrica total del sistema
es igual a:
U = Ui + U 2+ U 12
POTENCIAL DE TIERRA
Consideramos "Tierra" como un conduc­
tor esférico de radio "R" muy grande (R -» ~),
para valores de cargas comunes en elec­
trostática (microcoulomb a lo más) el poten­
cial de este gran conductor esférico es igual
a cero.
Cualquier cuerpo conductor conectado al
gran conducto esférico Tierra, tomará de (o
cederá) Tierra las cargas necesarias para
que el potencial eléctrico de ambos sea igual
a cero. El potencial de Tierra no se modifica
cuando gana o pierde electrones Luego: el
potencial eléctrico de cualquier cuerpo con­
ductor conectado a Tierra es cero.
1. La figura (1) un cuerpo conductor "A" con
carga inicial "qo", alrededor del cual no
hay otras cargas, se conecta a Tierra,
entonces'al final de la carga es igual a
cero entonces decidimos que el cuerpo
"A“ se ha descargado.
4tce0 R
= 0
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
2. La figura " 2 " muestra un cuerpo conduc­
tor "B", inicialmente neutro alrededor del
cual hay un cuerpo "C" cargado con mag­
nitud “Q", puede haber mas cuerpos car­
gados, luego "B“ se conecta a Tierra.
Entonces el cuerpo “B" y Tierra forman
un solo gran conductor neutro y debido a
la presencia de “C" cerca de “B“, las
cargas del conductor ib + Tierra) se re­
distribuyen de tal manera que en ”B" hay
cargas de signo contrario a “O" y en la
Tierra cargas del mismo signo de Q pero
muy alejadas, osea neutralizadas. El
cuerpo “B“ conectada a Tierra y por lo
tanto con potencial eléctrico CERO, tiene
ertonces carga neta NO nula
Hemos explicado así que un conductor
conectado a Tierra (“
B*i siempre el po­
tencial es NULO, pero la <
: ?.rg<j neta no es
necesariamente nula

617. Una esfera conductora metálica de ra­
dio "a" y cargado con magnitud ,,+q" se
rodea con una envoltura esférica conduc­
tora de radio "b“ sin carga.
Hallar el nuevo potencial de la esfera
de radio "a", cuando la envoltura de radio
"b” se conecta a "Tierra".
SOLUCION:
*
*
*
*
* PROBLEMA N- 2
1. El potencial en la superficie de la
envoltura es igual a cero, por estar
conectado a "Tierra", entonces, la
carga ,,+q'' induce una carga neta
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
La figura muestra un sistema que sirve
para cargar una esfera conductora de ra­
dio "R“ por el método de inducción. La
carga puntual "q" se encuentra a una dis­
tancia "d" del centro del cuerpo esférico.
El interruptor K está cerrado inicialmente
luego se abre: Determinar la carga de la
esfera.
Sugerencia: El potencial eléctrico de la
Tierra es igual a cero.
.... (2)
Reemplazando (1) en (2) tenemos-
VA= kq
Va = k . q
í 1
a b
(b-a)
a b
El potencial eléctrico inicial de la
esfera era igual a: V0 = kq/a, esto
significa que su potencial disminuye
cuando la envoltura se conecta a
Tierra.
*
*
*
*
*
*
*
*
*
*
*■
*
*
m
*
*
Ü
í
*
*
*
*
*
»
!•
*
*
*
*
guíente la esfera se carga con signo
opuesto a la carga inductora.
Después que se abre el interruptor
K la esfera conductora no podrá
descargarse

618. Pero, sabemos que el potencial de
Tierra es igual a cero, entonces el
potencial de la superficie esférica es
igual a cero, por consiguiente el po­
tencial en el centro de la esfera tam­
bién es igual a cero, cuando el inte­
rruptor K está cerrado.
'centro "0"=-
1
47teo
9 .91 .92 ,33 .93 . ,92
d R R R R R
La carga neta del cuerpo esférico
será la sumatoria de las cargas su­
perficiales.
q’= Aqi + Aq2+ Aqs + Aq4
+ . . . + Aqn , . . (2)
Reemplazando (2) en (1):
La ecuación (3) igualando a cero:
[ OPTICA
CONCEPTO:
Es la parte de la física, estudia los fenó­
menos producidos por la luz.
Luz:
Es toda radiación de ondas electromag­
néticas que puede afectar al ojo humano.
NATURALEZA DE LA LUZ
1. Teoría Corpuscular:
Los primeros esquemas con bases mitad
científicas aparecen en la segunda mitad del
siglo XVII con Newton y Huygens.
Para Newton la luz estaba constituida por
pequeñísimas partículas que emitían los
*
*
*
*
*
*
*
*
*
*
#
*
*
ft
*
*
*
*
*
*
♦
•¥
*
*
*
X
»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
+
*
*
*
*■
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
cuerpos luminosos y que al llegar al ojo hu­
mano, propagándose en línea recta, pro­
ducían la sensación luminosa.
2. Teoría Ondulatoria:
Huygens por el contrario opinaba que la
luz constituía un movimiento ondulatorio lon­
gitudinal (como el sonido, aunque de fre­
cuencia mucho mayor) que se propaga en el
seno de un hipotético medio elástico ex­
tendido por todas partes: el éter Esta teoría,
además de la reflexión, explicaba de modo
más fácil la refracción luminosa. No obstante,
se objetó que si la luz tenía carácter de onda,
como estas podían doblar los obstáculos, se
debería poder ver detrás de una esquina, no
habría sombras, etc.
Con el comienzo del siglo XVII el pen­
samiento científico se inclina en favor de la
teoría ondulatoria gracias a los trabajos de
Young sobre los fenómenos de interferencia,
ya conocidos e inexplica- dos por Newton,
que demostraron que “luz más luz podía dar
oscuridad". Un poco más tarde es consoli­
dada con los estudios de Fresnel sobre la
difracción, explicando la propagación rec­
tilínea de la luz en base a su longitud de onda
muy corta. El mismo Fresnel demostró que
los fenómenos de polarización evidenciaban
que las ondas luminosas eran transversales.
Los fenómenos anteriores de INTERFE
RENCIA, difracción y POLARIZACION son
típicamente ONDULATORIOS e imposibles
de explicar con ninguna teoría corpuscular.
Fue MAXWELL, en 1 873, el autor de la
principal aportación a la teoría ondulatoria
Una consecuencia de su teoría electroma­
gnética era la posibilidad de existencia de
ondas electromagnéticas (o.e.m) cuya velo­
cidad de propagación, deducida de nagni-
tudes eléctricas y magnéticas, comprobo que
coincidía con la calculada experimentalmen­
te para la luz. Esto le llevó a la hipótesis de
que la luz tenía una naturaleza ondulatoria
de tipo electromagnético y no mecánico, co­
mo hasta entonces se había admitido.
Quince años más tarde, H elz confirmó
las previsiones de Maxwell a . lograr producir

619. o.e.m. mediante un ci/cuito oscilante y de­
mostrar que poseían todas las propiedades
de la luz, salvo las diferencias derivadas de
su longitud de onda mucho mayor.
La teoría electromagnética de Maxwell
ha sido una de las más brillantes de la física
y permitió englobar en su seno a la electrici­
dad y la óptica, hasta entonces indepen­
dientes entre sí. Tras ella se pensó que los
conocimientos acerca de la naturaleza de la
luz se habían completado totalmente.
3. Teoría Cuántica:
Ahora bien, a tiñes del siglo XIX la teoría
electromagnética comienza a tambalearse al
ser incapaz de explicar los datos experimen­
tales de la luz emitida por un cuerpo sólido
caliente. Entonces, en 1 900, Max Planck (P.
Nóbel 1 918) estableció la sorprendente hi­
pótesis de que los cuerpos (concretamente,
sus átomos en oscilación) no pueden ab­
sorber ni emitir energía radiante (luz) de for­
ma continua, sino en unidades discretas
(E = h./) llamadas CUANTOS.
Esta afirmación equivalía a romper con la
física clásica, para quien "la naturaleza no da
saltos"'. La teoría cuántica, con la que surge
una nueva física, viene a ser como una teoría
atómica de la energía, aunque la magnitud
del cuanto no es fija sino que depende de (/)
la frecuencia.
Aunque el efecto fotoeléctrico estaba
previsto por la teoría electromagnética (la
energía de las o.e.m, podía extraer elec­
trones), el hecho experimental de que exis­
tiera una frecuencia umbral de la luz inci­
dente por debajo de la cual no se produjera
la emisión de electrones, y que la velocidad
de éstos no dependiese de la intensidad de
la luz sino de su frecuencia, era inexplica­
bles, puesto que, de acuerdo con la teoría
electromagnética, la intensidad de una ra­
diación de tal tipo dependía de su energía
que a su vez era proporciona! a,cuadrado de
su amplitud máxima de sus campos eléctrico
y magnético:
Ilu z = K E 2 + B 2 1
max max
*
*
$
*
$
0
$
*
♦
*
*
m
*
*
m
*
*
m
*
*
#
*
*
#
*
$
*
*
*
*
*
#
*
«tí
$
$
*
$
$
¡t»
*
*
*
*
*
*
*
*
#
<
s
*
*
$
$
*
*
*
*
$
*
*
*
*
*
En 1 905, Albert Einstein explica ei etecto
fotoeléctrico extendiendo las ideas cuánticas
de Planck a la luz misma y estableciendo que
el cuanto de energfa conserva su individuali­
dad tras haber sido emitido (cuanto de luz o
fotón) y se mueve con la velocidad de ésta.
El que la luz esté conformada por fotones
supone en cierto modo volver a la teoría
corpuscular, aunque la energía del fotón y,
por tanto, de la luz viene en función de una
magnitud típicamente ondulatoria como es
(/) la frecuencia.
La teoría fotonica fue confirmada en
1 922 por Compton (P, Nóbel 1 927), al
estudiar ciertos choques entre fotones (de
rayos x o gamma) y electrones en los que el
fotón cede sólo parte de su energía al elec­
trón (a diferencia del efecto fotoeléctrico),
transformándose en otro de menor energía o
frecuencia que sale dispersado en distinta
dirección, de acuerdo con las leyes del cho­
que elástico entre cuerpos materiales.
¿Está entonces compuesta la luz por on­
das o por partículas? Como hay apoyo para
ambas representaciones, la física actual no
considera como contradicción admitir que la
luz tiene a la vez caracter de onda y corpús­
culo. De esta forma, unas veces manifiesta
su naturaleza ondulatoria (en los fenómenos
de propagación) y otras su naturaleza cor­
puscular (en los de interacción con la mate­
ria).
Ahora bien esta dualidad se ha com­
probado que es una ley general de la natu­
raleza y que también la materia participa
de ella.
Esta proposición fue hecha en 1 923 por
De Broglie (P. Nóbel 1 929) quien sugirió que
los electrones, aparte de su carácter corpus­
cular, en determinadas circunstancias po­
dían comportarse como ondas, lo que fue
comprobado unos años más tarde (1 927) a
lograrse la difracción de haces de electrones,
puede hablarse, por tanto, de ONDAS DE
MATERIA.
De la hipótesis de De Broglie arranca la
mecánica cuántica u ondulatoria, desarro­
llada entre 1 925 - 1 927 por Heisenberg,
Shródinger y Dirac (P. Nóbel 1 932 y 1 933,

620. éste compartido por los últimos), que reúne
en un solo tronco la mecánica, la electricidad
y la óptica, y ha venido a substituir todo el
cuerpo de doctrina de la física clásica.
De acuerdo con ella todo corpúsculo (fo­
tón, electrón, etc.) que se mueve lleva aso­
ciada una onda que se propaga de tal modo
que esta determina la mayor o menor posi­
bilidad de encontrar al corpúsculo en un sitio
u otro dei espacio (no se puede conocer su
posición exacta). Como la probalidad es pro­
porcional al cuadrado de la amplitud de la
onda, cuanto mayor sea la amplitud en un
punto, más probable será eocontrarlo allí, es
decir, la onda es en realidad una ONDA DE
PROBABILIDAD de la presencia del corpús­
culo.
La física actual, según vemos, ha hecho
desaparecer toda imagen intuitiva de los fe­
nómenos a escala atómica a que tan acos­
tumbrados nos tenía la física clásica.
*
*
♦
$
i»
♦
♦
*
*
*•
*
#
*
♦
i*
*
*
*
*
*
*
i#
*
*
*
*
♦
$
*
$
*
*
$
*
*
♦
*
*
♦
SIMPLICIO:
La experiencia cotidiana nos muestra
que la propagación de la luz es instantánea,
porque cuando vemos que se dispara un
cañón a gran distancia el fogonazo llega a
nuestros ojos sin que transcurra ningún tiem­
po, mientras el sonido llega a nuestros oídos
sólo después de un intervalo de tiempo per­
ceptible
SAGREDO:
Bien, Simplicio, lo único que yo puedo
inferir de ésta experiencia tan común es que
el sonido al llegar a nuestros oídos viaja más
lentamente que la luz, no me informa si la
llegada de la luz es instantánea o no. Aún
cuando sea sumamente rápida, de todas ma­
neras invierte un tiempo....
"Sagredo, quien evidentemente es Gali-
leo mismo, describe entonces un método
posible para medir la velocidad de la luz ..."
James Maxwell (1 873) demostró que la
luz es uno de los componentes del "espectro
electromagnético" que se muestra en la fi­
gura (1).
VELOCIDAD Y PROPAGACION
DE LA LUZ
¿Con qué rapidez se mueve la luz?
Galileo se hizo esta pregunta y trató de
contestarla experimentalmente. Su obra
principal "Dos nuevas ciencias", publicada
en Holanda en 1 638, está escrita en forma
de una conversación entre tres personajes
ficticios llamados: Salviati, Sagredo y Simpli­
cio. Reproducimos una parte de los que de­
cían acerca de la velocidad de la luz.
*
*
*
♦
*
*
*
*
m
♦
$
*
*
*
*
$
*
Todas estas ondas son de carácter elec­
tromagnético y tienen la misma velocidad “C"
en el espacio libre (vacío). Difieren sólo en
su longitud de onda (X) y por consiguiente
en frecuencia (/). El producto de longitud
de onda por su frecuencia es una con­
stante e igual a la velocidad de la luz
^
■
i - /l= A
.1 . Í2 = ^3 ■/3 = C

621. El espectro electromagnético no tiene lí­
mites definidos ni superior ni inferior.
Definiremos aquí a la "luz” como toda
radiación de ondas electromagnéticas que
puede efectuar al ojo humano.
LUZ O ESPECTRO VISIBLE
Es una banda angosta del espectro elec­
tromagnético formado por las longitudes de
onda a las cuales nuestra retina es sensible.
Se extiende en longitudes de onda desde 7,6
x 1C f’ m. hasta 3,8 x 10- 7m. yen frecuencias
desde 4 x 1014Hz. hasta 8 x 1014 Hz.
La luz es tan importante que ha dado
lugar al desarrollo de una rama de la física
aplicada, llamada OPTICA. La óptica trata
los fenómenos luminosos y la visión, inclu­
yendo el diseño de instrumentos ópticos. El
campo de la óptica incluye actualmente, ade­
más del espectro visible, el infrarrojo y el
ultravioleta.
Las diferentes sensaciones que la luz
produce en el ojo, que se denominan COLO­
RES, dependen de la frecuencia (o de la
longitud de onda) de la onda electromag­
nética y corresponden a los siguientes inter­
valos para la persona promedio:
COLOR LONGITUD DE ONDA (m)
Violeta 3,90 -4 ,5 5 x 10~7
Azul 4 ,5 5 -4 ,9 2 x 1 0-7
Verde 4,92 - 5,77 x 10“7
Amarillo 5,77-5,97 x 10~7
Naranja 5,97 - 6,22 x 10"7
Rojo 6,22 - 7,80 x 10-7
*
&
*
*
m
$
*
*
*
*
*
*
$
*
*
$
#
*
i
*
*
«
S
*
*
*
$
¥
*
*
*
*
*
*
*
*
m
&
*
*
*
v
*
$
*
*
*
*
*
s
is
*
m
m
*
La sensibilidad del ojo también depende
de la longitud de onda de la luz esta sensi­
bilidad es máxima para longitudes de onda
de 5,6 x 10 metros aproximadamente. Es
por la relación entre color y longitud de onda
o frecuencia de la luz que una onda electro­
magnética de frecuencia o longitud de onda
definida se denomina también onda MONO­
CROMATICA (mono: uno: chromos: color).
La visión es el resultado de señales trans­
mitidas al cerebro por dos elementos presen­
tes en una membrana llamada RETINA, la
cual está en el fondo del ojo; estos elementos
son los CONOS y los BASTONCILLOS. Los
conos son los elementos activos en la pre­
sencia de la luz intensa, como las que hay
durante las horas de sol, y son sensibles al
color. Los bastoncillos, por otra parte, son
elementos capaces de actuar con una ilumi­
nación muy intenue, como la que hay en una
habitación en penumbra, y son insensibles al
color.
OPTICA GEOMETRICA
El dominio de la óptica geométrica a dife­
rencia de la óptica física, se limita a las
situaciones donde los efectos de la difracción
que tiene lugar debido a la naturaleza ondu­
latoria inherente de la luz son despreciables.
Esta simplificación equivale a exigir una
propagación rectilínea en un medio ho­
mogéneo, esto es, se supone que ios rayos
luminosos siguen líneas rectas.
En un medio homogéneo y transparente
la luz se propaga en forma rectilínea, alcan­
zando su máxima velocidad en el vacío:
GE300 000 km/s
Bspeci
III
tro
[ectromagnéu
inélijo
violeta azul verde Naj. R O J O

622. Cuerpos Luminosos:
Son aquellos cuerpos que tienen la ca­
pacidad de emitir luz propia.
Ejemplo: el sol.
Cuerpos Opacos:
Aon aquellos cuerpos que no dejan pasar
la lo' a través de su masa.
Cuerpos Transparentes:
Son aquellos cuerpos que dejan pasar a
la luz a través de su masa, de tal manera que
los cuerpos ubicados detrás de ellos pueden
ser vistos en su totalidad.
Cuerpos Translúcidos:
Son aquellos cuerpos que dejan pasar
parcialmente la luz a través de su masa, de
tal manera que los cuerpos ubicados detrás
de ellos pueden ser vistos en su contorno
(silueta).
INDICE DE REFRACCION (n)
La velocidad V que lleva la luz al atrave­
sar un medio material (vidrio, agua, aire, etc.)
es propia del mismo y siempre inferior a la
del vacío, C
Se define como índice de refracción "n“
de un medio al cociente:
Es evidente que siempre n > 1, excepto
para el vacío en que n = 1 (también para el
aire es muy aproximadamente 1) y tanto
mayor cuanto menor sea V.
Por otra parte, la disminución brusca de
la velocidad al pasar la luz del vacío (o aire)
al medio no es de igual magnitud para todas
las longitudes de onda o colores, sino que es
más intensa a medida que la longitud de
onda es menor, es decir, que mientras todos
los colores se propagan a igual velocidad en
el vacío, no lo hacen así por un medio mate­
rial; o en otras palabras, el índice de refrac­
ción “n" de un medio material es función de
la frecuencia (/) de la radiación. A este fe­
nómeno se le llama DISPERSION. Vemos,
pues, que el vacío (o aire) no es dispersivo.
Por lo dicho anteriormente, los "n“ de los
distintos medios se hacen todos con referen­
cia a una misma frecuencia (/), puesto que
un mismo medio tiene “n" diferentes para
cada color (al ser la frecuencia de ellos dife­
rente). Así, el agua presenta para la luz roja
un n =1,329, y para luz violeta, n =1,340,
Como todo color se caracteriza por una
frecuencia (/) fija, a consecuencia de la dis­
minución de la velocidad de la luz, también
lo hace la longitud de onda (X).
En general, al pasar de un medio a otro,
la frecuencia (color) de una onda luminosa (y
toda o.e.m.) no varía haciéndolo en cambio
su longitud de onda. De ésta manera siempre
que definamos a un color por su longitud de
onda se sobreentenderá que es la corres­
pondiente al vacío.
Indice de refracción referida
a la luz amarilla
Longitud de onda = 5,890 x 10“ ' m.
Aire .............. 1,0003
Agua ............. 1,333
Alcohol .............. 1,361
Benceno .............. 1,504
Cuarzo .............. 1,544
Sal común............. 1,544
Diamante .......... 2,427
Vidrio .............. 1,5-1,9
REFLEXION Y REFRACCION DE LA LUZ
Concepto:
Cuando un haz luminoso que se propaga
por un medio se encuentra con otro medio de
índice de refracción diferente, se desdobla
en dos haces que se apartan de la dirección
original. Uno continúa por el mismo medio y
el otro penetra en el segundo. Son, respecti­
vamente, el haz reflejado y el refractado.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
❖
*
*
*
*
*
«
*
«
*
*
*
#
*
*
*
*
*
*
*
*
*
*
#
*
*
♦
*
♦
*
*
¡t*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
*
&

623. Si m > n2entonces el rayo refractado se
aleja de la normal.
Elementos:
1. Rayo incidente (R.i.), es aquel haz lumi­
noso que llega a la superficie que separa
dos medios materiales diferentes
2. Rayo reflejado (R.r.), es aquel haz lumi­
noso que aparentemente sale de la su­
perficie.
3. Rayo refractado (R.R), es aquel haz lu­
minoso que atraviesa a la superficie que
divide dos medios diferentes
4. Normal (N), es la perpendicular trazada a
la superficie.
A
5. Angulo de incidencia (i), es el ángulo que
forma el haz incidente con la normal.
A
6. Angulo de reflexión (r), es el ángulo que
forma el rayo reflejado con la normal.
A
7. Angulo de refracción (R), es el ángulo
que forma el rayo refractado con la nor­
mal.
Leyes de la reflexión y refracción:
1o El rayo incidente, la normal y los rayos
reflejado y refractado están en el mismo
plano, además dicho plano es perpen­
dicular a la superficie que divide dos me­
dios diferentes.
fc
*
fc
»
fc
1
=
fc
*
fc
fc
*
fc
fc
*
fc
fc
fc
fc
fc
*
fc
fc
fc
fc
*
fc
fc
*
fc
*
fc
fc
fc
fc
*
*
*
fc
fc
fc
fc
fc
fc
*
fc
fc
♦
fc
2o El ángulo de incidencia es igual al ángulo
de reflexión.
3o (Ley de SNELL) el ángulo de refracción
depende del ángulo de incidencia y de los
ángulos de refracción de los medios, se­
gún la expresión:
n i . Sen 1 = n2 . Sen
D
Se sobreentiende para una radiación mo­
nocromática (una sola longitud de onda),
pues, en caso contrario, habría disper­
sión.
Aplicación de la Ley de Snell
A A
n i . Sen 1 = n2 . Sen R
Según la ecuación anterior, si el ángulo
de incidencia es igual a cero entonces el
ángulo de refracción es igual a cero, es decir,
no hay desviación para los rayos que inciden
perpendicularmente.
Fácilmente se comprueba que cuando un
rayo luminoso se deplaza de un medio de
menor densidad a otro de mayor densidad,
el rayo refractado se acerca a la normal, y
viceversa, esto quiere decir que cuando el
rayo luminoso se desplaza de un medio de
mayor densidad a otro de menor densidad,
entonces el rayo refractado se aleja de la
normal.
A
Angulo Límite (L)
Se denomina así al ángulo de incidencia
que produce un ángulo de refracción igual a
90°. Para que exista ángulo límite es indis­
pensable que el rayo luminoso se propague
de un medio de mayor densidad a otro de
menor densidad.
Para el sistema óptico mostrado, en la
figura:
A
Por Snell: ni . Sen L = n2 . Sen 90°
Sen L = Ü2
ni

624. Si, ahora el foco luminoso se encuentra
en el medio n2, por el principio de reversi­
bilidad de las trayectorias luminosas, los ra­
yos irán por el mismo camino pero en sentido
opuesto.
Reflexión Total (0)
Es aquel fenómeno que se produce cuan­
do el ángulo de incidencia es mayor que el
ángulo limite Consiste en que el rayo lumi­
noso no emerge, sino que se refleja con un
ángulo igual al de incidencia. La superficie,
pues, se comporta como un espejo.
0 > L
Por tanto, para que se verifique la re­
flexión total son necesarias dos condiciones
a) Que la luz vaya de un medio más refrin-
gente a otro menos, y
b) Que incida con un ángulo superior al án­
gulo límite L .
El llamado PRISMA DE REFLEXION TO­
TAL tiene su fundamento en este fenómeno.
Suponiendo que el vidrio que lo constituye
posee un n = 1,5 , el ángulo límite de la
superfic¡e de separación aire (n = 1) y vidrio
será, por la Ley de Snell
A
1 . Sen 90° = 15 Sen L
A
entonces. L = 42°
De este modo el rayo luminoso llega a la
cara A, penetra en el prisma sin desviación
(incidencia normal), pero toca a la cara B con
un ángulo (i = ¿5o) superior al límite,
*
*
*
*
*
*
*
*
*
*
*
*
ts
*
*
*
*
*
*
*
*
*
*
$
*
£
*
*
*
ifí
*
<*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
I»
(L = 42°), siendo reflejado totalmente y
saliendo sin desviación por la cara C, como
indica la figura posterior
Fundamentos en que se basa la OPTICA
GEOMETRICA:
Principalmente son tres:
1B En un medio isótropo y homogéneo
la luz se propaga en línea recta.
2 - Se cumplen las leyes de la reflexión
y la refracción
3e El camino óptico de los rayos lumi­
nosos es reversible.
La Ley de Reflexión fue conocida por
Euclides. La de la refracción fue descubier­
ta experimentalmente por Willebrod Snell
(1 591-1 626) y fue deducida de la primitiva
teoría corpuscular de la luz por René Des­
cartes (1 596-1 650). La Ley de la refracción
se conoce como Ley de Snell o Ley de Des­
cartes, en Francia.
Las Leyes de la reflexión y de la refrac­
ción se pueden derivar de las ecuaciones de
MAXWELL, lo cual quiere decir que estas
leyes son válidas para todas las regiones del
espectro electromagnético.
A

625. REFLEXION DE LA LUZ
Concepto:
Este fenómeno consiste en el cambio de
dirección que experimentan los rayos lumi­
nosos cuando inciden sobre una superficie
que no permite su refracción, se refleja prác­
ticamente el 100% de la luz incidente, retor­
nando el rayo luminoso al medio en el cual
se propagaba inicialmente.
LEYES DE LA REFLEXION DE LA LUZ
R . i : Rayo incidente
R . r : Rayo reflejado
N : Normal
1C El rayo incidente, la normal y el rayo
reflejado se encuentran en el mismo
plano, el cual es perpendicular al
plano relectante.
2® El ángulo de incidencia es igual al
ángulo de reflexión.
Se dice que la reflexión es regular cuando
un conjunto de rayos luminosos paralelos
inciden sobre una superficie plana pulimen­
tada, el conjunto de rayos reflejados siguen
siendo paralelos.
Reflexión Regular:
Si los rayos incidentes son paralelos y los
mismos ya reflejados son no-paralelos en­
tonces la reflexión se denomina difusa, esto
ocurre cuando la superficie plana es rugosa.
*
*
*
*
*
*
*
«
«
*
*
*
*
*
*
*
$
*
*
*
*
m
*
$
*
♦
*
«
*
«
3
#
V
*
*
*
*
*
En el sistema óptico mostrado el rayo
luminoso incide c o i un ángulo de 53°
respecto de la normal. Determinar el án­
gulo de refracción "6".
o AIRE .
5 3 ^ ^
-----------------jS 6
- z i T - i r -- - ".“ i:
_________/ __________________
SOLUCION:
Ley de Snell
naire Sen 53° —nagua Sen 0
Reemplazando:
4 4-
1‘ 5 = 3 0
Sen 0 - ~
5
0 = 37°
PROBLEMA 2
Una lámina de vidrio de caras para­
lelas se encuentra sobre la superficie libre
del agua contenida en un recipiente. De­
terminar el ángulo de refracción ”0" para
un rayo luminoso proveniente del aire que
incide en la lámina con un ángulo de inci­
dencia igual a 53°.
4
nagua = ~
_AGUA________

626. b) 37°
e) Ninguna
PROBLEMA 3
Un rayo de luz incide sobre un cuerpo
transparente, cuyo índice de refracción es
"n“, formando un ángulo "0”. ¿Qué re­
lación debe haber entre "n" y ''0", para que
el rayo reflejado sea perpendicular al rayo
refractado.
SOLUCION
Aplicando la Ley de Snell:
na¡re ■Sen 0 = n . Sen (90° - 0)
Reemplazando:
1 . Sen 0 = n Cos 0
PROBLEMA 4
En la figura el haz luminoso pasa del
medio (II) de índice de refracción 2,0;
hacia el medio (I) de índice de refracción
1,0. Indique Ud. el posible rayo luminoso
refractado.
*
»
*
*
*
*
*
*
#
*
*
♦
$
*
♦
d) Cuatro e) Ninguna
PROBLEMA 5
La figura muestra una lámina de vidrio
delgada de caras paralelas, en el aire. De­
muestre, que el rayo luminoso incidente y
el mismo rayo ya refractado al aire son
paralelos.
*
*
*
*
>
*
m
$
*
#
*
*
*
*
*
*
*
*
En la entrada:
na)re - Sen a = n Sen 0 .... (1)
En la salida:
n Sen 0 = na¡re ■Sen p .... (2)
Aplicando la propiedad transitiva:
na¡re . Sen a = na¡re Sen p
Sen a = Sen p
a = p
"El rayo luminoso incidente y emergente
son paralelos'.

627. La figura muestra una lámina delgada
de vidrio de índice de refracción: nv = 1,5
sumergido en un líquido de índico de re­
fracción nL = 2,0. Indique Ud. el posible
rayo luminoso emergente del vidrio.
PROBLEMA 7
En el sistema óptico mostrado, hallar
la medida del ángulo “6", sabiendo que el
rayo de luz incide perpendicularmente y
se refracta finalmente paralelo a la cara
AB. Indique la refracción del prisma, n =
5/4.
SOLUCION:
Aplicando la Ley de Snell, cuando el haz
de luz emerge al aire
*
*
#
i»
♦
y. Cos 6 = 1 .(1)
4
Cos 6 =
0 = 37°
PROBLEMA 8
La figura muestra dos porciones de
vidrio de índices de refracción n y ni. Si
un rayo de luz incide con un óngulo ”0",
siguiendo la trayectoria mostrada, emer-
qido sobre la cara vertical. Calcular "n".
0 = 45°
n . Sen (90° - 0) = na . Sen 90°
*
m
<
¡*
<
K
*
*
$
*
*
$
*
*
#
*
*
*
*
*
*
#
*
*
v
#
♦
*
*
<
t*
*
*
*
*
*
*
a) 1,5
d)3
PROBLEMA 9
b) 1,8 c) 2
e) Ninguna
Un rayo luminoso incide perpendicu­
larmente sobre un prisma isósceles de
vidrio. ¿Cuál será la trayectoria que se­
guirá, si el ángulo crítico vidrio-aire es
igual a:
a) L = 40°
b) L = 45°
c) L = 50°
SOLUCION:
a) Sí el ángulo de incidencia es mayor
que el ángulo crítico, se produce la
reflexión interna.

628. b) Si el ángulo de incidencia es igual al
ángulo crítico, entonces el ángulo
de refracción es igual a 90°
*
*
#
#
*
*
*
#
*
*
*
$
*
*
♦
<
K
*
*
*
*
*
*
*
c) Si el ángulo de incidencia es menor
que el ángulo crítico, entonces el
rayo de luz emerge, vidrio-aire ale­
jándose de la normal.
#
*
*
*
*
#
*
a) 0 > 30° b) 0 > 37°
c) 0 > 45° d) 0 > 45°
e) Ninguna
PROBLEMA 11
Determinar el índice de refracción de
un cristal cúbico, sabiendo que un rayo
luminoso incide en una de las caras del
cubo con un ángulo de incidencia igual a
45°, y emerge coincidiendo con una de las
caras del cubo.
SOLUCION:
PROBLEMA 10
*
*
*
*
<
C
*
*
Aplicando la Ley de Snell:
Aire - Cristal:
na . Sen 45° = n . Sen 0 ... (1)
Cristal - Aire.
n . Sen (90° - 0) = na . Sen 90° ... (2)
Reemplazando valores en (1) y (2), luego
acomodando convenientemente:
m
*
*
*
$
*
*
4
*
$
*
*
*
*
*
0
*
4
*
#
«
tí
♦
1 = n Cos 0
(3)
(4)
Elevando al cuadrado (3) y (4), luego
sumando:
—= n2. {Sen20 + Cos20)
En el sistema óptico mostrado, ¿Con
qué ángulo "0" debe incidir el rayo lumi­
noso mostrado, para que pueda reflejarse
totalmente sobre la cara AB.

629. Un foco luminoso se encuentra en el
centro de un pozo que contiene un líquido
de índice de refracción n = 5/4. Si se logra
ver la emergencia de la luz del foco, ¿A
qué profundidad se encuentra el foco, si
el diámetro del pozo es 16 metros?. Dar
como respuesta la altura máxima, tal que
el pozo se encuentra totalmente ilumi­
nado.
a) 3 b) 4m c) 6m
d) 8m e) 10m
PROBLEMA 13
Sobre la mitad de una esfera de radio
r = 3,0 cm, hecha de vidrio de índice de
refracción n = 5/4, incide un haz de rayos
paralelos como indica la figura. Determi­
nar el radio del círculo brillante que se
formará sobre la pantalla situada a la dis­
tancia d = 13,0 cm del centro de la esfera.
P
A
N
T
A
L
L
A
SOLUCION:
A
Debido al ángulo crítico L, de la semies­
fera sólo emergen los rayos que inciden
sobre la superficie interna con un ángulo
menor o igual al ángulo límite.
Ley de Snell, para Vidrio - aire.
A
n . Sen L = na¡re Sen 90°
5 A
—. Sen L = 1 x 1
4
A 4
Sen L = ~
O
A
L = 53° ... (1)
Identificando en la figura:
a = 5,0 cm
b = 8,0 cm
Luego, el radio del círculo brillante será:
R = 6,0 cm
PROBLEMA 14
Un rayo luminoso incide formando un
ángulo de 53° respecto de la normal, so­
bre una esfera de vidrio de índice de re­
fracción 4/3. Determinar el ángulo "0" que
forma el rayo emergente respecto de inci­
dente.
d) 48° e) N.A.
PROBLEMA 15
Una moneda está sumergida en el
agua a una profundidad "H". Si miramos
desde arriba y en dirección vertical ¿A
qué profundidad vemos la moneda?
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
H
*
*
*
*
*
*
%
*
*
*
*
*
*
*
*
*
*
*
*
5
)5
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

630. Ley de Snell: Agua - Aire
nagua .SenC
t = naire ■Sen (3 .... (1)
Pero: a y p son pequeños:
X
Sena = Taga = — ....(2)
H
Senp =TagP =^ ....(3)
Reemplazando en (1):
nagua
¿Y qué sucede si miramos la moneda no
verticalmente sino de un lado?
- En este caso veremos la moneda no
solamente más arriba, sino también des­
plazada.
Una piscina de 4m. de profundidad se
* encuentra totalmente llena de agua (n =4/3).
* ¿A qué profundidad aparente se verá el
* fondo?
* a)3,0m b) 1,5m c)2,0m
d) 2,5m e) Ninguna
* PROBLEMA 17
* En el sistema óptico mostrado, el pía-
J no inclinado es un espejo sumergido en
* agua. El rayo luminoso incide en la super-
* ficie del agua con un ángulo de 53°. Deter-
* minar el ángulo que forman los rayos re-
^ flejados en el agua y en el espejo.
SOLUCION:
Cálculo del ángulo de refracción "0" apli­
cando la Ley de Snell:
naíre ■Sen 53 = nagua ■Sen 0
4 4
1 ‘ 5 = 3 ' Sen 6
Sen 0 = f
5

631. En el AAOB, la suma de los ángulos,
interiores es igual a 180°.
30° +(90° + 37°) + (90° - P) = 180°
p = 67° .... (1)
En el AACB, el ángulo exterior en el
vértice "B“ es:
A
2 p = x + 90° .,..(2)
Reemplazando (1) en (2)-
PROBLEMA 18
En la figura mostrada, hallar “x", si el
ángulo de incidencia G = 53° y el mu­
chacho logra ver el PEZ que está en el
agua de índice de refracción n = 4/3.
a)1,5m b) 2,0m c)2,5m
d) 3,0m e) Ninguna
PROBLEMA 19
Demuestre que en un sistema de va­
rias láminas transparentes, el rayo lumi­
noso incidente y el mismo rayo ya re­
fractado al mismo medio son paralelos.
«
*
*
*
+
*
ü
*
*
$
*
*
*
*
*
#
* '
*
«
*
#
*
#
#
*
¥
*
*
m
*
*
#
*
*
*
*
#
*
*
#
*
*
*
*
*
$
#
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
m
*
*
*
■
¥
*
*
*
*
*
SOLUCION:
1. Aplicando la Ley de Snell:
n . Sen ao = ni . Sen ai ... (1)
ni . Sen a i = n2 . Sen ... (2)
r 2 . Sen a2= n3. Sen cí3 ... (3)
n3. Sen 03 = n4. Sen 04 ... (4)
2 Aplicando la propiedad transitiva:
n . Sen a0 = n .Sen 04
Sen ao = Sen 04
Luego ao =04
Por consiguiente el rayo luminoso inci­
dente y emergente son paralelos
PROBLEMA 20
Una lámina de vidrio de caras para­
lelas se encuentra sobre la superficie libre
del agua contenido sobre un recipiente.
Determinar el ángulo de refracción sobre
el agua, para un rayo luminoso provenien­
te del aire que incide en la cara superior
de la lámina con una ángulo de incidencia
iguales a 53°'
4
nagua - g
naire —1

632. 2.
Resolución:
1. Aplicando la Ley de Snell
Aire - Vidrio:
na . Sen 53° = n . Sen a ... (1)
Vidrio - Agua:
n Sen a = n8gua Sen a ... (2)
Analizando las relaciones anterio­
res.
(1)= (2)
na . Sen 53° = nagua . Sen 0
Reemplazando valores:
4 4
1 x —= —. Sen 0
5 O
Sen 0 = §
5
Entonces: 0 = 37°
PROBLEMA 21
Un buceador se encuentra sumergido
en el fondo de un lago. Si la distancia
entre los ojos del buceador y la superficie
libre del lago es "H". Hallar el radio del
círculo luminoso, que verá sobre él. El
índice de refracción del lago es "n".
#
S
jí
*
*
*
*
*
*
*
*
*
#
$
*
*
$
*
*
*
*
$
#
*
n . Sen a = 1 . 1
Luego: Sen a = ~ .... (1)
2. Del gráfico:
r
Tan a =
H
Entonces: r = H . Tan a
Sen a
I T — - 2 - <
3)
V 1 - Sen a
3 . Reemplazando (1) en (3):
1
Tana = — —
Vn -1
En (2): r -
"El resto de la superficie se comporta
como un espejo para el buzo"
PROBLEMA 22
Un rayo luminoso incide sobre una
lámina transparente de índice de refrac­
ción "n" y espesor "d". Determinar el des­
plazamiento lateral "x" del haz emergente,
sabiendo que el ángulo de incidencia en
el aire es igual al doble del ángulo de
refracción sobre el material de la lámina.
1. El último rayo que se refracta es
aquel que su ángulo de incidencia
A
es L.
Por Snell:
1. Igualdad de triángulos:
AABD = AACD
2. Ley de Snell en A:
na¡re. Sen 2 0 = n . Sen 0
1.2 Sen 0 . Cos 9 - n . San 0

633. Cos 0 =
3 En el triángulo ABD:
Tan 6 ......x = d . Tan 6 ... (2)
ti
Pero de (1):
CONCEPTO:
Se denomina así a toda aquella superfi­
cie perfectamente pulida en la cual se pro­
duce solamente reflexión regular.
OBJETO:
Es aquel punto o conjunto de puntos a
partir de los cuales se "originan" los rayos
luminosos que van a incidir en el espejo.
IMAGEN:
Es el punto o conjunto de puntos que se
forma mediante la intersección de los rayos
reflejados o de sus prolongaciones.
Las imágenes pueden ser "reales o virtu­
ales'. En el caso de una imagen real, la
energía luminosa pasa realmente por la im­
agen virtual se forma por la intersección de
los rayos reflejados, esta imagen es vista
directamente dentro del espejo.
Todo espejo tiene convencionalmente
dos zonas bien definidas denominadas zona
real y zona virtual.
1. Zona real (Z.R):
Es aquella en el cual se encuentra el
objeto, donde cualquier distancia es po­
sitiva.
*
*
«fe
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
$
*
#
♦
*
*
*
«
fe
*
Es aquella región que se encuentra de­
trás del espejo, donde cualquier distancia es
negativa.
ESPEJO PLANO
Concepto:
Es aquella superficie plana perfec­
tamente pulida Es una superficie lisa capaz
de reflejar prácticamente el 100% de la luz
incidente. Los espejos ordinarios constan de
una lámina de vidrio que lleva en el reverso
una delgada capa de plata donde se produce
la reflexión.
Características:
1. Las imágenes en los espejos planos son
siempre virtuales, su posición parece de­
finida en el espacio detrás del espejo.
2. Las imágenes en los espejos planos di­
fieren de los objetos en que la derecha y
la izquierda están intercambiados.
3. La imagen y el objeto se encuentran equi­
distantes con respecto al espejo plano.
#
*
*
*
*
*
$
*
*
*
*
*
#
*
*
*
*
*
Z R (+ )
au s tro
■
-k—
Z V (-)
iMAfetN
■
--------V
donde: o + i = 0 , o = - i
Número de Imágenes entre dos espejos
planos

634. Experimentalmente, disponemos de una
bicolor colocado simétricamente con los
espejos planos. Si el ángulo que forman
los espejos tienen la siguiente forma
6 n = 2 n . . . ( 1)
0 Angulo que forman los espejos (en
radianes).
n : Numero entero y positivo
Entonces se observa que el objeto y las
imágenes forman un polígono regular de
n lados, inscrito en una circunferencia.
Por consiguiente el número de imágenes
será:
N = n - 1 .... (2)
Reemplazando (1) en (2):
N = —
——1
0
Si, 0 se mide en grados sexagesimales:
n = 3 §0^ _ i
*
*
m
*
*
*
*¡i
*
*
*
#
*
*
*
*
&
*
*
*
*
*
*
*
PROBLEMA 1
Una rana se encuentra frente a dos
espejos m utuam ente perpendiculares.
¿Cuántas imágenes verá la rana?
SOLUCION
1 Ve tres imágenes.
2 Dos imágenes resultan de las reflex­
iones de los rayos en cada uno de
los espejos.
3. La tercera imagen resulta cuando el
rayo de luz se refleja sobre ambos
espejos.
Un sapo se encuentra frente a dos
espejos que forman entre sí un ángulo de
120°. ¿Cuántas imágenes verá el sapo?
a) Uno b) Dos c)Tres
d) Cuatro e) Ninguna
PROBLEMA 3
En un espejo plano incide un rayo lu­
minoso. Demostrar que cuando se gira el
espejo plano un ángulo "0", sus rayos
reflejados se desvían ”2 ft".
SOLUCION
Consideremos un espejo horizontal, al
cual lo haremos girar un ángulo "6" en
sentido horario.
* 0 + (90° + a) + (90° - P) = 180°
a = p - u ... (1)

635. En el AACB, el ángulo exterior en el vér­
tice "B" es:
A
2 P = x + 2 a
x = 2 ( p - a ) ....(2)
Reemplazando (1) en (2)
x = 2 0
PROBLEMA 4
Dos espejos planos forman un ángulo
de 50° entre sí. Determinar el ángulo "6"
que el rayo reflejado forma con el rayo
incidente.
a) 50° b) 80° c) 100°
d)120° e) Ninguna
PROBLEMA 5
Una persona de estatura "H" se en­
cuentra parado frente a un espejo plano
vertical, considerando que sus ojos se
encuentran a una distancia "d" por debajo
del límite superior de su cabeza, determi­
nar:
a) La altura mínima que debe tener el
espejo.
b) A que altura con respecto al piso
debe ser colocado, tal que pueda
ver su imagen completa
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
•K
*
*
*
*
a) Teorema de los puntos medios:
APON - ATOB
Los valores de X e y son independientes
de la d.stanc¡a 'a“
PROBLEMA 6
Para el esquema mostrado, calcular la
altura mínima que debe tener el espejo
plano en la pared vertical AB, para que la
persona (1) pueda ver al muchacho (2)
íntegramante.
d) 1,0m e) Ninguna
ESPEJOS ESFERICOS
Concepto:
Se denomina así a todo aquel casquete
de espejo esférico cuya superficie interna o
externa es reflectante.
Cuando la superficie interna es la reflec­
tante se denomina espejo CONCAVO y,
cuando es la externa reflectante se de­
nomina espejo CONVEXO,
1. CONCAVO

636. 1. Centro de Curvatura (C):
Es el centro geométrico de la cual forma
parte el casquete.
2. Radio de Curvatura (R):
Es el radio de la esfera de la cual forma
parte el espejo.
3. Vértice (V):
Es el centro geométrico del espejo.
4. Eje Principal (X’X):
Es la recta que pasa por el centro de
curvatura y el vértice.
5. Foco (F):
Es aquel punto situado en el eje principal
entre el vértice y el centro de curvatura.
El foco se caracteriza porque por él pasa
los rayos reflejados a sus prolongacio­
nes, provenientes de rayos incidentes al
espejo paralelos al eje principal.
6. Distancia Focal (f):
Es la distancia que existe entre el foco y
el vértice del espejo, cumpliéndose que
dicha distancia es igual a la mitad del
radio de curvatura, f = R/2
7. Abertura (MN):
Es aquel segmento o cuerda que une los
puntos extremos del espejo, cuando la
abertura es muy grande se produce el
fenómeno de “aberración esférica", el
cual consiste en la formación de una ima­
gen borrosa de tal manera que el foco
deja de ser un punto para convertirse en
una mancha Para observar una imagen
nítida se exige que el ángulo central cor­
respondiente al arco MN debersermenor
de 20°.
*
*
*
#
*
*
♦
*
*
¥
*
«
*
$
*
*
*
*
*
#
*
<
¡*
*
*
¡»
*
*
*
♦
*
#
Rayos Principales:
Para la formación de imágenes en espe­
jos esféricos, se toman en cuenta tres rayos
luminosos como los principales, resultando
indispensables dos de ellos, y son los si­
guientes:
1. Un rayo luminoso que incide paralela­
mente al eje principal se refleja pasando
él o su prolongación por el foco.
2. Un rayo luminoso incidente que pasa él o
su prolongación por el foco se refleja
paralelamente al eje principal.
3. Un rayo luminoso incidente que pasa él o
su prolongación por el centro de cur­
vatura se refleja sobre sí misma.
*
*
*
$
*
*
Su imagen es virtual, derecha y de menor
tamaño que el objeto.

637. B) ESPEJO CONCAVO:
Su imagen es real, invertida y de menor
tamaño.
2do. Caso: El objeto en C. Su imagen
es rea), invertida y de igual
tamaño.
3er. Caso: El objeto entre C y F. Su
imagen es real, invertida y
más grande.
4to. Caso: Objeto en el foco F. No hay
imagen.
*
*
*
*
*
*
*
*
*
*
i
*
«
*
#
*
*
*
*
<
t
>
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
5to. Caso: Objeto entre F y V. Su ima­
gen es virtual derecha y más
grande que el objeto.
Ecuaciones:
CONVEXO CONCAVO
0 (+) siempre (+) siempre
i (-) siempre (+) I. real
f {-) siempre (+) I. virtual
I. Ecuaciones de los focos conjugados:
1 1 1
f ~ o + i
J II. Aumento (A)
Tamaño delalmagen
" Tamaño del objeto
*
<
¡*
*
*
*
*
*
*
*
*
*
*
*
Ü
c
*
*
*
*
*
*
*
*
*
*
*
*
*
A = —
(+) I. Derecha
(-) I. Invertida
ESPEJOS ESFERICOS
PROBLEMA 1
¿Cuál e9 el radio de curvatura de un
espejo de afeitar que da un aumento doble
de su rostro situado a 30 cm. def espejo?
SOLUCION:
El espejo cóncavo, es el único espejo
esférico, que da un aumento mayor que
la unidad (A >1).

638. Aumento =— = 2
o
£=20
i = 60 cm.
Ecuación de los focos conjugados:
2 _ ± _ 1 _
R 30 + - 60
R = 120 cm.
PROBLEMA 2
Se tiene un espejo cóncavo de 80 cm.
de radio de curvatura y un objeto de 5 cm.
de altura ubicado a 60 cm del espejo.
Determinar el tamaño de su imagen.
a) 5 cm.
d) 15 cm.
PROBLEMA 3
b)10cm. c) 8 cm.
e) Ninguna
*
*
*
*
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
«
<
¡
>
*
#
*
*
*
*
*
*
*
*
*
*
Un objeto frente a un espejo esférico
genera una imagen virtual de tamaño do­
ble, si la distancia entre el objeto y la
imagen es 30 cm. ¿A qué distancia del
espejo se encuentra el objeto.
SOLUCION:
El único espejo esférico, que genera una
imagen de mayor tamaño que el objeto
(A >1) es el espejo cóncavo.
Del dato:
o + i =30 cm .
Reemplazando (1) en (2):
¿=20 ....(1)
..(
2)
o = 1 0 cm.
PROBLEMA 4
Un objeto se encuentra frente a un es­
pejo esférico, obteniéndose una imagen vir­
tual y tamaño cinco veces, el objeto. Cal­
cular la distancia focal del espejo, si la dis­
tancia entre el objeto y la imagen es 120 cm.
a) f = - 25 cm.
c) f = - 5 cm.
PROBLEMA 5
b) f = + 25 cm.
d) f = + 50 cm.
Con un espejo cóncavo se obtiene una
imagen invertida tres veces el tamaño ob­
jeto, si la distancia que le separa respecto
a su imagen formada es de 28 cm. Hallar
el radio de curvatura del espejo.

639. Aumento = — = 3
o
Del gráfico: ¿ - o =28 cm. ......(2)
Reemplazando (1) en (2):
o = l 4 c m ......(3)
Ecuación de los focos conjugados:
2 _ ± JL
R - o + ¿
2
R 14 + 42
R = 21 cm.
PROBLEMA 6
Un objeto de 5 cm. de altura está si­
tuado a 180 cm. de un espejo convexo
esférico que tiene un radio de curvatura
de 90 cm. Determinar el tamaño de la
imagen.
a)1,0cm. b)1,5cm.
c) 2,0 cm. d) 2,5 cm.
e) Ninguna
PROBLEMA 7
Un espejo esférico cóncavo de 20 cm.
de radio se utiliza para proyectar la im­
agen de un cuerpo sobre una pantalla
situado a 110 cm. ¿Dónde debe ser colo­
cado el cuerpo y cómo se verá la imagen?
SOLUCION:
— = - + —
10 o 110
o = 11cm
Aumento =
t/
o
.... (1)
110
11
"La imagen es real, invertida y de mayor
tamaño”.
PROBLEMA 8
Un espejo cóncavo y otro convexo de
igual longitud focal f = 28 cm, estén uno
en frente de otro de tal manera que coin­
ciden sus ejes, y la distancia entre espe­
jos es de 90 cm. ¿A qué distancia del
espejo convexo habrá que colocar un ob­
jeto de altura "h" para que las imágenes
formadas tengan igual tamaño.
--------«------
*
*
#
#
*
*
*
*
*
#
*
m
*
*
*
*
*
#
*
*
*
*
*
*
*
a) 15 cm. b) 17 cm.
c)12cm. d)19cm.
e) Ninguna
PROBLEMA 9
Dos objetos se encuentran frente a un
espejo cóncavo de 60 cm. de radio de
curvatura, el primero se encuentra 10 cm.
delante del foco y el segundo 10 cm. de­
trás del foco. Determinar la distancia que
existe entre las imágenes de los objetos.
SOLUCION:
Ecuación de los focos conjugados:

640. i 1 j l .
f " o *
Cálculo para el primer objeto:
_1__ J_ JL
30 " 40 + ¿1
i, =+120cm ... (1)
Cálculo para el segundo objeto:
J ___ i I
30 ~ 20 + ¿i
¡2= - 60 cm .... (2)
De la figura, la distancia entre las
imágenes es:
d = 120+ 60
d = 180 cm.
PROBLEMA 10
Un automovilista que se encuentra de­
tenido al borde de una autopista, observa
por su espejo retrovisor convexo de radio
de curvatura 10m, y ve que un motoci­
clista se le acerca tai que en dos segun­
dos la imagen que se observa se duplica.
Si inicialmente el motociclista estaba 75m
de! auto, hallar su velocidad media.
a) 10 m/s b) 15 m/s
c) 20 m/s d) 25 m/s
e) Ninguna
PROBLEMA 11
Obtener una expresión para el aumen­
to producido por un espejo esférico, en
este caso particular para un espejo cón­
cavo.
#
*
*
*
«i
s
t»
*
m
*
*
*
*
m
*
m
*
•
m
m
m
#
*
«
#
*
*
#
#
*
*
*
«
K
*
«
I*
*
*
*
m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
#
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
ah
abv = Tag 6 = .... (I)
AR
AABV: Tg 0 = ....(II)
2. Igualando I y II:
AB ab
o ~ *
ab - i
— o
AB
3 Pero el aumento A de un sistema
óptico se define como el cociente
entre el tamaño imagen y el objeto,
de (III):
A - ——_ ~ i/
~ — ~ o
AB
Elsiqnomenos(-)sedebealhecho
que ab es negativo, ya que la ima­
gen es invertida.
PROBLEMA 12
Demostrar la ecuación de René Des­
cartes, para el caso de un espejo cóncavo.
1. De la figura:
AOPC . p = 0 + ai ....(1)
ACPI • C
X
2 = 0 + p (2)
Restando: p - ct2= ai - p
de donde: 2 p = ai + ct2 .... (3)
2 Los ángulos a i, 0.2 y p son muy
pequeños, es decir los rayos son
parciales.
T h
ai s T g a i = -
a2 s T g a i
P s Tg p =y, f = ^
Reemplazando en (3):
2 . Ü , ñ h
r o /

641. 2 _ _ ! _L
jr_~ o ¿
2
1 1 _L
f - o i'
El segmento VB tiende a cero. .

642. LENTES
CONCEPTO.
Es aquella sustancia transparente limi­
tada por dos superficies, de las cuales por lo
menos una de ellas debe ser esférica, de
modo que su espesor es despreciable en
relación a la longitud de los radios de cur­
vatura, también se les fiama 'lentes del­
gadas".
TIPOS DE LENTES
L. plano convexa
L menisco convergente
*
*
#
*
1. Lentes Convergentes:
Son aquellos lentes cuya parte central es
más ancha que sus extremos, estas lentes
se caracterizan porque hacen concurrir a los
rayos refractados provenientes de rayos in­
cidentes paralelos en un punto del plano
focal.
Son aquellos lentes cuya parte central es
más delgada que sus extremos, estas lentes
se caracterizan porque hacen divergentes a
los rayos refractados en la lente provenientes
de rayos incidentes paralelos. Los rayos re­
fractados divergentes, sus concurrentes en
un punto del plano focal.
L. bicóncava
*
«
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
L. plano cóncava
L. menisco divergente
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
*
*
*
*
*
Elementos:
1. Centro Optico (C):
Es el centro geométrico de la lente. Este
punto se caracteriza porque todo rayo
luminoso que pasa por él no sufre nin­
guna desviación.
2 . Centro de Curvatura (Ci, C2):
Son los centros geométricos de las su­
perficies esféricas que limitan la lente.

643. 3. Radio de Curvatura (Ri, R2):
Son los radios de las superficies esféri­
cas que limitan la lente.
Se denomina "R," al radio de la esfera
que está frente al objeto y '^ 2 “la radio
de la esfera que no está frente al ob­
jeto
4. Eje Principal (X' X):
Es aquella recta que pasa por los centros
de curvatura y el centro óptico.
5. Foco Objeto (Fo):
Es el foco de la lente que se encuentra
en la región donde está el objeto.
6. Foco Imagen (Fi):
Es el foco de la lente que se encuentra
en la región donde no está el objeto.
7. Foco Principal (F):
Es aquel punto situado en el eje principal
por el cual van a pasar los rayos refrac­
tados osus prolongaciones de éstos, pro­
venientes de rayos incidentes a la lente
paralelos al eje principal. El foco principal
puede ser el foco objeto o el foco imagen.
8. Distancia Focal (f):
Es la distancia que existe entre el foco
principal y el centro óptico de la lente.
9. Zonas:
Toda lente divide al espacio en el espacio
en el cual se encuentra en dos zonas
denominadas, ZONA REAL a aquella en
la cual no se encuentra el objeto y ZONA
VIRTUAL a aquella en la cual se encuen­
tra el objeto, convencionalmente. En la
zona real las distancias son positivas y en
la zona virtual las distancias son negati­
vas.
10. Aberración:
Cuando los rayos luminosos pasan cerca
a los extremos de la lente se produce el
*
m
*
*
*
*
*
#
*
*
*
*
*
*
fenómeno denominado “aberración cro­
mática” de la lente, en el cual la imagen
que se forma es coloreada como resul­
tado que la luz se dispersa o se descom­
pone en sus colores componentes.
FORMACION DE IMAGENES
$ Rayos Principales:
*
*
*
*
*
*
*
*
H
e
*
*
*
*
*
*
#
*
n
#
#
*
*
*
*
H
>
*
*
Para la formación de imágenes en una
lente se tomaran en cuenta tres rayos lumi­
nosos considerados como los principales, de
los cuales resultan indispensables solamen­
te dos resultados el tercero de comproba­
ción.
1® Un rayo luminoso que partiendo del ob­
jeto incide en la lente paralelamente al eje
principal, se refracta para luego pasar él
o su prolongación por el foco principal.
2® Un rayo luminoso que participa del objeto
incide en la lente pasando previamente él
o su prolongación por el foco NO PRIN­
CIPAL, para luego refractarse emergien­
do de la lente paralelamente al eje princi­
pal.
3® Un rayo luminoso que parte del objeto,
pasa por el centro óptico sin desviarse.

644. que el objeto.
B) Lentes convergentes: En este caso el foco principal es el foco imagen.
Su imagen es real, invertida y de mayor
tamaño.
Su imagen es real, invertida y de igual
tamaño que el objeto.
4to. Caso: El objeto en el foco
No hay imagen
1er. Caso: El objeto más allá de C2.
Z.V Z.R
1 . 1
.
2. 1. invertida
3 .1
. de menor tamaño
3er Caso: El objeto entre C2y F0.
2do. Caso: El objeto en C2
Z.V Z.R

645. 5to. Caso : Objeto entre F0 y el centro
óptico.
Z .V B Z R(+)
Su imagen es:
virtual, derecha y mayor que el objeto
ECUACIONES:
o (+) siempre
i (+) I. real (-) 1 virtual
f (+) ¿. Convergente (-) £. Divergente
A (+) I. derecha {-) I Invertida
I) Ecuación de los focos conjugados o de
GAUSS.
II) Aumento (A):
A =
tamaño imagen
tamaño objeto
A = —
o
III) Ecuación de los Fabricantes de Lentes:
n . Indice de refracción de la lente.
n0 : Indice de refracción dei medio en
que se encuentra el lente, para el
aire es igual a uno.
*
*
♦
«
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
*
*
#
$
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
V
*
*
*
*
*
*
*
*
*
*
=
t>
*
*
*
*
*
*
*
P =
,-1
Unidades: dioptrías = mt."
V) Lente equivalente al sistema:
a) En contacto
1 _ ± 1
f ” fi + f2
f. f,
b) Separadas
1 1 1 ó_
f " fi + fe fi fe
VI) Ecuación de Newton
i¿= Xi . X2
X t: Distancia del objeto al foco objeto.
X¿: Distancia de la imagen al foco ima­
gen.
f : Distancia al foco principal.
LENTES
PROBLEMA 1
En el siguiente sistema óptico, deter­
minar geométricamente el foco principal y
la trayectoria que seguirá el rayo luminoso
(1)- "

646. La lente convergente, hace concurrir a
los rayos refractados en la lente pro­
venientes de rayos incidentes paralelos
en un punto del plano focal. Todo rayo
luminoso que pasa por el centro óptico
(C), no experimenta desviación.
El foco principal se encuentra en la inter­
sección del plano focal y el eje principal
(horizontal).
PROBLEMA 2
Con una lente convergente se obtiene
una imagen de tamaño 4 veces el tamaño
dei objeto. Si dicho objeto lo alejamos 5
cm, el aumento disminuye a la mitad. En­
contrar la distancia focal de la lente.
a)18cm. b)19cm.
c) 20 cm. d) 21 cm.
e) Ninguna
PROBLEMA 3
La figura muestra una lente cuyo ín­
dice de refracción es n = 1,5.
SI, x = 30 cm ; y 60 = cm.
Hallar la distancia focal de la lente.
Imaginariamente ubicamos al objeto a la
izquierda de la lente convergente
Escribimos la ecuación de los Fabrican­
tes de Lentes:
Ri: Radio de la superficie de la lente,
frente al objeto.
Ri: X = +30 cm. (Zona Real)
R2 : Y = - 60 cm (Zona Virtual)
Reemplazando:
30 -6oj
Resolviendo:
f = + 40 cm.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
+
*
#
*
*
+
*
*
*
*
*
*
*
*
*
*
(+): Lente Convergente
PROBLEMA 4
La figura muestra dos lentes planos
convexo A y B en contacto, cuyos índices
de refracción son:
nA = 1,3 ; X = 60 cm.
ne = 1,5 ; y = 60 cm.
Hallar la distancia focal de la lente
equivalente al sistema óptico así for­
mado.
c) f = 75 cm.
e) Ninguna

647. La figura muestra una lente de material
sintético de índice de refracción n = 1,5,
sumergido en un líquido transparente de
índice de refracción n0 = 2,0. Hallar la
distancia focal de la lente. X = 40 cm.
¿La lente es convergente o diver­
gente?
LIQUIDO
----- rio—
SOLUCION:
Fórmula del Fabricante de Lentes
1 n - n0
f ~ no
J_ 1
Ri R2
n0 : Indice de refracción del medio que
rodea a ia lente
R i: Radio de la superficie de la lente,
frente al objeto.
Imaginariamente ubicamos el objeto a la
izquierda de la lente.
R-i = «
R2= X = - 40 cm.
Reemplazando:
1 (1,5-2,0)
f ~ 2,0
1
-40
Resolviendo-
f = —160 cm
(-): Lente Divergente
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
s
¡s
»
*
*
*
*
*
*
*
*
#
*
*
*
*
*
íí«
*
*
*
*
*
*
*
*
*
m
*
m
*
*
*
*
*
*
*
*
*
*
_______
i
H o t m a i l
V . X . ------------------
—
PROBLEMA 6
La figura muestra una lente de material
sintético de índice de refracción n = 1,5,
sumergido en un líquido transparente de
índice de refracción n0 = 2,0. Hallar la
distancia focal de la lente.
R = 20 cm.
¿La lente es convergente o diver­
gente?
LIQUIDO
______________________
a) f = - 80 cm. b) f =+80 cm
c) f = - 40 cm. d) f =+40 cm.
e) Ninguna
PROBLEMA 7
Delante de una lente convergente de
10 cm. de distancia focal, se coloca a 4
cm. del mismo, un objeto luminoso de 12
cm. de tamaño. Calcular el tamaño de la
imagen.
SOLUCION
Cálculo de la distancia imagen:

648. . 20
" = ~ T cm
... (i)
. . Tamaño Imagen i
Aumento = —------ — -T^rr-r- - —
Tamaño Objeto o
T.l
20
3cm
12cm 4cm
T I = 20cm.
PROBLEMA 8
La figura muestra una lente conver­
gente biconvexa de igual radio de cur­
vatura (Ri = R2). La distancia del objeto al
foco objeto es 8 cm. La distancia de la
imagen al foco imagen es 2 cm. Hallar la
distancia Imagen "ff.
a) 3 m.
d) 6 m.
b) 4 m.
e) N.A.
c)5m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
i
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
+
*
*
*
*
*
*
*
*
Un objeto está ubicado a 100 cm. de
una pantalla, ¿A qué distancia del objeto
debe colocarse una lente convergente de
distancia focal f =16 cm para que en la
pantalla se pueda ver una imagen nítida
del objeto?
SOLUCION:
Ecuación de los focos conjugados:
1
JL _±
16 - X + (100 —X)
x¿- 100x + 1 600 = 0
X1 = 20 cm
Y'¿ = 80 cm
Existe dos posibilidades, en cada caso la
imagen tendrá tamaño diferente.
PROBLEMA 10
¿A qué distancia máxima "X" de una
pantalla, una lente convergente de 4,2 cm.
de longitud focal formará la imagen de un
objeto luminoso situado a 2Qm. de la pan­
talla.
i -
— y o
20 n
a) 10 m
d) 16 m.
b) 12 m.
e) Ninguna
c) 14 m

649. La figura muestra una lente cuyo ín­
dice de refracción es n = 1,5. Hallar la
distancia focal de la lente.
X = 30 cm.
SOLUCION-
Imaginariamente ubicamos al objeto a la
izquierda de la lente divergente. Ecua­
ción de los Fabricantes de Lentes;
f
= (n -1)
Ri
J l
Ra
Ri: Radio de la superficie de la lente,
frente al objeto.
Ri : Y = - 60 cm. (Zona Virtual)
R2 : X = + 30 cm. (Zona Real)
Reemplazando:
f (1,5 1)[-6 0 30
Despejando:
f = - 40 cm.
(-): Lente Divergente
PROBLEMA 12
La figura muestra dos lentes cóncavos
A y B, cuyos índices de refracción son:
nA = 1,4
ne = 1,5
X = 40 cm.
Y = 50 cm.
o
»
*
*
&
$
4
*
*
*
*
$
*
*
*
*
&
sj*
4
*
$
*
*
*
*
*
*
*
*
*
*
4
*
Determinar la distancia focal de la len­
te equivalente al sistema óptico así for~
mado:
c) f = - 40 cm.
e) Ninguna
PROBLEMA 13
d) f = - 50 cm.
En el sistema óptico mostrado, deter­
minar geométricamente el foco principal
y la trayectoria que seguirá el rayo lumi­
noso (1).
4
*
*
*
*
*
*
*
*
*
*
*
*
*
*
«
La lente divergente, hace divergentes a
los rayos refractados en la lente pro­
venientes de rayos incidentes paralelos.
La prolongación de los rayos refractados,
son concurrentes en un punto del plano
focal.
Todo rayo luminoso que pasa por el cen­
tro óptico (C), no experimenta desvia­
ción.
El foco principal (F) se encuentra en la
intersección del plano focal y el eje prin­
cipal (horizontal).

650. Ia
PROBLEMA 14
Calcular el índice de refracción de una
lente convergente, si su distancia focal en
el agua, es el triple de su distancia focal
en el aire.
a) 1 4
d) 1,8
PROBLEMA 15
b) 1,5 c) 1,6
e) Ninguna
Una lámpara A de intensidad luminosa
16 candelas y otra B de 9 candelas distan
e^tre sí 1,4 m. ¿A qué distancia de la
lámpara A hay que colocar una pantalla
para que esté igualmente iluminada por
ambos focos?
La figura muestra el denominado "Fo­
tómetro de Bunsen".
SOLUCION:
Iluminación (A) = Iluminación (B)
l(B)
,2
“ 1 “2
I Intensidad luminosa (candela).
d : Distancia entre la pantalla y la lám­
para.
Reemplazando en (1):
16 9
(1,4 - X f
Resolviendo:
X = 0,8 m.
*
#
*
*
n
»
*
*
*
*
*
*
*
*
*
*
*
n
»
♦
*
*
m
*
*
*
*
*
*
*
<
¥
*
*
*
*
*
*
*
*
*
*
*
*
*
#
*
*
*
O
PROBLEMA 16
Una lámpara A de intensidad luminosa
25 candelas y otra B de 16 candelas distan
entre sí 1,8m. ¿A qué distancia de la lám­
para A hay que poner una pantalla para
que esté igualmente iluminada por ambos
focos?
a) 0,8 m.
d) 1,1 m.
PROBLEMA 17
b) 0,9 m.
e) Ninguna
c)1,0 m.
La cara convexa de una lente plano
convexa cuyo radio de curvatura es R y su
índice de refracción “n" se cubre con una
capa de plata y debido a esto obtendre­
mos un espejo cóncavo peculiar. Encon­
trar la distancia focal de dicho espejo (al
sistema óptico así formado).
M es punto medio de VU. La lente es
delgada, VT tiende a cero.

651. 1) El rayo incidente, paralelamente el
eje principal, se refleja en el espejo
esferico dirigiéndose al foco del es­
pejo, o sea el punto M, pero debido
a la lente se refracta y se desvia
para pasar por el foco del sistema,
el punto F.
2) Aplicando la Ley de Snell:
n . Sen a i = na . Sen a2 .... (1)
3) Los ángulos a i y 02 son muy pe­
queños de (1):
Sen ai 2 Tan ai
Sen a2 n Tan 0.2
4) De la figura:
.... (2)
h = f . Tan a2= — . Tan a.
Despejando:
f _ 5 Tanai
2 Tan 0.2
5) Reemplazando (2) en (3):
... (3)
#
*
*
*
*
*
*
*
*
*
*
*
#
*
*
♦
*
*
*
*
*
*
*
*
*
*
#
*
*
*
*
I»
*
*
*
*
*
slí
*
*
*
*
*
PROBLEMA 18
La cara convexa de una lente plano
convexa cuyo radio de curvatura es de 60
cm. es plateada y debido a esto se obtiene
un espejo cóncavo peculiar. Delante de
este espejo y a una distancia de 25 cm. de
éste se coloca un objeto. Encontrar la
distancia entre el espejo y la imagen del
objeto, si el índice de refracción de la lente
es igual a 1,5.
SOLUCION
1. Usando el resultado anterior deter­
minamos la distancia focal del sis­
tema óptico
, R , , 60 cm
f = — entonces f = — - —
2n 2x1,5
Luego: f = 20 cm
2. Ecuación de los fabricantes de es­
pejos esféricos:
1 1
f ~ o +
i = 100 cm.

652. PROBLEMA 19
Un objeto se coloca a 14 cm. delante
de una lente convergente de 10 cm. de
distancia focal. Otra lente convergente de
7 cm. de distancia focal se coloca a 40 cm.
detrás de la primera lente. Determinar ia
posición de la imagen.
SOLUCION:
1 Cálculo de la posición de h
=
=
> = 35 cm.
2. De la figura: ¿2+ o2 = 40 cm.
Entonces: 02 = 5 cm.
3. Cálculo de la posición de imagen (I2)
1 1 1
*1 '= 01 + i /
1 1 1
10 =
: 14 + '1
1 = 1 1
f.
r = 17,5 cm.
La imagen se forma a 17,5 cm. a la
izquierda de la segunda lente.
<
¥
*
*
i
*
#
*
$
*
*
#
*
*
*
*
W
#
*
*
#
*
*
*
*
*
*
#
*
¥
#
*
&
$
*
*
*
+
*
*
*
*
*
*
- -_:
■
■
■
: ........ ■
■
■
■
_A Vq
I PRINCIPIO DE FERM AT 4
A
Un soldado de caballería debe llevar una
parte desde el punto A a la tienda de cam­
paña de su jefe, el cual se encuentra en el
punto C (ver figura). Le separan de dicha
tienda dos zonas, una formada por arenas
profundas y otra por un prado, divididas entre
sí por la línea recta EF. Por la arena, el
caballo marcha con la mitad de la velocidad
que por el prado. ¿Qué camino deberá seguir
el jinete para llegar en el tiempo mínimo a la
tienda de su jefe?
En el segmento EF, existe un punto de
“Refracción'' donde se cumple la siguiente
relación:
V i _ V 2
Sen a ” Sen p
“Toda onda electromagnética y en par­
ticular la luz busca el camino más rápido ".

653. El principio de Fermat, es compatible con
la Ley de Snell (óptico).
En 1 650, el matemático francés Pierre
de Fermat (1 601 - 1 665) descubrió un
notable principio que actualmente expresa­
mos a menudo en los siguientes términos:
"Un rayo luminoso que va de un punto a
otro sigue una trayectoria tal que, comparada
con otras trayectorias cercanas, el tiempo
que emplea para recorrerla es mínimo".
También se puede enunciar de los si­
guientes modos:
”Toda onda electromagnética, en particu­
lar la luz busca el camino mas rápido”.
"Al pasar de un punto a otro, el rayo
luminoso elige el camino para el cual el tiem­
po de propagación es mínimo".
Las leyes de reflexión y la de refracción
se pueden derivar fácilmente de este prin­
cipio.
No entraremos en más detalles acerca de
cómo se puede usar el principio de Fermat
para trazar el camino de un rayo en un medio
no homogéneo, sino que sólo verificaremos
que este principio es compatible con la ley de
Snell.
PROBLEMA 1
Sobre una mesa de billar, la bola 13
situado en A pretende chocar a la bola 7
situado en B, chocando, previamente la
banda horizontal.
Si la velocidad de la bola es 0,5 m/s y
todos los choques son perfectamente
elásticos, hallar el tiempo mínimo emplea­
do. Las dimensiones, se indica en la fi­
gura.
" t
ü f
20on
*
*
*
$
*
*
*
$
*
#
*
♦
«
*
*
*
*
*
*
*
*
s
H
*
$
*
*
*
$
«le
«
H
*
*
«
I*
*
*
*
*
*
*
*
*
*
*
m
*
*
#
*
*
1. La bola N° 13 puede seguir muchas
trayectorias pero la más rápida será
cuando se comporta como un rayo
luminoso y la banda horizontal como
un espejo.
De la figura se puede observar que
el espacio recorrido por la bola es
igual al espacio recorrido en la linea
recta hacia la imagen de la bola 7
AÑ + ÑB = AB = 100 cm ....(1)
2. Cálculo del tiempo mínimo
_ e AN + NB
V ~ V
Reemplazando (1) en (2):
10Ocm
(2)
t =
0,5
m
t = 2s
PROBLEMA 2
Juanito se encuentra en la posición A
de un lago, donde desarrolla una veloci­
dad de 3 m/s y en la orilla desarrolla una
velocidad de 5 m/s. Determinar el tiempo
mínimo que emplea en llegar a la cabaña
situado en la posición B. Las dimensiones
se indica en la figura.
(Ver figura)
390m

654. SOLUCION-
1. Cálculo del tiempo mínimo:
t = ti + t2
, AN NB ...
I = v7 + W - (1)
2. Del gráfico
x + y = 390 m ....(2)
3. DelprincipiodeFermat:
n i . Sen a = n2. Sen 90°
C „ C
T, v ¡
„ Vi
Sen a = —
V2
Luego:a = 37°
4. En el AMN
x 3
Tan a = —— = —=> x = 90 m
120C 4
en (2): y = 300 m.
5. Otra vez en el ! AMN
120 _ 1
_ 3
c 3
Sen a = —
5
Cos a = -
AN
ÁÑ = 150 m y ÑB = 300 m
Reemplazando en (1):
150 300
t = 110s
*
*
m
*
$
*
*
*
*
*
*
*
*
*
*
*
TEORIA ESPECIAL DE LA
RELATIVIDAD
Por relatividad queremos decir la apa­
riencia que presenta la naturaleza a un ob­
servador y su relación con la apariencia que
presenta la naturaleza a otro observador,
que puede estar en movimiento con respecto
al primero.
Por ejemplo, un avión de guerra se des­
plaza a velocidad constante respecto a ¡a
Tierra, si el piloto abandona una bomba res­
pecto al avión la trayectoria que describe el
proyectil es diferente para el piloto y un ob­
servador en la Tierra.
#
*
*
*
m
*
*
*
*
#
*
*
*
El hombre en tierra observa que la trayec­
toria que describe el proyectil es una pará­
bola
El piloto de avión observa que el proyectil
cae en línea recta
,00 C

655. Luego:
Donde
Como: Vi -p 2 <
De este modo, la longitud de la barra en
movimiento resulta ser menor que su longi­
tud propia.
*
*
#
*
*
♦
*
*
*
#
#
*
#
*
*
*
Sea que la barra se mueve con relación
al sistema "S* de referencia a velocidad
constante "V" en línea recta y que la longitud
de la barra en el sistema de referencia "S“
ligado con ella, es igual a “L".
Nuestro problema es determinar la longi­
tud “L” de la barra desde el sistema "S".
La longitud “L” , medida en el sistema de
referencia "SB
I, donde la barra está inmóvil,
se denomina Longitud propia.
Que la barra se mueve con velocidad
constante "V" respecto al sistema "S“ de
referencia o que el sistema de referencia "S"
se mueve respecto a la barra con una velo­
cidad constante V" es físicamente idéntico.
PROBLEMA NB1
La barra en el sistema de referencia
ligado con ia barra, su longitud
propia es L’ = 5rn., en tanto que el sistema
"S", con relación al cual la barra se mueve
a la velocidad V = 4/5 C. Hallar su longitud
en movimiento, respecto al sistema de
referencia “S“.
#
*
*
*
*
#
#
*
#
*
«
#
#
*
*
Usando la transformación de Lorentz.
L = L’ . ( V l - p 2 ) ....(1)
Pero, p = — , para nuestro caso:
O
p=-
Reemplazando en (1):
P2 = ^
p 25
i L < L ’ i
*
«
*
*
*
L = 5m .
fi) - L = 3 m.
1
5
J
Esta transformación de coordenadas del
sistema S’ a "S" es denominado "Transfor­
mación de Lorentz" debido a que fue ob­
tenido por primera vez por el físico holandés
Hendrik Lorentz, en 1 890, en conexión con
el problema del campo electromagnético de
una carga eléctrica en movimiento
#
*
*
4
>
*
0
*
Así pqes, la longitud de una misma barra
resulta ser diferente en distintos sistemas
inerciales de referencia. Con otras pala­
bras, la longitud es un concepto relativo
que tiene sentido sólo respecto a uno u
otro sistema de referencia.

656. M - S 6 o O O
9 -
o L _____
Jll .■
■
■
W B
r
L=3m
I V
^==t!lll!ll lililí III iiinnv— —
v _ y
■
"
ítr-irran'
■
t -
.
1
"nevj1
--
.
vív.
r"
"^i
Para nuestro caso:
p - f - 02= !
Reemplazando en (1):
x = 4m
[ * l -
X
II
ro
3
¿ )
*
*
*
*
*
*
PROBLEMA N92
Una lámina de forma rectangular en el
sistema de referencia "S’“, ligado al rec­
tángulo, tiene longitudes propias x’ = 4m,
y’ = 2m. El sistema "S"' se mueve con
respecto al sistema "S" con una velocidad
constante V = >/3/2C. Hallar las dimensio­
nes de la lámina respecto al sistema iner­
cial "S“.
- Señaiamos, que la contracción se refiere
sólo a las medidas longitudinales de los
cuerpos en la dirección del movimiento,
las medidas transversales no varían, por
lo tanto: y = y' = 2 m.
La contracción de la longitud se da en el
eje x paralelo al movimiento. Usando la
transformación de Lorentz.
X = X'. Vi - p2 , p = ~ ..(1)
Para el sistema de referencia
”S" x = 2m , y = 2m.
*
*
*
$
*
*
*
*
*
*
*
*
*
#
*
*
♦
♦
*
*
j
¡*
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
$
>
¡»
*
*
*
#
*
PROBLEMA Ne3
En el sistema "S"' de referencia se
encuentra una barra inmóvil de L' = 5m de
longitud, orientada un ángulo, 0’ =37° res­
pecto al eje X’.
Encontrar su longitud L y el ángulo 6,
correspondiente al sistema "S" de refe­
rencia. S’ se mueve a velocidad constante
v = %
Í7/4 C respecto ai sistema "S".
No hay contracción de la componente
perpendicular al movimiento, por lo tanto:
y = y’ = 3rn
Existe contracción de la componente pa­
ralela al movimiento.
x = x .... (1)

657. x = 4m .
/ 31
14
=» x - 3m
y )
Luego:
L = "/x2+ y2 = 3>/2 m
_ . y 3m .
Tan 6 = = - — = 1 =>
x 3m
2. Dilatación del tiempo:
6=45°
En la teoría de la relatividad se acostum­
bra hablar de la comparación de la
marcha de los relojes idénticos en dife­
rentes sistemas inerciales de referencia.
Un intervalo de tiempo puede definirse
como el tiempo que transcurre entre dos
eventos, medido por un observador.
Un evento es una ocurrencia específica
que sucede en un punto particular del
espacio y en un tiempo particular.
o
>
*
<
t»
*
n
*
*»
*
*
*
*
*
*
*
*
*
*
*
*
*
*
0
«
*
«I
o
»
m
*
o
»
*
<
*
■
<
¡
í
*
$
Así, en función de estas definiciones,
cuando la masa de un péndulo alcanza
su máxima altura durante una oscilación,
esto constituye un evento. Después de
un cierto perforado de tiempo retornará a
la misma posición, esto es un segundo
evento.
El tiempo transcurrido entre dos eventos
es entonces un intervalo. Así un intervalo
es el tiempo que toma hacer algo: oscilar
para un péndulo, girar alrededor del nú­
cleo para un electrón, latir para un co­
razón, etc.
El reloj asociado al sistema de referencia
S’ se mueve con velocidad constante "V"
en línea recta respecto al sistema “S" de
referencia.
Supongamos que, estamos midiendo el
periodo de un péndulo oscilatorio respec­
to al sistema de referencia S’ el cual nos
da un valor T ”, el mismo fenómeno me­
dido con un reloj en el sistema “S" indi­
cará T igual a:
Donde:
Además:
1 - < 1
i reposo > T ’i
movimiento
Es decir, el mismo reloj en diferentes
sistemas inerciales de referencia marcha
de modo distinto
“El reloj en movimiento marcha más len­
tamente que el que está en reposo”

658. El tiempo registrado por un reloj que se
mueve junto con un cuerpo [péndulo] en
el que transcurre algún proceso, se de­
nomina “tiempo propio" de este cuerpo y
se designa por T . Como se puede obser­
var de la relación anterior el tiempo propio
es más corto.
"Los relojes en movimiento acelerado,
respecto a otro, marchan más despacio
que los estacionarios”.
Cálculos detallados, que salen de los lí­
mites de la teoría especial de la Relativi­
dad, muestran que el reloj que se mueve
con aceleración, marcha con mayor len­
titud, respecto a otro estacionadp.
PROBLEMA
Dos hermanos mellizos a la edad de 20
años se separaron. Uno de ellos, A sale en
un cohete hacia una estrella, con velocidad
V3
constante V = — C. y el hermano B, se
queda en el planeta Tierra llevando una vida
normal
Cuando el hermano A llega al otro sis­
tema estelar, otro planeta, su reloj indica un
intervalo de tiempo igual a 30 años
Edad de los mellizos A y B 20 años.
r
1 986 i
£
1 le
4
H í ■ ■ -
I . .....
*
*
♦
*
*
*
*
*
*
*
*
*
*
*
*
*
♦
*
*
*
*
*
*
*
*
#
*
*
i
*
+
*
*
*
#
*
*
*
*
*
*
#
*
*
*
*
*
*
$
*
*
*
*
*
*
*
*
*
Los hermanos A y B se despiden en 1 986
cuando ambos tienen la misma edad, 20
años, y tienen relojes idénticos.
El mellizo A llega al otro planeta en el año
2 016 respecto al sistema de referencia iner-
cial [S'] ligado al cohete T = 30 años. Según
la transformación de Lorentz, el tiempo trans­
currido para el hermano B será:
T =
T
V i - p 2
. - ( 1 )
En este caso
p = — = —
p C 2
Reemplazando en (1):
30 años
T = ■
0,5
Cuando A llegó al otro planeta, B en la
Tierra tiene 80 años, respecto a “S".
En otro planeta, bajo otro cielo el her­
mano A. Edad = 50 años.
r
L / ;
2 016
■ •
En la tierra el hermano B.
Edad = 80 años.
^------- ------¿
n;
2 076
í » . .

659. 3. La masa aumenta:
La masa en reposo "m0“de una partícula,
respecto al sistema de referencia inercial
’S” .
La masa aumenta cuando se mueva res­
pecto a un sistema de referencia, en ese
caso el sistema S de referencia, el valor de
la masa es:
Donde
m = masa de la partícula en movimiento.
P = ^ < 1
- La masa “m" se denomina "relativista".
- Esta última, como se ve de la ecuación
anterior es mayor que la masa en reposo
y depende de la velocidad V de la par­
tícula. ,
- De este rríodo, llegamos a una importante
deducción. La masa relativista de la par­
tícula depende de su velocidad
- Con otras palabras, la masa de una mis­
ma partícula será diferente en los distin­
tos sistemas inerciales de referencia.
- A diferencia de la masa relativista, la
masa en reposo "mo" de la partícula es
una magnitud invariante, es decir, igual
en todos los sistemas de referencia.
- Por esta causa se puede afirmar que
precisamente la masa en reposo "mo”es
la característica de una partícula.
Cuando la velocidad de la partícula V es
despreciable comparada con la veloci­
dad C, de luz en el vacío, la masa rela­
tivista tiende a la masa en reposo.
Si:
=> m = m0
Este es el caso de la mecánica c'ásica,
movimientos lentos comparado con la ve­
locidad de la luz.
PROBLEMA
Una partícula cuya masa en reposo
mc = 15 gramos se mueve con una velo­
cidad constante V = V3/2 C respecto a un
sistema de referencia "S”. Hallar la masa
relativista respecto al sistema "S“
* La masa en reposo respecto al sistema
S, m0 = 15g.
f
y i Si: V = 0
0 f , Q .
V j
De la ecuación que relaciona la masa en
reposo con la masa relativista:
m = •
m0
Vi - p 2
Para nuestro caso:
r
P - c - 2 =»
....(1)

660. 15 gramos
m = -
0,5
Luego:
m = 30 gramos
La masa relativista es el doble de la masa
de la partícula en reposo.
4. Energía Cinética de la partícula rela­
tivista:
La energía cinética de una partícula en
movimiento con una velocidad y compa­
rable con la velocidad de la luz, C en el
vacio es:
.... (1)
Esta es la expresión de la energía ci­
nética relativista:
f
V
V
---------------- - . - V
Donde:
m0 = masa de la partícula en reposo.
m = masa relativista de la partícula
C = Velocidad de la luz en el vacío.
- La masa relativista de la partícula en
reposo es igual a:
m = m0
- Por consiguiente en (1) la energía
cinética de la partícula en reposo es
igual a cero.
Ek = Cero
- La masa relativista en función de la
masa en reposo:
m0
m =-
Vi-p2
Reemplazando (2) en (1) tenemos:
.... (2)
*
*
*
*
*
$
$
ft
*
*
$
*
*
*
*
$
$
#
*
$
$
«
$
o
$
*
*
<
¡
s
$
*
#
$
$
*
$
*
*
*
*
*
$
*
*
*
*
«
*
*
*
P =
V
.... (3)
Debemos recordar que en mecá­
nica clasica la energía cinética es:
Ek = m0 . (4)
Si la velocidad de la partícula es
pequeña comparada con C, enton­
ces la fórmula (3) pasa a ser igual a
la fórmula (4); Cerciorémonos si:
P « 1
Para esto hacemos uso de la fór­
mula del binomio de Newton, según
la cual:
1
;= < 1 -p 2)-1/2=
= 1 ^ P 2 + | P 4
Cuando p « 1 podemos limitarnos a los
dos primeros términos de la serie y en­
tonces reemplazamos en (3):
Ek = m0 . Cz 4 - p2 - 1
Ek= m 0 .C 2 . |
Pero:
V
Ek = mc . C
Finalmente:
2 1
2
Ek = ^ . m0 . V2
- Por lo tanto, a grandes velocidades
la energía cinética de la partícula se
determina por la fórmula (3) rela­
tivista diferente a:

661. - Señalemos que no se puede escribir
la fórmula:
Ek =
mV
Donde m es la masa relativista.
PROBLEMA N» 1
Una partícula en reposo tiene una ma­
sa m0= 1,0 kg, si la partícula se mueve con
una velocidad constante, v = ^3. C/2 ,x
cuál es el valor de su energía cinética,
respecto al observador [S].
SOLUCION:
Masa en reposo: m0 = 1,0 kg.
Fórmula de la energía cinética relativista:
Ek = ( m - m 0) C 2 ....(1)
Calculo de la masa relativista:
m0
m = -
1 - p 2
Donde:
R - Y - 2 Ü
.... (2)
Reemplazando datos en (2):
m
1,0 kq.
4
La masa se duplica respecto a m0
Reemplazando en (1):
$
<*
*
*
«
*
*
*
#
+
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
<
s
*
#
*
*
#
*
*
*
♦
*
*
*
#
*
*
*
*
*
*
*
*
*
m
*
*
*
*
*
*
*
*
*
Ek = (2kg - 1kg). 32 . 1016 ~
s
Ek = 9 . 10,6J
Debemos recordar que:
C = 3 . 10e m/s
PROBLEMA 2
¿Qué trabajo es necesario realizar pa­
ra aumentar la velocidad de una partícula
de masa en reposo m0 = 1 gramo desde
Vi = 0,6C hasta V2 = 0,8C
Aplicando el teorema de la energía ci­
nética conocido en mecánica clásica- “El
trabajo realizado por todas las fuerzas es
igual a la variación de la energía cinética".
W = Ek(final) - Ek(inicial) .... (1)
Pero la energía cinética relativista es:
Ek = (m - m0) C2
Reemplazando en (1):
W = (m2- m0)C2 - (mi - m0)C2
W = ( m 2 - m i ) C 2 ....(2)
Cálculo de la masa relativista:
ÍTÍq ITio m 0
mi =
rr»2=
V í —0,36 0,8
m0 m0 mQ
/1 - 0,64 0,6
V2 V2
2 1 P 2
PI = - 2 =0,36, p‘ = - f =0,64

662. E0 = M0 . C2 .... (3)
5) Ley de Interacción de la masa y la
energía:
Albert Einstein llegó a la siguiente deduc­
ción fundamental:
La energía tota! del cuerpo (o sistema de
cuerpos), independientemente de que ti­
po de energía ella se componga [cinética,
eléctrica, química, etc.], se liga con la
masa de este cuerpo por la relación:
E = M . C 2 ....(1)
E : energía total del cuerpo,
m : masa relativista del cuerpo,
c : velocidad de la luz en el vacío.
Para evitar incompresiones prestamos
atención que en la energía total E no se
incluye la energía potencial del cuerpo en
el campo externo, si tal actúa sobre el
cuerpo
- Esta fórmula expresa una de las
leyes más fundamentales de la na­
turaleza.
- Se puede escribir de otro modo la
energía total del cuerpo:
E = Mo. C2 + Ek .... (2)
m0 es la masa en reposo del cuerpo.
Ek : es la energía cinética del cuerpo
- De aquí (2) se deduce directamente,
que el cuerpo en reposo (Ek = 0)
también posee energía.
*
#
“Esta energía se denomina energía de
reposo o energía propia".
Vemos, que la masa de un cuerpo que en
mecánica clásica actuaba como medida
de ia inercia (en la segunda Ley de New­
ton) o como medida de acción de gravi­
tación (en la Ley de gravitación univer­
sal), ahora actúa como una nueva fun­
ción, o sea, como la medida del Conteni­
do de energía del cuerpo.
Incluso el cuerpo en reposo posee según
la Teoría de la relatividad, reserva de
energía, es decir, la energía de reposo.
¿Qué, energía de reposo posee una par­
tícula cuya masa en reposo es m0 = 1
gramo?
De la ecuación:
Eo = m0 . C2 =1 g 32 . 1016—
Eo = 9 . 1013J
Es la energía en reposo .. imagínate.
La variación de la energía total del cuerpo
(o del sistema de partículas) va acom­
pañada por la variación equivalente de su
masa.
(mi - m¡) =
( E f - E ¡ ,
Durante los procesos macroscópicos co­
munes la variación de la masa del cuerpo
es extraordinariamente pequeña, inac­
cesible para la medición.
Esto se puede ilustrar en los siguientes
ejemplos:
1er. Ejemplo:
Para lograr un satélite de masa m0 = 100
kg. a la órbita alrededor de la Tierra, le
comunicamos la velocidad de V = 8 km/s.
Esto significa, que su energía aumenta
en:
.(1)
El aumento correspondiente de la masa
del satélite será:
Am =
A E m0 V
(2)

663. Reemplazando datos numéricos en la
ecuación (2) tenemos:
Am = 3,5 . 10-8 kg.
La masa del satélite a aumentado debido
al aumento de la energía, se puede ver:
2
Etotal —moC + Ek
p "
I p
Etotal = moC1
-+ —moV¿
2do. Ejemplo:
Un resorte con coeficiente de elasticidad
k = 1 OOON/cm, se comprime en x = 1 cm.
Con esto el resorte adquiere la energía:
E ~ 2 k ' x2 - 0 )
El aumento correspondiente de su masa
será:
Am =
AE_
AC2
... (2)
Reemplazando (1) en (2):
m =
Inicial Mnal
De los datos:
A m = 0,50 .1 0-16 kg.
“La masa del resorte a aumentado”.
3er. Ejemplo:
Para calentar un litro de agua desde 0
hasta 100°C se le comunica la energía:
AE = m Cp. A t ... (1)
joule
donde, Cp = 4,2 es la capacidad
gr. °C
calorífica del agua a presión constante, At es
la diferencia de temperaturas.
El aumento correspondiente de la masa
del agua será:
Am = - ... (2)
Reemplazando (1) en (2):
m . Cp . t
Am = -
C2
De los datos numéricos:
A m = 0,47 . 10-10 kg.
“La masa del agua a aumentado"

664. BIBLIOGRAFIA
I. TEXTOS DE TEORIA
1. Título: Física
Autor: Marcelo Alonso - Edward Finn
2. Título: Introducción a la Física
Autor: Marcelo Alonso - Virgilio Acosta
3. Título: Física - 1; 2; 3; 4
Autor: Piórishkin - Ródina, Ed. MIR
4. Título: Curso de Física General
Autor: Landau - Lifshitz, Ed. MIR
5. Título- Física Molecular
Autor: A. Kikoín, Ed. MIR
6. Título: Física Molecular
Autor: A.N. Matveev, Ed. MIR
7. Título: Fundamentos de Electrodinámica
Autor: N.N. Fiódorov, Ed. MIR
8. Título: Electricidad y Magnetismo
Autor: A.N. Matvéet, Ed. MIR
9. Título: Fundamentos de ia Teoría Electromagnética
Autor: Reditz - Milford
10 Título: Curso Breve de Mecánica Teórica
Autor. Simón Targ, Ed. MIR
II. TEXTOS DE PROBLEMAS
1. Título: Problemas de Mecánica Teórica
Autor: I. Mesherski, Ed. M|R
2. Título: Problemas de Física
Autor: O. Ya. Sávchenko, Ed. MIR
3. Título: Problemas Seleccionados de la Física Elemental
Autor: I.M. Saráeva, Ed. MIR
4. Título: Problemas de Física
Autor: Irodov, Ed. MIR
5. Título: Problemas de Física General
Autor: V. Volkenshtein, Ed MIR
6. Título: Problemas de Física
Autor: S. Kósel Ed. MIR