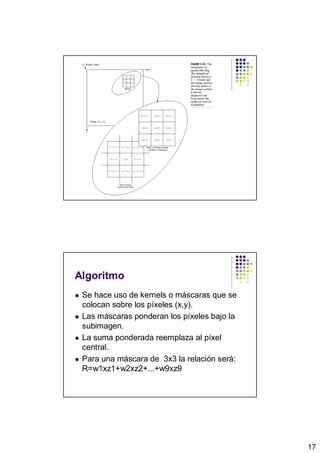
El documento describe diferentes técnicas de procesamiento digital de imágenes como mejora de imágenes, histograma, aumento y disminución de brillo, corrección de contraste, funciones de transformación, ecualización de histograma, filtrado espacial y de ruido. Explica conceptos como histograma, función de transferencia, kernel, convolución y cómo estas técnicas se pueden aplicar para mejorar atributos de una imagen como brillo, contraste y eliminar ruido.

1. Procesamiento Digital
de Imágenes 2
Profesor: Andrés Flores
Mejora de imágenes
Se busca transformar la imagen mediante
una relación matemática con la intención de
mejorarla.
La mejora se puede realizar en el dominio
espacial o el domini
1

2. El Histograma
Es la representación gráfica de las frecuencias
relativas con las que aparecen los distintos colores
en una determinada imagen.
Proporciona información sobre el brillo y el contraste
de la imagen, y puede ser utilizado para ajustar
estos parámetros, eliminar ciertas tonalidades
molestas, etc.
Es un función que muestra, para cada nivel de gris,
el número de pixels de la imagen que tienen ese
nivel de gris.
2

3. Algoritmo
Sea Imagen la variable que contiene la imagen.
int Histograma[256];
for (i=0;i<AnchoImagen;i++)
for (j=0;j<AltoImagen;j++)
Histograma[Imagen[i][j]]++;
3

4. Nos proporciona información global de la
imagen.
Nos da idea acerca de la iluminación (brillo) y
el contraste de la imagen.
4

5. Aumento del brillo (sumando 30 a cada pixel)
Disminución del brillo (restando 30 a cada pixel)
5

6. Contraste
El contraste mide, en cierto modo, el rango
dinámico de los colores en la imagen, es
decir, una imagen muy contrastada tiene un
amplio abanico de colores (o tonos de gris)
desde valores muy bajos a valores muy altos.
Para una imagen con poco contraste los
colores están muy juntos, el margen
dinámico es pequeño.
Imagen con buen contraste
6

7. Imagen de bajo contraste
Funciones de Transformación
Son operaciones que se realizan sobre cada
píxel y están representado mediante una función.
7

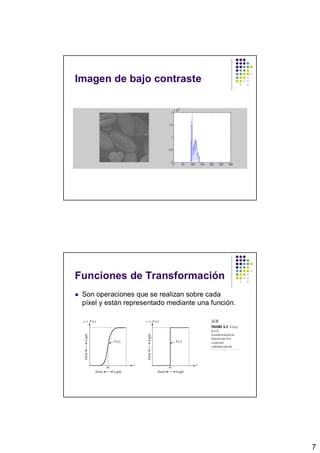
8. Función en el dominio espacial se
representa: g(x,u))= T[f(x,y)]
f es la imagen de entrada.
g es la imagen procesada.
T es un operador que actúa sobre f definido
en algun entorno de (x,y).
Algunas Funciones de
transfomación
8

9. Negativo
La operación sobre cada uno de los píxeles
de nuestra imagen en escala de grises:
nuevo_pixel=255-viejo_pixel
Imagen de
salida
Imagen de entrada
Ejemplos
9

10. Función Logarítmica
10

11. Corrección Gamma
En un monitor o en un
televisor, la señal que le
entra es un voltaje que en
la pantalla del tubo de rayos
catódicos se transforma en
luz que nosotros vemos.
La relación es
aproximadamente
cuadrática. La relación no
lineal entre luz emitida y
tensión de entrada se g = c. f γ
puede expresar.
Compensación
11

12. Corrección Gamma
Aplicación en Imágenes
12

13. Ecualización del Histograma
Si dividimos cada componente del
histograma por el número total de píxeles
que tiene la imagen, obtenemos una función
de probabilidad (fdp) de cierto tono de gris en
la imagen.
Podemos hallar la función de distribución
(FD) de esta fdp. Pues si usamos la FD como
función de transferencia de la imagen de
entrada, obtendremos una imagen igualada o
ecualizada.
13

14. El histograma de una imagen digital con L niveles de gris en
la amplitud de [0;L - 1], como una distribución de
probabilidad
donde:
rk es el k-ésimo nivel de gris,
nk es el número de píxeles de la imagen con tal nivel de gris,
n es el número total de píxeles, y
k = 0, 1, 2, … , L - 1 nivel de gris.
Proceso de Ecualización
Se desea que el histograma exprese una distribución uniforme
de todos los píxeles.
Esto se consigue determinando el Histograma Acumulado. Y
aplicándolo como función de Transformación sobre la imagen.
Con esto se consigue realzar el contraste de la imagen
para k = 0, 1… L - 1, y donde Imax = L - 1 sirve para escalar al
máximo nivel de gris.
14

15. Ejemplos
15

16. Filtraje Espacial
Los filtros lineales realizan una operación
conocida como convolución discreta
bidimensional, entre la imagen y un filtro.
Un filtro lineal estará compuesto por:
Matriz de Coeficientes coef[i][j]: pueden ser de
3x3, 5x5,…
Bias (bias): valor de continua a añadir al resultado
de la operación sobre cada pixel
Factor de Escala (factor): Para normalizar el
resultado
16

17. Algoritmo
Se hace uso de kernels o máscaras que se
colocan sobre los píxeles (x,y).
Las máscaras ponderan los píxeles bajo la
subimagen.
La suma ponderada reemplaza al píxel
central.
Para una máscara de 3x3 la relación será:
R=w1xz1+w2xz2+...+w9xz9
17

18. w1 w2 w3
w4 w5 w6
z1 z2 z3
w7 w8 w9
z4 z5 z6
Máscara
z7 z8 z9
SubImagen
18

19. Tipos de Filtros
Dependiendo de las ponderaciones de las
máscaras (kernels) se tienen:
Filtros Suavizantes (smoothing, blurring)
Pasabajo
Filtros Realzantes (sharpening).
Pasaalto
Diferenciales.
Filtros suavizantes
Suavizado de la imagen. Producen un cierto
desenfoque de la misma. Tienden a hacer
una media de tono entre el píxel que
procesamos y sus vecinos, dándole mayor o
menor peso a uno o a otros según la
intensidad de desenfoque deseada.
19

20. Filtros suavizantes
20

21. Filtros Realzantes
(Sharpening)
Producen un realzado de los bordes que
aparecen en la imagen. Marcan más la
diferencia entre el píxel procesado y los de
su vecindad (de ahí que usen valores
negativos en la matriz).
21

22. Filtros Realzantes
(Sharpening)
22

23. Filtros Gaussianos
Corresponden a kernels que tienen una
distribución Gaussiana de dos dimensiones
Permiten suavizar una imagen.
Se determina el kernel mediante la relación:
Ejemplos
Filtrado con
Sigma = 3
Imagen Original Filtrado con
Sigma = 1
23

24. Filtraje de ruido
Imagen con ruido
Filtro Mediana
Filtro no Lineal
Consiste en escoger una máscara o kernel.
Generalmente cuadrada de 3x3, 5x5, etc.,
aunque puede ser de cualquier forma
Se reemplaza el píxel central por la mediana
de los píxeles.
24

25. Ejemplo
ejemplos
Imagen Original Imagen con
ruido Impulsivo
25

26. Al aplicar filtro
Luego de aplicar filtro Luego de aplicar filtro
mediana de 3x3 mediana de 5x5
Comparación
Luego de aplicar filtro Luego de aplicar filtro
mediana de 3x3, 3 veces promedio de 5x5
26