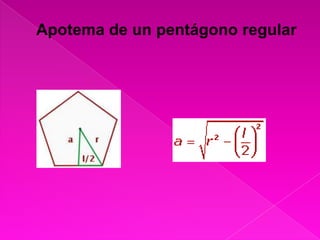
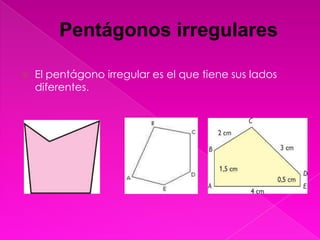
El documento describe las propiedades de los pentágonos regulares e irregulares. Un pentágono regular tiene todos sus lados iguales y sus ángulos internos miden 108 grados. El perímetro de un pentágono regular se calcula multiplicando la longitud de un lado por cinco.

1.  Pentágono. Denominado en geometría,
como polígono de cinco lados y cinco
vértices. Pueden ser regulares o
irregulares.

2. Pentágonos regulares
 El pentágono regular es aquél que tiene
todos sus lados iguales.

3. Elementos de un polígono regular
Centro
 Punto interior que equidista de cada vértice
Radio
 Es el segmento que va del centro a cada vértice.
Apotema
 Distancia del centro al punto medio de un lado.

4. Propiedades
 Los lados son iguales
 Los ángulos internos son congruentes.
 Cada ángulo interno mide 108 grados.
 La suma de los ángulos internos de un pentágono
regular es de 540° ó 3π radianes.
 El apotema.

5. Ángulos de un pentágono
 Suma de ángulos interiores de un pentágono = (5 −
2) · 180° = 540°
 El valor de un ángulo interior del pentágono
regular es: 540º / 5 = 108º
 El ángulo central del pentágono regular mide: 360º
/ 5 = 72º

6. Diagonales de un pentágono
 Número de diagonales = 5 x (5 − 3) / 2 = 5

7. Apotema de un pentágono regular

8. Perímetro de un pentágono regular
 Perímetro = 5 · l

9. Área de un pentágono regular

10. Pentágonos irregulares
 El pentágono irregular es el que tiene sus lados
diferentes.

11.  El área de un pentágono convexo regular de
lado a se puede obtener de la siguiente
fórmula:
 De forma general si tenemos que el radio de la
circunferencia circunscrita es ru
 o también:

12.  Siempre que supongamos que el pentágono tiene
lado a:
 ó también:
 Para obtener el perímetro P de un pentágono
regular, multiplíquese la longitud t de uno de sus
lados por cinco (el número de lados n del
polígono).