Jorge Didier Obando Montoya, profile picture
Subido porJorge Didier Obando Montoya
DOCX, PDF234 vistas

Plan de area matematicas 2014 (1)

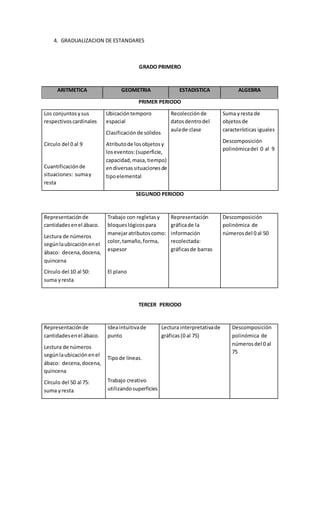
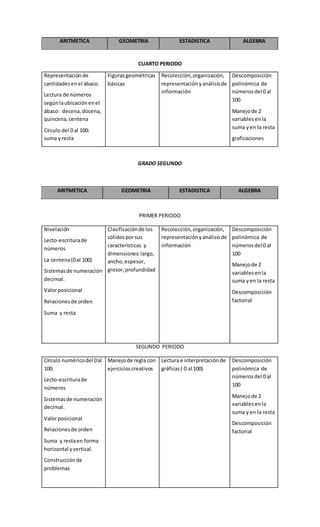
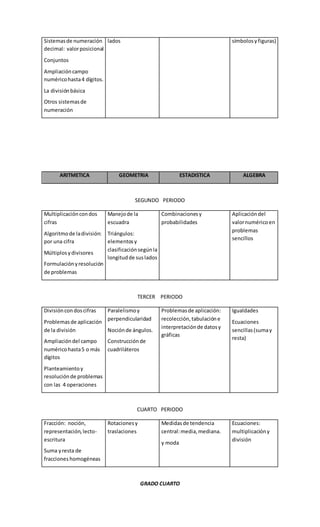
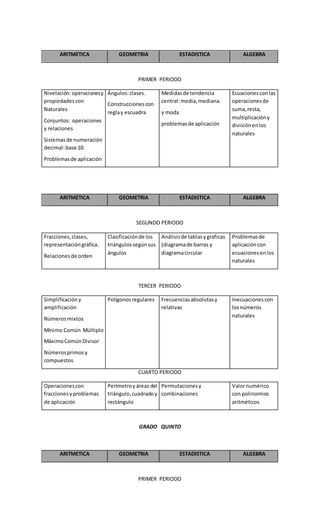
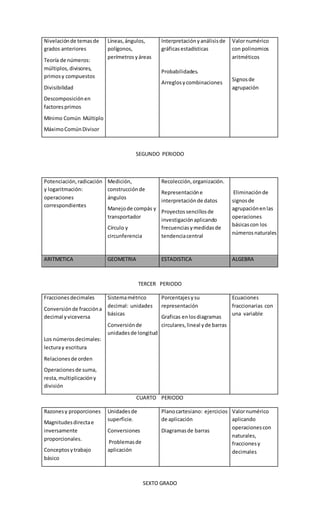
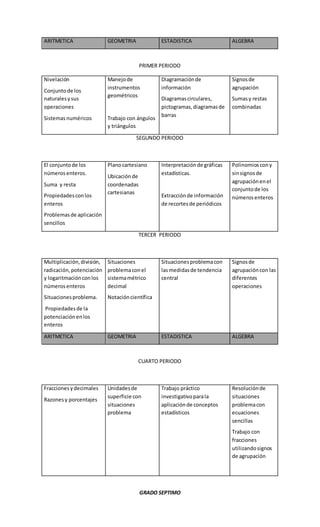
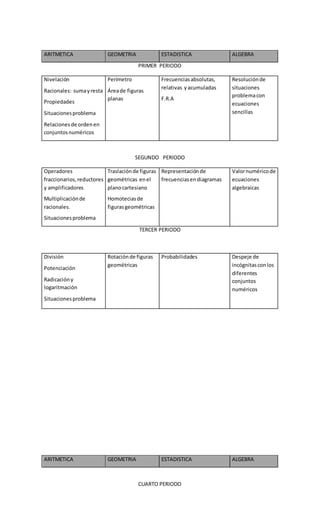
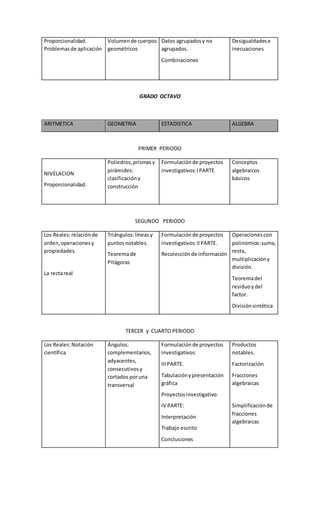
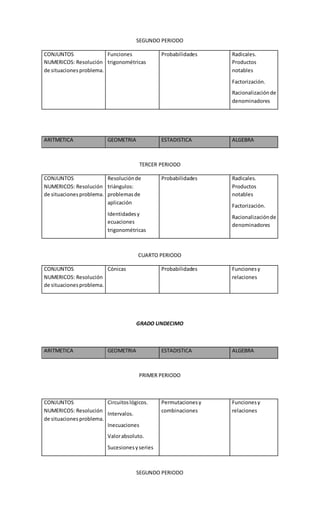
Este documento presenta el plan de área de matemáticas de una institución educativa. Explica la importancia de las matemáticas y los objetivos generales y específicos del área. Además, incluye la gradualización de estándares por grados, abarcando temas de aritmética, geometría, estadística y álgebra. Finalmente, establece el marco legal en el que se fundamenta el plan de acuerdo a la ley educativa colombiana.

Incrustar presentación

Descargar para leer sin conexión
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL PLAN DE ÁREA MATEMÁTICAS RESPONSABLES: ALBA ROCIO VELEZ AMZOLICREYTH GALARCIO AURA MUÑOZ DIOSELINA MENA FANNY MESA GLORIA AMPARO LONDOÑO S JORGE DIDIER OBANDO JORGE SÁNCHEZ SILVIA RIOS SUD MARIA MOSQUERA 2014
PLAN DEL AREA DE MATEMÁTICAS 1. JUSTIFICACION Nuestra civilización apenas existiría sin las leyes físicas y las técnicas desarrolladas como producto conjunto con la investigación matemática. Nadie puede construir una pared sin utilizar las técnicas de medición geométrica desarrolladas por los Matemáticos Egipcios. Los actuales avances tecnológicos a las postrimerías del siglo XX y a las puertas del siglo XXI ha necesitado y necesita por doquiera del aporte matemático: Los computadores, la estadística, la contabilidad, las ingenierías, los viajes espaciales y muchas más. El estudio de las Matemáticas busca de que el estudiante se apropie de los conocimientos básicos, repasando las operaciones usuales (suma, resta, multiplicación y división) en el conjunto de los Enteros, hasta llegar a manejar operaciones más complejas que necesitan de conocimientos más avanzados y un análisis más profundo en el conjunto de los Reales. La enseñanza de las matemáticas retoma la labor ya iniciada en el grado anterior; utiliza muchos de los conceptos antes vistos para fundamentar otros nuevos. Poco a poco y con confianza, el alumno irá construyendo las bases de una ciencia que se precia de ser la piedra angular de todas las ciencias exactas, y por ende sustentador del avance científico y tecnológico de nuestros días. Nuestra tarea será de adoptar el estudio de la Aritmética, el álgebra, la Geometría, la estadística y el análisis según lo que corresponda en cada curso. Creemos que el estudio paciente y disciplinado de esta área le dará las bases necesarias para abordar con confianza y sin traumatismos otras asignaturas científicas. En este plan la geometría aparecerá en la básica primaria y la básica secundaria como una exploración sistematizada del espacio. Desde el grado cero (0) al grado undécimo (11°) se incluye el estudio de las matemáticas con el fin de contribuir decididamente a la educación integral del individuo, reconceptualizando las estrategias didácticas, para un mejoramiento en las habilidades y competencias comunicativas – comprensión, análisis, síntesis y resolución de problemas. Se hace necesario entonces crear núcleos temáticos que sean el resultado de la integración de diferentes disciplinas académicas y no académicas (la cotidianidad), que aporten su saber en el estudio, la interpretación, la explicación y solución de problemas detectados. 2. OBJETIVOS GENERALES DEL AREA 1.) Generar en todos los estudiantes una actitud positiva hacia las Matemáticas y estimular en ellos el interés por el estudio. 2.) Desarrollar en los estudiantes una sólida comprensión de los conceptos, procesos y estrategias básicas de las Matemáticas e, igualmente la capacidad de utilizar todo ello en la solución de problemas. 3.) Estimular en los estudiantes el uso creativo de las Matemáticas para expresar nuevas ideas y descubrimientos, así como para reconocer los elementos Matemáticos presentes en otras actividades creativas.
OBJETIVOS ESPECIFICOS DEL AREA 1.) Desarrollar habilidades que le permitan razonar lógica, crítica y objetivamente 2.) Adquirir precisión en la expresión verbal y familiaridad con el lenguaje y expresiones simbólicas. 3.) Suministrar a los estudiantes el lenguaje apropiado que les permita comunicar de manera eficaz sus ideas y experiencias Matemáticas. 4.) Desarrollar habilidades en los procedimientos operativos, aritméticos y geométricos. 5.) Desarrollar en los estudiantes, la habilidad para reconocer la presencia de las Matemáticas en diversas situaciones de la vida real. 3. MARCO LEGAL DEL AREA La Ley 115 de 1994 en su artículo 23 establece para el logro de los objetivos de la educación básica como área obligatoria y fundamental del conocimiento y de la formación que necesariamente se tendrá que ofrecer de acuerdo con el currículo y con el PEI, a la matemática, además es innegable que esta ciencia no puede aislarse de la historia de la humanidad, ya que le ha dado progreso tanto a lo científico como a lo tecnológico. Todos en la práctica cotidiana necesitamos efectuar cálculos y estimar rápidamente algunos resultados, por tanto es indispensable insistir en la operación y cálculo mental, en la comprensión de conceptos y procesos, en la formulación y solución de problemas para motivar el ejercicio de los algoritmos de cálculo. Teniendo en cuenta una visión global e integral del quehacer matemático de debe tener en cuenta tres grandes aspectos para organizar el currículo en un todo armonioso: 1) PROCESOS GENERALES. Que tienen que ver con el aprendizaje tales como: el razonamiento, la resolución y planteamiento de problemas, la comunicación, la modelación y elaboración, comparación y ejercitación de procedimientos. 2) CONOCIMIENTOS BÁSICOS. Que tienen que ver con procesos específicos que desarrollan el pensamiento matemático y con sistemas propios de la matemática. Estos procesos específicos se relacionan con el desarrollo del pensamiento numérico, el espacial, el métrico, el aleatorio y el variacional entre otros. Los sistemas son aquellos propuestos desde la renovación curricular: sistemas numéricos, sistemas geométricos, sistemas de medida, sistema de datos y sistemas algebraicos y analíticos. 3) EL CONTEXTO. Que tiene que ver con los ambientes que rodean al estudiante y que le dan sentido a las matemáticas que aprende. Variables como las condiciones sociales y culturales tanto locales como internacionales, el tipo de interacciones, los intereses que se generan, las creencias, así como las condiciones económicas del grupo social en el que se concreta el acto educativo, deben tenerse en cuenta en el diseño y ejecución de experiencias didácticas.
4. GRADUALIZACION DE ESTANDARES GRADO PRIMERO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO Los conjuntosysus respectivoscardinales Círculo del 0 al 9 Cuantificaciónde situaciones: sumay resta Ubicacióntemporo espacial Clasificaciónde sólidos Atributode losobjetosy loseventos:(superficie, capacidad,masa,tiempo) endiversassituacionesde tipoelemental Recolecciónde datosdentrodel aulade clase Suma yresta de objetosde características iguales Descomposición polinómicadel 0 al 9 SEGUNDO PERIODO Representaciónde cantidadesenel ábaco. Lectura de números segúnlaubicación enel ábaco: decena,docena, quincena Círculo del 10 al 50: suma yresta Trabajo con regletasy bloqueslógicospara manejaratributoscomo: color,tamaño,forma, espesor El plano Representación gráficade la información recolectada: gráficasde barras Descomposición polinómica de númerosdel 0 al 50 TERCER PERIODO Representaciónde cantidadesenel ábaco. Lectura de números segúnlaubicaciónenel ábaco: decena,docena, quincena Círculo del 50 al 75: suma yresta Ideaintuitivade punto Tipode líneas. Trabajo creativo utilizandosuperficies Lectura interpretativade gráficas(0 al 75) Descomposición polinómica de númerosdel 0 al 75
ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA CUARTO PERIODO Representaciónde cantidadesenel ábaco. Lectura de números segúnlaubicaciónenel ábaco: decena,docena, quincena,centena Círculo del 0 al 100: suma yresta Figurasgeométricas básicas Recolección,organización, representaciónyanálisisde información Descomposición polinómica de númerosdel 0 al 100 Manejode 2 variablesenla suma yen la resta graficaciones GRADO SEGUNDO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO Nivelación Lecto-escriturade números La centena(0al 100) Sistemasde numeración decimal. Valorposicional Relacionesde orden Suma y resta Clasificaciónde los sólidosporsus características y dimensiones:largo, ancho,espesor, grosor,profundidad Recolección,organización, representaciónyanálisisde información Descomposición polinómica de númerosdel 0 al 100 Manejode 2 variablesenla suma yen la resta Descomposición factorial SEGUNDO PERIODO Círculo numéricodel 0al 100. Lecto-escriturade números Sistemasde numeración decimal. Valorposicional Relacionesde orden Suma y restaen forma horizontal yvertical. Construcciónde problemas Manejode regla con ejercicioscreativos Lectura e interpretaciónde gráficas( 0 al 100) Descomposición polinómica de númerosdel 0 al 100 Manejode 2 variablesenla suma yen la resta Descomposición factorial
ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA TERCER PERIODO Tablasde multiplicar: algoritmo. Sumasde sumandos iguales Conjuntos seriación Recta numérica, perímetro Áreas: cuadriláteros Tablasde multiplicar: gráficasde barras Descomposición polinómicay factorial enel círculo de númerosdel 0 al 100 Manejode 3 o más variables CUARTO PERIODO Tablasde multiplicar: algoritmo. Sumasde sumandos iguales Conjuntos Seriación Formulación y planteamientode problemas Propiedadesde la multiplicación Iniciaciónala división Recta numérica, perímetro Áreas: cuadriláteros Sistemasde medidas Utilizacióndel metro Tablasde multiplicar: gráficasde barras Probabilidades Descomposición polinómicay factorial enel círculo de númerosdel 0 al 100 Manejode 3 o más variables GRADO TERCERO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO Nivelación: suma,resta, multiplicación Clasesde polígonos segúnel númerode Combinacionesy probabilidades Valornumérico (relacionadocon
Sistemasde numeración decimal: valorposicional Conjuntos Ampliacióncampo numéricohasta4 dígitos. La divisiónbásica Otros sistemasde numeración lados símbolosyfiguras) ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA SEGUNDO PERIODO Multiplicacióncondos cifras Algoritmode ladivisión: por una cifra Múltiplosydivisores Formulaciónyresolución de problemas Manejode la escuadra Triángulos: elementosy clasificaciónsegúnla longitudde suslados Combinacionesy probabilidades Aplicacióndel valornuméricoen problemas sencillos TERCER PERIODO Divisióncondoscifras Problemasde aplicación de la división Ampliacióndel campo numéricohasta5 o más dígitos Planteamientoy resoluciónde problemas con las 4 operaciones Paralelismoy perpendicularidad Nociónde ángulos. Construcciónde cuadriláteros Problemasde aplicación: recolección,tabulacióne interpretaciónde datosy gráficas Igualdades Ecuaciones sencillas(sumay resta) CUARTO PERIODO Fracción: noción, representación,lecto- escritura Suma yresta de fracciones homogéneas Rotacionesy traslaciones Medidasde tendencia central:media,mediana. y moda Ecuaciones: multiplicacióny división GRADO CUARTO
ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO Nivelación:operacionesy propiedadescon Naturales Conjuntos: operaciones y relaciones Sistemasde numeración decimal:base 10. Problemasde aplicación Ángulos:clases. Construccionescon reglay escuadra Medidasde tendencia central:media,mediana. y moda problemasde aplicación Ecuacionesconlas operacionesde suma,resta, multiplicacióny divisiónenlos naturales ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA SEGUNDO PERIODO Fracciones,clases, representacióngráfica. Relacionesde orden Clasificaciónde los triángulossegúnsus ángulos Análisisde tablasygraficas (diagramade barras y diagramacircular Problemasde aplicacióncon ecuacionesenlos naturales TERCER PERIODO Simplificacióny amplificación Números mixtos Mínimo Común Múltiplo MáximoComúnDivisor Númerosprimosy compuestos Polígonosregulares Frecuenciasabsolutasy relativas Inecuacionescon losnúmeros naturales CUARTO PERIODO Operacionescon fraccionesyproblemas de aplicación Perímetroy áreas del triángulo,cuadradoy rectángulo Permutacionesy combinaciones Valornumérico con polinomios aritméticos GRADO QUINTO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO
Nivelaciónde temasde grados anteriores Teoría de números: múltiplos,divisores, primosy compuestos Divisibilidad Descomposiciónen factoresprimos Mínimo Común Múltiplo MáximoComúnDivisor Líneas,ángulos, polígonos, perímetrosyáreas Interpretaciónyanálisisde gráficasestadísticas Probabilidades. Arreglosycombinaciones Valornumérico con polinomios aritméticos Signosde agrupación SEGUNDO PERIODO Potenciación,radicación y logaritmación: operaciones correspondientes Medición, construcciónde ángulos Manejode compás y transportador Círculo y circunferencia Recolección,organización. Representacióne interpretaciónde datos Proyectossencillosde investigaciónaplicando frecuenciasymedidasde tendenciacentral Eliminaciónde signosde agrupaciónenlas operaciones básicascon los númerosnaturales ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA TERCER PERIODO Fraccionesdecimales Conversiónde fraccióna decimal yviceversa Los númerosdecimales: lecturay escritura Relacionesde orden Operacionesde suma, resta,multiplicacióny división Sistemamétrico decimal: unidades básicas Conversiónde unidadesde longitud Porcentajesysu representación Graficas enlosdiagramas circulares,lineal yde barras Ecuaciones fraccionarias con una variable CUARTO PERIODO Razonesy proporciones Magnitudesdirectae inversamente proporcionales. Conceptosytrabajo básico Unidadesde superficie. Conversiones Problemasde aplicación Planocartesiano: ejercicios de aplicación Diagramasde barras Valornumérico aplicando operacionescon naturales, fraccionesy decimales SEXTO GRADO
ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO Nivelación Conjuntode los naturalesysus operaciones Sistemasnuméricos Manejode instrumentos geométricos Trabajo con ángulos y triángulos Diagramaciónde información Diagramascirculares, pictogramas,diagramasde barras Signosde agrupación Sumasy restas combinadas SEGUNDO PERIODO El conjuntode los númerosenteros. Suma y resta Propiedadesconlos enteros Problemasde aplicación sencillos Planocartesiano Ubicaciónde coordenadas cartesianas Interpretaciónde gráficas estadísticas. Extracciónde información de recortesde periódicos Polinomioscony sinsignosde agrupaciónenel conjuntode los númerosenteros TERCER PERIODO Multiplicación,división, radicación,potenciación y logaritmaciónconlos númerosenteros Situacionesproblema. Propiedadesde la potenciaciónenlos enteros Situaciones problemaconel sistemamétrico decimal Notacióncientífica Situacionesproblemacon lasmedidasde tendencia central Signosde agrupacióncon las diferentes operaciones ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA CUARTO PERIODO Fraccionesydecimales Razonesy porcentajes Unidadesde superficie con situaciones problema Trabajo práctico investigativoparala aplicaciónde conceptos estadísticos Resoluciónde situaciones problemacon ecuaciones sencillas Trabajo con fracciones utilizandosignos de agrupación GRADO SEPTIMO
ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO Nivelación Racionales: sumayresta Propiedades Situacionesproblema Relacionesde ordenen conjuntosnuméricos Perímetro Áreade figuras planas Frecuenciasabsolutas, relativas y acumuladas F.R.A Resoluciónde situaciones problemacon ecuaciones sencillas SEGUNDO PERIODO Operadores fraccionarios,reductores y amplificadores Multiplicaciónde racionales. Situacionesproblema Traslaciónde figuras geométricas enel planocartesiano Homoteciasde figurasgeométricas Representaciónde frecuenciasendiagramas Valornuméricode ecuaciones algebraicas TERCER PERIODO División Potenciación Radicacióny logaritmación Situacionesproblema Rotaciónde figuras geométricas Probabilidades Despeje de incógnitasconlos diferentes conjuntos numéricos ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA CUARTO PERIODO
Proporcionalidad. Problemasde aplicación Volumende cuerpos geométricos Datos agrupadosy no agrupados. Combinaciones Desigualdadese inecuaciones GRADO OCTAVO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO NIVELACION Proporcionalidad. Poliedros,prismasy pirámides: clasificacióny construcción Formulaciónde proyectos investigativos:IPARTE Conceptos algebraicos básicos SEGUNDO PERIODO Los Reales:relaciónde orden,operacionesy propiedades. La rectareal Triángulos:líneasy puntosnotables. Teoremade Pitágoras Formulaciónde proyectos investigativos:IIPARTE. Recolección de información Operacionescon polinomios:suma, resta, multiplicacióny división. Teoremadel residuoydel factor. Divisiónsintética TERCER y CUARTO PERIODO Los Reales:Notación científica Ángulos: complementarios, adyacentes, consecutivosy cortados poruna transversal Formulaciónde proyectos investigativos: IIIPARTE. Tabulaciónypresentación gráfica Proyectosinvestigativo: IV PARTE: Interpretación Trabajo escrito Conclusiones Productos notables. Factorización Fracciones algebraicas Simplificaciónde fracciones algebraicas
GRADO NOVENO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER Y SEGUNDO PERIODO Númeroscomplejose imaginarios Poliedros,prismasy pirámides: clasificacióny construcción Formulaciónde proyectos investigativos:IPARTE Conceptos algebraicos básicos TECER PERIODO Progresionesaritméticas y geométricas Conos,cilindrosy esferas Variación Desviaciónestándar Ecuaciones cuadráticas CUARTO PERIODO Progresionesaritméticas y geométricas Proporcionalidady semejanza Variación Desviaciónestándar Potenciación, radicación. Racionalizaciónde denominadores GRADO DECIMO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Ecuacionesde la línearecta Probabilidades Radicales. Productos notables Factorización. Racionalizaciónde denominadores
SEGUNDO PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Funciones trigonométricas Probabilidades Radicales. Productos notables Factorización. Racionalizaciónde denominadores ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA TERCER PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Resoluciónde triángulos: problemasde aplicación Identidadesy ecuaciones trigonométricas Probabilidades Radicales. Productos notables Factorización. Racionalizaciónde denominadores CUARTO PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Cónicas Probabilidades Funcionesy relaciones GRADO UNDECIMO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Circuitoslógicos. Intervalos. Inecuaciones Valorabsoluto. Sucesionesyseries Permutacionesy combinaciones Funcionesy relaciones SEGUNDO PERIODO
CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Limites Sumatoriay productoria Funcionesy relaciones Productos notables Factorización. Racionalizaciónde denominadores TERCER PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Derivadas probabilidades Funcionesy relaciones Productos notables Factorización. Racionalizaciónde denominadores ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA CUARTO PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Integrales probabilidades Funcionesy relaciones Productos notables Factorización. Racionalizaciónde denominadores 5. COMPETENCIAS ESPECÍFICAS DEL ÁREA  INTERPRETATIVA: encontrar el sentido de una proposición de un problema, de un gráfico, de los argumentos en contra o en pro de una teoría.  ARGUMENTATIVA: dar razón de una afirmación, explicar el porqué de una proposición, justificar una afirmación mediante articulación. La articulación de conceptos y teorías.  PROPOSITIVA: generar hipótesis en la resolución de problemas, proposición de alternativas de solución de problemas y conflictos. Explicación de una proposición a través de conceptos lógicos.  NUMÉRICA OPERATIVA: hace referencia a la parte operativa o resolución de problemas en cada uno de los conjuntos numéricos (R, I, N, Q, Q”)
 GEOMÉTRICA MÉTRICA: transformaciones geométricas en el plano, comprensión de conceptos geométricos.  COGNITIVA: hace referencia al reconocimiento de conceptos previos, aplicación de conocimientos, procesos y solución de problemas a través de la reproducción de conceptos básicos. NIVELES DE COMPETENCIA – DESEMPEÑO EN MATEMÁTICAS Y METAS DE CALIDAD NIVEL DE COMPETENCIA DESEMPEÑO 01. RECONOCIMIENTO Y DISTINCIÓN - Reconocer figuras geométricas y atributos medibles: Identificar los efectos de las transformaciones - Reconocer, leer y distinguir diferentes representaciones y usos del número en contextos con significado. 02. INTERPRETACIÓN - Interpretar y describir información gráfica. - Expresar patrones de variación y establecer relaciones de proporcionalidad. - Resolver problemas de estructura aditiva o multiplicativa. - Interpretar y analizar fenómenos aleatorios: hacer arreglos y combinaciones. - Resolver situaciones problemáticas que requieren la utilización de propiedades métricas, geométricas o aritméticas. - Dar significado a información numérica y traducir entre diferentes representaciones. 03. PRODUCCIÓN - Ordenar, comparar, estimar, predecir o transformar expresiones numéricas o algebraicas relativas a situaciones problemáticas. - Resolver problemas geométricos o métricos usando argumentaciones deductivas e inductivas. 6. ESTRATEGIAS METODOLOGÍA APLICABLES AL AREA Los procesos presentes en toda la actividad matemática tienen que ver con:  La resolución y el planteamiento de problemas.  El razonamiento.  La comunicación.  La modelación: elaboración, comparación y ejercitación de procedimientos. LA RESOLUCIÓN Y EL PLANTEAMIENTO DE PROBLEMAS
La resolución de problemas debe ser eje central del currículo de matemáticas, y como tal, debe ser un objetivo primario de la enseñanza y parte integral de la actividad matemática. En la medida en que los estudiantes van resolviendo problemas, van ganando confianza en el uso de las matemáticas, van desarrollando una mente inquisitiva y perseverante, va aumentado su capacidad de comunicarse matemáticamente y su capacidad para utilizar procesos de pensamiento de más alto nivel. Las investigaciones que han reconocido la resolución de problemas como una actividad muy importante para aprender matemáticas, proponen considerar en el currículo escolar de matemáticas aspectos como los siguientes:  Formulación de problemas a partir de situaciones dentro y fuera de las matemáticas.  Desarrollo y aplicación de diversas estrategias para resolver problemas.  Verificación e interpretación de resultados a la luz del problema original.  Generalización de soluciones y estrategias para nuevas situaciones de problemas.  Adquisición de confianza en el uso significativo de las matemáticas. EL RAZONAMIENTO El razonamiento matemático tiene que ver estrechamente con las matemáticas como comunicación, como modelación y como procedimiento. El razonamiento matemático es necesario para tener en cuenta de una parte, la edad de los estudiantes y su nivel de desarrollo y, de otra, que cada logro alcanzado en un conjunto de grados se retoma y amplía en los conjuntos de grados siguientes. Asimismo, se debe partir de los niveles informales del razonamiento en los conjuntos de grados inferiores, hasta llegar a niveles más elaborados del razonamiento. Razonar en matemáticas tiene que ver con:  Dar cuenta del cómo y del porqué de los procesos que se siguen para llegar a conclusiones.  Justificar las estrategias y los procedimientos puestos en acción en el tratamiento de problemas.  Formular hipótesis, hacer conjeturas y predicciones, encontrar contraejemplos, usar hechos conocidos, propiedades y relaciones para explicar otros hechos.  Encontrar patronos y expresarlos matemáticamente.  Utilizar argumentos propios para expresar ideas, comprendiendo que las matemáticas más que una memorización de reglas y algoritmos, son lógicas y potencian la capacidad de pensar. LA COMUNICACIÓN Una necesidad común que tenemos todos los seres humanos en todas las actividades, disciplinas, profesiones y sitios de trabajo es la habilidad para comunicarnos. Los retos que nos plantea el siglo XXI requiere que en todas las profesiones científicas y técnicas, las personas sean capaces de:  Expresar ideas hablando, escribiendo, demostrando y describiendo visualmente de diferentes formas.  Construir, interpretar y ligar varias representaciones de ideas y de relaciones.  Hacer observaciones y conjeturas, formular preguntas, reunir y evaluar información.  Producir y presentar argumentos persuasivos y convincentes. Se ha identificado la comunicación como uno de los procesos más importantes para aprender matemáticas y para resolver problemas. La comunicación juega un papel fundamental al ayudar a los niños a construir los vínculos entre sus nociones informales e intuitivas y el lenguaje abstracto y simbólico de las matemáticas; cumple también una función clave como ayuda para que los alumnos tracen importantes conexiones entre
las representaciones físicas, pictóricas, gráficas, simbólicas, verbales y mentales de las ideas matemáticas. Thomas A. Romberg en su artículo “características problemáticas del currículo escolar de matemáticas” (página 375) destaca la comunicación verbal y escrita como una parte crucial del proceso enseñanza y aprendizaje de las matemáticas, por las siguientes razones:  En primer lugar la comunicación en forma de argumento lógico es fundamental para el discurso matemático.  En segundo lugar, la comunicación es el medio por el cual los conocimientos personales se sistematizan en un ámbito y, por tanto, se aceptan como conocimientos nuevos.  En tercer lugar, el desarrollo en las categorías y estructuras del sistema lingüístico, estructura la comprensión del niño y la hace progresar hacia un modelo de conocimiento público. De esta manera las funciones y el trabajo de los alumnos y de los educadores, se consideran complementarias. El educador debe guiar, escuchar, discutir, sugerir, preguntar y clarificar el trabajo de los alumnos a través de actividades apropiadas e interesantes. La comunicación es la esencia de la enseñanza, el aprendizaje y la evaluación de las matemáticas. LA MODELACIÓN Actualmente, la aparición de la era Informática, uno de los énfasis que se hace es la búsqueda y construcción de modelos matemáticos. La tecnología moderna sería imposible sin las matemáticas y prácticamente ningún proceso técnico podría llevarse a cabo en ausencia del modelo matemático que lo sustenta. Cuando hablamos de la actividad matemática en la escuela, destacamos que el alumno aprende matemática “haciendo matemáticas”, lo que supone como esencial la resolución de problemas de la vida diaria, lo que implica que desde el principio se integre al currículo una variedad de problemas relacionados con el contexto de los estudiantes. La resolución de problemas en un amplio sentido, se considera siempre en conexión con las aplicaciones y la modelación. La forma de describir ese juego o interrelación entre el mundo real y las matemáticas es la modelación. El punto de partida de la modelación es una situación problemática real. Esto conduce a una formulación del problema. Los datos, conceptos, relaciones, condiciones y suposiciones del problema enunciado matemáticamente deben trasladarse a las matemáticas, es decir, deben ser matematizados y así resulta un modelo matemático de la situación original. El proceso de resolución de problemas continúa mediante el trabajo de sacar conclusiones, calcula y revisa ejemplos concretos, aplica métodos y resultados matemáticos conocidos; como también desarrollando otros nuevos. En conjunto se obtienen ciertos resultados matemáticos, estos resultados tienen que ser validados, es decir, se tienen que volver a trasladar al mundo real, para ser interpretados en relación con la situación original. De esta manera, el que resuelve el problema también valida el modelo, si se justifica usarlo para el propósito que fue construido. En conclusión, la modelación es el proceso completo que conduce desde la situación problemática real original hasta un modelo matemático en el cual el conocimiento y las habilidades adquiridas se utilizan para descubrir regularidades, relaciones y estructuras desconocidas.
7. CRITERIOS Y PROCEDIMIENTOS PARA EVALUAR EL APRENDIZAJE, RENDIMIENTO Y DESARROLLO DE LA CAPACIDAD DE LOS EDUCANDOS La evaluación cualitativa debe ser formativa, continua, sistemática y flexible, centrada en el propósito de producir y recoger información necesaria sobre los procesos de enseñanza aprendizaje que tienen lugar en el aula y por fuera de ella. La evaluación debe ser más una reflexión que un instrumento de medición para poner etiquetas a los individuos; lo que no excluye el reconocimiento de las diferencias individuales. Evaluar el estado cognoscitivo y afectivo del estudiante, frente a un área del conocimiento, significa considerar todos aquellos elementos necesarios para diagnosticar los estados del aprendizaje, los factores formativos y los logros alcanzados de acuerdo con los propósitos y las estrategias de intervención utilizadas durante el proceso educativo. Con base en lo anterior, en el área de matemáticas evaluaremos teniendo en cuenta los siguientes aspectos:  Comportamiento de los estudiantes en su trabajo cotidiano, como su actitud, dedicación, interés, participación, capacidad de diferenciación, su habilidad para asimilar y comprender informaciones y procedimientos, su refinamiento progresivo en los métodos para conocer, para analizar, crear y resolver problemas, en su inventiva o tendencia a buscar nuevos métodos o respuestas para las diversas situaciones.  Las concepciones de los alumnos sobre los conceptos.  Los cambios que se presentan en las concepciones mediante la participación activa de los estudiantes durante la construcción de los conocimientos.  La comprensión de los conocimientos básicos en un momento dado.  El estado de conceptualización alcanzado frente a los saberes formales.  Las formas de comunicación de concepciones y conceptos.  La capacidad para aplicar los conceptos.  La capacidad para interpretar, plantear y resolver problemas.  Las estrategias y procedimientos utilizados para plantear y resolver problemas.  Los estilos de trabajo: individual y colectivo.  La adquisición de destrezas.  La participación individual en tareas colectivas.  El interés por ampliar los conocimientos discutidos en el aula.  La capacidad de lectura y escritura de temas relacionados con el área.  La capacidad de reflexionar críticamente sobre lo que se aprende, lee o escribe. PLANES ESPECIALES DE APOYO PARA ESTUDIANTES CON MARCADAS DIFICULTADES Se implementaran las siguientes estrategias:  Refuerzo constante de las operaciones básicas.  Formar un grupo de alumnos con dificultades en matemáticas para reforzar en jornada contraria, se llamaría semillero de alumnos con dificultades  Crear estímulos que motiven a los estudiantes a pertenecer al semillero como: izar bandera, resaltar en público los avances que van teniendo, mención de honor, entre otras.  Aprovechar el recurso de los alumnos más avanzados de cada grupo para que apoyen o sirvan de monitores en el semillero de alumnos con dificultades  Crear concursos y eventos matemáticos entre los alumnos del semillero a nivel institucional e interinstitucional como: juegos, carreras de observación, entre otros.  Integrar a padres de familia en forma periódica al semillero para que realicen actividades en común y juegos didácticos, para que sirvan de multiplicadores en el manejo del juego y temas aprendidos. PARA ESTUDIANTES CON DESEMPEÑO SUPÈRIOR EN EL AREA DE MATEMATICAS. Se implementaran las siguientes estrategias:
 Realizar convocatorias a estudiantes con desempeño superior en el área de matemáticas que deseen hacer parte de las monitorias.  Crear las monitorias con los estudiantes que presentan desempeño superior en el área.  Fortalecer habilidades que permitan orientar el trabajo de los monitores.  Motivar a los estudiantes monitores de los diferentes grados incluyendo a los estudiantes de 10º y 11º que deseen prestar su servicio social como monitores a estudiantes con dificultades en matemáticas; resaltando la importancia de las competencias ciudadanas para el bienestar académico propio y de los demás.  Involucrar al padre de familia dentro del proyecto de asesoráis tanto para los estudiantes con dificultades en el área como a los que colaboraran en las asesoráis.  Estimular a los estudiantes monitores con una valoración académica (nota en el periodo), un incentivo económico que le permita subsanar algunas de sus necesidades y eximirlo de algunas actividades escolares.  Crear espacios de asesoráis personalizadas que le permita avanzar en su desempeño en el área, elaborar material didáctico o profundizar en algunos temas y procedimientos matemáticos.  Participación en talleres y seminarios programados por la institución, el municipio o el departamento y que sean costeados por quien los organice.  Organizar encuentros interinstitucionales dentro y fuera del municipio, buscando mostrar experiencias y enriquecernos con nuevas propuestas.  Crear clubes o grupos de estudios dentro de las instituciones y luego a nivel municipal que faciliten el proceso de aprendizaje de las matemáticas en los estudiantes que presentan dificultades especificas del área, creando y fortaleciendo los semilleros existentes en el municipio.  Crear espacios de asesoráis a estudiantes con desempeño superior en el área del grado noveno para que elijan adecuadamente la modalidad, que le sirva de visión futura hacia sus expectativas universitarias y laborales.  Asignar espacios para la capacitación, integración, concursos y demás actividades que beneficien el desarrollo normal del proyecto del área en cada institución.  Recibir apoyo de la secretaria de educación municipal, de la junta municipal de educación (JUME) y de las diferentes instituciones para la creación y fortalecimiento de los clubes o grupos de estudiantes con desempeño superior en esta y otras áreas, asignando para ello presupuesto municipal que mejore la calidad de la educación. 4. INDICADORES DEL AREA POR GRADOS, SEGÚN LA RESOLUCION 2343 GRADO: PRIMERO 1. Expresa Ideas y situaciones que involucran conceptos matemáticos mediante lenguaje natural y representaciones físicas, pictóricas, gráficas, simbólicas y establece conexiones entre ellas. 2. Identifica y clasifica fronteras y regiones de objetos en el plano y en el espacio, reconoce en ellos formas y figuras a través de la imaginación del dibujo o de la construcción con materiales apropiados y caracteriza triángulos, cuadrados, rectángulos y círculos. 3. Identifica en objetos y situaciones de su entorno las magnitudes de longitud, volumen, y capacidad; reconoce procesos de conservación y desarrolla procesos de medición de dichas magnitudes, con patrones arbitrarios y con algunos patrones estandarizados. GRADO: SEGUNDO 1. Identifica en objetos y situaciones de su entorno las magnitudes de longitud, volumen, y capacidad; reconoce procesos de conservación y desarrolla procesos de medición de dichas magnitudes, con patrones arbitrarios y con algunos patrones estandarizados. 2. Relaciona los algoritmos convencionales o propios con los conceptos matemáticos que los sustentan, identifica esquemas y patrones que le permiten llegar a conclusiones. 3. Explora y descubre propiedades interesantes y regularidades de los números, efectúa cálculos con datos de la realidad y utiliza creativamente materiales y medios. GRADO: TERCERO 1. Compara, describe, denomina y cuantifica situaciones de la vida cotidiana, utilizando con sentido números por lo menos hasta de cinco cifras.
2. Identifica en objetos y situaciones de su entorno las magnitudes de longitud, volumen, y capacidad; reconoce procesos de conservación y desarrolla procesos de medición de dichas magnitudes, con patrones arbitrarios y con algunos patrones estandarizados. 3. Relaciona los algoritmos convencionales o propios con los conceptos matemáticos que los sustentan, identifica esquemas y patrones que le permiten llegar a conclusiones. 4. Explora y descubre propiedades interesantes y regularidades de los números, efectúa cálculos con datos de la realidad y utiliza creativamente materiales y medios. GRADO: CUARTO 1. Investiga y comprende contenidos matemáticos a partir de enfoques de resolución de problemas, formula y resuelve problemas derivados de situaciones cotidianas y matemáticas, examina y valora los resultados teniendo en cuenta el planteamiento original del problema. 2. Reconoce características de sólidos, figuras planas y líneas, los utiliza en su vida cotidiana en trabajos prácticos como mediciones, elaboración de dibujos y construcción de modelos. 3. Explica sus ideas y justifica sus respuestas mediante el empleo de modelos, la interpretación de hechos conocidos y la aplicación de propiedades y relaciones matemáticas. GRADO: QUINTO 1. Identifica los números naturales y los racionales positivos en su expresión decimal y fraccionaria, los usa en diferentes contextos y los representa de distintas formas. 2. Construye y utiliza significativamente en una amplia variedad de situaciones las operaciones de adición, sustracción, multiplicación y división con números naturales y con números racionales positivos, establece relaciones entre estas operaciones y usa sus propiedades para la elaboración del cálculo mental y escrito. 3. Interpreta datos presentados en talas y en diagramas, comprende y usa la media, la mediana y la moda en un conjunto pequeño de datos y saca conclusiones estadísticas. 4. Reconoce la importancia de averiguar datos y procesar información para tomar decisiones, y de conocer y evaluar sus características en relación con las decisiones que se tomen. 5. Reconoce características de sólidos, figuras planas y líneas, los utiliza en su vida cotidiana en trabajos prácticos como mediciones, elaboración de dibujos y construcción de modelos. 6. Explica sus ideas y justifica sus respuestas mediante el empleo de modelos, la interpretación de hechos conocidos y la aplicación de propiedades y relaciones matemáticas. GRADO: SEXTO 1. Identifica los números naturales y los racionales positivos en su expresión decimal y fraccionaria, los usa en diferentes contextos y los representa de distintas formas. 2. Explora y descubre propiedades interesantes y regularidades de los números, utiliza habitual y críticamente materiales y medios para verificar predicciones, realizar y comprobar cálculos y resolver problemas. 3. Interpreta datos presentados en tablas y en diagramas, comprende y usa la media, la mediana y la moda en un conjunto pequeño de datos y saca conclusiones estadísticas. 4. Reconoce la importancia de averiguar datos y procesar información para tomar decisiones, y de conocer y evaluar sus características en relación con las decisiones que se tomen.
5. Reconoce características de sólidos, figuras planas y líneas, los utiliza en su vida cotidiana en trabajos prácticos como mediciones, elaboración de dibujos y construcción de modelos. 6. aplica movimientos rígidos en el plano como traslaciones, rotaciones y reflexiones, identifica las propiedades que se conservan en cada movimiento y visualiza transformaciones simples para descubrir reglas de combinación que permitan crear patrones. 7. Identifica en objetos y situaciones de su entorno las magnitudes de longitud, área, volumen, capacidad, peso, masa, amplitud de ángulos y duración. Reconoce procesos de conservación y desarrolla procesos de medición y estimación de dichas magnitudes y las utiliza en situaciones de la vida diaria. 8. Formula, argumenta y somete a prueba conjeturas y elabora conclusiones lógicas. 9. Explica sus ideas y justifica sus respuestas mediante el empleo de modelos, la interpretación de hechos conocidos y la aplicación de propiedades y relaciones matemáticas. GRADO: SÉPTIMO 1. Identifica y usa los números enteros y los racionales en diferentes contextos, los representa de diversas formas y establece relaciones entre ellos; redefine las operaciones básicas en los sistemas formados con estos números y establece conexiones entre ellas. 2. Investiga y comprende contenidos y procedimientos matemáticos, a partir de enfoques de tratamiento y resolución de problemas y generaliza soluciones y estrategias para nuevas situaciones. 3. Formula problemas a partir de situaciones dentro y fuera de las matemáticas, desarrolla y aplica diversas estrategias para resolverlos, verifica e interpreta los resultados en relación con el problema original. 4. Formula inferencias y argumentos coherentes, utilizando medidas de tendencia central y de dispersión para el análisis de los datos, interpreta estadísticos y elabora críticamente conclusiones. 5. Visualiza, reconoce y efectúa transformaciones de polígonos en el plano y las utiliza para establecer congruencia, semejanza y simetría entre figuras. 6. Comprende y usa la proporcionalidad directa e inversa de magnitudes, en distintos contextos de la vida cotidiana y utiliza diferentes procedimientos para efectuar cálculos de proporcionalidad. GRADO: OCTAVO 1. Formula, argumenta y pone a prueba hipótesis, las modifica o descarta y reconoce las condiciones necesarias para que una propiedad matemática se cumpla; aplica estos procedimientos en la formulación, análisis y resolución de problemas. 2. Formula inferencias y argumentos coherentes, utilizando medidas de tendencia central y de dispersión para el análisis de los datos, interpreta estadísticos y elabora críticamente conclusiones. 3. Construye e interpreta formulas, ecuaciones e inecuaciones para presentar situaciones que requieren variables, opera con cualquiera de ellas y encuentra procedimientos para resolver ecuaciones e inecuaciones. 4. Construye modelos geométricos, esquemas, planos y maquetas utilizando escalas, instrumentos y técnicas apropiadas y visualiza, interpreta y efectúa representaciones gráficas de objetos tridimensionales en el plano.
5. Visualiza, reconoce y efectúa transformaciones de polígonos en el plano y las utiliza para establecer congruencia, semejanza y simetría entre figuras. 6. Comprende y usa la proporcionalidad directa e inversa de magnitudes, en distintos contextos de la vida cotidiana y utiliza diferentes procedimientos para efectuar cálculos de proporcionalidad. GRADO: NOVENO 1. Hace estimaciones sobre numerosidad, resultados de cálculos y medición de magnitudes concretas, a partir de sus propias estrategias y las utiliza como criterio para verificar lo razonable de los resultados. 2. Elabora modelos de fenómenos del mundo real y de las matemáticas a través de sucesiones, de series y de las funciones lineal, constante, idéntica, opuesta, de gráfica lineal, cuadrática y cúbica. 3. Representa y analiza funciones utilizando para ello tablas, expresiones orales, expresiones algebraicas, ecuaciones y gráficas y hace traducciones entre estas representaciones. 4. Interpreta listas de instrucciones, expresiones algebraicas y diagramas operacionales y de flujo, traduce de unos a otros y opera con ellos utilizando diferentes tipos de número. 5. Construye modelos geométricos, esquemas, planos y maquetas utilizando escalas, instrumentos y técnicas apropiadas y visualiza, interpreta y efectúa representaciones gráficas de objetos tridimensionales en el plano. GRADO: DECIMO 1. Da razones del porqué de los números reales y explica por qué unos son racionales y otros irracionales. 2. Utiliza el sentido de las operaciones y de las relaciones en sistemas de números reales. 3. Interpreta instrucciones, expresiones algebraicas, diagramas operacionales y de flujo y traduce de unos a otros, en el sistema de los números reales. 4. Aplica modelos de funciones para tratar matemáticamente situaciones financieras y transacciones comerciales frecuentes en la vida real. 5. Hace inferencias a partir de diagramas, tablas y gráficas que recojan datos de situaciones del mundo real; estima, interpreta y aplica medidas de tendencia central, de dispersión y de correlación. 6. Reconoce fenómenos aleatorios de la vida cotidiana y del conocimiento científico, formula y comprueba conjeturas sobre el comportamiento de los mismos y aplica los resultados en la toma de decisiones. 7. elabora argumentos informales pero coherentes y sólidos para sustentar la ordenación lógica de una serie de proposiciones. 8. Detecta y aplica distintas formas de razonamiento y métodos de argumentación en la vida cotidiana, en las ciencias sociales, en las ciencias naturales y en las matemáticas; analiza ejemplos y contraejemplos para cambiar la atribución de necesidad o suficiencia a una condición dada. 9. Disfruta y se recrea en exploraciones que retan su pensamiento y saber matemático y exigen la manipulación creativa de objetos, instrumentos de medida y materiales y medios. GRADO: UNDÉCIMO
1. Investiga y comprende contenidos matemáticos a través del uso de distintos enfoques para el tratamiento y resolución de problemas; reconoce, formula y resuelve problemas del mundo real aplicando modelos matemáticos e interpreta los resultados a la luz de la situación inicial. 2. Elabora modelos de fenómenos del mundo real y de las matemáticas con funciones polinómicas, escalonadas, exponenciales, logarítmicas, circulares y trigonométricas; las representa y traduce mediante expresiones orales, tablas, gráficas y expresiones algebraicas. 3. Aplica modelos de funciones para tratar matemáticamente situaciones financieras y transacciones comerciales frecuentes en la vida real. 4. analiza situaciones de la vida diaria generadoras de las ideas fuertes del cálculo, tales como tasa de cambio, tasa de crecimiento y total acumulado; descubre y aplica modelos de variación para tratarlas matemáticamente. 5. Hace inferencias a partir de diagramas, tablas y gráficas que recojan datos de situaciones del mundo real; estima, interpreta y aplica medidas de tendencia central, de dispersión y de correlación. 6. Reconoce fenómenos aleatorios de la vida cotidiana y del conocimiento científico, formula y comprueba conjeturas sobre el comportamiento de los mismos y aplica los resultados en la toma de decisiones. 7. Formula hipótesis, las pone a prueba, argumenta a favor y en contra de ellas y las modifica o las descarta cuando no resisten la argumentación. 8. Planifica colectivamente tareas de medición previendo lo necesario para llevarlas a cabo, el grado de precisión exigido, los instrumentos adecuados y confronta los resultados con las estimaciones. 9. Disfruta y se recrea en exploraciones que retan su pensamiento y saber matemático y exigen la manipulación creativa de objetos, instrumentos de medida y materiales y medios. METAS DE CALIDAD POR GRADO Al finalizar el año escoñar los estudiantes que hayan adquirido los contenidos mínimos establecidos en el currículo estarán en capacidad de: GRADO PRIMERO  Identificará y contará los elementos de conjuntos diversos, clasificándolos y buscándolas semejanzas y relaciones con situaciones de la vida cotidiana.  Desarrollará habilidades lógicas y críticas, mediante nociones y procedimientos de razonamiento elemental, alcanzando la construcción de estructuras matemáticas básicas, la ordenación de datos basado en la posicionalidad del sistema numérico, reconocimiento y definición de figuras geométricas elementales. GRADO SEGUNDO 1. Utilizará las operaciones básicas en situaciones de la vida diaria, identificando el valor posicional, estableciendo relaciones numéricas y espaciales y utilizando conjuntos de datos dentro del círculo numérico del 1000 al 99.999, GRADO TERCERO 1. Situación de la competencia matemática 2. 16 Manejan procesos de pensamiento matemático Que les permiten diseñar sus propias formas de resolver un problema: trazan las estrategias para solucionarlo y reorganizan o transforman los datos. 3. 35 Están en capacidad de resolver problemas que Involucran un sólo tópico (aritmética, geometría, estadística) y tienen toda la información en el enunciado, pero ésta requiere reorganización.
4. 30 Pueden resolver problemas concretos de un solo tópico cuyo enunciado contiene toda la información en el orden exacto para solucionarlos. GRADO CUARTO 1. Generar una actitud favorable hacia las matemáticas y estimular el interés por su estudio. 2. Obtener los mejores resultados posibles en las pruebas institucionales. 3. Obtener mínimo un promedio de 50 puntos en el área de matemáticas en las pruebas SABER. (50). 4. Reducir al máximo el índice de repitencia en el grado 4º. 5. Orientar los estudiantes para que su trabajo en clase, su capacidad de lenguaje matemático, la excelencia en los trabajos que se realicen y el resultado en las diferentes pruebas pueden llegar a los mejores resultados. 6. Implementar diferentes acciones y/o estrategias preventivas en materia de pérdida, reprobación y/o repitencia GRADO QUINTO 1. Tener un 60% de los estudiantes con capacidad argumentativa coherente. 2. Llegar a un 50% de estudiantes propositivos en las diferentes temáticas trabajadas. 3. Ofrecer una educación de calidad, propiciando espacios de aprendizaje, práctica de valores, lenguaje simbólico e investigación, así como adquirir conceptos y dominio de pensamiento matemático que sean ampliamente aplicables y útiles a diferentes situaciones de la vida diaria y en el desarrollo de la competencia laborales generales. 4. Reducir en un 5% el índice de reprobación en el área de matemáticas. 5. Disminuir en un 1% los índices de deserción escolar de los estudiantes. 6. Fortalecer, con la participación de los estudiantes, los eventos que tradicionalmente organiza el área de matemáticas. 7. El 65%de los estudiantes de la I.E Luis Eduardo Arias Reinel aprendan a desarrollar competencias básicas y específicas del área de matemáticas. GRADO SEXTO 1. Que al culminar el año 2013 los Jóvenes de los grados sextos en un 75% reconozcan, utilicen y solucionen problemas que involucren los números naturales. 2. Reconocer la importancia de averiguar datos y procesar información para tomar decisiones, y evaluar sus características en relación con las decisiones que se tomen. 3. Reconocer características de sólidos, figuras planas y líneas y utilizarlas en su vida cotidiana en trabajos prácticos como mediciones, elaboración de dibujos y construcción de modelos. GRADO SEPTIMO 1. Al culminar el grado séptimo como mínimo el 70% estarán en capacidad de identificar y usar los números enteros y los racionales en diferentes contextos, representaciones de diversas formas y establecer relaciones entre ellos. 2. Redefinir las operaciones básicas en los sistemas formados con los números racionales y decimales y establecer conexiones entre ellas. 3. Los estudiantes estarán en capacidad de investigar y comprender contenidos y procedimientos matemáticos, a partir de enfoques de tratamiento y resolución de problemas y generalizar soluciones y estrategias para nuevas situaciones. 4. Estarán en capacidad de formular inferencias y argumentos coherentes, utilizando medidas de tendencia central y de dispersión para el análisis de los datos, interpretar estadísticos y elaborar críticamente conclusiones. 5. Visualizar, reconocer y efectuar transformaciones de polígonos en el plano y utilizarlas para establecer congruencia, semejanza y simetría entre figuras. 6. Comprender y usar la proporcionalidad directa e inversa de magnitudes, en distintos contextos de la vida cotidiana y utilizar diferentes procedimientos para efectuar cálculos de proporcionalidad.
GRADO OCTAVO 1. Utilizar estrategias y técnicas simples de resolución de problemas de la vida cotidiana, tales como el análisis del Enunciado, el planteamiento de la situación y la resolución de la misma, con los números reales que conlleva a comprobar la Solución obtenida y así expresarlo en el lenguaje matemático propio de su nivel. 2. Los jóvenes del grado octavo en un 80% al culminar el año puedan reconocer, realizar operaciones básicas, solucionen problemas de la vida diaria con los números reales GRADO NOVENO 1. Organizar e interpretar informaciones diversas mediante tablas y gráficas estadísticas, e identificar relaciones de dependencia en situaciones cotidianas en cuanto a las medidas de tendencia central y las de dispersión. 2. Utilizar estrategias y técnicas simples de resolución de problemas de la vida diaria, tales como el análisis del Enunciado, el planteamiento de la situación y la resolución de la misma, utilizando ecuaciones lineales con dos y tres variables que conlleva a comprobar la Solución obtenida y así expresarlo en el lenguaje matemático propio de su nivel. GRADO DECIMO 1. Tener una aprobación del 95% del área de matemáticas. 2. Tener un manejo mínimo del 60% de los siguientes pensamientos: numérico, métrico, geométrico y aleatorio. 3. Tener un manejo mínimo del 60% en los siguientes temas: - Conversión de ángulos - Triángulos rectángulos - Triángulos oblicuángulos - Ángulos de depresión y elevación - Identidades trigonométricas - Ecuaciones trigonométricas - Secciones cónicas - estadística 4. Hacer incentivos y reconocimientos establecidos y promover el desarrollo del talento estudiantil en el área de las matemáticas en participación de diferentes eventos como: olimpiadas de matemáticas es diferentes instituciones. 5. Realizar una evaluación por periodo y anual de los resultados en el área de matemáticas y establecer metas de mejoramiento futuro. 6. Implementar de manera integral las matemáticas con las demás áreas del conocimiento. 7. Permitir el acceso a INTERNET como herramienta de enseñanza y de aprendizaje en el área de matemáticas como fuente de información para la investigación de tareas y proyectos. 8. 0% de deserción. Buscar estrategias para que sus estudiantes no abandonen las aulas, crear las condiciones y resolver las situaciones para evitar la deserción durante el año escolar. 9. Mantener un alto nivel de Eficiencia Interna dada por los porcentajes anuales de aprobación, repitencia y optimización del tiempo escolar. GRADO UNDECIMO 1. Tener una aprobación del 95% del área de matemáticas.
2. Tener un manejo mínimo del 60% de los siguientes pensamientos: numérico, métrico, geométrico y aleatorio. 3. Tener un manejo mínimo del 60% en los siguientes temas: - Secciones cónicas - Estadística descriptiva - Funciones - Concepto de limite formal e informal - Derivación - integración 4. Hacer incentivos y reconocimientos establecidos y promover el desarrollo del talento estudiantil en el área de las matemáticas en participación de diferentes eventos como: olimpiadas de matemáticas es diferentes instituciones. 5. Realizar una evaluación por periodo y anual de los resultados en el área de matemáticas y establecer metas de mejoramiento futuro. 6. Implementar de manera integral las matemáticas con las demás áreas del conocimiento. 7. Permitir el acceso a INTERNET como herramienta de enseñanza y de aprendizaje en el área de matemáticas como fuente de información para la investigación de tareas y proyectos. 8. 0% de deserción. Buscar estrategias para que sus estudiantes no abandonen las aulas, crear las condiciones y resolver las situaciones para evitar la deserción durante el año escolar. 9. Mantener un alto nivel de Eficiencia Interna dada por los porcentajes anuales de aprobación, repitencia y optimización del tiempo escolar. RECURSOS Los recursos son escogidos con la siguiente intencionalidad: Suministrar al área de matemáticas recursos didácticos que generen en los estudiantes una actitud favorable frente al área y que estimulen en ellos el interés por su estudio. Estimular en los estudiantes el uso creativo de las matemáticas para expresar nuevas ideas y descubrimientos, así como para reconocer los elementos matemáticos presentes en otras actividades creativas. Familiarizar a los estudiantes desde temprana edad con el mundo de las matemáticas en una forma analítica, experimental y crítica. Brindar una enseñanza de cada uno de los pensamientos matemáticos basada en la experimentación, el juego y el constructivismo. Después de mencionar las intencionalidades generales que se pretenden alcanzar al utilizar cada uno de los recursos es importante ser específicos y categorizar cada uno de ellos: El material Impreso: donde se pretende hacer uso exclusivo de la biblioteca teniendo como finalidad la realización de actividades pedagógicas como talleres, tareas, entre otras. Además la fotocopiadora se convierte en ese medio tecnológico que permite la multiplicación de guías de trabajo. Material Didáctico: a través del manejo de sólidos, reglas, compás, transportador, bloques lógicos, algunas láminas entre otros materiales que se pueden manipular y que permiten el aprendizaje lúdico. Equipos y Materiales Audiovisuales: esta categoría permite la utilización de las sala de video, donde se puede hacer uso del televisor, los proyectores, entre otros medios todo con el fin de dinamizar el aprendizaje y ampliar los contenidos.
Programas y Servicios Informáticos: a futuro se puede hacer uso del aula de Medellín digital pues este recurso proporciona herramientas para mejorar los procesos académicos a partir del uso de las Tics. Materiales impresos 1. Talleres construidos por el docente en base al plan de área de matemáticas, con el eje de situaciones problema. Copias Clases Maestras y documentos creados por los docentes: libros, fotocopias, periódicos, documentos. 2. Textos De Apoyo: Serie Espiral,SerieNova, Serie Santillana,Serie McGraw Hill,entre otros libros que la I.E. disponga en su biblioteca. Materiales didácticos: 1. Escuadras, reglas, transportadores 2. Tangram 3. Pentóminos 4. Domino de fracciones 5. Guías (orientadas desde la Escuela del Maestro) 6. Materiales para niños de transición a 5º de primaria Equipos y materiales audiovisuales: 1. Sala de Proyecciones: Video Beam 2. Sala de Televisión: TV 3. Sala de Informática: PC Programas y servicios informáticos: Servicios telemáticos:páginas web, blogs,tours virtuales,webquest, cazas del tesoro, correo electrónico,chats,foros, unidades didácticasy cursos on-line. Cabri: Para aprender geometría 2. Geogebra 3. Flechas: números y formas. Infantil y primaria 4. Funciones: representa funciones. Postalcardware 5. HungryFrog. Juego para trabajar álgebra básica 6. Módulo para Derive. Puntos, rectas y planos. 7. Las plantas. Infantil y primaria. Reconocimiento de los números 8. Plot3D. Representación gráfica de funciones. 9. Juego con 250 problemas de geometría 10. Primtres. Aritmética y geometría para primaria 11. SerpikGraphs 1.2. Funciones 12. Simetría. Para trabajar las simetrías en infantil y primara 13. UniGraph. Representación de funciones 14. Cantidades. Juego para aprender números y seriaciones. Infantil y primaria. 15. Colores. Juego para familiarizarse con los números. Infantil 16. Trigonometría: Software freeware para trabajar con funciones trigonométricas 17. Programa para aprender el área de figuras planas 18. Programa para resolver ecuaciones de segundo grado 19. Cálculos de geometría. Áreas y volúmenes. 20. KapGram. Juego similar al Tangram 21. El proyecto descartes. 22. Blogs disponibles en Internet en páginas como multiply.com, www.entrepares.com Otros: recursos humanos como los docentes (matemáticas y todas las áreas) y los alumnos. Con recurso físico las instalaciones del colegio, tanto aula como espacios al aire libre. Además se debe involucrar el contexto que rodea a la institución como garante de aprendizajes porque El ambiente educativo no se limita a las condiciones materiales necesarias para la implementación del currículo, cualquiera que sea su concepción, o a las relaciones interpersonales básicas entre maestros y alumnos. Por el contrario, se instaura en las dinámicas que constituyen los procesos educativos y que involucran acciones, experiencias vivencias por cada uno de los participantes; actitudes, condiciones materiales y socio afectivo, múltiples relaciones con el entorno y la infraestructura necesaria para la concreción de los propósitos culturales que se hacen explícitos en toda propuesta educativa.
4. MALLAS CURRICULARES: INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: PRIMERO PERIODO: 1 ESTÁNDAR: Reconozco significados del número en diferentes contextos (medición, conteo, comparación codificación, localización, entre otros). Describo, comparo y cuantifico situaciones con números, en diferentes contextos y con diversas representaciones EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATI VA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué es importante saber contar y conocer las características de los objetos que nos rodean?  Cantidades  Relación de orden  Adición  Sustracción  Situaciones problémicas  Valor posicional  Conjuntos  Clases de líneas  Patrones de medida  Secuencias  Características de los objetos.  Distancia y posición.  Posición y lugar.  Ubicación espacial.  Conjuntos, números del 0 al 9, orden de los números, adición y sustracción de números, problemas de adicción y sustracción y representación en la recta numérica.  Líneas curvas, rectas, abiertas y cerradas,  mediciones, patrones de medida  Secuencias de números y figuras.  Números ordinales.  Comparación y clasificación de pequeñas colecciones de objetos teniendo en cuenta sus cualidades o características.  Ordenamiento y relación de dígitos con la cantidad de elementos.  Organización de objetos y eventos de acuerdo con su posición y patrón de orden.  Establecimiento de relaciones de distancia y ubicación espacial de los objetos: Largo- Corto, alto - bajo, en medio de, dentro – fuera, izquierda – derecha, primero – último.  Interprete situaciones matemáticas aditivas.  Reconozca los números hasta 9 y su valor de posición.  Argumente sobre la solución de una situación o problema presentando y organizando procedimientos lógicos.  Proponga solución a las situaciones problemáticas presentadas.  Prediga y estime resultados numéricos.  Establecimiento de relaciones de orden entre los números.  Reconocimiento de cantidades, utilizando números cardinales y ordinales.  Descubrimiento de que la suma y la resta sirven para resolver problemas.  Encuentro del patrón de cambio en secuencias de objetos diversos y numéricos.  Organización de secuencias utilizando patrones.  Ubicación de objetos en relación con su posición en el espacio.  Realización de graficas utilizando diversos tipos de líneas.   Solución de situaciones problema, utilizando los números para contar y medir.  Aporte de sus conocimientos y capacidades al proceso de conformación de un equipo de trabajo y contribuye al desarrollo de las acciones orientadas.  Expresa sus ideas, sentimientos e intereses en el salón.  escucha respetuosamente a los demás miembros del grupo.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: PRIMERO PERIODO: 2 ESTÁNDAR: Reconozco significados del número en diferentes contextos (medición, conteo, comparación, codificación, localización, entre otros). Describo situaciones o eventos a partir de un conjunto de datos. Describo cualitativamente situaciones de cambio y variación utilizando el lenguaje natural, dibujos y gráficas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué los números tienen diferente nombre y valor? • Cantidades: • El reloj: • El calendario • Adición • Sustracción • Organización de datos. • Eventos seguros • Decenas, docenas, quincena. • Horas, minutos, segundos. • Los días de la semana, los meses del año • Adición de números hasta 99 • Sustracción de números hasta 99 • Números ordenados hasta 99. • Utilice el reloj para medir el tiempo de sucesos cotidianos. • Resuelva situaciones aditivas en el ámbito 0 a 99. • De y siga instrucciones en que aparecen relaciones de distancia y dirección. • Reconocimiento del efecto que tienen las operaciones básicas (suma y resta) sobre los números • Identificación de los atributos mesurables de los objetos y eventos de tiempo en diversas situaciones. • Reconocimiento del calendario con meses y días. • Reconocimiento y manejo del reloj u sus manecillas.  Explicación, desde su experiencia, de la posibilidad o imposibilidad de ocurrencia de eventos cotidianos.  Suma en el ámbito de los números de 0 a 99  Resto en el ámbito de números del 0 a 99.  Solución de problemas con operaciones de suma y resta.  Uso de su experiencia para predecir si algo va a suceder, o la probabilidad de ocurrencia.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: PRIMERO PERIODO: 3 ESTÁNDAR: Describo cualitativamente situaciones de cambio y variación, utilizando el lenguaje natural, dibujos y gráficas. Construyo secuencias numéricas y geométricas, utilizando propiedades de los números y de las figuras geométricas EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento variacional. ¿Cómo realizar operaciones de suma y resta con centenas? • Cantidades: • Lectura y escritura de números. • Adición. • Sustracción • Secuencias. • Sólidos • Figuras planas • La moneda • La centena: • Identificación del orden de números de tres cifras. • Lectura y escritura de números hasta 999. • Comparación de números hasta 999. • Adición sin agrupamiento hasta 999. • Adición agrupando. • Sustracción sin desagrupar. • Sustracción desagrupando. • Identificación de secuencias numéricas y geométricas. • Sólidos geométricos. • Identificación de las características de los objetos en tres dimensiones • Identificación de formas y figuras planas. • El peso colombiano, dólar, euro… Identificación de la moneda colombiana para hacer transacciones. • Identificación de eventos imposibles • Interprete la suma y la resta como operaciones internas de los números naturales y resuelva problemas con esas operaciones. • Explique las características de las figuras geométricas, las compare y las organice por una característica o medida. • Describa lo que cambia y cómo cambia usando dibujos, palabras, números o gráficos. • Identifique correctamente las centenas como aquellas conformadas por 100 unidades o por 10 decenas, logrando con ello mayor y mejor dominio del área. • Reconocimiento de los nombres de los números hasta 999 y sabe cuál es su valor según el lugar que ocupa. • Conteo, y organización de cantidades con tres dígitos y establecimiento de relaciones de orden entre ellos. • Distinción de las características de los objetos en tres dimensiones. • Descripción y señalamiento de los bordes y los vértices en una figura geométrica.  Conteo de números hasta 999.  Resolución de situaciones que requieran adición y sustracción con números de hasta tres dígitos.  Reconocimiento y trazo de diferentes clases de líneas y figuras geométricas.  Organización de datos usando tablas de secuencia.  Análisis y organización de tablas de frecuencia para resolver preguntas planteadas por el grupo de estudiantes.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: PRIMERO PERIODO: 4 ESTÁNDAR: Describo, comparo y cuantifico situaciones con diversas representaciones de los números, en diferentes contextos. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento espacial.  Pensamiento variacional. ¿Cómo seguir contando números después del 999 y en qué orden se clasifica el número 1.000? • La unidad de mil. • Igualdades. • Estimación. • La mitad. • Resolución de problemas con números hasta 1.000. • El centímetro. • El decímetro. • El metro. • Simetría. • Traslación. • Diagrama de barras horizontales, verticales. • Lectura y escritura de las unidades de mil. • Identificación y representación de igualdades. • El centímetro. • El decímetro. • Equivalencia con medidas de longitud. • Noción de simetría. • Traslaciones realizadas sobre objetos. • Estimaciones con suma y resta hasta 1.000. • Repartición de conjuntos en mitades. • Resolución de problemas con números hasta 1000. • Medida de objetos en centímetros. • Medida de objetos en decímetros. • Interpretación y lectura de los diagramas de barras. • Identifique los números hasta el mil para contar, medir, comparar y describir situaciones que requieran solución, logrando con ello un mayor dominio de la matemática. • Interprete situaciones aditivas según la información proporcionada. • Argumente los procedimientos y algoritmos utilizados para resolver una situación presentada. • Proponga solución a los problemas presentados usando los procedimientos matemáticos con creatividad. • Solución a situaciones matemáticas aditivas en el ámbito de los naturales hasta 1.000. • Lectura y análisis de las situaciones presentadas en el ámbito numérico de 0 a 1.000. • Encuentro de los procedimientos y algoritmos correspondientes para dar solución a situaciones presentadas de 0 a 1.000. • Comparación y ordenamiento de objetos de acuerdo con sus tamaños y medidas, utilizando medidas e instrumentos adecuados. • Utilización de los números para contar, medir, comparar y describir situaciones que requieran solución. • Análisis de datos para resolver preguntas. • Utilización de las medidas de longitud y la información de los gráficos en la solución de las situaciones planteadas en clase. • Participación en el desarrollo de las clases. • Escucha respetuosa a los demás miembros del grupo
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SEGUNDO PERIODO: 1 ESTÁNDAR: Reconozco significados del número en diferentes contextos (medición, conteo, comparación, codificación, localización, entre otros). Describo situaciones o eventos a partir de un conjunto de datos. Reconozco y describo regularidades y patrones en distintos contextos (numérico, geométrico, musical, entre otros). Describo cualitativamente situaciones de cambio y variación utilizando el lenguaje natural, dibujos y gráficas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento Numérico y Sistemas Numéricos  Pensamiento Aleatorio y Sistemas de Datos  Pensamiento Variacional y Sistemas Algebraicos y Analíticos ¿Por qué es indispensable que el hombre ubique adecuadamente el valor posicional de un número?  Conjuntos – subconjuntos.  Propiedades y relaciones de conjuntos  Unidad, decena centena, unidades de mil.  Composición de números.  Valor posicional.  Datos en pictogramas.  Diferencias entre un conjunto y un subconjunto.  Reconocimiento y ubicación de unidades, decenas centenas, en números de tres cifras.  Adición y sustracción con y sin agrupación.  Análisis de datos presentados en pictogramas. • Diferencie entre un conjunto y un subconjunto. • Reconozca y ubique las unidades, decenas, centenas, en números de tres cifras. • Sume y reste con y sin agrupación • Valore las operaciones básicas y las propiedades de la adición y sustracción. • Clasifique y organice datos reales de acuerdo con sus cualidades y atributos; describiendo situaciones o eventos a partir de estos, explicando la posibilidad o imposibilidad desde su experiencia cotidiana. • Análisis de las características comunes entre elementos para formar conjuntos. • Ampliación del concepto de suma mediante la composición de números hasta 1.000. • Utilización de la información presentada en pictogramas para solucionar problemas de la vida cotidiana. • Expresión del significado de una unidad, decena, centena. • Establecimiento de relaciones de pertenencia entre un elemento y un conjunto. • Reconocimiento y utilización de los números naturales y ordinales en diferentes situaciones de la cotidianidad. • Resolución de ejercicios en donde se combinan operaciones de adición y sustracción. • Aporte de sus conocimientos y capacidades al proceso de conformación de un equipo de trabajo y contribuye al desarrollo de las acciones orientadas. • Expresión de sus ideas, sentimientos e intereses en el salón. • Cumplimiento de las reglas básicas del diálogo. • Resolución de conflictos con los demás de manera pacífica. • Presentación de sus trabajos en forma clara y ordenada.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SEGUNDO PERIODO: 2 ESTÁNDAR: Reconozco significados del número en diferentes contextos (medición, conteo, comparación, codificación, localización, entre otros). Resuelvo y formulo problemas aditivos de composición y transformación (Pensamiento numérico y sistemas numéricos) Reconozco en los objetos propiedades o atributos que se puedan medir (longitud, área, volumen, capacidad, peso y masa) y, en l os eventos, su duración. Clasifico, organizo e interpreto datos de acuerdo a cualidades y atributos y los presento en tablas. Reconozco y genero equivalencias entre expresiones numéricas y describo cómo cambian los símbolos aunque el valor siga igual. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Cómo beneficia al hombre el conocer las medidas de longitud, superficie y tiempo?  Números hasta el 99.999  Comparación y descomposición entre números  Adición y sustracción  Medidas de longitud, superficie y tiempo  Lectura y escritura de números de 5 cifras.  Orden, comparación, composición y descomposición de secuencias numéricas y geométricas.  Suma y resta agrupando y desagrupando  Ejercicios con unidad de medida de longitud, de superficie y de tiempo.  Propiedades de la adición y sustracción.  Lea y escriba números de 5 cifras.  Ordene, compare, componga y descomponga secuencias numéricas y geométricas.  Calcule sumas y restas agrupando y desagrupando.  Solucione ejercicios con unidad de medida de longitud, de superficie y de tiempo.  Valore las operaciones básicas y las propiedades de la adición y sustracción. • Valore la adición como sistema de resolución de situaciones reales que impliquen agrupar. • Reconocimiento de la cantidad que representa un número de 5 cifras. • Composición y descomposición de números de 5 cifras. • Resolución de adiciones y sustracciones. • Conocimiento de la unidad de medida de tiempo y superficie.  Ubicación de números de 5 cifras en la tabla de posición.  Establecimiento d relaciones de orden entre números de 5 cifras.  Planteamiento y solución de problemas que involucran situaciones aditivas.  Uso del centímetro, el decímetro y el metro como unidades de medida y longitud. • Expresión de sus ideas, sentimientos e intereses en el salón. • Escucha respetuosa a los demás miembros del grupo. • Participación con responsabilidad en las actividades individuales y grupales. • Resolución de los conflictos con los demás de manera pacífica.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SEGUNDO PERIODO: 3 ESTÁNDAR: Reconozco propiedades de los números (ser par, ser impar, etc.) y relaciones entre ellos (ser mayor que, ser menor que, ser múltiplo de, ser divisiblepor, etc.) en diferentes contextos. Uso diversas estrategias de cálculo (especialmente cálculo mental) y de estimación para resolver problemas en situaciones aditivas y multiplicativas. Realizo construcciones y diseños utilizando cuerpos y figuras geométricas tridimensionales y dibujos o figuras geométricas bidimensionales. Reconozco en los objetos propiedades o atributos que se puedan medir (longitud, área, volumen, capacidad, peso y masa) y, en los eventos, su duración. Represento datos relativos a su entorno usando objetos concretos, pictogramas o diagrama de barras EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATI VA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Qué importancia tiene para el hombre el usar diversas estrategias de cálculo y representación de sus resultados?  La multiplicación:  Sólidos y figuras geométricas.  Gráficas de barras:  Relación entre adición y multiplicación.  Propiedades de la multiplicación.  Procedimiento para el cálculo de productos.  Diferencias entre sólidos geométricos y figuras planas.  Los datos en las gráficas de barras. • Relacione la adición y la multiplicación. • Aplique las propiedades de la multiplicación. • Calcule productos. • Diferencie entre sólidos geométricos y figuras planas. • Acepte de buen agrado, las opiniones ajenas, valorándolas críticamente. • Grafique e interprete información en diagramas de barras. • Reconocimiento del signo equis (X), el asterisco (*) y el punto (.) como operadores o signos de la multiplicación. • Comparación de la multiplicación como una adición de sumandos iguales. • Identificación de las figuras planas y los cuerpos geométricos. • Graficación de información en diagramas de barras. • Interpretación de la información dada en un diagrama de barras. • Realización de multiplicaciones por una cifra. • Resolución de ejercicios con los factores dados. • Graficación de sólidos geométricos y figuras planas. • Ubicación de información en diagramas de barras. • Aporte de sus conocimientos y capacidades al proceso de conformación de un equipo de trabajo y contribuye al desarrollo de las acciones orientadas. • Expresión de sus ideas, sentimientos e intereses en el salón. • Escucha respetuosa a los demás miembros del grupo. • Aceptación de buen agrado, las opiniones ajenas, valorándolas Críticamente. • Uso de los diagramas de barras para interpretar situaciones de la vida real.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SEGUNDO PERIODO: 4 ESTÁNDAR: Resuelvo y formulo problemas en situaciones de variación proporcional. Represento datos relativos a mi entorno usando objetos concretos, pictogramas y diagramas de barras. Resuelvo y formulo preguntas que requieran para su solución coleccionar y analizar datos del entorno próximo Construyo secuencias numéricas y geométricas utilizando propiedades de los números y de las figuras geométricas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué las matemáticas se integran con otras áreas del saber y en nuestra vida diaria?  División  Estadística y probabilidad.  Permutaciones y combinaciones de elementos.  Calculo de cocientes.  Prueba de la división.  Calculo de la división,  La mitad, tercera, cuarta parte de una cantidad.  Clasificación de datos en tablas estadísticas.  Clases de división, términos de la división • Calcule cocientes. • Realice la prueba de divisiones. • Calcule la mitad, tercera, cuarta parte de una cantidad. • Clasifique datos en tablas estadísticas. • Reconozca las combinaciones y las permutaciones de diferentes elementos. • Encuentre la forma como se ordenan diferentes objetos. • Reconocimiento de la división como una distribución en partes iguales. • Diferenciación de la división exacta e inexacta. • Interpretación de datos representados en un diagrama. • Reconocimiento de combinaciones de diferentes elementos. • Realización de divisiones exactas con dividendo hasta de 3 cifras. • Aplicación del algoritmo de la división. • Clasificación de divisiones exactas e inexactas.  Realización de tablas y gráficos utilizando la información.  Elaboración de diferentes permutaciones de elementos:  Aporte de sus conocimientos y capacidades al proceso de conformación de un equipo de trabajo y contribuye al desarrollo de las acciones orientadas.  Escucha respetuosa a los demás miembros del grupo. • Interés manifestado por desarrollar y conocer elementos nuevos o más  complejos.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: TERCERO PERIODO: 1 ESTÁNDAR: Reconozco propiedades de los números (ser par, ser impar, etc.) y relaciones entre ellos (ser mayor que, ser menor que, ser múltiplo de, ser divisiblepor, etc.) en diferentes contextos. Realizo construcciones y diseños utilizando cuerpos y figuras geométricas tridimensionales y dibujos o figuras geométricas bidimensionales. Realizo estimaciones de medidas requeridas en la resolución de problemas relativos particularmente a la vida social, económica y de las ciencias. Represento datos relativos a mi entorno usando objetos concretos, pictogramas y diagramas de barras. Describo cualitativamente situaciones de cambio y variación utilizando el lenguaje natural, dibujos y gráficas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué el hombre a través de la historia se ha interesado en representar de diversas formas sus conocimientos?  Sistema de numeración Romana.  Números de cinco dígitos.  Múltiplos y submúltiplos  Datos pictográficos.  Formas y figuras • Orden de objetos. • Formas de figuras. • Las tablas de multiplicar de doble entrada hasta el 12. • Solución de problemas • Normas de comportamiento cotidianos. • Recolección, interpretación, tabulación y traficación de datos pictográficos. • Construcción las tablas de multiplicar de doble entrada hasta el 12. • Identificación el sistema de numeración romana. • Organización y representación de datos en tablas y gráficos. • Realización de traslaciones y rotaciones de figuras. • Identificación de las características de algunas formas y figuras, y establece relaciones entre ellas. • Formulación y solución de problemas sencillos de la cotidianidad, utilizando las operaciones básicas. • Reconocimiento del sistema de numeración romano y lo compara con el sistema de numeración decimal. • Identificación de las características de los números hasta de cinco dígitos. • Explicación del antecesor y el sucesor de un elemento en una secuencia y el establecimiento de relaciones entre ellos. • Representación e interpretación de pictogramas a partir de un conjunto de datos. • Construcción y aplicación de las tablas de multiplicar hasta el doce. • Aplicación de los múltiplos y submúltiplos en diferentes situaciones de la vida. • Elaboración de traslaciones y rotaciones para crear nuevas figuras del Entorno. • Formulación y resolución de problemas que requieran el uso de la suma, la resta, la multiplicación y la división. • Respeto a las reglas básicas del dialogo. • Resolución de los conflictos con los demás de manera pacífica y/o respetuosa.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: TERCERO PERIODO: 2 ESTÁNDAR: Uso diversas estrategias de cálculo (especialmente cálculo mental) y de estimación para resolver problemas en situaciones aditivas y multiplicativas. Identifico regularidades y propiedades de los números utilizando diferentes instrumentos de cálculo (calculadoras, ábacos, bloques, etc.). Reconozco nociones de horizontalidad, verticalidad, paralelismo y perpendicularidad en distintos contextos y su condición relativa con respecto a diferentes sistemas de referencia. Realizo estimaciones de medidas requeridas en la resolución de problemas relativos particularmente a la vida social, económica y de las ciencias. Clasifico y organizo datos de acuerdo a cualidades y atributos y los presento en tablas. EJE GENERADOR PREGUNTA PROBLEMATIZAD ORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué es importante para el hombre aprender a analizar y resolver problemas? • Datos pictogramas. • Problemas de adición y sustracción desagrupar y agrupando. • Ángulos y triángulos. • La suma y sus propiedades. • Conteo y probabilidad. • Multiplicació n y división. • Medición de objetos del entorno. • Medición del tiempo y el espacio. • Realización de repartos. • Calculo mental con operaciones de suma, resta, multiplicaron y división. • Normas de comportamie nto. • Interpretación de información representada en pictogramas. • Identificación de situaciones cuya solución requiera de la adición y la sustracción. • Identificación y aplicación de las propiedades de la adición o suma. • Realización de sustracciones agrupando y desagrupando. • Identificación y aplicación de los conceptos de ángulos y triángulos. • Solución de operaciones de multiplicación y división por una cifra. • Construcción e identificación de ángulos y triángulos de acuerdo con sus características. • Aplicación de la propiedad conmutativa y asociativa de la suma en la resolución de diferentes problemas. • Identificación de datos como elementos que adquieren significado, cuando ofrecen información confiable de un contexto dado. • Resolución de situaciones planteadas en pictogramas. • Medición y establecimiento de congruencias y semejanzas entre varios objetos. • Utilización y establecimiento de relaciones entre las medidas de longitud, de superficie y de tiempo. • Interpretación y resolución de situaciones por medio del algoritmo de la multiplicación y la división. • Desarrollo de habilidades de cálculo mental en la resolución de problemas. • Utilización de la información presentada en pictogramas para solucionar problemas de la vida cotidiana. • Respeto por los aportes propios y de los demás. • Cooperación en las actividades propuestas en clase.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: TERCERO PERIODO: 3 ESTÁNDAR: Identifico regularidades y propiedades de los números utilizando diferentes instrumentos de cálculo (calculadoras, ábacos, bloques multibase, etc.). Represento el espacio circundante para establecer relaciones espaciales. Realizo construcciones y diseños utilizando cuerpos y figuras geométricas tridimensionales y dibujos o figuras geométricas bidimensionales Reconozco en los objetos propiedades o atributos que se puedan medir (longitud, área, volumen, capacidad, peso y masa) y, en los eventos, su duración. Comparo y ordeno objetos respecto a atributos medibles. EJE GENERADOR PREGUNTA PROBLEMATIZA DORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Cómo realizar procesos de medición con patrones arbitrarios y estandarizados?  Clases de división:  Equivalencia entre Medidas.  Gráficos:  Ubicación en el espacio:  Área y perímetro  Números primos y compuestos, operaciones combinadas • Exacta e inexacta. • Aplicación de la división • Volumen, capacidad, peso • Diagramas de barra. • Arriba, abajo, centro, afuera, derecha, izquierda, adelante, atrás, zurdo, diestro. • Reglas básicas del diálogo. • Identificación y aplicación de las clases de división. • Reconocimiento de la noción de volumen, peso y capacidad en objetos de su entorno. • Formulación y solución de problemas de multiplicación y división. • Descripción de los conceptos de espacio y tiempo en su contexto. • Identificación y clasificación de números primos y compuestos. • Determinación del m.c.m. y el m.c.d de dos o más números. • Identificación y aplicación de los conceptos de área y perímetro. • Reconocimiento de la división exacta e inexacta. • Indagación del área y el perímetro de figuras geométricas y de objetos del entorno. • Descripción de la posición de un objeto con relación a un punto en el espacio. • Identificación de números primos y compuestos. • Comparación, medición y relación de diferentes elementos, utilizando medidas de capacidad, volumen y peso • Planteamiento y resolución de problemas que requieran de la división. • Elaboración de diagramas de barras para representar y analizar datos. • Escritura de los submúltiplos de un número dado. • Encuentro el m.c.d entre dos números • Resolución de los conflictos con los demás de manera pacífica. • Respeto de las reglas básicas del diálogo.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: TERCERO PERIODO: 4 ESTÁNDAR: Describo situaciones de medición utilizando fracciones comunes. Reconozco propiedades de los números (ser par, ser impar, etc.) y relaciones entre ellos (ser mayor que, ser menor que, ser múltiplo de, ser divisible por, etc.) en diferentes contextos. Resuelvo y formulo problemas en situaciones de variación proporcional. Reconozco y genero equivalencias entre expresiones numéricas y describo cómo cambian los símbolos aunque el valor siga igual. EJE GENERADOR PREGUNTA PROBLEMATIZA DORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento aleatorio.  Pensamiento variacional. ¿Qué actividades puedo realizar para ayudar a mejorar la economía familiar y escolar de mi comunidad? • División por una y dos cifras en el divisor. • Fracciones como parte de la unidad. • Estadística, azar y probabilidad. • El ahorro. • Números primos y compuestos. • Operaciones combinadas. • Prueba de la división. • Cálculo de la división, la mitad, tercera, cuarta parte de una cantidad. • Clasificación de datos en diagramas horizontales. • Azar, probabilidad. • Partes fraccionadas de un conjunto, fracciones homogéneas. Orden de las fracciones, equivalentes. • Adición y sustracción de fracciones, problemas con fracciones. • La cooperación. • Realización y prueba de divisiones de una y dos cifras en el divisor. • Identificación y representación del concepto de fracciones. • Identificación y aplicación de las clases de fracciones. • Reconocimiento de la división como mitad, tercera o cuarta parte de una cantidad. • Formulación de problemas cuya solución involucran la multiplicación y la división. • Realización de adiciones y sustracciones con fracciones. • Realización de congruencias y semejanzas entre cuerpos y figuras geométricas. • Comprensión y empleo correcto de las fracciones en diferentes situaciones. • Establecimiento de relaciones de congruencia, semejanza y diferencia entre figuras y cuerpos sólidos. • Ejecución de sumas y restas de fracciones homogéneas, con el fin de interpretar y argumentar la solución de diversas situaciones. • Construcción de diferentes sólidos geométricos a partir de diseños. • Creación de diseños utilizando la ampliación y reducción de figuras. • Organización y comparación de datos en diagramas de barras horizontales. • Aplicación del concepto de probabilidad en la solución de problemas. • Respeto de las reglas básicas del diálogo. • Resolución de los conflictos con los demás de manera pacífica. • Manifestación de conciencia del valor del ahorro a través de la creación de su alcancía.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL. MALLAS CURRICULARES MATEMÁTICAS. GRADO: CUARTO PERIODO: 1 ESTÁNDAR: Resuelvo y formulo problemas cuya estrategia de solución requiera de las relaciones y propiedades de los números naturales y sus operaciones. Comparo y clasifico figuras bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. Identifico, represento y utilizo ángulos en giros, aberturas, inclinaciones, figuras, puntas y esquinas en situaciones estáticas y dinámicas. Construyo y descompongo figuras y sólidos a partir de condiciones dadas. EJE GENERADOR PREGUNTA PROBLEMATIZA DORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial. ¿Qué importancia tiene para el hombre aprender a diferencias figuras bidimensionales y tridimensionales ? • Relaciones de los números naturales: • Objetos geométricos de dos y tres dimensiones: • Múltiplos y divisores, Mínimo Común Múltiplo, Máximo Común Divisor, Criterios de divisibilidad. Números naturales de más de seis cifras y operaciones básicas con ellos. • Componentes de los objetos tridimensionales (caras, lados). • Componentes de las figuras bidimensionales (ángulos, vértices). • Propiedades de los objetos geométricos. • Ejercicios de transformación de objetos bidimensionales dando cuenta de las relaciones y diferencias entre ellas. • -Identificar y representar los números naturales explicando su aplicación en la solución de situaciones de la vida cotidiana. • -Usar significativamente los conocimientos geométricos para solucionar problemas. • -Utilizar y proponer estrategias de cálculo y de estimación para resolver situaciones donde es necesario la aplicación de las operaciones básicas (suma, resta, multiplicación y división). • -Descomponer números naturales en factores primos y/o divisores. • -Hallar el M.C.M y M.C.D. entre números. • Identificar y relacionar los componentes de una figura bidimensional (ángulos y vértices). • -Diferenciar los componentes que tiene un objeto tridimensional y uno bidimensional. • -Transformar objetos bidimensionales dando cuenta de las relaciones y diferencias entre ellas. • -Estimación de resultados en operaciones básicas de: suma, resta, multiplicación y división con números naturales. • -Reconocimiento del M.C.M y M.C.D. • -Identificación y relación entre los componentes de una figura bidimensional (ángulos y vértices) • -Identificación y relación entre los componentes de una figura bidimensional (ángulos y vértices) • -Diferenciación de los componentes que tiene un objeto tridimensional y uno bidimensional. • -Descomposición de números naturales en factores primos y/o divisores. • -Construcción y clasificación de objetos geométricos. • -Elaboración de figuras bidimensionales y tridimensionales. • -Cumplimiento y organización en la elaboración y entrega de los trabajos propuestos. • -Interés por indagar y dar respuesta a las preguntas. • -Interés por aprender sobre los números naturales y sus operaciones. • -Valoración del aprendizaje de las operaciones básicas. • -Perseverancia en la construcción de objetos geométricos. • -Reconocimiento de la importancia que tiene el uso de los números naturales y sus propiedades en la vida diaria.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: CUARTO PERIODO: 2 ESTANDAR: Interpreto las fracciones en diferentes contextos: situaciones de medición, relaciones parte todo, cociente, razones y proporciones. Utilizo la notación decimal para expresar fracciones en diferentes contextos y relaciono estas dos notaciones con la de los porcentajes. Comparo y clasifico objetos tridimensionales de acuerdo con componentes (caras, lados) y propiedades. Comparo y clasifico figuras bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. Construyo objetos tridimensionales a partir de representaciones bidimensionales y puedo realizar el proceso contrario en contextos de arte, diseño y arquitectura EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DELOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamient o numérico.  Pensamient o espacial. ¿Por qué en el mundo actual el hombre maneja cantidades con fracciones y decimales? • Números fraccionarios: • Números decimales: • Objetos geométricos de dos y tres dimensiones: • Interpretación del número fraccionario como partidor, medidor y porcentaje. • Equivalencia de fracciones. • Fracciones decimales. • Fracciones Mixtas. • Conceptualización de Fracciones propias e impropias. • Conceptualización sobre 1implificación y amplificación. • Adición y sustracción de fracciones. • Potencias de 10. • Concepto del número decimal y su forma de expresarlo. • Componentes de los • objetos tridimensionales • (Caras, lados). • Propiedades de los objetos geométricos. • Polígonos regulares e irregulares. • El círculo y la • circunferencia: • Partes del círculo y elementos de la circunferencia. • -Explicar del cómo y el porqué de los procesos que se siguen para llegar a conclusiones apoyándose en estrategias a nivel matemático. • -Diferenciar las distintas clases de fracciones y su representación para interpretarlas en contexto. • -Utilizar significativamente los conocimientos geométricos para solucionar problemas. • -Identificar características tangibles de objetos del entorno estableciendo relaciones con los elementos de los cuerpos geométricos. • -Identificación de la fracción como partidor y medidor estableciendo relaciones de ella con el porcentaje. • -Interpretación de problemas de adicción y sustracción utilizando fracciones y decimales. • -Comprensión de las diferencias que hay entre círculo y circunferencia. • -Comparación de números decimales. • -Diferenciación de los componentes que tiene un objeto tridimensional y uno bidimensional. • -Diferenciación entre polígonos regulares e irregulares. • -Comparación entre objetos geométricos a través de la congruencia y • -Simplificación y amplificación de fracciones. • -Realización de operaciones básicas (suma, resta, multiplicación y división) con números fraccionarios. • -Expresión oral y escrita del número decimal a partir de las potencias de 10. • Realización de adiciones y sustracciones entre números naturales y decimales. • -Diseños de objetos con • -Disposición para realizar el trabajo propuesto dentro y fuera del aula. • -Respeto y valoración por el trabajo propio y el de los demás. • -Cumplimiento y organización en la elaboración y entrega de los trabajos propuestos. • -Interés por indagar y dar respuesta a las preguntas. • -Valoración sobre los conocimientos relacionados con la geometría
semejanza. círculos. INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: CUARTO PERIODO: 3 ESTÁNDAR: Construyo objetos tridimensionales a partir de representaciones bidimensionales y puedo realizar el proceso contrario en contextos de arte, diseño y arquitectura Reconozco el uso de algunas magnitudes (longitud, área, volumen, capacidad, peso y masa, duración, rapidez, temperatura) y de algunas de las unidades que se usan para medir cantidades de la magnitud respectiva en situaciones aditivas y multiplicativas. Describo y argumento relaciones entre el perímetro y el área de figuras diferentes, cuando se fija una de estas medidas. Describo e interpreto variaciones representadas en gráficos. Construyo igualdades y desigualdades numéricas como representación de relaciones entre distintos datos. EJE GENERADOR PREGUNTA PROBLEMATIZA DORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio. ¿Qué beneficio le da el hombre al conocimiento que tiene de las unidades de medidas? • Objetos geométricos de dos y tres dimensiones: • Magnitudes: • La noción de ecuación e igualdad. • Secuencias : • Propiedades de los objetos geométricos.: Transformaciones: simetría, rotación y reflexión. • Conceptualización del concepto de congruencia y semejanza. • Perímetro, Concepto de área y superficie. Unidades de medida: De longitud y área. Propiedades o atributos medibles con magnitudes discretas. • La letra como incógnita. • Patrones y regularidades. • Secuencias numéricas y Geométricas. • -Reconocer las propiedades de los objetos geométricos. • -Realizar y explicar las transformaciones al momento de manipular los objetos bidimensionales. • -Diferenciar los conceptos de congruencia y semejanza en objetos bidimensionales. • -Plantear y resolver problemas relacionados con las magnitudes perímetro y área. • -Reconocer y utilizar el metro cuadrado como la unidad de área en situaciones cotidianas. • -Identificar y relacionar una expresión numérica con el concepto de ecuación. • • -Diferenciación entre polígonos regulares e irregulares. • -Comparación entre objetos geométricos a través de la congruencia y semejanza. • -Reconocimiento de los atributos medibles en los objetos geométricos a través de ejercicios. • -Identificación y diferenciación del papel de la letra cuando es una incógnita. • -Predicción de patrones utilizando secuencias numéricas y geométricas. • -Transformación de objetos bidimensionales dando cuenta de las relaciones y diferencias entre ellas. • -Resolución de problemas con modelos geométricos. • Medición de objetos del entorno, utilizando diferentes unidades de medida. • -Construcción de objetos geométricos con medidas específicas. • -Construcción de ecuaciones sencillas a partir de ejemplos cotidianos. • -Aplicación de modelos para hallar el perímetro y área de polígonos regulares e irregulares. • -Participación activa durante el desarrollo de las actividades propuestas. • -Interés para el cumplimiento del trabajo propuesto. • -Reconocimiento de sus errores y aprender a corregirlos. • -Cumplimiento y organización en la elaboración y entrega de los trabajos propuestos. • -Interés por indagar y dar respuesta a las preguntas
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: CUARTO PERIODO: 4 ESTÁNDAR: Interpreto y represento información presentada en tablas y gráficas. (Pictogramas, gráficas de barras, diagramas de líneas, diagramas circulares). Resuelvo y formulo problemas a partir de un conjunto de datos provenientes de observaciones, consultas o experimentos. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio. ¿Cómo los rangos de variación me permiten conocer e intervenir con más acierto en la solución de problemas? • Magnitudes: • Patrones y regularidades. • Secuencias numéricas y Geométricas. • Interpretación de información: • Conceptualización de: Media (o promedio) y mediana. • Magnitudes discretas. • Propiedades o atributos medibles con magnitudes discretas. • Nociones de masa, temperatura y capacidad. • Conjunto de datos. • Variables cuantitativas y cualitativas. • Sistemas de • representación gráficos: Pictogramas, gráficas de • barras, diagramas • circulares. • Sistematización de datos. • -Predecir patrones utilizando secuencias numéricas y geométricas. • -Representar información en pictogramas, gráficas de barras y diagramas circulares. • -Recolectar, organizar, registrar y analizar información en tablas datos. • -Reconocimiento de las nociones de masa y capacidad en objetos de su entorno. • -Interpretación de la noción de temperatura en situaciones cotidianas. • -Interpretación de datos de una información estadística y utilizarlos significativamente. • -Comparación y establecimiento de diferencias entre la Media (o promedio) y la Mediana. • -Explicación del por qué una magnitud es o no discreta. • -Realización de diagramas para representar la información más relevante. • -Proposición de secuencias numéricas o geométricas estableciendo un patrón para su construcción • -Realización de forma organizada y responsable el trabajo que se le propone en el área. • -Organización al momento de leer e interpretar la información. • -Cumplimiento y organización en la elaboración y entrega de los trabajos propuestos.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: Quinto PERIODO: 1 ESTÁNDAR: Justifico el valor de posición en el sistema de numeración decimal en relación con el conteo recurrente de unidades. Represento datos usando tablas y gráficas (pictogramas, gráficas de barras, diagramas de líneas, diagramas circulares). Resuelvo y formulo problemas a partir de un conjunto de datos provenientes de observaciones, consultas o experimentos. Predigo patrones de variación en una secuencia numérica, geométrica o gráfica. Construyo igualdades y desigualdades numéricas como representación de relaciones entre distintos datos. EJE GENERADOR PREGUNTA PROBLEMATIZAD ORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS EINDICADORES DELOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento variacional ¿Por qué desarrollo mi intuición y pensamiento lógico a través de ejercicios de equivalencias y relaciones? • Números decimales: • Equivalencias y relaciones: • La recta numérica: • Objetos planos: • Patrones numéricos: • Representaci ón de gráficas: • Conceptualización del Sistema de numeración decimal. • Equivalencia y relaciones entre números fraccionarios y decimales. • La recta numérica. • Objetos planos y sus componentes (ángulos, vértices). • Patrones numéricos utilizando diversas secuencias. • Gráficas de barras y diagramas circulares. • Utilice y proponga estrategias de cálculo y de estimación para resolver situaciones donde es necesario la aplicación de las estructuras aditivas y multiplicativas. • Use significativamente los conocimientos geométricos para solucionar problemas. • Formule preguntas, respuestas y conjeturas coherentes a interrogantes de ¿por qué?, ¿dónde? y ¿cuándo? en situaciones problémicas propias de las matemáticas; tanto en forma oral como escrita. • Exponga sus ideas, sentimientos e intereses dando cuenta de su capacidad de escucha, respeto y tolerancia frente a los pensamientos e intereses de los demás miembros del grupo. • Elija y lleve a la práctica diferentes estrategias que le permiten la solución de situaciones del diario vivir. • Represente datos, los compare en diferentes representaciones, y los interprete a través de diagramas de barras, de líneas y circulares, formando conjeturas a través de formular y resolver problemas a partir de un conjunto de datos provenientes de la observación, la • Reconocimiento de las propiedades y relaciones del sistema de numeración decimal. • Reconocimiento y explicación de las relaciones existentes entre los componentes de los objetos tridimensionales y bidimensionales, sus ángulos y vértices. • Reconocimiento y planteamiento de patrones numéricos en secuencias dadas. • Realización de diagramas de barras y circulares para representar la información más relevante. • Aplicación de las propiedades del sistema de numeración decimal con el conjunto de los números naturales. • Conversión de números fraccionarios a decimales y viceversa. • Desarrollo de operaciones básicas (suma, resta, multiplicación y división) entre números fraccionarios, naturales y decimales. • Ubicación y representación de números naturales, fraccionarios y decimales en la recta numérica. • Realización de forma organizada y responsable del trabajo que se le propone en el área. • Respeto y valoración por el trabajo propio y el de los demás. • Valoración del aprendizaje de las operaciones básicas. • Valoración sobre los conocimientos relacionados con la geometría.
experimentación y la consulta. INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: QUINTO PERIODO: 2 ESTÁNDAR: Identifico la potenciación y la radicación en contextos matemáticos y no matemáticos Comparo y clasifico figuras Bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. Conjeturo y pongo a prueba predicciones acerca de la posibilidad de ocurrencia de eventos. Predigo patrones de variación en una secuencia numérica, geométrica o gráfica. EJE GENERADOR PREGUNTA PROBLEMATI ZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico. ¿Cómo el logaritmo transforma un producto en una suma, un cociente en una resta, una potencia en una multiplicación sencilla y una raíz en una división sencilla? • Potenciación, Radicación y Logaritmación: • Objetos geométricos de dos y tres dimensiones: • Conceptualización de la Potenciación. • Radicación y Logaritmación. Potencias y raíces cuadradas y cúbicas. • Logaritmación. • Objetos planos y sus componentes (ángulos, vértices). • Relaciones Intra-figurales e Inter-figurales en los objetos geométricos. • Propiedades de los Polígonos (cuadriláteros y triángulos). • Transformaciones en el plano: Rotación, Traslación, Simetría, Homotecia. • Relaciones de congruencia y semejanza. • Identifique la potenciación y la radicación en contextos matemáticos y no matemáticos. • Justifique regularidades y propiedades de los números, sus relaciones y operaciones. • Compare y clasifique figuras bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. • Prediga patrones de variación en una secuencia numérica, geométrica o gráfica. • Identificación de las potencias cuadradas y cúbicas en un número natural. • Identificación de las raíces cuadradas y cúbicas en un número natural. • Diferenciación de los componentes que tiene un objeto tridimensional y uno Bidimensional. • Diferenciación de los conceptos de congruencia y semejanza al momento de trabajar con objetos geométricos. • Reconocimiento y explicación de las relaciones existentes entre los componentes de los objetos tridimensionales y bidimensionales. • Construcción y clasificación de objetos geométricos. • Resolución de problemas utilizando representaciones con polígonos. • Realización de movimientos de figuras planas en el plano cartesiano. • Resolución de problemas con modelos geométricos. • Aplicación del concepto de congruencia utilizando la simetría entre figuras bidimensionales. • Disposición para realizar el trabajo propuesto dentro y fuera del aula. • Respeto y valoración por el trabajo propio y el de los demás. • Interés por indagar y dar respuesta a las preguntas. • Perseverancia en la • construcción de objetos geométricos. • Valoración sobre los conocimientos relacionados con la geometría.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: QUINTO PERIODO: 3 ESTÁNDAR: Interpreto las fracciones en diferentes contextos: situaciones de medición, relaciones parte todo, cociente, razones y proporciones. Reconozco el uso de algunas magnitudes (longitud, área, volumen, capacidad, peso y masa, duración, rapidez, temperatura) y de algunas de las unidades que se usan para medir cantidades de la magnitud respectiva en situaciones aditivas y multiplicativas. Construyo igualdades y desigualdades numéricas como representación de relaciones entre distintos datos. EJE GENERADOR PREGUNTA PROBLEMATIZAD ORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento métrico.  Pensamiento aleatorio. ¿P ara qué me sirve resolver ecuaciones o pensar? • Números fraccionarios: • Magnitudes: • Diagramas circulares • El número fraccionario como porcentaje. Equivalencia y relaciones entre números fraccionarios y decimales. • Multiplicación y divisiónde fracciones. • Magnitudes: Área y superficie. Volumen y capacidad. Relaciones entre área y volumen. • Nociones de masa, temperatura y capacidad. • Razón, Proporcionalidad simple y compuesta. Ecuación lineal. • Análisis de información en diagramas. • Reconoce fracciones y números decimales. • Aplique algoritmos para hacer operaciones con decimales y resuelva situaciones que requieren el uso de decimales. • Identifique la variación en una secuencia geométrica o en una secuencia numérica. • Interpreto el significado de una fracción decimal como porcentaje. • Represente información en diagramas circulares. • Analice información presentada en diagramas circulares. • Resuelva situaciones que requieren analizar información en diagramas circulares • Aplicación de modelos para hallar el volumen y la capacidad de algunos objetos geométricos. • Identificación del uso de las magnitudes masa, temperatura o capacidad. • Desarrollo de operaciones básicas con números fraccionarios. • Lectura y escritura de porcentajes en problemas cotidianos. • Conversión de números fraccionarios a decimales y viceversa. • Solución de problemas sencillos utilizando el concepto de razón. • Desarrollo de ejercicios de identificación de la proporcionalidad simple o compuesta. • Participación activa durante el desarrollo de las actividades propuestas. • Interés para el cumplimiento del trabajo propuesto. • Interés por aprender sobre los números naturales y sus operaciones. • Valoración del aprendizaje de las operaciones básicas. • Perseverancia y constancia para resolver problemas cotidianos con números fraccionarios y decimales. • Organización y rigor al momento de realizar medidas específicas.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: QUINTO PERIODO: 4 ESTÁNDAR: Modelo situaciones de dependencia mediante la proporcionalidad directa e inversa. Selecciono unidades, tanto convencionales como estandarizadas, apropiadas para diferentes mediciones. Uso e interpreto la media (o promedio) y la mediana y comparo lo que indican. Resuelvo y formulo problemas a partir de un conjunto de datos provenientes de observaciones, consultas o experimentos Describo e interpreto variaciones representadas en gráficos. Analizo y explico relaciones de dependencia entre cantidades que varían en el tiempo con cierta regularidad en situaciones económicas, sociales y de las ciencias naturales. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATI VA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional ¿Qué son y para qué sirven las indicadoras razón y proporción? • Números decimales: • Sistema métrico decimal: • Unidades de medida: • Conceptualizació n de razones y proporciones: Diagramas lineales. • Datos: • Equivalencia y relaciones entre números fraccionarios y decimales. • Multiplicación y división de decimales. • Unidades de longitud, superficie, volumen y capacidad. • Masa, tiempo y temperatura. • Razones, Proporciones. • Propiedades fundamentales de las proporciones, escalas. • Moda y promedio. • Resuelva problemas de multiplicación y división utilizando los números decimales. • Aplique el concepto de razón y proporción al momento de interpretar y solucionar un problema sencillo. • Exponga sus ideas y sentimientos de forma respetuosa y asertiva. • Reconozca las magnitudes directamente proporcionales e inversamente proporcionales. • Resuelva situaciones que involucran distinta variación entre las magnitudes. • Conversión de números fraccionarios a decimales y viceversa. • Reconocimiento de magnitudes directamente proporcionales e inversamente proporcionales. • Desarrollo de operaciones básicas (suma, resta, multiplicación y división) con números decimales. • Elaboración de ejercicios donde se identifique el uso de las magnitudes masa, temperatura o capacidad. • Resolución de problemas sencillos utilizando el concepto de razón y proporción. • Calculo de situaciones que involucran distinta variación entre las magnitudes. • Disposición para realizar el trabajo propuesto dentro y fuera del aula. • Perseverancia y constancia en concluir el trabajo iniciado. • Interés por indagar y dar respuesta a las preguntas. • Organización y rigor al momento de realizar medidas específicas.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: SEXTO PERIODO: 1 ESTÁNDAR: Clasificarpolígonosenrelación con sus propiedades EJE GENERADOR PREGUNTA PROBLEMATIZAD ORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. ¿En qué situaciones de la vida diaria utilizamos los números naturales y aplicamos principios de asociación? Apreciemos las formas y descubramos sus lenguajes. • Los Números Naturales. • Polígonos Y Ángulos. • Operación con números naturales. • Suma • Resta • *Multiplicación • División • Clasificación de Polígonos y ángulos. • Interpretación y resolución de problemas, haciendo uso de las operaciones con números naturales. • Aplicación de reglas para eliminar sistemáticamente signos de agrupación en la resolución de operaciones combinadas. • Medición y clasificación de polígonos y ángulos. • Reconozco las operaciones básicas con los números naturales para resolver problemas y operaciones combinadas. • Identificación de figuras, sus formas y medidas utilizando medios tecnológicos como: Transportador, compas e indaga sobre su importancia en estructuras físicas y naturales. • Interpretación de las operaciones básicas con los números naturales para resolver problemas y problemas combinados. • Caracterización de las diferentes figuras por su forma, patrones de medida y funcionalidad de contesto real. • Elaboración situaciones problemas que involucran las operaciones básicas con los números naturales. • Observación directa que posibles construcciones se pueden elaborar y son necesarias en el municipio.
Pensamiento aleatorio Pensamiento geométrico Que aportes hacen la estadística para el análisis y la mejor comprensión de hechos y fenómenos de la vida cotidiana • Organización y tabulación de datos. Conjuntos • Conceptos básicos: población muestra, características y variables. • Frecuencias absolutas, relativas y acumulada • Datos agrupados. Proposición Conjuntos Subconjuntos Unión Intersección • Identificación de diferentes frecuencias. Identificación de la condición o condiciones que cumplen los elementos de un conjunto y utilizarlas en la solución de un problema • Comparación de diferentes tipos de información expresadas en frecuencia y datos agrupados Identificación de diferentes relaciones entre conjuntos • Elaboración de situaciones problemas utilizando el lenguaje, notación y símbolos matemáticos. Resolución de problemas utilizando las diferentes teorías de conjuntos • Construcción de tablas de información utilizando mecanismo de recolección para plantar alternativas de solución a las necesidades de la comunidad educativa. Proposición de situaciones en los que se hace necesario utilizar la teoría de conjuntos
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: SEXTO PERIODO: 2 ESTÁNDAR: Resolver y solucionar problemas cuya solución requieran sobre la potenciación o radiación EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPOSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. Pensamiento aleatorio ¿En qué situaciones de la vida diario utilizamos los números naturales y aplicar principios de asociación? Porque son importantes los instrumentos de medición. ¿Qué importancia tiene la recolección de datos en situaciones de la Los Números Naturales. Triángulos Y Cuadriláteros. Medida de tendencia central. Operaciones con los números naturales potenciación, radicación y logaritmación. Clasificación de triángulos y cuadriláteros. Moda, promedio y mediana Representación gráficamente de números naturales y sus respectivas operaciones. Identificación de las clases de triángulos y cuadriláteros. Identificación en diferentes situaciones las medidas de Operación de: Potenciación, radicación, logaritmación con los números naturales. Investigación de figuras, sus formas y medidas utilizando medios tecnológicos como: regla y compas e indaga sobre su importancia en estructuras físicas y naturales. Comparación de diferente tipos de información expresada en gráficas, tablas Interpretación de las operaciones de Potenciación, radicación, logaritmación con los números naturales Para solucionar problemas. Caracterización de las diferentes figuras por su forma, patrones de medida y funcionalidad de contesto real. Elaboración de situaciones problemas utilizando el lenguaje, Elaboración situaciones problemas que involucran las operaciones de: Potenciación, radicación, logaritmación con los números naturales. Observación directa que posibles construcciones se pueden elaborar y son necesarias en el municipio. Construcción de tablas de información utilizando
vida real? Problemas de aplicación tendencia central Solución de problemas aplicando una de las medidas de tendencia central Organización adecuadamente datos. estableciendo conexiones entre ellas y descubrimiento nuevas maneas de descubrir el mundo real. notación y símbolos matemáticos, para elaborar estructurar conceptuales y prácticas. mecanismo de recolección para plantar alternativas de solución a las necesidades de la comunidad educativa, atreves de encuestas, diagramas y gráficas.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: SEXTO PERIODO: 3 ESTÁNDAR: Identificar relaciones entre unidades para medir diferentes magnitudes EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. ¿En qué situaciones de la vida diaria empleamos los números enteros? ¿Sería práctico medir la distancia de aquí a Medellín usando milímetros? Números enteros. El metro como unidad patrón. Concepto de número entero Valor absoluto Operaciones con enteros: Suma Resta Problemas de aplicación. Sistema métrico decimal (SMD) El metro como unidad fundamental Conversación de unidades de longitud Representación de los enteros en la recta numérica. Resolución de operaciones con suma y resta de enteros. Realización de conversiones entre las diferentes unidades y magnitudes del sistema métrico decimal. Identificación de la importancia de reconocer el orden en el conjunto de los números enteros. Descubro la importancia de reconocer el metro comunidad patrón de medida. Elaboración de situaciones problemas y las desarrollo argumentando su respuesta desde conceptos adquiridos previamente de suma y resta con los números enteros. Elaboración del metro para medir, comparar y describir diferentes sitios de nuestra institución. Construcción de conceptos nuevos atreves de la puesta en práctica de los diferentes conjuntos de números, su relación con el contexto real y propone actividades utilizando dichos conceptos de manera dinámica. Construcción de conceptos nuevos atreves de la puesta en práctica de los diferentes múltiplos y sub múltiplos del metro, su relación
Pensamiento aleatorio ¿Qué aportes hace la estadística para el análisis y mejor comprensión de hechos y fenómenos de la vida cotidiana? Diagrama. Diagramas De barras Circulares Pictogramas. Interpretación de graficas estadísticas. Representación y análisis de datos utilizando tablas y gráficos. Comparación tipos de información expresadas en diferentes diagramas estableciendo conexiones entre ellas y descubriendo nuevas maneras de ver el mundo real. Representación de diferente tipos de información presentada en los diagramas. con el contexto real y propone actividades utilizando dichos conceptos de manera dinámica. Construcción de diferentes diagramas a partir de una situación problema.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: SEXTO PERIODO: 4 ESTÁNDAR: Identificarlas características de las diversasgraficas cartesianas (De puntos,Continuas,Formadas por Segmentos etc.) En relacióncon la situaciónque presentas EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico-variaciones. Pensamiento geométrico – métrico. ¿Qué aplicabilidad le encuentras a las ecuaciones para resolver situaciones que se presentan en la vida diaria? ¿Qué aplicabilidad le puedes dar al sistema geométrico en la solución de situaciones problemas? Números enteros. Área y perímetro Teorema de Pitágoras. Operaciones con números enteros: multiplicación y división. Polinomio con y sin signos de agrupación. Área y perímetro de algunas figuras planas como: Cuadrado, rectángulo, triangulo, paralelogramo, trapecio y hexágono. Aplicación del teorema de Resolución de problemas que involucran las operaciones con números enteros. Resolución de situaciones, problemas que involucran ecuaciones. Aplicación de técnicas apropiadas, herramientas y fórmulas para determinar las medidas. Operación básica entre números enteros. Descubro la importancia de manejar correctamente los conceptos de: Área, perímetro y el teorema de Pitágoras y su necesidad de aplicación en el contexto real. Elaboración de situaciones problemas y las desarrollo argumentando su respuesta desde conceptos adquiridos previamente de suma y resta con los números enteros. Elaboración de situaciones problemas y las desarrollo argumentando su respuesta desde conceptos adquiridos previamente de área, perímetro y el teorema de Pitágoras Construcción de conceptos nuevos atreves de la puesta en práctica de los diferentes conjuntos de números, su relación con el contexto real y propone actividades utilizando dichos conceptos de manera dinámica. Proposición de situaciones problemas atreves de la puesta en práctica de los diferentes conceptos de área, perímetro y el teorema de Pitágoras, su relación con el contexto real.
Pensamiento aleatorio ¿Qué es un plano cartesiano? Plano cartesiano. Pitágoras. Plano cartesiano Parejas ordenadas Movimientos en el plano. Ubicación de pares ordenados en el plano cartesiano. Ubicación correctamente pares ordenados en el plano cartesiano. Elaboración de situaciones problema donde halla la necesidad de construir figuras geométricas en el plano cartesiano. Proposición de situaciones problemas atreves de la puesta en práctica de los diferentes conceptos del plano cartesiano.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO SEPTIMO PERIODO: 1 ESTÁNDAR: Utilizar el concepto de número entero y analizo las operaciones que se dan entre ellos para establecer relaciones. Resolver y formular problemas utilizando propiedades fundamentales de la teoría de los números. Resolver y formular problemas cuya solución requiere de la potenciación y radicación. Generalizar propiedades y relaciones de los números enteros, racionales y decimales. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento geométrico.  Pensamiento Variacional y Aleatorio. ¿Cuál es la importancia de reconocer los conjuntos de números y sus operaciones en la cotidianidad? .Números enteros. .Números racionales. .Números decimales. Concepto de número entero Valor absoluto Adición y sustracción de números enteros Propiedades de la suma de los números enteros Multiplicación y división de entero Propiedades de la multiplicación de los números enteros Potenciación de números enteros Radicación de números enteros Situaciones problema .Interpretación, ordenación, comparación y representación gráfica con los racionales y decimales sus respectivas operaciones. . Interpretación y resuelvo problemas haciendo uso de las operaciones con racionales. Comunicación de un racional como decimal y viceversa. .Identificación y uso los enteros en diferentes contextos, los representa de diversas formas y establece relaciones entre ellos; Redefine las operaciones básicas en los sistemas formados con éstos números y establece conexiones entre ellas. .Argumentación de situaciones problema haciendo uso de las operaciones con números enteros Argumentación respuestas de situaciones desde sus conceptos adquiridos previamente de suma, resta, multiplicación y división, potenciación de números enteros, racionales y decimales. • Proposición de situaciones que involucran solución de problemas de la vida cotidiana. • Socialización de conceptos nuevos a través de la puesta práctica de los números con su relación con el contexto real y propone actividades de manera dinámica.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO SEPTIMO PERIODO: 2 ESTÁNDAR: Utilizar el concepto de número racional y decimal y analizo las operaciones que se dan entre ellos para establecer relaciones. Resolver y formular problemas utilizando propiedades fundamentales de la teoría de los números. Resolver y formular problemas cuya solución requiere de la potenciación y radicación. Generalizar propiedades y relaciones de los números enteros, racionales y decimales. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento geométrico.  Pensamiento Variacional y Aleatorio. ¿Cuál es la importancia de reconocer los conjuntos de números y sus operaciones en la cotidianidad? .Números enteros. .Números racionales. .Números decimales. .Concepto de número racional. (Q). Representación en la recta numérica. Fracciones equivalentes. Relación de orden. Adición y sustracción de racionales. Multiplicación y división de racionales. Propiedades. Situaciones problema. Expresión racional de un decimal y viceversa. .Resuelvo problemas con ecuaciones de primer grado. .Interpretación ordenación, comparación y representación gráfica con los racionales y decimales sus respectivas operaciones. . Interpretación y resolución problemas haciendo uso de las operaciones con racionales. Expreso un racional como decimal y viceversa. .Identificación y uso los enteros y los racionales en diferentes contextos, los representa de diversas formas y establece relaciones entre ellos; Redefine las operaciones básicas en los sistemas formados con éstos números y establece conexiones entre ellas. .Argumentación de situaciones problema haciendo uso de las operaciones con números enteros, racionales y decimales. Argumenta respuestas de situaciones desde sus conceptos adquiridos previamente de suma, resta, multiplicación y división, potenciación de números enteros, racionales y decimales. • Proposición de situaciones que involucran solución de problemas de la vida cotidiana. • Socialización de conceptos nuevos a través de la puesta práctica de los números con su relación con el contexto real y propone actividades de manera dinámica.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SÉPTIMO PERIODO: 3 ESTANDAR: Utilizar técnicas y herramientas para la construcción de figuras planas y cuerpos con medidas dadas. Clasificar polígonos en relación con sus propiedades. Resolver y formulo problemas usando modelos geométricos. Hacer conjeturas y verificar propiedades de congruencia y semejanza entre figuras bidimensionales en la solución de problemas. Calcular áreas y volúmenes a través de composición y descomposición de figuras y cuerpos. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento geométrico.  Pensamiento geométrico. ¿Cómo posibilitar la percepción de las construcciones, formas y medidas geométricas que afiancen su conocimiento? • .Concepto de Geometría. • Plano cartesiano, transformaciones y composiciones en el mismo. • Congruencias y semejanzas de figuras. • Área de polígonos. • Clasificación de los triángulos, ángulos y teorema de Pitágoras. • Medidas de longitud, volumen, capacidad y tiempo. • Construcción de conceptos en el plano cartesiano. • Construcción de figuras planas, triángulos, ángulos utilizando herramientas didácticas como: regla, transportador y compás. • Clasificación de figuras reales de acuerdo a características de peso, altura, forma, hallando en ellas sus medidas. • Rotación de polígonos en el plano. • Aplicación de transformaciones y usar la simetría para analizar situaciones matemáticas. • Construcción figuras planas utilizando materiales didácticos. • Aplicación transformaciones y usa la simetría para analizar situaciones matemáticas. • Identificación en objetos y situaciones de su entorno las magnitudes de longitud, perímetro, área, volumen, capacidad y desarrolla procesos de medición y estimación de dichas magnitudes y las utiliza en situaciones de la vida diaria. • Representación de figuras y formas utilizando medios tecnológicos como: regla, transportador, compás e indaga sobre su importancia en estructuras físicas y naturales. • Caracterización de las diferentes figuras por su forma, patrones de medida y funcionalidad en el contexto real. . Observación directa qué posibles construcciones se pueden elaborar y son necesarias en el Municipio para mejorar la calidad de vida de sus habitantes, presentando diseños que involucren el uso de las herramientas naturales y tecnológicas.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SÉPTIMO PERIODO: 4 ESTÁNDAR: Justificar el uso de representaciones y procedimientos en situaciones de proporcionalidad directa e inversa. Reconocer relación entre un conjunto de datos y su representación. Utilizar y justificar el uso de la estimación para resolver problemas relativos a la vida social, económica. Hacer conjeturas acerca del resultado de un experimento aleatorio usando proporcionalidad y nociones básicas de proporcionalidad. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento geométrico.  Pensamiento Variacional. ¿Qué mecanismos usa el estudiante para adquirir información, inferir y utilizarla para su bienestar y el de los demás? • Razones y Proporciones. • Magnitudes: Directa e inversamente proporcionales. • Regla de tres simple y compuesta. • Probabilidad. • Medidas de tendencia central: Media, Mediana, Moda. • Tablas y gráficas. • Combinaciones y permutaciones. • Identificación de las razones y proporciones como relaciones entre magnitudes. • Solución de problemas de proporcionalidad. • Orden y relaciones. • Uso de gráficas estadísticas y medidas de tendencia central • Evaluación de la probabilidad de ocurrencia de un evento. • Comprensión de la probabilidad como un número entre 0 y 1. • Formulación de inferencias y argumentos lógicos que se basan en el análisis y manejo de datos estadísticos agrupados, y hace su representación gráfica. • Interpretación de datos de una información estadística y los usa significativamente. • Identificación de cálculos de proporcionalidad directa e inversa. • Comparación de diferentes tipos de información expresada en proporciones gráficas, tablas, estableciendo conexiones entre ellas y descubriendo el mundo real. • Planeación y resolución de problema utilizando el lenguaje, notación y símbolos matemáticos para elaborar estructuras conceptuales y gráficas. • Construcción de tablas de información utilizando mecanismos de proporcionalidad para plantear alternativas de solución a las necesidades de la comunidad educativa a través de encuestas, diagramas y gráficas. • Realización de forma organizada y responsable el trabajo que se le propone en el área. • Organización al momento de leer e interpretar la información.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: OCTAVO PERIODO: 1 ESTÁNDAR: Utilizar números reales en sus diferentes representaciones en diversos contextos. Usar representaciones geométricas para resolver y formular problemas en la matemática y en otras disciplinas. Hacer conjeturas acerca del resultado de un experimento aleatorio usando proporcionalidad y nociones básicas de proporcionalidad. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿En qué situaciones de la vida se aplican y se utilizan los sistemas numéricos, y qué funcionalidad le ves a los poliedros? • Sistemas numéricos. • Ángulos complementarios, adyacentes, consecutivos cortados por una transversal. • Poliedros. • Proporcionalidad. • Conjunto de los números reales: Operaciones y propiedades, relación de orden, recta real. • Clasificación y construcción de Poliedros: Pirámides, prismas, conos y cilindros. • Aplicaciones a la proporcionalidad. • Formulación de proyecto investigativo estadístico (primera parte). • Identificación y representación de conjuntos numéricos en la recta real. • Aplicación de propiedades de los conjuntos numéricos a través de la solución de problemas. • Identificación, clasificación y construcción de poliedros. • Calcula la probabilidad de ocurrencia de un evento. • Comprensión de la probabilidad como un número entre 0 y 1. • Formulación de inferencias y argumentos lógicos que se basan en el análisis y manejo de datos estadísticos agrupados, y hace su representación gráfica. • Resolución de operaciones por medio de los conjuntos numéricos. • Interpretación de datos de una información estadística y los usa significativamente. • Identificación y clasificación de poliedros. • Construcción de poliedros de acuerdo a sus características. • Planeación de situaciones problema utilizando el lenguaje, notación y símbolos matemáticos para elaborar estructuras conceptuales y gráficas. • Argumentación y descripción utilizando adecuadamente propiedades de los conjuntos numéricos. • Proposición de proyectos de investigación estadística. • Construcción de tablas de información utilizando mecanismos de proporcionalidad para plantear alternativas de solución a las necesidades de la comunidad educativa a través de encuestas, diagramas y gráficas.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: OCTAVO PERIODO: 2 ESTÁNDAR: Usar procesos inductivos y lenguaje algebraico para verificar conjeturas. Construir expresiones algebraicas equivalentes a una expresión algebraica dada. Reconocer y contrastar propiedades y relaciones geométricas utilizadas en demostración de teoremas (Pitágoras y Thales.) Interpretar analítica y críticamente información estadística proveniente de diversas fuentes 8prensa, revista, televisión, consultas, entrevista, etc.) Compara resultados experimentales con probabilidad matemática esperada. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento Variacional.  Pensamiento geométrico. ¿En qué situaciones de la vida le encuentras aplicación y funcionabilidad al álgebra? • Conceptos básicos algebraicos. • Triángulos, líneas y puntos notables • Teorema de Pitágoras. • Medidas de tendencia central: Media, Mediana, Moda. • Tablas y gráficas. • Combinaciones y permutaciones. • Conceptos básicos del álgebra en la solución de problemas. • Identificación del triángulo rectángulo aplicando el Teorema de Pitágoras. • Identificación de las razones y proporciones como relaciones entre magnitudes. • Solución de problemas de proporcionalidad. • Orden y relaciones. • Uso de gráficas estadísticas y medidas de tendencia central. • Resolución de ejercicios y problemas a partir de los conceptos del álgebra. • Deducción y aplicación del teorema de Pitágoras a través de un triángulo rectángulo. • Interpretación y resolución de datos algebraicos en la solución de problemas. • Interpretación e identificación del triángulo rectángulo aplicando el teorema de Pitágoras. • Comparación de diferentes tipos de datos estadísticos para aplicar a la vida real. Argumentación de operaciones básicas en la utilización del álgebra. Argumentación de problemas relacionados con la aplicación del teorema de Pitágoras en la solución de los mismos. • Proposición de datos algebraicos en la solución de problemas. • Construcción de tablas de información y uso de gráficas estadísticas para el análisis de datos.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: OCTAVO PERIODO: 3 ESTÁNDAR: Usar procesos inductivos y lenguaje algebraico para verificar conjeturas. Modelar situaciones de variación con funciones polinómicas. Seleccionar y usar algunos métodos estadísticos adecuados, según el tipo de información. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento Variacional. ¿En qué situaciones de la vida le encuentras aplicabilidad a los productos notables y a la factorización? • Operaciones con polinomios. • Productos y cocientes notables. • Factorización. • Tabulación y representación gráfica de frecuencias (Absoluta, relativa y acumulada) • Operaciones de suma, resta, multiplicación y divisiónde polinomios. • Divisiónsintética. • Identifico y aplico los diversos productos y cocientes notables. • Diferentes casos de factorización. • Tabulación y representación gráfica de frecuencias. • Resolución de sumas y restas entre polinomios. • Resolución de multiplicaciones y diversas divisiones de polinomios. • Resolución y aplicación de los productos notables. • Resolución y aplicación de cocientes notables. • Identificación y aplicación de cada uno de los casos de factorización. • Aplicación de frecuencias, tabulo y represento datos por medio de gráficas. • Resolución de las operaciones con productos y cocientes notables. • Identificación y resolución de los casos de factorización. • Interpretación de datos de una información estadística y los usa significativamente. • Identificación y tabulación de datos para diferentes tipos de información expresada en proporciones gráficas, tablas permitiendo el análisis entre ellos. • Expresión de situaciones problema utilizando el lenguaje, notación y símbolos matemáticos aplicados a la vida cotidiana. • Caracterización de las operaciones con polinomios y factorización según los conocimientos adquiridos. • Sugiere operaciones desde los conocimientos adquiridos y ve su funcionalidad con la vida real. • Construcción de tablas, diagramas y gráficas mediante la tabulación de datos estadísticos. • Realización de forma organizada y responsable el trabajo que se le propone en el área. • Organización al momento de leer e interpretar la información.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: OCTAVO PERIODO: 4 ESTÁNDAR: Utilizar números reales en sus diferentes representaciones en diversos contextos. Utilizar la notación científica para representar cantidades y medidas. Usar representaciones geométricas para resolver y formular problemas en la matemática y en otras disciplinas. Interpretar conceptos de media, mediana y moda. Modelar situaciones de variación con funciones polinómicas. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento Variacional.  Pensamiento geométrico. ¿Qué función y aplicabilidad le ves a la estadística en tu vida? • Fracciones algebraicas. • Simplificación de fracciones. • Operaciones básicas con fracciones algebraicas. • Notación científica • Cuadriláteros: Clasificación y propiedades. • Medidas de tendencia central (promedio, moda, mediana). • Operaciones básicas con fracciones algebraicas. • Simplificación de fracciones algebraicas. • Expresión de cantidades en notación científica. • Identificación y construcción de cuadriláteros. • Aplicación e interpretación de gráficas a partir de las medidas de tendencia central. • Resolución de la factorización, traduciendo expresiones algebraicas. • Identificación y simplificación de fracciones algebraicas. • Solución de las medidas de tendencia central desde una población de datos. • Expresión de cantidades en notación científica. • Identificación, construcción y clasificación de cuadriláteros. • Interpretación de datos de una información estadística y los usa significativamente. • Interpretación de gráficas, y planteamiento de las conclusiones de datos y .gráficos. • Explicación y argumentación de la simplificación de fracciones algebraicas. • Argumentación y expresión de operaciones con fracciones algebraicas. • Caracterización de situaciones problema utilizando el lenguaje, notación y símbolos matemáticos. • Solución de fracciones algebraicas. • Construcción de tablas de información. • Extracción de conclusiones de datos y gráficos aplicando las medidas de tendencia central. • Organización al momento de leer e interpretar la información.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: NOVENO PERIODO: 1º ESTÁNDAR: Identificar los números reales, sus propiedades y las aplico en la ejecución de ejercicios y situaciones problemas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Numérico y Variacional. Métrico Geométrico ¿Son necesarios los números reales como concepto previo para la concepción en el área de matemáticas y en otras aéreas? En que situaciones de la vida real halla la distancia entre dos puntos. Números reales. Funciones lineales Conjuntos numéricos Radicación Racionalización de denominadores. Potenciación Ubicaciones en la recta numérica. Resolución de ecuaciones Distancia entre dos Identificación de los números reales. Realización correctamente las operaciones básicas en los reales. Resolución de potencias y raíces con números reales. Solución de la ecuación de una recta que pasas por dos puntos. Comprensión correctamente los reales en la recta numérica. Identificación y comprensión las propiedades de los números reales. Identificación de funciones lineales a través de su estructura gráfica. Comprensión la conformación y características particulares de los conjuntos numéricos. Justificación de la importancia de los números reales en la resolución de algoritmos, ecuaciones, funciones interpretación de gráficas. . Obtención de información a través de la distancia entre dos puntos. Sugiero situaciones problemas que involucren las operaciones con los números reales. Proposición de ejercicios y situaciones problemas para la adquisición de conceptos de manera didáctica y la aplicación de dichos conceptos en su cotidianidad. Proposición de ejercicios en los que aplico los conocimientos
Aleatorio ¿En que situaciones de la vida aplico los conceptos de medida de tendencia central? Medidas de tendencia central. puntos. Moda- Mediana- Promedio- Varianza y desviación estándar. Interpretación de datos y gráficos relacionados con información significativa. Comprensión de relaciones con informaciones estadísticas. Formulación de inferencias y argumentos lógicos que se basan en el análisis de datos. adquiridos. Representación de datos estadísticos
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: NOVENO PERIODO: 2º ESTÁNDAR: Identificar relaciones entre propiedades de las gráficas y propiedades de las ecuaciones algebraicas EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATIVA PROPÓSITIVA Numérico Variacional. Métrico Geométrico ¿Para qué se crearon las ecuaciones? ¿En qué situaciones de la vida real observas la pendiente de una recta? Función lineal. Función lineal. Ecuación de una recta Punto medio Pendiente de una recta. Resolución de situaciones cotidianas mediante ecuaciones lineales Solución de forma correcta la pendiente de una recta. Determinación y graficación de la pendiente de una recta. Comprensión del significado de ecuaciones lineales y cuadráticas. Identificación de situaciones que se resuelven utilizando ecuaciones. Relación entre los conceptos básicos de punto medio, pendiente y ecuación de una recta. Obtención de información a partir de una gráfica. Justificación de un procedimiento para resolver ecuaciones y desigualdades. Identificación del método mediante el cual grafico la pendiente de una recta. Proposición de ejercicios cotidianos en los que aplico los conceptos adquiridos. Solución de problema derivados de situaciones cotidianas utilizando ecuaciones. Representación correcta desituaciones reales por medio de funciones lineales.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: NOVENO PERIODO: 3º ESTÁNDAR: Identifico diferentes métodos para solucionar sistemas de ecuaciones lineales EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATIVA PROPÓSITIVA Numérico Variacional. ¿Interpreto en mi entorno una situación donde se evidencie un sistema de ecuación lineal? Sistemas de Ecuaciones lineales. Solución Grafica Métodos de solución algebraicos sistemas 2x2 y 3x3: igualación. Sustitución, reducción, determinantes Resolución de problemas aplicando ecuaciones de primer grado. Diferenciación de métodos para resolver ecuaciones lineales. Resolución de situaciones cotidianas mediante ecuaciones lineales y cuadráticas Comprendo el significado de ecuaciones lineales Identificación de situaciones que se resuelven utilizando ecuaciones. Obtención de información a partir de una gráfica. Justificación de un procedimiento para resolver ecuaciones. Proposición de ejercicios cotidianos en los que aplico los conceptos adquiridos. Solución de problema derivados de situaciones cotidianas utilizando ecuaciones.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: NOVENO PERIODO: 4º ESTÁNDAR: Reconocer y realizar correctamente operaciones básicas con las ecuaciones lineales y cuadráticas. Identificar la parte real y la parte imaginaria de un número complejo EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATIVA PROPÓSITIVA Numérico Variacional. Pensamiento numérico ¿Para qué se crearon las ecuaciones? ¿Solo existen los números reales? Ecuaciones cuadráticas Números complejos Regla de la función cuadrática Grafica de una función cuadrática Aplicaciones de una función cuadrática Notación Operaciones con números complejos Conjugado de un numero complejo Planeación y resolución de problemas aplicando ecuaciones de segundo grado. Resolución de situaciones cotidianas mediante ecuaciones cuadráticas Diferenciación entre un número real y un número imaginario Comprensión del significado de ecuaciones lineales y cuadráticas. Identificación de situaciones que se resuelven utilizando ecuaciones. Identificación entre un número real y un número imaginario Obtención de información a partir de una gráfica. Justificación de un procedimiento para resolver ecuaciones Enunciación entre un número real y un número imaginario Proposición de ejercicios cotidianos en los que aplico los conceptos adquiridos. Solución de problema derivados de situaciones cotidianas utilizando ecuaciones. Proposición de un número real y un número imaginario
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: DÉCIMO PERIODO: 1 ESTÁNDAR: Comparar y contrastar las propiedades de los números (enteros, racionales, reales) sus relaciones y operaciones (sistemas numéricos). Utilizar argumentos de la teoría de números para justificar relaciones que involucran números naturales. Usar argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. Predecir y justificar razonamientos y conclusiones usando información estadística. Resolver y formular problemas usando conceptos básicos de conteo y probabilidad. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Es importante el conocimiento e identificación de los conjuntos numéricos y la solución de problemas afines? • Los conjuntos numéricos. • Combinaciones. • Productos notables. • Factorización. • Los números reales. • Propiedades y gráfica de los números reales R. • Conjuntos. • Nociones de probabilidad. • Medida de ángulos. • Combinaciones. • Aplicación de distintos sistemas numéricos en la solución de situaciones problema. • Solución de la pendiente de una recta a partir de sus coordenadas. • Relación de dependencia entre las variables que se ven involucradas en situaciones reales. • Identificación y resolución de productos notables y factoriza polinomios algebraicos aplicando la descomposición en factores. • Aplicación de las propiedades de los números reales en la solución de problemas algebraicos. • Apropiación de la teoría combinatoria. • Diferenciación de los números racionales de los irracionales a partir de su representación. • Reconoce la importancia de la representación gráfica de un problema como herramienta didáctica. • Caracterización de las propiedades de los números reales. • Interpretación de gráficas que involucran relaciones entre tres conjuntos. • Comprensión, relación y aplicación de la diferencia entre tipos de variables en la resolución de problemas. • Utilización correcta del lenguaje matemático. • Representación de cualquier número real en la recta numérica. • Generación de algoritmos para la resolución de problemas que involucran elementos geométricos. • Realización de forma organizada y responsable el trabajo que se le propone en el área.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: DÉCIMO PERIODO: 2 ESTÁNDAR: Identificar características de localización de objetos geométricos en sistemas de representación cartesiana y otros. Describir y modelar fenómenos periódicos del mundo real usando relaciones y funciones trigonométricas. Usar argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. Diseñar estrategias para abordar situaciones de medición que requieran grados de precisión específicos. Modelar situaciones de variación periódica con funciones trigonométricas. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento Numérico  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento Variacional. ¿Por qué es importante la Geometría y qué aplicación tiene en la sociedad moderna? • Representación gráfica de los reales. • Ángulos positivos y negativos. • Definición de las funciones trigonométricas. • Gráfica de las funciones y sus variaciones. • Permutaciones y variaciones. • Circunferencia trigonométrica. • Líneas trigonométricas de las funciones. • Gráfica de las funciones trigonométricas: Seno, Coseno, Tangente, cosecante, cosecante, secante y cotangente. • Generalización de las funciones: Traslación, amplitud, período. • • Graficación de diferentes números reales sobre una recta numérica. • Conversión de grados sexagesimales a Radianes y viceversa. • Identificación de funciones trigonométricas de ángulos agudos. • Graficación de las funciones trigonométricas y determina sus variaciones. • Resolución de problemas sobre permutaciones y Variaciones. • Utilización de herramientas tecnológicas para trazar gráficas de • Reconoce la circunferencia trigonométrica y traza las seis funciones trigonométricas. • Identificación de regularidades en las funciones trigonométricas. • Identificación de las propiedades de las funciones y las usa para resolver situaciones problema. • Identificación y solución de problemas sobre • Comprensión de la importancia de las funciones trigonométricas en el desarrollo de la sociedad. • Expone y grafica las funciones trigonométricas y determina sus variaciones. • Definición de las funciones que permiten el estudio del triángulo en todas sus formas. • Construcción correctamente degráficas de las funciones trigonométricas con base en la circunferencia trigonométrica. • Socialización de conversión de grados sexagesimales a radianes y viceversa.
funciones trigonométricas. Permutaciones y Variaciones. INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: DÉCIMO PERIODO: 3 ESTÁNDAR: Establecer relaciones y diferencias entre diferentes notaciones de números reales para decidir sobre su uso en una situación dada. Usar argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. Reconocer y describir curvas o lugares geométricos. Justificar inferencias provenientes de los medios o de estudios diseñados en el ámbito escolar. Interpretar conceptos de probabilidad condicional e independencia de eventos. Proponer inferencias a partir del estudio de muestras probabilísticas. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento Métrico.  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento Variacional. ¿Qué importancia tiene la estadística en el diagnóstico y solución de problemas a nivel general? • Resolución de Triángulos Rectángulos. • Resolución de triángulos oblicuángulos. • Teorema del Seno • Teorema del Coseno. • Ángulos de elevación y depresión. • Probabilidad. • Solución de triángulos rectángulos. • Ley del seno. • Ley del coseno. • Ángulos de elevación. • Ángulos de depresión. • Probabilidad condicional. • Resolución de triángulos rectángulos aplicando las fórmulas respectivas. • Resolución de triángulos oblicuángulos aplicando las fórmulas del Teorema del Seno y del Coseno respectivamente. • Resolución de problemas sobre ángulos de Elevación y de Depresión. • Aplicación de los principios básicos de la probabilidad. • Apropiación de la teoría de la probabilidad. Identificación y aplicación de forma geométrica la solución de triángulos. Indagación y comparación sobre la importancia de la aplicación de ángulos en la vida real. Interpretación de conceptos de probabilidad condicional e • Comprensión de la importancia de la solución de triángulos rectángulos y oblicuángulos en la aplicación de los problemas de la vida cotidiana. • Construcción y análisis de los planteamientos utilizados para resolver problemas en la solución de triángulos. • Realización de forma organizada y responsable el trabajo que se le propone en el área. • • Organización al momento de leer e interpretar la información.
independencia de eventos. INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: DÉCIMO PERIODO: 4 ESTÁNDAR: Describir y modelar fenómenos periódicos del mundo real usando relaciones y funciones trigonométrica. Usar argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. Diseñar estrategias para abordar situaciones de medición que requieran grados de precisión específicos. Justificar inferencias provenientes de los medios o de estudios diseñados en el ámbito escolar. Interpretar conceptos de probabilidad condicional e independencia de eventos. Proponer inferencias a partir del estudio de muestras probabilísticas. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento Variacional. ¿Qué papel desempeñan las operaciones algebraicas en la solución de problemas trigonométricos? • Demostración de identidades. • Ecuaciones trigonométricas. • Funciones de la suma y diferencia de dos ángulos. • Propiedades de la probabilidad. • Racionalización. • Identidades trigonométricas: Relaciones pitagóricas. • Identidades para la suma y diferencia de ángulos. • Identidades para ángulos dobles y medios. • Probabilidad condicional. • Diagrama de árbol. • Probabilidad total. • Demostración identidades y soluciono ecuaciones trigonométricas. • Identificación y aplición de las propiedades de la probabilidad en la solución de problemas. • Racionalización de denominadores mediante la aplicación de expresiones conjugadas Establezco procesos lógicos para verificar identidades • Identificación de cada una de las funciones por medio de la aplicación de problemas a la vida real. • Interpretación de las propiedades de ecuaciones trigonométricas para el desarrollo de la habilidad mental. • Inferenciación en el • Racionalización de denominadores por medio de expresiones conjugadas para la aplicación de problemas algebraicos. • Utilización de los argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. • Representación de alternativas en la aplicación de la solución de problemas de la comunidad educativa a través de conocimientos adquiridos. • Realización de forma organizada y responsable el trabajo que se le propone en el área. • Organización al
Pensamiento espacial ¿En la vida cotidiana donde se observan las figuras cónicas? Secciones cónicas Circunferencia, parábola, elipse e hipérbola trigonométricas. Diferenciación entre las combinaciones y permutaciones Resolución de problemas en los que se usen propiedades geométricas de figuras cónicas de manera algebraica conocimiento adquirido a través del desarrollo matemático para afrontar situaciones de la vida cotidiana. Interpretación de un polinomio una ecuación con C(o, o) y C(h, k) • Exposición mediante diagrama de árbol situaciones relacionadas con el contexto educativo. Argumentación de ejercicios de aplicación con lo cotidiano momento de leer e interpretar la información. Proposición de ejercicios de aplicación con lo cotidiano.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: UNDÉCIMO PERIODO: 1 ESTÁNDAR: Establecer relaciones y diferencias entre números reales, expresiones algebraicas y las gráficas de funciones polinómicas y racionales EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. Pensamiento aleatorio ¿Por qué es importante conocer conjuntos numéricos con situaciones problemáticas en nuestro mundo matemático? ¿Por qué es importante la geometría y que aplicación tiene en nuestra sociedad? ¿Para qué nos sirve las permutaciones y las combinaciones? Conjunto de los números reales Desigualdades e inecuaciones Estadística Conjunto numérico con situaciones problemas Intervalo Valor absoluto Inecuaciones al infinito Inecuaciones simultaneas Inecuaciones con valor absoluto Permutación y combinación Planeación y resolución de situaciones problemas Solución de diferentes clases de intervalos Diferenciación entre las combinaciones y permutaciones Interpretación y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Interpretación de diferentes clases de inecuaciones Interpretación de ejercicios de aplicación con arreglos cotidianos prácticos Solución de situaciones problemas enfocados a pruebas ICFES. Argumentación de diferentes clases de inecuaciones Argumentación de ejercicios de aplicación con arreglos cotidianos prácticos Construcción y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Proposición de diferentes clases de intervalos Proposición de ejercicios de aplicación con arreglos cotidianos prácticos
Pensamiento espacial ¿En la vida cotidiana donde se observan las figuras cónicas? Secciones cónicas Estadística descriptiva Tablas de frecuencias Medida de tendencia central Interpretación de datos estadísticos Circunferencia, parábola, elipse e hipérbola Solución de diferentes datos estadísticos ya sea de forma gráfica o en tablas de frecuencias Resolución de problemas en los que se usen propiedades geométricas de figuras cónicas de manera algebraica Interpretación de diferentes datos estadísticos ya sea de forma gráfica o en tablas de frecuencias Interpretación de un polinomio una ecuación con C(o, o) y C(h, k) Argumentación de diferentes datos estadísticos ya sea de forma gráfica o en tablas de frecuencias Argumentación de ejercicios de aplicación con lo cotidiano Proposición de soluciones de diferentes datos estadísticos ya sea de forma gráfica o en tablas de frecuencias Proposición de ejercicios de aplicación con lo cotidiano.
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: UNDÉCIMO PERIODO: 2 ESTÁNDAR: Usar argumentos geométricos para resolver y formular problemas en contestos matemáticos y en otras ciencias EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIV A Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. Pensamiento aleatorio ¿Por qué es importante conocer conjuntos numéricos con situaciones problemáticas en nuestro mundo matemático? ¿Por qué es importante la geometría analítica en el estudio de la función lineal ¿Para qué nos sirve las permutaciones y las combinaciones? Conjunto de los números reales Función lineal Estadística Conjunto numérico con situaciones problemas Distancia entre dos puntos Pendiente de una recta Coordenadas del punto medio Permutación y combinación Planeación y resolución de situaciones problemas Solución de la distancia entre dos puntos y las coordenadas del punto medio Verificación de la pendiente de una recta a partir de sus coordenadas Combinación y arreglos de objetos, a partir de situaciones problemas Interpretación y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Interpretación y resolución de situaciones problemas que me permiten encontrar la distancia entre dos puntos y las coordinadas del punto medio y la pendiente de una recta Interpretación de ejercicios de aplicación con arreglos cotidianos prácticos Solución de situaciones problemas enfocados a pruebas ICFES. Solución de situaciones problemas que involucran: distancia entre dos puntos y las coordinadas del punto medio y la pendiente de una recta Argumentación de ejercicios de aplicación con arreglos cotidianos Construcción y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Construcción y resolución de situaciones problemas que involucran: distancia entre dos puntos y las coordinadas del punto medio y la pendiente de una recta Proposición de ejercicios de aplicación con arreglos cotidianos
Establezco diferencias entre las combinaciones y permutaciones prácticos prácticos
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: UNDÉCIMO PERIODO: 3 ESTÁNDAR: Justificar resultados obtenidos mediante procesos de aproximación sucesiva, rangos de variación y límites en situaciones de medición. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. ¿Qué beneficios y funcionalidad le encuentra al estudio de las funciones y relaciones? ¿Por qué es importante desarrollar la intuición y que aplicación tiene en las sucesiones de números reales? Funciones y relaciones Sucesiones de números reales Relaciones reales, dominio y rango Clases de funciones reales Sucesiones y series Termino general o N-eximo Caracterización geométrica de una función, con ayuda de su grafica Relación y diferenciación entre funciones y relaciones Determinación del dominio y rango en una función Identificación y clasificación de sucesiones y serie de los números reales Determinación del termino general N-eximo de una sucesión real Identificación del dominio y el rango de una función Determinación de los términos de una sucesión a partir de un ecuación Justificación geométrica y analíticamente la inversa de una función respecto a las operaciones, determino si es o no biyectiva Identificación de asíntotas verticales y horizontales de funciones reales Clasificación de las sucesiones en categorías : Creciente, De Creciente, Aritméticas y Geométricas Proposición de argumentos geométricos y analíticos para construir las gráficas de las funciones reales Proposición de sucesiones donde haya la necesidad de desarrollar la intuición para encontrar el termino general o N-eximo
Pensamiento aleatorio ¿Será importante estudiar la probabilidad de que ocurran ciertos sucesos naturales o de nuestra vida diaria? Probabilidad l Medidas de localización y dispersión. Experimentos Aleatorios. Variables aleatorias discretas y continuas Realización de experimentos o fenómenos aleatorios. Identificar las propiedades de la probabilidad. Diferenciación de las variables aleatorias y continuas. Estudio la posibilidad de que ocurran sucesos. Interpretación de los resultados numéricos obtenidos al hallar el valor esperado y la varianza de una variable aleatoria Exposición de los pasos generados para determinar el valor esperado, la varianza y la desviación estándar de una variable aleatoria Solución por pasos generales para determinar el valor esperado, la varianza y desviación típica de una variable aleatoria
INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: UNDÉCIMO PERIODO: 4 ESTÁNDAR: - Identificar el concepto de sucesiones para encontrar el límite de una función y representarla en diferentes formas, en el plano cartesiano, describiendo el límite hacia un valor real - Interpretar la noción de derivada como razón de cambio y desarrolla métodos para hallar la derivada de funciones básicas. - Utilizar las técnicas de aproximación en procesos infinitos numéricos. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento geométrico – métrico. ¿Para qué nos sirve el estudio de los límites y que aplicabilidad tiene en nuestra vida cotidiana? Limites Derivada Límite de funciones Limite directos Limites con racionalización Limites con factorización Limites indeterminados Límites al infinito Derivada y el problema de la recta Solución del límite de una función aplicando sus propiedades Solución de limites aplicando conjugadas Identificación de limites infinitos y al infinito Solución de la derivada como razón de cambio y desarrolla métodos para Aplicación de nociones fundamentales de los límites de una sucesión para calcular algunos límites de funciones. Aplicación de técnicas de factorización en el cálculo de limites Interpretación de la noción de derivada como razón de Utilización de técnicas de sustitución para calcular límites alrededor de un punto distinto de cero. Utilización de sucesiones para aprobar la no existencia de limites Argumentación de la noción de derivada como razón de cambio Construcción y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Proposición de la noción de derivada como razón de cambio
Pensamiento aleatorio ¿Será importante estudiar la probabilidad de que ocurran ciertos sucesos naturales o de nuestra vida diaria? Integración Probabilidad ll tangente Velocidad, aceleración y otras razones de cambio Reglas de derivación Regla de la cadena Derivación implícita Primitivas e Integración indefinida Integración definida Teorema fundamental del cálculo Integración por sustitución Modelo de Poisson Modelo Binomial Modelo Normal hallar la derivada de funciones básicas. Utilización de técnicas de aproximación en procesos infinitos numéricos. Identificación y aplicación de la distinción Binomial en nuevos experimentos dados. Identificación y aplicación de la distribución de Poisson en nuevos experimentos dados. Identificación y aplicación de la distribución normal cambio y desarrolla métodos para hallar la derivada de funciones básicas. Interpretación de las técnicas de aproximación en procesos infinitos numéricos. Utilización de la tabla de la distribución normal estándar en la búsqueda de probabilidades de modelos normales y desarrolla métodos para hallar la derivada de funciones básicas. Argumentación de las técnicas de aproximación en procesos infinitos numéricos. Interpretación de los valores de la medidas de tendencia central de los modelos probabilísticos discretos, Binomial y de Poisson Interpretación de los problemas enmarcados en el modelo normal e interpreta gráficamente las probabilidades y desarrolla métodos para hallar la derivada de funciones básicas. Explicación de las técnicas de aproximación en procesos infinitos numéricos. Presentación del modelo de probabilidad discreto que modele más adecuadamente, la información presentada en una situación problema Proposición de un modelo de probabilidad para interpretar la naturaleza aleatoria de algún fenómeno
en nuevos experimentos dados. Utilizo los modelos de distribución de probabilidades: Binomial, Poisson y normal, en el planteamiento y resolución de problemas. encontradas presentado en forma de problema
Plan de area matematicas 2014 (1)

Más contenido relacionado

DOC
Proyecto
porJaime Saltarin Viloria
 
DOC
Plan de area
porladanzadelosnumeros
 
DOC
Programación curricular anual desarrollada mat 1230-cuarto sec.
porJulia Garcia
 
PDF
Mod matecompleto
porEdgar Sanchez
 
PDF
Plan de area de matemáticas 2015
porBladimir Marin
 
DOC
Plan de estudios matematicas 2010
porNixonivan Romero
 
PDF
Chile Curriculo Matematicas Tics
porRommel Gutierrez Roa
 
PDF
Tema 25
porMovb Glez
 
Proyecto
porJaime Saltarin Viloria
 
Plan de area
porladanzadelosnumeros
 
Programación curricular anual desarrollada mat 1230-cuarto sec.
porJulia Garcia
 
Mod matecompleto
porEdgar Sanchez
 
Plan de area de matemáticas 2015
porBladimir Marin
 
Plan de estudios matematicas 2010
porNixonivan Romero
 
Chile Curriculo Matematicas Tics
porRommel Gutierrez Roa
 
Tema 25
porMovb Glez
 

La actualidad más candente

PDF
Plan de area matematicas
porJader Mario Mendoza
 
PPS
Competencias en Matemáticas
poreuclidesmurcia
 
PDF
Modulo matematica eba
porIrfa Peru
 
PDF
Pensamiento numerico y algebraico
porcbt_hueypoxtla
 
PDF
Tema 22
porMovb Glez
 
PDF
Tema 20
porMovb Glez
 
DOCX
Plan de area matematicas 2014
porNora Elena Orrego García
 
PDF
Didactica matemática
porElva Reyes
 
DOC
Cursodidactica1
porfavalenc
 
PDF
Rutas del Aprendizaje : Fasciculo general matematica
porsisicha3
 
PDF
1 1°programación anual 2014
porReymundosalcedovalencia
 
DOC
Programacion matematicas 1º olga
porOlgaSainz1
 
PDF
Ross mate y su enseñanza puc
porNancy Ross
 
PDF
Cultivos urbanos en un aula de matemáticas inclusiva
porCompartir Palabra Maestra
 
PPTX
Lineamientos curriculares de matematicas
porEstefaniaroldan94
 
Plan de area matematicas
porJader Mario Mendoza
 
Competencias en Matemáticas
poreuclidesmurcia
 
Modulo matematica eba
porIrfa Peru
 
Pensamiento numerico y algebraico
porcbt_hueypoxtla
 
Tema 22
porMovb Glez
 
Tema 20
porMovb Glez
 
Plan de area matematicas 2014
porNora Elena Orrego García
 
Didactica matemática
porElva Reyes
 
Cursodidactica1
porfavalenc
 
Rutas del Aprendizaje : Fasciculo general matematica
porsisicha3
 
1 1°programación anual 2014
porReymundosalcedovalencia
 
Programacion matematicas 1º olga
porOlgaSainz1
 
Ross mate y su enseñanza puc
porNancy Ross
 
Cultivos urbanos en un aula de matemáticas inclusiva
porCompartir Palabra Maestra
 
Lineamientos curriculares de matematicas
porEstefaniaroldan94
 

Destacado

PPS
Elsecretoparaserfeliz (1)
porVanessa Benavides
 
PPTX
Osteoporosis
porKaren Urquijo
 
DOCX
Epson l355 diego
porDiego Narvaez
 
PDF
Studentische Softwareentwicklung - Warum es keine Alternative zu agilen Metho...
porWolfgang Reinhardt
 
DOCX
Formato agenda digital online matematicas grado 11ºa y 11ºb
porJorge Didier Obando Montoya
 
PPTX
4 grandes religiones
porJulian Galeano
 
DOCX
Paso a paso para crear un archivo de audio con audacity
porguillermo campos
 
PPTX
Historia de los portatiles
porArmando Alvarez
 
PPTX
Justin mitologia griega
porjustin-1031
 
PPTX
Informatica medica danna ceballos
porDanna Sierra
 
PPT
Gute Freunde Horst
porderdirk20
 
PPTX
mtn u
porgroup eight256
 
PPTX
La célula
porSofi Chaves
 
PPTX
Estrategias avanzadas de docencia en línea en entornos de enseñanza-aprendizaje
porMartin López Villa
 
PPTX
Mi biografía-carlos zuleta
porKrlos Zuleta Hernandez
 
PPT
introduccion al internet
porRoney Kevin Pozo Andía
 
PPTX
Proyecto videojuego (Estructuras Narrativas)
porAlexandra Plascencia
 
PPTX
Proyecto formativo
porMercado Yerwin
 
PPTX
La culpa es de la vaca sandra
porJeison Medina©
 
PPTX
La Europa de la restauración y las revoluciones
porProfesora de Geografía e Historia
 
Elsecretoparaserfeliz (1)
porVanessa Benavides
 
Osteoporosis
porKaren Urquijo
 
Epson l355 diego
porDiego Narvaez
 
Studentische Softwareentwicklung - Warum es keine Alternative zu agilen Metho...
porWolfgang Reinhardt
 
Formato agenda digital online matematicas grado 11ºa y 11ºb
porJorge Didier Obando Montoya
 
4 grandes religiones
porJulian Galeano
 
Paso a paso para crear un archivo de audio con audacity
porguillermo campos
 
Historia de los portatiles
porArmando Alvarez
 
Justin mitologia griega
porjustin-1031
 
Informatica medica danna ceballos
porDanna Sierra
 
Gute Freunde Horst
porderdirk20
 
mtn u
porgroup eight256
 
La célula
porSofi Chaves
 
Estrategias avanzadas de docencia en línea en entornos de enseñanza-aprendizaje
porMartin López Villa
 
Mi biografía-carlos zuleta
porKrlos Zuleta Hernandez
 
introduccion al internet
porRoney Kevin Pozo Andía
 
Proyecto videojuego (Estructuras Narrativas)
porAlexandra Plascencia
 
Proyecto formativo
porMercado Yerwin
 
La culpa es de la vaca sandra
porJeison Medina©
 
La Europa de la restauración y las revoluciones
porProfesora de Geografía e Historia
 

Similar a Plan de area matematicas 2014 (1)

PPT
Plan de área matemáticas 2015
pordianazuluaga1
 
PPTX
Plan de area matematicas 2014
pordianazuluaga1
 
PPTX
Plan de area matematicas 2013
pordianazuluaga1
 
DOC
Plan de area matematicas
poredilbertotorrescatalan
 
PPTX
1. Plan de área Matemáticas 2012
pordianazuluaga1
 
PPTX
plandeareamatematicas2014-140309212018-phpapp02 (1).pptx
porLuzFortuna2
 
DOCX
Plan de area_mat 4°-5°
porjackelinpreciosa
 
PPTX
1. PLAN DE AREA MATEMATICAS 2012
pordianazuluaga1
 
PPT
Trabajo calculo
porCarlos Guillermo Triana Lopez
 
PDF
Plan de estudios
porierepublicadehonduras
 
PDF
Plan de estudios matematicas
porierepublicadehonduras
 
PPTX
1 plandeareamatematicas2012-120305155534-phpapp02
porDocente en el Instituto Mundo de Colores
 
PPTX
Plan de área de matematicas
porLeobaldo Palacio
 
PPTX
8. presentacion matemáticas ser
porYesid Guarin
 
DOC
Mate. tercer grado
porMiguel Angel de la Cruz
 
PDF
Unidad didáctica integrada
porMaría José Rey
 
DOC
PLANIFICACIÓN DE MATEMATICA 4 Y 2 AÑO.doc
porEduardoDanielBonetto1
 
PDF
Malla de matematicas hecha para cada uno de los grados del colegio
porDanielaRiveraArenas
 
PDF
matematicas
porPedro Escalonilla Torres
 
PDF
Matemáticas pd todo23 (1)
porÁlvaro Gutierrez Perez-Cejuela
 
Plan de área matemáticas 2015
pordianazuluaga1
 
Plan de area matematicas 2014
pordianazuluaga1
 
Plan de area matematicas 2013
pordianazuluaga1
 
Plan de area matematicas
poredilbertotorrescatalan
 
1. Plan de área Matemáticas 2012
pordianazuluaga1
 
plandeareamatematicas2014-140309212018-phpapp02 (1).pptx
porLuzFortuna2
 
Plan de area_mat 4°-5°
porjackelinpreciosa
 
1. PLAN DE AREA MATEMATICAS 2012
pordianazuluaga1
 
Trabajo calculo
porCarlos Guillermo Triana Lopez
 
Plan de estudios
porierepublicadehonduras
 
Plan de estudios matematicas
porierepublicadehonduras
 
1 plandeareamatematicas2012-120305155534-phpapp02
porDocente en el Instituto Mundo de Colores
 
Plan de área de matematicas
porLeobaldo Palacio
 
8. presentacion matemáticas ser
porYesid Guarin
 
Mate. tercer grado
porMiguel Angel de la Cruz
 
Unidad didáctica integrada
porMaría José Rey
 
PLANIFICACIÓN DE MATEMATICA 4 Y 2 AÑO.doc
porEduardoDanielBonetto1
 
Malla de matematicas hecha para cada uno de los grados del colegio
porDanielaRiveraArenas
 
matematicas
porPedro Escalonilla Torres
 
Matemáticas pd todo23 (1)
porÁlvaro Gutierrez Perez-Cejuela
 

Último

PPTX
TALLER INTEGRAL VI. Elaboración (DTT) para Titulación
porEstudiosendiseoAM
 
PDF
Seminario "Patrimonio inteligente: cómo la IA redefine el acceso, la autoría ...
porUniversidad Internacional de Andalucía
 
PDF
Leyes de la Logica Proposicional LP2 Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Ecuaciones de Segundo Grado Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Estrés , Sufrimiento y Felicidad - Daniel Lopez Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Esc. Sab. Lec. 4. Unidad mediante la humildad.pdf
porAlejandrino Halire Ccahuana
 
PDF
Seminario "La IA, entre alucinaciones y aciertos: marco de trabajo para tarea...
porUniversidad Internacional de Andalucía
 
PDF
Inteligencia Social. La Nueva Ciencia de las Relaciones Humanas Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Fundamentos de Algebra Lineal - Ron Larson Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Evaluación Educativa. José Francisco Lukas Mujika Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Física Universitaria - Francis Sears, Mark Zemansky Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Estrategias de Evaluación Formativa. Mariana Morales Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Hebreos 1 (1a. Parte) El Mesías, superior a los ángeles. Por Humberto Rendon.pdf
porHumberto Rendon
 
PDF
Fundamentos Matemáticos de la Cibernética - Korshunov Editorial Mir Ccesa00...
porDemetrio Ccesa Rayme
 
PDF
Paradigmas-de-Investigacion-Epistemologia-y-Verdad-Cientifica.pdf
porAlberto Soto
 
PDF
Unidad 8: Teoría de la Estimación - Probabilidad y Variables Aleatorias
porFrancisco Sandoval
 
PDF
MONOGRAFIA. CURRÍCULUM.LYA-2.pdftrabajofinal
porantoniomiguel2011201
 
PPTX
SPAN 102 - Repaso para la prueba 1.ppt. x
porbrianjars
 
PDF
tema 10 La Civilización griega. presentación
porVasallo1
 
PDF
INTEGRACIÓN STL, DICOM, TOMOGRAFÍA PREVIO A TRATAMIENTO DE ORTODONCIA.
porpaolamejiac
 
TALLER INTEGRAL VI. Elaboración (DTT) para Titulación
porEstudiosendiseoAM
 
Seminario "Patrimonio inteligente: cómo la IA redefine el acceso, la autoría ...
porUniversidad Internacional de Andalucía
 
Leyes de la Logica Proposicional LP2 Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Ecuaciones de Segundo Grado Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Estrés , Sufrimiento y Felicidad - Daniel Lopez Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Esc. Sab. Lec. 4. Unidad mediante la humildad.pdf
porAlejandrino Halire Ccahuana
 
Seminario "La IA, entre alucinaciones y aciertos: marco de trabajo para tarea...
porUniversidad Internacional de Andalucía
 
Inteligencia Social. La Nueva Ciencia de las Relaciones Humanas Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Fundamentos de Algebra Lineal - Ron Larson Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Evaluación Educativa. José Francisco Lukas Mujika Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Física Universitaria - Francis Sears, Mark Zemansky Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Estrategias de Evaluación Formativa. Mariana Morales Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Hebreos 1 (1a. Parte) El Mesías, superior a los ángeles. Por Humberto Rendon.pdf
porHumberto Rendon
 
Fundamentos Matemáticos de la Cibernética - Korshunov Editorial Mir Ccesa00...
porDemetrio Ccesa Rayme
 
Paradigmas-de-Investigacion-Epistemologia-y-Verdad-Cientifica.pdf
porAlberto Soto
 
Unidad 8: Teoría de la Estimación - Probabilidad y Variables Aleatorias
porFrancisco Sandoval
 
MONOGRAFIA. CURRÍCULUM.LYA-2.pdftrabajofinal
porantoniomiguel2011201
 
SPAN 102 - Repaso para la prueba 1.ppt. x
porbrianjars
 
tema 10 La Civilización griega. presentación
porVasallo1
 
INTEGRACIÓN STL, DICOM, TOMOGRAFÍA PREVIO A TRATAMIENTO DE ORTODONCIA.
porpaolamejiac
 

Plan de area matematicas 2014 (1)

  • 1.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL PLAN DE ÁREA MATEMÁTICAS RESPONSABLES: ALBA ROCIO VELEZ AMZOLICREYTH GALARCIO AURA MUÑOZ DIOSELINA MENA FANNY MESA GLORIA AMPARO LONDOÑO S JORGE DIDIER OBANDO JORGE SÁNCHEZ SILVIA RIOS SUD MARIA MOSQUERA 2014
  • 3.
    PLAN DEL AREADE MATEMÁTICAS 1. JUSTIFICACION Nuestra civilización apenas existiría sin las leyes físicas y las técnicas desarrolladas como producto conjunto con la investigación matemática. Nadie puede construir una pared sin utilizar las técnicas de medición geométrica desarrolladas por los Matemáticos Egipcios. Los actuales avances tecnológicos a las postrimerías del siglo XX y a las puertas del siglo XXI ha necesitado y necesita por doquiera del aporte matemático: Los computadores, la estadística, la contabilidad, las ingenierías, los viajes espaciales y muchas más. El estudio de las Matemáticas busca de que el estudiante se apropie de los conocimientos básicos, repasando las operaciones usuales (suma, resta, multiplicación y división) en el conjunto de los Enteros, hasta llegar a manejar operaciones más complejas que necesitan de conocimientos más avanzados y un análisis más profundo en el conjunto de los Reales. La enseñanza de las matemáticas retoma la labor ya iniciada en el grado anterior; utiliza muchos de los conceptos antes vistos para fundamentar otros nuevos. Poco a poco y con confianza, el alumno irá construyendo las bases de una ciencia que se precia de ser la piedra angular de todas las ciencias exactas, y por ende sustentador del avance científico y tecnológico de nuestros días. Nuestra tarea será de adoptar el estudio de la Aritmética, el álgebra, la Geometría, la estadística y el análisis según lo que corresponda en cada curso. Creemos que el estudio paciente y disciplinado de esta área le dará las bases necesarias para abordar con confianza y sin traumatismos otras asignaturas científicas. En este plan la geometría aparecerá en la básica primaria y la básica secundaria como una exploración sistematizada del espacio. Desde el grado cero (0) al grado undécimo (11°) se incluye el estudio de las matemáticas con el fin de contribuir decididamente a la educación integral del individuo, reconceptualizando las estrategias didácticas, para un mejoramiento en las habilidades y competencias comunicativas – comprensión, análisis, síntesis y resolución de problemas. Se hace necesario entonces crear núcleos temáticos que sean el resultado de la integración de diferentes disciplinas académicas y no académicas (la cotidianidad), que aporten su saber en el estudio, la interpretación, la explicación y solución de problemas detectados. 2. OBJETIVOS GENERALES DEL AREA 1.) Generar en todos los estudiantes una actitud positiva hacia las Matemáticas y estimular en ellos el interés por el estudio. 2.) Desarrollar en los estudiantes una sólida comprensión de los conceptos, procesos y estrategias básicas de las Matemáticas e, igualmente la capacidad de utilizar todo ello en la solución de problemas. 3.) Estimular en los estudiantes el uso creativo de las Matemáticas para expresar nuevas ideas y descubrimientos, así como para reconocer los elementos Matemáticos presentes en otras actividades creativas.
  • 4.
    OBJETIVOS ESPECIFICOS DELAREA 1.) Desarrollar habilidades que le permitan razonar lógica, crítica y objetivamente 2.) Adquirir precisión en la expresión verbal y familiaridad con el lenguaje y expresiones simbólicas. 3.) Suministrar a los estudiantes el lenguaje apropiado que les permita comunicar de manera eficaz sus ideas y experiencias Matemáticas. 4.) Desarrollar habilidades en los procedimientos operativos, aritméticos y geométricos. 5.) Desarrollar en los estudiantes, la habilidad para reconocer la presencia de las Matemáticas en diversas situaciones de la vida real. 3. MARCO LEGAL DEL AREA La Ley 115 de 1994 en su artículo 23 establece para el logro de los objetivos de la educación básica como área obligatoria y fundamental del conocimiento y de la formación que necesariamente se tendrá que ofrecer de acuerdo con el currículo y con el PEI, a la matemática, además es innegable que esta ciencia no puede aislarse de la historia de la humanidad, ya que le ha dado progreso tanto a lo científico como a lo tecnológico. Todos en la práctica cotidiana necesitamos efectuar cálculos y estimar rápidamente algunos resultados, por tanto es indispensable insistir en la operación y cálculo mental, en la comprensión de conceptos y procesos, en la formulación y solución de problemas para motivar el ejercicio de los algoritmos de cálculo. Teniendo en cuenta una visión global e integral del quehacer matemático de debe tener en cuenta tres grandes aspectos para organizar el currículo en un todo armonioso: 1) PROCESOS GENERALES. Que tienen que ver con el aprendizaje tales como: el razonamiento, la resolución y planteamiento de problemas, la comunicación, la modelación y elaboración, comparación y ejercitación de procedimientos. 2) CONOCIMIENTOS BÁSICOS. Que tienen que ver con procesos específicos que desarrollan el pensamiento matemático y con sistemas propios de la matemática. Estos procesos específicos se relacionan con el desarrollo del pensamiento numérico, el espacial, el métrico, el aleatorio y el variacional entre otros. Los sistemas son aquellos propuestos desde la renovación curricular: sistemas numéricos, sistemas geométricos, sistemas de medida, sistema de datos y sistemas algebraicos y analíticos. 3) EL CONTEXTO. Que tiene que ver con los ambientes que rodean al estudiante y que le dan sentido a las matemáticas que aprende. Variables como las condiciones sociales y culturales tanto locales como internacionales, el tipo de interacciones, los intereses que se generan, las creencias, así como las condiciones económicas del grupo social en el que se concreta el acto educativo, deben tenerse en cuenta en el diseño y ejecución de experiencias didácticas.
  • 5.
    4. GRADUALIZACION DEESTANDARES GRADO PRIMERO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO Los conjuntosysus respectivoscardinales Círculo del 0 al 9 Cuantificaciónde situaciones: sumay resta Ubicacióntemporo espacial Clasificaciónde sólidos Atributode losobjetosy loseventos:(superficie, capacidad,masa,tiempo) endiversassituacionesde tipoelemental Recolecciónde datosdentrodel aulade clase Suma yresta de objetosde características iguales Descomposición polinómicadel 0 al 9 SEGUNDO PERIODO Representaciónde cantidadesenel ábaco. Lectura de números segúnlaubicación enel ábaco: decena,docena, quincena Círculo del 10 al 50: suma yresta Trabajo con regletasy bloqueslógicospara manejaratributoscomo: color,tamaño,forma, espesor El plano Representación gráficade la información recolectada: gráficasde barras Descomposición polinómica de númerosdel 0 al 50 TERCER PERIODO Representaciónde cantidadesenel ábaco. Lectura de números segúnlaubicaciónenel ábaco: decena,docena, quincena Círculo del 50 al 75: suma yresta Ideaintuitivade punto Tipode líneas. Trabajo creativo utilizandosuperficies Lectura interpretativade gráficas(0 al 75) Descomposición polinómica de númerosdel 0 al 75
  • 6.
    ARITMETICA GEOMETRIA ESTADISTICAALGEBRA CUARTO PERIODO Representaciónde cantidadesenel ábaco. Lectura de números segúnlaubicaciónenel ábaco: decena,docena, quincena,centena Círculo del 0 al 100: suma yresta Figurasgeométricas básicas Recolección,organización, representaciónyanálisisde información Descomposición polinómica de númerosdel 0 al 100 Manejode 2 variablesenla suma yen la resta graficaciones GRADO SEGUNDO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO Nivelación Lecto-escriturade números La centena(0al 100) Sistemasde numeración decimal. Valorposicional Relacionesde orden Suma y resta Clasificaciónde los sólidosporsus características y dimensiones:largo, ancho,espesor, grosor,profundidad Recolección,organización, representaciónyanálisisde información Descomposición polinómica de númerosdel 0 al 100 Manejode 2 variablesenla suma yen la resta Descomposición factorial SEGUNDO PERIODO Círculo numéricodel 0al 100. Lecto-escriturade números Sistemasde numeración decimal. Valorposicional Relacionesde orden Suma y restaen forma horizontal yvertical. Construcciónde problemas Manejode regla con ejercicioscreativos Lectura e interpretaciónde gráficas( 0 al 100) Descomposición polinómica de númerosdel 0 al 100 Manejode 2 variablesenla suma yen la resta Descomposición factorial
  • 7.
    ARITMETICA GEOMETRIA ESTADISTICAALGEBRA TERCER PERIODO Tablasde multiplicar: algoritmo. Sumasde sumandos iguales Conjuntos seriación Recta numérica, perímetro Áreas: cuadriláteros Tablasde multiplicar: gráficasde barras Descomposición polinómicay factorial enel círculo de númerosdel 0 al 100 Manejode 3 o más variables CUARTO PERIODO Tablasde multiplicar: algoritmo. Sumasde sumandos iguales Conjuntos Seriación Formulación y planteamientode problemas Propiedadesde la multiplicación Iniciaciónala división Recta numérica, perímetro Áreas: cuadriláteros Sistemasde medidas Utilizacióndel metro Tablasde multiplicar: gráficasde barras Probabilidades Descomposición polinómicay factorial enel círculo de númerosdel 0 al 100 Manejode 3 o más variables GRADO TERCERO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO Nivelación: suma,resta, multiplicación Clasesde polígonos segúnel númerode Combinacionesy probabilidades Valornumérico (relacionadocon
  • 8.
    Sistemasde numeración decimal: valorposicional Conjuntos Ampliacióncampo numéricohasta4dígitos. La divisiónbásica Otros sistemasde numeración lados símbolosyfiguras) ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA SEGUNDO PERIODO Multiplicacióncondos cifras Algoritmode ladivisión: por una cifra Múltiplosydivisores Formulaciónyresolución de problemas Manejode la escuadra Triángulos: elementosy clasificaciónsegúnla longitudde suslados Combinacionesy probabilidades Aplicacióndel valornuméricoen problemas sencillos TERCER PERIODO Divisióncondoscifras Problemasde aplicación de la división Ampliacióndel campo numéricohasta5 o más dígitos Planteamientoy resoluciónde problemas con las 4 operaciones Paralelismoy perpendicularidad Nociónde ángulos. Construcciónde cuadriláteros Problemasde aplicación: recolección,tabulacióne interpretaciónde datosy gráficas Igualdades Ecuaciones sencillas(sumay resta) CUARTO PERIODO Fracción: noción, representación,lecto- escritura Suma yresta de fracciones homogéneas Rotacionesy traslaciones Medidasde tendencia central:media,mediana. y moda Ecuaciones: multiplicacióny división GRADO CUARTO
  • 9.
    ARITMETICA GEOMETRIA ESTADISTICAALGEBRA PRIMER PERIODO Nivelación:operacionesy propiedadescon Naturales Conjuntos: operaciones y relaciones Sistemasde numeración decimal:base 10. Problemasde aplicación Ángulos:clases. Construccionescon reglay escuadra Medidasde tendencia central:media,mediana. y moda problemasde aplicación Ecuacionesconlas operacionesde suma,resta, multiplicacióny divisiónenlos naturales ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA SEGUNDO PERIODO Fracciones,clases, representacióngráfica. Relacionesde orden Clasificaciónde los triángulossegúnsus ángulos Análisisde tablasygraficas (diagramade barras y diagramacircular Problemasde aplicacióncon ecuacionesenlos naturales TERCER PERIODO Simplificacióny amplificación Números mixtos Mínimo Común Múltiplo MáximoComúnDivisor Númerosprimosy compuestos Polígonosregulares Frecuenciasabsolutasy relativas Inecuacionescon losnúmeros naturales CUARTO PERIODO Operacionescon fraccionesyproblemas de aplicación Perímetroy áreas del triángulo,cuadradoy rectángulo Permutacionesy combinaciones Valornumérico con polinomios aritméticos GRADO QUINTO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO
  • 10.
    Nivelaciónde temasde grados anteriores Teoríade números: múltiplos,divisores, primosy compuestos Divisibilidad Descomposiciónen factoresprimos Mínimo Común Múltiplo MáximoComúnDivisor Líneas,ángulos, polígonos, perímetrosyáreas Interpretaciónyanálisisde gráficasestadísticas Probabilidades. Arreglosycombinaciones Valornumérico con polinomios aritméticos Signosde agrupación SEGUNDO PERIODO Potenciación,radicación y logaritmación: operaciones correspondientes Medición, construcciónde ángulos Manejode compás y transportador Círculo y circunferencia Recolección,organización. Representacióne interpretaciónde datos Proyectossencillosde investigaciónaplicando frecuenciasymedidasde tendenciacentral Eliminaciónde signosde agrupaciónenlas operaciones básicascon los númerosnaturales ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA TERCER PERIODO Fraccionesdecimales Conversiónde fraccióna decimal yviceversa Los númerosdecimales: lecturay escritura Relacionesde orden Operacionesde suma, resta,multiplicacióny división Sistemamétrico decimal: unidades básicas Conversiónde unidadesde longitud Porcentajesysu representación Graficas enlosdiagramas circulares,lineal yde barras Ecuaciones fraccionarias con una variable CUARTO PERIODO Razonesy proporciones Magnitudesdirectae inversamente proporcionales. Conceptosytrabajo básico Unidadesde superficie. Conversiones Problemasde aplicación Planocartesiano: ejercicios de aplicación Diagramasde barras Valornumérico aplicando operacionescon naturales, fraccionesy decimales SEXTO GRADO
  • 11.
    ARITMETICA GEOMETRIA ESTADISTICAALGEBRA PRIMER PERIODO Nivelación Conjuntode los naturalesysus operaciones Sistemasnuméricos Manejode instrumentos geométricos Trabajo con ángulos y triángulos Diagramaciónde información Diagramascirculares, pictogramas,diagramasde barras Signosde agrupación Sumasy restas combinadas SEGUNDO PERIODO El conjuntode los númerosenteros. Suma y resta Propiedadesconlos enteros Problemasde aplicación sencillos Planocartesiano Ubicaciónde coordenadas cartesianas Interpretaciónde gráficas estadísticas. Extracciónde información de recortesde periódicos Polinomioscony sinsignosde agrupaciónenel conjuntode los númerosenteros TERCER PERIODO Multiplicación,división, radicación,potenciación y logaritmaciónconlos númerosenteros Situacionesproblema. Propiedadesde la potenciaciónenlos enteros Situaciones problemaconel sistemamétrico decimal Notacióncientífica Situacionesproblemacon lasmedidasde tendencia central Signosde agrupacióncon las diferentes operaciones ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA CUARTO PERIODO Fraccionesydecimales Razonesy porcentajes Unidadesde superficie con situaciones problema Trabajo práctico investigativoparala aplicaciónde conceptos estadísticos Resoluciónde situaciones problemacon ecuaciones sencillas Trabajo con fracciones utilizandosignos de agrupación GRADO SEPTIMO
  • 12.
    ARITMETICA GEOMETRIA ESTADISTICAALGEBRA PRIMER PERIODO Nivelación Racionales: sumayresta Propiedades Situacionesproblema Relacionesde ordenen conjuntosnuméricos Perímetro Áreade figuras planas Frecuenciasabsolutas, relativas y acumuladas F.R.A Resoluciónde situaciones problemacon ecuaciones sencillas SEGUNDO PERIODO Operadores fraccionarios,reductores y amplificadores Multiplicaciónde racionales. Situacionesproblema Traslaciónde figuras geométricas enel planocartesiano Homoteciasde figurasgeométricas Representaciónde frecuenciasendiagramas Valornuméricode ecuaciones algebraicas TERCER PERIODO División Potenciación Radicacióny logaritmación Situacionesproblema Rotaciónde figuras geométricas Probabilidades Despeje de incógnitasconlos diferentes conjuntos numéricos ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA CUARTO PERIODO
  • 13.
    Proporcionalidad. Problemasde aplicación Volumende cuerpos geométricos Datosagrupadosy no agrupados. Combinaciones Desigualdadese inecuaciones GRADO OCTAVO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO NIVELACION Proporcionalidad. Poliedros,prismasy pirámides: clasificacióny construcción Formulaciónde proyectos investigativos:IPARTE Conceptos algebraicos básicos SEGUNDO PERIODO Los Reales:relaciónde orden,operacionesy propiedades. La rectareal Triángulos:líneasy puntosnotables. Teoremade Pitágoras Formulaciónde proyectos investigativos:IIPARTE. Recolección de información Operacionescon polinomios:suma, resta, multiplicacióny división. Teoremadel residuoydel factor. Divisiónsintética TERCER y CUARTO PERIODO Los Reales:Notación científica Ángulos: complementarios, adyacentes, consecutivosy cortados poruna transversal Formulaciónde proyectos investigativos: IIIPARTE. Tabulaciónypresentación gráfica Proyectosinvestigativo: IV PARTE: Interpretación Trabajo escrito Conclusiones Productos notables. Factorización Fracciones algebraicas Simplificaciónde fracciones algebraicas
  • 14.
    GRADO NOVENO ARITMETICA GEOMETRIAESTADISTICA ALGEBRA PRIMER Y SEGUNDO PERIODO Númeroscomplejose imaginarios Poliedros,prismasy pirámides: clasificacióny construcción Formulaciónde proyectos investigativos:IPARTE Conceptos algebraicos básicos TECER PERIODO Progresionesaritméticas y geométricas Conos,cilindrosy esferas Variación Desviaciónestándar Ecuaciones cuadráticas CUARTO PERIODO Progresionesaritméticas y geométricas Proporcionalidady semejanza Variación Desviaciónestándar Potenciación, radicación. Racionalizaciónde denominadores GRADO DECIMO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Ecuacionesde la línearecta Probabilidades Radicales. Productos notables Factorización. Racionalizaciónde denominadores
  • 15.
    SEGUNDO PERIODO CONJUNTOS NUMERICOS: Resolución desituacionesproblema. Funciones trigonométricas Probabilidades Radicales. Productos notables Factorización. Racionalizaciónde denominadores ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA TERCER PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Resoluciónde triángulos: problemasde aplicación Identidadesy ecuaciones trigonométricas Probabilidades Radicales. Productos notables Factorización. Racionalizaciónde denominadores CUARTO PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Cónicas Probabilidades Funcionesy relaciones GRADO UNDECIMO ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA PRIMER PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Circuitoslógicos. Intervalos. Inecuaciones Valorabsoluto. Sucesionesyseries Permutacionesy combinaciones Funcionesy relaciones SEGUNDO PERIODO
  • 16.
    CONJUNTOS NUMERICOS: Resolución de situacionesproblema. LimitesSumatoriay productoria Funcionesy relaciones Productos notables Factorización. Racionalizaciónde denominadores TERCER PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Derivadas probabilidades Funcionesy relaciones Productos notables Factorización. Racionalizaciónde denominadores ARITMETICA GEOMETRIA ESTADISTICA ALGEBRA CUARTO PERIODO CONJUNTOS NUMERICOS: Resolución de situacionesproblema. Integrales probabilidades Funcionesy relaciones Productos notables Factorización. Racionalizaciónde denominadores 5. COMPETENCIAS ESPECÍFICAS DEL ÁREA  INTERPRETATIVA: encontrar el sentido de una proposición de un problema, de un gráfico, de los argumentos en contra o en pro de una teoría.  ARGUMENTATIVA: dar razón de una afirmación, explicar el porqué de una proposición, justificar una afirmación mediante articulación. La articulación de conceptos y teorías.  PROPOSITIVA: generar hipótesis en la resolución de problemas, proposición de alternativas de solución de problemas y conflictos. Explicación de una proposición a través de conceptos lógicos.  NUMÉRICA OPERATIVA: hace referencia a la parte operativa o resolución de problemas en cada uno de los conjuntos numéricos (R, I, N, Q, Q”)
  • 17.
     GEOMÉTRICA MÉTRICA:transformaciones geométricas en el plano, comprensión de conceptos geométricos.  COGNITIVA: hace referencia al reconocimiento de conceptos previos, aplicación de conocimientos, procesos y solución de problemas a través de la reproducción de conceptos básicos. NIVELES DE COMPETENCIA – DESEMPEÑO EN MATEMÁTICAS Y METAS DE CALIDAD NIVEL DE COMPETENCIA DESEMPEÑO 01. RECONOCIMIENTO Y DISTINCIÓN - Reconocer figuras geométricas y atributos medibles: Identificar los efectos de las transformaciones - Reconocer, leer y distinguir diferentes representaciones y usos del número en contextos con significado. 02. INTERPRETACIÓN - Interpretar y describir información gráfica. - Expresar patrones de variación y establecer relaciones de proporcionalidad. - Resolver problemas de estructura aditiva o multiplicativa. - Interpretar y analizar fenómenos aleatorios: hacer arreglos y combinaciones. - Resolver situaciones problemáticas que requieren la utilización de propiedades métricas, geométricas o aritméticas. - Dar significado a información numérica y traducir entre diferentes representaciones. 03. PRODUCCIÓN - Ordenar, comparar, estimar, predecir o transformar expresiones numéricas o algebraicas relativas a situaciones problemáticas. - Resolver problemas geométricos o métricos usando argumentaciones deductivas e inductivas. 6. ESTRATEGIAS METODOLOGÍA APLICABLES AL AREA Los procesos presentes en toda la actividad matemática tienen que ver con:  La resolución y el planteamiento de problemas.  El razonamiento.  La comunicación.  La modelación: elaboración, comparación y ejercitación de procedimientos. LA RESOLUCIÓN Y EL PLANTEAMIENTO DE PROBLEMAS
  • 18.
    La resolución deproblemas debe ser eje central del currículo de matemáticas, y como tal, debe ser un objetivo primario de la enseñanza y parte integral de la actividad matemática. En la medida en que los estudiantes van resolviendo problemas, van ganando confianza en el uso de las matemáticas, van desarrollando una mente inquisitiva y perseverante, va aumentado su capacidad de comunicarse matemáticamente y su capacidad para utilizar procesos de pensamiento de más alto nivel. Las investigaciones que han reconocido la resolución de problemas como una actividad muy importante para aprender matemáticas, proponen considerar en el currículo escolar de matemáticas aspectos como los siguientes:  Formulación de problemas a partir de situaciones dentro y fuera de las matemáticas.  Desarrollo y aplicación de diversas estrategias para resolver problemas.  Verificación e interpretación de resultados a la luz del problema original.  Generalización de soluciones y estrategias para nuevas situaciones de problemas.  Adquisición de confianza en el uso significativo de las matemáticas. EL RAZONAMIENTO El razonamiento matemático tiene que ver estrechamente con las matemáticas como comunicación, como modelación y como procedimiento. El razonamiento matemático es necesario para tener en cuenta de una parte, la edad de los estudiantes y su nivel de desarrollo y, de otra, que cada logro alcanzado en un conjunto de grados se retoma y amplía en los conjuntos de grados siguientes. Asimismo, se debe partir de los niveles informales del razonamiento en los conjuntos de grados inferiores, hasta llegar a niveles más elaborados del razonamiento. Razonar en matemáticas tiene que ver con:  Dar cuenta del cómo y del porqué de los procesos que se siguen para llegar a conclusiones.  Justificar las estrategias y los procedimientos puestos en acción en el tratamiento de problemas.  Formular hipótesis, hacer conjeturas y predicciones, encontrar contraejemplos, usar hechos conocidos, propiedades y relaciones para explicar otros hechos.  Encontrar patronos y expresarlos matemáticamente.  Utilizar argumentos propios para expresar ideas, comprendiendo que las matemáticas más que una memorización de reglas y algoritmos, son lógicas y potencian la capacidad de pensar. LA COMUNICACIÓN Una necesidad común que tenemos todos los seres humanos en todas las actividades, disciplinas, profesiones y sitios de trabajo es la habilidad para comunicarnos. Los retos que nos plantea el siglo XXI requiere que en todas las profesiones científicas y técnicas, las personas sean capaces de:  Expresar ideas hablando, escribiendo, demostrando y describiendo visualmente de diferentes formas.  Construir, interpretar y ligar varias representaciones de ideas y de relaciones.  Hacer observaciones y conjeturas, formular preguntas, reunir y evaluar información.  Producir y presentar argumentos persuasivos y convincentes. Se ha identificado la comunicación como uno de los procesos más importantes para aprender matemáticas y para resolver problemas. La comunicación juega un papel fundamental al ayudar a los niños a construir los vínculos entre sus nociones informales e intuitivas y el lenguaje abstracto y simbólico de las matemáticas; cumple también una función clave como ayuda para que los alumnos tracen importantes conexiones entre
  • 19.
    las representaciones físicas,pictóricas, gráficas, simbólicas, verbales y mentales de las ideas matemáticas. Thomas A. Romberg en su artículo “características problemáticas del currículo escolar de matemáticas” (página 375) destaca la comunicación verbal y escrita como una parte crucial del proceso enseñanza y aprendizaje de las matemáticas, por las siguientes razones:  En primer lugar la comunicación en forma de argumento lógico es fundamental para el discurso matemático.  En segundo lugar, la comunicación es el medio por el cual los conocimientos personales se sistematizan en un ámbito y, por tanto, se aceptan como conocimientos nuevos.  En tercer lugar, el desarrollo en las categorías y estructuras del sistema lingüístico, estructura la comprensión del niño y la hace progresar hacia un modelo de conocimiento público. De esta manera las funciones y el trabajo de los alumnos y de los educadores, se consideran complementarias. El educador debe guiar, escuchar, discutir, sugerir, preguntar y clarificar el trabajo de los alumnos a través de actividades apropiadas e interesantes. La comunicación es la esencia de la enseñanza, el aprendizaje y la evaluación de las matemáticas. LA MODELACIÓN Actualmente, la aparición de la era Informática, uno de los énfasis que se hace es la búsqueda y construcción de modelos matemáticos. La tecnología moderna sería imposible sin las matemáticas y prácticamente ningún proceso técnico podría llevarse a cabo en ausencia del modelo matemático que lo sustenta. Cuando hablamos de la actividad matemática en la escuela, destacamos que el alumno aprende matemática “haciendo matemáticas”, lo que supone como esencial la resolución de problemas de la vida diaria, lo que implica que desde el principio se integre al currículo una variedad de problemas relacionados con el contexto de los estudiantes. La resolución de problemas en un amplio sentido, se considera siempre en conexión con las aplicaciones y la modelación. La forma de describir ese juego o interrelación entre el mundo real y las matemáticas es la modelación. El punto de partida de la modelación es una situación problemática real. Esto conduce a una formulación del problema. Los datos, conceptos, relaciones, condiciones y suposiciones del problema enunciado matemáticamente deben trasladarse a las matemáticas, es decir, deben ser matematizados y así resulta un modelo matemático de la situación original. El proceso de resolución de problemas continúa mediante el trabajo de sacar conclusiones, calcula y revisa ejemplos concretos, aplica métodos y resultados matemáticos conocidos; como también desarrollando otros nuevos. En conjunto se obtienen ciertos resultados matemáticos, estos resultados tienen que ser validados, es decir, se tienen que volver a trasladar al mundo real, para ser interpretados en relación con la situación original. De esta manera, el que resuelve el problema también valida el modelo, si se justifica usarlo para el propósito que fue construido. En conclusión, la modelación es el proceso completo que conduce desde la situación problemática real original hasta un modelo matemático en el cual el conocimiento y las habilidades adquiridas se utilizan para descubrir regularidades, relaciones y estructuras desconocidas.
  • 20.
    7. CRITERIOS YPROCEDIMIENTOS PARA EVALUAR EL APRENDIZAJE, RENDIMIENTO Y DESARROLLO DE LA CAPACIDAD DE LOS EDUCANDOS La evaluación cualitativa debe ser formativa, continua, sistemática y flexible, centrada en el propósito de producir y recoger información necesaria sobre los procesos de enseñanza aprendizaje que tienen lugar en el aula y por fuera de ella. La evaluación debe ser más una reflexión que un instrumento de medición para poner etiquetas a los individuos; lo que no excluye el reconocimiento de las diferencias individuales. Evaluar el estado cognoscitivo y afectivo del estudiante, frente a un área del conocimiento, significa considerar todos aquellos elementos necesarios para diagnosticar los estados del aprendizaje, los factores formativos y los logros alcanzados de acuerdo con los propósitos y las estrategias de intervención utilizadas durante el proceso educativo. Con base en lo anterior, en el área de matemáticas evaluaremos teniendo en cuenta los siguientes aspectos:  Comportamiento de los estudiantes en su trabajo cotidiano, como su actitud, dedicación, interés, participación, capacidad de diferenciación, su habilidad para asimilar y comprender informaciones y procedimientos, su refinamiento progresivo en los métodos para conocer, para analizar, crear y resolver problemas, en su inventiva o tendencia a buscar nuevos métodos o respuestas para las diversas situaciones.  Las concepciones de los alumnos sobre los conceptos.  Los cambios que se presentan en las concepciones mediante la participación activa de los estudiantes durante la construcción de los conocimientos.  La comprensión de los conocimientos básicos en un momento dado.  El estado de conceptualización alcanzado frente a los saberes formales.  Las formas de comunicación de concepciones y conceptos.  La capacidad para aplicar los conceptos.  La capacidad para interpretar, plantear y resolver problemas.  Las estrategias y procedimientos utilizados para plantear y resolver problemas.  Los estilos de trabajo: individual y colectivo.  La adquisición de destrezas.  La participación individual en tareas colectivas.  El interés por ampliar los conocimientos discutidos en el aula.  La capacidad de lectura y escritura de temas relacionados con el área.  La capacidad de reflexionar críticamente sobre lo que se aprende, lee o escribe. PLANES ESPECIALES DE APOYO PARA ESTUDIANTES CON MARCADAS DIFICULTADES Se implementaran las siguientes estrategias:  Refuerzo constante de las operaciones básicas.  Formar un grupo de alumnos con dificultades en matemáticas para reforzar en jornada contraria, se llamaría semillero de alumnos con dificultades  Crear estímulos que motiven a los estudiantes a pertenecer al semillero como: izar bandera, resaltar en público los avances que van teniendo, mención de honor, entre otras.  Aprovechar el recurso de los alumnos más avanzados de cada grupo para que apoyen o sirvan de monitores en el semillero de alumnos con dificultades  Crear concursos y eventos matemáticos entre los alumnos del semillero a nivel institucional e interinstitucional como: juegos, carreras de observación, entre otros.  Integrar a padres de familia en forma periódica al semillero para que realicen actividades en común y juegos didácticos, para que sirvan de multiplicadores en el manejo del juego y temas aprendidos. PARA ESTUDIANTES CON DESEMPEÑO SUPÈRIOR EN EL AREA DE MATEMATICAS. Se implementaran las siguientes estrategias:
  • 21.
     Realizar convocatoriasa estudiantes con desempeño superior en el área de matemáticas que deseen hacer parte de las monitorias.  Crear las monitorias con los estudiantes que presentan desempeño superior en el área.  Fortalecer habilidades que permitan orientar el trabajo de los monitores.  Motivar a los estudiantes monitores de los diferentes grados incluyendo a los estudiantes de 10º y 11º que deseen prestar su servicio social como monitores a estudiantes con dificultades en matemáticas; resaltando la importancia de las competencias ciudadanas para el bienestar académico propio y de los demás.  Involucrar al padre de familia dentro del proyecto de asesoráis tanto para los estudiantes con dificultades en el área como a los que colaboraran en las asesoráis.  Estimular a los estudiantes monitores con una valoración académica (nota en el periodo), un incentivo económico que le permita subsanar algunas de sus necesidades y eximirlo de algunas actividades escolares.  Crear espacios de asesoráis personalizadas que le permita avanzar en su desempeño en el área, elaborar material didáctico o profundizar en algunos temas y procedimientos matemáticos.  Participación en talleres y seminarios programados por la institución, el municipio o el departamento y que sean costeados por quien los organice.  Organizar encuentros interinstitucionales dentro y fuera del municipio, buscando mostrar experiencias y enriquecernos con nuevas propuestas.  Crear clubes o grupos de estudios dentro de las instituciones y luego a nivel municipal que faciliten el proceso de aprendizaje de las matemáticas en los estudiantes que presentan dificultades especificas del área, creando y fortaleciendo los semilleros existentes en el municipio.  Crear espacios de asesoráis a estudiantes con desempeño superior en el área del grado noveno para que elijan adecuadamente la modalidad, que le sirva de visión futura hacia sus expectativas universitarias y laborales.  Asignar espacios para la capacitación, integración, concursos y demás actividades que beneficien el desarrollo normal del proyecto del área en cada institución.  Recibir apoyo de la secretaria de educación municipal, de la junta municipal de educación (JUME) y de las diferentes instituciones para la creación y fortalecimiento de los clubes o grupos de estudiantes con desempeño superior en esta y otras áreas, asignando para ello presupuesto municipal que mejore la calidad de la educación. 4. INDICADORES DEL AREA POR GRADOS, SEGÚN LA RESOLUCION 2343 GRADO: PRIMERO 1. Expresa Ideas y situaciones que involucran conceptos matemáticos mediante lenguaje natural y representaciones físicas, pictóricas, gráficas, simbólicas y establece conexiones entre ellas. 2. Identifica y clasifica fronteras y regiones de objetos en el plano y en el espacio, reconoce en ellos formas y figuras a través de la imaginación del dibujo o de la construcción con materiales apropiados y caracteriza triángulos, cuadrados, rectángulos y círculos. 3. Identifica en objetos y situaciones de su entorno las magnitudes de longitud, volumen, y capacidad; reconoce procesos de conservación y desarrolla procesos de medición de dichas magnitudes, con patrones arbitrarios y con algunos patrones estandarizados. GRADO: SEGUNDO 1. Identifica en objetos y situaciones de su entorno las magnitudes de longitud, volumen, y capacidad; reconoce procesos de conservación y desarrolla procesos de medición de dichas magnitudes, con patrones arbitrarios y con algunos patrones estandarizados. 2. Relaciona los algoritmos convencionales o propios con los conceptos matemáticos que los sustentan, identifica esquemas y patrones que le permiten llegar a conclusiones. 3. Explora y descubre propiedades interesantes y regularidades de los números, efectúa cálculos con datos de la realidad y utiliza creativamente materiales y medios. GRADO: TERCERO 1. Compara, describe, denomina y cuantifica situaciones de la vida cotidiana, utilizando con sentido números por lo menos hasta de cinco cifras.
  • 22.
    2. Identifica enobjetos y situaciones de su entorno las magnitudes de longitud, volumen, y capacidad; reconoce procesos de conservación y desarrolla procesos de medición de dichas magnitudes, con patrones arbitrarios y con algunos patrones estandarizados. 3. Relaciona los algoritmos convencionales o propios con los conceptos matemáticos que los sustentan, identifica esquemas y patrones que le permiten llegar a conclusiones. 4. Explora y descubre propiedades interesantes y regularidades de los números, efectúa cálculos con datos de la realidad y utiliza creativamente materiales y medios. GRADO: CUARTO 1. Investiga y comprende contenidos matemáticos a partir de enfoques de resolución de problemas, formula y resuelve problemas derivados de situaciones cotidianas y matemáticas, examina y valora los resultados teniendo en cuenta el planteamiento original del problema. 2. Reconoce características de sólidos, figuras planas y líneas, los utiliza en su vida cotidiana en trabajos prácticos como mediciones, elaboración de dibujos y construcción de modelos. 3. Explica sus ideas y justifica sus respuestas mediante el empleo de modelos, la interpretación de hechos conocidos y la aplicación de propiedades y relaciones matemáticas. GRADO: QUINTO 1. Identifica los números naturales y los racionales positivos en su expresión decimal y fraccionaria, los usa en diferentes contextos y los representa de distintas formas. 2. Construye y utiliza significativamente en una amplia variedad de situaciones las operaciones de adición, sustracción, multiplicación y división con números naturales y con números racionales positivos, establece relaciones entre estas operaciones y usa sus propiedades para la elaboración del cálculo mental y escrito. 3. Interpreta datos presentados en talas y en diagramas, comprende y usa la media, la mediana y la moda en un conjunto pequeño de datos y saca conclusiones estadísticas. 4. Reconoce la importancia de averiguar datos y procesar información para tomar decisiones, y de conocer y evaluar sus características en relación con las decisiones que se tomen. 5. Reconoce características de sólidos, figuras planas y líneas, los utiliza en su vida cotidiana en trabajos prácticos como mediciones, elaboración de dibujos y construcción de modelos. 6. Explica sus ideas y justifica sus respuestas mediante el empleo de modelos, la interpretación de hechos conocidos y la aplicación de propiedades y relaciones matemáticas. GRADO: SEXTO 1. Identifica los números naturales y los racionales positivos en su expresión decimal y fraccionaria, los usa en diferentes contextos y los representa de distintas formas. 2. Explora y descubre propiedades interesantes y regularidades de los números, utiliza habitual y críticamente materiales y medios para verificar predicciones, realizar y comprobar cálculos y resolver problemas. 3. Interpreta datos presentados en tablas y en diagramas, comprende y usa la media, la mediana y la moda en un conjunto pequeño de datos y saca conclusiones estadísticas. 4. Reconoce la importancia de averiguar datos y procesar información para tomar decisiones, y de conocer y evaluar sus características en relación con las decisiones que se tomen.
  • 23.
    5. Reconoce característicasde sólidos, figuras planas y líneas, los utiliza en su vida cotidiana en trabajos prácticos como mediciones, elaboración de dibujos y construcción de modelos. 6. aplica movimientos rígidos en el plano como traslaciones, rotaciones y reflexiones, identifica las propiedades que se conservan en cada movimiento y visualiza transformaciones simples para descubrir reglas de combinación que permitan crear patrones. 7. Identifica en objetos y situaciones de su entorno las magnitudes de longitud, área, volumen, capacidad, peso, masa, amplitud de ángulos y duración. Reconoce procesos de conservación y desarrolla procesos de medición y estimación de dichas magnitudes y las utiliza en situaciones de la vida diaria. 8. Formula, argumenta y somete a prueba conjeturas y elabora conclusiones lógicas. 9. Explica sus ideas y justifica sus respuestas mediante el empleo de modelos, la interpretación de hechos conocidos y la aplicación de propiedades y relaciones matemáticas. GRADO: SÉPTIMO 1. Identifica y usa los números enteros y los racionales en diferentes contextos, los representa de diversas formas y establece relaciones entre ellos; redefine las operaciones básicas en los sistemas formados con estos números y establece conexiones entre ellas. 2. Investiga y comprende contenidos y procedimientos matemáticos, a partir de enfoques de tratamiento y resolución de problemas y generaliza soluciones y estrategias para nuevas situaciones. 3. Formula problemas a partir de situaciones dentro y fuera de las matemáticas, desarrolla y aplica diversas estrategias para resolverlos, verifica e interpreta los resultados en relación con el problema original. 4. Formula inferencias y argumentos coherentes, utilizando medidas de tendencia central y de dispersión para el análisis de los datos, interpreta estadísticos y elabora críticamente conclusiones. 5. Visualiza, reconoce y efectúa transformaciones de polígonos en el plano y las utiliza para establecer congruencia, semejanza y simetría entre figuras. 6. Comprende y usa la proporcionalidad directa e inversa de magnitudes, en distintos contextos de la vida cotidiana y utiliza diferentes procedimientos para efectuar cálculos de proporcionalidad. GRADO: OCTAVO 1. Formula, argumenta y pone a prueba hipótesis, las modifica o descarta y reconoce las condiciones necesarias para que una propiedad matemática se cumpla; aplica estos procedimientos en la formulación, análisis y resolución de problemas. 2. Formula inferencias y argumentos coherentes, utilizando medidas de tendencia central y de dispersión para el análisis de los datos, interpreta estadísticos y elabora críticamente conclusiones. 3. Construye e interpreta formulas, ecuaciones e inecuaciones para presentar situaciones que requieren variables, opera con cualquiera de ellas y encuentra procedimientos para resolver ecuaciones e inecuaciones. 4. Construye modelos geométricos, esquemas, planos y maquetas utilizando escalas, instrumentos y técnicas apropiadas y visualiza, interpreta y efectúa representaciones gráficas de objetos tridimensionales en el plano.
  • 24.
    5. Visualiza, reconocey efectúa transformaciones de polígonos en el plano y las utiliza para establecer congruencia, semejanza y simetría entre figuras. 6. Comprende y usa la proporcionalidad directa e inversa de magnitudes, en distintos contextos de la vida cotidiana y utiliza diferentes procedimientos para efectuar cálculos de proporcionalidad. GRADO: NOVENO 1. Hace estimaciones sobre numerosidad, resultados de cálculos y medición de magnitudes concretas, a partir de sus propias estrategias y las utiliza como criterio para verificar lo razonable de los resultados. 2. Elabora modelos de fenómenos del mundo real y de las matemáticas a través de sucesiones, de series y de las funciones lineal, constante, idéntica, opuesta, de gráfica lineal, cuadrática y cúbica. 3. Representa y analiza funciones utilizando para ello tablas, expresiones orales, expresiones algebraicas, ecuaciones y gráficas y hace traducciones entre estas representaciones. 4. Interpreta listas de instrucciones, expresiones algebraicas y diagramas operacionales y de flujo, traduce de unos a otros y opera con ellos utilizando diferentes tipos de número. 5. Construye modelos geométricos, esquemas, planos y maquetas utilizando escalas, instrumentos y técnicas apropiadas y visualiza, interpreta y efectúa representaciones gráficas de objetos tridimensionales en el plano. GRADO: DECIMO 1. Da razones del porqué de los números reales y explica por qué unos son racionales y otros irracionales. 2. Utiliza el sentido de las operaciones y de las relaciones en sistemas de números reales. 3. Interpreta instrucciones, expresiones algebraicas, diagramas operacionales y de flujo y traduce de unos a otros, en el sistema de los números reales. 4. Aplica modelos de funciones para tratar matemáticamente situaciones financieras y transacciones comerciales frecuentes en la vida real. 5. Hace inferencias a partir de diagramas, tablas y gráficas que recojan datos de situaciones del mundo real; estima, interpreta y aplica medidas de tendencia central, de dispersión y de correlación. 6. Reconoce fenómenos aleatorios de la vida cotidiana y del conocimiento científico, formula y comprueba conjeturas sobre el comportamiento de los mismos y aplica los resultados en la toma de decisiones. 7. elabora argumentos informales pero coherentes y sólidos para sustentar la ordenación lógica de una serie de proposiciones. 8. Detecta y aplica distintas formas de razonamiento y métodos de argumentación en la vida cotidiana, en las ciencias sociales, en las ciencias naturales y en las matemáticas; analiza ejemplos y contraejemplos para cambiar la atribución de necesidad o suficiencia a una condición dada. 9. Disfruta y se recrea en exploraciones que retan su pensamiento y saber matemático y exigen la manipulación creativa de objetos, instrumentos de medida y materiales y medios. GRADO: UNDÉCIMO
  • 25.
    1. Investiga ycomprende contenidos matemáticos a través del uso de distintos enfoques para el tratamiento y resolución de problemas; reconoce, formula y resuelve problemas del mundo real aplicando modelos matemáticos e interpreta los resultados a la luz de la situación inicial. 2. Elabora modelos de fenómenos del mundo real y de las matemáticas con funciones polinómicas, escalonadas, exponenciales, logarítmicas, circulares y trigonométricas; las representa y traduce mediante expresiones orales, tablas, gráficas y expresiones algebraicas. 3. Aplica modelos de funciones para tratar matemáticamente situaciones financieras y transacciones comerciales frecuentes en la vida real. 4. analiza situaciones de la vida diaria generadoras de las ideas fuertes del cálculo, tales como tasa de cambio, tasa de crecimiento y total acumulado; descubre y aplica modelos de variación para tratarlas matemáticamente. 5. Hace inferencias a partir de diagramas, tablas y gráficas que recojan datos de situaciones del mundo real; estima, interpreta y aplica medidas de tendencia central, de dispersión y de correlación. 6. Reconoce fenómenos aleatorios de la vida cotidiana y del conocimiento científico, formula y comprueba conjeturas sobre el comportamiento de los mismos y aplica los resultados en la toma de decisiones. 7. Formula hipótesis, las pone a prueba, argumenta a favor y en contra de ellas y las modifica o las descarta cuando no resisten la argumentación. 8. Planifica colectivamente tareas de medición previendo lo necesario para llevarlas a cabo, el grado de precisión exigido, los instrumentos adecuados y confronta los resultados con las estimaciones. 9. Disfruta y se recrea en exploraciones que retan su pensamiento y saber matemático y exigen la manipulación creativa de objetos, instrumentos de medida y materiales y medios. METAS DE CALIDAD POR GRADO Al finalizar el año escoñar los estudiantes que hayan adquirido los contenidos mínimos establecidos en el currículo estarán en capacidad de: GRADO PRIMERO  Identificará y contará los elementos de conjuntos diversos, clasificándolos y buscándolas semejanzas y relaciones con situaciones de la vida cotidiana.  Desarrollará habilidades lógicas y críticas, mediante nociones y procedimientos de razonamiento elemental, alcanzando la construcción de estructuras matemáticas básicas, la ordenación de datos basado en la posicionalidad del sistema numérico, reconocimiento y definición de figuras geométricas elementales. GRADO SEGUNDO 1. Utilizará las operaciones básicas en situaciones de la vida diaria, identificando el valor posicional, estableciendo relaciones numéricas y espaciales y utilizando conjuntos de datos dentro del círculo numérico del 1000 al 99.999, GRADO TERCERO 1. Situación de la competencia matemática 2. 16 Manejan procesos de pensamiento matemático Que les permiten diseñar sus propias formas de resolver un problema: trazan las estrategias para solucionarlo y reorganizan o transforman los datos. 3. 35 Están en capacidad de resolver problemas que Involucran un sólo tópico (aritmética, geometría, estadística) y tienen toda la información en el enunciado, pero ésta requiere reorganización.
  • 26.
    4. 30 Puedenresolver problemas concretos de un solo tópico cuyo enunciado contiene toda la información en el orden exacto para solucionarlos. GRADO CUARTO 1. Generar una actitud favorable hacia las matemáticas y estimular el interés por su estudio. 2. Obtener los mejores resultados posibles en las pruebas institucionales. 3. Obtener mínimo un promedio de 50 puntos en el área de matemáticas en las pruebas SABER. (50). 4. Reducir al máximo el índice de repitencia en el grado 4º. 5. Orientar los estudiantes para que su trabajo en clase, su capacidad de lenguaje matemático, la excelencia en los trabajos que se realicen y el resultado en las diferentes pruebas pueden llegar a los mejores resultados. 6. Implementar diferentes acciones y/o estrategias preventivas en materia de pérdida, reprobación y/o repitencia GRADO QUINTO 1. Tener un 60% de los estudiantes con capacidad argumentativa coherente. 2. Llegar a un 50% de estudiantes propositivos en las diferentes temáticas trabajadas. 3. Ofrecer una educación de calidad, propiciando espacios de aprendizaje, práctica de valores, lenguaje simbólico e investigación, así como adquirir conceptos y dominio de pensamiento matemático que sean ampliamente aplicables y útiles a diferentes situaciones de la vida diaria y en el desarrollo de la competencia laborales generales. 4. Reducir en un 5% el índice de reprobación en el área de matemáticas. 5. Disminuir en un 1% los índices de deserción escolar de los estudiantes. 6. Fortalecer, con la participación de los estudiantes, los eventos que tradicionalmente organiza el área de matemáticas. 7. El 65%de los estudiantes de la I.E Luis Eduardo Arias Reinel aprendan a desarrollar competencias básicas y específicas del área de matemáticas. GRADO SEXTO 1. Que al culminar el año 2013 los Jóvenes de los grados sextos en un 75% reconozcan, utilicen y solucionen problemas que involucren los números naturales. 2. Reconocer la importancia de averiguar datos y procesar información para tomar decisiones, y evaluar sus características en relación con las decisiones que se tomen. 3. Reconocer características de sólidos, figuras planas y líneas y utilizarlas en su vida cotidiana en trabajos prácticos como mediciones, elaboración de dibujos y construcción de modelos. GRADO SEPTIMO 1. Al culminar el grado séptimo como mínimo el 70% estarán en capacidad de identificar y usar los números enteros y los racionales en diferentes contextos, representaciones de diversas formas y establecer relaciones entre ellos. 2. Redefinir las operaciones básicas en los sistemas formados con los números racionales y decimales y establecer conexiones entre ellas. 3. Los estudiantes estarán en capacidad de investigar y comprender contenidos y procedimientos matemáticos, a partir de enfoques de tratamiento y resolución de problemas y generalizar soluciones y estrategias para nuevas situaciones. 4. Estarán en capacidad de formular inferencias y argumentos coherentes, utilizando medidas de tendencia central y de dispersión para el análisis de los datos, interpretar estadísticos y elaborar críticamente conclusiones. 5. Visualizar, reconocer y efectuar transformaciones de polígonos en el plano y utilizarlas para establecer congruencia, semejanza y simetría entre figuras. 6. Comprender y usar la proporcionalidad directa e inversa de magnitudes, en distintos contextos de la vida cotidiana y utilizar diferentes procedimientos para efectuar cálculos de proporcionalidad.
  • 27.
    GRADO OCTAVO 1. Utilizarestrategias y técnicas simples de resolución de problemas de la vida cotidiana, tales como el análisis del Enunciado, el planteamiento de la situación y la resolución de la misma, con los números reales que conlleva a comprobar la Solución obtenida y así expresarlo en el lenguaje matemático propio de su nivel. 2. Los jóvenes del grado octavo en un 80% al culminar el año puedan reconocer, realizar operaciones básicas, solucionen problemas de la vida diaria con los números reales GRADO NOVENO 1. Organizar e interpretar informaciones diversas mediante tablas y gráficas estadísticas, e identificar relaciones de dependencia en situaciones cotidianas en cuanto a las medidas de tendencia central y las de dispersión. 2. Utilizar estrategias y técnicas simples de resolución de problemas de la vida diaria, tales como el análisis del Enunciado, el planteamiento de la situación y la resolución de la misma, utilizando ecuaciones lineales con dos y tres variables que conlleva a comprobar la Solución obtenida y así expresarlo en el lenguaje matemático propio de su nivel. GRADO DECIMO 1. Tener una aprobación del 95% del área de matemáticas. 2. Tener un manejo mínimo del 60% de los siguientes pensamientos: numérico, métrico, geométrico y aleatorio. 3. Tener un manejo mínimo del 60% en los siguientes temas: - Conversión de ángulos - Triángulos rectángulos - Triángulos oblicuángulos - Ángulos de depresión y elevación - Identidades trigonométricas - Ecuaciones trigonométricas - Secciones cónicas - estadística 4. Hacer incentivos y reconocimientos establecidos y promover el desarrollo del talento estudiantil en el área de las matemáticas en participación de diferentes eventos como: olimpiadas de matemáticas es diferentes instituciones. 5. Realizar una evaluación por periodo y anual de los resultados en el área de matemáticas y establecer metas de mejoramiento futuro. 6. Implementar de manera integral las matemáticas con las demás áreas del conocimiento. 7. Permitir el acceso a INTERNET como herramienta de enseñanza y de aprendizaje en el área de matemáticas como fuente de información para la investigación de tareas y proyectos. 8. 0% de deserción. Buscar estrategias para que sus estudiantes no abandonen las aulas, crear las condiciones y resolver las situaciones para evitar la deserción durante el año escolar. 9. Mantener un alto nivel de Eficiencia Interna dada por los porcentajes anuales de aprobación, repitencia y optimización del tiempo escolar. GRADO UNDECIMO 1. Tener una aprobación del 95% del área de matemáticas.
  • 28.
    2. Tener unmanejo mínimo del 60% de los siguientes pensamientos: numérico, métrico, geométrico y aleatorio. 3. Tener un manejo mínimo del 60% en los siguientes temas: - Secciones cónicas - Estadística descriptiva - Funciones - Concepto de limite formal e informal - Derivación - integración 4. Hacer incentivos y reconocimientos establecidos y promover el desarrollo del talento estudiantil en el área de las matemáticas en participación de diferentes eventos como: olimpiadas de matemáticas es diferentes instituciones. 5. Realizar una evaluación por periodo y anual de los resultados en el área de matemáticas y establecer metas de mejoramiento futuro. 6. Implementar de manera integral las matemáticas con las demás áreas del conocimiento. 7. Permitir el acceso a INTERNET como herramienta de enseñanza y de aprendizaje en el área de matemáticas como fuente de información para la investigación de tareas y proyectos. 8. 0% de deserción. Buscar estrategias para que sus estudiantes no abandonen las aulas, crear las condiciones y resolver las situaciones para evitar la deserción durante el año escolar. 9. Mantener un alto nivel de Eficiencia Interna dada por los porcentajes anuales de aprobación, repitencia y optimización del tiempo escolar. RECURSOS Los recursos son escogidos con la siguiente intencionalidad: Suministrar al área de matemáticas recursos didácticos que generen en los estudiantes una actitud favorable frente al área y que estimulen en ellos el interés por su estudio. Estimular en los estudiantes el uso creativo de las matemáticas para expresar nuevas ideas y descubrimientos, así como para reconocer los elementos matemáticos presentes en otras actividades creativas. Familiarizar a los estudiantes desde temprana edad con el mundo de las matemáticas en una forma analítica, experimental y crítica. Brindar una enseñanza de cada uno de los pensamientos matemáticos basada en la experimentación, el juego y el constructivismo. Después de mencionar las intencionalidades generales que se pretenden alcanzar al utilizar cada uno de los recursos es importante ser específicos y categorizar cada uno de ellos: El material Impreso: donde se pretende hacer uso exclusivo de la biblioteca teniendo como finalidad la realización de actividades pedagógicas como talleres, tareas, entre otras. Además la fotocopiadora se convierte en ese medio tecnológico que permite la multiplicación de guías de trabajo. Material Didáctico: a través del manejo de sólidos, reglas, compás, transportador, bloques lógicos, algunas láminas entre otros materiales que se pueden manipular y que permiten el aprendizaje lúdico. Equipos y Materiales Audiovisuales: esta categoría permite la utilización de las sala de video, donde se puede hacer uso del televisor, los proyectores, entre otros medios todo con el fin de dinamizar el aprendizaje y ampliar los contenidos.
  • 29.
    Programas y ServiciosInformáticos: a futuro se puede hacer uso del aula de Medellín digital pues este recurso proporciona herramientas para mejorar los procesos académicos a partir del uso de las Tics. Materiales impresos 1. Talleres construidos por el docente en base al plan de área de matemáticas, con el eje de situaciones problema. Copias Clases Maestras y documentos creados por los docentes: libros, fotocopias, periódicos, documentos. 2. Textos De Apoyo: Serie Espiral,SerieNova, Serie Santillana,Serie McGraw Hill,entre otros libros que la I.E. disponga en su biblioteca. Materiales didácticos: 1. Escuadras, reglas, transportadores 2. Tangram 3. Pentóminos 4. Domino de fracciones 5. Guías (orientadas desde la Escuela del Maestro) 6. Materiales para niños de transición a 5º de primaria Equipos y materiales audiovisuales: 1. Sala de Proyecciones: Video Beam 2. Sala de Televisión: TV 3. Sala de Informática: PC Programas y servicios informáticos: Servicios telemáticos:páginas web, blogs,tours virtuales,webquest, cazas del tesoro, correo electrónico,chats,foros, unidades didácticasy cursos on-line. Cabri: Para aprender geometría 2. Geogebra 3. Flechas: números y formas. Infantil y primaria 4. Funciones: representa funciones. Postalcardware 5. HungryFrog. Juego para trabajar álgebra básica 6. Módulo para Derive. Puntos, rectas y planos. 7. Las plantas. Infantil y primaria. Reconocimiento de los números 8. Plot3D. Representación gráfica de funciones. 9. Juego con 250 problemas de geometría 10. Primtres. Aritmética y geometría para primaria 11. SerpikGraphs 1.2. Funciones 12. Simetría. Para trabajar las simetrías en infantil y primara 13. UniGraph. Representación de funciones 14. Cantidades. Juego para aprender números y seriaciones. Infantil y primaria. 15. Colores. Juego para familiarizarse con los números. Infantil 16. Trigonometría: Software freeware para trabajar con funciones trigonométricas 17. Programa para aprender el área de figuras planas 18. Programa para resolver ecuaciones de segundo grado 19. Cálculos de geometría. Áreas y volúmenes. 20. KapGram. Juego similar al Tangram 21. El proyecto descartes. 22. Blogs disponibles en Internet en páginas como multiply.com, www.entrepares.com Otros: recursos humanos como los docentes (matemáticas y todas las áreas) y los alumnos. Con recurso físico las instalaciones del colegio, tanto aula como espacios al aire libre. Además se debe involucrar el contexto que rodea a la institución como garante de aprendizajes porque El ambiente educativo no se limita a las condiciones materiales necesarias para la implementación del currículo, cualquiera que sea su concepción, o a las relaciones interpersonales básicas entre maestros y alumnos. Por el contrario, se instaura en las dinámicas que constituyen los procesos educativos y que involucran acciones, experiencias vivencias por cada uno de los participantes; actitudes, condiciones materiales y socio afectivo, múltiples relaciones con el entorno y la infraestructura necesaria para la concreción de los propósitos culturales que se hacen explícitos en toda propuesta educativa.
  • 30.
    4. MALLAS CURRICULARES: INSTITUCIÓNEDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: PRIMERO PERIODO: 1 ESTÁNDAR: Reconozco significados del número en diferentes contextos (medición, conteo, comparación codificación, localización, entre otros). Describo, comparo y cuantifico situaciones con números, en diferentes contextos y con diversas representaciones EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATI VA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué es importante saber contar y conocer las características de los objetos que nos rodean?  Cantidades  Relación de orden  Adición  Sustracción  Situaciones problémicas  Valor posicional  Conjuntos  Clases de líneas  Patrones de medida  Secuencias  Características de los objetos.  Distancia y posición.  Posición y lugar.  Ubicación espacial.  Conjuntos, números del 0 al 9, orden de los números, adición y sustracción de números, problemas de adicción y sustracción y representación en la recta numérica.  Líneas curvas, rectas, abiertas y cerradas,  mediciones, patrones de medida  Secuencias de números y figuras.  Números ordinales.  Comparación y clasificación de pequeñas colecciones de objetos teniendo en cuenta sus cualidades o características.  Ordenamiento y relación de dígitos con la cantidad de elementos.  Organización de objetos y eventos de acuerdo con su posición y patrón de orden.  Establecimiento de relaciones de distancia y ubicación espacial de los objetos: Largo- Corto, alto - bajo, en medio de, dentro – fuera, izquierda – derecha, primero – último.  Interprete situaciones matemáticas aditivas.  Reconozca los números hasta 9 y su valor de posición.  Argumente sobre la solución de una situación o problema presentando y organizando procedimientos lógicos.  Proponga solución a las situaciones problemáticas presentadas.  Prediga y estime resultados numéricos.  Establecimiento de relaciones de orden entre los números.  Reconocimiento de cantidades, utilizando números cardinales y ordinales.  Descubrimiento de que la suma y la resta sirven para resolver problemas.  Encuentro del patrón de cambio en secuencias de objetos diversos y numéricos.  Organización de secuencias utilizando patrones.  Ubicación de objetos en relación con su posición en el espacio.  Realización de graficas utilizando diversos tipos de líneas.   Solución de situaciones problema, utilizando los números para contar y medir.  Aporte de sus conocimientos y capacidades al proceso de conformación de un equipo de trabajo y contribuye al desarrollo de las acciones orientadas.  Expresa sus ideas, sentimientos e intereses en el salón.  escucha respetuosamente a los demás miembros del grupo.
  • 31.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: PRIMERO PERIODO: 2 ESTÁNDAR: Reconozco significados del número en diferentes contextos (medición, conteo, comparación, codificación, localización, entre otros). Describo situaciones o eventos a partir de un conjunto de datos. Describo cualitativamente situaciones de cambio y variación utilizando el lenguaje natural, dibujos y gráficas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué los números tienen diferente nombre y valor? • Cantidades: • El reloj: • El calendario • Adición • Sustracción • Organización de datos. • Eventos seguros • Decenas, docenas, quincena. • Horas, minutos, segundos. • Los días de la semana, los meses del año • Adición de números hasta 99 • Sustracción de números hasta 99 • Números ordenados hasta 99. • Utilice el reloj para medir el tiempo de sucesos cotidianos. • Resuelva situaciones aditivas en el ámbito 0 a 99. • De y siga instrucciones en que aparecen relaciones de distancia y dirección. • Reconocimiento del efecto que tienen las operaciones básicas (suma y resta) sobre los números • Identificación de los atributos mesurables de los objetos y eventos de tiempo en diversas situaciones. • Reconocimiento del calendario con meses y días. • Reconocimiento y manejo del reloj u sus manecillas.  Explicación, desde su experiencia, de la posibilidad o imposibilidad de ocurrencia de eventos cotidianos.  Suma en el ámbito de los números de 0 a 99  Resto en el ámbito de números del 0 a 99.  Solución de problemas con operaciones de suma y resta.  Uso de su experiencia para predecir si algo va a suceder, o la probabilidad de ocurrencia.
  • 32.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: PRIMERO PERIODO: 3 ESTÁNDAR: Describo cualitativamente situaciones de cambio y variación, utilizando el lenguaje natural, dibujos y gráficas. Construyo secuencias numéricas y geométricas, utilizando propiedades de los números y de las figuras geométricas EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento variacional. ¿Cómo realizar operaciones de suma y resta con centenas? • Cantidades: • Lectura y escritura de números. • Adición. • Sustracción • Secuencias. • Sólidos • Figuras planas • La moneda • La centena: • Identificación del orden de números de tres cifras. • Lectura y escritura de números hasta 999. • Comparación de números hasta 999. • Adición sin agrupamiento hasta 999. • Adición agrupando. • Sustracción sin desagrupar. • Sustracción desagrupando. • Identificación de secuencias numéricas y geométricas. • Sólidos geométricos. • Identificación de las características de los objetos en tres dimensiones • Identificación de formas y figuras planas. • El peso colombiano, dólar, euro… Identificación de la moneda colombiana para hacer transacciones. • Identificación de eventos imposibles • Interprete la suma y la resta como operaciones internas de los números naturales y resuelva problemas con esas operaciones. • Explique las características de las figuras geométricas, las compare y las organice por una característica o medida. • Describa lo que cambia y cómo cambia usando dibujos, palabras, números o gráficos. • Identifique correctamente las centenas como aquellas conformadas por 100 unidades o por 10 decenas, logrando con ello mayor y mejor dominio del área. • Reconocimiento de los nombres de los números hasta 999 y sabe cuál es su valor según el lugar que ocupa. • Conteo, y organización de cantidades con tres dígitos y establecimiento de relaciones de orden entre ellos. • Distinción de las características de los objetos en tres dimensiones. • Descripción y señalamiento de los bordes y los vértices en una figura geométrica.  Conteo de números hasta 999.  Resolución de situaciones que requieran adición y sustracción con números de hasta tres dígitos.  Reconocimiento y trazo de diferentes clases de líneas y figuras geométricas.  Organización de datos usando tablas de secuencia.  Análisis y organización de tablas de frecuencia para resolver preguntas planteadas por el grupo de estudiantes.
  • 33.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: PRIMERO PERIODO: 4 ESTÁNDAR: Describo, comparo y cuantifico situaciones con diversas representaciones de los números, en diferentes contextos. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento espacial.  Pensamiento variacional. ¿Cómo seguir contando números después del 999 y en qué orden se clasifica el número 1.000? • La unidad de mil. • Igualdades. • Estimación. • La mitad. • Resolución de problemas con números hasta 1.000. • El centímetro. • El decímetro. • El metro. • Simetría. • Traslación. • Diagrama de barras horizontales, verticales. • Lectura y escritura de las unidades de mil. • Identificación y representación de igualdades. • El centímetro. • El decímetro. • Equivalencia con medidas de longitud. • Noción de simetría. • Traslaciones realizadas sobre objetos. • Estimaciones con suma y resta hasta 1.000. • Repartición de conjuntos en mitades. • Resolución de problemas con números hasta 1000. • Medida de objetos en centímetros. • Medida de objetos en decímetros. • Interpretación y lectura de los diagramas de barras. • Identifique los números hasta el mil para contar, medir, comparar y describir situaciones que requieran solución, logrando con ello un mayor dominio de la matemática. • Interprete situaciones aditivas según la información proporcionada. • Argumente los procedimientos y algoritmos utilizados para resolver una situación presentada. • Proponga solución a los problemas presentados usando los procedimientos matemáticos con creatividad. • Solución a situaciones matemáticas aditivas en el ámbito de los naturales hasta 1.000. • Lectura y análisis de las situaciones presentadas en el ámbito numérico de 0 a 1.000. • Encuentro de los procedimientos y algoritmos correspondientes para dar solución a situaciones presentadas de 0 a 1.000. • Comparación y ordenamiento de objetos de acuerdo con sus tamaños y medidas, utilizando medidas e instrumentos adecuados. • Utilización de los números para contar, medir, comparar y describir situaciones que requieran solución. • Análisis de datos para resolver preguntas. • Utilización de las medidas de longitud y la información de los gráficos en la solución de las situaciones planteadas en clase. • Participación en el desarrollo de las clases. • Escucha respetuosa a los demás miembros del grupo
  • 34.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SEGUNDO PERIODO: 1 ESTÁNDAR: Reconozco significados del número en diferentes contextos (medición, conteo, comparación, codificación, localización, entre otros). Describo situaciones o eventos a partir de un conjunto de datos. Reconozco y describo regularidades y patrones en distintos contextos (numérico, geométrico, musical, entre otros). Describo cualitativamente situaciones de cambio y variación utilizando el lenguaje natural, dibujos y gráficas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento Numérico y Sistemas Numéricos  Pensamiento Aleatorio y Sistemas de Datos  Pensamiento Variacional y Sistemas Algebraicos y Analíticos ¿Por qué es indispensable que el hombre ubique adecuadamente el valor posicional de un número?  Conjuntos – subconjuntos.  Propiedades y relaciones de conjuntos  Unidad, decena centena, unidades de mil.  Composición de números.  Valor posicional.  Datos en pictogramas.  Diferencias entre un conjunto y un subconjunto.  Reconocimiento y ubicación de unidades, decenas centenas, en números de tres cifras.  Adición y sustracción con y sin agrupación.  Análisis de datos presentados en pictogramas. • Diferencie entre un conjunto y un subconjunto. • Reconozca y ubique las unidades, decenas, centenas, en números de tres cifras. • Sume y reste con y sin agrupación • Valore las operaciones básicas y las propiedades de la adición y sustracción. • Clasifique y organice datos reales de acuerdo con sus cualidades y atributos; describiendo situaciones o eventos a partir de estos, explicando la posibilidad o imposibilidad desde su experiencia cotidiana. • Análisis de las características comunes entre elementos para formar conjuntos. • Ampliación del concepto de suma mediante la composición de números hasta 1.000. • Utilización de la información presentada en pictogramas para solucionar problemas de la vida cotidiana. • Expresión del significado de una unidad, decena, centena. • Establecimiento de relaciones de pertenencia entre un elemento y un conjunto. • Reconocimiento y utilización de los números naturales y ordinales en diferentes situaciones de la cotidianidad. • Resolución de ejercicios en donde se combinan operaciones de adición y sustracción. • Aporte de sus conocimientos y capacidades al proceso de conformación de un equipo de trabajo y contribuye al desarrollo de las acciones orientadas. • Expresión de sus ideas, sentimientos e intereses en el salón. • Cumplimiento de las reglas básicas del diálogo. • Resolución de conflictos con los demás de manera pacífica. • Presentación de sus trabajos en forma clara y ordenada.
  • 35.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SEGUNDO PERIODO: 2 ESTÁNDAR: Reconozco significados del número en diferentes contextos (medición, conteo, comparación, codificación, localización, entre otros). Resuelvo y formulo problemas aditivos de composición y transformación (Pensamiento numérico y sistemas numéricos) Reconozco en los objetos propiedades o atributos que se puedan medir (longitud, área, volumen, capacidad, peso y masa) y, en l os eventos, su duración. Clasifico, organizo e interpreto datos de acuerdo a cualidades y atributos y los presento en tablas. Reconozco y genero equivalencias entre expresiones numéricas y describo cómo cambian los símbolos aunque el valor siga igual. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Cómo beneficia al hombre el conocer las medidas de longitud, superficie y tiempo?  Números hasta el 99.999  Comparación y descomposición entre números  Adición y sustracción  Medidas de longitud, superficie y tiempo  Lectura y escritura de números de 5 cifras.  Orden, comparación, composición y descomposición de secuencias numéricas y geométricas.  Suma y resta agrupando y desagrupando  Ejercicios con unidad de medida de longitud, de superficie y de tiempo.  Propiedades de la adición y sustracción.  Lea y escriba números de 5 cifras.  Ordene, compare, componga y descomponga secuencias numéricas y geométricas.  Calcule sumas y restas agrupando y desagrupando.  Solucione ejercicios con unidad de medida de longitud, de superficie y de tiempo.  Valore las operaciones básicas y las propiedades de la adición y sustracción. • Valore la adición como sistema de resolución de situaciones reales que impliquen agrupar. • Reconocimiento de la cantidad que representa un número de 5 cifras. • Composición y descomposición de números de 5 cifras. • Resolución de adiciones y sustracciones. • Conocimiento de la unidad de medida de tiempo y superficie.  Ubicación de números de 5 cifras en la tabla de posición.  Establecimiento d relaciones de orden entre números de 5 cifras.  Planteamiento y solución de problemas que involucran situaciones aditivas.  Uso del centímetro, el decímetro y el metro como unidades de medida y longitud. • Expresión de sus ideas, sentimientos e intereses en el salón. • Escucha respetuosa a los demás miembros del grupo. • Participación con responsabilidad en las actividades individuales y grupales. • Resolución de los conflictos con los demás de manera pacífica.
  • 36.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SEGUNDO PERIODO: 3 ESTÁNDAR: Reconozco propiedades de los números (ser par, ser impar, etc.) y relaciones entre ellos (ser mayor que, ser menor que, ser múltiplo de, ser divisiblepor, etc.) en diferentes contextos. Uso diversas estrategias de cálculo (especialmente cálculo mental) y de estimación para resolver problemas en situaciones aditivas y multiplicativas. Realizo construcciones y diseños utilizando cuerpos y figuras geométricas tridimensionales y dibujos o figuras geométricas bidimensionales. Reconozco en los objetos propiedades o atributos que se puedan medir (longitud, área, volumen, capacidad, peso y masa) y, en los eventos, su duración. Represento datos relativos a su entorno usando objetos concretos, pictogramas o diagrama de barras EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATI VA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Qué importancia tiene para el hombre el usar diversas estrategias de cálculo y representación de sus resultados?  La multiplicación:  Sólidos y figuras geométricas.  Gráficas de barras:  Relación entre adición y multiplicación.  Propiedades de la multiplicación.  Procedimiento para el cálculo de productos.  Diferencias entre sólidos geométricos y figuras planas.  Los datos en las gráficas de barras. • Relacione la adición y la multiplicación. • Aplique las propiedades de la multiplicación. • Calcule productos. • Diferencie entre sólidos geométricos y figuras planas. • Acepte de buen agrado, las opiniones ajenas, valorándolas críticamente. • Grafique e interprete información en diagramas de barras. • Reconocimiento del signo equis (X), el asterisco (*) y el punto (.) como operadores o signos de la multiplicación. • Comparación de la multiplicación como una adición de sumandos iguales. • Identificación de las figuras planas y los cuerpos geométricos. • Graficación de información en diagramas de barras. • Interpretación de la información dada en un diagrama de barras. • Realización de multiplicaciones por una cifra. • Resolución de ejercicios con los factores dados. • Graficación de sólidos geométricos y figuras planas. • Ubicación de información en diagramas de barras. • Aporte de sus conocimientos y capacidades al proceso de conformación de un equipo de trabajo y contribuye al desarrollo de las acciones orientadas. • Expresión de sus ideas, sentimientos e intereses en el salón. • Escucha respetuosa a los demás miembros del grupo. • Aceptación de buen agrado, las opiniones ajenas, valorándolas Críticamente. • Uso de los diagramas de barras para interpretar situaciones de la vida real.
  • 37.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SEGUNDO PERIODO: 4 ESTÁNDAR: Resuelvo y formulo problemas en situaciones de variación proporcional. Represento datos relativos a mi entorno usando objetos concretos, pictogramas y diagramas de barras. Resuelvo y formulo preguntas que requieran para su solución coleccionar y analizar datos del entorno próximo Construyo secuencias numéricas y geométricas utilizando propiedades de los números y de las figuras geométricas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué las matemáticas se integran con otras áreas del saber y en nuestra vida diaria?  División  Estadística y probabilidad.  Permutaciones y combinaciones de elementos.  Calculo de cocientes.  Prueba de la división.  Calculo de la división,  La mitad, tercera, cuarta parte de una cantidad.  Clasificación de datos en tablas estadísticas.  Clases de división, términos de la división • Calcule cocientes. • Realice la prueba de divisiones. • Calcule la mitad, tercera, cuarta parte de una cantidad. • Clasifique datos en tablas estadísticas. • Reconozca las combinaciones y las permutaciones de diferentes elementos. • Encuentre la forma como se ordenan diferentes objetos. • Reconocimiento de la división como una distribución en partes iguales. • Diferenciación de la división exacta e inexacta. • Interpretación de datos representados en un diagrama. • Reconocimiento de combinaciones de diferentes elementos. • Realización de divisiones exactas con dividendo hasta de 3 cifras. • Aplicación del algoritmo de la división. • Clasificación de divisiones exactas e inexactas.  Realización de tablas y gráficos utilizando la información.  Elaboración de diferentes permutaciones de elementos:  Aporte de sus conocimientos y capacidades al proceso de conformación de un equipo de trabajo y contribuye al desarrollo de las acciones orientadas.  Escucha respetuosa a los demás miembros del grupo. • Interés manifestado por desarrollar y conocer elementos nuevos o más  complejos.
  • 38.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: TERCERO PERIODO: 1 ESTÁNDAR: Reconozco propiedades de los números (ser par, ser impar, etc.) y relaciones entre ellos (ser mayor que, ser menor que, ser múltiplo de, ser divisiblepor, etc.) en diferentes contextos. Realizo construcciones y diseños utilizando cuerpos y figuras geométricas tridimensionales y dibujos o figuras geométricas bidimensionales. Realizo estimaciones de medidas requeridas en la resolución de problemas relativos particularmente a la vida social, económica y de las ciencias. Represento datos relativos a mi entorno usando objetos concretos, pictogramas y diagramas de barras. Describo cualitativamente situaciones de cambio y variación utilizando el lenguaje natural, dibujos y gráficas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué el hombre a través de la historia se ha interesado en representar de diversas formas sus conocimientos?  Sistema de numeración Romana.  Números de cinco dígitos.  Múltiplos y submúltiplos  Datos pictográficos.  Formas y figuras • Orden de objetos. • Formas de figuras. • Las tablas de multiplicar de doble entrada hasta el 12. • Solución de problemas • Normas de comportamiento cotidianos. • Recolección, interpretación, tabulación y traficación de datos pictográficos. • Construcción las tablas de multiplicar de doble entrada hasta el 12. • Identificación el sistema de numeración romana. • Organización y representación de datos en tablas y gráficos. • Realización de traslaciones y rotaciones de figuras. • Identificación de las características de algunas formas y figuras, y establece relaciones entre ellas. • Formulación y solución de problemas sencillos de la cotidianidad, utilizando las operaciones básicas. • Reconocimiento del sistema de numeración romano y lo compara con el sistema de numeración decimal. • Identificación de las características de los números hasta de cinco dígitos. • Explicación del antecesor y el sucesor de un elemento en una secuencia y el establecimiento de relaciones entre ellos. • Representación e interpretación de pictogramas a partir de un conjunto de datos. • Construcción y aplicación de las tablas de multiplicar hasta el doce. • Aplicación de los múltiplos y submúltiplos en diferentes situaciones de la vida. • Elaboración de traslaciones y rotaciones para crear nuevas figuras del Entorno. • Formulación y resolución de problemas que requieran el uso de la suma, la resta, la multiplicación y la división. • Respeto a las reglas básicas del dialogo. • Resolución de los conflictos con los demás de manera pacífica y/o respetuosa.
  • 39.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: TERCERO PERIODO: 2 ESTÁNDAR: Uso diversas estrategias de cálculo (especialmente cálculo mental) y de estimación para resolver problemas en situaciones aditivas y multiplicativas. Identifico regularidades y propiedades de los números utilizando diferentes instrumentos de cálculo (calculadoras, ábacos, bloques, etc.). Reconozco nociones de horizontalidad, verticalidad, paralelismo y perpendicularidad en distintos contextos y su condición relativa con respecto a diferentes sistemas de referencia. Realizo estimaciones de medidas requeridas en la resolución de problemas relativos particularmente a la vida social, económica y de las ciencias. Clasifico y organizo datos de acuerdo a cualidades y atributos y los presento en tablas. EJE GENERADOR PREGUNTA PROBLEMATIZAD ORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Por qué es importante para el hombre aprender a analizar y resolver problemas? • Datos pictogramas. • Problemas de adición y sustracción desagrupar y agrupando. • Ángulos y triángulos. • La suma y sus propiedades. • Conteo y probabilidad. • Multiplicació n y división. • Medición de objetos del entorno. • Medición del tiempo y el espacio. • Realización de repartos. • Calculo mental con operaciones de suma, resta, multiplicaron y división. • Normas de comportamie nto. • Interpretación de información representada en pictogramas. • Identificación de situaciones cuya solución requiera de la adición y la sustracción. • Identificación y aplicación de las propiedades de la adición o suma. • Realización de sustracciones agrupando y desagrupando. • Identificación y aplicación de los conceptos de ángulos y triángulos. • Solución de operaciones de multiplicación y división por una cifra. • Construcción e identificación de ángulos y triángulos de acuerdo con sus características. • Aplicación de la propiedad conmutativa y asociativa de la suma en la resolución de diferentes problemas. • Identificación de datos como elementos que adquieren significado, cuando ofrecen información confiable de un contexto dado. • Resolución de situaciones planteadas en pictogramas. • Medición y establecimiento de congruencias y semejanzas entre varios objetos. • Utilización y establecimiento de relaciones entre las medidas de longitud, de superficie y de tiempo. • Interpretación y resolución de situaciones por medio del algoritmo de la multiplicación y la división. • Desarrollo de habilidades de cálculo mental en la resolución de problemas. • Utilización de la información presentada en pictogramas para solucionar problemas de la vida cotidiana. • Respeto por los aportes propios y de los demás. • Cooperación en las actividades propuestas en clase.
  • 40.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: TERCERO PERIODO: 3 ESTÁNDAR: Identifico regularidades y propiedades de los números utilizando diferentes instrumentos de cálculo (calculadoras, ábacos, bloques multibase, etc.). Represento el espacio circundante para establecer relaciones espaciales. Realizo construcciones y diseños utilizando cuerpos y figuras geométricas tridimensionales y dibujos o figuras geométricas bidimensionales Reconozco en los objetos propiedades o atributos que se puedan medir (longitud, área, volumen, capacidad, peso y masa) y, en los eventos, su duración. Comparo y ordeno objetos respecto a atributos medibles. EJE GENERADOR PREGUNTA PROBLEMATIZA DORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Cómo realizar procesos de medición con patrones arbitrarios y estandarizados?  Clases de división:  Equivalencia entre Medidas.  Gráficos:  Ubicación en el espacio:  Área y perímetro  Números primos y compuestos, operaciones combinadas • Exacta e inexacta. • Aplicación de la división • Volumen, capacidad, peso • Diagramas de barra. • Arriba, abajo, centro, afuera, derecha, izquierda, adelante, atrás, zurdo, diestro. • Reglas básicas del diálogo. • Identificación y aplicación de las clases de división. • Reconocimiento de la noción de volumen, peso y capacidad en objetos de su entorno. • Formulación y solución de problemas de multiplicación y división. • Descripción de los conceptos de espacio y tiempo en su contexto. • Identificación y clasificación de números primos y compuestos. • Determinación del m.c.m. y el m.c.d de dos o más números. • Identificación y aplicación de los conceptos de área y perímetro. • Reconocimiento de la división exacta e inexacta. • Indagación del área y el perímetro de figuras geométricas y de objetos del entorno. • Descripción de la posición de un objeto con relación a un punto en el espacio. • Identificación de números primos y compuestos. • Comparación, medición y relación de diferentes elementos, utilizando medidas de capacidad, volumen y peso • Planteamiento y resolución de problemas que requieran de la división. • Elaboración de diagramas de barras para representar y analizar datos. • Escritura de los submúltiplos de un número dado. • Encuentro el m.c.d entre dos números • Resolución de los conflictos con los demás de manera pacífica. • Respeto de las reglas básicas del diálogo.
  • 41.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: TERCERO PERIODO: 4 ESTÁNDAR: Describo situaciones de medición utilizando fracciones comunes. Reconozco propiedades de los números (ser par, ser impar, etc.) y relaciones entre ellos (ser mayor que, ser menor que, ser múltiplo de, ser divisible por, etc.) en diferentes contextos. Resuelvo y formulo problemas en situaciones de variación proporcional. Reconozco y genero equivalencias entre expresiones numéricas y describo cómo cambian los símbolos aunque el valor siga igual. EJE GENERADOR PREGUNTA PROBLEMATIZA DORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento aleatorio.  Pensamiento variacional. ¿Qué actividades puedo realizar para ayudar a mejorar la economía familiar y escolar de mi comunidad? • División por una y dos cifras en el divisor. • Fracciones como parte de la unidad. • Estadística, azar y probabilidad. • El ahorro. • Números primos y compuestos. • Operaciones combinadas. • Prueba de la división. • Cálculo de la división, la mitad, tercera, cuarta parte de una cantidad. • Clasificación de datos en diagramas horizontales. • Azar, probabilidad. • Partes fraccionadas de un conjunto, fracciones homogéneas. Orden de las fracciones, equivalentes. • Adición y sustracción de fracciones, problemas con fracciones. • La cooperación. • Realización y prueba de divisiones de una y dos cifras en el divisor. • Identificación y representación del concepto de fracciones. • Identificación y aplicación de las clases de fracciones. • Reconocimiento de la división como mitad, tercera o cuarta parte de una cantidad. • Formulación de problemas cuya solución involucran la multiplicación y la división. • Realización de adiciones y sustracciones con fracciones. • Realización de congruencias y semejanzas entre cuerpos y figuras geométricas. • Comprensión y empleo correcto de las fracciones en diferentes situaciones. • Establecimiento de relaciones de congruencia, semejanza y diferencia entre figuras y cuerpos sólidos. • Ejecución de sumas y restas de fracciones homogéneas, con el fin de interpretar y argumentar la solución de diversas situaciones. • Construcción de diferentes sólidos geométricos a partir de diseños. • Creación de diseños utilizando la ampliación y reducción de figuras. • Organización y comparación de datos en diagramas de barras horizontales. • Aplicación del concepto de probabilidad en la solución de problemas. • Respeto de las reglas básicas del diálogo. • Resolución de los conflictos con los demás de manera pacífica. • Manifestación de conciencia del valor del ahorro a través de la creación de su alcancía.
  • 42.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL. MALLAS CURRICULARES MATEMÁTICAS. GRADO: CUARTO PERIODO: 1 ESTÁNDAR: Resuelvo y formulo problemas cuya estrategia de solución requiera de las relaciones y propiedades de los números naturales y sus operaciones. Comparo y clasifico figuras bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. Identifico, represento y utilizo ángulos en giros, aberturas, inclinaciones, figuras, puntas y esquinas en situaciones estáticas y dinámicas. Construyo y descompongo figuras y sólidos a partir de condiciones dadas. EJE GENERADOR PREGUNTA PROBLEMATIZA DORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial. ¿Qué importancia tiene para el hombre aprender a diferencias figuras bidimensionales y tridimensionales ? • Relaciones de los números naturales: • Objetos geométricos de dos y tres dimensiones: • Múltiplos y divisores, Mínimo Común Múltiplo, Máximo Común Divisor, Criterios de divisibilidad. Números naturales de más de seis cifras y operaciones básicas con ellos. • Componentes de los objetos tridimensionales (caras, lados). • Componentes de las figuras bidimensionales (ángulos, vértices). • Propiedades de los objetos geométricos. • Ejercicios de transformación de objetos bidimensionales dando cuenta de las relaciones y diferencias entre ellas. • -Identificar y representar los números naturales explicando su aplicación en la solución de situaciones de la vida cotidiana. • -Usar significativamente los conocimientos geométricos para solucionar problemas. • -Utilizar y proponer estrategias de cálculo y de estimación para resolver situaciones donde es necesario la aplicación de las operaciones básicas (suma, resta, multiplicación y división). • -Descomponer números naturales en factores primos y/o divisores. • -Hallar el M.C.M y M.C.D. entre números. • Identificar y relacionar los componentes de una figura bidimensional (ángulos y vértices). • -Diferenciar los componentes que tiene un objeto tridimensional y uno bidimensional. • -Transformar objetos bidimensionales dando cuenta de las relaciones y diferencias entre ellas. • -Estimación de resultados en operaciones básicas de: suma, resta, multiplicación y división con números naturales. • -Reconocimiento del M.C.M y M.C.D. • -Identificación y relación entre los componentes de una figura bidimensional (ángulos y vértices) • -Identificación y relación entre los componentes de una figura bidimensional (ángulos y vértices) • -Diferenciación de los componentes que tiene un objeto tridimensional y uno bidimensional. • -Descomposición de números naturales en factores primos y/o divisores. • -Construcción y clasificación de objetos geométricos. • -Elaboración de figuras bidimensionales y tridimensionales. • -Cumplimiento y organización en la elaboración y entrega de los trabajos propuestos. • -Interés por indagar y dar respuesta a las preguntas. • -Interés por aprender sobre los números naturales y sus operaciones. • -Valoración del aprendizaje de las operaciones básicas. • -Perseverancia en la construcción de objetos geométricos. • -Reconocimiento de la importancia que tiene el uso de los números naturales y sus propiedades en la vida diaria.
  • 43.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: CUARTO PERIODO: 2 ESTANDAR: Interpreto las fracciones en diferentes contextos: situaciones de medición, relaciones parte todo, cociente, razones y proporciones. Utilizo la notación decimal para expresar fracciones en diferentes contextos y relaciono estas dos notaciones con la de los porcentajes. Comparo y clasifico objetos tridimensionales de acuerdo con componentes (caras, lados) y propiedades. Comparo y clasifico figuras bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. Construyo objetos tridimensionales a partir de representaciones bidimensionales y puedo realizar el proceso contrario en contextos de arte, diseño y arquitectura EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DELOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamient o numérico.  Pensamient o espacial. ¿Por qué en el mundo actual el hombre maneja cantidades con fracciones y decimales? • Números fraccionarios: • Números decimales: • Objetos geométricos de dos y tres dimensiones: • Interpretación del número fraccionario como partidor, medidor y porcentaje. • Equivalencia de fracciones. • Fracciones decimales. • Fracciones Mixtas. • Conceptualización de Fracciones propias e impropias. • Conceptualización sobre 1implificación y amplificación. • Adición y sustracción de fracciones. • Potencias de 10. • Concepto del número decimal y su forma de expresarlo. • Componentes de los • objetos tridimensionales • (Caras, lados). • Propiedades de los objetos geométricos. • Polígonos regulares e irregulares. • El círculo y la • circunferencia: • Partes del círculo y elementos de la circunferencia. • -Explicar del cómo y el porqué de los procesos que se siguen para llegar a conclusiones apoyándose en estrategias a nivel matemático. • -Diferenciar las distintas clases de fracciones y su representación para interpretarlas en contexto. • -Utilizar significativamente los conocimientos geométricos para solucionar problemas. • -Identificar características tangibles de objetos del entorno estableciendo relaciones con los elementos de los cuerpos geométricos. • -Identificación de la fracción como partidor y medidor estableciendo relaciones de ella con el porcentaje. • -Interpretación de problemas de adicción y sustracción utilizando fracciones y decimales. • -Comprensión de las diferencias que hay entre círculo y circunferencia. • -Comparación de números decimales. • -Diferenciación de los componentes que tiene un objeto tridimensional y uno bidimensional. • -Diferenciación entre polígonos regulares e irregulares. • -Comparación entre objetos geométricos a través de la congruencia y • -Simplificación y amplificación de fracciones. • -Realización de operaciones básicas (suma, resta, multiplicación y división) con números fraccionarios. • -Expresión oral y escrita del número decimal a partir de las potencias de 10. • Realización de adiciones y sustracciones entre números naturales y decimales. • -Diseños de objetos con • -Disposición para realizar el trabajo propuesto dentro y fuera del aula. • -Respeto y valoración por el trabajo propio y el de los demás. • -Cumplimiento y organización en la elaboración y entrega de los trabajos propuestos. • -Interés por indagar y dar respuesta a las preguntas. • -Valoración sobre los conocimientos relacionados con la geometría
  • 44.
    semejanza. círculos. INSTITUCIÓN EDUCATIVALUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: CUARTO PERIODO: 3 ESTÁNDAR: Construyo objetos tridimensionales a partir de representaciones bidimensionales y puedo realizar el proceso contrario en contextos de arte, diseño y arquitectura Reconozco el uso de algunas magnitudes (longitud, área, volumen, capacidad, peso y masa, duración, rapidez, temperatura) y de algunas de las unidades que se usan para medir cantidades de la magnitud respectiva en situaciones aditivas y multiplicativas. Describo y argumento relaciones entre el perímetro y el área de figuras diferentes, cuando se fija una de estas medidas. Describo e interpreto variaciones representadas en gráficos. Construyo igualdades y desigualdades numéricas como representación de relaciones entre distintos datos. EJE GENERADOR PREGUNTA PROBLEMATIZA DORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio. ¿Qué beneficio le da el hombre al conocimiento que tiene de las unidades de medidas? • Objetos geométricos de dos y tres dimensiones: • Magnitudes: • La noción de ecuación e igualdad. • Secuencias : • Propiedades de los objetos geométricos.: Transformaciones: simetría, rotación y reflexión. • Conceptualización del concepto de congruencia y semejanza. • Perímetro, Concepto de área y superficie. Unidades de medida: De longitud y área. Propiedades o atributos medibles con magnitudes discretas. • La letra como incógnita. • Patrones y regularidades. • Secuencias numéricas y Geométricas. • -Reconocer las propiedades de los objetos geométricos. • -Realizar y explicar las transformaciones al momento de manipular los objetos bidimensionales. • -Diferenciar los conceptos de congruencia y semejanza en objetos bidimensionales. • -Plantear y resolver problemas relacionados con las magnitudes perímetro y área. • -Reconocer y utilizar el metro cuadrado como la unidad de área en situaciones cotidianas. • -Identificar y relacionar una expresión numérica con el concepto de ecuación. • • -Diferenciación entre polígonos regulares e irregulares. • -Comparación entre objetos geométricos a través de la congruencia y semejanza. • -Reconocimiento de los atributos medibles en los objetos geométricos a través de ejercicios. • -Identificación y diferenciación del papel de la letra cuando es una incógnita. • -Predicción de patrones utilizando secuencias numéricas y geométricas. • -Transformación de objetos bidimensionales dando cuenta de las relaciones y diferencias entre ellas. • -Resolución de problemas con modelos geométricos. • Medición de objetos del entorno, utilizando diferentes unidades de medida. • -Construcción de objetos geométricos con medidas específicas. • -Construcción de ecuaciones sencillas a partir de ejemplos cotidianos. • -Aplicación de modelos para hallar el perímetro y área de polígonos regulares e irregulares. • -Participación activa durante el desarrollo de las actividades propuestas. • -Interés para el cumplimiento del trabajo propuesto. • -Reconocimiento de sus errores y aprender a corregirlos. • -Cumplimiento y organización en la elaboración y entrega de los trabajos propuestos. • -Interés por indagar y dar respuesta a las preguntas
  • 45.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: CUARTO PERIODO: 4 ESTÁNDAR: Interpreto y represento información presentada en tablas y gráficas. (Pictogramas, gráficas de barras, diagramas de líneas, diagramas circulares). Resuelvo y formulo problemas a partir de un conjunto de datos provenientes de observaciones, consultas o experimentos. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio. ¿Cómo los rangos de variación me permiten conocer e intervenir con más acierto en la solución de problemas? • Magnitudes: • Patrones y regularidades. • Secuencias numéricas y Geométricas. • Interpretación de información: • Conceptualización de: Media (o promedio) y mediana. • Magnitudes discretas. • Propiedades o atributos medibles con magnitudes discretas. • Nociones de masa, temperatura y capacidad. • Conjunto de datos. • Variables cuantitativas y cualitativas. • Sistemas de • representación gráficos: Pictogramas, gráficas de • barras, diagramas • circulares. • Sistematización de datos. • -Predecir patrones utilizando secuencias numéricas y geométricas. • -Representar información en pictogramas, gráficas de barras y diagramas circulares. • -Recolectar, organizar, registrar y analizar información en tablas datos. • -Reconocimiento de las nociones de masa y capacidad en objetos de su entorno. • -Interpretación de la noción de temperatura en situaciones cotidianas. • -Interpretación de datos de una información estadística y utilizarlos significativamente. • -Comparación y establecimiento de diferencias entre la Media (o promedio) y la Mediana. • -Explicación del por qué una magnitud es o no discreta. • -Realización de diagramas para representar la información más relevante. • -Proposición de secuencias numéricas o geométricas estableciendo un patrón para su construcción • -Realización de forma organizada y responsable el trabajo que se le propone en el área. • -Organización al momento de leer e interpretar la información. • -Cumplimiento y organización en la elaboración y entrega de los trabajos propuestos.
  • 46.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: Quinto PERIODO: 1 ESTÁNDAR: Justifico el valor de posición en el sistema de numeración decimal en relación con el conteo recurrente de unidades. Represento datos usando tablas y gráficas (pictogramas, gráficas de barras, diagramas de líneas, diagramas circulares). Resuelvo y formulo problemas a partir de un conjunto de datos provenientes de observaciones, consultas o experimentos. Predigo patrones de variación en una secuencia numérica, geométrica o gráfica. Construyo igualdades y desigualdades numéricas como representación de relaciones entre distintos datos. EJE GENERADOR PREGUNTA PROBLEMATIZAD ORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS EINDICADORES DELOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento variacional ¿Por qué desarrollo mi intuición y pensamiento lógico a través de ejercicios de equivalencias y relaciones? • Números decimales: • Equivalencias y relaciones: • La recta numérica: • Objetos planos: • Patrones numéricos: • Representaci ón de gráficas: • Conceptualización del Sistema de numeración decimal. • Equivalencia y relaciones entre números fraccionarios y decimales. • La recta numérica. • Objetos planos y sus componentes (ángulos, vértices). • Patrones numéricos utilizando diversas secuencias. • Gráficas de barras y diagramas circulares. • Utilice y proponga estrategias de cálculo y de estimación para resolver situaciones donde es necesario la aplicación de las estructuras aditivas y multiplicativas. • Use significativamente los conocimientos geométricos para solucionar problemas. • Formule preguntas, respuestas y conjeturas coherentes a interrogantes de ¿por qué?, ¿dónde? y ¿cuándo? en situaciones problémicas propias de las matemáticas; tanto en forma oral como escrita. • Exponga sus ideas, sentimientos e intereses dando cuenta de su capacidad de escucha, respeto y tolerancia frente a los pensamientos e intereses de los demás miembros del grupo. • Elija y lleve a la práctica diferentes estrategias que le permiten la solución de situaciones del diario vivir. • Represente datos, los compare en diferentes representaciones, y los interprete a través de diagramas de barras, de líneas y circulares, formando conjeturas a través de formular y resolver problemas a partir de un conjunto de datos provenientes de la observación, la • Reconocimiento de las propiedades y relaciones del sistema de numeración decimal. • Reconocimiento y explicación de las relaciones existentes entre los componentes de los objetos tridimensionales y bidimensionales, sus ángulos y vértices. • Reconocimiento y planteamiento de patrones numéricos en secuencias dadas. • Realización de diagramas de barras y circulares para representar la información más relevante. • Aplicación de las propiedades del sistema de numeración decimal con el conjunto de los números naturales. • Conversión de números fraccionarios a decimales y viceversa. • Desarrollo de operaciones básicas (suma, resta, multiplicación y división) entre números fraccionarios, naturales y decimales. • Ubicación y representación de números naturales, fraccionarios y decimales en la recta numérica. • Realización de forma organizada y responsable del trabajo que se le propone en el área. • Respeto y valoración por el trabajo propio y el de los demás. • Valoración del aprendizaje de las operaciones básicas. • Valoración sobre los conocimientos relacionados con la geometría.
  • 47.
    experimentación y laconsulta. INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: QUINTO PERIODO: 2 ESTÁNDAR: Identifico la potenciación y la radicación en contextos matemáticos y no matemáticos Comparo y clasifico figuras Bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. Conjeturo y pongo a prueba predicciones acerca de la posibilidad de ocurrencia de eventos. Predigo patrones de variación en una secuencia numérica, geométrica o gráfica. EJE GENERADOR PREGUNTA PROBLEMATI ZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico. ¿Cómo el logaritmo transforma un producto en una suma, un cociente en una resta, una potencia en una multiplicación sencilla y una raíz en una división sencilla? • Potenciación, Radicación y Logaritmación: • Objetos geométricos de dos y tres dimensiones: • Conceptualización de la Potenciación. • Radicación y Logaritmación. Potencias y raíces cuadradas y cúbicas. • Logaritmación. • Objetos planos y sus componentes (ángulos, vértices). • Relaciones Intra-figurales e Inter-figurales en los objetos geométricos. • Propiedades de los Polígonos (cuadriláteros y triángulos). • Transformaciones en el plano: Rotación, Traslación, Simetría, Homotecia. • Relaciones de congruencia y semejanza. • Identifique la potenciación y la radicación en contextos matemáticos y no matemáticos. • Justifique regularidades y propiedades de los números, sus relaciones y operaciones. • Compare y clasifique figuras bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. • Prediga patrones de variación en una secuencia numérica, geométrica o gráfica. • Identificación de las potencias cuadradas y cúbicas en un número natural. • Identificación de las raíces cuadradas y cúbicas en un número natural. • Diferenciación de los componentes que tiene un objeto tridimensional y uno Bidimensional. • Diferenciación de los conceptos de congruencia y semejanza al momento de trabajar con objetos geométricos. • Reconocimiento y explicación de las relaciones existentes entre los componentes de los objetos tridimensionales y bidimensionales. • Construcción y clasificación de objetos geométricos. • Resolución de problemas utilizando representaciones con polígonos. • Realización de movimientos de figuras planas en el plano cartesiano. • Resolución de problemas con modelos geométricos. • Aplicación del concepto de congruencia utilizando la simetría entre figuras bidimensionales. • Disposición para realizar el trabajo propuesto dentro y fuera del aula. • Respeto y valoración por el trabajo propio y el de los demás. • Interés por indagar y dar respuesta a las preguntas. • Perseverancia en la • construcción de objetos geométricos. • Valoración sobre los conocimientos relacionados con la geometría.
  • 48.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: QUINTO PERIODO: 3 ESTÁNDAR: Interpreto las fracciones en diferentes contextos: situaciones de medición, relaciones parte todo, cociente, razones y proporciones. Reconozco el uso de algunas magnitudes (longitud, área, volumen, capacidad, peso y masa, duración, rapidez, temperatura) y de algunas de las unidades que se usan para medir cantidades de la magnitud respectiva en situaciones aditivas y multiplicativas. Construyo igualdades y desigualdades numéricas como representación de relaciones entre distintos datos. EJE GENERADOR PREGUNTA PROBLEMATIZAD ORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento métrico.  Pensamiento aleatorio. ¿P ara qué me sirve resolver ecuaciones o pensar? • Números fraccionarios: • Magnitudes: • Diagramas circulares • El número fraccionario como porcentaje. Equivalencia y relaciones entre números fraccionarios y decimales. • Multiplicación y divisiónde fracciones. • Magnitudes: Área y superficie. Volumen y capacidad. Relaciones entre área y volumen. • Nociones de masa, temperatura y capacidad. • Razón, Proporcionalidad simple y compuesta. Ecuación lineal. • Análisis de información en diagramas. • Reconoce fracciones y números decimales. • Aplique algoritmos para hacer operaciones con decimales y resuelva situaciones que requieren el uso de decimales. • Identifique la variación en una secuencia geométrica o en una secuencia numérica. • Interpreto el significado de una fracción decimal como porcentaje. • Represente información en diagramas circulares. • Analice información presentada en diagramas circulares. • Resuelva situaciones que requieren analizar información en diagramas circulares • Aplicación de modelos para hallar el volumen y la capacidad de algunos objetos geométricos. • Identificación del uso de las magnitudes masa, temperatura o capacidad. • Desarrollo de operaciones básicas con números fraccionarios. • Lectura y escritura de porcentajes en problemas cotidianos. • Conversión de números fraccionarios a decimales y viceversa. • Solución de problemas sencillos utilizando el concepto de razón. • Desarrollo de ejercicios de identificación de la proporcionalidad simple o compuesta. • Participación activa durante el desarrollo de las actividades propuestas. • Interés para el cumplimiento del trabajo propuesto. • Interés por aprender sobre los números naturales y sus operaciones. • Valoración del aprendizaje de las operaciones básicas. • Perseverancia y constancia para resolver problemas cotidianos con números fraccionarios y decimales. • Organización y rigor al momento de realizar medidas específicas.
  • 49.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: QUINTO PERIODO: 4 ESTÁNDAR: Modelo situaciones de dependencia mediante la proporcionalidad directa e inversa. Selecciono unidades, tanto convencionales como estandarizadas, apropiadas para diferentes mediciones. Uso e interpreto la media (o promedio) y la mediana y comparo lo que indican. Resuelvo y formulo problemas a partir de un conjunto de datos provenientes de observaciones, consultas o experimentos Describo e interpreto variaciones representadas en gráficos. Analizo y explico relaciones de dependencia entre cantidades que varían en el tiempo con cierta regularidad en situaciones económicas, sociales y de las ciencias naturales. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATI VA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento espacial.  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento variacional ¿Qué son y para qué sirven las indicadoras razón y proporción? • Números decimales: • Sistema métrico decimal: • Unidades de medida: • Conceptualizació n de razones y proporciones: Diagramas lineales. • Datos: • Equivalencia y relaciones entre números fraccionarios y decimales. • Multiplicación y división de decimales. • Unidades de longitud, superficie, volumen y capacidad. • Masa, tiempo y temperatura. • Razones, Proporciones. • Propiedades fundamentales de las proporciones, escalas. • Moda y promedio. • Resuelva problemas de multiplicación y división utilizando los números decimales. • Aplique el concepto de razón y proporción al momento de interpretar y solucionar un problema sencillo. • Exponga sus ideas y sentimientos de forma respetuosa y asertiva. • Reconozca las magnitudes directamente proporcionales e inversamente proporcionales. • Resuelva situaciones que involucran distinta variación entre las magnitudes. • Conversión de números fraccionarios a decimales y viceversa. • Reconocimiento de magnitudes directamente proporcionales e inversamente proporcionales. • Desarrollo de operaciones básicas (suma, resta, multiplicación y división) con números decimales. • Elaboración de ejercicios donde se identifique el uso de las magnitudes masa, temperatura o capacidad. • Resolución de problemas sencillos utilizando el concepto de razón y proporción. • Calculo de situaciones que involucran distinta variación entre las magnitudes. • Disposición para realizar el trabajo propuesto dentro y fuera del aula. • Perseverancia y constancia en concluir el trabajo iniciado. • Interés por indagar y dar respuesta a las preguntas. • Organización y rigor al momento de realizar medidas específicas.
  • 50.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: SEXTO PERIODO: 1 ESTÁNDAR: Clasificarpolígonosenrelación con sus propiedades EJE GENERADOR PREGUNTA PROBLEMATIZAD ORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. ¿En qué situaciones de la vida diaria utilizamos los números naturales y aplicamos principios de asociación? Apreciemos las formas y descubramos sus lenguajes. • Los Números Naturales. • Polígonos Y Ángulos. • Operación con números naturales. • Suma • Resta • *Multiplicación • División • Clasificación de Polígonos y ángulos. • Interpretación y resolución de problemas, haciendo uso de las operaciones con números naturales. • Aplicación de reglas para eliminar sistemáticamente signos de agrupación en la resolución de operaciones combinadas. • Medición y clasificación de polígonos y ángulos. • Reconozco las operaciones básicas con los números naturales para resolver problemas y operaciones combinadas. • Identificación de figuras, sus formas y medidas utilizando medios tecnológicos como: Transportador, compas e indaga sobre su importancia en estructuras físicas y naturales. • Interpretación de las operaciones básicas con los números naturales para resolver problemas y problemas combinados. • Caracterización de las diferentes figuras por su forma, patrones de medida y funcionalidad de contesto real. • Elaboración situaciones problemas que involucran las operaciones básicas con los números naturales. • Observación directa que posibles construcciones se pueden elaborar y son necesarias en el municipio.
  • 51.
    Pensamiento aleatorio Pensamiento geométrico Que aportes hacen la estadísticapara el análisis y la mejor comprensión de hechos y fenómenos de la vida cotidiana • Organización y tabulación de datos. Conjuntos • Conceptos básicos: población muestra, características y variables. • Frecuencias absolutas, relativas y acumulada • Datos agrupados. Proposición Conjuntos Subconjuntos Unión Intersección • Identificación de diferentes frecuencias. Identificación de la condición o condiciones que cumplen los elementos de un conjunto y utilizarlas en la solución de un problema • Comparación de diferentes tipos de información expresadas en frecuencia y datos agrupados Identificación de diferentes relaciones entre conjuntos • Elaboración de situaciones problemas utilizando el lenguaje, notación y símbolos matemáticos. Resolución de problemas utilizando las diferentes teorías de conjuntos • Construcción de tablas de información utilizando mecanismo de recolección para plantar alternativas de solución a las necesidades de la comunidad educativa. Proposición de situaciones en los que se hace necesario utilizar la teoría de conjuntos
  • 52.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: SEXTO PERIODO: 2 ESTÁNDAR: Resolver y solucionar problemas cuya solución requieran sobre la potenciación o radiación EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPOSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. Pensamiento aleatorio ¿En qué situaciones de la vida diario utilizamos los números naturales y aplicar principios de asociación? Porque son importantes los instrumentos de medición. ¿Qué importancia tiene la recolección de datos en situaciones de la Los Números Naturales. Triángulos Y Cuadriláteros. Medida de tendencia central. Operaciones con los números naturales potenciación, radicación y logaritmación. Clasificación de triángulos y cuadriláteros. Moda, promedio y mediana Representación gráficamente de números naturales y sus respectivas operaciones. Identificación de las clases de triángulos y cuadriláteros. Identificación en diferentes situaciones las medidas de Operación de: Potenciación, radicación, logaritmación con los números naturales. Investigación de figuras, sus formas y medidas utilizando medios tecnológicos como: regla y compas e indaga sobre su importancia en estructuras físicas y naturales. Comparación de diferente tipos de información expresada en gráficas, tablas Interpretación de las operaciones de Potenciación, radicación, logaritmación con los números naturales Para solucionar problemas. Caracterización de las diferentes figuras por su forma, patrones de medida y funcionalidad de contesto real. Elaboración de situaciones problemas utilizando el lenguaje, Elaboración situaciones problemas que involucran las operaciones de: Potenciación, radicación, logaritmación con los números naturales. Observación directa que posibles construcciones se pueden elaborar y son necesarias en el municipio. Construcción de tablas de información utilizando
  • 53.
    vida real? Problemasde aplicación tendencia central Solución de problemas aplicando una de las medidas de tendencia central Organización adecuadamente datos. estableciendo conexiones entre ellas y descubrimiento nuevas maneas de descubrir el mundo real. notación y símbolos matemáticos, para elaborar estructurar conceptuales y prácticas. mecanismo de recolección para plantar alternativas de solución a las necesidades de la comunidad educativa, atreves de encuestas, diagramas y gráficas.
  • 54.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: SEXTO PERIODO: 3 ESTÁNDAR: Identificar relaciones entre unidades para medir diferentes magnitudes EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. ¿En qué situaciones de la vida diaria empleamos los números enteros? ¿Sería práctico medir la distancia de aquí a Medellín usando milímetros? Números enteros. El metro como unidad patrón. Concepto de número entero Valor absoluto Operaciones con enteros: Suma Resta Problemas de aplicación. Sistema métrico decimal (SMD) El metro como unidad fundamental Conversación de unidades de longitud Representación de los enteros en la recta numérica. Resolución de operaciones con suma y resta de enteros. Realización de conversiones entre las diferentes unidades y magnitudes del sistema métrico decimal. Identificación de la importancia de reconocer el orden en el conjunto de los números enteros. Descubro la importancia de reconocer el metro comunidad patrón de medida. Elaboración de situaciones problemas y las desarrollo argumentando su respuesta desde conceptos adquiridos previamente de suma y resta con los números enteros. Elaboración del metro para medir, comparar y describir diferentes sitios de nuestra institución. Construcción de conceptos nuevos atreves de la puesta en práctica de los diferentes conjuntos de números, su relación con el contexto real y propone actividades utilizando dichos conceptos de manera dinámica. Construcción de conceptos nuevos atreves de la puesta en práctica de los diferentes múltiplos y sub múltiplos del metro, su relación
  • 55.
    Pensamiento aleatorio ¿Qué aportes hacela estadística para el análisis y mejor comprensión de hechos y fenómenos de la vida cotidiana? Diagrama. Diagramas De barras Circulares Pictogramas. Interpretación de graficas estadísticas. Representación y análisis de datos utilizando tablas y gráficos. Comparación tipos de información expresadas en diferentes diagramas estableciendo conexiones entre ellas y descubriendo nuevas maneras de ver el mundo real. Representación de diferente tipos de información presentada en los diagramas. con el contexto real y propone actividades utilizando dichos conceptos de manera dinámica. Construcción de diferentes diagramas a partir de una situación problema.
  • 56.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: SEXTO PERIODO: 4 ESTÁNDAR: Identificarlas características de las diversasgraficas cartesianas (De puntos,Continuas,Formadas por Segmentos etc.) En relacióncon la situaciónque presentas EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico-variaciones. Pensamiento geométrico – métrico. ¿Qué aplicabilidad le encuentras a las ecuaciones para resolver situaciones que se presentan en la vida diaria? ¿Qué aplicabilidad le puedes dar al sistema geométrico en la solución de situaciones problemas? Números enteros. Área y perímetro Teorema de Pitágoras. Operaciones con números enteros: multiplicación y división. Polinomio con y sin signos de agrupación. Área y perímetro de algunas figuras planas como: Cuadrado, rectángulo, triangulo, paralelogramo, trapecio y hexágono. Aplicación del teorema de Resolución de problemas que involucran las operaciones con números enteros. Resolución de situaciones, problemas que involucran ecuaciones. Aplicación de técnicas apropiadas, herramientas y fórmulas para determinar las medidas. Operación básica entre números enteros. Descubro la importancia de manejar correctamente los conceptos de: Área, perímetro y el teorema de Pitágoras y su necesidad de aplicación en el contexto real. Elaboración de situaciones problemas y las desarrollo argumentando su respuesta desde conceptos adquiridos previamente de suma y resta con los números enteros. Elaboración de situaciones problemas y las desarrollo argumentando su respuesta desde conceptos adquiridos previamente de área, perímetro y el teorema de Pitágoras Construcción de conceptos nuevos atreves de la puesta en práctica de los diferentes conjuntos de números, su relación con el contexto real y propone actividades utilizando dichos conceptos de manera dinámica. Proposición de situaciones problemas atreves de la puesta en práctica de los diferentes conceptos de área, perímetro y el teorema de Pitágoras, su relación con el contexto real.
  • 57.
    Pensamiento aleatorio ¿Qué es unplano cartesiano? Plano cartesiano. Pitágoras. Plano cartesiano Parejas ordenadas Movimientos en el plano. Ubicación de pares ordenados en el plano cartesiano. Ubicación correctamente pares ordenados en el plano cartesiano. Elaboración de situaciones problema donde halla la necesidad de construir figuras geométricas en el plano cartesiano. Proposición de situaciones problemas atreves de la puesta en práctica de los diferentes conceptos del plano cartesiano.
  • 58.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO SEPTIMO PERIODO: 1 ESTÁNDAR: Utilizar el concepto de número entero y analizo las operaciones que se dan entre ellos para establecer relaciones. Resolver y formular problemas utilizando propiedades fundamentales de la teoría de los números. Resolver y formular problemas cuya solución requiere de la potenciación y radicación. Generalizar propiedades y relaciones de los números enteros, racionales y decimales. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento geométrico.  Pensamiento Variacional y Aleatorio. ¿Cuál es la importancia de reconocer los conjuntos de números y sus operaciones en la cotidianidad? .Números enteros. .Números racionales. .Números decimales. Concepto de número entero Valor absoluto Adición y sustracción de números enteros Propiedades de la suma de los números enteros Multiplicación y división de entero Propiedades de la multiplicación de los números enteros Potenciación de números enteros Radicación de números enteros Situaciones problema .Interpretación, ordenación, comparación y representación gráfica con los racionales y decimales sus respectivas operaciones. . Interpretación y resuelvo problemas haciendo uso de las operaciones con racionales. Comunicación de un racional como decimal y viceversa. .Identificación y uso los enteros en diferentes contextos, los representa de diversas formas y establece relaciones entre ellos; Redefine las operaciones básicas en los sistemas formados con éstos números y establece conexiones entre ellas. .Argumentación de situaciones problema haciendo uso de las operaciones con números enteros Argumentación respuestas de situaciones desde sus conceptos adquiridos previamente de suma, resta, multiplicación y división, potenciación de números enteros, racionales y decimales. • Proposición de situaciones que involucran solución de problemas de la vida cotidiana. • Socialización de conceptos nuevos a través de la puesta práctica de los números con su relación con el contexto real y propone actividades de manera dinámica.
  • 59.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO SEPTIMO PERIODO: 2 ESTÁNDAR: Utilizar el concepto de número racional y decimal y analizo las operaciones que se dan entre ellos para establecer relaciones. Resolver y formular problemas utilizando propiedades fundamentales de la teoría de los números. Resolver y formular problemas cuya solución requiere de la potenciación y radicación. Generalizar propiedades y relaciones de los números enteros, racionales y decimales. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento geométrico.  Pensamiento Variacional y Aleatorio. ¿Cuál es la importancia de reconocer los conjuntos de números y sus operaciones en la cotidianidad? .Números enteros. .Números racionales. .Números decimales. .Concepto de número racional. (Q). Representación en la recta numérica. Fracciones equivalentes. Relación de orden. Adición y sustracción de racionales. Multiplicación y división de racionales. Propiedades. Situaciones problema. Expresión racional de un decimal y viceversa. .Resuelvo problemas con ecuaciones de primer grado. .Interpretación ordenación, comparación y representación gráfica con los racionales y decimales sus respectivas operaciones. . Interpretación y resolución problemas haciendo uso de las operaciones con racionales. Expreso un racional como decimal y viceversa. .Identificación y uso los enteros y los racionales en diferentes contextos, los representa de diversas formas y establece relaciones entre ellos; Redefine las operaciones básicas en los sistemas formados con éstos números y establece conexiones entre ellas. .Argumentación de situaciones problema haciendo uso de las operaciones con números enteros, racionales y decimales. Argumenta respuestas de situaciones desde sus conceptos adquiridos previamente de suma, resta, multiplicación y división, potenciación de números enteros, racionales y decimales. • Proposición de situaciones que involucran solución de problemas de la vida cotidiana. • Socialización de conceptos nuevos a través de la puesta práctica de los números con su relación con el contexto real y propone actividades de manera dinámica.
  • 60.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SÉPTIMO PERIODO: 3 ESTANDAR: Utilizar técnicas y herramientas para la construcción de figuras planas y cuerpos con medidas dadas. Clasificar polígonos en relación con sus propiedades. Resolver y formulo problemas usando modelos geométricos. Hacer conjeturas y verificar propiedades de congruencia y semejanza entre figuras bidimensionales en la solución de problemas. Calcular áreas y volúmenes a través de composición y descomposición de figuras y cuerpos. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento geométrico.  Pensamiento geométrico. ¿Cómo posibilitar la percepción de las construcciones, formas y medidas geométricas que afiancen su conocimiento? • .Concepto de Geometría. • Plano cartesiano, transformaciones y composiciones en el mismo. • Congruencias y semejanzas de figuras. • Área de polígonos. • Clasificación de los triángulos, ángulos y teorema de Pitágoras. • Medidas de longitud, volumen, capacidad y tiempo. • Construcción de conceptos en el plano cartesiano. • Construcción de figuras planas, triángulos, ángulos utilizando herramientas didácticas como: regla, transportador y compás. • Clasificación de figuras reales de acuerdo a características de peso, altura, forma, hallando en ellas sus medidas. • Rotación de polígonos en el plano. • Aplicación de transformaciones y usar la simetría para analizar situaciones matemáticas. • Construcción figuras planas utilizando materiales didácticos. • Aplicación transformaciones y usa la simetría para analizar situaciones matemáticas. • Identificación en objetos y situaciones de su entorno las magnitudes de longitud, perímetro, área, volumen, capacidad y desarrolla procesos de medición y estimación de dichas magnitudes y las utiliza en situaciones de la vida diaria. • Representación de figuras y formas utilizando medios tecnológicos como: regla, transportador, compás e indaga sobre su importancia en estructuras físicas y naturales. • Caracterización de las diferentes figuras por su forma, patrones de medida y funcionalidad en el contexto real. . Observación directa qué posibles construcciones se pueden elaborar y son necesarias en el Municipio para mejorar la calidad de vida de sus habitantes, presentando diseños que involucren el uso de las herramientas naturales y tecnológicas.
  • 61.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: SÉPTIMO PERIODO: 4 ESTÁNDAR: Justificar el uso de representaciones y procedimientos en situaciones de proporcionalidad directa e inversa. Reconocer relación entre un conjunto de datos y su representación. Utilizar y justificar el uso de la estimación para resolver problemas relativos a la vida social, económica. Hacer conjeturas acerca del resultado de un experimento aleatorio usando proporcionalidad y nociones básicas de proporcionalidad. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento geométrico.  Pensamiento Variacional. ¿Qué mecanismos usa el estudiante para adquirir información, inferir y utilizarla para su bienestar y el de los demás? • Razones y Proporciones. • Magnitudes: Directa e inversamente proporcionales. • Regla de tres simple y compuesta. • Probabilidad. • Medidas de tendencia central: Media, Mediana, Moda. • Tablas y gráficas. • Combinaciones y permutaciones. • Identificación de las razones y proporciones como relaciones entre magnitudes. • Solución de problemas de proporcionalidad. • Orden y relaciones. • Uso de gráficas estadísticas y medidas de tendencia central • Evaluación de la probabilidad de ocurrencia de un evento. • Comprensión de la probabilidad como un número entre 0 y 1. • Formulación de inferencias y argumentos lógicos que se basan en el análisis y manejo de datos estadísticos agrupados, y hace su representación gráfica. • Interpretación de datos de una información estadística y los usa significativamente. • Identificación de cálculos de proporcionalidad directa e inversa. • Comparación de diferentes tipos de información expresada en proporciones gráficas, tablas, estableciendo conexiones entre ellas y descubriendo el mundo real. • Planeación y resolución de problema utilizando el lenguaje, notación y símbolos matemáticos para elaborar estructuras conceptuales y gráficas. • Construcción de tablas de información utilizando mecanismos de proporcionalidad para plantear alternativas de solución a las necesidades de la comunidad educativa a través de encuestas, diagramas y gráficas. • Realización de forma organizada y responsable el trabajo que se le propone en el área. • Organización al momento de leer e interpretar la información.
  • 62.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: OCTAVO PERIODO: 1 ESTÁNDAR: Utilizar números reales en sus diferentes representaciones en diversos contextos. Usar representaciones geométricas para resolver y formular problemas en la matemática y en otras disciplinas. Hacer conjeturas acerca del resultado de un experimento aleatorio usando proporcionalidad y nociones básicas de proporcionalidad. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico.  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿En qué situaciones de la vida se aplican y se utilizan los sistemas numéricos, y qué funcionalidad le ves a los poliedros? • Sistemas numéricos. • Ángulos complementarios, adyacentes, consecutivos cortados por una transversal. • Poliedros. • Proporcionalidad. • Conjunto de los números reales: Operaciones y propiedades, relación de orden, recta real. • Clasificación y construcción de Poliedros: Pirámides, prismas, conos y cilindros. • Aplicaciones a la proporcionalidad. • Formulación de proyecto investigativo estadístico (primera parte). • Identificación y representación de conjuntos numéricos en la recta real. • Aplicación de propiedades de los conjuntos numéricos a través de la solución de problemas. • Identificación, clasificación y construcción de poliedros. • Calcula la probabilidad de ocurrencia de un evento. • Comprensión de la probabilidad como un número entre 0 y 1. • Formulación de inferencias y argumentos lógicos que se basan en el análisis y manejo de datos estadísticos agrupados, y hace su representación gráfica. • Resolución de operaciones por medio de los conjuntos numéricos. • Interpretación de datos de una información estadística y los usa significativamente. • Identificación y clasificación de poliedros. • Construcción de poliedros de acuerdo a sus características. • Planeación de situaciones problema utilizando el lenguaje, notación y símbolos matemáticos para elaborar estructuras conceptuales y gráficas. • Argumentación y descripción utilizando adecuadamente propiedades de los conjuntos numéricos. • Proposición de proyectos de investigación estadística. • Construcción de tablas de información utilizando mecanismos de proporcionalidad para plantear alternativas de solución a las necesidades de la comunidad educativa a través de encuestas, diagramas y gráficas.
  • 63.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: OCTAVO PERIODO: 2 ESTÁNDAR: Usar procesos inductivos y lenguaje algebraico para verificar conjeturas. Construir expresiones algebraicas equivalentes a una expresión algebraica dada. Reconocer y contrastar propiedades y relaciones geométricas utilizadas en demostración de teoremas (Pitágoras y Thales.) Interpretar analítica y críticamente información estadística proveniente de diversas fuentes 8prensa, revista, televisión, consultas, entrevista, etc.) Compara resultados experimentales con probabilidad matemática esperada. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento Variacional.  Pensamiento geométrico. ¿En qué situaciones de la vida le encuentras aplicación y funcionabilidad al álgebra? • Conceptos básicos algebraicos. • Triángulos, líneas y puntos notables • Teorema de Pitágoras. • Medidas de tendencia central: Media, Mediana, Moda. • Tablas y gráficas. • Combinaciones y permutaciones. • Conceptos básicos del álgebra en la solución de problemas. • Identificación del triángulo rectángulo aplicando el Teorema de Pitágoras. • Identificación de las razones y proporciones como relaciones entre magnitudes. • Solución de problemas de proporcionalidad. • Orden y relaciones. • Uso de gráficas estadísticas y medidas de tendencia central. • Resolución de ejercicios y problemas a partir de los conceptos del álgebra. • Deducción y aplicación del teorema de Pitágoras a través de un triángulo rectángulo. • Interpretación y resolución de datos algebraicos en la solución de problemas. • Interpretación e identificación del triángulo rectángulo aplicando el teorema de Pitágoras. • Comparación de diferentes tipos de datos estadísticos para aplicar a la vida real. Argumentación de operaciones básicas en la utilización del álgebra. Argumentación de problemas relacionados con la aplicación del teorema de Pitágoras en la solución de los mismos. • Proposición de datos algebraicos en la solución de problemas. • Construcción de tablas de información y uso de gráficas estadísticas para el análisis de datos.
  • 64.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: OCTAVO PERIODO: 3 ESTÁNDAR: Usar procesos inductivos y lenguaje algebraico para verificar conjeturas. Modelar situaciones de variación con funciones polinómicas. Seleccionar y usar algunos métodos estadísticos adecuados, según el tipo de información. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento Variacional. ¿En qué situaciones de la vida le encuentras aplicabilidad a los productos notables y a la factorización? • Operaciones con polinomios. • Productos y cocientes notables. • Factorización. • Tabulación y representación gráfica de frecuencias (Absoluta, relativa y acumulada) • Operaciones de suma, resta, multiplicación y divisiónde polinomios. • Divisiónsintética. • Identifico y aplico los diversos productos y cocientes notables. • Diferentes casos de factorización. • Tabulación y representación gráfica de frecuencias. • Resolución de sumas y restas entre polinomios. • Resolución de multiplicaciones y diversas divisiones de polinomios. • Resolución y aplicación de los productos notables. • Resolución y aplicación de cocientes notables. • Identificación y aplicación de cada uno de los casos de factorización. • Aplicación de frecuencias, tabulo y represento datos por medio de gráficas. • Resolución de las operaciones con productos y cocientes notables. • Identificación y resolución de los casos de factorización. • Interpretación de datos de una información estadística y los usa significativamente. • Identificación y tabulación de datos para diferentes tipos de información expresada en proporciones gráficas, tablas permitiendo el análisis entre ellos. • Expresión de situaciones problema utilizando el lenguaje, notación y símbolos matemáticos aplicados a la vida cotidiana. • Caracterización de las operaciones con polinomios y factorización según los conocimientos adquiridos. • Sugiere operaciones desde los conocimientos adquiridos y ve su funcionalidad con la vida real. • Construcción de tablas, diagramas y gráficas mediante la tabulación de datos estadísticos. • Realización de forma organizada y responsable el trabajo que se le propone en el área. • Organización al momento de leer e interpretar la información.
  • 65.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: OCTAVO PERIODO: 4 ESTÁNDAR: Utilizar números reales en sus diferentes representaciones en diversos contextos. Utilizar la notación científica para representar cantidades y medidas. Usar representaciones geométricas para resolver y formular problemas en la matemática y en otras disciplinas. Interpretar conceptos de media, mediana y moda. Modelar situaciones de variación con funciones polinómicas. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento aleatorio.  Pensamiento Variacional.  Pensamiento geométrico. ¿Qué función y aplicabilidad le ves a la estadística en tu vida? • Fracciones algebraicas. • Simplificación de fracciones. • Operaciones básicas con fracciones algebraicas. • Notación científica • Cuadriláteros: Clasificación y propiedades. • Medidas de tendencia central (promedio, moda, mediana). • Operaciones básicas con fracciones algebraicas. • Simplificación de fracciones algebraicas. • Expresión de cantidades en notación científica. • Identificación y construcción de cuadriláteros. • Aplicación e interpretación de gráficas a partir de las medidas de tendencia central. • Resolución de la factorización, traduciendo expresiones algebraicas. • Identificación y simplificación de fracciones algebraicas. • Solución de las medidas de tendencia central desde una población de datos. • Expresión de cantidades en notación científica. • Identificación, construcción y clasificación de cuadriláteros. • Interpretación de datos de una información estadística y los usa significativamente. • Interpretación de gráficas, y planteamiento de las conclusiones de datos y .gráficos. • Explicación y argumentación de la simplificación de fracciones algebraicas. • Argumentación y expresión de operaciones con fracciones algebraicas. • Caracterización de situaciones problema utilizando el lenguaje, notación y símbolos matemáticos. • Solución de fracciones algebraicas. • Construcción de tablas de información. • Extracción de conclusiones de datos y gráficos aplicando las medidas de tendencia central. • Organización al momento de leer e interpretar la información.
  • 66.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: NOVENO PERIODO: 1º ESTÁNDAR: Identificar los números reales, sus propiedades y las aplico en la ejecución de ejercicios y situaciones problemas. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Numérico y Variacional. Métrico Geométrico ¿Son necesarios los números reales como concepto previo para la concepción en el área de matemáticas y en otras aéreas? En que situaciones de la vida real halla la distancia entre dos puntos. Números reales. Funciones lineales Conjuntos numéricos Radicación Racionalización de denominadores. Potenciación Ubicaciones en la recta numérica. Resolución de ecuaciones Distancia entre dos Identificación de los números reales. Realización correctamente las operaciones básicas en los reales. Resolución de potencias y raíces con números reales. Solución de la ecuación de una recta que pasas por dos puntos. Comprensión correctamente los reales en la recta numérica. Identificación y comprensión las propiedades de los números reales. Identificación de funciones lineales a través de su estructura gráfica. Comprensión la conformación y características particulares de los conjuntos numéricos. Justificación de la importancia de los números reales en la resolución de algoritmos, ecuaciones, funciones interpretación de gráficas. . Obtención de información a través de la distancia entre dos puntos. Sugiero situaciones problemas que involucren las operaciones con los números reales. Proposición de ejercicios y situaciones problemas para la adquisición de conceptos de manera didáctica y la aplicación de dichos conceptos en su cotidianidad. Proposición de ejercicios en los que aplico los conocimientos
  • 67.
    Aleatorio ¿En quesituaciones de la vida aplico los conceptos de medida de tendencia central? Medidas de tendencia central. puntos. Moda- Mediana- Promedio- Varianza y desviación estándar. Interpretación de datos y gráficos relacionados con información significativa. Comprensión de relaciones con informaciones estadísticas. Formulación de inferencias y argumentos lógicos que se basan en el análisis de datos. adquiridos. Representación de datos estadísticos
  • 68.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: NOVENO PERIODO: 2º ESTÁNDAR: Identificar relaciones entre propiedades de las gráficas y propiedades de las ecuaciones algebraicas EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATIVA PROPÓSITIVA Numérico Variacional. Métrico Geométrico ¿Para qué se crearon las ecuaciones? ¿En qué situaciones de la vida real observas la pendiente de una recta? Función lineal. Función lineal. Ecuación de una recta Punto medio Pendiente de una recta. Resolución de situaciones cotidianas mediante ecuaciones lineales Solución de forma correcta la pendiente de una recta. Determinación y graficación de la pendiente de una recta. Comprensión del significado de ecuaciones lineales y cuadráticas. Identificación de situaciones que se resuelven utilizando ecuaciones. Relación entre los conceptos básicos de punto medio, pendiente y ecuación de una recta. Obtención de información a partir de una gráfica. Justificación de un procedimiento para resolver ecuaciones y desigualdades. Identificación del método mediante el cual grafico la pendiente de una recta. Proposición de ejercicios cotidianos en los que aplico los conceptos adquiridos. Solución de problema derivados de situaciones cotidianas utilizando ecuaciones. Representación correcta desituaciones reales por medio de funciones lineales.
  • 69.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: NOVENO PERIODO: 3º ESTÁNDAR: Identifico diferentes métodos para solucionar sistemas de ecuaciones lineales EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATIVA PROPÓSITIVA Numérico Variacional. ¿Interpreto en mi entorno una situación donde se evidencie un sistema de ecuación lineal? Sistemas de Ecuaciones lineales. Solución Grafica Métodos de solución algebraicos sistemas 2x2 y 3x3: igualación. Sustitución, reducción, determinantes Resolución de problemas aplicando ecuaciones de primer grado. Diferenciación de métodos para resolver ecuaciones lineales. Resolución de situaciones cotidianas mediante ecuaciones lineales y cuadráticas Comprendo el significado de ecuaciones lineales Identificación de situaciones que se resuelven utilizando ecuaciones. Obtención de información a partir de una gráfica. Justificación de un procedimiento para resolver ecuaciones. Proposición de ejercicios cotidianos en los que aplico los conceptos adquiridos. Solución de problema derivados de situaciones cotidianas utilizando ecuaciones.
  • 70.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES DE MATEMATICAS GRADO: NOVENO PERIODO: 4º ESTÁNDAR: Reconocer y realizar correctamente operaciones básicas con las ecuaciones lineales y cuadráticas. Identificar la parte real y la parte imaginaria de un número complejo EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATIVA PROPÓSITIVA Numérico Variacional. Pensamiento numérico ¿Para qué se crearon las ecuaciones? ¿Solo existen los números reales? Ecuaciones cuadráticas Números complejos Regla de la función cuadrática Grafica de una función cuadrática Aplicaciones de una función cuadrática Notación Operaciones con números complejos Conjugado de un numero complejo Planeación y resolución de problemas aplicando ecuaciones de segundo grado. Resolución de situaciones cotidianas mediante ecuaciones cuadráticas Diferenciación entre un número real y un número imaginario Comprensión del significado de ecuaciones lineales y cuadráticas. Identificación de situaciones que se resuelven utilizando ecuaciones. Identificación entre un número real y un número imaginario Obtención de información a partir de una gráfica. Justificación de un procedimiento para resolver ecuaciones Enunciación entre un número real y un número imaginario Proposición de ejercicios cotidianos en los que aplico los conceptos adquiridos. Solución de problema derivados de situaciones cotidianas utilizando ecuaciones. Proposición de un número real y un número imaginario
  • 71.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: DÉCIMO PERIODO: 1 ESTÁNDAR: Comparar y contrastar las propiedades de los números (enteros, racionales, reales) sus relaciones y operaciones (sistemas numéricos). Utilizar argumentos de la teoría de números para justificar relaciones que involucran números naturales. Usar argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. Predecir y justificar razonamientos y conclusiones usando información estadística. Resolver y formular problemas usando conceptos básicos de conteo y probabilidad. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento numérico  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento variacional. ¿Es importante el conocimiento e identificación de los conjuntos numéricos y la solución de problemas afines? • Los conjuntos numéricos. • Combinaciones. • Productos notables. • Factorización. • Los números reales. • Propiedades y gráfica de los números reales R. • Conjuntos. • Nociones de probabilidad. • Medida de ángulos. • Combinaciones. • Aplicación de distintos sistemas numéricos en la solución de situaciones problema. • Solución de la pendiente de una recta a partir de sus coordenadas. • Relación de dependencia entre las variables que se ven involucradas en situaciones reales. • Identificación y resolución de productos notables y factoriza polinomios algebraicos aplicando la descomposición en factores. • Aplicación de las propiedades de los números reales en la solución de problemas algebraicos. • Apropiación de la teoría combinatoria. • Diferenciación de los números racionales de los irracionales a partir de su representación. • Reconoce la importancia de la representación gráfica de un problema como herramienta didáctica. • Caracterización de las propiedades de los números reales. • Interpretación de gráficas que involucran relaciones entre tres conjuntos. • Comprensión, relación y aplicación de la diferencia entre tipos de variables en la resolución de problemas. • Utilización correcta del lenguaje matemático. • Representación de cualquier número real en la recta numérica. • Generación de algoritmos para la resolución de problemas que involucran elementos geométricos. • Realización de forma organizada y responsable el trabajo que se le propone en el área.
  • 72.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: DÉCIMO PERIODO: 2 ESTÁNDAR: Identificar características de localización de objetos geométricos en sistemas de representación cartesiana y otros. Describir y modelar fenómenos periódicos del mundo real usando relaciones y funciones trigonométricas. Usar argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. Diseñar estrategias para abordar situaciones de medición que requieran grados de precisión específicos. Modelar situaciones de variación periódica con funciones trigonométricas. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento Numérico  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento Variacional. ¿Por qué es importante la Geometría y qué aplicación tiene en la sociedad moderna? • Representación gráfica de los reales. • Ángulos positivos y negativos. • Definición de las funciones trigonométricas. • Gráfica de las funciones y sus variaciones. • Permutaciones y variaciones. • Circunferencia trigonométrica. • Líneas trigonométricas de las funciones. • Gráfica de las funciones trigonométricas: Seno, Coseno, Tangente, cosecante, cosecante, secante y cotangente. • Generalización de las funciones: Traslación, amplitud, período. • • Graficación de diferentes números reales sobre una recta numérica. • Conversión de grados sexagesimales a Radianes y viceversa. • Identificación de funciones trigonométricas de ángulos agudos. • Graficación de las funciones trigonométricas y determina sus variaciones. • Resolución de problemas sobre permutaciones y Variaciones. • Utilización de herramientas tecnológicas para trazar gráficas de • Reconoce la circunferencia trigonométrica y traza las seis funciones trigonométricas. • Identificación de regularidades en las funciones trigonométricas. • Identificación de las propiedades de las funciones y las usa para resolver situaciones problema. • Identificación y solución de problemas sobre • Comprensión de la importancia de las funciones trigonométricas en el desarrollo de la sociedad. • Expone y grafica las funciones trigonométricas y determina sus variaciones. • Definición de las funciones que permiten el estudio del triángulo en todas sus formas. • Construcción correctamente degráficas de las funciones trigonométricas con base en la circunferencia trigonométrica. • Socialización de conversión de grados sexagesimales a radianes y viceversa.
  • 73.
    funciones trigonométricas. Permutacionesy Variaciones. INSTITUCIÓN EDUCATIVA LUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: DÉCIMO PERIODO: 3 ESTÁNDAR: Establecer relaciones y diferencias entre diferentes notaciones de números reales para decidir sobre su uso en una situación dada. Usar argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. Reconocer y describir curvas o lugares geométricos. Justificar inferencias provenientes de los medios o de estudios diseñados en el ámbito escolar. Interpretar conceptos de probabilidad condicional e independencia de eventos. Proponer inferencias a partir del estudio de muestras probabilísticas. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento Métrico.  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento Variacional. ¿Qué importancia tiene la estadística en el diagnóstico y solución de problemas a nivel general? • Resolución de Triángulos Rectángulos. • Resolución de triángulos oblicuángulos. • Teorema del Seno • Teorema del Coseno. • Ángulos de elevación y depresión. • Probabilidad. • Solución de triángulos rectángulos. • Ley del seno. • Ley del coseno. • Ángulos de elevación. • Ángulos de depresión. • Probabilidad condicional. • Resolución de triángulos rectángulos aplicando las fórmulas respectivas. • Resolución de triángulos oblicuángulos aplicando las fórmulas del Teorema del Seno y del Coseno respectivamente. • Resolución de problemas sobre ángulos de Elevación y de Depresión. • Aplicación de los principios básicos de la probabilidad. • Apropiación de la teoría de la probabilidad. Identificación y aplicación de forma geométrica la solución de triángulos. Indagación y comparación sobre la importancia de la aplicación de ángulos en la vida real. Interpretación de conceptos de probabilidad condicional e • Comprensión de la importancia de la solución de triángulos rectángulos y oblicuángulos en la aplicación de los problemas de la vida cotidiana. • Construcción y análisis de los planteamientos utilizados para resolver problemas en la solución de triángulos. • Realización de forma organizada y responsable el trabajo que se le propone en el área. • • Organización al momento de leer e interpretar la información.
  • 74.
    independencia de eventos. INSTITUCIÓN EDUCATIVALUIS EDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: DÉCIMO PERIODO: 4 ESTÁNDAR: Describir y modelar fenómenos periódicos del mundo real usando relaciones y funciones trigonométrica. Usar argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. Diseñar estrategias para abordar situaciones de medición que requieran grados de precisión específicos. Justificar inferencias provenientes de los medios o de estudios diseñados en el ámbito escolar. Interpretar conceptos de probabilidad condicional e independencia de eventos. Proponer inferencias a partir del estudio de muestras probabilísticas. Predecir y justificar razonamientos y conclusiones usando información estadística. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGRO(S) COMPETENCIAS E INDICADORES DE LOGROS INTERPRETATIVA ARGUMENTATIVA PROPOSITIVA  Pensamiento métrico.  Pensamiento geométrico.  Pensamiento aleatorio.  Pensamiento Variacional. ¿Qué papel desempeñan las operaciones algebraicas en la solución de problemas trigonométricos? • Demostración de identidades. • Ecuaciones trigonométricas. • Funciones de la suma y diferencia de dos ángulos. • Propiedades de la probabilidad. • Racionalización. • Identidades trigonométricas: Relaciones pitagóricas. • Identidades para la suma y diferencia de ángulos. • Identidades para ángulos dobles y medios. • Probabilidad condicional. • Diagrama de árbol. • Probabilidad total. • Demostración identidades y soluciono ecuaciones trigonométricas. • Identificación y aplición de las propiedades de la probabilidad en la solución de problemas. • Racionalización de denominadores mediante la aplicación de expresiones conjugadas Establezco procesos lógicos para verificar identidades • Identificación de cada una de las funciones por medio de la aplicación de problemas a la vida real. • Interpretación de las propiedades de ecuaciones trigonométricas para el desarrollo de la habilidad mental. • Inferenciación en el • Racionalización de denominadores por medio de expresiones conjugadas para la aplicación de problemas algebraicos. • Utilización de los argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias. • Representación de alternativas en la aplicación de la solución de problemas de la comunidad educativa a través de conocimientos adquiridos. • Realización de forma organizada y responsable el trabajo que se le propone en el área. • Organización al
  • 75.
    Pensamiento espacial ¿En la vidacotidiana donde se observan las figuras cónicas? Secciones cónicas Circunferencia, parábola, elipse e hipérbola trigonométricas. Diferenciación entre las combinaciones y permutaciones Resolución de problemas en los que se usen propiedades geométricas de figuras cónicas de manera algebraica conocimiento adquirido a través del desarrollo matemático para afrontar situaciones de la vida cotidiana. Interpretación de un polinomio una ecuación con C(o, o) y C(h, k) • Exposición mediante diagrama de árbol situaciones relacionadas con el contexto educativo. Argumentación de ejercicios de aplicación con lo cotidiano momento de leer e interpretar la información. Proposición de ejercicios de aplicación con lo cotidiano.
  • 76.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: UNDÉCIMO PERIODO: 1 ESTÁNDAR: Establecer relaciones y diferencias entre números reales, expresiones algebraicas y las gráficas de funciones polinómicas y racionales EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. Pensamiento aleatorio ¿Por qué es importante conocer conjuntos numéricos con situaciones problemáticas en nuestro mundo matemático? ¿Por qué es importante la geometría y que aplicación tiene en nuestra sociedad? ¿Para qué nos sirve las permutaciones y las combinaciones? Conjunto de los números reales Desigualdades e inecuaciones Estadística Conjunto numérico con situaciones problemas Intervalo Valor absoluto Inecuaciones al infinito Inecuaciones simultaneas Inecuaciones con valor absoluto Permutación y combinación Planeación y resolución de situaciones problemas Solución de diferentes clases de intervalos Diferenciación entre las combinaciones y permutaciones Interpretación y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Interpretación de diferentes clases de inecuaciones Interpretación de ejercicios de aplicación con arreglos cotidianos prácticos Solución de situaciones problemas enfocados a pruebas ICFES. Argumentación de diferentes clases de inecuaciones Argumentación de ejercicios de aplicación con arreglos cotidianos prácticos Construcción y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Proposición de diferentes clases de intervalos Proposición de ejercicios de aplicación con arreglos cotidianos prácticos
  • 77.
    Pensamiento espacial ¿Enla vida cotidiana donde se observan las figuras cónicas? Secciones cónicas Estadística descriptiva Tablas de frecuencias Medida de tendencia central Interpretación de datos estadísticos Circunferencia, parábola, elipse e hipérbola Solución de diferentes datos estadísticos ya sea de forma gráfica o en tablas de frecuencias Resolución de problemas en los que se usen propiedades geométricas de figuras cónicas de manera algebraica Interpretación de diferentes datos estadísticos ya sea de forma gráfica o en tablas de frecuencias Interpretación de un polinomio una ecuación con C(o, o) y C(h, k) Argumentación de diferentes datos estadísticos ya sea de forma gráfica o en tablas de frecuencias Argumentación de ejercicios de aplicación con lo cotidiano Proposición de soluciones de diferentes datos estadísticos ya sea de forma gráfica o en tablas de frecuencias Proposición de ejercicios de aplicación con lo cotidiano.
  • 78.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: UNDÉCIMO PERIODO: 2 ESTÁNDAR: Usar argumentos geométricos para resolver y formular problemas en contestos matemáticos y en otras ciencias EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIV A Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. Pensamiento aleatorio ¿Por qué es importante conocer conjuntos numéricos con situaciones problemáticas en nuestro mundo matemático? ¿Por qué es importante la geometría analítica en el estudio de la función lineal ¿Para qué nos sirve las permutaciones y las combinaciones? Conjunto de los números reales Función lineal Estadística Conjunto numérico con situaciones problemas Distancia entre dos puntos Pendiente de una recta Coordenadas del punto medio Permutación y combinación Planeación y resolución de situaciones problemas Solución de la distancia entre dos puntos y las coordenadas del punto medio Verificación de la pendiente de una recta a partir de sus coordenadas Combinación y arreglos de objetos, a partir de situaciones problemas Interpretación y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Interpretación y resolución de situaciones problemas que me permiten encontrar la distancia entre dos puntos y las coordinadas del punto medio y la pendiente de una recta Interpretación de ejercicios de aplicación con arreglos cotidianos prácticos Solución de situaciones problemas enfocados a pruebas ICFES. Solución de situaciones problemas que involucran: distancia entre dos puntos y las coordinadas del punto medio y la pendiente de una recta Argumentación de ejercicios de aplicación con arreglos cotidianos Construcción y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Construcción y resolución de situaciones problemas que involucran: distancia entre dos puntos y las coordinadas del punto medio y la pendiente de una recta Proposición de ejercicios de aplicación con arreglos cotidianos
  • 79.
    Establezco diferencias entre lascombinaciones y permutaciones prácticos prácticos
  • 80.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: UNDÉCIMO PERIODO: 3 ESTÁNDAR: Justificar resultados obtenidos mediante procesos de aproximación sucesiva, rangos de variación y límites en situaciones de medición. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento numérico- variaciones. Pensamiento geométrico – métrico. ¿Qué beneficios y funcionalidad le encuentra al estudio de las funciones y relaciones? ¿Por qué es importante desarrollar la intuición y que aplicación tiene en las sucesiones de números reales? Funciones y relaciones Sucesiones de números reales Relaciones reales, dominio y rango Clases de funciones reales Sucesiones y series Termino general o N-eximo Caracterización geométrica de una función, con ayuda de su grafica Relación y diferenciación entre funciones y relaciones Determinación del dominio y rango en una función Identificación y clasificación de sucesiones y serie de los números reales Determinación del termino general N-eximo de una sucesión real Identificación del dominio y el rango de una función Determinación de los términos de una sucesión a partir de un ecuación Justificación geométrica y analíticamente la inversa de una función respecto a las operaciones, determino si es o no biyectiva Identificación de asíntotas verticales y horizontales de funciones reales Clasificación de las sucesiones en categorías : Creciente, De Creciente, Aritméticas y Geométricas Proposición de argumentos geométricos y analíticos para construir las gráficas de las funciones reales Proposición de sucesiones donde haya la necesidad de desarrollar la intuición para encontrar el termino general o N-eximo
  • 81.
    Pensamiento aleatorio ¿Será importante estudiar laprobabilidad de que ocurran ciertos sucesos naturales o de nuestra vida diaria? Probabilidad l Medidas de localización y dispersión. Experimentos Aleatorios. Variables aleatorias discretas y continuas Realización de experimentos o fenómenos aleatorios. Identificar las propiedades de la probabilidad. Diferenciación de las variables aleatorias y continuas. Estudio la posibilidad de que ocurran sucesos. Interpretación de los resultados numéricos obtenidos al hallar el valor esperado y la varianza de una variable aleatoria Exposición de los pasos generados para determinar el valor esperado, la varianza y la desviación estándar de una variable aleatoria Solución por pasos generales para determinar el valor esperado, la varianza y desviación típica de una variable aleatoria
  • 82.
    INSTITUCIÓN EDUCATIVA LUISEDUARDO ARIAS REINEL MALLAS CURRICULARES MATEMÁTICAS GRADO: UNDÉCIMO PERIODO: 4 ESTÁNDAR: - Identificar el concepto de sucesiones para encontrar el límite de una función y representarla en diferentes formas, en el plano cartesiano, describiendo el límite hacia un valor real - Interpretar la noción de derivada como razón de cambio y desarrolla métodos para hallar la derivada de funciones básicas. - Utilizar las técnicas de aproximación en procesos infinitos numéricos. EJE GENERADOR PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES OBJETOS DE ENSEÑANZA LOGROS COMPETENCIAS E INDICADORES DE LOGRO INTERPRETATIVA ARGUMENTATITVA PROPÓSITIVA Pensamiento geométrico – métrico. ¿Para qué nos sirve el estudio de los límites y que aplicabilidad tiene en nuestra vida cotidiana? Limites Derivada Límite de funciones Limite directos Limites con racionalización Limites con factorización Limites indeterminados Límites al infinito Derivada y el problema de la recta Solución del límite de una función aplicando sus propiedades Solución de limites aplicando conjugadas Identificación de limites infinitos y al infinito Solución de la derivada como razón de cambio y desarrolla métodos para Aplicación de nociones fundamentales de los límites de una sucesión para calcular algunos límites de funciones. Aplicación de técnicas de factorización en el cálculo de limites Interpretación de la noción de derivada como razón de Utilización de técnicas de sustitución para calcular límites alrededor de un punto distinto de cero. Utilización de sucesiones para aprobar la no existencia de limites Argumentación de la noción de derivada como razón de cambio Construcción y resolución de situaciones problemas, en el mundo matemático que nos permitan afianzar conceptos Proposición de la noción de derivada como razón de cambio
  • 83.
    Pensamiento aleatorio ¿Será importante estudiar laprobabilidad de que ocurran ciertos sucesos naturales o de nuestra vida diaria? Integración Probabilidad ll tangente Velocidad, aceleración y otras razones de cambio Reglas de derivación Regla de la cadena Derivación implícita Primitivas e Integración indefinida Integración definida Teorema fundamental del cálculo Integración por sustitución Modelo de Poisson Modelo Binomial Modelo Normal hallar la derivada de funciones básicas. Utilización de técnicas de aproximación en procesos infinitos numéricos. Identificación y aplicación de la distinción Binomial en nuevos experimentos dados. Identificación y aplicación de la distribución de Poisson en nuevos experimentos dados. Identificación y aplicación de la distribución normal cambio y desarrolla métodos para hallar la derivada de funciones básicas. Interpretación de las técnicas de aproximación en procesos infinitos numéricos. Utilización de la tabla de la distribución normal estándar en la búsqueda de probabilidades de modelos normales y desarrolla métodos para hallar la derivada de funciones básicas. Argumentación de las técnicas de aproximación en procesos infinitos numéricos. Interpretación de los valores de la medidas de tendencia central de los modelos probabilísticos discretos, Binomial y de Poisson Interpretación de los problemas enmarcados en el modelo normal e interpreta gráficamente las probabilidades y desarrolla métodos para hallar la derivada de funciones básicas. Explicación de las técnicas de aproximación en procesos infinitos numéricos. Presentación del modelo de probabilidad discreto que modele más adecuadamente, la información presentada en una situación problema Proposición de un modelo de probabilidad para interpretar la naturaleza aleatoria de algún fenómeno
  • 84.
    en nuevos experimentos dados. Utilizolos modelos de distribución de probabilidades: Binomial, Poisson y normal, en el planteamiento y resolución de problemas. encontradas presentado en forma de problema