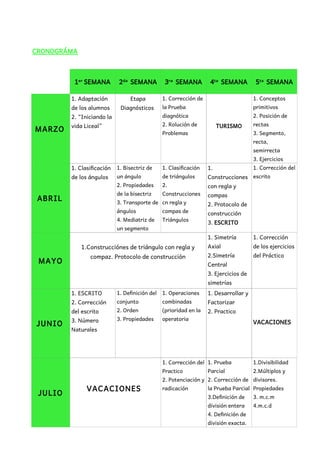
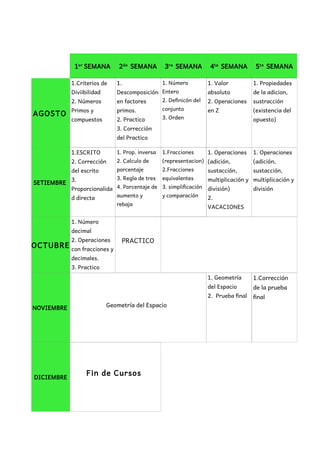
Este documento presenta una planificación anual para la asignatura de matemáticas. Describe los objetivos generales para los estudiantes y profesores, las estrategias metodológicas, los materiales didácticos, y la evaluación. Además, detalla tres bloques temáticos que serán cubiertos: geometría plana, números, y geometría espacial. Cada bloque contiene varias unidades con los temas que se abordarán.

1. Planificación Anual
Para este curso debemos de tener en cuenta: que es la continuación del alumno,
en contacto con la matemática. De una forma más profunda y compleja, porque se
implementa un lenguaje en donde el alumno va a hacer novato. Es por este motivo,
entre otros, que el educador cumple un rol muy importante a la hora de motivar al
alumno. Con lo dicho anteriormente nos referimos a: que los temas, ejercicios y
problemas deben de ser muy bien escogidos para dinamizar el ambiente áulico.
Si profundizamos en la matemática, principalmente debemos de tener en cuenta
que le debemos de acercar una metodología tentativa de: comprensión, resolución y
producción (problemas, ejercicios, reflexiones y aplicaciones). Esto significa que el
educando debería de ser un individuo crítico y reflexivo, pero partiendo siempre de su
logro personal, vinculandolo con lo teórico o contrastandolo con la realidad en el que
se encuentra inmerso.
Lo primero que debe de tener encuenta el educador y el educando es que la
matemática no solo es un conjunto de números, símbolos y estructuras lógicas,sino
que también es una forma de pensar y de actuar.
Dicha es una herramienta para la vida cotidiana, pero también lo es para las diversas
ciencias. Con estos último punto nos referimos a que la mátematica es incluida en el
curriculum como indispensable para el desarrollo personal del individuo.
Dentro de esta planificacion se pretende utilizar diversos materiales didacticos
(detallados más adelante). Esto se debe a que basándonos en el paradigma
constructivista, se busca que el alumno sea totalmente activo; siendo el protagonista
de su aprendizaje.

2. Mi rol como docente será el de promover el desarrollo y autonomía de los alumnos,
continuando así con la construcción del aprendizaje mediante de la enseñanza a partir
de la experiencia.
Como nos plantea Ausubel el aprendizaje de nuestros alumnos va a depender de la
estructuracognitiva previa de los mismos, que se relacionará con una nueva
formación, creando un nuevo conocimiento. Por tanto nos basamos en este autor
debedio a que consideramos que el uso de los recusos didacticos son muy importantes
para el aprendizaje
Debido a que con estos recusos el educando establece una relación entre sus
ideas previas y conocimiento adquiridos. En este punto nonde logramos el aprendizaje
significativo, como lo denomina el autor.
También nos basaremos en Bruner para trabajar el área sicológica porque él mismo
trabaj el tema “andamiaje”: costrucción del conocimiento mediante su descubrimiento,
el aprendizaje es un proceso activo de información donde cada alumno organiza y
construye desde su punto de vista. Es por esto que durante todo el transcurso del año
se plantearan preguntas diverguentes, para que el alumno pueda formar conjeturas y
exponer su propio punto de vista.
Por otra parte debemos de tener en cuenta que como docentes nos vamos a
encontrar con el autor Gastón Bachelard denomina obstáculos epistemológicos: son
ciertas dificultades que no permiten una correcta apropiación del conocimiento,
algunas de estas dificultades son los conocimientos previos. Se debe a que los
individuos tienen un conjuntos de ideas acerca de algo, que en ocasiones limita el
aprendizaje.

3. UN ejemplo de esto son los obstáculos verbales que se dan cuando el estudiante
mediante una palabra o imagen intenta explicar un concepto. Es por esto que debemos
de tratar de llegar a un conocimiento nuevo, partiendo de esas ideas previas y
utilizando un lenguaje acorde al contexto, para poder derribar esos obstáculos que se
presentan a la hora de aprender.
OBJETIVOS GENERALES:
EL PROFESOR DEBERÁ:
✔ Desarrollar el sentido crítico del estudiante, crear en el aula debates y críticas
constructivas potenciando la autoevaluación y el espíritu democrático
participativo.
✔ Generar en los alumnos el hábito de trabajo fomentando la tarea domiciliaria
mediante “repartidos” de los temas en el curso del año lectivo, incentivando
de esta forma una rutina de estudio a diario.
✔ Incentivar el gusto por la asignatura.
✔ Introducir el lenguaje matemático.
✔ Revalorizar el rol de estudiante introduciendo la labor grupal
✔ Fomentar la reflexión sobre los propios razonamientos y modos de pensar a
través del trabajo en el cuaderno y la lectura del libro de texto o selección de
lecturas apropiadas.
✔ Crear en el aula un buen clima de relacionamiento, transmitiendo valores
como; solidaridad, tolerancia, equidad y respeto (cuidando así las relaciones
humanas y públicas)

4. ✔ Fomentar el trabajo de coordinación entre las diferentes disciplinas sin perder
el perfil de la asignatura( problemas, procedimientos, soluciones y modelos).
✔ Evaluar sin separar el proceso de enseñanza aprendizaje y teniendo en
cuenta: considerando el desarrollo de las macrohabilidades- competencias y a
la diversidad, basadas en múltiples inteligencias y capacidades de cada
alumno;( diferentes formas de aprendizaje) en el momento de realizar las
propuestas.
✔ Introducir el uso de las XO y las tic’s en general como una herramienta más en
el proceso de aprendizaje.
EL ALUMNO SERÁ CAPAZ DE:
✔ Desarrollar competencias y procesos que le permiten aprender matemática y
otras disciplinas
✔ Introducir el trabajo grupal con motivo de respetar las ideas y dificultades de
sus compañeros
✔ Aplicar la resolución de problemas como herramienta necesaria para la vida
cotidiana
✔ Producir el desarrollo fundamentado de sus descubrimientos procurando
luego la consolidación precisa y rigurosa en lo conceptual para motivar y
enriquecer sus capacidades.( Justificar, argumentar, mostrar)
✔ Utilizar la calculadora y la computadora con sentido crítico.
✔ Incorporar el sentido de responsabilidad y orden a través del cuaderno.

5. ESTRATEGIAS METODOLÓGICAS
En el marco de modernas y diversas estrategias metodológicas se propone desarrollar
en los alumnos habilidades -competencias tales como, deberán plantearse a los
alumnos, situaciones problemáticas que deberán resolver con los insuficientes
elementos que disponen, con el propósito de que propicié el sentido de
descubrimiento, investigación y justificación, reafirmando conocimientos o
adquiriendo nuevos, aplicando procedimientos o conceptos para su resolución ya sea
de forma conjunta, en equipo, por parejas o individualmente.
Este sistema agudizará sus conocimientos fomentando la autocrítica y haciendo
prosperar los conceptos de cooperación y socialización en el ámbito comunitario donde
se desarrolla su actividad intelectual y extendiendo estas prácticas en un futuro a su
vida como ciudadano autónomo y reflexivo, útil para la sociedad. Se implementaran
estrategias que permitan desarrollar en los alumnos las siguientes habilidades o
competencias donde se tratan de centrar la educación en el estudiante, en su
aprendizaje y en el significado funcional de dicho proceso: pensar y razonar,
argumentar, comunicar, plantear y resolver problemas, representar, utilizar el
lenguaje simbólico, formal y técnico y las operaciones.
Algunos indicadores que ejemplifican cada una de las competencias.
Pensar y Razonar
Incluye las capacidades de:
✔ Plantear cuestiones propias de las matemáticas (¿Cuántos hay? ¿Cómo
encontrarlo? Si es así, …entonces etc.).
✔ Conocer los tipos de respuestas que ofrecen las matemáticas a estas cuestiones.

6. ✔ Distinguir entre diferentes tipos de enunciados (definiciones, teoremas,
conjeturas, hipótesis, ejemplos).
✔ Entender y utilizar los conceptos matemáticos.
Argumentar
Incluye las capacidades de:
✔ Conocer lo que son las pruebas matemáticas y cómo se diferencian de otros
tipos de razonamiento matemático.
✔ Seguir y valorar cadenas de argumentos matemáticos de diferentes tipos.
✔ Disponer de sentido para la heurística (¿Qué puede (o no) ocurrir y por qué?).
✔ Crear y expresar argumentos matemáticos.
Comunicar
Incluye las capacidades de:
✔ Expresarse en una variedad de vías, sobre temas de contenido matemático, de
forma oral y también escrita,
✔ Entender enunciados de otras personas sobre estas materias en forma oral y
escrita.
Plantear y resolver problemas
Incluye las capacidades de:
✔ Plantear, formular y definir diferentes tipos de problemas matemáticos.
✔ Resolver diferentes tipos de problemas matemáticos mediante una diversidad
de vías.
Representar
Incluye las capacidades de:

7. ✔ Decodificar, interpretar y distinguir entre diferentes tipos de representación de
objetos matemáticos y situaciones, así como las interrelaciones entre las
distintas representaciones.
✔ Escoger y relacionar diferentes formas de representación de acuerdo con la
situación y el propósito.
Utilizar el lenguaje simbólico, formal y técnico y las operaciones
Incluye las capacidades de:
✔ Decodificar e interpretar el lenguaje simbólico y formal y entender sus
relaciones con el lenguaje natural.
✔ Traducir desde el lenguaje natural al simbólico y formal.
✔ Manejar enunciados y expresiones que contengan símbolos y fórmulas.
✔ Utilizar variables, resolver ecuaciones y comprender los cálculos.
La utilización de diferentes medios de comunicación al alcance de los alumnos
(informática, audiovisuales, etc…) será la vía más frecuente a proponer para lograr la
motivación.
Un punto a incrementar en el transcurso del año será todas las formas de expresión de
los alumnos fundamentalmente incentivando las competencias comunicativas escritas
y verbales promoviendo la alfabetización matemática.
MATERIAL DIDÁCTICO
Se emplearán durante el año:
✔ Pizarrón, marcadores y borrador.
✔ Fotocopias ( Resúmenes, actividades y prácticos)

8. ✔ Útiles de geometría.
✔ Material concreto.
✔ Juegos didácticos.
✔ Selección de problemas.
✔ Calculadora.
✔ Libro de Texto del curso ( Selección de lecturas)
✔ Se promoverá el uso de imágenes, videos y series de TV.
✔ Procesador “XO” (uso de la web y software que propicié la investigación de
propiedades y relaciones. Logrando los alumnos formular conjeturas e
investigar justificando sus reflexiones)
EVALUACIÓN
La misma corresponde a la sumatoria de los diversos aspectos que componen los
fundamentales elementos que habrán de determinar un ajustado resultado de la
actividad personal del alumno:
✔ Capacidad de aprendizaje.
✔ Tarea domiciliaria.
✔ Comportamiento en clase a nivel intelectual, emocional, frente al grupo y frente
al profesor.
✔ Interés en la asignatura.
✔ El cuaderno de clase.
✔ Las intervenciones orales y escritas grupales e individuales.
El promedio final estará formado por una serie de cuestiones que responde a una

9. conciencia en la aplicación de los procedimientos y actividades, como en un objetivo
análisis individual lo que habrá de conjugar en una justa evolución. Tomando en
cuenta a cada alumno con sus capacidades y respuesta en el grupo inserto en
particular. El cuaderno tendrá un papel significativo en la evaluación debido a que
para incorporar sus saberes, se permitirá el uso de su material de apoyo durante el
proceso de evaluación, para evaluar algunas de las competencias indicadas en el perfil
al que se aspira alcanzar; en evaluaciones escritas se puede pedir la realización de
actividades nuevas, contemplando diferentes dimensiones del saber ya sean cognitivas
procedimentales o actitudinales.
Al inicio del año en la etapa diagnóstica se realizan actividades grupales con fichas de
actividades y observaciones, donde se registra el proceso de aprendizaje de cada
estudiante, este mismo proceso se reiterará a lo largo del año de forma continua.
El proceso de evaluación llevara a lo largo del año incorporado una autoevaluación del
docente y a partir de los resultados obtenidos se realizaran la replanificación y ajustes
pertinentes para mejorar el proceso de enseñanza y aprendizaje.
El perfil a alcanzar será que el alumno se capaz de aplicar los conocimientos,
habilidades y destrezas en la comprensión, explicación y transformación de diferentes
fenómenos y situaciones matemáticas en la vida cotidiana.

10. DESARROLLO DEL PLAN ANUAL
Dicho programa estará fragmentado en tres grandes bloques; el primero será
geometría en el plano, el segundo números y el último será geometría en el espacio .
Bloque I: GEOMETRÍA
Dentro de este bloque lo fundamental sera la resolución de problemas, que permita al
alumno identicicar situaciones geométricas y tenga la capacidad de realizar
construcciones, en las cuales utilicen conocimientos adquiridos en años anteriores.
Otras veces serán las mismas construcciones geométricas las que generarán la
problemática a estudiar.
GEOMETRÍA EN EL PLANO
Unidad 1: Resolución de problemas que involucren el uso de concepts geométrcios, de
instrumentos de dibujo y medida
i. Conceptos primitivos: Punto, recta y plano . Notación
ii. Segmento,Semirrecta, Recta
iii.Posiciones de dos rectas en el plano
iv. Ángulo
v. Transporte de ángulos
vi. Bisectriz de un ángulo
vii. Mediatriz de un segmento
viii. Triángulos. Clasificación
ix. Construcción de triángulos con regla y compás
Unidad 2: Simetría Axial y Simetría Central. Aplicaciones

11. Bloque II: NÚMEROS
Unidad 1: Números Naturales.
➔ Definición del conjunto
➔ Orden
➔ Propiedades
➔ Operaciones combinadas (prioridad en la operatoria
➔ Desarrollar y Factorizar
➔ Potenciación y Radicación
Unidad 2: Divisibilidad
➔ Definición de división entera
➔ Definición de división exacta
➔ Divisibilidad
➔ Divisores y multiplos
➔ Múltiplos comunes
➔ Propiedades de los múltiplos
➔ Mínimo común múltiplo
➔ Máximo común divisor
➔ Criterios de divisibilidad
➔ Números primos y compuestos
➔ Descomposición en factores primos
Unidad 3: Números Enteros
➔ Definición del conjunto
➔ Orden

12. ➔ Valor absoluto de un número
➔ Operaciones en Z (adición, sustracción, multiplicación y división)
➔ Propiedades de la adición y sustracción (existencia del opuesto)
Unidad 4: Porcentaje, proporcionalidad, número decimal y fracciones
➔ Proporcionalidad Directa e inversa
➔ Determinación del coeficiente de proporcionalidad
➔ Cálculo de porcentajes (resolución de problemas en diversas áreas)
➔ Regla de tres
➔ Porcentaje de aumento y de rebaja
➔ Conocer diveras formas de representar una fracción
➔ Representación de fracciones en la la recta numérica
➔ Fracciones equivalentes
➔ Simplificación de fracciones
➔ Comaparación y ordenación de fracciones
➔ Operaciones con fracciones
➔ Número decimal
➔ Operaciones con fracciones y números decimales
Bloque III: GEOMETRÍA EN EL ESPACIO
➔ Rectas y planos en el espacio
➔ Descripción y representación de prismas, cilindros, pirámides y conos
➔ Cálculo de volúmenes

13. CRONOGRÁMA
MARZO
1er
SEMANA 2da
SEMANA 3ra
SEMANA 4ta
SEMANA 5ta
SEMANA
1. Adaptación
de los alumnos
2. “Iniciando la
vida Liceal”
Etapa
Diagnósticos
TURISMO
1. Corrección de
la Prueba
diagnótica
2. Rolución de
Problemas
1. Conceptos
primitivos
2. Posición de
rectas
3. Segmento,
recta,
semirrecta
3. Ejercicios
ABRIL
1. Clasificación
de los ángulos
1. Bisectriz de
un ángulo
2. Propiedades
de la bisectriz
3. Transporte de
ángulos
4. Mediatriz de
un segmento
1.
Construcciones
con regla y
compas
2. Protocolo de
construcción
3. ESCRITO
1. Clasificación
de triángulos
2.
Construcciones
cn regla y
compas de
Triángulos
1. Corrección del
escrito
MAYO
1.Construcciónes de triángulo con regla y
compaz. Protocolo de construcción
1. Simetría
Axial
2.Simetría
Central
3. Ejercicios de
simetrías
1. Corrección
de los ejercicios
del Práctico
JUNIO
1. ESCRITO
2. Corrección
del escrito
3. Número
Naturales
1. Definición del
conjunto
2. Orden
3. Propiedades
1. Desarrollar y
Factorizar
2. Practico
1. Operaciones
combinadas
(prioridad en la
operatoria
VACACIONES
JULIO
VACACIONES
1. Prueba
Parcial
2. Corrección de
la Prueba Parcial
3.Definición de
división entera
4. Definición de
división exacta.
1. Corrección del
Practico
2. Potenciación y
radicación
1.Divisibilidad
2.Múltiplos y
divisores.
Propiedades
3. m.c.m
4.m.c.d

14. AGOSTO
1er
SEMANA 2da
SEMANA 3ra
SEMANA 4ta
SEMANA 5ta
SEMANA
1.Criterios de
Diviibilidad
2. Números
Primos y
compuestos
1.
Descomposición
en factores
primos.
2. Practico
3. Corrección
del Practico
1. Valor
absoluto
2. Operaciones
en Z
1. Número
Entero
2. Definicón del
conjunto
3. Orden
1. Propiedades
de la adicion,
sustracción
(existencia del
opuesto)
SETIEMBRE
1.ESCRITO
2. Corrección
del escrito
3.
Proporcionalida
d directa
1. Prop. inversa
2. Calculo de
porcentaje
3. Regla de tres
4. Porcentaje de
aumento y
rebaja
1. Operaciones
(adición,
sustacción,
multiplicación y
división)
2.
VACACIONES
1.Fracciones
(representacion)
2.Fracciones
equivalentes
3. simplificación
y comparación
1. Operaciones
(adición,
sustacción,
multiplicación y
división
OCTUBRE
NOVIEMBRE Geometría del Espacio
1. Geometría
del Espacio
2. Prueba final
1.Corrección
de la prueba
final
DICIEMBRE
Fin de Cursos
1. Número
decimal
2. Operaciones
con fracciones y
decimales.
3. Practico
PRACTICO

15. BBIBLIOGRAFÍA
Para el alumno:
✔ Matemática1º- Prácticas Santillana. Ed. Bicentenario. Montevideo, 2011.
✔ "COLECCIÓN GAUSS tomos 1,2 y 3." Luis Belcredi, Mónica Zambra. Editorial la flor de
Itapebí, Montevideo, 1998
✔ "Matemáticas1." Luis Pancorbo, Ma. Victoria Becerra, Rafael Martínez, Rosario
Rodríguez. Impreso en Torán S.A.
✔ "Matemática 1 curso". Autores: Juliana Cabrera, Alicia Fort, María Sánchez.
✔ “Matemática c. b. 1º parte uno y dos “Autor: M. Bonifacino, C Fernández, M. González.
1996-Monteverde – Montevideo (Uruguay).
✔ “Matemática 1º ESO” Autores: Francisco González, Carmen López, Begoña Martínez,
✔ Matemática 1º” Grupo Botadá: M. Barbonet, B.Burgos, Ana S. Martínez, N. Ravaioli.
Colección textos de Fín de Siglo. 2008- Montevideo (Uruguay).
✔ “Matemática 1º” Luis Belcredi y Mónica Zambra. Nuevos Mosaicos Ediciones de la
Plaza. 2009- Montevideo (Uruguay).
✔ "Matemáticas 1°" B. Sánchez, J Agrasot - 1991-Editorial Técnica SRL. Montevideo.
✔ “Matemática 1º ESO” Autores: Luis Pancorbo, Ma. Becerra, R. Martínez, R. Rodriguez
-1995- Mc Graw Hill. (España)
Para el docente:
✔ “Juegos matemáticos para secundaria y bachillerato”. F. Corbalán. Editorial Síntesis
✔ "La matemática aplicada a la vida cotidiana." F. Corbalán.
✔ “Geometría métrica, plano y espacio” W. F. Val
✔ “Geometría metríca” P. Adam. Euler Editorial
✔ “Calculus vol. I y II” T. Apostol. Editorial Reverté