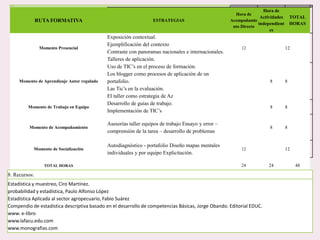
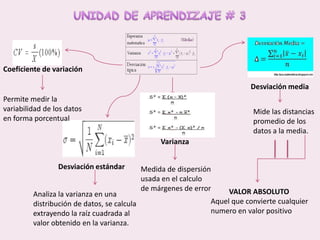
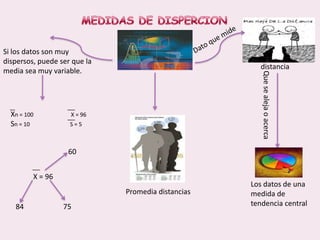
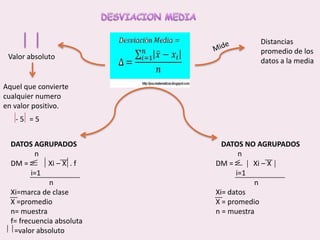
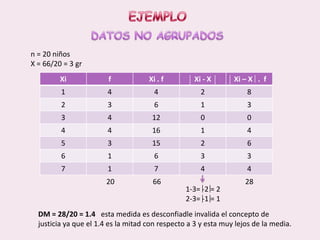
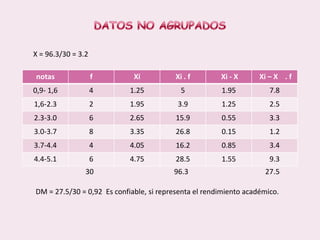
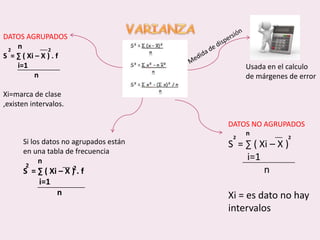
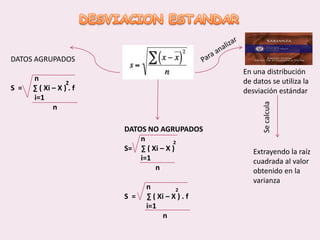
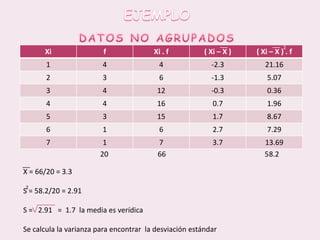
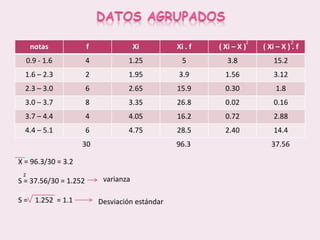
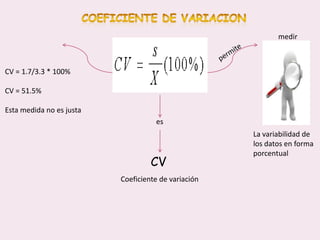
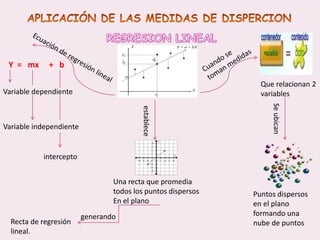
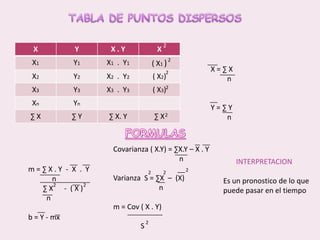
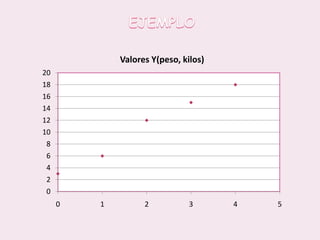
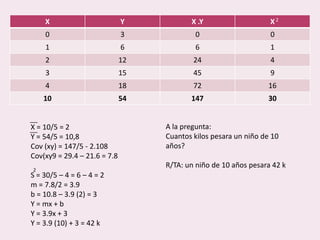
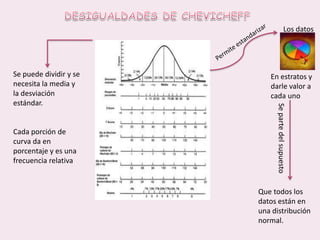
Este documento contiene las hojas de vida de tres estudiantes de contaduría pública y conceptos sobre estadística descriptiva como desviación media, varianza, desviación estándar, coeficiente de variación y regresión lineal. También incluye ejemplos de cálculo de estas medidas y su aplicación en la estimación de pesos de niños.

1. PORTAFOLIOESTADISTICA DESCRIPTIVA

2. ESTADISTICA DESCRIPTIVA DOCENTE: ALEJANDRO OBANDOINTEGRANTES: CARLOS RUEDA YENNY QUINTERO ANDREA CERONgrupo : 504 UNIVERSIDAD COOPERATIVA DE COLOMBIACONTADURIA PUBLICA III SEMESTRE

3. IDENTIFICACION

4. HOJA DE VIDACARLOS RUEDANOMBRE: CARLOS ENRIQUE RUEDA OLMOSFECHA DE NACIMIENTO 23 DE AGOSTO DEL 1990LUGAR DE NACIMIENTO: BOGOTA D.CESTADO CIVIL: SOLTERODIRECCION: CLL 24B No 19B-34 CANAIMATELEFONO 311 503 5366ESTUDIOS REALIZADOSBACHILLER: NORMAL SUPERIOR DE V/CIOTECNICO: CONTABILIDAD Y FINANZASUNIVERSIDAD: COOPERATIVA DE COLOMBIA

5. HOJA DE VIDAYENNY SULAY QUINTERONOMBRE: YENNY SULAY QUINTERO BOHORQUEFECHA DE NACIMIENTO 28 DE DICIEMBRE DEL 1985LUGAR DE NACIMIENTO: VILLAVICENCIO METAESTADO CIVIL: SOLTERADIRECCION: ALTOS DE PANORAMA IITELEFONO 3202366377ESTUDIOS REALIZADOSPRIMARIA: ESCULA EL JORDANSEGUNDARIA: COLEGIO JUANPABLO IITECNICO: SECRETARIADO CONTABLEUNIVERSIDAD: COOPERATIVA DE COLOMBIA

6. HOJA DE VIDAANDREA CERON CHAVEZ INFORMACION PERSONALFecha de Nacimiento 04 Febrero 1980 Lugar de Nacimiento Cosaca - Nariño. Estado Civil: Soltera Edad: 30 Años Tel: 3132706474 Dirección: Cll 35D # 20C–21 Jordán reservado e-mail: ceronchavez@hotmail.com FORMACION ACADEMICAPrimaria: Centro educativo mercedario Pasto – Nariño 1991Secundaria: Colegio Sta. Rita de Casia Villavicencio-Meta 1997Universitarios: Universidad Cooperativa de Colombia IIISem contaduría publica 2.010

7. LEGAL

11. UNIDAD DE APRENDIZAJE # 3Coeficiente de variaciónDesviación mediaPermite medir la variabilidad de los datos en forma porcentualMide las distancias promedio de los datos a la media.VarianzaDesviación estándarMedida de dispersión usada en el calculo de márgenes de errorVALOR ABSOLUTOAquel que convierte cualquier numero en valor positivoAnaliza la varianza en una distribución de datos, se calcula extrayendo la raíz cuadrada al valor obtenido en la varianza.

12. TERCER CORTE

13. MEDIDAS DE DISPERCIONDato que mideSi los datos son muy dispersos, puede ser que la media sea muy variable.distanciaQue se aleja o acercaXn = 100 X = 96Sn = 10 S = 560X = 96Los datos de una medida de tendencia centralPromedia distancias7584

14. DESVIACION MEDIADistancias promedio de los datos a la mediaMide Valor absolutoAquel que convierte cualquier numero en valor positivo.- 5 = 5DATOS AGRUPADOS nDM = Xi – X . f i=1 nXi=marca de claseX =promedion= muestraf= frecuencia absoluta =valor absoluto DATOS NO AGRUPADOS nDM = Xi – X i=1 nXi= datosX = promedion = muestra

15. EJEMPLODATOS NO AGRUPADOSn = 20 niñosX = 66/20 = 3 gr 20 66 281-3= -2 = 22-3= -1 = 1DM = 28/20 = 1.4 esta medida es desconfiadle invalida el concepto de justicia ya que el 1.4 es la mitad con respecto a 3 y esta muy lejos de la media.

16. DATOS NO AGRUPADOSX = 96.3/30 = 3.2 30 96.3 27.5DM = 27.5/30 = 0,92 Es confiable, si representa el rendimiento académico.

17. VARIANZADATOS AGRUPADOSnS = ∑ ( Xi – X ) . f i=1 nXi=marca de clase ,existen intervalos.Medida de dispersión22Usada en el calculo de márgenes de errorDATOS NO AGRUPADOSnS = ∑ ( Xi – X ) i=1 nXi = es dato no hay intervalos22Si los datos no agrupados están en una tabla de frecuencianS = ∑ ( Xi – X ) . f i=1 n22

18. DESVIACION ESTANDARPara analizarDATOS AGRUPADOSnS = ∑ ( Xi – X ) . f i=1 nEn una distribución de datos se utiliza la desviación estándar2Se calcula DATOS NO AGRUPADOS n S= ∑ ( Xi – X ) i=1 nn S = ∑ ( Xi – X ) . f i=1 n2Extrayendo la raíz cuadrada al valor obtenido en la varianza 2

19. EJEMPLODATOS NO AGRUPADOS2 20 66 58.2X = 66/20 = 3.3S = 58.2/20 = 2.91S = 2.91 = 1.7 la media es verídicaSe calcula la varianza para encontrar la desviación estándar 2

20. DATOS AGRUPADOS22 30 96.3 37.56X = 96.3/30 = 3.2S = 37.56/30 = 1.252S = 1.252 = 1.12varianzaDesviación estándar

21. COEFICIENTE DE VARIACIONmedirpermite CV = 1.7/3.3 * 100% CV = 51.5% Esta medida no es justa esLa variabilidad de los datos en forma porcentualCVCoeficiente de variación

22. APLICACIÓN DE LAS MEDIDAS DE DISPERCION REGRESION LINEALCuando se toman medidasEcuación de regresión linealY = mx + bQue relacionan 2 variablesVariable dependienteSe ubican estableceVariable independiente interceptoUna recta que promedia todos los puntos dispersosEn el planoPuntos dispersos en el plano formando una nube de puntosgenerandoRecta de regresión lineal.

23. TABLA DE PUNTOS DISPERSOS22X = ∑ X nY = ∑ Y n222FORMULASCovarianza ( X.Y) = ∑X.Y – X . Y nVarianza S = ∑X – (X) nm = Cov ( X . Y) S INTERPRETACIONEs un pronostico de lo que puede pasar en el tiempom = ∑ X . Y - X . Y n ∑ X - ( X ) nb = Y - mx222222

24. EJEMPLO

25. 2A la pregunta:Cuantos kilos pesara un niño de 10 años?R/TA: un niño de 10 años pesara 42 kX = 10/5 = 2Y = 54/5 = 10,8Cov (xy) = 147/5 - 2.108Cov(xy9 = 29.4 – 21.6 = 7.8S = 30/5 – 4 = 6 – 4 = 2m = 7.8/2 = 3.9b = 10.8 – 3.9 (2) = 3Y = mx + bY = 3.9x + 3Y = 3.9 (10) + 3 = 42 k 2

26. DESIGUALDADES DE CHEVICHEFFLos datosPermite estandarizarSe puede dividir y se necesita la media y la desviación estándar.Cada porción de curva da en porcentaje y es una frecuencia relativaEn estratos y darle valor a cada unoSe parte del supuestoQue todos los datos están en una distribución normal.