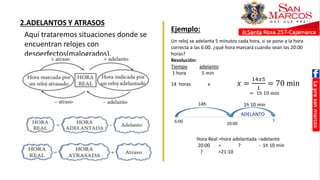
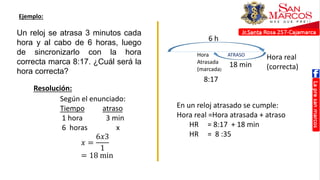
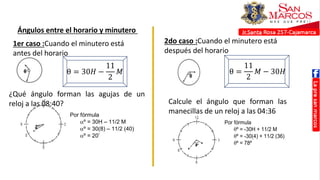
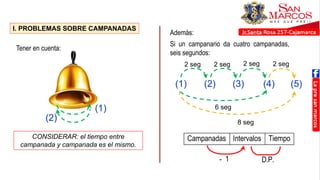
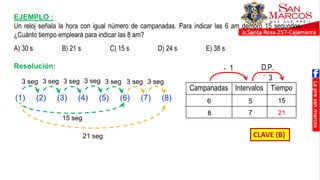
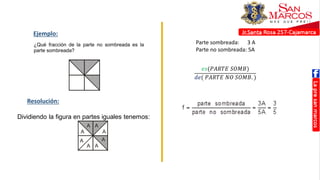
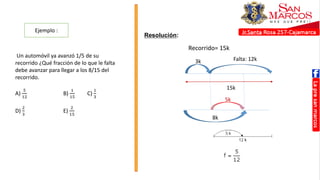
Este documento presenta temas sobre cronometría y fracciones. En la sección de cronometría, se explican problemas sobre tiempo transcurrido y por transcurrir usando esquemas lineales. También se cubren temas como adelantos y atrasos de relojes. La sección de fracciones incluye reducción a la unidad, fracciones de fracciones, y problemas con mezclas y partes.

1. Curso: Razonamiento matemático
UNC 2022
DOCENTE: Kerry Cárdenas Ronceros
ACADEMIA PRE UNIVERSITARIA
TEMA: Cronometría y Fracciones

2. CRONOMETRÍA I
1.Problemas sobre tiempo transcurrido
y por transcurrir
En este tipo de problemas para su mejor
comprensión y análisis emplearemos un
esquema lineal donde se ubique en primer
lugar la hora actual y luego los tiempos de
referencia que se indicarán en cada
enunciado. HORA
Tiempo
transcurrido
Tiempo que falta
transcurrir
1 día <> 24 horas
x 24-x
Ejemplo:¿Qué hora es, si el tiempo
transcurrido del día es 1/5 del tiempo que
falta transcurrir?
Resolución:
HORA
x 24-x
1 día <> 24 horas
Dato: X =
1
5
(24-X)
5X=24-X
X=4
∴ son las 4 am

3. OTRA FORMA :
1 día <> 24 horas
HORA
a 5a
Luego:
a+ 5a =24
a = 4
∴ son las 4 am
Ejemplo:
¿Qué día es del mes de junio , si los
días que faltan transcurrir son 2/3 de
los días transcurridos?
junio <> 30 días
DÍA
n 30-n
Dato: 30-n =
2
3
(n)
90-3n=2n
n=18
∴ es el 18 de junio

4. EJEMPLO :

5. EJEMPLO :
Si el doble de las horas transcurridas en un día es
igual al cuádruple de las que faltan transcurrir.
¿Qué hora es?
Resolución:
Según el enunciado: 2x = 4(24 – x)
2x = 96 – 4x
6x = 96
x = 16
 Son las 4:00 p.m.
EJEMPLO :
Faltan para las 8:00 a.m. la mitad de los minutos
que pasarán desde las 6:00 a.m. de esta mañana
hasta la hora actual. ¿Qué hora indica el reloj?
Resolución:
2x + x = 120  3x = 120  x = 40 min
Hora exacta: 6 h + 2x = 7:20

6. 2.ADELANTOS Y ATRASOS
Ejemplo:
Un reloj se adelanta 5 minutos cada hora, si se pone a la hora
correcta a las 6:00. ¿qué hora marcará cuando sean las 20:00
horas?
Resolución:
Tiempo adelanto
1 hora 5 min
14 horas x 𝑥 =
14𝑥5
1
= 70 min
= 1h 10 min
Aquí trataremos situaciones donde se
encuentran relojes con
desperfectos(malogrados).
20:00
6:00 ?
ADELANTO
14h 1h 10 min
Hora Real =hora adelantada –adelanto
20:00 = ? - 1h 10 min
? =21:10

7. Un reloj se atrasa 3 minutos cada
hora y al cabo de 6 horas, luego
de sincronizarlo con la hora
correcta marca 8:17. ¿Cuál será la
hora correcta?
Ejemplo:
Resolución:
Según el enunciado:
Tiempo atraso
1 hora 3 min
6 horas x
𝑥 =
6𝑥3
1
= 18 min
Hora real
(correcta)
Hora
Atrasada
(marcada)
6 h
18 min
ATRASO
8:17
En un reloj atrasado se cumple:
Hora real =Hora atrasada + atraso
HR = 8:17 + 18 min
HR = 8 :35

8. EJEMPLO :
Un reloj se adelanta 10 minutos cada hora. Si son
las 8:00 a.m. ¿Qué hora marcará el reloj a las 2
p.m.?
Resolución:
El tiempo transcurrido desde las 8:00 a.m.
hasta las 2 p.m. es 6 horas.
Entonces:
1 h - - - - 10 min
6 h - - - - x
 x = 60 min  1h
Luego, la hora que marca es:
2 p.m. + 1 h = 3 p.m.
EJEMPLO :
Un reloj se retrasa 10 minutos por día. ¿En cuántos
días volverá a marcar la hora exacta?
Resolución:
Para que vuelva a marcar la hora exacta se
debe retrasar 12 h = 720 min.
Luego:
10 min - - - - 1 día
720 min - - - - x
10x = 720  x = 72 días

9. CRONOMETRÍA II
RELOJES
x12
𝑅𝑒𝑐𝑜𝑟𝑟𝑖𝑑𝑜 𝑑𝑒𝑙 ℎ𝑜𝑟𝑎𝑟𝑖𝑜
𝑅𝑒𝑐𝑜𝑟𝑟𝑖𝑑𝑜 𝑑𝑒𝑙 𝑚𝑖𝑛𝑢𝑡𝑒𝑟𝑜
=
1
12

10. Ángulos entre el horario y minutero
1er caso :Cuando el minutero está
antes del horario
θ = 30𝐻 −
11
2
𝑀
2do caso :Cuando el minutero está
después del horario
θ =
11
2
𝑀 − 30𝐻
¿Qué ángulo forman las agujas de un
reloj a las 08:40?
Por fórmula
º = 30H – 11/2 M
º = 30(8) – 11/2 (40)
º = 20’
Calcule el ángulo que forman las
manecillas de un reloj a las 04:36
Por fórmula
º = -30H + 11/2 M
º = -30(4) + 11/2 (36)
º = 78º

11. I. PROBLEMAS SOBRE CAMPANADAS
Tener en cuenta:
(1)
(2)
CONSIDERAR: el tiempo entre
campanada y campanada es el mismo.
Además:
Si un campanario da cuatro campanadas,
seis segundos:
(1) (2) (3) (4)
6 seg
2 seg 2 seg 2 seg
(5)
2 seg
8 seg
Campanadas Intervalos Tiempo
1
- D.P.

12. Ejemplo:
Un campanario tarda 8 segundos en
dar 5 campanadas. ¿Cuánto tiempo
tardará en dar 8 campanadas?

13. EJEMPLO :
Un reloj señala la hora con igual número de campanadas. Para indicar las 6 am demoró 15 segundos.
¿Cuánto tiempo empleará para indicar las 8 am?
A) 30 s B) 21 s C) 15 s D) 24 s E) 38 s
(1) (2) (3) (4) (5) (6)
15 seg
3 seg 3 seg 3 seg 3 seg 3 seg
(7) (8)
3 seg 3 seg
21 seg
Campanadas Intervalos Tiempo
1
- D.P.
6 5 15
8 7
3
´
21
CLAVE (B)
Resolución:

14. FRACCIONES
FRACCIÓN DE FRACCIÓN
DE
DEL
DE LOS
ES
SON
REPRESENTA
X =
Donde a y b ∈ 𝑍+ ∧ a≠ ሶ
𝑏

15. Ejemplo:
¿Cuánto le debemos quitar a los 2/3 de los
5/7 de los 6/5 de los 3/4 de 21 para que sea
igual a la mitad de 1/3 de 2/5 de 3/4 de 80?
2
3
𝑥
5
7
𝑥
6
5
𝑥
3
4
𝑥21
9 4
9 –x = 4
x = 5
− 𝑋 =
1
2
𝑥
1
3
𝑥
2
5
𝑥
3
4
𝑥80

16. Ejemplo:
¿Qué parte de 15 es 10?
X. 15=10
X=
10
15
X=
2
3
Otra forma:
Ejemplo:
¿Qué parte de 18 es 27?
𝑒𝑠
𝑑𝑒
27
18
=
3
2

17. Ejemplo:
¿Qué fracción de la parte no sombreada es la
parte sombreada?
Dividiendo la figura en partes iguales tenemos:
A A
A A
A
A
A
A
Parte sombreada: 3 A
Parte no sombreada: 5A
𝑒𝑠(𝑃𝐴𝑅𝑇𝐸 𝑆𝑂𝑀𝐵)
𝑑𝑒( 𝑃𝐴𝑅𝑇𝐸 𝑁𝑂 𝑆𝑂𝑀𝐵. )
Resolución:

19. Dos tercios de los profesores de un colegio son
mujeres. Doce de los profesores varones son
solteros, mientras que los 3/5 son casados. ¿Cuál
es el número de profesores?
Ejemplo:
Resolución:
Número de profesores: P

20. FRACCIÓN CON MEZCLA
Ejemplo:
En un depósito hay 30 litros de vino y 40
litros de agua. Si al extraer cierta cantidad de
la mezcla en el depósito quedan 24 litros de
agua, qué cantidad de mezcla se ha retirado.
Se extrae
Vino
Agua

21. REDUCCIÓN A LA UNIDAD
Ronaldo hizo 240 pataditas en 10 minutos
¿Cuántas pataditas hizo en 1 min?
240 𝑝𝑎𝑡𝑎𝑑𝑖𝑡𝑎𝑠
10 𝑚𝑖𝑛𝑢𝑡𝑜𝑠
=
24 𝑝𝑎𝑡𝑎𝑑𝑖𝑡𝑎𝑠
1 𝑚𝑖𝑛𝑢𝑡𝑜
En 1 minuto hizo 24 pataditas .
Es el procedimiento mediante
el cual se calcula la parte de la
obra realizada en cada unidad
de tiempo
Ejemplos:
2h-------1 examen
1h-------
1
2
examen
30 min-----1 tanque
1min-------
1
30
tanque
18 días----1 obra
1día-------
1
18
obra
X horas-----1 trabajo
1hora------
1
𝑥
trabajo

22. Un obrero puede realizar un trabajo solo
en 20 horas, otro obrero puede hacerlo
en 30 horas. Si trabajan los dos juntos,
qué tiempo se tardarán en realizar dicho
trabajo?
A) 15 h B) 12 h C) 23 h
D) 18 h E) 16 h
1
t 20h

2
t 30h

Por reducción a la unida
tenemos:
1 1 1
T 12h
20 30 T
   
Tiempo (1er obrero) =20 h
Tiempo( 2do obrero)=30 h
Tiempo de ambos= T
Ejemplo: 1er obrero
En 1 hora
2do obrero
En 1 hora
Los 2 juntos
En 1 hora
1
20
1
30
1
𝑇
Por reducción a la unidad tenemos :
Resolución:
30 + 20
20𝑥30
=
1
𝑇
50T=600
T=12 h

23. OTRA FORMA:
Caño A Caño B Los 2 juntos
4h 6h X h
1
4
1
6
1
𝑋
1
4
+
1
6
=
1
𝑋
X=
12
5
h = 2
2
5
h

24. Ejemplo :
Resolución:
En una reunión de 38 personas, se
observa que la quinta parte de las
mujeres son delgadas y la séptima parte
de los hombres son gordos. ¿Cuántos
hombres son delgados?
A) 8 B) 12 C) 18
D) 24 E) 32
RESOLUCIÓN
H + M = 38
7 h + 5 m = 38
4 2
Gordos:
1
7
 H =28
Delgados:  
6
28 24
7

RESOLUCIÓN
H + M = 38
7 h + 5 m = 38
4 2
Gordos:
1
7
 H =28
Delgados:  
6
28 24
7

RESOLUCIÓN
H + M = 38
7 h + 5 m = 38
4 2
Gordos:
1
7
 H =28
Delgados:  
6
28 24
7

RESOLUCIÓN
H + M = 38
7 h + 5 m = 38
4 2
Gordos:
1
7
 H =28
Delgados:  
6
28 24
7


25. Ejemplo :
Resolución:
Si 1/5 de “x” es igual a los 2/5 de “y”, ¿qué
parte de (2x+y) es (x - y)?
A) 1/3 B) 2/3 C) 1/5
D) 2/5 E) 3/5
1
5
𝑋 =
2
5
Y
X=2Y
𝑒𝑠(𝑋 − 𝑌)
𝑑𝑒( 2𝑋 + 𝑌)
F=
2𝑌−𝑌
2 2𝑌 +𝑌
=
𝑌
5𝑌
=
1
5

26. Ejemplo :
Resolución:
Un automóvil ya avanzó 1/5 de su
recorrido ¿Qué fracción de lo que le falta
debe avanzar para llegar a los 8/15 del
recorrido.
A)
5
12
B)
1
15
C)
1
3
D)
2
3
E)
2
15
Recorrido= 15k
15k
3k Falta: 12k
8k
5k

27. Ejemplo :
Resolución:
1. Dos señoras compran una bolsa
cada una del mismo detergente; la
primera emplea los
4
7
en su
lavado, mientras que la segunda
emplea los
2
5
del suyo. ¿Qué
fracción del total comprado queda
sin usar?
A)
36
35
B)
9
17
C)
18
35
D)
12
35
E)
6
35
RESOLUCIÓN
4
7

1
S : B
3
B
7
2
5

2
S : B
3
B
5
Total comprado: 2B
Queda sin usar:
3 3 36
B B B
7 5 35
 
36
18
35
f
2 35
 
RESOLUCIÓN
4
7

1
S : B
3
B
7
2
5

2
S : B
3
B
5
Total comprado: 2B
Queda sin usar:
3 3 36
B B B
7 5 35
 
36
18
35
f
2 35
 
RESOLUCIÓN
4
7

1
S : B
3
B
7
2
5

2
S : B
3
B
5
Total comprado: 2B
Queda sin usar:
3 3 36
B B B
7 5 35
 
36
18
35
f
2 35
 

28. Ejemplo :
Resolución:
Un estudiante tiene que resolver cierta
cantidad de problemas en 3 días. El
primer día resuelve 3/10 del total, el
segundo 4/7 del resto y el último día los
27 restantes. ¿Cuántos problemas
resolvió?
A) 120 B) 100 C) 90
D) 80 E) 70
Sea “x” la cantidad de problemas que resolvió
lo que iba quedando.
3 7
x 27
7 10
270
x
3
x 90



NUMERO DE PROBLEMAS = X
1er día
3
10
2er día
4
7
Queda:
7
10
3
7
Queda:
7
10
.
3
7
. X = 27

29. Ejemplo :
1. En un depósito se mezcla 30 litros
de agua y 50 litros de leche; luego
se extrae 16 litros de la mezcla y
se le reemplaza por la misma
cantidad de agua. Si de la nueva
mezcla se extrae 18 litros,
¿Cuántos litros de leche salen?
A) 5 B) 6 C) 8
D) 9 E) 10
RESOLUCIÓN
Agua: 30
3
8
Leche: 50
5
8
Agua: 6 Agua: 24
64
Leche: 10 Leche: 40
+ 16 agua
Agua: 40
1
2
Leche: 40
1
2
Agua: 9
Leche: 9
80
-16
80
-18
Resolución:
RESOLUCIÓN
Agua: 30
3
8
Leche: 50
5
8
Agua: 6 Agua: 24
64
Leche: 10 Leche: 40
+ 16 agua
Agua: 40
1
2
Leche: 40
1
2
Agua: 9
Leche: 9
80
-16
80
-18
RESOLUCIÓN
Agua: 30
3
8
Leche: 50
5
8
Agua: 6 Agua: 24
64
Leche: 10 Leche: 40
+ 16 agua
Agua: 40
1
2
Leche: 40
1
2
Agua: 9
Leche: 9
80
-16
80
-18