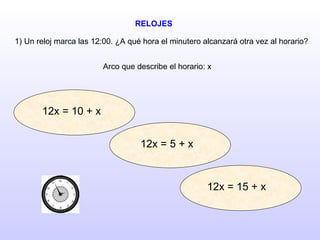
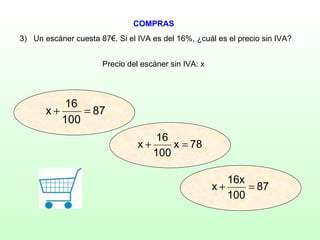
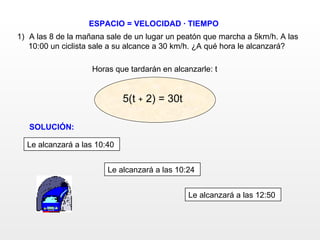
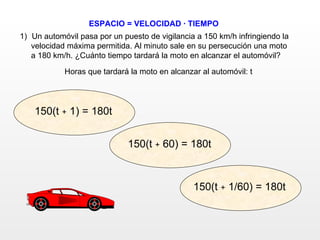
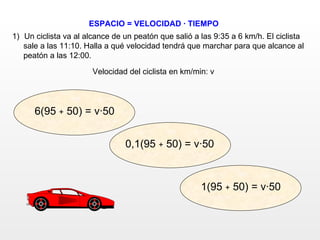
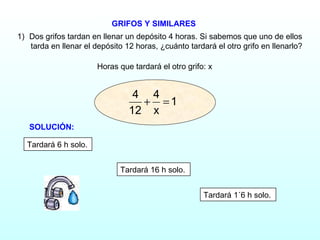
Este documento presenta una serie de 10 problemas de ecuaciones de primer grado. Cada problema contiene un enunciado y tres opciones de respuesta, de las cuales solo una es correcta. El objetivo es seleccionar la opción correcta para cada problema. Al final, se indica que se han acertado todos los problemas correctamente.