2010 i semana 13

UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS
Universidad del Perú, DECANA DE AMÉRICA
CENTRO PREUNIVERSITARIO
Habilidad Verbal
SEMANA 13 A
EL TEXTO NARRATIVO
Las narraciones ponen en juego una trama en la que el desarrollo de
acontecimientos es el eje fundamental. Los textos narrativos más útiles para los fines de
medir la capacidad académica son los que sazonan la narración con ciertas reflexiones
que le dan densidad conceptual a la estructura diegética (la configuración de la historia).
TEXTO DE EJEMPLO
Alcalde de corte en 1752 era el licenciado D. Gonzalo de Vallés. Una mañana
encaminose a la cárcel de la Pescadería para despachar con destino al presidio de
Chagres trece reos condenados a expiar allí sus delitos durante quince años.
Despidiéndose de uno de los reos, sentenciado por ladrón y asesino, hallábase su
hermana, una bellísima mulata, la que se arrojó a los pies de D. Gonzalo pidiéndole la
libertad del pez. El demonio de la lujuria mordió los sentidos del licenciado, y a trueque de
los apetitosos favores de la muchacha, convino en sacrificar sus deberes de juez y su
conciencia de hombre.
Pero presentábase una pequeña dificultad. Siendo trece los condenados, había que
arbitrar la manera de no cambiar el número. El Sr. De Vallés mandó poner preso al
primer pobre diablo que pasara por la calle, y haciéndose sordo a sus protestas lo envió,
poco después de oraciones, al Callao en trahilla. El buque que debía transportarlos al
presidio zarpó aquella misma noche llevando junto con los doce pícaros al honradísimo
leñador, que dejaba mujer e hijos, ignorantes del cruel destino que le había cabido.
Quince años pasó el infeliz en Chagres devorando en silencio su amargura, pero
acariciando un pensamiento de legítima venganza. En 1767 ocupaba ya D. Gonzalo de
Vallés plaza de oidor en la Real Audiencia de Lima; y una tarde en que regresaba de su
cotidiano paseo por la Alameda, al pasar bajo el arco del Puente arrojose sobre él un
hombre, y clavándole un puñal en el pecho, le dijo:
—Yo soy Tomás el leñador, a quien tuvo su señoría quince años en el presidio.
Y empapándose las manos en la sangre caliente que a borbotones salía de la
herida, y bañándose con ella la cabeza, exclamó con una espantosa carcajada:
—¡Ya me lavé las canas que me salieron en el presidio de Chagres!
En el acto Tomás fue sentenciado «a horca, cortándole antes el verdugo la mano
derecha». Y habríase cumplido la terrible sentencia a no existir en la escolta del virrey
Amat un soldado, hijo del leñador, quien puso en antecedentes a su excelencia, el
justificado Amat envió la causa a España, y en 1769 volvió ésta con el real y definitivo
fallo. Su majestad declaraba que el oidor Vallés había sido muerto en buena ley, y que de
sus bienes se pagara a Tomás durante su vida una pensión de diez pesos fuertes al mes.
Solucionario de la semana Nº 13 Pág. 1

1. El fallo real significó, en última instancia, un
A) error irreparable. B) equívoco más. C) acto de justicia.
D) deslinde casual. E) favor interesado.
Solución:
El fallo real se sustentó en un análisis y en un concepto de justicia retributiva.
Clave: C
2. Es incompatible afirmar que la exclamación «¡YA ME LAVÉ LAS CANAS…!»
connote
A) frenesí. B) venganza. C) denuedo.
D) ecuanimidad. E) vehemencia.
Solución:
Es un gesto que lo muestra desquiciado.
Clave: D
3. En virtud del sentido del texto, se puede inferir que un crimen
A) es siempre un acto abominable.
B) puede tener alguna justificación.
C) es moralmente irreprochable.
D) merece perdón en todos los casos.
E) siempre debe recibir un gran castigo.
Solución:
El texto dice: Quince años pasó el infeliz en Chagres devorando en silencio su
amargura, pero acariciando un pensamiento de LEGÍTIMA venganza.
Clave: B
4. La expresión ARBITRAR puede entenderse como
A) inhibirse. B) abstenerse. C) resolver.
D) restablecer. E) castigar.
Solución:
Arbitrar es dar una resolución.
Clave: C
5. Se infiere que Gonzalo de Vallés no pudo hacer nada, pues el ataque del leñador fue
A) súbito. B) tardío. C) inminente.
D) elusivo. E) incruento.
Solución:
Fue un acto tan súbito que impidió cualquier defensa.
Clave: A
6. Se deduce del texto que Gonzalo de Vallés actuaba bajo el imperio de

A) la magnificencia. B) la sindéresis. C) la venganza.
D) la insania. E) la lascivia.
Solución:
Liberó al delincuente por el pedido de la hermosa mulata que despertó en él un
deseo pasional, lascivo.
Clave: E
7. En el relato, la sentencia del Rey se presenta como
A) intempestiva. B) irracional. C) apresurada.
D) inapelable. E) hiperbólica.
Solución:
Se trata de un fallo definitivo, o sea, inapelable.
Clave: D
8. En síntesis, el relato presenta una historia
A) cuya génesis es un acto de injusticia y se resuelve con un acto de venganza
justificado por el monarca español.
B) un tanto tétrica y pasmosa que se centra en los arrebatos violentos de un leñador,
muy pobre pero honrado.
C) detallada sobre las injusticias cometidas por las autoridades virreinales y la
manera cómo eran castigadas.
D) que trata de poner de relieve el criterio de justicia en las autoridades más altas
del imperio de España.
E) que describe con lujo de detalles las artimañas cometidas por Gonzalo de Vallés
para llegar al cargo de oidor.
Solución:
La historia presenta un acto de injusticia (la condena de un inocente) y el acto de
legítima venganza justificado por el monarca.
Clave: A
COMPRENSIÓN DE LECTURA
TEXTO 1
En la náutica se conoce como espolón a la prolongación de la proa de un buque de
guerra ubicada por debajo de la línea de flotación que es usada para embestir y
eventualmente hundir a otras embarcaciones. El espolón fue inventado por los fenicios en
el siglo VIII a. C. Fue usado durante la antigüedad y era una parte importante de las
galeras fenicias, griegas y romanas. El uso de la artillería en el siglo XV tuvo como
consecuencia el fin de su utilización como arma de guerra.
El espolón tuvo un breve renacimiento durante la segunda mitad del siglo XIX,
debido a la incapacidad de la artillería naval para penetrar el blindaje de la primera
generación de buques acorazados, es así como el espolón fue usado por el blindado
peruano Huáscar para hundir a la corbeta Esmeralda en el combate naval de Iquique
durante la guerra del Pacífico.

El único uso efectivo del espolón entre blindados en tiempos de guerra se dio
durante la batalla de Lissa entre Austria e Italia. El blindado italiano Re d'Italia, dañado y
sin gobierno, fue espoloneado por el blindado austriaco Ferdinand Max, buque insignia del
almirante Tegetthoff. El buque austriaco resultó indemne, mientras que el buque italiano
zozobró y se hundió. Ningún otro buque blindado fue hundido por un buque enemigo
mediante el uso del espolón. Sin embargo, el espolón fue considerado el arma principal
de los buques blindados durante más de treinta años por las marinas más importantes del
mundo. Resulta curioso el hecho de que varios buques resultaran espoloneados por otros
de sus propias escuadras en tiempos de paz.
A fines del siglo XIX, la introducción del cañón de retrocarga, que era capaz de
penetrar el blindaje a grandes distancias, marcó el fin del espolón como arma de guerra.
1. El término BLINDAJE implica
A) ataque. B) antigüedad. C) elegancia. D) defensa. E) latrocinio.
Solución:
El blindaje es una característica del acorazado y, por ello, implica defensa.
Clave: D
2. Dentro de la lógica de la exposición, se infiere que la corbeta Esmeralda se
menciona para enfatizar que era un buque
A) europeo. B) ultramoderno. C) con misiles.
D) antiquísimo. E) de madera.
Solución:
Si la corbeta Esmeralda fue espoloneada, cabe deducir que era de material ligero,
como la madera.
Clave: E
3. Resulta incompatible con el texto afirmar que el manejo del espolón
A) data de tiempos antiguos en la humanidad.
B) se documenta en la histórica batalla de Lissa.
C) se podía describir por la falibilidad en el ataque.
D) estaba totalmente controlado por los mandos.
E) fue considerado como un arma bélica crucial.
Solución:
Resulta curioso el hecho de que varios buques resultaran espoloneados por otros de
sus propias escuadras en tiempos de paz.
Clave: D
4. La mención de la batalla de Lissa sirve para ilustrar que el espolón demostró eficacia
para __________ embarcaciones.
A) construir B) atemorizar C) acorazar D) abatir E) absterger
Solución:
Estaba ubicado por debajo de la línea de flotación para embestir y eventualmente
hundir a otras embarcaciones.
Clave: D

5. Si una nave tuviese una artillería pesada, eficaz y efectiva,
A) ya no necesitaría contar con un espolón en su proa.
B) podría prescindir de acorazar su estructura física.
C) podría haber sido inventada por los antiguos fenicios.
D) sería capaz de vencer por sí sola a una gran escuadra.
E) no tendría necesidad de un buen cañón de retrocarga.
Solución:
El espolón implica un ataque de contacto. Con una artillería así, el espolón resulta
prescindible.
Clave: A
TEXTO 2
Émile Durkheim fue, entre otras cosas, un pionero en la sociología de la religión.
Otros pensadores del siglo XIX analizaron el tema de la religión desde perspectivas
diferentes. Algunos contemporáneos de Durkheim, como sir James Frazer y Edward B.
Tylor, estaban interesados en los orígenes históricos de la religión y especularon respecto
de la evolución de las creencias «primitivas». Por consiguiente, vieron la religión como
una reliquia de fases más tempranas de la evolución social humana. Otros, como
Sigmund Freud y William James, se preocuparon por la influencia psicológica y las
funciones de la religión, y sondearon los motivos individuales, los propósitos y las
experiencias religiosas; estos autores percibieron la religión como una profunda
necesidad psicológica. En contraste, Durkheim estaba interesado en las fuentes sociales
de la religión y en lo que su estudio podría revelar sobre la naturaleza de la vida social. El
estudio de Durkheim sobe literatura histórica y etnográfica lo convenció de que todas las
sociedades distinguen entre lo «sagrado» (lo que es divino, inspira temor y debe tratarse
con respeto) y lo «profano» (cosas ordinarias y cotidianas que pueden tratarse en forma
casual). Si la religión es universal, razonó Durkheim, debe realizar alguna función vital en
la sociedad humana, que rechaza la búsqueda de principios y motivos psicológicos como
no científicos. Durkheim buscó las «causas siempre presentes» de la religión, las fuerzas
sociales que mantienen la religión en todas las sociedades. Empezó su búsqueda con
descripciones del totemismo entre grupos aborígenes australianos, que representaban la
forma más simple de la sociedad humana y revelarían por consiguiente «las formas
elementales» de la vida religiosa. Un tótem es un emblema sagrado que los miembros de
un grupo o clan tratan con reverencia y temor. Las cosas escogidas como tótems (lagarto,
oruga, pez, árbol) no son, en sí mismos, inspiradoras de temor; pero los miembros de un
clan ven el objeto como intermediario entre ellos y lo sobrenatural. Un tótem es un
símbolo de dios y del clan, esta asociación, según Durkheim, es una pista para entender
la función de la religión, ya que al adorar al tótem, los miembros del clan adoran la
sociedad. Además, argumentó que muchos de los sentidos y las experiencias que las
personas categorizan como religiosas son respuestas a fuerzas sociales inadvertidas pero
poderosas. Por ejemplo, la creencia religiosa de que los humanos son el producto de la
creación divina refleja el hecho social de que somos criaturas de la cultura y el tiempo; de
la misma manera la sensación religiosa de eternidad refleja el hecho de que la sociedad
existió antes de que el individuo naciera y continuará después de que muera.

1. El texto se centra básicamente en
A) la explicación de la religión a partir de un análisis etnológico del totemismo.
B) la consideración del trasfondo social que entraña la religión según Durkheim.
C) una distinción entre lo profano y lo sagrado como elementos histórico-literarios.
D) la necesidad psicológica que determina la religiosidad en las minorías étnicas.
E) las propuestas indiscernibles de Frazer, Durkheim y Freud acerca de la religión.
Solución:
El texto aborda la propuesta de Durkheim acerca de la religión, la cual se evalúa en
el marco de las redes sociales.
Clave: B
2. La palabra SONDEAR adquiere el sentido de
A) indagar. B) recusar. C) corroborar.
D) penetrar. E) planificar.
Solución:
Freud y William James «sondearon»; a saber, hicieron las primeras averiguaciones
acerca de los motivos individuales de la religión como necesidad psicológica. Por
eso el sinónimo contextual es INDAGAR.
Clave: A
3. Resulta incompatible respecto de la propuesta de sir James Frazer afirmar que
A) era distinta a la propuesta sociológica de Durkheim.
B) asumía que las creencias eran pasibles de desarrollo.
C) presentaba una visión historicista acerca de la religión.
D) este veía a la religión como un relicto de la vida social.
E) la vida social humana se caracteriza por ser inmutable.
Solución:
James Frazer sostiene que la vida social humana evoluciona (es dinámica) y la
religión constituye la huella de ese marco evolutivo.
Clave: E
4. Se deduce del texto que, para Durkheim, religiones como el islamismo y el
catolicismo
A) son explicables a partir de modelos sociales divergentes.
B) mantienen un mismo marco causal de naturaleza social.
C) son representaciones modernas de creencias totémicas.
D) son incapaces de distinguir entre lo sagrado y lo profano.
E) constituyen una corroboración de la propuesta de Freud.
Solución:
Para Durkheim las religiones obedecen a «causas siempre presentes»: las fuerzas
sociales que mantienen la religión en todas las sociedades.
Clave: B

5. Si Durkheim sostuviera que la capacidad de algunos monjes para soportar el dolor a
través de la meditación obedece a un proceso psicológico de sugestión temporal,
A) el tótem sería explicable mediante una hipótesis de tipo cientificista.
B) el modelo funcionalista se erigiría como un aporte instrumental válido.
C) su propuesta estaría más acorde con la de Freud y William James.
D) la distinción entre lo sagrado y lo profano adquiriría mayor validez.
E) no existirían las formas elementales de vida religiosa en el mundo.
Solución:
La religiosidad se explica, según Freud y James, como una profunda necesidad
psicológica. Así, la meditación se explicaría de esta manera.
Clave: C
6. En la perspectiva de Durkheim, el tótem
A) tiene una eminente capacidad vicarial.
B) refleja un pensamiento muy alambicado.
C) se explica solamente por lo psicológico.
D) inspira veneración, pero no un temor.
E) carece de significación en la sociedad.
Solución:
El tótem es un intermedio y, por ello, cumple con una función vicarial.
Clave: A
SERIES VERBALES
1. Mudable, voluble; fértil, feraz; inconstante, veleidoso;
A) veraz, estéril. B) caliginoso, diáfano C) enteco, versátil.
D) caprichoso, yermo. E) copioso, ubérrimo.
Solución:
Se trata de completar la serie sinonímica.
Clave: E
2. Entronizar, ungir, ensalzar,
A) implicar. B) encumbrar. C) liberar.
D) excluir. E) penetrar.
Solución:
La serie verbal está formada por sinónimos, el campo del elogio y reconocimiento se
completa con ENCUMBRAR.
Clave: B
3. Elija el término que no cabe incluir en la serie PUSILÁNIME, MEDROSO,
APOCADO.
A) cobarde. B) timorato. C) miedoso.
D) asustadizo. E) fanfarrón.

Solución:
Fanfarrón no pertenece al campo semántico del temor.
Clave: E
4. Restaurar, deteriorar; remudar, reemplazar; disipar, desvanecer;
A) deglutir, regurgitar. B) soslayar, socavar. C) obligar, vetar.
D) reeditar, redimir. E) incoar, iniciar.
Solución:
Series de sinónimos.
Clave: E
5. Noble, vil; ponzoñoso, inocuo; vacuo, pletórico;
A) abyecto, siniestro. B) émulo, ignaro. C) bisoño, baquiano.
D) adosado, propincuo. E) yerto, muerto.
Solución:
Serie de antónimos
Clave: C
6. Equilibrio, acróbata; destreza, cirujano;
A) ciencia, filósofo. B) vehemencia, pensador. C) belleza, atleta.
D) elocuencia, rétor. E) rebeldía, político.
Solución:
En la serie, las palabras guardan la siguiente relación: característica inherente,
sujeto.
Clave: D
7. Pintor, mural; matemático, teorema; escultor, busto;
A) vate, discurso. B) sacerdote, homilía.
C) exégeta, comentario. D) historiador, panfleto.
E) artesano, buril.
Solución:
La serie de palabras guardan la relación de agente-producto de su creación; por lo
tanto, la alternativa sería exégeta, comentario.
Clave: C
8. Científico, objetividad; bailarín, ritmo; actor, expresividad;
A) abogado, persuasión. B) político, iracundia.
C) sacerdote, salvación. D) anacoreta, erudición.
E) filósofo, irracionalidad.
Solución:
En la serie verbal se observa la relación sujeto-práctica que lo caracteriza.
Clave: A

9. Escudriñar, inquirir, examinar,
A) razonar. B) conjeturar. C) confutar.
D) escrutar. E) escamotear.
Solución:
Serie de sinónimos.
Clave: D
10. Elija la tríada de sinónimos.
A) flamígero, abrasador, hidratante. B) fiero, siniestro, torvo.
C) adocenado, ramplón, selecto. D) veraz, sicofante, embustero.
E) áureo, ebúrneo, marfileño.
Tres palabras que guardan sinonimia.
Clave: B
SEMANA 13 B
EL TEXTO DESCRIPTIVO
En este tipo de textos, el autor hace referencia a un objeto sobre la base de la
presentación de sus propiedades o rasgos más notables. La descripción tiende a la
neutralidad en la medida en que el texto intenta dar una visión muy aproximada del objeto.
TEXTO DE EJEMPLO
Más de 100 millones de años de evolución han proporcionado a la tortuga laúd
capacidades para nadar, bucear y sobrevivir en aguas heladas con gran eficiencia, todo
esto con una dieta de medusas baja en calorías. Esta tortuga cuenta con placas de hueso
del tamaño de una moneda, las cuales se entrecruzan en una concha flexible que podría
comprimirse a profundidades extremas. La forma de gota de su cuerpo y las crestas en
forma de quillas facilitan el flujo a lo largo del caparazón. Un área de piel pálida permite
que la luz llegue a la glándula pineal, la cual podría detectar cambios en la duración de los
días, así como dirigir migraciones. Las glándulas salinas retienen el exceso de sal en la
dieta de medusas de la tortuga y lo excretan en lágrimas viscosas. El esfínter cierra el
flujo de sangre hacia los pulmones, lo que conserva la energía. Las puntas como espinas
cubren el esófago para atrapar presas resbalosas. Además, la sangre fría que regresa de
las aletas se calienta con la sangre que llega a ellas antes de alcanzar el centro del
cuerpo. En aguas muy frías, el flujo sanguíneo hacia la superficie de las aletas podría
suspenderse intermitentemente. Finalmente, una masa enorme (de hasta 900 kilogramos)
ayuda a la tortuga a permanecer tibia en aguas frías.
1. El texto aborda centralmente el tema de
A) la sangre fría de las tortugas. B) la flexibilidad de la tortuga laúd.
C) las medusas y las tortugas laúd. D) la masa corporal de la tortuga.
E) las características de la tortuga laúd.

Solución:
El texto trata acerca de las características más notables de la tortuga laúd.
Clave: E
2. ¿Cuál es la idea central del texto?
A) La tortuga laúd ha desarrollado a lo largo de los años capacidades notables.
B) Las tortugas laúd pueden suspender el flujo sanguíneo intermitentemente.
C) La gran masa corporal de la tortuga laúd le permite regular su temperatura.
D) La tortuga laúd ha desarrollado la capacidad para alimentarse de medusas.
E) En términos evolutivos, la tortuga laúd se considera un espécimen frágil.
Solución:
El texto se centra en el notable desarrollo evolutivo de la tortuga laúd, el cual ha
determinado que sea un espécimen capaz de sobrevivir en un ambiente adverso.
Clave: A
3. El adverbio INTERMITENTEMENTE implica un proceso que se ejecuta
A) fortuitamente. B) interrumpidamente. C) fugazmente.
D) paralelamente. E) continuamente.
Solución:
«Intermitentemente» alude a un proceso que se realiza de manera interrumpida.
Clave: B
4. De acuerdo con el texto, es incompatible afirmar que las tortugas laúd
A) poseen una zona de piel que les posibilita dirigir las migraciones.
B) presentan una dieta baja en calorías conformada por medusas.
C) capturan presas resbaladizas gracias a las espinas de su esófago.
D) pierden de manera inevitable ingentes cantidades de energía.
E) poseen un cuerpo que facilita el flujo sanguíneo en su caparazón.
Solución:
Las tortugas laúd son capaces de conservar la energía gracias al esfínter que cierra
el flujo sanguíneo.
Clave: D
5. Si las tortugas laúd no contaran con zonas de piel que recepcionen y procesen la luz
solar,
A) la suspensión del flujo sanguíneo se daría de forma continua.
B) recurrirían a la forma de su caparazón para detectar a sus presas.
C) disminuirían su capacidad para ubicarse en lugares muy gélidos.
D) perderían la capacidad para que la glándula pineal la obstaculice.
E) serían incapaces de detectar lugares hacia donde puedan migrar.
Solución:
Las áreas de piel pálida le permiten a la tortuga laúd dirigir las migraciones y
percatarse de los cambios en la duración de los días.
Clave: E

6. Se deduce del texto que, gracias a su enorme tamaño, las tortuga laúd
A) retienen la ingesta de mucha sal. B) habitan en lugares muy profundos.
C) pueden retrasar la pérdida de calor. D) se alimentan de medusas grandes.
E) presentan placas óseas pequeñas.
Solución:
Su gran tamaño les permite permanecer tibia en aguas frías, esto es, retrasa la pérdida
de calor corporal.
Clave: C
COMPRENSIÓN DE LECTURA
TEXTO 1
Los estudios sociales de la ciencia desarrollados en las últimas décadas han puesto
de manifiesto la naturaleza social de la práctica científica y su consecuente compromiso
con los valores, prioridades e intereses propios de la estructura y los agentes sociales. Es
decir, la ciencia es una actividad social vinculada a las restantes formas de la actividad
humana. Los procesos de producción, difusión y aplicación de conocimientos propios de
la actividad científica son inexplicables al margen de los intereses económicos, políticos,
militares, entre otros, que caracterizan los diversos contextos sociales. En esta
perspectiva, la ciencia es una actividad institucionalizada, permeable a los valores e
intereses sociales y no puede ser neutral. Sin embargo, esta conclusión no podría ser tan
rotunda si se presta atención a la ciencia como conocimiento, es decir, si prestamos
atención al valor cognoscitivo de las teorías y otras expresiones del saber. Si de manera
apresurada se extiende la no neutralidad, predicada para la ciencia como actividad, a la
comprensión de la ciencia como saber, se puede llegar a la negación de la objetividad
científica. Se podría sostener un ideal de compromiso social para la ciencia, pero en este
camino no veo la forma de retener el sentido de la honestidad intelectual entendida como
compromiso con la objetividad. Agazzi lo expresa así: "Se ha de concluir que la ciencia no
puede ser neutral como actividad mientras lo es y debe serlo como saber".
La ciencia es actividad y es saber. Ni lo uno ni lo otro por separado. Los límites entre
ambas expresiones de la ciencia sólo pueden reconocerse con un propósito analítico. Sin
embargo, como se verá de inmediato, esa distinción puede ser útil para explorar los
diferentes sentidos de neutralidad mencionados antes. Comencemos por la neutralidad
como "desinterés". La actividad científica es inexplicable al margen de los intereses
sociales. Esos intereses se expresan, por ejemplo, en el financiamiento de la ciencia, en
las prioridades que para ella se establecen. Esos intereses, sin embargo, no niegan el
interés por producir conocimiento objetivo, los intereses propiamente cognoscitivos que
favorecen la objetividad. Más aún, los intereses que intentan instrumentalizar la ciencia y
ponerla al servicio de los más variados fines, requieren del conocimiento objetivo que
haga de la ciencia un saber útil. Las políticas científicas, los programas de investigación,
las instituciones que articulan el trabajo científico no son neutrales respecto a los fines
sociales que les dan vida, pero ello no hace del conocimiento obtenido la expresión de un
interés económico o político particular, aunque su utilización sí suele subordinarse a ellos.
Veamos la idea de neutralidad como "independencia de prejuicios". Aquí la palabra
prejuicio no tiene un sentido peyorativo; se refiere a "un cierto complejo preconstituido de
convicciones, actitudes intelectuales, hábitos mentales, valoraciones, etc." La ciencia vista
como actividad no puede ser neutral respecto de los prejuicios así definidos. Cada
individuo, colectividad, sociedad, época, portan tales prejuicios que influyen sobre el modo
de hacer ciencia, en la elección de los campos de la investigación, prioridades en la

enseñanza y otras expresiones de la práctica científica. Debemos reconocer que esos
prejuicios también influyen sobre la ciencia como saber. Los criterios de objetividad y
racionalidad están sometidos a cierta contingencia y determinación histórica. La
construcción de un saber objetivo siempre se logra dentro de marcos conceptuales y
metodológicos preestablecidos. Los científicos deben tomar conciencia de los límites que
imponen a la objetividad dichos marcos y esforzarse por subordinar sus conclusiones a
las "buenas razones" (teóricas, lógicas, empíricas) que puedan aportarse dentro de esos
marcos cuyos límites han sido críticamente evaluados. De este modo, la ciencia como
saber logra cierta neutralidad respecto de los prejuicios: "La ciencia como saber puede y
debe ser neutral respecto de los prejuicios, tomando conciencia de ellos y de su
parcialidad".
1. En el texto, el vocablo PERMEABLE connota
A) estar sujeto a determinadas influencias.
B) representar determinados intereses.
C) asumir diversas perspectivas teóricas.
D) estar condicionado por ciertos intereses.
E) renunciar a la objetividad científica.
Solución:
En el texto, este vocablo connota la idea de que la ciencia está influenciada por los
valores e intereses sociales que asume el científico y, por ello, la ciencia no puede
ser neutral.
Clave: A
2. El tema central que se expone en texto es
A) la incompatibilidad entre compromiso social y objetividad en la ciencia como
cognosis.
B) el “desinterés” y la “independencia de prejuicios”: expresiones de la objetividad
científica.
C) el compromiso social de la actividad científica y la neutralidad de la ciencia como
saber.
D) los requisitos esenciales del conocimiento científico: objetividad, neutralidad y
unicidad.
E) los prejuicios conceptuales y metodológicos como escollos para la objetividad
científica.
Solución:
Tal como expresa Agazzi: "se ha de concluir que la ciencia no puede ser neutral
como actividad mientras lo es y debe serlo como saber"
Clave: C
3. Es incompatible con el texto aseverar que la objetividad científica
A) es posible alcanzar aun asumiendo un compromiso.
B) requiere conciencia de la determinación histórica.
C) es indispensable para alcanzar una ciencia útil.
D) es fruto, sobre todo, de la honestidad intelectual.
E) resulta imposible por causa de los prejuicios.

Solución:
Según el texto, el científico puede y debe ser neutral respecto a los prejuicios,
tomando conciencia de ellos y de su parcialidad. De este modo, la objetividad
científica, garantizada por la neutralidad, no se vería afectada.
Clave: E
4. Se deduce que un científico debe estar comprometido, sobre todo, con
A) el saber objetivo. B) la utilidad. C) la política.
D) los fines sociales. E) la investigación.
Solución:
La ciencia como cognosis es saber objetivo. Este es el compromiso de la ciencia.
Clave: A
5. Si un científico promoviera la neutralidad como "desinterés", probablemente
A) estaría en inmejorables condiciones para alcanzar el saber objetivo.
B) desarrollaría su actividad encerrado herméticamente en su laboratorio.
C) su labor se caracterizaría por ser más rigurosa, objetiva y proficua.
D) se desenvolvería al margen de las políticas oficiales de investigación.
E) sería reconocido como un paradigma en el campo de la investigación.
Solución:
Dicho científico desconocería los intereses sociales que intervienen en la actividad
científica, intereses que se expresan, entre otros, en las políticas de investigación.
En consecuencia, la actividad de este científico se desenvolvería al margen de
dichas políticas.
Clave: D
6. A partir del texto se puede afirmar que las investigaciones científicas
A) están totalmente determinadas por el interés general del Estado.
B) están sujetas a las determinaciones conceptuales de su tiempo.
C) deben cuestionar y desechar el marco conceptual predominante.
D) para ser objetivas, deben recusar al marco metodológico existente.
E) requieren una actitud eminentemente crítica y sin ningún prejuicio.
Solución:
Según el texto, la construcción de un saber objetivo siempre se logra dentro de
marcos conceptuales y metodológicos preestablecidos. En consecuencia, las
investigaciones científicas están sujetas a estos marcos, a estas determinaciones.
Clave: B
TEXTO 2
La sonrisa es parte integral de la interacción social cotidiana. En algunos casos, la
sonrisa es el signo consciente e intencional de felicidad, fraternidad o diversión; en otros,
la sonrisa es también un tipo de comunicación que traiciona las emociones de la persona
que quería ocultarla, sobre todo el nerviosismo o el ridículo. En algunas situaciones
sociales, sonreír es requerido como cuando un vendedor saluda a un cliente, un anfitrión
presenta a un recién llegado a una fiesta, o un actor acepta el aplauso del público. En
otras situaciones, sonreír es considerado inapropiado; por ejemplo, cuando le dicen que

alguien que usted conoce (de hecho, cualquiera) está agonizando o cuando ve a otra
persona con dolor físico o emocional.
¿Las normas para sonreír son variables en las diversas culturas? Para investigar
esta pregunta, los sociólogos Kenji Nagashima y James Schellenberg presentaron a 42
estudiantes de una universidad en Estados Unidos y 48 en Japón, con tres situaciones
que involucran interacción estudiante-profesor o estudiante-estudiante: a) un estudiante
va hacia el profesor u otro estudiante para preguntar por el trabajo de la clase (una
sonrisa amistosa); b) un estudiante oye a otro estudiante decir un chiste que él o ella no lo
considera cómico (una sonrisa forzada); c) un estudiante recibe la información que él o
ella querían de un profesor u otro estudiante (una sonrisa genuina). Los investigadores
pidieron a los estudiantes de ambos países medir la probabilidad de que el estudiante
sonreiría en cada una de esas situaciones, en una escala de 7 puntos: partiendo de 1 (si
no sonreía) hasta 7 (si sonreía mucho). Los estereotipos culturales sostienen que el
japonés es más formal y cortés, y muestra más respeto por las jerarquías que los
estadounidenses. Nagashima y Schellenberg supusieron que en una situación que no
implicara respeto por diferencia de estatus, los estudiantes japoneses serían menos
propensos que los estadounidenses a sonreír cuando preguntaban a un profesor
(situación 1) y más probablemente sonreirían al chiste del profesor (situación 2). Ellos no
hicieron ninguna predicción para la situación 3: ¿los resultados?
Tanto los estudiantes estadounidenses como japoneses mostraron el mismo
comportamiento en las mismas situaciones. En concreto, no encontraron ninguna
diferencia cultural significativa. ¿El estudio fue un fracaso? No. La investigación
transcultural es igual de importante si detecta similitudes, tanto como diferencias. La
muestra fue demasiado pequeña para establecer generalizaciones; no obstante, sugiere
que las expresiones de emoción pueden ser universales, es decir, una forma no verbal de
comunicación que todos los humanos usan y entienden.
1. El texto trata centralmente acerca de
A) los rasgos de la comicidad en la historia de la humanidad.
B) la interacción cotidiana a través de gestos faciales de la risa.
C) las formas no verbales de la comicidad en Japón y en USA.
D) un estudio sobre la posible variabilidad cultural de la sonrisa.
E) la diferencia del respeto entre los occidentales y los orientales.
Solución:
El texto trata acerca de un estudio acerca de las diferencias involucradas en las
reglas que permiten sonreír.
Clave: D
2. En el texto, la palabra TRANSCULTURAL connota
A) universalidad en los rasgos étnicos. B) semejanza en las normas culturales.
C) parangón entre culturas diferentes. D) diferencias al interior de una cultura.
E) fuerza de un grupo cultural particular.
Solución:
El término transcultural se usa para hacer referencia a un estudio de contrastación
entre la cultura japonesa y la estadounidense; es decir, entre dos culturas diferentes.
Clave: C

3. En el primer párrafo del texto, la palabra TRAICIONAR connota
A) revelar involuntariamente lo que se intenta ocultar.
B) actuar de manera desleal y alevosa ante un enemigo.
C) delatarse a sí mismo por espontánea y propia voluntad.
D) abandonar a alguien en un momento de suma urgencia.
E) fracasar en el intento de descubrir diferencias culturales.
Solución:
«Traicionar» hace alusión a un acto de descubrimiento involuntario de aquello que
se quería ocultar, como el ridículo o el nerviosismo.
Clave: A
4. Resulta incompatible respecto de las normas culturales de la sonrisa afirmar que
A) son casi indiscernibles en los japoneses y los americanos.
B) pueden ser formas no verbales de interacción comunicativa.
C) es probable que presenten rasgos de carácter ecuménico.
D) forman parte esencial de la comunicación no verbal humana.
E) evidencian diferencias palmarias en las relaciones culturales.
Solución:
Las normas culturales de la sonrisa, por lo menos en el estudio comparativo
presentado en el texto, no ofrecen distingos concluyentes. Afirmar lo contrario
resulta incongruente.
Clave: E
5. De acuerdo con el texto, resulta compatible afirmar que la sonrisa
A) no se usaría jamás para vender un determinado producto.
B) está involucrada en el devenir cotidiano de las personas.
C) nunca aparece en situaciones de jolgorio y festividad.
D) se utiliza únicamente para encubrir una intención aleve.
E) solamente puede ser un gesto voluntario de fría cortesía.
Solución:
En efecto, es congruente con el texto afirmar que la sonrisa está involucra en la
interacción social cotidiana de los individuos.
Clave: B
6. Si la investigación de Nagashima y Schellenberg hubiese arrojado diferencias
significativas en las actitudes de los japoneses y los estadounidenses,
A) la sonrisa no sería un objeto de estudio asequible.
B) las normas que regulan la risa serían insondables.
C) se podría objetar la universalidad de toda sonrisa.
D) tendría que abordarse la sonrisa fuera de lo social.
E) la sonrisa dejaría de ser un fenómeno heteróclito.
Solución:
Los estudios transculturales sirven para definir similitudes y diferencias. Al hallar
diferencias, se erosiona el carácter universal.
Clave: C

7. En última instancia, para el autor, la investigación llevada a cabo se puede calificar
de
A) contraproducente. B) inviable. C) irrefragable.
D) paradójica. E) relevante.
Solución:
La interrogante, al final del texto, se plantea para argumentar a favor de la
importancia de una investigación de este tipo, la cual puede definir generalizaciones
o no.
Clave: E
8. Se deduce del texto que una investigación de tipo transcultural
A) permite, en algunos casos, establecer generalizaciones.
B) únicamente está encaminada a determinar diferencias.
C) está constreñida a predecir patrones culturales universales.
D) resulta ineficaz al abordar lo abigarrada que es la sonrisa.
E) es plausible cuando el grupo observado es minúsculo.
Solución:
El estudio presentado, de tipo transcultural en la medida en que contrasta dos
realidades culturales, no arrojó generalizaciones, pero es posible que sí permita
determinarlas.
Clave: A
9. Nagashima y Schellenberg suponían que un japonés, a diferencia de un
estadounidense,
A) se caracterizaría por una dura parquedad en toda circunstancia.
B) sonreiría con más facilidad ante un mal chiste de un catedrático.
C) nunca sonreiría ante la broma proferida por un norteamericano.
D) expresaría una amplia sonrisa al dirigirse a un profesor japonés.
E) se podría describir por una actitud jovial en toda eventualidad.
Solución:
Por respeto, el estudiante japonés sonreiría ante el chiste de un profesor, por más
que no fuera un buen chiste.
Clave: B
10. Si alguien sonríe porque se siente azorado, es una sonrisa
A) política. B) deliberada. C) formal.
D) involuntaria. E) sarcástica.
Solución:
Se trataría de una sonrisa natural, causada por el sentimiento de vergüenza.
Clave: D

SEMANA 13 C
TEXTO 1
Entre las doctrinas de Tlön, ninguna ha merecido tanto escándalo como el
materialismo. Algunos pensadores lo han formulado, con menos claridad que fervor, como
quien adelanta una paradoja. Para facilitar el entendimiento de esa tesis inconcebible, un
heresiarca de Tlön ideó el sofisma de las nueve monedas de cobre, cuyo renombre
escandaloso equivale para nosotros al de las aporías eleáticas. De ese razonamiento
especioso hay muchas versiones, que varían el número de monedas y el número de
hallazgos; he aquí la más común:
El martes, X atraviesa un camino desierto y pierde nueve monedas
de cobre. El jueves, Y encuentra en el camino cuatro monedas, algo
herrumbradas por la lluvia del miércoles. El viernes, Z descubre tres
monedas en el camino. El viernes de mañana, X encuentra dos
monedas en el corredor de su casa. El heresiarca quería deducir de
esa historia la realidad –id est, la continuidad– de las nueve
monedas recuperadas. Es absurdo (afirmaba) imaginar que cuatro
de las monedas no han existido entre el martes y el jueves, tres
entre el martes y la tarde del viernes, dos entre el martes y la
madrugada del viernes. Es lógico pensar que han existido –siquiera
de algún modo secreto, de comprensión vedada a los hombres– en
todos los momentos de esos tres plazos.
El lenguaje de Tlön se resistía a formular esa paradoja, los más no la entendieron.
Los defensores del sentido común se limitaron, al principio, a negar la veracidad de la
anécdota. Repitieron que era una falacia verbal, basada en el empleo temerario de dos
voces neológicas, no autorizadas por el uso y ajenas a todo pensamiento severo: los
verbos “encontrar” y “perder”, que comportaban una petición de principio, porque
presuponían la identidad de las nueve primeras monedas y de las últimas. Recordaron
que todo sustantivo (hombre, moneda, jueves, miércoles, lluvia) sólo tiene un valor
metafórico. Denunciaron la pérfida circunstancia “algo herrumbradas por la lluvia del
miércoles”, que presupone lo que se trata de demostrar: la persistencia de las cuatro
monedas, entre el jueves y el martes. Explicaron que una cosa es igualdad y otra
identidad y formularon una especie de reductio ad absurdum, o sea el caso hipotético de
nueve hombres que en nueve sucesivas noches padecen un vivo dolor. ¿No sería ridículo
–interrogaron– pretender que ese dolor es el mismo? Dijeron que al heresiarca no lo
movía sino el blasfematorio propósito de atribuir la divina categoría de ser a unas simples
monedas y que a veces negaba la pluralidad y otras no. Argumentaron: si la igualdad
comporta la identidad, habría que admitir asimismo que las nueve monedas son una sola.
1. El texto versa fundamentalmente sobre
A) la ambigüedad de los postulados metafísicos de Tlön.
B) el rechazo del materialismo en la metafísica de Tlön.
C) el materialismo como postura filosófica inequívoca.
D) una herejía en torno a la naturaleza del dios de Tlön.
E) la historia de un heresiarca revolucionario de Tlön.

Solución:
El texto centra su atención en el materialismo como postura inconcebible para la
metafísica de Tlön. Se propone un razonamiento para intentar probar el materialismo
y se procede a criticar ásperamente el mismo.
Clave: B
2. En el primer párrafo del texto, el término ESPECIOSO podría ser reemplazado por
A) sofisticado. B) cuidadoso. C) engañoso.
D) ampuloso. E) extravagante.
Solución:
En el texto se afirma que un heresiarca ideó un sofisma, es decir un razonamiento
falaz, para poder introducir el materialismo en Tlön.
Clave: C
3. Resulta incongruente con lo afirmado en el texto sostener que
A) la continuidad temporal de la materia resulta del todo inverosímil en Tlön.
B) la refutación del razonamiento de las nueve monedas no se hizo esperar.
C) el relato acerca de las nueve monedas de cobre tiene múltiples versiones.
D) la recusación del materialismo en Tlön no tomó en cuenta criterios lógicos.
E) el materialismo es una postura inadmisible para los metafísicos de Tlön.
Solución:
Al rechazar el materialismo se sostuvo que el uso de las palabras “encontrar” y
“perder” comportaba una petición de principio, es decir, la falacia que presupone lo
que se quiere demostrar.
Clave: D
4. Se puede inferir que las aporías eleáticas
A) representan una inviabilidad de índole racional.
B) fueron muy censuradas por los metafísicos de Tlön.
C) son razonamientos que aluden a la numismática.
D) son un obstáculo para el desarrollo de la ciencia.
E) constituyen un problema sólo para los matemáticos.
Solución:
En el primer párrafo se compara el razonamiento de las nueve monedas con las
famosas aporías de Zenón. Cabe inferir que tales aporías, al igual que el
razonamiento de las monedas, quiebran un cierto orden racional.
Clave: A
5. Si el materialismo fuese una postura plausible en Tlön, la historia de las nueve
monedas de cobre
A) habría sido recibida con gran escepticismo.
B) tendría una enorme variedad de versiones.
C) generaría una fuerte adhesión al idealismo.
D) sería catalogada como una fábula especiosa.
E) constituiría un relato verosímil y fundamentado.

Solución:
La historia de las monedas es asombrosa en Tlön debido a que allí no se concibe el
materialismo. Si ocurriese lo contrario, la historia de las monedas no resultaría
extravagante o asombrosa.
Clave: E
TEXTO 2
El surgir o el resurgir de las ciudades en la Europa de los siglos XI-XII marcó un giro
en la historia de la civilización europea y preparó nuevos destinos para el mundo entero.
Las ciudades habían prosperado y proliferado en el mundo grecorromano, pero la
decadencia del imperio señaló también su decadencia y las invasiones germánicas
decretaron su muerte. Si sobrevivieron núcleos urbanos, su papel se limitó simplemente y
sobre todo al de centros de la administración religiosa y sedes de guarniciones militares.
El mundo de la Alta Edad Media fue un mundo primitivo dominado por el campo.
El empobrecimiento de las sociedades europeas fue característico de las zonas de
Europa que habían sido parte del Imperio romano. Al margen del Imperio, nada había
existido en el continente europeo en materia de ciudades, y poco en materia de
manufacturas y comercios. Con la caída del Imperio, el Norte mejoró lentamente. El
violento contraste que había dividido netamente el Norte y el Sur en la época de Roma se
atenuó. Por otra parte, las invasiones musulmanas debilitaron los lazos que habían unido
el Sur de Europa con el norte de África y con el Próximo Oriente. En tiempos de Roma
habían existido dos mundos separados: el mundo mediterráneo y el mundo nórdico. En el
siglo VIII el mundo mediterráneo quedó cortado en dos, y la parte europea, empobrecida,
se ligó más estrechamente con la parte septentrional del subcontinente. Bajo la égida de
un común credo religioso emergió en embrión Europa.
Era una Europa pobre y primitiva. Una Europa compuesta por muchos microcosmos
rurales –las curtes– ampliamente autosuficientes, cuya autarquía era en parte
consecuencia de la decadencia del comercio y en buena parte también causa de ello. La
sociedad estaba dominada por un espíritu de renuncia, de sospecha y de miedo hacia el
mundo exterior. La gente se aislaba en la autarquía económica de las curtes o se
encerraba en la meditación religiosa de los claustros.
La situación de las artes, la instrucción, el comercio y la división del trabajo estaban
reducidos a niveles mínimos. El uso de la moneda había desaparecido casi por completo.
La población era escasa, pero la producción más escasa aún, y máxima la pobreza. Las
estructuras sociales eran primitivas. Unos rezaban, otros combatían y otros trabajaban. Y
quienes trabajaban eran considerados siervos. Predominaba el bosque, habitado por
animales salvajes y, según las fantasías de la gente, también por gnomos y hadas, por
brujas y geniecillos. En este mundo deprimido y deprimente, donde la vida era tan mísera
que los hombres ponían su única esperanza de algún gozo en el más allá, el surgir de las
ciudades entre los siglos XI y XIII representó un hecho nuevo que cambió el curso de la
historia de la Europa occidental.
En el mundo de las curtes los raros intercambios se producían en los escasos
mercados que tenían lugar una vez a la semana, o una vez al mes, o una vez al año. En
las ciudades el intercambio es continuo: el mercado no sufre interrupciones. La ciudad era
el mercado por antonomasia. El desarrollo de las ciudades significó el desarrollo de la
economía de mercado.

1. La idea principal del texto sostiene que
A) el surgimiento de las ciudades trae aparejado un gran desarrollo económico y
político de las mismas.
B) hay solución de continuidad entre las ciudades del mundo grecorromano y las de
los siglos XI y XIII.
C) la economía de mercado es un modelo económico cuyo advenimiento es
absolutamente ineluctable.
D) Europa es un continente que experimentó múltiples y trascendentales cambios en
su desarrollo histórico.
E) el resurgimiento de las ciudades europeas estimuló el desarrollo mercantil de
Europa y del mundo entero.
Solución:
El texto afirma que Europa, y con ella el mundo entero, experimentó un cambio
notable que se tradujo en el desarrollo de la economía de mercado tras el
resurgimiento de las urbes entre los siglos XI y XIII.
Clave: E
2. El sentido contextual de la palabra DEPRIMIDO es
A) apesadumbrado. B) desagradable. C) pobre.
D) golpeado. E) tortuoso.
Solución:
La etapa previa al resurgimiento de las urbes europeas se describe como un mundo
signado por la pobreza, el miedo y la superstición. En suma, se advierte un clima
decadente o de declive de la sociedad europea.
Clave: C
3. Se puede colegir que durante la vigencia del Imperio romano, el Norte
A) era un espacio donde había gran flujo comercial.
B) se encontraba en una situación de marginalidad.
C) no tenía ningún tipo de comunicación con el Sur.
D) constituyó un área de interés para los romanos.
E) pugnaba por formar parte de la ecúmene romana.
Solución:
En el texto se afirma que el Norte mejoró lentamente tras la caída del Imperio
romano y que el mundo nórdico estaba al margen del mundo mediterráneo en los
tiempos de Roma.
Clave: B
4. Del texto se infiere que, durante la Alta Edad Media, la religión
A) inculcó valores muy practicados después en las incipientes urbes.
B) fomentó deliberadamente una gran diversidad de supersticiones.
C) preparó el camino para el surgimiento de las ciudades europeas.
D) terminó por instalarse definitivamente en la subjetividad europea.
E) fue una esfera de total significación para algunos sujetos europeos.

Solución:
Durante la Alta Edad Media algunas personas se encerraban en los claustros
religiosos como alternativa a la autarquía de las curtes. La sociedad misma estaba
dividida en gente que rezaba, que luchaba y que trabajaba.
Clave: E
5. Si durante los siglos XI y XIII no hubieran resurgido las ciudades europeas,
A) la miseria de Europa se habría extendido por el planeta.
B) el desarrollo económico europeo no habría sido posible.
C) habría sido imposible sostener la autarquía de las curtes.
D) el Imperio romano habría logrado un segundo gran apogeo.
E) los pueblos musulmanes habrían logrado todo el predominio.
Solución:
El resurgimiento de las ciudades europeas después de la Alta Edad Media generó el
desarrollo de la economía de mercado y la prosperidad de Europa. Sin la presencia
de las urbes, la producción habría quedado estancada en los microcosmos rurales.
Clave: B
TEXTO 3
Si la economía del mundo del siglo XIX se formó principalmente bajo la influencia de
la Revolución industrial inglesa, su política e ideología se formaron principalmente bajo la
influencia de la Revolución francesa. Gran Bretaña proporcionó el modelo para sus
ferrocarriles y fábricas y el explosivo económico que hizo estallar las tradicionales
estructuras económicas y sociales del mundo no europeo, pero Francia hizo sus
revoluciones y les dio sus ideas, hasta el punto de que cualquier cosa tricolor se convirtió
en el emblema de todas las nacionalidades nacientes. Entre 1789 y 1917, las políticas
europeas (y las de todo el mundo) lucharon ardorosamente en pro o en contra de los
principios de 1789 o los más incendiarios todavía de 1793. Francia proporcionó el
vocabulario y los programas de los partidos liberales, radicales y democráticos de la
mayor parte del mundo. Francia ofreció el primer gran ejemplo, el concepto y el
vocabulario del nacionalismo. Francia proporcionó los códigos legales, el modelo de
organización científica y técnica y el sistema métrico decimal a muchísimos países. La
ideología del mundo moderno penetró por primera vez en las antiguas civilizaciones, que
hasta entonces habían resistido a las ideas europeas, a través de la influencia francesa.
Esta fue la obra de la Revolución francesa.
1. El tema que desarrolla el texto es
A) el poderoso impacto de la gran revolución industrial inglesa.
B) la revolución francesa como una expresión política moderna.
C) el surgimiento intempestivo de las diversas nacionalidades.
D) el parangón entre la revolución industrial y la gesta francesa.
E) la profunda significación política de la Revolución francesa.
Solución:
El texto inicia con una alusión a la revolución industrial inglesa para, de manera
análoga, destacar primordialmente las implicancias políticas que el mundo moderno
experimentó tras la revolución francesa.
Clave: E

2. Resulta incompatible con lo afirmado en el texto decir que
A) la Revolución francesa repercutió en el terreno científico.
B) las civilizaciones antiguas se resistieron al influjo europeo.
C) Francia no es afín a los ideales del pensamiento liberal.
D) Inglaterra influyó en el desarrollo económico mundial.
E) la Revolución francesa reviste importancia ecuménica.
Solución:
Francia es el país que con su poderoso influjo logra que la ideología moderna
penetre incluso en las civilizaciones antiguas.
Clave: C
3. Del texto cabe colegir que la revolución bolchevique de 1917
A) desencadenó un movimiento contrarrevolucionario en territorio francés.
B) fue un evento semejante en trascendencia a la Revolución francesa.
C) se gestó por los ideales nacionalistas propios de la tradición europea.
D) significó el fin del influjo en el mundo de la Revolución francesa de 1789.
E) creó las bases para una nueva revolución industrial en el mundo occidental.
Solución:
La revolución francesa es un hito en la historia y se sostiene que hasta 1917 marca
el derrotero del acontecer político mundial. Si se pone 1917 como límite, cabe inferir
que en esa fecha ocurrió otro evento de similar trascendencia: la revolución rusa.
Clave: B
4. Se puede inferir que la bandera tricolor de una república joven
A) acusa falta de imaginación y arte por parte de sus diseñadores.
B) es la representación de tres poderosas influencias para ese país.
C) revela la intención de emular el espíritu y la ideología franceses.
D) representa necesariamente un gran desarrollo económico nacional.
E) apela a la emotividad que la impresión visual es capaz de despertar.
Solución:
El tricolor se convirtió en emblema de todas las nacionalidades nacientes que
quieren seguir el derrotero trazado por la ideología francesa.
Clave: C
5. Si la revolución industrial inglesa hubiese también desarrollado una radical influencia
política,
A) sería posible establecer una gran semejanza entre su influjo y el de Francia.
B) Francia habría asumido la gran responsabilidad de industrializar el mundo.
C) no se habría producido la revolución francesa ni ninguna otra revolución.
D) la producción material en Francia se habría tecnificado en un nivel superlativo.
E) se habría producido una gran cantidad de convulsiones sociales en el orbe.
Solución:
Al inicio del texto se formula una relación de semejanza entre el influjo de Inglaterra
en lo económico y el de Francia en lo político.
Clave: A

ELIMINACIÓN DE ORACIONES
1. I) El Ayurveda, la ciencia de la vida, prevención y longevidad, es el sistema médico
holístico más antiguo y completo disponible en el mundo. II) Sus principios básicos
pueden encontrarse en las escrituras hindúes llamadas Vedas, los antiguos libros
indios de sabiduría escritos hace más de 5 000 años. III) El Ayurveda usa los
principios inherentes a la naturaleza para ayudar a preservar la salud de una
persona manteniendo el cuerpo, la mente y el espíritu del individuo en perfecto
equilibrio con la naturaleza. IV) India Herbs Ltda. cuenta con un experimentado
grupo de doctores ayurvédicos expertos en Kaya Chikitsa, una de las 8
especialidades del Ayurveda que se ocupa de la Medicina Interna. V) El Ayurveda
ofrece terapias para la purificación y desintoxicación, explica muy bien la causa
primordial de una enfermedad y prescribe el uso terapéutico de varias hierbas y
tratamientos holísticos.
A) IV B) I C) III D) II E) V
Solución:
No pertinencia. La referencia a la empresa India Herbs Ltda. se elimina por
impertinencia.
Clave: A
2. I) La medicina occidental recurre a medicamentos recetados agresivos y a cirugía
prohibitivamente cara para tratar muchos problemas relacionados con la toxicidad
del cuerpo. II) Estos métodos generalmente tratan sólo los síntomas de toxicidad y
no las causas subyacentes. III) Tan pronto como deja de consumir los
medicamentos, los problemas de toxicidad regresan y estos medicamente a menudo
tienen efectos secundarios no deseados y peligrosos. IV) Por ejemplo, las migrañas
son frecuentemente causadas por la concentración de toxinas en el cuerpo. V) La
Amitriptilina, Desipramina y Doxepina son prescritos comúnmente para aliviar las
migrañas.
A) III B) I C) IV D) V E) II
Solución:
No pertinencia. El tema es las toxinas, no los medicamentos específicos.
Clave: D
3. I) Intentar definir a Tony Évora, musicólogo, percusionista, destacado dibujante,
grabador, diseñador gráfico, profesor de arte y caribeño universal, resulta una tarea
ardua. II) Este cubano, nacido en La Habana hace 62 años, también se ha dedicado
a hacer la historia de la música cubana. III) Licenciado en Bellas Artes, es pionero
del arte gráfico en su país, ex-director artístico del Instituto Cubano del Libro y
peregrino por Europa desde 1968. IV) Tony Évora, artista pionero y polifacético, vive
exiliado en España. V) Hoy vive en Valencia dedicado al grabado, la enseñanza y la
investigación sobre la música popular del Caribe.
A) III B) V C) II D) I E) IV
Solución:
Redundancia. El contenido de la oración IV repite información.
Clave: E

4. I) Lev Semionovich Vygotsky nació en Orsha, pequeña ciudad de Bielorrusia, el 17
de noviembre de 1896. II) Tras concluir la enseñanza secundaria en la ciudad de
Gomel, a partir de 1912, cursó estudios universitarios de derecho, filosofía e historia
en Moscú. III) Durante sus estudios secundarios y universitarios, Vygotsky adquirió
una excelente formación en la esfera de las ciencias humanas (lenguas y lingüística,
estética y literatura, filosofía e historia). IV) Ya a la edad de 20 años escribió un
estudio voluminoso sobre Hamlet. V) Vygotsky fue calificado por el filósofo
S.Toulmin como el “Mozart de la psicología”.
A) V B) II C) I D) III E) IV
Solución:
Se elimina V por impertinente. El tema se refiere a la biografía de Vygotsky.
Clave: A
5. I) Por origen y por naturaleza el ser humano no puede existir ni experimentar el
desarrollo propio de su especie como una mónada aislada, de modo aislado no es
un ser completo. II) Para el desarrollo del niño, especialmente en su primera
infancia, revisten primordial importancia las interacciones con los adultos portadores
de todos los mensajes de la cultura. III) En este tipo de interacción, el papel esencial
corresponde a los signos, a los distintos sistemas semióticos. IV) Estos, desde el
punto de vista genético, tienen una función de comunicación y de instrumentos de
organización y de control del comportamiento individual. V) La interacción social fue
un concepto básico sobre el que Vygotsky erigió su concepción psicológica del
desarrollo integral del niño.
A) IV B) III C) II D) I E) V
Solución:
Se elimina V por impertinente. Tema La importancia de la interacción en el desarrollo
del niño.
Clave: E
Habilidad Lógico Matemática
EJERCICIOS DE CLASE Nº 13
1. En la figura se tiene un trozo de madera cuadriculada de 1 cm de espesor, el cual
será cortado por una sierra eléctrica para obtener cinco cuadraditos con las letras, P,
R, E, S y M. Si la sierra no corta más de 1 cm de espesor, ¿cuántos corte rectos
como mínimo deberán realizarse?
A) 3
B) 4
C) 5
D) 6
E) 7
R
P E
S M

Solución:
Se necesitan 3 cortes como mínimo
2. En la figura, se tiene un trozo de madera de forma circular de 1 cm de espesor, el
cual será cortado por una sierra eléctrica para obtener tres sectores circulares con
las letras P, R y E. Si la sierra no corta más de 1 cm de espesor, ¿cuántos cortes
rectos como mínimo deberán realizarse?
A) 2
B) 3
C) 4
D) 5
E) 6
Solución:
Se necesitan 3 cortes
Como mínimo
Nota: el tercer corte se hace recto acomodando las piezas después de haber
realizado los dos primeros cortes.
P
R
E
R
P E
S M
R
P E
S M
1º 2º
3º
P
R
E
P
R
E
1º
2º
3º

1º corte 2º corte
3º corte
4º corte
5º corte
6º corte
7º corte
2 dobladas
1 doblada
3. Se dispone de una tela cuadrada de 6 m de lado y de una guillotina que puede cortar
una longitud máxima de 2 m y a lo más tres capas a la vez de esta tela. Si se desea
obtener trozos rectangulares de 2 m por 1 m de esta tela, ¿cuántos cortes como
mínimo deberá realizarse para obtener el máximo número de trozos?
A) 9 B) 8 C) 6 D) 7 E) 5
Solución:
1) Marcas para los cortes:
2) Doblando en las líneas punteadas, se tiene los cortes:
3) Luego sobreponiendo las tres piezas, resultan los cortes:
4) Número mínimo de cortes: 7
4. En la figura se muestra una hoja de papel cuadriculada y deseamos seccionar los 6
cuadrados de la cuadrícula. ¿Cuántos cortes rectos como mínimo debemos realizar
con una tijera de costura, para lograr el objetivo?
A) 4
B) 3
C) 1
D) 5
E) 2
Solución:

1 doblada
1 corte
1) Primera acción:
2) Segunda acción:
3) Tercera acción:
4) Cuarta acción:
5) Número de cortes: 1.
5. Un alambre, de “n” cm de longitud, se divide mediante un corte en dos partes de
igual longitud, luego en cada parte se realizan nuevos cortes y se obtiene un número
exacto de trozos, en el primero trozos de n/16 cm, y en el segundo trozos de n/32
cm. Halle el número total de cortes realizados, si estos se hicieron uno a uno.
A) n B) 12 C) 24n D) 23 E) 48n
Solución:
= + − + − = + + =
   
   
   
n / 2 n / 2
Nro cortes 1 1 1 1 7 15 23
n / 16 n / 32
6. En una reunión el promedio de las edades de 50 personas presentes es 60 años. Si
se retiran 5 personas cuya edad promedio es 15 años, ¿en cuánto varía el
promedio?
A) 15 años B) 5 años C) 8 años D) 2 años E) 10 años
Solución:
Sean las edades: 1 2 3 4 50; ; ; ; .... ;a a a a a
Promedio de todos:
50
50
1
1
60 3000
50
i
i
a
a= ⇒ =
∑
∑
Promedio de los que se retiran:
5
5
1
1
15 75
5
i
i
a
a= ⇒ =
∑
∑
Promedio de los que se quedan:
50 50 5
6 1 1
2925i i ia a a= − =∑ ∑ ∑
50
6 2925
65
45 45
ia
⇒ = =
∑
∴ Varía en 5
n/2 n/2

7. En una empresa la edad promedio de los trabajadores varones es de 35 años y el de
las mujeres es de 28 años. Si las mujeres representan el 75% del número de
varones, ¿cuál es la edad promedio de los trabajadores de la empresa?
Solución:
1. # hombres: h, # mujeres: m khkmhmh%m 43
4
3
75 =∧=⇒=⇒=⇒
años32
k7
)k3)(28()k4)(35(
k7
mujeresedadesbreshomedades
promedioEdad.2
=
+
=
Σ+Σ
=
8. El promedio de un conjunto de números es K. Si se eliminan 29 números cuya suma
es 377, el promedio de los restantes sigue siendo K. Halle la suma de cifras de K.
A) 4 B) 5 C) 6 D) 7 E) 8
Solución:
Sean los números: 1 2 3 4; ; ; ; .... ; na a a a a
El promedio es: 1
1
n
i n
i
a
K a nK
n
= ⇒ =
∑
∑
Eliminado 29 números: 1
1
377
377 ( 29)
29
n
i n
i
a
K a n K
n
−
= ⇒ − = −
−
∑
∑
377 ( 29) 29 377nK n K K⇒ − = − ⇒ =
∴ K = 13
9. Ricardo, tiene 64 figuritas para llenar su álbum del mundial mientras que Julián no
tiene ninguno. Ricardo como buen amigo que es le regala cierta cantidad, dándose
cuenta que el producto de los números que cada uno tiene de figuritas es el mayor
posible. ¿Con cuántas figuritas se quedó Ricardo?
A) 16 B) 18 C) 20 D) 32 E) 24
Solución:
1) # figuritas que regaló Ricardo: x


 −
⇒
x:tieneJulián
x:tieneRicardo 64

Así el producto será: 10243210246464 22
=⇒−−=−=−= maxP)x(xx)x(xP
cuando 32=x .
Luego Ricardo se queda con 32 figuritas.
10. Miguel, tiene una lámina de hojalata que tiene la forma de un triángulo isósceles de
la cual desea recortar una pieza rectangular como se indica en la figura. Determinar
la altura del rectángulo si tiene la máxima área.
A) 1 m
B) 1,5 m
C) 1,25 m
D) 1,75 m
E) 2 m
Solución:
1) ABC∆ ~ MBN∆
)xh(
h
a
y
h
xh
a
y
−=⇒
−
=⇒
2) El área del rectángulo es:






−−=−== 2
2
2
24
)
h
x(
h
h
a
)xhx(
h
a
xyA
Luego A es máxima cuando 251
2
52
2
,
,h
x === m
11. Dos líneas férreas se cruzan formando un ángulo recto. Los trenes parten al mismo
tiempo y se acercan a gran velocidad hacia el cruce. Uno parte de cierta estación
que dista 40 km del cruce; el otro de una estación que dista 50 km del cruce con
velocidades constantes de 800 m/min y 600 m/min, respectivamente. ¿Qué tiempo
tiene que transcurrir para que la distancia que separa a los trenes sea mínima?
A) 1h 2 min B) 45 min C) 1 h 8 min D) 1h 15min E) 59 min
3 m
2,5 m
3 m
2,5 m
x
h
h-x
a
yA
B
C
M N

Solución:
Datos:
VA=800 m/min; VB=600 m/min
Tiempo transcurrido : t minutos
Distancia mínima :
0d ≥ .
2 2 2 2
2 2
( ) ( ) (40 0,8 ) (50 0,6 )
124 4100 ( 62) 256
d ON OM t t
t t t
⇒ = + = − + −
= − + = − +
Luego min 256 16d km= = esto ocurre cuando 62t = min o su equivalente
t = 1h 2 min.
12. En la figura mostrada, ABCD es un trapecio con AD//BC y CN = ND.
Si 2
18 cmyz =+ , halle x.
A) 20 cm²
B) 27 cm²
C) 9 cm²
D) 10 cm²
E) 18 cm²
Solución:
= =
+ = +
∴ = 2
1
Area(BMLA) Area(ABCD) Area(BNA)
2
S 18 S x
x 18 cm
B C
A D
y
x
z
M
L
N
50 km
40 km
d
A
B
O M
N
B C
A D
y
x
z
M
L
N
B C
A D
y
x
z
M
L
NS

13. En la figura, se indica un cuadrado de lado 5 cm, el cual se ha dividido en
cuadrados congruentes. Si las cuatro regiones sombreadas en el cuadrado son
congruentes y sus dimensiones son como se indica, determine el área de la región
equivalente a las cuatro regiones sombreadas.
A) 10 cm 2
B) 5 cm2
C) 2 cm 2
D) 15 cm 2
E) 7,5 cm2
Solución:
1) Los puntos E, F, G y H son los vértices de un cuadrado.
2) El cuadrado EFGH es equivalente a las cuatro regiones sombreadas.
3) Por propiedad: Area EFGH 2
525
5
1
5
1
cmABCDArea =×==
14. En la figura, se muestra una red formada por paralelogramos congruentes de área
igual a 1 cm 2
. Determine el área de la región sombreada.
A) 8 cm2
B) 12 cm 2
C) 9 cm 2
D) 8,5 cm 2
E) 6,5 cm2
Solución:
1cm2
2a
2a
a
a
2a
2a
a
a
A
A
A
A
AA
AA
E
F
G
H
5cm
A
B C
D

1) La región sombreada tiene un área igual a la suma de
las áreas de las regiones que se indica en la figura.
2) 2
9
2
5
2
6
2
3
2 cmDCBAAsomb =+++=+++=
EVALUACIÓN DE CLASE Nº 13
1. En la figura se muestra una hoja de papel cuadriculada. ¿Cuántos cortes rectos
como mínimo debemos realizar para separar los 10 cuadrados de la cuadrícula?
A) 4
B) 1
C) 2
D) 3
E) 5
Solución:
2. ¿Cuál es el máximo número de trozos de papel que se puede obtener haciendo 10
cortes rectos a una hoja de papel de forma circular, sin doblar ni superponer en
ningún momento y también sin separar las partes más allá del grosor del instrumento
cortante?
A) 53 B) 54 C) 57 D) 55 E) 56
Solución:
1) Por inducción, se obtiene para n cortes:
A
D
B
C
doblamosdoblamos
1 corte

( )1
# 1
2
n n
Trozos
+
= +
.
2) Para 10n = , se obtiene
( )10 10 1
# 1 56
2
Trozos
+
= + =
.
3. La figura representa un pedazo de madera que tiene la forma de un triángulo
equilátero, el cual va a ser cortado total y exactamente en 16 trozos que tengan la
forma de triángulos equiláteros congruentes. ¿Cuántos cortes rectos como mínimo
son necesarios realizar para lograr el objetivo?
A) 3
B) 4
C) 5
D) 6
E) 7
Solución:
. los tres primeros cortes lo dividen 6 trozos
. los trozos obtenidos se sobreponen y se realizan 2 cortes más
. por lo tanto
Total de cortes = 3 + 2 = 5
4. De las edades de 5 personas, si sumamos la edad promedio de cuatro de ellos a la
edad de la quinta persona, se obtienen los números 26, 29, 32, 35 y 38. Halle la
suma de las edades de las 5 personas.

Solución:
Sean las edades: a, b, c, d, e
Por dato tenemos:
26
4
29
4
32
4
35
4
38
4
b c d e
a
a c d e
b
a b d e
c
a b c e
d
a b c d
e
+ + +
+ =
+ + +
+ =
+ + +
+ =
+ + +
+ =
+ + +
+ =
Sumando obtenemos: 2(a + b + c + d + e) = 160
∴ (a + b + c + d + e) = 80 años
5. Una empresa tiene 12 trabajadores de edades diferentes y ninguno es menor de
20 años. Si la edad promedio es de 28 años, ¿cuál es la máxima edad que puede
tener uno de los trabajadores?
Solución:
1. Edad máxima de uno de los trabajadores: maxe .
2. Suma de las otras edades: 11S
3. 
33630212033628
12
11
11
=++++⇒=+⇒=
+
)(eSe
Se
max
imomin
max
max

4. 61=maxe años
6. Halle el mayor valor de “k” en k
abc
)cba(
≥
++ 3
, si a, b y c son números reales
positivos.
A) 30 B) 27 B) 9 C) 12 D) 24
Solución:
Tenemos MA ≥ MG
3
3
abc
cba
≥
++

27
)( 3
≥
++
abc
cba
luego K=27
7. Jaime, ingeniero de una empresa que se dedica a la producción de harina de
pescado, observa que la producción mensual (en toneladas) sigue la regla:
45102
+−= xx)x(P , donde x indica el mes del año. Determine cuál fue la producción
mínima y en qué mes ocurrió.
A) 20 ton, junio B) 25 ton, mayo C) 30 ton, setiembre
D) 20 ton, mayo E) 30 ton, agosto
Solución:
1) 2054510 22
+−=+−= )x(xx)x(P
La producción mínima será de 20 toneladas, y ello ocurre cuando x=5, luego en el
mes de mayo la producción alcanzó su mínimo valor.
8. En la figura, CD//AB , DE//BC , = 2
1S 3m y = 2
2S 27m . Determine el área de la
región triangular BCD.
A) 8 m²
B) 9 m²
C) 7 m²
D) 6 m²
E) 10 m²
Solución:
Propiedad
= ⇒ =
→ =
∴ =
2
2
2
2
3 (ak)
a 27(3)
27 (27k)
a 9
A(BDC) 9m
9. En la figura se indica un rectángulo que ha sido dividido en regiones mediante arcos
de circunferencias congruentes, cuyo ángulo central mide 45º, con centros en los
puntos que se indican y de radio 4cm. Determine el área de la región sombreada.
B
C
A
D
E
S1
S2
B
CA
D
E
S =31
S =272
27k
ak
ak
a
a

A) 16 cm 2
B) 24 cm 2
C) 36 cm 2
D) 20 cm 2
E) 12 cm 2
Solución:
1) Completamos los sectores circulares.
2) La región sombreada queda dividida como se indica en la figura.
3) Trasladando regiones equivalentes se tiene:
2
24833 cm)SA(Asomb =×=+=
Aritmética
1. Una cuadrilla de obreros emplea 10 días trabajando 12 hrs. por día en realizar
una obra. Si hubiera trabajado 2 hrs. menos por día ¿En cuántos días habría
terminado la obra?
A) 10 B) 12 C) 14 D) 16 E) 18
Solución:
10 12
x 10
∴
10.12
x 12
10
= = Clave: B
2. Nueve hombres pueden hacer una obra en 10 días ¿Cuántos hombres más
harían falta para hacer la obra en 2 días?
A) 45 B) 40 C) 36 D) 30 E) 25
4cm
12 cm
A
B C
EG
S
A
S
S
A
A
S
SS
4cm
4cm 4cm 4cm

Solución:
9 10
x 2
∴
9.10
x 45
2
= =
Clave: C
3. Los
5
13
de un terreno esta valorizado en 15,300 soles. ¿A cuánto se debe
vender la otra parte para ganar su 25%?
A) S/.
30600 B) S/.
20600 C) S/.
26600 D) S/.
28000 E) S/.
30000
Solución:
5
13
15300
8
13
x
8
.15300
13x 24480
5
13
= =
Pv = 24480 + 25% 24480
= 30600
Clave: A
4. Se tiene dos cuadrillas de obreros; la primera tiene 100 hombres y puede hacer
una obra en 30 días, la segunda tiene 60 hombres y puede hacer la misma obra
en 40 días. Si sólo tomamos los
3
4
de la primera y los
5
6
de la segunda, ¿en
cuántos días se terminará la obra?
A)
1
18
3
B)
9
21
11
C)
1
23
3
D)
1
24
2
E)
1
25
3
Solución:
100 30 60 40
1 x 1 x
x = 3000 x = 2400
En un día:
( ) ( )
3 1 5 1 11
100 . 60 .
4 3000 6 2400 240
+ =

Toda la obra se hará en:
240 9
21
11 11
= días
Clave: B
5. Cuarenta kilogramos de agua salada contienen 7kg de sal. ¿Qué cantidad de
agua se debe dejar evaporar para que 20kg de la nueva mezcla contengan 6kg
de sal?
A)
2
16 kg
3
B)
1
15 kg
3
C)
2
14 kg
3
D)
1
13 kg
3
E)
2
12 kg
3
Solución:
20 kg de mezcla 6kg sal
x 7kg sal
20.7 70
x
6 3
= =
Se deben evaporar
70 50 2
40 16
3 3 3
− = =
Clave: A
6. Cierta cantidad de obreros prometen hacer una obra en 30 días pero cuando ya
habían trabajado cinco días contratan 8 obreros más con lo que terminan el
trabajo 5 días antes. ¿Cuántos días demorará un sólo obrero en hacer dicha
obra?
A) 900 B) 930 C) 960 D) 990 E) 1020
Solución:
x 30 1 x 30 1
x 5 y x+8 20
5
6
∴
1
y
6
= x + 8 =
5
x.30.
6
20.1
x = 32
32 30 1
1 x 1
x = 30.32 = 960
Clave: C

7. Un grupo de 40 obreros se comprometen terminar una obra en 40 días
trabajando 8 h/d. Luego de 10 días de trabajo se contrató 10 obreros
doblemente hábiles que los anteriores y juntos trabajan 8 días a razón de 6 h/d,
al cabo del cual se despidió a todos y se contrató 8 obreros triplemente
hábiles que los del inicio terminando la obra 2 días antes. ¿Cuántos h/d
trabajaron estos últimos?
A)
9
2
B) 5 C) 7 D) 10 E) 14
Solución:
40 40 8 1 40 40 8 1
40 10 8 x 60 8 6 y
→ x =
1
4
→ y =
9
40
40 40 8 1
24 20 z
21
40
→ z = 14
Clave: E
8. Un empleado observa que su sueldo ha sido descontado en un 20% ¿Cuál será
el porcentaje de aumento para que reciba su salario original?
A) 10% B) 15% C) 20% D) 25% E) 30%
Solución:
80%S + x% 80%S = S
x = 25
Clave: D
9. Un comerciante compra un artículo de S/.
8000 ¿Cuál será el precio fijado para
que al rebajarlo el 20% aún se gane el 30% de su costo?
A) S/.
12000 B) S/.
13000 C) S/.
14000 D) S/.
15000 E) S/.
16000
Solución:
80%PF = 130%PC
= 130% 8000
→ PF = 13000 Clave: B
10. El número de artículos que se pueden comprar con una suma de dinero
aumentaría en 5, si se variase en 20% el precio de compra de cada artículo.
¿Cuál es dicho número de artículos?
A) 10 B) 15 C) 20 D) 25 E) 30

Solución:
nP = ( n + 5 )( 80%P )
→ n = 20
Clave: C
11. Una persona gasta el 20% de lo que tiene, luego el 30% de lo que le queda y
por último gasta el 40% del nuevo resto, quedándole S/.
33600. ¿Cuánto tenía al
principio?
A) 80000 B) 90000 C) 100000 D) 110000 E) 120000
Solución:
Queda: 80%. 70%. 60%T = 33600
T = 100000
Clave: C
12. En la venta de un artículo se obtiene un beneficio del 20% sobre el precio de
costo. Si se hubiera ganado el 20% sobre el precio de venta se habría obtenido
S/.
3,5 más. ¿Cuál fue el precio de venta?
A) S/.
90 B) S/.
95 C) S/.
100 D) S/.
105 E) S/.
110
Solución:
PV = 120% PC G2 – G1 = 3,5
G1 = 20% PC 20%PV – 20%PC = 3,5
G2 = 20% PV C C
1 6 1
P P 3,5
5 5 5
 
− = 
 
C
175
P
2
=
∴ V
6 175
P 105
5 2
 
= = 
 
Clave: D

EVALUACIÓN DE CLASE N° 13
1. Una cuadrilla de obreros emplea 7 días trabajando 8hrs. por día en realizar una
obra. Si se hubiera trabajado 1hr. menos por días. ¿En cuántos días habría
terminado la obra?
A) 8 B) 9 C) 10 D) 11 E) 12
Solución:
7 8
x 7
∴x = 8
Clave: A
2. Nueve obreros pueden hacer una obra en 5 días. ¿Cuántos hombres habría
que disminuir para hacer la obra en 15 días?
A) 7 B) 6 C) 5 D) 4 E) 3
Solución:
9 5
9 – x 15
9.5
9 x x 6
15
− = → =
Clave: B
3. Para pintar 180m2 se necesitan 24kg de pintura. ¿Cuántos kg se necesitaran
para pintar una superficie rectangular de 12m de largo por 10 de ancho?
A) 14 B) 15 C) 16 D) 17 E) 18
Solución:
180 24
12.10 x
x = 16
Clave: C

4. Para hacer una obra se tiene dos cuadrillas, la primera tiene 80 hombres y
pueden hacer la obra en 40 días, la segunda tiene 40 hombres y pueden hacer
la obra en 20 días si tomamos la mitad de ambas cuadrillas. ¿En cuántos días
dos se terminaría?
A)
2
26
3
B) 27 C)
2
27
3
D) 28 E)
2
28
3
Solución:
80 40 40 20
1 x 1 x
x = 3200 x = 800
En un día:
1 1 3
40. 20
3200 800 80
 
+ = 
 
Toda la obra se hará en:
80 2
26
3 3
= días
Clave: A
5. Quince obreros hacen una obra en 9 días, 18 mujeres hacen el 80% de la obra
en 12 días y 15 niños hacen el 75% de la obra en 18 días. ¿En cuántos días dos
niños harán lo que hacen juntos un hombre y una mujer en 24 días?
A) 48 B) 36 C) 54 D) 60 E) 64
Solución:
15 9 18
4
5
12
1 x 1 1 x
x = 135 x = 270
15
3
4
18
1 1 x
x = 360
→
1 1 1
2. t 24
360 135 270
 
= + 
 
t = 48
Clave: A

6. Cierta cantidad de obreros se comprometen hacer una obra en 40 días. Pero
cuando ya habían trabajado 10 días contratan 10 obreros más con lo que
terminan la obra 10 días antes. ¿Cuántos días demorarán 2 obreros en hacer la
obra?
A) 800 B) 400 C) 600 D) 700 E) 300
Solución:
n 40 1 n 40 1 20 40
n 10 x n+10 20
3
4
2 y
1
x
4
=
3
40.n.
4n 10
20
+ =
20.40
y 400
2
= =
n = 20
Clave: B
7. En una granja el 25% son patos, el 40% son gallinas y el 35% son pavos. Si el
número de gallinas fuera el doble ¿Qué porcentaje del total serán pavos?
A) 21% B) 22% C) 23% D) 24% E) 25%
Solución:
Patos =
5
T
20
Gallinas =
8
T
20
Pavos =
7
T
20
Clave: E
8. En que porcentaje se debe aumentar el precio de un artículo de tal manera que
aún haciendo un descuento del 20% del precio fijado se gane el 40% del
costo?
A) 75% B) 60% C) 50% D) 45% E) 25%
Solución:
PF = PC + x% PC 4( PC + x%PC) = 7 PC
PV = 80% PF = 140% PC → x = 75
4PF = 7PC
Clave: A
→
7 5 16 7
x%
20 20 20 20
 
= + + 
 
→ x = 25

9. Al aumentar el precio de la localidad de un espectáculo en 20% la asistencia
baja en el 10%. ¿En qué porcentaje aumenta la recaudación?
A) 8% B) 10% C) 12% D) 14% E) 16%
Solución:
T1 = np → T2 – T1 =
8
np
100
T2 = (90%n)(120%p) = 8% np
Aumenta en 8%
Clave: A
10. En un salón de clase; el 60% son mujeres, 24 son hombres con reloj mientras
que el 40% son hombres sin reloj. Hallar el total de alumnos del aula.
A) 60 B) 170 C) 80 D) 90 E) 100
Solución:
24 = 60% H → H = 40 = 40%
→ H = 40 ∴ M = 60
∴ H + M = 100
Clave: E
Álgebra
SOLUCIONARIO SEMANA Nº 13
EJERCICIOS DE CLASE
1. Si 3m7
m3m
32m
−=
−
+
, hallar la suma de los cuadrados de los valores de m.
A) 34 B) 25 C) 40 D) 53 E) 13
Solución:
De la ecuación:
( ) ( )
( )( )
.4026
2m6m02m6m
012m8m3m73m3m2m
22
2
=+∴
=∨=⇒=−−⇒
=+−⇒−=−−+
Clave: C

2. Hallar los valores de n para que el sistema en x e y
( ) ( )
( )


−=++
=+++
7ny2x1n
4y2nx1n2
tenga solución única.
A) R –{ }1,2− B) R –






−−
3
2
,1 C) R –






− 1,
3
2
D) R –{ }1,1− E) R –{ }1,2 −−
Solución:
Sistema de solución única: 0s ≠∆
( ) ( )( )
( )( )
.1,
3
2
Rn
1n
3
2
n01n2n3
02nn302n1nn21n2
0
n21n
2n1n2
2
s






−−∈∴
≠∧−≠⇒≠−+⇒
≠−−⇒≠++−+⇒
≠
+
++
=∆
Clave: C
3. Hallar el valor de m para que el sistema en x e y
( ) ( )




=+
−=++−
4y2x5
1y1m3x2m3 2
sea compatible indeterminado.
A) –
4
1
B)
2
1
C) –
8
1
D) –
2
1
E)
4
1
Solución:
Sistema compatible indeterminado:
4
1
2
1m3
5
2m3 2
−=
+
=
−
.
2
1
m
2
1
m12m6
4
1
2
1m3
de
2
1
m
2
1
m3m12
4
1
5
2m3
de 2
2
−=∴
−=⇒−=+⇒−=
+
−=∨=⇒=⇒−=
−
Clave: D

4. Hallar el valor de n para que el sistema en x e y
( )




−=+
=++
3nyx5
4y4x4n2
sea
incompatible.
A) 4 B) – 3 C) 2 D) – 2 E) – 4
Solución:
Sistema incompatible:
3n
4
1
4
5
4n2
−
≠=
+
.4n
4n13n
3n
4
1
4
de
4n4n16n
1
4
5
4n
de 2
2
−=∴
≠⇒≠−⇒
−
≠
−=∨=⇒=⇒=
+
Clave: E
5. Al resolver el sistema de ecuaciones




=+
=++
7y3x2
37y9xy6x4 22
, hallar el mayor
valor de y – x.
A) –
6
1
B) –
2
1
C) – 1 D) 1 E)
6
1
Solución:
( )
( )( )
.
6
1
xyMayor
1xy2x1ySi
6
1
xy
2
3
x
3
4
ySi:
1y
3
4
y01y4y3
04y7y37y3
y
2
2
73y2xEn:
y
2
x2xy37xy67
37xy6y3x2
379y6xy4xDe:
2
2
2
22
−=−∴
−=−⇒=⇒=
−=−⇒=⇒=
=∨=⇒=−−⇒
=+−⇒=+







⇒
=+
=⇒=⇒=−⇒
=−+⇒
=++
III
II
I
Clave: A

6. Si ∈x R , determinar el conjunto solución de la siguiente ecuación
0
x31x
x2xx2
02x
2
=
−+
+ .
A) { }2,0 B) { }2,0,1− C) { }1 D) { }0 E) { }2
Solución:
x 2 0
2x x + 2 x
0 x + 1 3 – x2
– x3
(x + 2)
3x2
x 2 0 0
– 4x3
2x x + 2 x 2x(x+1)
N M
( ) ( ) ( )
( ) ( ) ( ) ( )
{ } .2,0CS
0x2x
01xx2x2xx2xx
0x2xx2x
0x4x3x2x2x2x
0x4x31xx22xx
0NM
23
234
32234
323
=∴
=∨=⇒
=+−=−+−⇒
=−+−⇒
=+−++−−⇒
=−−+++−⇒
=−⇒
+

Clave: A
7. Si βα y tal que β>α son las soluciones de la ecuación
( )
432
36x12x9x6x5x
30xx15x2x25x
x3x3x3
222
222
=
+−+−−
−−−+− , hallar .
7
52
β
−α
A) 2 B) 21 C) 96 D) 7 E) 12
Solución:

( )( ) ( )( ) ( )( )
( ) ( ) ( )
( )
( ) ( ) ( )
( ) ( )( ) ( )( ) ( )( )
( )( )( )( )
( )( )
( )
.24042
78
532
7
52
:
8,33x8x03x8x
024x5x4323125xx3
4323x6x5x6x5x3x5xx3
432
6x3x5x
6x3x5x
111
5xx3
432
6x3x5x
6x5x3x5x5x5x
x3x3x3
:
2
222
222
=−=
−
−
=
β
−α
−=β=α⇒=∨−=⇒=−+⇒
=−+⇒=−−+⇒
=−−−−−−−−−+⇒
=
−−−
−−−+⇒
=
−−−
−+−+−+
II
I
Clave: A
8. Hallar el valor de m para que el sistema en x, y, z
( )
( )
( ) 2zyx1m
2zy1mx
41mzyx
=++−
=+−+
−=−++
sea incompatible.
A) – 1 B) – 2 C) 2 D) 1 E) 0
Solución:
( )( )( ) ( )( )( ) ( )( )( ) ( ) ( )( )( ) ( )( )( )( )
( ) ( )
.2m:leincompatibSistema
2zyx2
2zy2x
4z2yx
1m
leincompatibsistema24
2zyx
2zyx
4zyx
2m
:ecuacionesdesistemaelenplazandomeRe:
1m2m01m2m04m3m
021m3m3m3m3
01111111m111m1m1111m1
0
111m
11m1
1m11
0:
223
23
3
s
=∴
⇒





=++−
=+−
−=−+
⇒−=
=−⇒





=++
=++
−=++
⇒=
−=∨=⇒=+−⇒=+−⇒
=−+−+−−⇒
=++−−−+−+−⇒
=
−
−
−
=∆
II
I
Clave: C
Sumando las ecuaciones
Se tiene 0 = 0
Sistema de Infinitas soluciones

9. Hallar el valor de x que satisface el sistema de ecuaciones
27yzxzxy
1
z
1
y
1
x
1
9zyx
=++
=++
=++
.
A) 2 B) 4 C)
2
5
D) 3 E)
2
7
Solución:
En el sistema
( )
( )
( )






=++
=++
=++
III
II
I
...27yzxzxy
...1
z
1
y
1
x
1
...9zyx
( ) ( )
( )
( ) ( )
( )
( )
.3x
03x027x27x9x
x2727xx927
x
27
x9x
27yzzyx:en
x9zy:de
x
27
yz27xyzy1
xyz
xyxzyz
:de
323
32
=∴
=−⇒=−+−⇒
=+−⇒=+−⇒
=++
−=+
=⇒=⇒=
++
III
I
IIIII
Clave: D
9zyx
14yzxzxy
29zyx 222
=++
=−+
=++
, hallar la suma de los
valores de x.
A) 7 B) 8 C) 9 D) 6 E) 10
Solución:
Sabemos que:
( ) ( )
( )
( ) ( )α=+⇒=+⇒
=−+
=++⇒
+++=⇒
+++++=++
...20zyx40xz2xy2
14yzxzxy:dato
26yzxzxy
yzxzxy2299
yzxzxy2zyxzyx
2
2222

( ) ( )
( )( )
.954:xsuma
5x4x05x4x
020x9x20x9x:enluego
x9zy9zyx:dato
2
=+∴
=∨=⇒=−−⇒
=+−⇒=−α
−=+⇒=++
Clave: C
EJERCICIOS DE EVALUACIÓN
1. Si 7
b24
a3
=
−
, hallar el valor de
b4b104
a2a53
+−
+
.
A) 14 B) 28 C) 21 D) 7 E) 35
Solución:
( ) ( ) ( ) ( ) 1472a4b62a2b104b4a53
b4b104
a2a53
:
7a4b67
b24
a3
:
==+=+−−+=
+−
+
=+⇒=
−
II
I
Clave: A
2. Hallar el valor de n para que el sistema en x e y
( )
( ) ( )


−=+−−
−=+−
1n2y7nx2n
14n3y2nx4
sea compatible indeterminado.
A) 8 B) – 4 C)
5
6
D)
3
2
E)
3
4
Solución:
Sistema compatible indeterminado:
( )
( ) 1n2
14n3
7n
2n
2n
4
−
−
=
+−
+−
=
−
( )
( )
.8n
3
4
n8n032n28n3
1n2
14n3
2n
4
de
4n8n032n4n
7n
2n
2n
4
de
2
2
=∴
=∨=⇒=+−⇒
−
−
=
−
−=∨=⇒=−−⇒
+−
+−
=
−
Clave: A





=+−−−+
=+−+−+
14y5x39y5x3
74y5x39y5x3
, hallar el
valor de x + y.
A) 9 B) 7 C) 5 D) 6 E) 8
Solución:
En el sistema
( )
( )



β=+−−−+
α=+−+−+
...14y5x39y5x3
...74y5x39y5x3
( ) ( )
( ) ( )
.7yx
2y20y105x30x6
5y5x364y5x32:
25y5x389y5x32:
=+∴
=⇒=∧=⇒=⇒
=−⇒=+−β−α
=+⇒=−+β+α
Clave: B
4. Si x e y tal que x < y son los valores positivos que se obtienen al resolver
el sistema de ecuaciones
( )( )
xy
72
1y1x
18yxyx 22
=++
=+++
, hallar el valor de xy
.
A) 5 B) 8 C) 9 D) 10 E) 6
Solución:
En el sistema
( )
( )( ) ( )




=++
=+++
II
I
...
xy
72
1y1x
....18yxyx 22
( ) ( )( ) ( )
( ) ( )
( ) ( )( ) ( )
( ) ( ) ( )( )
( )( )
( ) ( )
( )
( )( )
( ) ( ) 3x4x012xx72xx6:en
2y3y02y3y6yxSi)
.yx3y,2x
2x3x06xx72xx12:en
3y4y03y4y12yySi)
6yy12yy
06yy12yy072yy18yy
72yyyy18:en
yy18xx18yyxx:de
...72yyxx:de
22
2
22
2
22
22222
22
2222
22
=∨−=⇒=−+⇒=+α
=∨−=⇒=−+⇒=+∗
<==⇒
=∨−=⇒=−+⇒=+α
=∨−=⇒=−+⇒=+∗
=+∨=+⇒
=−+−+⇒=++−+⇒
=++−α
+−=+⇒=+++
α=++
I
II
No cumple la condición x, y positivos tal que x < y
.82x 3y
==∴
Clave: B

5. Si
bb
2a
bab
aba
2=
+
−
donde 0a ≠ , hallar el valor de
2222
baab
abba
111
+
.
A) 0 B) 1 C) – 1 D) 2 E) – 2
Solución:
0
a2aa
aaa
111
baab
abba
111
:
ba0bab2a
bb
2a
bab
aba
:
222
2
2222
22
2
==
+
=⇒=+−⇒=
+
−
II
I
Clave: A
6. Hallar los valores de m para que el sistema en x, y, z
19zy2x3
7z2myx3
6z3y2x
=++
−=++
=++
tenga solución única.
A) R –






5
2
B) R






−
5
4
C) R






−
3
5
D) R






−
2
5
E) R






−
5
3
Solución:
Sistema de solución única: 0s ≠∆
( )( )( ) ( )( )( ) ( )( )( ) ( )( )( ) ( )( )( ) ( )( )( )( )
.
2
5
m
2
5
m01030m8
03211223m32233231m1
0
123
2m3
321
s






−∈∴
≠⇒≠−+−⇒
≠+++++⇒
≠=∆
R
Clave: D

7. Determinar el valor de ∈m Z para que el sistema de ecuaciones en x, y, z
mx + y + 2z = 2
x + (m–1) y + 2z = 1 sea compatible indeterminado.
x + 2 y + (m + 1)z = 3
A) – 2 B) – 1 C) 0 D) 2 E) 1
Solución:
( )( ) ( )( )( ) ( )( )( ) ( )( )( ) ( )( )( ) ( )( )( )( )
( )( )
.1madominerdetincompatibleSistema
solucionesinitasinf
1z2x
1y
3z2y2x
1z2x
2z2yx
1m
:ecuacionesdesistemaelenplazandomeRe:
1m07mm1m07m8m
0111mm2211m22112211m1mm
0
1m21
21m1
21m
0:
m
23
s
=∴



=+
=
⇒





=++
=+
=++
⇒=
=⇒=−+−⇒=+−⇒
=+++−−+++−⇒
=
+
−
=∆
∉
II
I
  
Z
Clave: E
8. Hallar un valor de x en el sistema de ecuaciones









=
=++
=++
1xyz
2
7
z
1
y
1
x
1
2
7
zyx
.
A)
4
1
B)
2
3
C)
4
3
D)
2
1
E)
4
5
Solución:

En el sistema
( )
( )
( )









=
=++
=++
III
II
I
...1zyx
...
2
7
z
1
y
1
x
1
...
2
7
zyx
( ) ( ) ( )
( ) ( )
( ) ( )
( )( )( )
.
2
1
xdevalorUn
2x
2
1
x1x02x1x21x
02x7x7x2
2
7
x
2
7
x
x
1
2
7
yzxyz:en
x
1
yz:x
2
7
zy:de
...
2
7
xyxzyzy
2
7
xyz
xyxzyz
:de
23
=∴
=∨=∨=⇒=−−−⇒
=−+−⇒=





−+⇒
=++α
=∧−=+
α=++⇒=
++
IIII
IIIII
Clave: D
Geometría
EJERCICIOS DE CLASE N° 13
1. En la figura, P – ABCD es una pirámide cuadrangular regular. Si PC = AC = m22 ,
hallar el área total de la pirámide.
A) ( ) 2
m174 +
B) ( ) 2
m172 +
C) ( ) 2
m172 −
D) ( ) 2
m174 −
E) ( ) 2
m274 +

D
B C
A
O
60º
H
Resolución:
1) PMC: 71)22(Ap 22
=−=
2) 74
2
724
2
ApP
A
xx
L ===
42A 2
B ==
3) )17(4474AAA BLT +=+=+=
Clave: A
2. En una pirámide cuadrangular regular, la arista de la base mide m24 y la arista
lateral 9 m. Hallar la distancia del centro de la base a una arista lateral.
A) m65
9
2
B) m65
9
4
C) m65
7
4
D) m65
9
5
E) m65
2
1
Resolución:
1) POC = 22
49 +
65h =
2) POC: R.M:
9x654 .. =
m
9
654
x =∴
Clave: B
3. En la figura, D–ABC es una pirámide regular, la altura DO mide m36 . Hallar el
área total de la pirámide.
A) 2
m3296 B) 2
m3348
C) 2
m3336 D) 2
m3280
E) 2
m3324
Resolución:

B
CA
D
D
B C
A
O
60º
l
B
CA
D
H
2 3
2 3
2 3
2 3
2
x - 92
Q
x
O
3
3
1) DOM: Notable: DM = 12 ∧ OM = 6
2) O: Baricentro del ∆ABC
3) 312
3
36
318 ==→= l
2
l
3324A
12
2
)312(3
4
3)312(
A
T
2
T
=
+= .
Clave: E
4. En la figura, D–ABC es una pirámide regular, el radio de la cirunferencia inscrita en
la base mide 2 cm y el radio de la circunferencia inscrita en la cara BDC mide 3 cm.
Hallar el área lateral de la pirámide.
A) 2
cm372 B) 2
cm3144
C) 2
cm348 D) 2
cm396
E) 2
cm336
Resolución:
1) DQO ∼ DHC
21
3x
9x
32
3
2
=→
+
−
=
2)
2
24)34(3
2
ApP
AL
..
==
3144AL =∴
Clave: B

45º
P
A
C
B
30º
45º
P
A
C
B
30º
63 2
3 6
A
V
C
Q
D
B
O
F
5. En la figura, P–ABC es una pirámide y PB = 6 cm. Hallar el volumen de la pirámide.
A) 3
cm218
B) 3
cm16
C) 3
cm224
D) 3
cm18
E) 3
cm24
Resolución:
1) PAB , PAC: Notables
2) ABC: Pitágoras
6BC
)63(BC)23( 222
=
=+
3) 23
2
236
3
1
V
x








=
V = 18
Clave: D
6. En la figura, V – ABCD es una pirámide cuadrangular regular y O es centro de la
base. Si su volumen es numéricamente igual al área lateral, hallar OF en
centímetros.
A) 4 cm
B) 3 cm
C) 5 cm
D) 1 cm
E) 2 cm

A
V
C
Q
D
B
O
F
H
Ap
a
a
2
Ap
D
B
C
A F
EO
M l
l
V
Resolución:
1) V = LA
2
Apa4
Ha
3
1 2 .
. =
2) VOQ: R.M: H . OFAp
2
a
.=
→
2
a
H..
OF
1
Ap =
3)
2
a
H
OF
1
a2Ha
3
1 2
... =
∴ OF = 3
Clave: B
7. El área lateral de una pirámide regular hexagonal es 48 m2
. Si el apotema de la
pirámide tiene una medida igual a 4 veces la medida del radio de la circunferencia
que circunscribe a la base, hallar la longitud del lado de la base.
A) 3 m B) 4 m C) 2 m D) 5 m E) 6 m
Resolución:
1) l4R4Ap48AL ==∧=
2) 48
2
46
48
2
ApP xxxB
=⇒=
ll
∴ l = 2
Clave: C
8. Una pirámide regular tiene 12 aristas en total, su apotema mide m212 y la base
está inscrita en una circunferencia cuyo radio mide 8 m. Hallar el volumen de la
pirámide.
A) 190 3 m3
B) 192 3 m3
C) 180 3 m3
D) 384 m3
E) 346 m3

A
V
M P
C
E
B
A
V
M P
C
E
B
h
a
a a
a
a
a
VX
H/2
V2
Resolución:
1) Propiedad: R = l = 8 , 21Ap =
2) VOM: 222
h)34()212( +=
84 = 48 + h2
h = 6
3) 31926
4
38
6
3
1
V
2
=








= ..
Clave: B
9. En la figura, V–ABC es una pirámide regular cuyo volumen es 72 m3
, M, E y P son
puntos medios de las aristas VA , VB y VC . Hallar el volumen de la pirámide
E – AMPC.
A) 9 m3
B) 18 m3
C) 27 m3
D) 38 m3
E) 36 m3
Resolución:
1) 9V
a2a2a2
aaa
V
V
1
1
=⇒=
..
..
2) 36V
HA
3
1
2
H
A
3
1
V
V
2
B
B
2
=⇒=
.
.
3) 7236V9 x =++
∴ xV = 27
Clave: C

A
P
C
Q
D
B
M
A
P
C
Q
D
B
M
3
3
3
L
30º30º
3 2
3 2
6
6
3 3
10. Una pirámide es seccionada por dos planos paralelos a la base de tal manera que
trisecan a la altura. Si el volumen del sólido central es 21 cm3
, hallar el volumen de la
pirámide original.
A) 96 cm3
B) 81 cm3
C) 72 cm3
D) 69 cm3
E) 75 cm3
Resolución:
3
total
3
3
total
3
3
cm81V
)h3(
)h2(
V
24
3V
)h2(
h
21V
V
=
=
=⇒=
+
∴
Clave: B
11. En la figura, P – ABCD es una pirámide regular, M es punto medio de la altura PQ,
mDMC = 60º y AD = 6 cm. Hallar el volumen de la pirámide.
A) 3
cm336
B) 3
cm264
C) 3
cm272
D) 3
cm368
E) 3
cm275
Resolución:
1) MQL: Pitágoras
26h23MQ
)33(3MQ 222
=→=
=+
2) 266
3
1
V xx
2
=
∴ 3
cm272V =
Clave: C

B
36
h=12
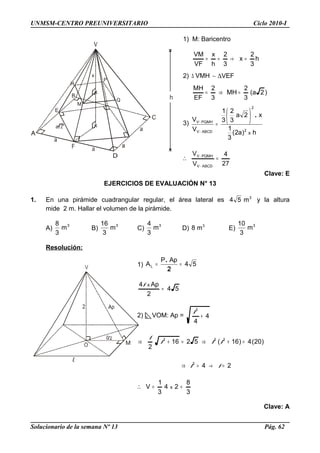
12. El volumen de un tronco de pirámide cuadrangular regular es 208 cm3
. Si su altura
mide 12 m y el área de una de sus bases es 36 cm2
, hallar el área de la otra base.
A) 5 cm2
B) 3 cm2
C) 4 cm2
D) 2 cm2
E) 6 cm2
Resolución:
[ ]
[ ]
4B
16B6BO
B3636B
3
12
208
B3636B
3
h
208V
2
=
−+=
++=
++==
∴
Clave: C
13. En una pirámide triangular, las aristas básicas miden 5 m, 6 m y 7 m, las caras
laterales determinan con la base diedros que miden 60º. Si el pie de la altura de la
pirámide es el incentro del triángulo ABC, hallar el volumen de la pirámide.
A) 3
m28 B) 3
m38 C) 3
m68 D) 3
m66 E) 3
m63
Resolución:
1) Por Herón 9
2
765
p =
++
=
662349A xxxb ==
2) 6
3
2
rr9
2
rP
66 x =⇒==
.
3) DOH: 2236
3
2
h == .
382266
3
1
V ==∴ ..
Clave: B
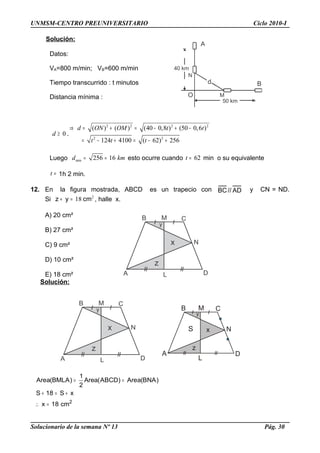
14. En una pirámide regular V – ABCD los puntos P, Q, M y H son baricentros de las
caras laterales VBC, VCD, VDA y VAB respectivamente. Hallar la relación entre los
volúmenes de las pirámides V – PQMH y V – ABCD.
A)
27
8
B)
25
9
C)
27
16
D)
9
4
E)
27
4
Resolución:

1) M: Baricentro
h
3
2
x
3
2
h
x
VF
VM
=→==
2) VMH∆ ∼ ∆VEF
)2a(
3
2
MH
3
2
EF
MH
=⇒=
3)
h)a2(
3
1
x2a
3
2
3
1
V
V
x
2
2
ABCDV
PQMHV
.





=
−
−
27
4
V
V
ABCDV
PQMHV
=
−
−
∴
Clave: E
EJERCICIOS DE EVALUACIÓN N° 13
1. En una pirámide cuadrangular regular, el área lateral es 2
m54 y la altura
mide 2 m. Hallar el volumen de la pirámide.
A)
3
m
3
8
B)
3
m
3
16
C)
3
m
3
4
D) 3
m8 E)
3
m
3
10
Resolución:
1) 54
ApP
AL ==
2
.
54
2
Ap4 x
=
l
2) VOM: Ap = 4
4
2
+
l
24
)20(4)16(5216
2
2
222
=→=⇒
=+⇒=+⇒
ll
lll
l
3
8
24
3
1
V x ==∴
Clave: A

H
2. En un tetraedro regular S – ABC, la distancia del ortocentro de la cara SAB a la
altura del tetraedro es cm3 . Hallar el área total de la pirámide S – ABC.
A) 2
cm374 B) 2
cm336 C) 2
cm381
D) 2
cm354 E) 2
cm345
Resolución:
1) QHS ∼ MGS
2
33
k
k
3
k3
k2
=→=
2) ABC:
2
3a
2
33
3 =







9a =→
3) 381
4
39
4A
2
T =







=
Clave: C
3. En una pirámide regular P–ABCD, la mediatriz de PC contiene al centro de la base
ABCD. Si AP = 6 m, hallar el volumen de la pirámide.
A) 3
m216 B) 3
m318 C) 3
m218 D) 3
m312 E) 3
m236
Resolución:
3
2
m236V
236
3
1
V
=
= .
Clave: E

h
h
d
36
S
4. En la figura, P–ABC es una pirámide regular, las regiones BPC y MNQ son
equivalentes y BC = 6 cm. Hallar el área lateral del tronco de pirámide MNQ – ABC.
A) ( ) 2
cm239 +
B) ( ) 2
cm339 +
C) ( ) 2
cm239 −
D) ( ) 2
cm339 −
E) 2
cm39
Resolución:
312b9
4
3b
)2
9
2
6
2
6
2
1
S)1
2
2
PBC
=→=
=











=
3) ∆QPN ∼ ∆CPB
)33(9A
339S
6
b
9
S9
L
2
2
−=
−=⇒=
−
∴
Clave: D
5. En un tronco de pirámide triangular las áreas de sus bases son 36 cm2
y 100 cm2
.
Si se traza un plano paralelo y equidistante a las bases, hallar el área de la sección
determinada en el tronco por dicho plano.
A) 81 cm2
B) 49 cm2
C) 64 cm2
D) 86 cm2
E) 90 cm2
Resolución:
1) 222
)h2d(
100
d
36
)hd(
S
+
==
+
2)
h2S
10
d
6
hd
S
+
==
+
⇒ Por razones y proporc.
h2
4
d
6
h
6S
==
−
64S =∴
Clave: C

A C
M N
P
D
A C
M N
P
D
aa
a a
2a
6. En la figura, B–ACD es un tetraedro regular cuya área total es 80 m2
, M, N y P son
puntos medios de las aristas BC,AB y BD . Hallar el área lateral del tronco de
pirámide MNP–ADC.
A) 38 m2
B) 45 m2
C) 30 m2
D) 40 m2
E) 42 m2
Resolución:
45)15(3A
15520S
5
3
20
3
20
4
3a
S)2
a
3
20
4
3)a2(
480A)1
tronoL
AMNC
2
MBN
2
2
T
x
==
=−=→
===
=⇒





==
∴
Clave: B

Trigonometría
EJERCICIOS DE LA SEMANA Nº 13
1. Si x ∈ [ π3,0 , halle la suma de las soluciones de la ecuación 2cosxsen
3
x
= cosx.
A)
2
3π
B) 2π C)
2
9π
D) π E)
2
5π
Solución:
2cosxsen
3
x
= cosx, x ∈ [ π3,0
2cosxsen
3
x
– cosx = 0
cosx 





− 1
3
x
sen2 = 0
cosx = 0, x =
2
π
,
2
3π
,
2
5π
sen
3
x
=
2
1
;
3
x
=
6
π
,
6
5π
⇒ x =
2
π
,
2
5π
x =
2
π
,
2
3π
,
2
5π
Σsol =
2
π
+
2
3π
+
2
5π
=
2
9π
Clave: C
2. Si x ∈ [ π2,0 , halle el número de soluciones de la ecuación tg2
xtg2x = tgxtg2x.
A) 3 B) 2 C) 1 D) 5 E) 4
Solución:
tg2
xtg2x = tgxtg2x, x ∈ [ π2,0
tg2
xtg2x – tgxtg2x = 0
tgxtg2x(tgx – 1) = 0
tgxtg2x = 0 ⇒ tgx 





− xtg1
tgx2
2 = 0 ⇒ tgx = 0, tg2
x ≠ 1
tgx = 0, x = 0,π
tgx – 1 = 0 ⇒ tgx = 1 no pues tgx ≠ 1
número de soluciones = 2
Clave: B

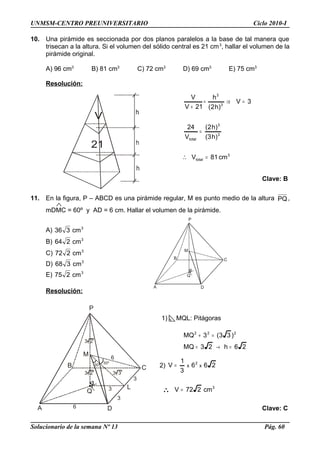
3. Si x ∈ [0, 2π], halle el número de soluciones de la ecuación
4sen
2
x
cos2x + 2sen
2
x
– 2cos2x – 1 = 0,
A) 2 B) 3 C) 1 D) 4 E) 5
Solución:
4sen
2
x
cos2x + 2sen
2
x
– 2cos2x – 1 = 0, x ∈ [0, 2π]
2sen
2
x
(2cos2x + 1) – (2cos2x + 1) = 0
(2cos2x + 1) 





− 1
2
x
sen2 = 0
sen
2
x
=
2
1
⇒
2
x
=
6
π
,
6
5π
⇒ x =
3
π
,
3
5π
cos2x = –
2
1
⇒ 2x =
3
2π
,
3
4π
,
3
8π
,
3
10π
⇒ x =
3
π
,
3
2π
,
3
4π
,
3
5π
x =
3
π
,
3
2π
,
3
4π
,
3
5π
n° de soluciones = 4
Clave: D
4. Halle la solución general de la ecuación 4sen2x(sen2x – 1) = 3.
A)






∈
π
−+
π +
Zn/
12
)1(
2
n 1n
B)






∈
π
−+π Zn/
6
)1(n
n
C)






∈
π
−+π Zn/
3
)1(n
n
D)






∈
π
−+
π +
Zn/
6
)1(
2
n 1n
E)






∈
π
−+
π
Zn/
3
)1(
2
n n
Solución:
4sen2x(sen2x – 1) = 3
4sen2
2x – 4sen2x – 3 = 0 ⇒ (2sen2x – 3)(2sen2x + 1) = 0
2 – 3
2 1
2sen2x – 3 = 0 ⇒ sen2x =
2
3

2sen2x + 1 = 0 ⇒ sen2x = –
2
1
2x = nπ + (– 1)n





 π
−
6
, n ∈ Z
2x = nπ + (– 1)n + 1
6
π
, n ∈ Z
x =
2
nπ
+ (– 1)n + 1
12
π
, n ∈ Z
Clave: A
5. El conjunto solución de la ecuación senx + 2 = cosx es
A)






∈
π−
Zn/
3
)1n4(
B)






∈
π
Zn/
3
n4
C)






∈
π−
Zn/
4
)1n8(
D)






∈
π+
Zn/
6
)1n4(
E)






∈
π−
Zn/
4
)1n2(
Solución:
senx + 2 = cosx
2 = cosx – senx
2
2
= cosx 





2
1
– 





2
1
senx
1 = cosxcos
4
π
– sen
4
π
senx
cos 




 π
+
4
x = 1
x +
4
π
= 2nπ ± 0, n ∈ Z
x = 2nπ –
4
π
, n ∈ Z ⇒ x =
4
)1n8( π−
, n ∈ Z
Clave: C
6. Halle el conjunto solución de la ecuación sen4x + cos4xctg2x + 1 = 0.
A)






∈
π
−
π
Zn/
42
n
B)






∈
π
+
π
Zn/
82
n
C)






∈
π
+
π
Zn/
122
n
D)






∈
π
+π Zn/
4
n2 E)






∈
π
−
π
Zn/
82
n

Solución:
sen4x + cos4xctg2x + 1 = 0
sen4x + cos4x
x2sen
x2cos
+ 1 = 0
x2sen
x2cosx4cosx2xsen4sen +
= – 1
x2sen
x2cos
= – 1 ⇒ ctg2x = – 1 ⇒ tg2x = – 1
2x = nπ –
4
π
, n ∈ Z
x =
2
nπ
–
8
π
, n ∈ Z
Clave: E
7. Halle la menor solución positiva de la ecuación cos6x = x2csc
x2sec
x6sen1





 +
.
A)
6
7π
B)
12
7π
C)
4
π
D)
6
5π
E)
4
3π
Solución:
cos6x = x2csc
x2sec
x6sen1





 +
cos6x = x2cos
x2sen
x6sen1





 +
, sen2x ≠ 0 ∧ cos2x ≠ 0
cos6xsen2x = cos2x + sen6xcos2x
cos2x + sen6xcos2x – cos6xsen2x = 0
cos2x + sen4x = 0
2sen2xcos2x + cos2x = 0
cos2x(2sen2x + 1) = 0
cos2x = 0 no pues cos2x ≠ 0
2sen2x + 1 = 0 ⇒ sen2x = –
2
1
⇒ 2x =
6
7π
⇒ x =
12
7π
Clave: B
8. Halle la mayor solución negativa de la ecuación cos8x + cos6x + cos7x = 0.
A) –
18
π
B) –
15
π
C) –
12
π
D) –
14
π
E) –
16
π
Solución:
cos8x + cos6x + cos7x = 0
2cos7xcosx + cos7x = 0
cos7x(2cosx + 1) = 0

cos7x = 0 ⇒ 7x = –
2
π
⇒ x = –
14
π
2cosx + 1 = 0 ⇒ cosx = –
2
1
⇒ x = –
3
2π
⇒ mayor solución negativa es –
14
π
Clave: D
9. Si x ∈ [0, π], halle el número de soluciones de la ecuación
x2sen
xcos4xcos3 3
−
= 0.
A) 1 B) 3 C) 4 D) 5 E) 2
Solución:
x2sen
xcos4xcos3 3
−
= 0, x ∈ [0, π]
– cos3x = 0, sen2x ≠ 0
cos3x = 0 ⇒ 3x =
2
π
,
2
3π
,
2
5π
⇒ x =
6
π
,
2
π
,
6
5π
pues sen2 




 π
2
= 0 ⇒ x =
6
π
,
6
5π
Clave: E
10. Si x ∈ [0, 2π], halle la suma de las soluciones de la ecuación
x2cos1
x2cos1
−
+
= tg2
x.
A) 2π B)
2
3π
C) 3π D) 4π E)
2
7π
Solución:
x2cos1
x2cos1
−
+
= tg2
x
xsen2
xcos2
2
2
= tg2
x ⇒ ctg2
x = tg2
x ⇒ tg4
x = 1 ⇒ tgx = 1 ó tgx = – 1
tgx = 1, x =
4
π
,
4
5π
tgx = – 1, x =
4
3π
,
4
7π
Σsol =
4
π
+
4
5π
+
4
3π
+
4
7π
= 4π
Clave: D

EVALUACIÓN Nº 13
1. Si α es la menor solución positiva de la ecuación cosx + ctg5°senx = 2cos5°,
halle tg9α.
A) – 1 B)
2
2
C) – 3 D) 1 E) –
3
3
Solución:
cosx + ctg5°senx = 2cos5°
cosx +
°
°
5sen
5cos
senx = 2cos5°
°
°+°
5sen
5cossenx5xsencos
= 2cos5°
sen(x + 5°) = 2cos5°sen5°
sen(x + 5°) = sen10°
x + 5° = 10° ⇒ x = 5° ⇒ α = 5°
tg9α = tg9(5°) = tg45° = 1
Clave: D
2. Si x ∈ [0, 2π], halle el número de soluciones de la ecuación tg
3
x
senx = 3 senx.
A) 3 B) 2 C) 4 D) 1 E) 5
Solución:
tg
3
x
senx = 3 senx, x ∈ [0, 2π]
tg
3
x
senx – 3 senx = 0
senx 





− 3
3
x
tg = 0
senx = 0 ⇒ x = 0, π, 2π
tg
3
x
– 3 = 0 ⇒ tg
3
x
= 3 ⇒
3
x
=
3
π
⇒ x = π
x = 0, π, 2π
Clave: A
3. Si x ∈ [0, π], halle la suma de las soluciones de la ecuación
senx
x2cosx3senxsenx3cosxcos −−
= 0.
A) 2π B)
2
3π
C) π D)
3
2π
E) 3π

Solución:
senx
x2cosx3senxsenx3cosxcos −−
= 0, x ∈ [0, π]
cos4x – cos2x = 0, senx ≠ 0
– 2sen3xsenx = 0
senx = 0 pues senx ≠ 0
sen3x = 0 ⇒ 3x = 0, π, 2π, 3π ⇒ x = 0,
3
π
,
3
2π
, π pues senx ≠ 0
⇒ x =
3
π
,
3
2π
Σsol =
3
π
+
3
2π
= π
Clave: C
4. Halle la solución general de la ecuación 4sen2
x – 3 = 0.
A)






∈
π
±π Zn/
3
n B)






∈
π
±π Zn/
6
n2 C)








∈π Zn/n2
D)






∈
π
±π Zn/
3
n2 E)






∈
π
±π Zn/
6
n
Solución:
4sen2
x – 3 = 0
4sen2
x = 3
2sen2
x =
2
3
1 – cos2x =
2
3
cos2x = –
2
1
2x = 2nπ ±
3
2π
, n ∈ Z
x = nπ ±
3
π
, n ∈ Z
Clave: A
5. Si x 




 π
∈
4
3
,0 , halle la suma de las soluciones de la ecuación cos2x + sen2x + 1 =
0.
A)
3
4π
B)
4
π
C)
4
3π
D)
4
5π
E)
8
3π

Solución:
cos2x + sen2x = – 1, x 




 π
∈
4
3
,0
sen2x
2
1
+
2
1
cos2x = –
2
1
sen2xcos
4
π
+ sen
4
π
cos2x = –
2
1
sen 




 π
+
4
x2 = –
2
1
2x +
4
π
=
4
5π
,
4
7π
⇒ 2x =
4
4π
,
4
6π
⇒ x =
8
4π
,
8
6π
Σsol =
8
4π
+
8
6π
=
8
10π
=
4
5π
Clave: D
Lenguaje
EVALUACIÓN DE CLASE Nº 13
1. Respecto del adverbio, seleccione la opción en la que se presenta la secuencia
correcta de verdad (V) o falsedad (F) de los siguientes enunciados.
A) Se caracteriza por ser una palabra variable. ( )
B) Su lexema no recibe morfemas flexivos. ( )
C) Aparece siempre en la frase verbal. ( )
D) Siempre deriva de adjetivos. ( )
E) Designa hechos o acontecimientos. ( )
A) FVVVF B) VVVFV C) FFVFV D) FVFFF E) VVFFF
Clave: D. FVFFF
2. Marque la opción en la que se presenta más adverbios.
A) En efecto, todos te apoyarán en esa decisión.
B) Anoche, Ana tomó café con bastante azúcar.
C) Ayer, pocos alumnos llegaron tarde, profesor.
D) Todas las tardes llueve a cántaros por aquí.
E) Él no la abrazó tierna y amorosamente.
Clave: E. Las palabras no, tierna y amorosamente son adverbios, pues modifican
semánticamente al verbo abrazar.

3. Señale la alternativa en la que la locución adverbial no expresa modo.
A) De pronto, Julia entró asustada al salón.
B) Ella aprendió la lección al pie de la letra.
C) Dejaron la puerta abierta de par en par.
D) Ella siempre entiende todo al revés.
E) Raquel salió de la casa a hurtadillas.
Clave: A. En esta alternativa, la locución adverbial de pronto expresa tiempo.
4. A la derecha de cada oración, escriba la clase a la que pertenece el adverbio.
A) Ana comía el chocolate lentamente. ________________
B) Llegamos temprano a la ceremonia. ________________
C) Aquel hombre comió demasiado. ________________
D) Dejaron el balón afuera, Antonio. ________________
E) Posiblemente, viaje con ustedes. ________________
Clave: A) modo, B) tiempo, C) cantidad, D) lugar, E) duda
5. Correlacione la columna de las palabras subrayadas con la columna de las
categorías de la derecha.
A) Iremos, aunque no quieras. 1. Conjunción adversativa
B) Nos quedamos adentro. 2. Adverbio de lugar
C) Siempre te recuerdo. 3. Adverbio de tiempo
D) Te busqué, pero no te encontré. 4. Conjunción completiva
E) Sé que lo encontrarás. 5. Conjunción concesiva
Clave: A5, B2, C3, D1, E4
6. Seleccione la alternativa en la que hay empleo correcto del adverbio.
Clave
A) Este chocolate está muy riquísimo. El chocolate está riquísimo.
B) María Jesús está sentada detrás tuyo. detrás de ti
C) Actuó amable, sincera y cortésmente.
D) Los niños llegaron medios cansados. medio cansados
E) Sus padres también no lo apoyaron. tampoco
Clave: C. Cuando se emplea dos o más adverbios terminados en –mente, solo el
último debe llevar el sufijo.
7. Elija la alternativa donde la frase adverbial presenta núcleo y modificador.
A) Esta noche luces muy hermosa.
B) Carla, lo redactaste muy bien.
C) Fuiste demasiado cruel con ella.
D) Carolina siempre viste a la moda.
E) Quizás ganes esta competencia.

Clave: B. La frase adverbial está estructurada por el núcleo bien y el modificador
muy.
8. En el enunciado “muchos alumnos siempre miran aquí y allá mientras explico
la lección. Los que están cerca procuran moverse despacio. Los que se
sientan atrás siempre hacen ruido y nunca parecen estar quietos. Yo no me
enfado con ellos: quiero que comprendan que solamente ellos pueden decidir
si quieren aprovechar el tiempo o no. Efectivamente, creo que eso es
importante aprender hoy. Quizá un día me den las gracias”, el número de
adverbios es
A) catorce. B) once. C) doce. D) quince. E) trece.
Clave: A. En el enunciado, los adverbios son siempre, aquí, allá, cerca, despacio,
atrás, siempre, nunca, no, solamente, no, efectivamente quizá y hoy. Mientras es
conjunción adverbial (tiempo).
9. Escriba la clase a la que corresponde la conjunción subrayada.
A) Acepto porque no tengo otra opción. ________________
B) Me contaron que volverás a casa pronto. ________________
C) Es vegetariano, es decir, no come carne. ________________
D) Comió tanto helado que se enfermó. ________________
E) Lo hicimos como tú nos lo pediste. ________________
F) Le dirás la verdad o no te perdonaré. ________________
G) Lorena me invitó, pero no pienso asistir. ________________
Clave: A) causal, B) completiva, C) explicativa, D) consecutiva, E) modal, F)
disyuntiva, G) adversativa.
10. Marque la opción en la que se presenta conjunción ilativa.
A) Le regalo rosas rojas o le compro bombones.
B) Como no vinimos ayer, no entendemos el tema.
C) Iremos bien vestidos, o sea, con traje de gala.
D) Llovió tanto que se inundaron todas las casas.
E) No conseguí el préstamo, por ello, no viajaré.
Clave: E. La conjunción ilativa por ello expresa relación de consecuencia y
secuencia lógica.
11. El enunciado “___________________ no se sentía bien, tuvo que levantarse
____________________ no podía faltar a la reunión” se completa con
A) aunque y porque.
B) no obstante y por lo que.
C) por más que y sin embargo.
D) ya que y debido a que.
E) a pesar de que y así que.

Clave: A. La conjunción concesiva aunque y la conjunción causal porque completan
el enunciado.
12. Seleccione el enunciado en el que se presenta conjunción coordinante.
A) Se avergonzó tanto que no quiso volver a la escuela.
B) Liliana es políglota, o sea, domina más de dos lenguas.
C) Resolvió los problemas tan rápido que me solicitó más.
D) Me contaron que te casarás con Roberto muy pronto.
E) Aunque me lo pidas de rodillas, no te disculparé, José.
Clave: B. La locución conjuntiva explicativa o sea es una conjunción coordinante.
13. Elija la alternativa en la que se presenta conjunción subordinante.
A) Ni José ni Julia han bailado en esa fiesta.
B) Está absolutamente inquieta: ya va, ya viene.
C) Ella es mi novia, mas su padre aún no lo sabe.
D) Antonio, no sé si ella te adivinará la suerte hoy.
E) Prepararé un pastel, así que compraré huevos.
Clave: D. La conjunción completiva si es una conjunción subordinante.
14. Marque el enunciado conceptualmente incorrecto con respecto a la
conjunción.
A) Enlaza proposiciones, frases y palabras.
B) Es un nexo coordinante y subordinante.
C) Las adversativas expresan contrariedad.
D) Se caracteriza por ser palabra invariable.
E) Las concesivas expresan consecuencias.
Clave: E. La conjunción concesiva aporta idea de objeción a lo expresado en la idea
principal de la oración.
15. Identifique las opciones que evidencian uso correcto (C) o incorrecto (I) de los
conectores.
A) Así que no estudias más, no aprobarás. ( )
B) Como no hice la tarea, me castigaron. ( )
C) Iré al cine con él, así no quieras, papá. ( )
D) Juan me quiere tanto que lo imaginé. ( )
E) Caminé tanto, entonces me cansé. ( )
Clave: ICCII. En las opciones incorrectas, los conectores posibles son A) si; D)
como y E) que.

16. Complete las oraciones con las conjunciones subordinantes adecuadas.
A) Llegó tan cansado _______ no quiso comer.
B) _______ Ana le diga que no, Luis irá de viaje.
C) _______ me das una flor, te doy mi amistad.
D) Me prometiste _______ llegarías a tiempo.
E) _______ no tenía interés, decidió no asistir.
Clave: A) que (consecutiva), B) aunque o así (concesiva), C) si (condicional), D)
que (completiva) y E) como o ya que (causal).
17. Seleccione la alternativa en la que se presenta la correlación correcta entre
ambas columnas.
A) Antiguamente, los piropos eran floridos. ( ) 1. Duda
B) Los leones dormían plácidamente. ( ) 2. Afirmación
C) Hace una semana llovió demasiado. ( ) 3. Tiempo
D) Probablemente, la tormenta perdure. ( ) 4. Cantidad
E) La pérdida fue verdaderamente cuantiosa. ( ) 5. Modo
A) A3, B1, C2, D5, E4 B) A3, B4, C5, D2, E1
C) A5, B4, C3, D2, E1 D) A2, B3, C5, D1, E4
E) A3, B5, C4, D1, E2
Clave: E.
18. Escriba a la derecha, si fuera necesario, los usos formales de las frases
subrayadas.
Clave.
A) Su conducta cambiará poco a poco. ____________ paulatinamente.
B) La clase empezará el día de mañana. ____________ mañana
C) Me llamas cualquier día, excepto el domingo.___________ Formal
D) Recién que llegó, vio a tus amigos. ____________ tan pronto como
E) El enfermo hablaba de lo más tranquilo. ____________ muy tranquilo /
tranquilamente
Clave: Los usos formales son respectivamente A) paulatinamente, B) mañana, D)
tan pronto como, D) Es formal, E) (muy tranquilo) tranquilamente.
19. Seleccione la alternativa que presenta uso correcto del adverbio.
Clave
A) Esta mesa de madera es demasiada larga. demasiado
B) No laves la fruta con agua media sucia. medio
C) Los niños se quedaron medios asustados. medio
D) Los alumnos se pusieron bastantes nerviosos. Bastante nerviosos
E) Sirvieron los anticuchos demasiado calientes. correcto
Clave: E. Las formas correctas son A) demasiado, B) medio, C) medio, D)
nerviosísimos.

20. Escriba a la derecha el adverbio apropiado para cada oración.
A) Llegó un amigo bruscamente. _______________________
B) Tan es así que estudió con ahínco. _______________________
C) Regresó anoche más antes que tú. _______________________
D) Ayer por la tarde, caminamos un poco. _______________________
E) Es un manual perfectamente inútil. _______________________
Clave: Las formas adecuadas son las siguientes: A) inesperadamente, B) tanto, C)
mucho, D) poco, E) completamente
21. Escriba a la derecha el adverbio que sustituye a la locución adverbial.
Clave
A) Repartió los regalos a manos llenas. ________________ generosamente
B) Luis vive en Hawai a cuerpo de rey. ________________ cómodamente
C) Pasó por su habitación de puntillas. ________________ sigilosamente
D) Solucionó el problema en un dos por tres. ________________ rápidamente
E) Caminaba con pies de plomo. ________________ lentamente
pesadamente
Clave: Las formas adecuadas son las siguientes: A) generosamente, B)
cómodamente C) sigilosamente D) rápidamente, E) lentamente, pesadamente.
22. Escriba a la derecha las palabras adecuadas que reemplazan las palabras
subrayadas.
Clave
A) Nosotros salimos más después que tú. Mucho después que tú
B) No pongas ese macetero tan allí. No pongas ese macetero allá.
C) Acudió al teatro más número de niños. Acudió mayor número de niños.
D) Este departamento se vende a más precio. se vende a mayor precio.
E) Ese banco ofrece mucha más que el otro. ofrece mucho más que el otro.
Clave: Las formas correctas son las siguientes: A) mucho, B) allá, C) mayor, D)
mayor, E) mucho
23. Marque la opción en la que se presenta uso formal del adverbio.
Clave
A) El sueldo que ganaba era tan poquito. exiguo (mínimo)
B) El concierto terminó tardísimo. muy tarde
C) Devolveré la llamada ahorita. enseguida
D) La iglesia se encuentra cerca. correcta
E) La entrevista se realizará tempranísimo. en las primeras horas
Clave: D. Las otras formas correctas de las demás opciones son las siguientes: A)
exiguo, B) muy tarde, C) enseguida, E) en las primeras horas.

24. Escriba a la derecha las formas adecuadas de las frases subrayadas.
Clave
A) En aquí esta mi casa. __________ Aquí está mi casa
B) El recién ganador viajó. __________ El reciente ganador
C) Ninguno sale de en aquí. __________ aquí
D) Describió lo más mínimo del accidente. __________ mínimo
E) La obra es tan modernísima que felicitaron a Juan. _____ tan moderna
Clave: Las formas correctas son A) Aquí está mi casa, B) El reciente ganador, C)
Ninguno sale de aquí. D) Describió lo mínimo del accidente y E) La obra es tan
moderna que felicitaron a Juan.
25. El enunciado “el lenguaje es una facultad universal” se completa
coherentemente con
A) o sea las personas hablan más de una lengua.
B) porque es propia de la especie humana.
C) pero se manifiesta en variedades lingüísticas.
D) es decir, pertenece a una comunidad lingüística.
E) para que todas las personas puedan entenderse.
Clave: B. El enunciado se completa coherentemente con el conector causal porque.
26. Marque la opción que presenta la conjunción completiva si.
A) Me inscribo en el curso si consigo el dinero de la matrícula.
B) En el último ensayo, el violín emitía un si desentonado.
C) Conversamos como si nos hubiéramos conocido antes.
D) El niño preguntó a su madre si las flores jugaban.
E) Si tan solo me dieras la oportunidad, no te defraudaría.
Clave: D. La conjunción si introduce la proposición subordinada sustantiva las flores
jugaban en función de objeto directo.
27. Elija la alternativa en la que se presenta uso correcto de porque.
Clave
A) No entendió porque había tanta algarabía en el patio. por qué
B) El noble ideal porque lucha es la razón de su vida. por el que
C) Las semillas no germinaron porque carecían de agua.
D) Los motivos porque renunciaste no fueron aceptados. por los que
E) Escucharon con asombro el porque de su gran éxito. porqué
Clave: C. La conjunción porque expresa causa. En las otras opciones, las formas
correctas son las siguientes: A) por qué, B) por el que, D) por los que, E) porqué.

28. Señale la opción en la que se presenta la conjunción como con valor causal.
A) Los miró como si fueran sospechosos.
B) Como no atendían, busqué por otras tiendas.
C) Instaló el circuito como indicaba el reglamento.
D) Donó tanto la mansión como sus joyas.
E) Como no pagues a tiempo, te cobrarán multa.
Clave: B. La conjunción como puede ser sustituida por porque con sentido causal.
En las otras alternativas los valores son de comparación supuesta, modal,
copulativo, condicional.
29. El enunciado “las diferentes autoridades municipales llevan a cabo programas
de asistencia social, ________ no proyectan su durabilidad; _________ es
dificultosa la evaluación de sus objetivos y el impacto en la cultura nacional”
se completa, respectivamente con las conjunciones
A) pero y por lo tanto.
B) aunque y pero.
C) por lo tanto y aunque.
D) mas y porque.
E) mas y aunque.
Clave: A. Las ideas contrarias se conectan con pero y la idea de secuencia con por
lo tanto.
30. El enunciado “la actitud, que los peruanos debemos asumir ante el TLC, no es
que nuestra economía se extranjerice; _________ que es crear las condiciones
________ el resto del mundo se peruanice” se completa, respectivamente, con
las conjugaciones
A) como y si.
B) o sea y por ello.
C) por tanto y así que.
D) sino y para que.
E) es decir y puesto que.
Clave: D. Sino conecta las ideas contrarias; para que indica la finalidad.
31. Marque la opción que se completa adecuadamente con la conjunción
“aunque”.
A) La pesca de anchoveta está prohibida, _______, hay veda.
B) Deseó tanto viajar a España ______ consiguió realizar su sueño.
C) Presentará el proyecto de inversión ______ no lo financien.
D) Se interrumpieron las clases ______ hubo presentación teatral.
E) No subió la cotización del dólar ________ estaba pronosticado.
Clave: C. Las conjunciones que completan las oraciones son las siguientes: A) es
decir, B) que, D) porque, E) tal como.

JUNTAS Y SEPARADAS
Sinrazón. Acción hecha contra justicia y fuera de lo razonable o debido. Ejemplo: Es
conocida la sinrazón de su conducta.
Sin razón (prep. + sustantivo). Que no tiene razón o motivo. Ejemplo: Discutía sin razón.
32. Complete los enunciados con sinrazón o sin razón según convenga.
A) Aquellas hermanas discutieron ____________.
B) La ____________de su renuncia sorprendió a todos.
C) Todos actuamos _____________ alguna vez.
D) Sus ______________ ya nos tienen cansados.
E) Me despidieron del trabajo _____________ alguna.
F) El negocio fue multado _______________ por la Sunat.
G) No me sorprende la ________________ de su actitud.
H) Aumentó ___________________ las tasas impositivas.
Clave: A) sin razón, B) sinrazón, C) sin razón, D) sinrazones, E) sin razón
F) sin razón G) sinrazón H) sin razón
33. Reconozca el enunciado en la que se presenta uso correcto de la palabra
sinrazón.
Clave
A) Abrazó fuertemente a su amiga _____________. sin razón
B) Abandonó la ceremonia abruptamente ___________. sin razón
C) El trabajador recibió bonos y aguinaldos __________. sin razón
D) __________ alguna lo gritó delante de los invitados. Sin razón
E) La ________ de su mal comportamiento no convenció a nadie. Sinrazón
Clave: E. El enunciado se completa con sinrazón.
34. Escriba los verbos precisos que le corresponden al verbo tener en cada
enunciado.
Clave
A) No tengo mucho tiempo para mis hijos. _____________ dispongo de
B) A él le gusta tener el mando de todo. _____________ ejercer
C) Tiene buena salud, aquel muchacho. _____________ goza de
D) Ana desea tener un cambio en su vida. _____________ experimentar
E) Este manuscrito tiene varias partes. _____________ consta de
F) Todos tenemos errores alguna vez. _____________ incurrimos en
G) Doctor, mi hijo tiene estos síntomas. _____________ presenta
35. Reemplace las palabras subrayadas por otra de la variedad estándar.
A) Se debe evitar hechos de sangre en Irak. _______________
B) Ten cuidado con la gasa estéril. _______________
C) La sopa que preparó Luisa está fea. _______________
D) El amigo de mi hermana me cae pesado. _______________
E) Los niños, a la cocina; los grandes, al comedor. _______________
Clave: A) sangrientos, B) esterilizada, C) desagradable, D) antipático, E) mayores.

Literatura
EJERCICIOS DE CLASE
1. Con respecto a la verdad (V) o falsedad (F) de los siguientes enunciados sobre la
literatura de la Emancipación, marque la alternativa que contiene la secuencia
correcta.
I. En los escritos se exalta el heroico patriotismo peruano.
II. Se expresó por medio de relatos, mitos, leyendas y crónicas.
III. Entre sus representantes destacan Melgar y Garcilaso de la Vega.
IV. En relación al contenido, se impuso la idea del americanismo.
V. La temática de la poesía emancipadora fue de carácter político.
A) VFFVV B) FVFVF C) VFVFV D) FFVFV E) VVFVF
Resp. A.)
I. En los escritos de la literatura del periodo emancipador, se exalta el patriotismo
peruano a través de uno poesía política. (V) II. Se expresó por medio de odas,
himnos, canciones, etc. (F) III. Garcilaso es un cronista de la época colonial. (F) IV.
En este periodo predominó la idea de unidad continental y se expresó a través del
americanismo. (V) V. La temática de la poesía emancipadora fue eminentemente
política. (V).
2. Los temas que plantea la poesía de la Emancipación son
A) las pasiones amorosas, la venganza, el libre albedrío.
B) el paisaje americano, el indio y los homenajes patrióticos.
C) las costumbres limeñas, el nacionalismo, el pasado incaico.
D) las luchas de los caudillos, la modernización, la religión.
E) los conflictos sociales, la naturaleza, la migración al Perú.
Resp. B)
La poesía de la Emancipación centra su temática en la política, por lo tanto, sus
temas son los homenajes patrióticos, el paisaje americano y el indio.
3. La literatura peruana de la Emancipación está bajo los cánones del
A) Barroco. B) Renacimiento C) Modernismo.
D) Neoclasicismo. E) Indigenismo.
Resp. D)
La literatura peruana de la emancipación se rige bajo los cánones del Neoclasicismo
español, es decir, sigue el estilo, la poética y la preceptiva de este periodo. Sin
embargo, se vislumbra el primer romanticismo con Mariano Melgar.
4. La obra literaria de Mariano Melgar tuvo influencia de los poetas latinos, tales como
Ovidio, Horacio y Virgilio. De Ovidio tradujo
A) El arte de amar. B) La metamorfosis. C) Geórgicas.
D) El arte de olvidar. E) Epístola a los Pisones.

Resp. D)
La formación humanística de Mariano Melgar le permitió el conocimiento de autores
clásicos latinos. Tradujo de Ovidio Remedios de amor, pero Melgar cambió el título y
le puso El arte de olvidar, traducción que es considerada la mejor en lengua
castellana.
5. El yaraví melgariano expresa la
A) angustia por la muerte de Silvia. B) plenitud del amor idealizado.
C) congoja por la ausencia de la amada. D) crítica satírica al sistema colonial.
E) exaltación del naciente patriotismo.
Resp. C)
El yaraví proviene del haraui que expresa el dolor del amor contrariado a causa de la
inconstancia de la amada, quien ha abandonado al poeta.
6. Son características del costumbrismo peruana, excepto
A) el tono realista y panfletario. B) la intensa actitud moralizante.
C) la descripción de tipos y costumbres. D) la tendencia sumamente satírica.
E) el interés por lo pasado y exótico.
Resp. E)
El interés por lo pasado y exótico es propio del romanticismo. El costumbrismo se
interesó e el presente describiendo tipos y costumbres de la ciudad.
7. El costumbrismo nace con la república y se halla en búsqueda de la expresión
A) colonial. B) nacional. C) castiza. D) indígena. E) moderna.
Resp. B)
Las primeras décadas del sistema republicano fueron de aprendizaje y formación; el
costumbrismo nace con la República y se hallaba en búsqueda de expresar lo
nacional.
8. La comedia Ña Catita pertenece al género
A) periodístico. B) lírico. C) ensayístico.
D) dramático. E) épico.
Resp. D)
La comedia Ña Catita, de Manuel Ascensio Segura, pertenece al género dramático.
9. ¿Qué sucede al final de Ña Catita?
A) Ña Catita llega a la casa de don Jesús.
B) Juliana fuga con su enamorado.
C) Alejo es descubierto por don Juan.
D) Don Jesús y doña Rufina se enemistan.
E) Manuel abandona a su suerte a Juliana.

Resp. C)
En la parte final de esta comedia de costumbres, Juan, amigo de don Jesús, llega de
visita y revela que Alejo es casado.
10. Con respecto a la verdad (V) o falsedad (F) de los siguientes enunciados sobre Ña
Catita, de Manuel Asencio Segura, marque la alternativa que contiene la secuencia
correcta.
I. Es una tragedia del costumbrismo peruano.
II. Emplea un lenguaje coloquial y popular criollo.
III. La hija rebelde, que rechaza a Alejo, se llama Juliana.
IV. El autor es considerado padre del teatro nacional.
V. Está escrita con el uso de tercetos endecasílabos.
A) VVFFV B) FVFVF C) VFVFV D) FFVVF E) FVVVF
Resp. E)
I. Ña Catita es una comedia del costumbrismo peruano. (F) II. La obra emplea un
lenguaje coloquial, criollo, de clase media. (V) III. Doña Juliana es la hija que se
revela contra la madre. (V) IV. Manuel Ascencio Segura es considerado padre del
teatro nacional. (V) V. La comedia está escrita en versos de métrica irregular. (F)
Educación Cívica
EJERCICIOS Nº 13
1. El ___________ es el elemento político por excelencia de un Estado moderno, como
la República del Perú.
A) poblador B) territorio C) ejército
D) presupuesto E) gobierno
Solución:
El Estado se organiza bajo la estructura de un gobierno unitario basado en la
existencia de un gobierno que constituye el elemento político. El elemento humano
es la nación, y el elemento geográfico es el territorio.
Clave: E
2. La defensa de los intereses del Estado peruano recaen en
A) los Fiscales Supremos. B) los Procuradores Públicos.
C) los Jueces de Paz. D) la Defensoría del Pueblo.
E) el Tribunal Constitucional.
Solución:
El Procurador vela por los intereses del Estado peruano. El Procurador Público
Nacional ejercita la representación y defensa en los procesos del sector al que
pertenece. Actúa en calidad de demandante, denunciante, o parte civil, pudiendo
prestar confesión en juicio en representación del Sector o Ministerio y convenir en la
demanda o desistirse de ella o transigir en juicio. Existen también Procuradores
Públicos regionales y municipales.
Clave: B

3. La separación de poderes en el Estado peruano posibilita la distribución en
funciones
A) políticas, económicas y sociales.
B) de gobierno, legislativas y de administración de justicia.
C) de planificación, organización y de control.
D) administrativas y de gestión nacional.
E) de dirección y manejo de los funcionarios públicos.
Solución:
Para garantizar eficientemente la sociedad e impedir la concentración de poder en
manos de una sola persona o de un solo organismo, se distribuye el poder en tres
funciones: de gobierno (Poder Ejecutivo), legislativas (Poder Legislativo) y de
administración de justicia (Poder Judicial).
Clave: B
4. Son atribuciones del Poder Legislativo.
1. Censurar a un Ministro de Estado.
2. Desacatar una norma constitucional.
3. Cambiar parcialmente una ley.
4. Exigirle explicaciones a un funcionario público.
5. Interpelar a los Congresistas.
A) 1-4-5 B) 1-2-3 C) 1-3-4 D) 2-3-4 E) 3-4-5
Solución:
El Poder Legislativo cumple dos funciones generales, una relativa a las leyes (dar,
interpretar, modificar y derogar) y otra de control político (censurar, interpelar,
fiscalizar). El Congreso investiga o fiscaliza los actos de todos los funcionarios
públicos, esto incluye a Ministros y Congresistas; puede censurar o negarle la
confianza a un Ministro, también puede interpelarlo, es decir exigirle explicaciones.
Clave: C
5. Si ninguno de los candidatos a la Presidencia de la República obtiene la mayoría
absoluta de los votos, se realiza una segunda votación entre
A) los tres postulantes más votados.
B) el Presidente electo y sus dos Vicepresidentes.
C) los militantes del Partido más votado.
D) los dos candidatos más votados.
E) los dos Congresistas más votados.
Solución:
Si ninguno de los candidatos obtiene la mayoría absoluta, se procede a una segunda
elección, dentro de los 30 días siguientes a la proclamación de los cómputos
generales, entre los candidatos que han obtenido las dos más altas mayorías.
Clave: D
6. Una de las atribuciones del Consejo de Ministros es
A) defender los derechos constitucionales de la persona.
B) dirigir y gestionar los servicios públicos.
C) fiscalizar la legalidad de las votaciones.
D) aceptar en última instancia un habeas corpus.
E) administrar las reservas internacionales.

Solución:
La dirección y gestión de los servicios públicos están confinadas al Consejo de
Ministros; y a cada Ministro en los asuntos que competen a la cartera a su cargo.
Clave: B
7. La supervisión del uso adecuado de los recursos del Estado le compete
A) a la Contraloría General de la República.
B) a la Superintendencia de Banca y Seguros.
C) al Consejo Nacional del Magistratura.
D) al Banco Central de Reserva.
E) al Banco de la Nación.
Solución:
El órgano superior del Sistema Nacional de Control es la Contraloría General de la
República y sus funciones están relacionadas al uso adecuado, por parte de las
autoridades y entidades públicas, de los recursos del Estado.
Clave: A
8. El órgano constitucional autónomo cuyos miembros son elegidos por el Congreso es
A) el Consejo Nacional de la Magistratura.
B) el Ministerio Público.
C) el Jurado Nacional de Elecciones.
D) el Tribunal Constitucional.
E) la Oficina Nacional de Procesos Electorales.
Solución:
Los miembros del Tribunal Constitucional son siete, elegidos por el Congreso con el
voto favorable de los dos tercios.
Clave: D
9. Los únicos jueces elegidos por elección popular son los
A) Vocales Supremos. B) Jueces provinciales.
C) Jueces especializados. D) Vocales Superiores.
E) Jueces de Paz.
Solución:
El Consejo Nacional de la Magistratura se encarga de la selección y nombramiento
de los jueces y fiscales. Los Jueces de Paz provienen de elección popular.
Clave: E
10. Las acciones de defensa civil son eficaces dependiendo fundamentalmente del
principio de _____________ que asuma la población.
A) transparencia B) supervisión C) previsión
D) austeridad E) evaluación
Solución:
Para que las acciones de defensa civil sean eficaces y cumplan sus objetivos, es
necesario que la población este organizada e involucrada en las tareas de previsión
y acción durante los desastres.
Clave: C

Psicología
PRÁCTICA Nº 13
Instrucciones: Leer detenidamente cada pregunta y elegir la respuesta que se estime
verdadera.
1. Es un ejemplo de la función elaborativa del pensamiento:
A) Leer a pesar del ruido. B) Tener imágenes oníricas.
C) Reconocer rostros. D) Hacer cálculo mental.
E) Recuperar ideas.
Solución:
Hacer cálculo mental es un ejemplo de función elaborativa, la cual construir
conocimientos, razonar, resolver problemas. Rpta.: D
2. Los números imaginarios son un ejemplo de conceptualización
A) sin referencia. B) por jerarquía. C) por abstracción.
D) por composición. E) sin extensión.
Solución:
Los números imaginarios son conceptos formados por abstracción o generalización.
Generalizar significa abstraer características o cualidades comunes en una clase o
categoría más amplia. Rpta.: C.
3. Los conceptos de Ciencias Sociales se forman por
A) comparación. B) composición. C) síntesis.
D) abstracción. E) introspección.
Solución:
Los conceptos científicos se forman por abstracción. Generalizar significa abstraer
características o cualidades comunes en una clase o categoría más amplia. Rpta.: D
4. La medicina tradicional que practican los chamanes se originó con la estrategia de
solución de problemas:
A) Heurística. B) Ensayo y error.
C) Algoritmo. D) Recuperación de información.
E) Experimentación.
Solución:
La estrategia de ensayo y error se basa en una teoría del aprendizaje que afirma
que éste es posible mediante tanteos y equivocaciones. No existe plan. La medicina
tradicional debió originarse así en un proceso de cientos o miles de años. Rpta.: B

5. Si un niño es premiado por incrementar su vocabulario de inglés, estamos ante un
caso de desarrollo del lenguaje por
A) condicionamiento clásico. B) condicionamiento operante.
C) aprendizaje imitativo. D) aprendizaje cognitivo.
E) aprendizaje por insight.
Solución:
Los niños aprenden su lengua materna y una segunda lengua por condicionamiento
operante, que consiste en premiar y castigar las conductas verbales. Rpta.: B.
6. El habla polisintética se caracteriza por ser
A) inmotivada. B) rígida. C) telegráfica.
D) explosiva. E) simpráxica.
Solución:
El estadio holofrásico es conocido también como fase de habla polisintética: una
sola frase o palabra es empleada en ese lapso para expresar toda una idea. En este
estadio, la palabra es acompañada de ademanes. Por ello se dice que el lenguaje
del niño de esa edad es simpráxico (está acompañado de acciones): el niño dice
“papá” y jala la mano del papá. Rpta.: E
7. Si un bebe de un año de edad se emociona igualmente ante la presencia de su
biberón como ante la palabra “biberón”, estamos ante un caso de adquisición del
lenguaje por
A) aprendizaje significativo. B) condicionamiento operante.
C) aprendizaje imitativo. D) condicionamiento clásico.
E) aprendizaje por insight.
Solución: Los bebes adquieren el significado de algunas palabras por
condicionamiento clásico cuando se aparea muchas veces un estímulo
incondicionado (biberón) con un estímulo neutro (palabra “biberón”) y este último
adquiere la capacidad de generar una respuesta condicionada (emoción ante el
alimento). Rpta.: D
8. El niño desarrolla la autorregulación atencional y la planificación de sus acciones en
el estadio
A) holofrásico B) explosión del lenguaje C) habla telegráfica
D) lenguaje egocéntrico E) lenguaje simpráxico
Solución: Estadio lenguaje egocéntrico. Según Lev Vigotsky, el habla egocéntrica
desarrolla gradualmente la autorregulación atencional y la planificación de las
acciones. Rpta.: D
9. Edad en la que se manifiesta el balbuceo:
A) Primer mes B) Seis semanas C) Seis meses
D) Ocho meses E) Al año.
Solución:
El balbuceo (combinación consonantes + vocales) se manifiesta a los seis meses de
edad. Rpta.: C

Historia
EVALUACIÓN Nº 13
1. De la imagen señalada se puede observar
A) La toma de la Bastilla por los sans culottes.
B) El golpe del 18 Brumario por Napoleón.
C) La caída del régimen de Robespierre.
D) La convocatoria de los Estados Generales.
E) El juramento del juego de la pelota.
“E” La imagen hace referencia al “juramento del juego de la pelota” cuando
miembros de la burguesía, la nobleza y el clero durante la Asamblea Nacional
reunidos en el salón de la pelota juran la redacción de una constitución política.
2. La Revolución francesa fue dirigida principalmente por
A) la burguesía B) el campesinado C) el proletariado
D) la nobleza E) la aristocracia.
“A” La Revolución francesa si bien contó con la participación de diversos sectores de
la sociedad fue dirigida principalmente por elementos de la burguesía que buscaban
desplazar del poder a la aristocracia y establecer un Estado liberal.
3. Doctrina política que buscaba acabar con el capitalismo a través de la lucha de
clases con una revolución proletaria.
A) Liberalismo. B) Socialismo utópico. C) Nacionalismo.
D) Socialismo científico. E) Anarquismo.
“D” El socialismo científico o marxismo es el sistema de ideas de Marx y Engels
elaborado a partir del análisis de la sociedad capitalista con el objetivo de

trasformarla a través de una revolución proletaria. Se plantea que la lucha de clases
explica el proceso histórico siendo la tendencia histórica del capitalismo el
socialismo y el comunismo.
4. Los sectores populares urbanos que participaron activamente en los
acontecimientos de la Revolución francesa, se denominaron
A) jacqueries. B) alodios. C) sans culottes.
D) proletariado. E) Termidorianos.
“C” Los sectores populares urbanos que participaron activamente en los
acontecimientos revolucionarios fueron llamados sans cullotes. La expresión sans
culottes significa literalmente "sin calzones". El término está relacionado con las
modas y costumbres de la época del siglo XVIII, ya que los sectores sociales más
acomodados vestían con unas calzas cortas y ajustadas (los culottes), mientras que
muchos miembros del Tercer Estado llevaban pantalones largos.
5. La Revolución francesa trajo como consecuencia principal
A) La consolidación del feudalismo señorial.
B) El encumbramiento del proletariado.
C) El auge de las ideas socialistas utópicas.
D) La destrucción del Antiguo Régimen feudal.
E) La socialización de los médios de producción.
“D” La mayor importancia de la Revolución Francesa radica en que destruyo el
antiguo régimen feudal en Francia caracterizado por el absolutismo, la sociedad
estamental y la servidumbre.
Filosofía
EVALUACIÓN Nº 13
1. Indicar los grupos en los que se encuentran las ciencias formales.
I. lógica
II. física
III. química
IV. matemática
A) sólo I B)I y II C) II y III D) I y IV * E) III y IV
“D” Matemática y lógica son ciencias formales o de estructuras.
2. Las ciencias fácticas se caracterizan sustancialmente porque
A) no tienen que ver directamente con el mundo físico.
B) no se ocupan de los hechos.
C) no necesitan usar la observación.
D) no tratan con entes físicos.
E) se apoyan en la inducción. *

“E” Las ciencias fácticas se apoyan en la inducción consistente en observar las
cosas individualmente para luego generalizar.
3. La ____________ es un intento previo de explicación de un fenómeno
problemático.
a) teoría
b) ley
c) metateoría
d) hipótesis *
e) verdad
“D” Las hipótesis son explicaciones tentativas a problemas científicos.
4. Cuando una hipótesis es confirmada con reiterados experimentos, ella
A) se convierte en conjetura.
B) se incorpora a la teoría.*
C) se declara como improbable.
D) forma parte del cuerpo de hipótesis.
E) reemplaza a la teoría vigente.
“B” Una hipótesis confirmada varias veces es incorporada a la teoría científica como
una ley, o como un conocimiento más.
5. Luego de que aparece un problema, en el método científico, se procede a
A) elaborar conocimientos.
B) experimentar.
C) plantear hipótesis. *
D) analizar los datos.
E) elaborar la ley.
“C” Cuando se establece un problema el siguiente paso, en el método científico, es
el planteamiento de la hipótesis.
6. La alternativa ajena al juicio de valor es
A) la rosa es vistosa.
B) el plomo es denso. *
C) Kathia es atractiva.
D) Pedro es justo.
E) Inés es buena.
“B” ‘El plomo es denso’ es un juicio de ser se refiere a características objetivas de la
cosa.

7. Marque la alternativa que representa un juicio de valor.
A) Muchos políticos no tienen calidad moral.*
B) Norma es secretaria ejecutiva.
C) Lima es una ciudad con mucha humedad.
D) El oro es el metal más dúctil.
E) Verónica es actriz y productora de videos.
“A” El enunciado a) contiene un valor por eso manifiesta una valoración axiológica.
8. El Güernica de Piccaso a Susana le parece un cuadro muy bello, en tanto que a
Guillermo le parece un cuadro muy lúgubre. Estas apreciaciones son expresio-
nes valorativas del
A) subjetivismo. *
B) naturalismo.
C) objetivismo.
D) socioculturalismo.
E) idealismo objetivo.
“A” El no ponerse de acuerdo respecto a la captación de un valor sería un hecho a
favor del subjetivismo en el cual cada quien tiene se propio criterio respecto a los
valores.
9. La característica de los predicados valorativos por la cual podemos hablar de
bueno y malo, justo e injusto, hermoso y feo, simpático y antipático es la
denominada
A) grado.
B) intensidad.
C) subjetividad.
D) polaridad. *
E) jerarquía.
“D” La polaridad expresa el hecho de que cada valor tiene su respectivo valor
contrario.
10. La afirmación “la ópera Don Giovanni de Mozart” es valiosa porque nos
produce placer al escucharla, se inscribe en la tesis valorativa del
A) utilitarismo.
B) objetivismo.
C) subjetivismo.
D) socioculturalismo.
E) hedonismo. *
“E” Para el hedonismo es valioso aquello que procure en nosotros algún placer.

Biología
1. Si leemos este párrafo ”El cirujano Ambroise Paré, que vivió en el siglo XVI, sostuvo
que había desenterrado en su viña una piedra hueca y cerrada por todas partes y
en su interior había un grueso sapo que sólo podía haber nacido de la humedad
putrefacta·”, llegamos a la conclusión que lo dicho coincide con la teoría denominada
A) panspermia. B) evolución. C) abiogénesis.
D) cosmogónica. E) biosintética.
Rpta.”C” La teoría e generación espontánea o abiogénesis sostiene que la vida se
origina a partir de la materia inerte, en este caso la humedad putrefacta habría dado
origen al sapo de Ambroise Paré.
2. Según la hipótesis de Oparin sobre el origen de la vida en la Tierra, es casi seguro
que la atmósfera primitiva era ________, quizá con altas concentraciones de metano
(CH4), vapor de agua (H2O), amoniaco (NH3) y algo de _____.
A) oxidante-O2 B) oxidante-SO2 C) reductora_HCl
D) reductora_H2 E) reductora_CO2
Rpta. “D” Según La hipótesis de Oparin sobre el origen de la vida Tierra, es casi
seguro que la atmósfera primitiva era reductora, quizá con altas concentraciones de
metano (CH4), vapor de agua (H2O), amoniaco (NH3) y algo de H2.
3. Respecto a las teorías sobre el origen de la vida, relacione
1. Aristóteles ( ) Cosmogónica.
2. Arrhenius ( ) Generación espontánea.
3. Spallanzani ( ) Quimiosintética.
4. Oparin ( ) No existe generación espontánea.
A) 2-1-4-3 B)1-2-4-3 C)2-1-3-4 D)1-2-3-4 E)2-3-1-4
Rpta. “A”
1. Aristóteles ( 2 ) Cosmogónica.
2. Arrhenius ( 1 ) Generación espontánea.
3. Spallanzani ( 4 ) Quimiosintética.
4. Oparin ( 3 ) No existe generación espontánea.
4. Refutó de manera absoluta la teoría de la generación espontánea.

A) Francisco Redi
B) Louis Pasteur
C) Lázaro Spallanzani
D) Alexander Oparin
E) John Haldane
Rpta. “B” Louis Pasteur en el siglo XIX en Francia refutó con un experimento
magistral que ningún ser vivo puedo originarse por generación espontánea.
5. Podemos resumir la concepción evolucionista de Lamarck en los siguientes
puntos excepto
A) Los cambios medioambientales provocan nuevas necesidades en los
organismos.
B) Los organismos deben competir entre si por la existencia.
C) Mecanísmo del uso y del desuso de sus órganos.
D) Los caracteres se adquieren gradualmente.
E) La evolución se explica por acumulación de caracteres adquiridos en el curso de
varias generaciones.
Rpta.”B” Los organismos deben competir entre sí por la existencia. Es uno de
los puntos en el que basa Darwin su teoría de la evolución por selección
natural.
6. La teoría _____________________sobre el origen de la biodiversidad se basa
principalmente en el proceso aleatorio por el cual a lo largo de varias
generaciones se modifica la estructura genética de las poblaciones.
A) creacionista B) neodarwinista C) lamarkiana
D) darwinista E) de evolución química.
Rpta. “B” La teoría neodarwinista o sintética de la evolución sobre el origen de
la biodiversidad se basa principalmente en el proceso aleatorio por el cual a lo
largo de varias generaciones se modifica la estructura genética de las
poblaciones.
7. Las pruebas anatómicas, quizá son las que más información nos pueden aportar
acerca de la evolución. Las alas del murciélago y la aleta del delfín son
____________, lo que nos permite concluir que ambas son especies cercanas
evolutivamente.
A) órganos análogos B) órganos vestigiales

C) órganos convergente D) órganos divergentes
E) órganos homólogos
Rpta. “E” Las alas del murciélago y la aleta del delfín son órganos homólogos ya
que tienen diferente función pero el mismo origen embriológico, lo que nos permite
concluir que ambas son especies cercanas evolutivamente.
8. Los tentáculos de un pulpo, las pinzas de un cangrejo y el brazo de un hombre
son__________________________ya que tienen la misma función pero
diferente origen embriológico.
A) órganos divergentes B) órganos vestigiales
C) órganos convergente D) órganos análogos
E) órganos homólogos
Rpta.”D” Los tentáculos de un pulpo, las pinzas de un cangrejo y el brazo de
un hombre son órganos análogos ya que tienen la misma función pero diferente
origen embriológico.
9. De las siguientes pruebas de la evolución que se indican ¿cuál sería de tipo
biogeográfico?
A) Distribución de las aves no voladoras.
B) Forma de un pez.
C) Huesos de una aleta.
D) Cariotipo.
E) Fósiles de tiranosaurios solo en América del Norte.
Rpta.”A” La distribución de las aves no voladoras. Las encontramos repartidas por
todo el planeta, y consisten en la existencia de grupos de especies más o menos
parecidas, emparentadas, que habitan lugares relacionados entre si por su
proximidad, situación o características.
10. La ciencia que nos da evidencias que los orangutanes y chimpancés son especies
muy cercanas filogenéticamente por tener el mismo número de cromosomas es la
A) Bioquímica comparada B) Anatomía Comparada
C) Embriología D) Citogenética
E) Genética
Rpta. “D” La ciencia que nos da evidencias que los orangutanes y chimpancés son
especies muy cercanas filogenéticamente por tener el mismo número de
cromosomas es la Citogenética.

11. Fue un homínido que vivió entre los 3,9 y 3 millones de años antes del presente.
Era de contextura delgada y grácil, y se cree que habitó sólo en Africa (Etiopía,
Tanzania y Kenia). Es aceptado entre la mayoría de la comunidad científica como el
ancestro del género Homo.
A) Australopithecus africanus B) Australopithecus afarensis
C) Australopithecus ramidus D) Australopithecus robustus
E) Australopithecus habili
Rpta.”A” Australopithecus africanus Fue un homínido que vivió entre los 3,9 y 3
millones de años antes del presente. Era de contextura delgada y grácil, y se cree
que habitó sólo en Africa (Etiopía, Tanzania y Kenia). Es aceptado entre la mayoría
de la comunidad científica como el ancestro del género Homo.a
12. Primera especie del género Homo, vivió aproximadamente desde 2,5 al comienzo
del Pleistoceno, sus fósiles fueron encontrados en Tanzania, Africa, entre 1962 y
1964.
A) Homo erectus B) Homo sapiens C) Homo habilis
D) Homo neardenthalesnsis E) Homo sapiens sapiens
Rpta.”C” Está generalmente aceptado que Homo habilis es la primera especie del
género Homo. Homo habilis (hombre hábil): el primer fabricante de herramientas de
piedra) HomoHomo habilis (hombre hábil) : Vivió aproximadamente desde 2,5, al
comienzo del Pleistoceno. El descubrimiento de esta especie se debe Mary y Louis
Leakey, quienes encontraron los fósiles en Tanzania, África, entre 1962 y 1964.
13. ¿Cuál de los siguientes caracteres aparece primero en los homínidos?
A) Uso del fuego B) Enterraban a sus muertos
C) La comunicación D) El bipedismo
E) La migración fuera del África.
Rpta.”D” El bipedismo es el primer carácter que aparece en los homínidos
14. El gallito de las rocas, ave nacional, cuyo nombre científico es Rupicola
peruvian y _____________
A) pertenece al género Rupicola
B) pertenece al género peruviana
C) es de la especie Rupicola

D) es de la familia peruviana
E) pertenece al género gallito de las rocas
Rpta.”A” La nomenclatura binomial está compuesto por el nombre del género y de
la especie, por tanto el gallito de las rocas pertenece al género Rupicola.
15. Es la forma correcta de escribir el nombre científico de una especie
A) Drosophyla melanogaster B) Boa constrictor
C) Zea Mays D) Thais chocolate
E) Kudoa sarmientae
Rpta. E es la forma correcta de escribir un nombre científico Kudoa sarmientae
Física
(Áreas: A, D y E)
1. Tres partículas ingresan en la región de un campo magnético describiendo las
trayectorias mostradas. Indicar la verdad (V) o falsedad (F) de las siguientes
proposiciones:
I. La partícula B tiene carga positiva.
II. La partícula A tiene carga negativa.
III. La partícula C tiene carga positiva.
A) FVF B) FFV C) VVF D) VFV E) FVV
Solución:
I) V II) V III) F
Clave: C

2. Un campo magnético uniforme de 2 T está orientado en la dirección del eje +z y la
corriente que circula por la barra ab es de intensidad 10A. Determine la magnitud
de la fuerza magnética sobre el conductor. El lado del cubo mide 10 cm.
A) 2 N
B) 2 2 N
C) 3 2 N
D) 3 N
E) 2 3 N
Solución:
F = Il Bsenθ
F = 2 × 10(10–1
3 )
3
2
= 2 2 N
Clave: B
3. En la figura se muestra una partícula de 0,01 kg y carga q+
= 2 mC moviéndose con
velocidad constante de magnitud 10 m/s. Al ingresar a una región donde existe un
campo magnético uniforme de magnitud B = 0,5 T, ¿cuál será su aceleración?
A) 2 m/s2
()
B) 4 m/s2
()
C) 3 m/s2
()
D) 5 m/s2
()
E) 1 m/s2
()
Solución:
Fm = ma = qvB ⇒ a =
m
qvB
= 1 m/s2
()
Clave: E

4. Una partícula con carga eléctrica q+
y masa m ingresa perpendicularmente en la
región de un campo magnético uniforme de magnitud B tal como se muestra en la
figura. Halle el tiempo que permanece la partícula en la región con campo
magnético.
A)
qB2
mπ
B)
qB
mπ
C)
qB3
m2π
D)
qB4
mπ
E)
qB4
m3π
Solución:
t =
4
1
T
T =
qB
m2π
⇒ t =
4
1
×
qB
m2π
=
qB2
mπ
Clave: A
5. En la figura, los campos eléctrico y magnético son uniformes, ¿qué magnitud debe
tener B para que la partícula, con carga q+
y de peso despreciable, describa una
trayectoria rectilínea horizontal?
A) 10 T
B) 12 T
C) 14 T
D) 16 T
E) 18 T
Solución:
qvB = qE ⇒ B =
v
E
=
15
180
= 12 T
Clave: B

6. En la posición A mostrada en la figura se abandona un bloque de 0,5 kg de masa y
carga eléctrica q+
= 0,1 C, el cual se desliza sobre la superficie cilíndrica lisa y
aislante de radio 1,25 m. Determine la magnitud de la fuerza normal en el punto más
bajo de su trayectoria (punto C). (g = 10 m/s2
)
A) 10 N
B) 14 N
C) 16 N
D) 18 N
E) 20 N
Solución:
Por conservación de la energía VC = 5 m/s
en C por dinámica circular: N – w – Fm =
R
mV 2
C
N = mg + qvB +
5
mV 2
C
= 16 N
Clave: C
7. En las siguientes proposiciones, los vectores E (campo eléctrico) B (campo
magnético) y v (velocidad de una partícula cargada) se encuentran en el plano del
papel. ¿En cuál de estos esquemas la partícula permanece en el plano del papel?
A) B) C)
D) E)
Solución:
Clave: C

8. En la figura se muestra un conductor por el cual circula una corriente de intensidad
I = 1A. Si la longitud PQ experimenta una fuerza de magnitud 100 N, determine la
magnitud de la fuerza resultante sobre el conductor.
A) 10 45 N
B) 10 55 N
C) 10 65 N
D) 10 75 N
E) 10 85 N
Solución:
FQR = il B = 50 N; FRES = °++ 127cos)50)(100(250100 22
∴FRES = 10 65 N
Clave: C
Física
(Áreas: B, C y F)
1. Calcule la magnitud de la fuerza magnética que actúa sobre la partícula con carga
q+
= 4 × 10–3
C cuando ingresa en la región de un campo magnético uniforme de
magnitud 1T con rapidez de 100 m/s y formando un ángulo de 30° con la dirección
del campo.
A) 0,2 N B) 0,3 N C) 0,4 N D) 0,5 N E) 0,6 N
Solución:
F = qvBsenθ = 4 × 10-3
× 100 × 1sen30° = 0,2 N
Clave: A
2. La figura muestra un conductor perpendicular a un campo magnético de magnitud
B = 2T. Si la intensidad de corriente por el conductor es I = 0,5 A. Halle la fuerza
magnética sobre el conductor.
A) 1 N
B) 2 N
C) 3 N
D) 4 N
E) 5 N

Solución:
F = Il Bsenθ =
2
1
A × 3 m × 2T sen90° = 3 N
Clave: C
3. Una partícula cargada, dentro de un campo magnético, describe la trayectoria
mostrada. Indicar la verdad (V) o falsedad (F) de las siguientes proposiciones:
I. La partícula tiene carga positiva.
II. La partícula tiene carga negativa.
III. La partícula es neutra eléctricamente.
A) FVF B) FFV C) VFF D) VFV E) FVV
Solución:
I) F II) V III) F
Clave: A
4. En la figura se muestra una partícula de 0,01 kg y carga q+
= 2 mC que se mueve
con velocidad constante de magnitud 10 m/s e ingresa a una región donde existe un
campo magnético uniforme de magnitud B = 0,5 T, ¿cuál será su aceleración?
A) 2 m/s2
()
B) 4 m/s2
()
C) 3 m/s2
()
D) 5 m/s2
()
E) 1 m/s2
()
Solución:
Fm = ma = qvB ⇒ a =
m
qvB
= 1 m/s2
()
Clave: E
5. En las siguientes proposiciones, los vectores E (campo eléctrico) B (campo
magnético) y v (velocidad de una partícula cargada) se encuentran en el plano del
papel. ¿En cuál de estos esquemas la partícula permanece en el plano del papel?

A) B) C)
D) E)
Solución:
Clave: C
Química
SEMANA N° 13: EJERCICIOS DE CLASE (AREAS - ADE)
1. Marque la alternativa que corresponda a las características generales de los
compuestos orgánicos.
I. Son inestables a altas temperaturas, pudiendo descomponerse
II. Tienen puntos de ebullición relativamente bajos.
III. La mayoría son poco solubles o insolubles en solventes orgánicos.
IV. Sólo se presentan en el estado gaseoso a condiciones ambientales.
A) I y II B) II y III C) III y IV D) I y IV E) II y IV
Solución:
I) CORRECTO, por lo general son termolábiles descomponiéndose por encima de
los 300 °C
II) CORRECTO, por lo general sus puntos de ebullición son bajos.
III) INCORRECTO, la mayoría son solubles en solventes orgánicos.
IV) INCORRECTO, se presentan en los tres estados de agregación.
Rpta. A

CH3 CH2 CH2 CH3 CH2 CH CH3
CH3 CH2 CH(CH )3 2 CH3 C C CH3
CH3 CH2 CH2 CH3
sp3
CH2 CH CH3
sp2
CH3 CH2 CH(CH )3 2
sp3
CH3 C C
sp
CH3
2. Sobre la hibridación del carbono, marque la secuencia correcta de verdadero (V) o
falso (F).
I. Se produce por la mezcla de sus orbitales de valencia.
II. Los orbitales híbridos tienen la misma energía.
III. Puede ser sp3
, sp2
, sp.
A) FFV B) FVF C) FVV D) FFF E) VVV
Solución:
I. VERDADERO, En la hibridación se produce la mezcla de los orbitales de
valencia.
II. VERDADERO, Los orbitales híbridos tienen igual energía.
III. VERDADERO, Puede ser sp3
, sp2
, sp.
Rpta. E
3. El tipo de hibridación del átomo de carbono marcado con asterisco (*), es
I. II.
III. IV.
A) sp2
, sp , sp2
, sp3
B) sp3
, sp2
, sp3
, sp
C) sp3
, sp , sp3
, sp2
D) sp3
, sp2
, sp , sp3
E) sp , sp3
, sp , sp2
Solución.
I. II.
III. IV.
Rpta. B

C C C C
C C C C
C C
C C C C
C C C C
C C
CH3 CH2 C C CH2 CH CH Cl
CH3
CH3
CH3
1
2
3
4
1
1 4 2
1
CH31
CH3
1
1
2
CH3 CH2 CH3
CH3
CH2 CHCH CH3
CH3
4. En la siguiente estructura, señale el número de enlaces sigma C – C y el número de
electrones pi.
A) 16 y 4 B) 16 y 2 C) 15 y 3 D) 16 y 6 E) 16 y 3
Solución.
Rpta. D
5. Indique el número de carbonos primarios, secundarios, terciarios y cuaternarios
respectivamente, que hay en el siguiente compuesto:
CH3 – CH2 – C(CH3)2 – C(CH3)2 – CH2 – CH(CH3) – CH2Cl
A) 7 ; 2 ; 1 ; 2 B) 6 ; 2 ; 1 ; 2 C) 7 ; 0 ; 3 ; 2
D) 6 ; 2 ; 0 ; 2 E) 7 ; 2 ; 0 ; 2
Solución.
Rpta. A
6. De acuerdo con la clasificación de los compuestos orgánicos indique la
correspondencia correcta
a) ( ) alicíclico, ramificado
b) ( ) insaturado, ramificado
c) ( ) lineal, saturado

CH2 CH3
CH3 CH2 CH3
CH3
CH2 CHCH CH3
CH3
CH2 CH3
C C C C C
C C OH
CH2 CH2 CH2 CH
CH2 CH2 OH
CH2
CH3 (CH )2 3 CH3 y CH3 CH2 CH(CH )3 2
CH2OH CO CH2OH y CH2OH CHOH CHO
CH3 CHOH COOH y CH2OH CH2 COOH
( ) de compensación
funcional
( ) de posición
( ) de cadena
a)
b)
c)
d) ( ) aromático, ramificado
A) dcba B) cdab C) dcab D) cdba E) abcd
Solución.
a) ( d ) alicíclico, ramificado
b) ( c ) insaturado, ramificado
c) ( a ) lineal, saturado
d) ( b ) aromático, ramificado
Rpta. C
7. Marque la alternativa con la formula global de la siguiente estructura
A) C15H28O B) C15H28 C) C15H30 D) C15H30O E) C15H27O
Solución.
Hay 15 C, 28 H y 1 O
Rpta. A
8. Establezca la correspondencia par de compuestos – tipo de isomería
A) abc B) cba C) bac D) bca E) cab

CH2 CH CH3 + H2 CH3 CH2 CH3 ( ) adición
CH3 CH2OH
H SO2 4
CH2 CH2 + H O2
CH4 + Br2 CH3Br + H
( ) sustitución
( ) eliminación
a)
b)
c) Br
CH3 (CH )2 3 CH3 y CH3 CH2 CH(CH )3 2
CH2OH CO CH2OH y CH2OH CHOH CHO
CH3 CHOH COOH y CH2OH CH2 COOH
( ) de compensación
funcional
( ) de posición
( ) de cadena
a)
b)
c)
b
c
a
CH3 CH2OH
H SO2 4
CH2 CH2 + H O2
CH4+ Br2 CH3Br + H
( ) sustitución
( ) eliminación
a)
b)
c)
a
c
bBr
Solución
Rpta. D
9. Marque la alternativa que establece la correspondencia correcta entre reacción y tipo
de reacción.
A) cba B) acb C) abc D) bca E) bac
Solución.
Rpta. B
10. Indique el grupo funcional de la función cetona
A) – COOH B) – CHO C) – CO – D) – OH E) – COO –
Solución
A) – COOH ácido carboxílico
B) – CHO aldehído
C) – CO – cetona
D) – OH alcohol
E) – COO – éster
Rpta. C

HC C CH CH C
CH3
CH CH2 CH3
HC C CH CH C
CH3
CH CH2 CH3
sp3
sp sp2sp sp2 sp2 sp2 sp2
sp3
C
C
C C C C C C C
C C
C C
CH3 CH2 CH2 CH CH CH CH2 CH3
HC CH2
H2
C H2 52º
2º2º2º2º
2º
C2º
EJERCICIOS DE REFORZAMIENTO
1. Determine respectivamente el número de carbonos con hibridación sp , sp2
y sp3
en el siguiente compuesto:
A) 3, 4, 2 B) 2, 4, 3 C) 4, 3, 2 D) 3, 5, 1 E) 2, 2, 5
Solución
Rpta. B
2. ¿Cuántos carbonos secundarios y enlace sigma C – H hay en la siguiente estructura?
A) 7 y 24 B) 4 y 2 C) 5 y 26 D) 6 y 26 E) 7 y 25
Solución
Rpta. E
3. ¿Cuál de los siguientes compuestos es isómero del CH3 – CH2 – COO – CH3?
A) CH2OH – CH2 – CH2 – CH2OH B) CH3 – O – CH2 – CHO
C) COOH – CH2 – C2H5 D) CHO – CH2 – CHO
E) CH3 – CHOH – CH2OH

+ 2
catalizador
+ H
CH3
CH CH3
OH
CH3
CH CH2 + H O2
CH3 CH CH2 + H2
catalizador
CH3 CH2 CH3
I.
II.
III.
Solución.
Fórmula Global
CH3 – CH2 – COO – CH3 C4H8O2 ISÓMERO
A) CH2OH – CH2 – CH2 – CH2OH C4H10O2
B) CH3 – O – CH2 – CHO C3H6O2
C) HOOC – CH2 – C2H5 C4H8O2 ISOMERO
D) CHO – CH2 – CHO C3H4O2
E) CH3 – CHOH – CH2OH C3H8O2
Rpta. C
4. Indique la reacción de eliminación y adición respectivamente
IV. CH4 + Cl2 CH3Cl + HCl
A) I y III B) II y IV C) I y II D) II y III E) III y IV
Solución: II es una reacción de eliminación, el producto es insaturado y III es una
reacción de adición.
Rpta. D
SEMANA N° 13: EJERCICIOS DE CLASE (AREAS - BCF)
1. Marque la alternativa que corresponda a las características generales de los
compuestos orgánicos.
I. Son inestables a altas temperaturas, pudiendo descomponerse
II. Tienen puntos de ebullición relativamente bajos.
III. La mayoría son poco solubles o insolubles en solventes orgánicos.
IV. Sólo se presentan en el estado gaseoso a condiciones ambientales.
A) I y II B) II y III C) III y IV D) I y IV E) II y IV

CH3 CH2 CH2 CH3 CH2 CH CH3
CH3 CH2 CH(CH )3 2 CH3 C C CH3
CH3 CH2 CH2 CH3
sp3
CH2 CH CH3
sp2
CH3 CH2 CH(CH )3 2
sp3
CH3 C C
sp
CH3
Solución:
I) CORRECTO, por lo general son termolábiles descomponiéndose por encima de
los 300 °C
II) CORRECTO, por lo general sus puntos de ebullición son bajos.
III) INCORRECTO, la mayoría son solubles en solventes orgánicos.
IV) INCORRECTO, se presentan en los tres estados de agregación.
Rpta. A
2. El tipo de hibridación del átomo de carbono marcado con asterisco (*), es
I. II.
III. IV.
A) sp2
, sp , sp2
, sp3
B) sp3
, sp2
, sp3
, sp
C) sp3
, sp , sp3
, sp2
D) sp3
, sp2
, sp , sp3
E) sp , sp3
, sp , sp2
Solución.
I. II.
III. IV.
Rpta. B

CH3 CH2 CH3
CH3
CH2 CHCH CH3
CH3
CH2 CH3
C
C
C C C C C C C
C C
C C
CH3 CH2 CH2 CH CH CH CH2 CH3
HC CH2
H2
C H2 52º
2º2º2º2º
2º
C2º
3. La fórmula global del hidrocarburo cuya cadena se representa por: C – C – C – C
es:
A) C7 H14 B) C6 H14 C) C5 H11 D) C6 H12 E) C7 H16
Solución:
CH3 – CH2 – CH – CH3 su formula global es C4H10
Rpta: A
4. ¿Cuántos carbonos secundarios y enlace sigma C – H hay en la siguiente estructura?
A) 7 y 24 B) 4 y 2 C) 5 y 26 D) 6 y 26 E) 7 y 25
Solución
Rpta. E
5. De acuerdo con la clasificación de los compuestos orgánicos indique la
correspondencia correcta
a) ( ) alicíclico, ramificado
b) ( ) insaturado, ramificado
c) ( ) lineal, saturado
d) ( ) aromático, ramificado

CH3 CH2OH
H SO2 4
CH2 CH2 + H O2
CH4 + Br2 CH3Br + H
( ) sustitución
( ) eliminación
a)
b)
c) Br
CH3 CH2OH
H SO2 4
CH2 CH2 + H O2
CH4+ Br2 CH3Br + H
( ) sustitución
( ) eliminación
a)
b)
c)
a
c
bBr
CH3 CH2 CH3
CH3
CH2 CHCH CH3
CH3
CH2 CH3
C C C C C
C C OH
A) dcba B) cdab C) dcab D) cdba E) abcd
Solución.
a) ( d ) alicíclico, ramificado
b) ( c ) insaturado, ramificado
c) ( a ) lineal, saturado
d) ( b ) aromático, ramificado
Rpta. C
6. Marque la alternativa que establece la correspondencia correcta entre reacción y tipo
de reacción.
A) cba B) acb C) abc D) bca E) bac
Solución.
Rpta. B
EJERCICIOS DE REFORZAMIENTO
1. Marque la alternativa con la formula global de la siguiente estructura
A) C15H28O B) C15H28 C) C15H30 D) C15H30O E) C15H27O

HC C CH CH C
CH3
CH CH2 CH3
HC C CH CH C
CH3
CH CH2 CH3
sp3
sp sp2sp sp2 sp2 sp2 sp2
sp3
CH2 CH2 CH2 CH
CH2 CH2 OH
CH2
+ 2
catalizador
+ H
CH3
CH CH3
OH
CH3
CH CH2 + H O2
CH3 CH CH2 + H2
catalizador
CH3 CH2 CH3
I.
II.
III.
Solución.
Hay 15 C, 28 H y 1 O
Rpta. A
2. Determine respectivamente el número de carbonos con hibridación sp , sp2
y sp3
en el siguiente compuesto:
A) 3, 4, 2 B) 2, 4, 3 C) 4, 3, 2 D) 3, 5, 1 E) 2, 2, 5
Solución
Rpta. B
3. Indique la reacción de eliminación y adición respectivamente
IV. CH4 + Cl2 CH3Cl + HCl
A) I y III B) II y IV C) I y II D) II y III E) III y IV

2010 i semana 13

Más contenido relacionado

La actualidad más candente

Similar a 2010 i semana 13

Más de IverSutizal1

2010 i semana 13