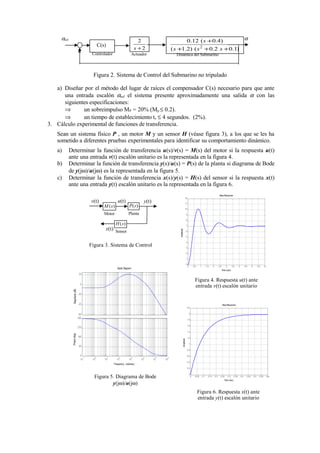
El documento describe tres sistemas de control automático: 1) Un sistema para controlar la trayectoria de un satélite espacial que debe seguir una referencia y rechazar perturbaciones, 2) Un sistema para controlar el ángulo de cabeceo de un submarino no tripulado mediante el diseño de un compensador, 3) Un sistema físico con un motor, planta y sensor para identificar sus funciones de transferencia mediante pruebas experimentales.

1. CONTROL AUTOMÁTICO
1. El diagrama de bloques de la figura 1 representa un sistema de control de un satélite
volando en espacio profundo. La nave debe seguir una trayectoria marcada por la
referencia r(s), rechazar perturbaciones gravitacionales y de viento solar d(s), y
atenuar el ruido en la medida n(s), creado por diversas radiaciones
electromagnéticas.
a) Calcular la función de transferencia que explique la influencia del ruido
electromagnético n(s) en la salida del controlador u(s), es decir u(s)/n(s).
b) Dibujar el diagrama de Bode la función u(jω)/n(jω).
c) Calcular la señal u(t) = B sen(ωt + φ) ante una entrada n(t) = A sen(ωt), siendo
A = 3 , ω = 2 π f , f = 100 Hz.
d) Mediante algún condensador y alguna resistencia, diseñar un filtro H(s) a
colocar en la realimentación, para atenuar el efecto del ruido electromagnético
n(s) de alta frecuencia en la salida del controlador u(s). Se pide que, sin
modificar apenas la estabilidad del sistema, la amplitud B obtenida en el caso
anterior para f = 100 Hz sea diez veces menor ante la misma entrada. Indicar la
expresión de H(s) en Laplace y su circuito electrónico asociado.
Figura 1. Sistema de Control del Satélite en Espacio Profundo
2. Sea el sistema de control del ángulo de cabeceo α de un submarino no tripulado (véase
figura 2).
2
5
s)14.0(
)13.1(
2.0
+
+
s
s
- Satélite
y(s)r(s) e(s)
Controlador
d(s)
n(s)
u(s)

2. Figura 2. Sistema de Control del Submarino no tripulado
a) Diseñar por el método del lugar de raíces el compensador C(s) necesario para que ante
una entrada escalón αref el sistema presente aproximadamente una salida α con las
siguientes especificaciones:
⇒ un sobreimpulso MP = 20% (Mp ≤ 0.2).
⇒ un tiempo de establecimiento ts ≤ 4 segundos. (2%).
3. Cálculo experimental de funciones de transferencia.
Sean un sistema físico P , un motor M y un sensor H (véase figura 3), a los que se les ha
sometido a diferentes pruebas experimentales para identificar su comportamiento dinámico.
a) Determinar la función de transferencia u(s)/v(s) = M(s) del motor si la respuesta u(t)
ante una entrada v(t) escalón unitario es la representada en la figura 4.
b) Determinar la función de transferencia y(s)/u(s) = P(s) de la planta si diagrama de Bode
de y(jω)/u(jω) es la representada en la figura 5.
c) Determinar la función de transferencia x(s)/y(s) = H(s) del sensor si la respuesta x(t)
ante una entrada y(t) escalón unitario es la representada en la figura 6.
)(sM
Planta
v(t)
)(sP
)(sH
u(t) y(t)
x(t)
Motor
Sensor
Step Response
Time (sec)
Amplitude
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 66
0
1
2
3
4
5
6
7
8
9
10
11
1212
Figura 3. Sistema de Control
Figura 4. Respuesta u(t) ante
entrada v(t) escalón unitario
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.60.6
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
2.22.2
Step Response
Time (sec)
Amplitude
Figura 6. Respuesta x(t) ante
entrada y(t) escalón unitario
Figura 5. Diagrama de Bode
y(jω)/u(jω)
-60
-40
-20
0
20
Magnitude(dB)
10
-1
10
0
10
1
10
2
10
3
10
4
10
5
10
6
0
90
180
270
360
Phase(deg)
Bode Diagram
Frequency (rad/sec)
C(s)
αref
-
α
)1.02.0()2.1(
)4.0(12.0
2
+++
+
sss
s
Actuador
2
2
+s
Dinámica del SubmarinoControlador

3. -20
-18
-16
-14
-12
-10
-8
-6
-4
-2
0
2
4
6
Magnitude(dB)
10
-3
10
-2
10
-1
10
0
10
1
10
2
10
3
-180
-165
-150
-135
-120
-105
-90
-75
-60
-45
-30
-15
0
15
30
45
60
75
9090
Phase(deg)
Bode Diagram
Frequency (rad/sec)