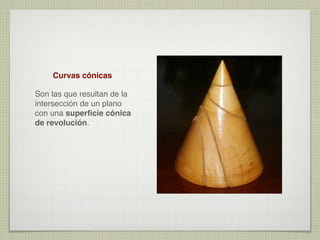
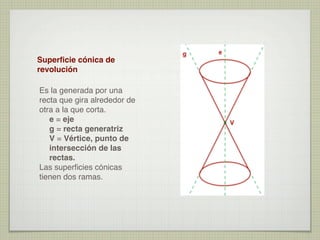
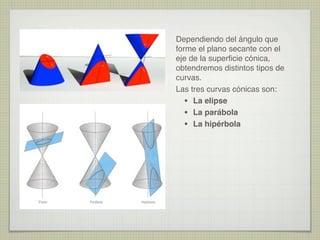
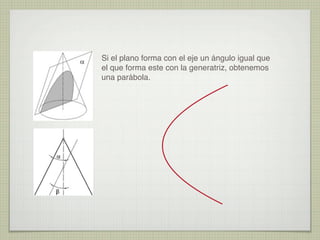
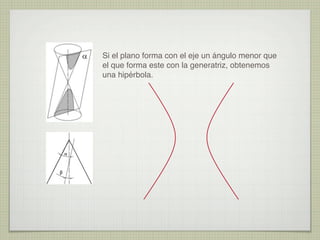
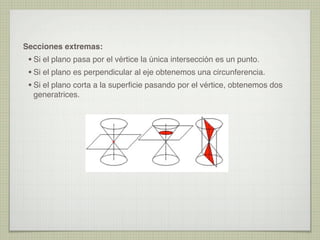
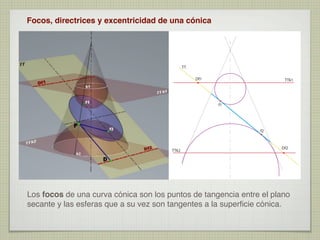
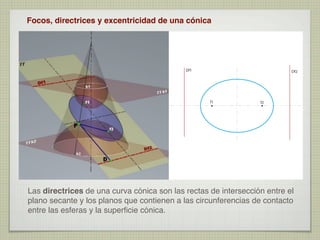
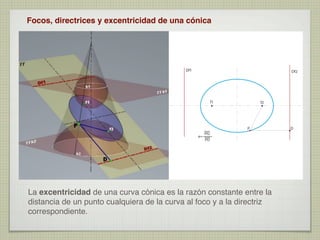
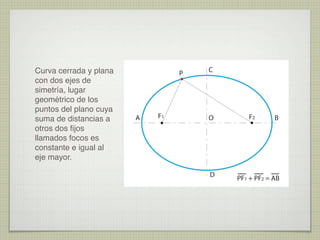
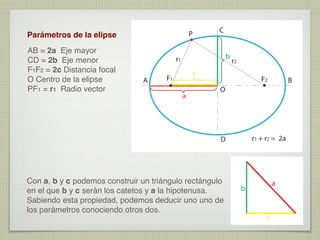
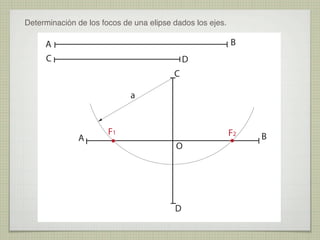
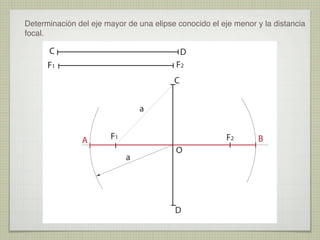
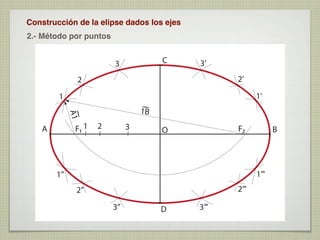
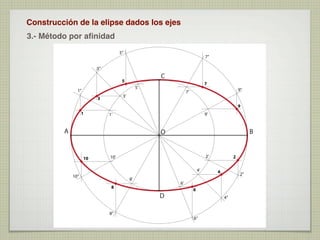
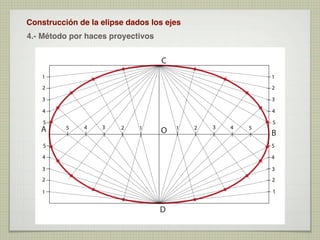
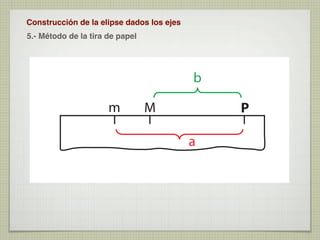
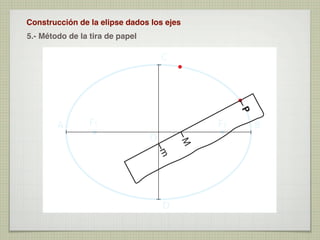
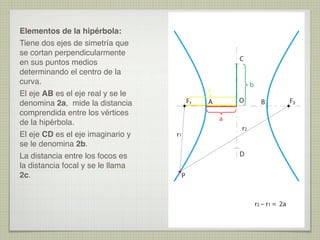
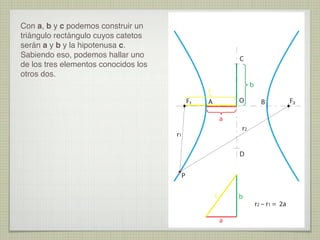
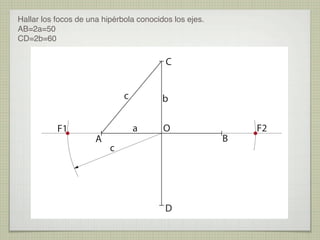
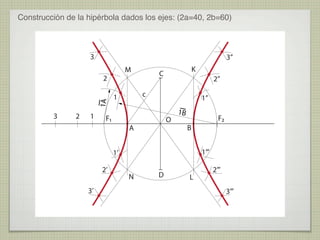
El documento explica las curvas cónicas, que son las que resultan de la intersección de un plano con una superficie cónica de revolución. Las tres curvas cónicas principales son la elipse, la parábola y la hipérbola. Se describen los elementos característicos de cada una como ejes, focos, directrices, así como métodos para su construcción.

1. CURVAS CÓNICAS
DIBUJO TÉCNICO 1º BACHILLERATO

2. Curvas cónicas
Son las que resultan de la
intersección de un plano
con una superficie cónica
de revolución.

3. Superficie cónica de
revolución
Es la generada por una
recta que gira alrededor de
otra a la que corta.
e = eje
g = recta generatriz
V = Vértice, punto de
intersección de las
rectas.
Las superficies cónicas
tienen dos ramas.

4. Dependiendo del ángulo que
forme el plano secante con el
eje de la superficie cónica,
obtendremos distintos tipos de
curvas.
Las tres curvas cónicas son:
• La elipse
• La parábola
• La hipérbola

5. Si el plano forma con el eje un ángulo mayor que
el que forma este con la generatriz, el plano
cortará a una sola rama de la superficie cónica y
a todas sus generatrices, la curva obtenida será
una elipse.

6. Si el plano forma con el eje un ángulo igual que
el que forma este con la generatriz, obtenemos
una parábola.

7. Si el plano forma con el eje un ángulo menor que
el que forma este con la generatriz, obtenemos
una hipérbola.

8. Secciones extremas:
• Si el plano pasa por el vértice la única intersección es un punto.
• Si el plano es perpendicular al eje obtenemos una circunferencia.
• Si el plano corta a la superficie pasando por el vértice, obtenemos dos
generatrices.

9. Focos, directrices y excentricidad de una cónica
TT
Df1
TTk1
f1
f2
TTk2
Df2
Los focos de una curva cónica son los puntos de tangencia entre el plano
secante y las esferas que a su vez son tangentes a la superficie cónica.

10. Focos, directrices y excentricidad de una cónica
Df1
Df2
f1
f2
Las directrices de una curva cónica son las rectas de intersección entre el
plano secante y los planos que contienen a las circunferencias de contacto
entre las esferas y la superficie cónica.

11. Focos, directrices y excentricidad de una cónica
Df1
Df2
f1
f2
P
Pf2
e=
PD
La excentricidad de una curva cónica es la razón constante entre la
distancia de un punto cualquiera de la curva al foco y a la directriz
correspondiente.
D

12. ELIPSE

13. Curva cerrada y plana
con dos ejes de
simetría, lugar
geométrico de los
puntos del plano cuya
suma de distancias a
otros dos fijos
llamados focos es
constante e igual al
eje mayor.
P
A
F1
C
O
D
F2
B
PF1 + PF2 = AB

14. P
Parámetros de la elipse
AB = 2a Eje mayor
CD = 2b Eje menor
F1F2 = 2c Distancia focal
O Centro de la elipse
PF1 = r1 Radio vector
C
b
r1
A
r2
c
F1
a
F2
B
O
r1 + r2 = 2a
D
Con a, b y c podemos construir un triángulo rectángulo
en el que b y c serán los catetos y a la hipotenusa.
Sabiendo esta propiedad, podemos deducir uno uno de
los parámetros conociendo otros dos.
a
b
c

15. Determinación de los focos de una elipse dados los ejes.
B
A
C
D
C
a
A
F1
F2
O
D
B

16. Determinación del eje menor de una elipse conocido el eje mayor y la distancia
focal.
B
A
F1
F2
C
a
A
F1
F2
O
D
B

17. Determinación del eje mayor de una elipse conocido el eje menor y la distancia
focal.
C
D
F2
F1
C
a
A
F1
F2
a
O
D
B

18. Construcción de la elipse dados los ejes
1.- Método del jardinero

19. Construcción de la elipse dados los ejes
2.- Método por puntos
C
3
3’
2’
2
1’
1
A1
1B
F1 1
A
2
3
F2
O
B
1’’’
1’’
2’’’
2’’
3’’
D
3’’’

20. Construcción de la elipse dados los ejes
3.- Método por afinidad
5’’
7’’
3’’
C
5
7
5’
1’’
3’
3
9’’
7’
9
1
9’
1’
A
B
O
10
2’
10’
4’
10’’
8’
4
2’’
6’
8
D
8’’
2
6
4’’
6’’

21. Construcción de la elipse dados los ejes
4.- Método por haces proyectivos
C
1
1
2
2
3
3
4
4
5
A
5
4
3
2
1
O
1
2
3
4
5
5
B
5
5
4
4
3
3
2
2
1
1
D

22. Construcción de la elipse dados los ejes
5.- Método de la tira de papel
b
m
P
M
a

23. Construcción de la elipse dados los ejes
5.- Método de la tira de papel
C
P
A
F1
F2
M
O
m
D
B

24. PARÁBOLA

25. Curva abierta y plana de una sola
rama. Se define como el lugar
geométrico de los puntos del plano
que equidistan de uno fijo llamado
foco (F) y de una recta llamada
directriz (d).
Tiene un solo eje de simetría (e),
sobre el que se sitúan el foco F y el
vértice V.
A la cuerda que pasa por el foco
paralela a la directriz se le llama
parámetro (2p). La distancia del foco
a la directriz (AF) será el
semiparámetro (p).
A los segmentos que unen un punto
cualquiera de la curva con el foco y
con la directriz perpendicularmente
se les llama radios vectores (r1, r2).
P
r1
r2
V
A
F
e
p
r1 = r2
d

26. Construcción de la parábola dados el foco y la directriz.
4’
d
3’
2’
P’
1’
1A
A
V
F
1
2
3
4
1’’
P’’
2’’
3’’
4’’
e

27. HIPÉRBOLA

28. Curva abierta y plana de dos
ramas que se define como el
lugar geométrico de los puntos
del plano cuya diferencia de
distancias a otros dos fijos
llamados focos es constante e
igual al eje real (AB).
C
F1
A
O
B
F2
D
P
PF2 – PF1 = AB

29. Elementos de la hipérbola:
Tiene dos ejes de simetría que
se cortan perpendicularmente
en sus puntos medios
determinando el centro de la
curva.
El eje AB es el eje real y se le
denomina 2a, mide la distancia
comprendida entre los vértices
de la hipérbola.
El eje CD es el eje imaginario y
se le denomina 2b.
La distancia entre los focos es
la distancia focal y se le llama
2c.
C
b
c
F1
O
A
B
a
r2
r1
D
P
r2 – r1 = 2a
F2

30. Con a, b y c podemos construir un
triángulo rectángulo cuyos catetos
serán a y b y la hipotenusa c.
Sabiendo eso, podemos hallar uno
de los tres elementos conocidos los
otros dos.
C
b
c
F1
O
A
B
a
r2
r1
D
P
c
b
a
r2 – r1 = 2a
F2

31. Hallar los focos de una hipérbola conocidos los ejes.
AB=2a=50
CD=2b=60
C
c
F1
A
b
a
O
c
D
B
F2

32. Hallar el eje imaginario de una hipérbola conociendo la distancia focal y el eje
real.
F1F2=2c=70
AB=2a=40
C
c
F1
A
a
b
O
D
B
F2

33. Hallar el eje real de una hipérbola conociendo la distancia focal y el eje
imaginario.
F1F2=2c=60
CD=2b=50
C
b
c
F1
A
a
O
D
B
F2

34. Asíntotas de la hipérbola
Las asíntotas de una
hipérbola son las tangentes
a la curva en el infinito.
La hipérbola tiene dos
asíntotas, que serán
simétricas respecto a los
ejes y pasarán por el centro
de la curva.
Cuando las asíntotas forman
45º con los ejes, decimos
que la hipérbola es
equilátera.
F1
A
O
B
F2

35. Dibujar las asíntotas de una hipérbola conocidos los focos y el eje real.
2c=70
2a=40
K
F1
A
N
M
O
B
L
F2

36. Construcción de la hipérbola dados los ejes: (2a=40, 2b=60)
3
3’’
M
1A
2
3
2
1
K
C
2’’
c
1
1’’
F1
O
A
1B
F2
B
1’’’
1’
2’
3’
N
D
L
2’’’
3’’’

37. F, MOHEDANO
DIBUJO TÉCNICO 1º BACH.
IES LOS MANANTIALES (TORREMOLINOS)