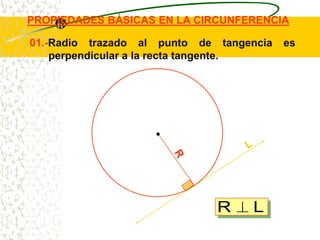
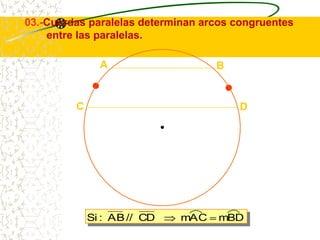
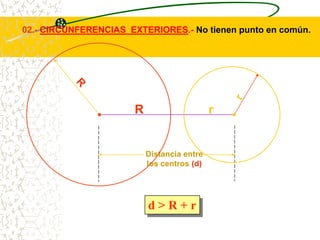
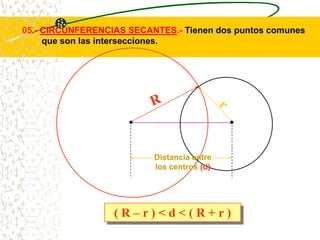
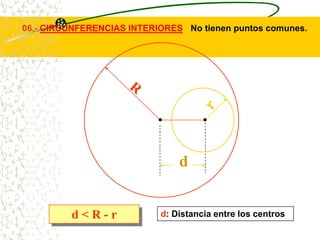
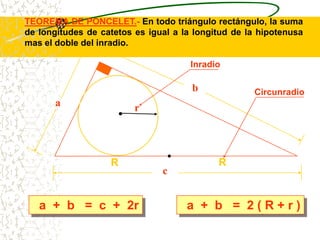
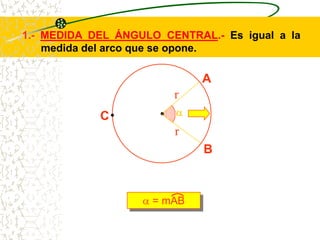
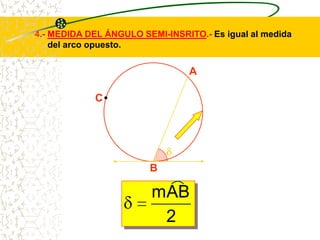
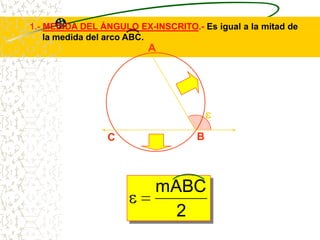
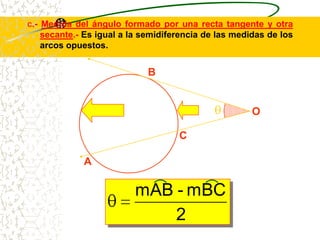
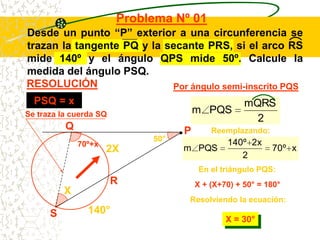
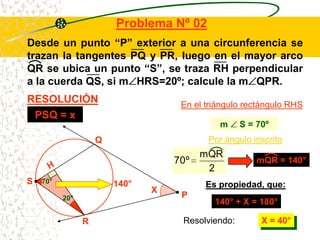
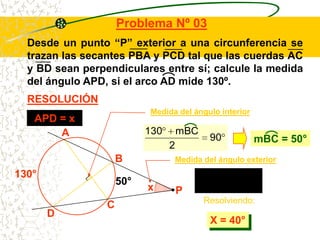
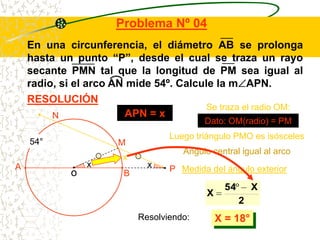
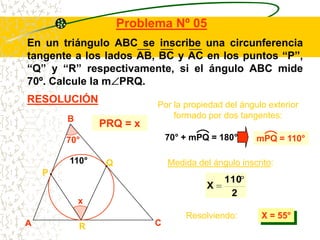
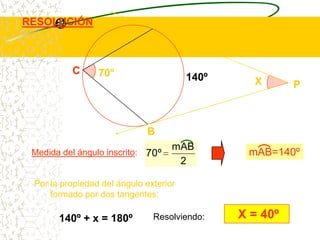
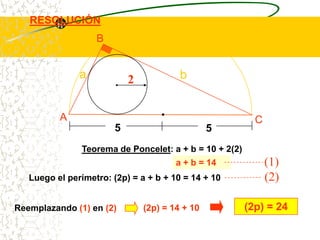
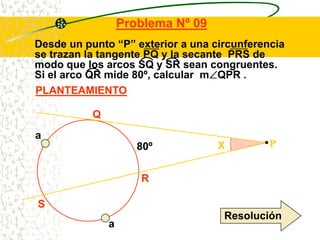
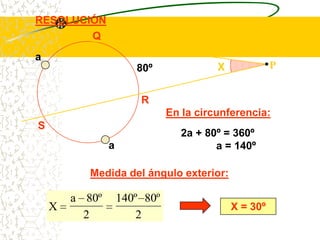
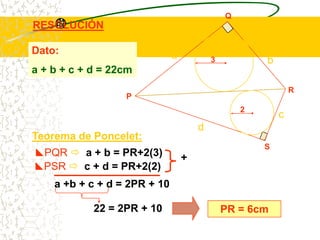
El documento describe las propiedades geométricas de las circunferencias. Define una circunferencia como un conjunto de puntos equidistantes de un punto central. Explica elementos como el radio, diámetro, cuerda, arco y tangente. Luego describe propiedades básicas como que un radio perpendicular a una cuerda la biseca. También cubre posiciones relativas de dos circunferencias como concentricas, tangentes o secantes. Finalmente, presenta teoremas sobre medidas de ángulos.

1. CIRCUNFERENCIA
Srta. Yanira Castro Lizana

2. CIRCUNFERENCIA.- Es un lugar geométrico
de un conjunto de infinitos puntos que
equidistan de un punto situado en el centro.

3. ELEMENTOS DE UNA CIRCUNFERENCIA
Flecha o
sagita Q

Cuerda PQ Recta
P secante

Radio
A  B
Arco BQ
Centro
Diámetro
( AB )
T

Recta
Punto de tangencia tangente

4. PROPIEDADES BÁSICAS EN LA CIRCUNFERENCIA
01.-Radio trazado al punto de tangencia es
perpendicular a la recta tangente.
R L

5. 02.- Radio o diámetro perpendicular a una cuerda
la biseca (divide en dos segmentos congruentes).
P
Q
R PQ PM MQ

6. 03.-Cuerdas paralelas determinan arcos congruentes
entre las paralelas.
A B
 
C D
Si : AB // CD mAC mBD

7. 04.- A cuerdas congruentes en una misma circunferencia
les corresponden arcos congruentes.
A C
Cuerdas congruentes
Arcos congruentes
B
Las cuerdas D
equidistan del
centro
Si : AB CD mAB mCD

8. POSICIONES RELATIVAS DE DOS
CIRCUNFERENCIAS
01.- CIRCUNFERENCIAS CONCENTRICAS.- Tienen el mismo centro.
r
d = Cero ; d : distancia

9. 02.- CIRCUNFERENCIAS EXTERIORES.- No tienen punto en común.
R r
Distancia entre
los centros (d)
d>R+r

10. 03.- CIRCUNFERENCIAS TANGENTES EXTERIORES.- Tienen Un
punto común que es la de tangencia.
Punto de tangencia
R r
Distancia entre
los centros (d)
d = R + r

11. 04.- CIRCUNFERENCIAS TANGENTES INTERIORES.- Tienen un
punto en común que es la de tangencia.
Punto de
tangencia
r
R
d
d=R-r d: Distancia entre los centros

12. 05.- CIRCUNFERENCIAS SECANTES.- Tienen dos puntos comunes
que son las intersecciones.
Distancia entre
los centros (d)
(R–r)<d<(R+r)

13. 06.- CIRCUNFERENCIAS ORTOGONALES.- Los radios son
perpendiculares en el punto de intersección.
Distancia entre
los centros (d)
d2 = R2 + r2

14. 06.- CIRCUNFERENCIAS INTERIORES.- No tienen puntos comunes.
d
d<R-r d: Distancia entre los centros

15. PROPIEDADES DE LAS TANGENTES
1.- Desde un punto exterior a una circunferencia se puede
trazar dos rayos tangentes que determinan dos
segmentos congruentes.
A
R
P
R
B AP = PB

16. 2.- TANGENTES COMUNES EXTERIORES.- Son congruentes
A
B
R
r
r
R
D
C
AB = CD

17. 3.- TANGENTES COMUNES INTERIORES.- Son congruentes.
A
R D
r
r
R B
C
AB = CD

18. TEOREMA DE PONCELET.- En todo triángulo rectángulo, la suma
de longitudes de catetos es igual a la longitud de la hipotenusa
mas el doble del inradio.
Inradio
b Circunradio
a r
R R
c
a + b = c + 2r a + b = 2(R+r)

19. TEOREMA DE PITOT.- En todo cuadrilátero circunscrito a una
circunferencia, se cumple que la suma de longitudes de los lados
opuestos son iguales.
b
Cuadrilátero circunscrito
c
a
d
a + c = b + d

20. Corolario:
Todo ángulo inscrito en una semi circunferencia es recto.
o

22. 1.- MEDIDA DEL ÁNGULO CENTRAL.- Es igual a la
medida del arco que se opone.
A
r
C
r
B
= mAB

23. 2.- MEDIDA DEL ÁNGULO INTERIOR.- Es igual a la
semisuma de las medidas de los arcos
opuestos
A D
C
B
mAB mCD
2

24. 3.- MEDIDA DEL ÁNGULO INSCRITO.- Es la mitad de la medida
del arco opuesto.
A
B
C
mAB
2

25. 4.- MEDIDA DEL ÁNGULO SEMI-INSRITO.- Es igual al medida
del arco opuesto.
A
C
B
mAB
2

26. 1.- MEDIDA DEL ÁNGULO EX-INSCRITO.- Es igual a la mitad de
la medida del arco ABC.
A
C B
mABC
2

27. 6.-ÁNGULOS EXTERIORES.- Son tres casos:
a.- Medida del ángulo formado por dos rectas tangentes.- Es
igual a la semidiferencia de las medidas de los arcos
opuestos.
A mACB - mAB
2
C O
B
+ mAB = 180°

28. b.- Ángulo formado por dos rectas secantes.- Es igual a la
semidiferencia de la medida de los arcos opuestos.
B
C
O
D
A
mAB - mCD
2

29. c.- Medida del ángulo formado por una recta tangente y otra
secante.- Es igual a la semidiferencia de las medidas de los
arcos opuestos.
B
O
C
A
mAB - mBC
2

31. Problema Nº 01
Desde un punto “P” exterior a una circunferencia se
trazan la tangente PQ y la secante PRS, si el arco RS
mide 140º y el ángulo QPS mide 50º. Calcule la
medida del ángulo PSQ.
RESOLUCIÓN Por ángulo semi-inscrito PQS
PSQ = x mQRS
Se traza la cuerda SQ m PQS
2
Q P Reemplazando:
50° 140º 2x
70º+x
2X m PQS 70º x
2
En el triángulo PQS:
R X + (X+70) + 50° = 180°
X
Resolviendo la ecuación:
S 140°
X = 30°

32. Problema Nº 02
Desde un punto “P” exterior a una circunferencia se
trazan la tangentes PQ y PR, luego en el mayor arco
QR se ubica un punto “S”, se traza RH perpendicular
a la cuerda QS, si m HRS=20º; calcule la m QPR.
RESOLUCIÓN En el triángulo rectángulo RHS
PSQ = x
m S = 70º
Q Por ángulo inscrito
mQR
70 º mQR = 140°
2
S 70° 140° Es propiedad, que:
X
20° P
140° + X = 180°
R Resolviendo: X = 40°

33. Problema Nº 03
Desde un punto “P” exterior a una circunferencia se
trazan las secantes PBA y PCD tal que las cuerdas AC
y BD sean perpendiculares entre sí; calcule la medida
del ángulo APD, si el arco AD mide 130º.
RESOLUCIÓN
Medida del ángulo interior
APD = x
A 130 mBC
90 mBC = 50°
2
B Medida del ángulo exterior
130° 130 50
50° X
x P 2
Resolviendo:
C
D
X = 40°

34. Problema Nº 04
En una circunferencia, el diámetro AB se prolonga
hasta un punto “P”, desde el cual se traza un rayo
secante PMN tal que la longitud de PM sea igual al
radio, si el arco AN mide 54º. Calcule la m APN.
RESOLUCIÓN
Se traza el radio OM:
N APN = x
Dato: OM(radio) = PM
Luego triángulo PMO es isósceles
54° M
Ángulo central igual al arco
x
A x x
o B P Medida del ángulo exterior
54 X
X
2
Resolviendo: X = 18°

35. Problema Nº 05
En un triángulo ABC se inscribe una circunferencia
tangente a los lados AB, BC y AC en los puntos “P”,
“Q” y “R” respectivamente, si el ángulo ABC mide
70º. Calcule la m PRQ.
RESOLUCIÓN Por la propiedad del ángulo exterior
B formado por dos tangentes:
PRQ = x
70° 70° + mPQ = 180° mPQ = 110°
110° Q Medida del ángulo inscrito:
P
110
X
2
x
Resolviendo: X = 55°
A R C

36. Problema Nº 06
Calcule la medida del ángulo “X”.
A
70°
X P
B Resolución

37. RESOLUCIÓN A
C 70° 140º X P
B
mAB
Medida del ángulo inscrito: 70 º mAB=140º
2
Por la propiedad del ángulo exterior
formado por dos tangentes:
140º + x = 180º Resolviendo: X = 40º

38. Problema Nº 07
Calcular la medida del ángulo “x”
A
130º X P
B
Resolución

39. A RESOLUCIÓN
260º X P
130º C
B
mAB
Medida del ángulo inscrito: 130 º mAB = 260º
2
En la circunferencia: 260º + mACB = 360º mACB = 100º
Por la propiedad del ángulo exterior
mACB + x = 100º X = 80º
formado por dos tangentes:

40. Problema Nº 08
Calcule el perímetro del triángulo ABC.
B
2
A C
5 5
Resolución

41. RESOLUCIÓN
B
a 2 b
A C
5 5
Teorema de Poncelet: a + b = 10 + 2(2)
a + b = 14 (1)
Luego el perímetro: (2p) = a + b + 10 = 14 + 10 (2)
Reemplazando (1) en (2) (2p) = 14 + 10 (2p) = 24

42. Problema Nº 09
Desde un punto “P” exterior a una circunferencia
se trazan la tangente PQ y la secante PRS de
modo que los arcos SQ y SR sean congruentes.
Si el arco QR mide 80º, calcular m QPR .
PLANTEAMIENTO
Q
a
80º X P
R
S
Resolución
a

43. RESOLUCIÓN
Q
a
80º X P
R
En la circunferencia:
S
2a + 80º = 360º
a a = 140º
Medida del ángulo exterior:
a 80º 140º 80º
X X = 30º
2 2

44. Problema Nº 10
En un cuadrilátero ABCD m Q = m S = 90º se traza
la diagonal PR. Los inradios de los triángulos PQR y
PRS miden 3cm y 2cm respectivamente. Si el
perímetro del cuadrilátero PQRS es 22cm. Calcule la
longitud de PR Q
PLANTEAMIENTO
3
R
P
2
Resolución
S

45. Q
RESOLUCIÓN
Dato: a 3 b
a + b + c + d = 22cm
R
P
2
c
d
Teorema de Poncelet:
S
PQR  a + b = PR+2(3) +
PSR  c + d = PR+2(2)
a +b + c + d = 2PR + 10
22 = 2PR + 10 PR = 6cm