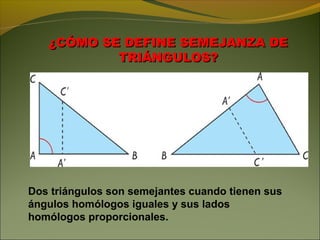
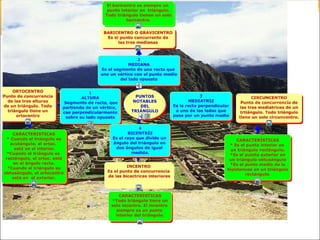
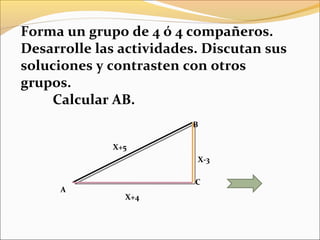
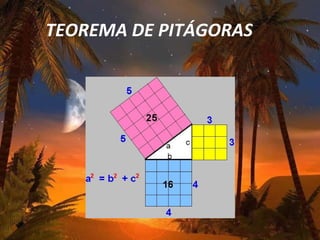
Este documento contiene preguntas y definiciones sobre conceptos geométricos como la semejanza de triángulos, líneas notables en triángulos, relaciones métricas en triángulos rectángulos, los teoremas de Pitágoras y Tales, y una prueba objetiva de matemática con ejercicios. También incluye instrucciones para que los estudiantes trabajen en grupos y discutan sus soluciones.