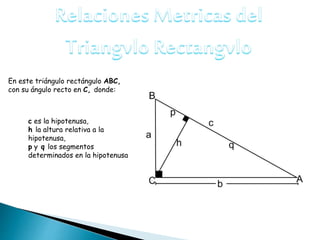
Este documento presenta las propiedades geométricas de un triángulo rectángulo, incluyendo que el cuadrado de un cateto es igual al producto de la hipotenusa por la proyección ortogonal de ese cateto sobre la hipotenusa, que el cuadrado de la altura es igual al producto de las proyecciones ortogonales de los catetos sobre la hipotenusa, y que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Se proporcionan ejemplos para ilustrar cada prop