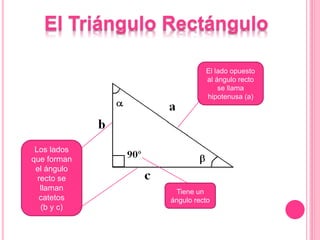
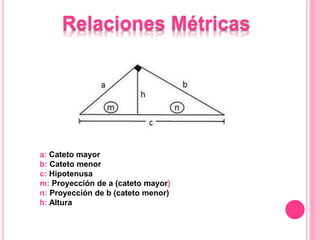
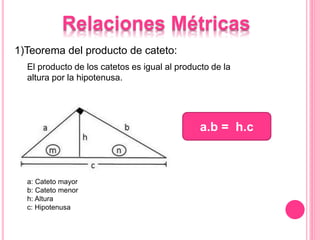
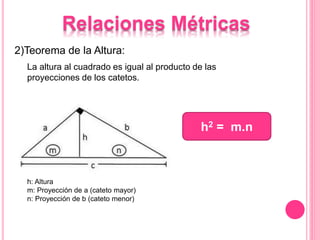
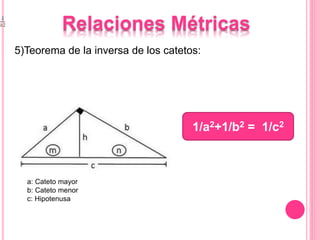
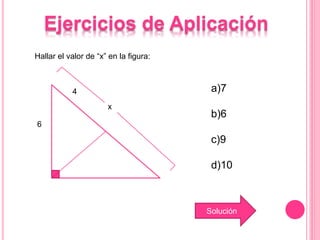
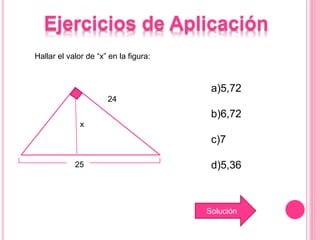
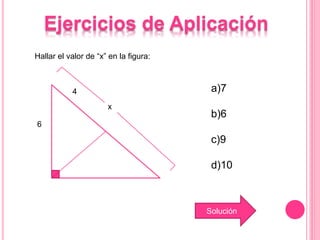
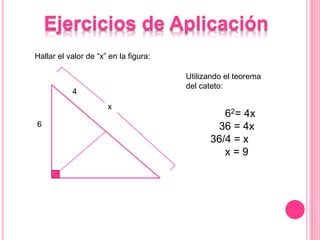
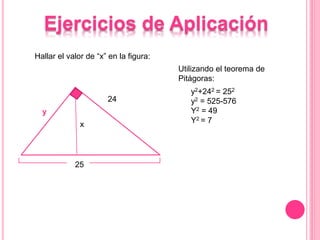
Este documento describe las propiedades del triángulo rectángulo, incluyendo las relaciones métricas y el Teorema de Pitágoras. Explica que el lado opuesto al ángulo recto se llama la hipotenusa, mientras que los lados que forman el ángulo recto son los catetos. Además, presenta cinco teoremas clave sobre las dimensiones de los catetos, la hipotenusa, la altura y las proyecciones en un triángulo rectángulo.

2. El Triángulo Rectángulo
El lado opuesto
al ángulo recto
se llama
hipotenusa (a)
Los lados
que forman
el ángulo
recto se
llaman
catetos
(b y c)
Tiene un
ángulo recto

3. Son cinco teoremas o propiedades, incluyendo
la ecuación del Teorema de Pitágoras. Estas
son válidas, exclusivamente, en el triángulo
rectángulo y se aplican sobre las dimensiones
de los catetos, hipotenusa, la altura relativa a la
hipotenusa y los segmentos determinados sobre
ésta como proyecciones de los catetos de
triángulo.
Relaciones Métricas

4. Relaciones Métricas
a: Cateto mayor
b: Cateto menor
c: Hipotenusa
m: Proyección de a (cateto mayor)
n: Proyección de b (cateto menor)
h: Altura

5. Relaciones Métricas
1)Teorema del producto de cateto:
El producto de los catetos es igual al producto de la
altura por la hipotenusa.
a.b = h.c
a: Cateto mayor
b: Cateto menor
h: Altura
c: Hipotenusa

6. Relaciones Métricas
2)Teorema de la Altura:
La altura al cuadrado es igual al producto de las
proyecciones de los catetos.
h2 = m.n
h: Altura
m: Proyección de a (cateto mayor)
n: Proyección de b (cateto menor)

7. Relaciones Métricas
3)Teorema del Cateto:
Cualquier cateto al cuadrado es igual al producto de su
producción por la hipotenusa.
a2 = m.c
b2 = n.c
a: Cateto mayor
b: Cateto menor
m: Proyección de a (cateto mayor)
n: Proyección de b (cateto menor)
c: Hipotenusa

8. Relaciones Métricas
5)Teorema de la inversa de los catetos:
1/a2+1/b2 = 1/c2
a: Cateto mayor
b: Cateto menor
c: Hipotenusa

9. Ejercicios de Aplicación
6
4
x
Hallar el valor de “x” en la figura:
a)7
b)6
c)9
d)10
Solución

10. Ejercicios de Aplicación
x
Hallar el valor de “x” en la figura:
a)5,72
b)6,72
c)7
d)5,36
Solución
24
25

11. Ejercicios de Aplicación
6
4
x
Hallar el valor de “x” en la figura:
a)7
b)6
c)9
d)10
Solución

12. Ejercicios de Aplicación
6
4
x
Hallar el valor de “x” en la figura:
Utilizando el teorema
del cateto:
62= 4x
36 = 4x
36/4 = x
x = 9

13. Ejercicios de Aplicación
x
Hallar el valor de “x” en la figura:
24
25
Utilizando el teorema de
Pitágoras:
y
y2+242 = 252
y2 = 525-576
Y2 = 49
Y2 = 7