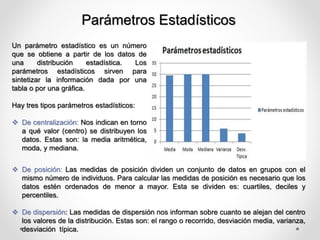
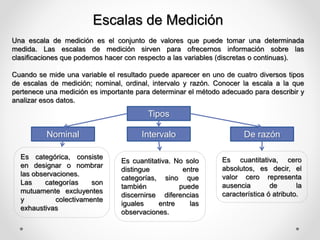
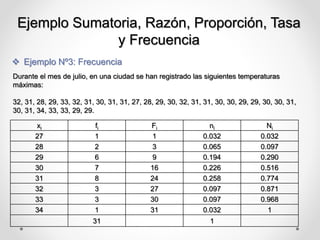
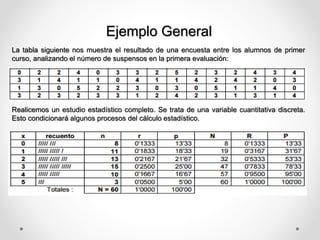
Este documento define conceptos estadísticos básicos como variables, población y muestra, parámetros estadísticos, escalas de medición, y sumatoria, razón, proporción, tasa y frecuencia. Explica que una variable puede ser cualitativa o cuantitativa, y describe tipos de variables, poblaciones y muestras. Además, define parámetros de centralización, posición y dispersión, y proporciona ejemplos de su cálculo. Finalmente, distingue entre las escalas nominal, ordinal, de intervalo y de raz

1. Republica Bolivariana de Venezuela
Ministerio del Popular para la Educación Superior
Instituto Universitario Politécnico “Santiago Mariño”
Profesor: Bachiller:
Pedro Beltrán Elena Vargas
Sección CV 26.756.592
Barcelona, Junio de 2016

2. Variables
Una variable estadística es cada una de las
características o cualidades que poseen los
individuos de una población. es una
propiedad que puede fluctuar y cuya
variación es susceptible de adoptar
diferentes valores, los cuales pueden
medirse u observarse.
Las variables adquieren valor cuando se
relacionan con otras variables, es decir, si
forman parte de una hipótesis o de una
teoría.
Una variable es la expresión simbólica representativa de un elemento no especificado
comprendido en un conjunto.

3. Variables
 Variables Cualitativas: se refieren a características o cualidades que no pueden ser
medidas con números. Podemos distinguir dos tipos:
 Variable cualitativa nominal: presenta modalidades no numéricas que no
admiten un criterio de orden. Puede ser: El estado civil, con las siguientes
modalidades: soltero, casado, separado, divorciado y viudo.
 Variable cualitativa ordinal: presenta modalidades no numéricas, en las
que existe un orden. Puede ser: La nota en un examen: suspenso,
aprobado, notable, sobresaliente.;
 Variable Cuantitativa: es la que se expresa mediante un número, por tanto se pueden
realizar operaciones aritméticas con ella. Podemos distinguir dos tipos:
 Variable discreta: es aquella que solo puede tomar un número finito de
valores entre dos valores cuales quiera de una característica. Puede ser:
El número de hermanos de 5 amigos: 2, 1, 0, 1, 3.
 Variable continua: es aquella que puede tomar un número infinito de
valores entre dos valores cuales quiera de una característica. Puede ser:
Velocidad de un vehículo: puede ser 20; 54,2; 100 ; ... km/h

4. Ejemplo Variables
 Ejemplo Nº1: Clasifica los siguientes caracteres estadísticos según sean cualitativos,
variables discretas ó continuas:
a) Marca de coches.
b) Peso de los coches.
c) Numero de coches vendidos de las diferentes marcas.
Solución:
a) Cualitativa.
b) Variable continua.
c) Variable discreta.
 Ejemplo Nº2: Con el fin de conocer mejor la forma de viajar de una población han
preparado una encuesta. Algunas de las preguntas trataron sobre: Nº de días de viaje,
dinero empleado, número de bultos, zonas geográficas, medio de transporte, naturaleza
del viaje (negocios, turismo, familiar, salud...) y nº de personas. Clasifica estas variables
estadísticas.
Solución:
a) V. cualitativa: Zonas geográficas, medio de transporte y naturaleza del viaje.
b) V. cuantitativa discreta: Nº de días, número de bultos y nº de personas.
c) V. cuantitativa continua: Dinero empleado.

5. Población y Muestra
Población: Es la colección de datos que
corresponde a las características de la totalidad
de individuos, objetos, cosas o valores en un
proceso de investigación.
Muestra: Es una parte representativa de la
población que es seleccionada para ser estudiada,
ya que la población es demasiado grande para ser
estudiada en su totalidad.
Cuando un investigador realiza en ciencias sociales un experimento, una encuesta o
cualquier tipo de estudio, trata de obtener conclusiones generales acerca de una población
determinada. Para el estudio de ese grupo, tomará un sector, al que se conoce como
muestra.

6. Población y Muestra
Tipos de Población:
 Poblaciones Finitas: Constan de un número
determinado de elementos, susceptible a ser
contado.
 Poblaciones Infinitas: Tienen un número
indeterminado de elementos, los cuales no
pueden ser contados.
Tipos de Muestra:
 Muestreo Probabilístico: Son aquellos que se basan en el principio de
equiprobabilidad. Es decir, aquellos en los que todos los individuos tienen la misma
probabilidad de ser elegidos para formar parte de una muestra.
 Muestreo al azar: Todos los individuos tienen la misma probabilidad de ser
seleccionados.
 Muestreo por conglomerados: Se utiliza cuando la población se encuentra dividida,
de manera natural, en grupos que se supone que contienen toda la variabilidad de la
población.

7. Ejemplo Población y Muestra
 Ejemplo Nº 1: Determine la población para cada uno de los siguientes casos:
a) Un agrónomo necesita realizar una investigación en los arbustos de café que se
encuentran en las fincas de Apaneca.
b) Se llevara a cabo una investigación sobre la calidad en la producción ininterrumpida de
las galletas en una fabrica.
Solución:
a) La población de los arbusto es grande, pero es finita.
b) La población son las galletas producidas y por producir es infinita.
 Ejemplo Nº 2: Una empresa de sondeos estadísticos tiene capacidad para entrevistar
a 1000 personas por semana. Si dispone de 4 semanas a qué porcentaje de una
población de 100.000 habitantes puede entrevistar para obtener una muestra.
Solución:
En 4 semanas puede entrevistar a 4000 personas. 4000 de 100.000 equivale a 4 de 100. Así
pues el 4%.

8. Parámetros Estadísticos
Un parámetro estadístico es un número
que se obtiene a partir de los datos de
una distribución estadística. Los
parámetros estadísticos sirven para
sintetizar la información dada por una
tabla o por una gráfica.
Hay tres tipos parámetros estadísticos:
 De centralización: Nos indican en torno
a qué valor (centro) se distribuyen los
datos. Estas son: la media aritmética,
moda, y mediana.
 De posición: Las medidas de posición dividen un conjunto de datos en grupos con el
mismo número de individuos. Para calcular las medidas de posición es necesario que los
datos estén ordenados de menor a mayor. Esta se dividen es: cuartiles, deciles y
percentiles.
 De dispersión: Las medidas de dispersión nos informan sobre cuanto se alejan del centro
los valores de la distribución. Estas son: el rango o recorrido, desviación media, varianza,
desviación típica.

9. Ejemplo Parámetros Estadísticos
 Ejemplo Nº1: Dadas las series
estadísticas:
3, 5, 2, 7, 6, 4, 9.
Calcular:
o La moda, la mediana y la media.
o La desviación media, la varianza y
la desviación típica.
o Los cuartiles 1º y 3º.
o Los deciles 2º y 7º.
o Los percentiles 32 y 85.
Solución
3, 5, 2, 7, 6, 4, 9.
Moda: No existe moda porque todas las
puntuaciones tienen la misma frecuencia.
Mediana: 2, 3, 4, 5, 6, 7, 9.
Me = 5
Media
Varianza
Desviación típica
Desviación media
Rango: r = 9 - 2 = 7
Cuartiles:
Deciles:
7 · (2/10) = 1.4 D2 = 3
7 · (7/10) = 4.9 D7 = 6
Percentiles:
7 · (32/100) = 2,2 P32 = 4
7 · (85/100) = 5.9 P85 = 7

10. Escalas de Medición
Una escala de medición es el conjunto de valores que puede tomar una determinada
medida. Las escalas de medición sirven para ofrecernos información sobre las
clasificaciones que podemos hacer con respecto a las variables (discretas o continuas).
Cuando se mide una variable el resultado puede aparecer en uno de cuatro diversos tipos
de escalas de medición; nominal, ordinal, intervalo y razón. Conocer la escala a la que
pertenece una medición es importante para determinar el método adecuado para describir y
analizar esos datos.
Tipos
Nominal Intervalo De razón
Es categórica, consiste
en designar o nombrar
las observaciones.
Las categorías son
mutuamente excluyentes
y colectivamente
exhaustivas
Es cuantitativa. No solo
distingue entre
categorías, sino que
también puede
discernirse diferencias
iguales entre las
observaciones.
Es cuantitativa, cero
absolutos, es decir, el
valor cero representa
ausencia de la
característica ó atributo.

11. Ejemplos Escalas de Medición
 Ejemplo Nº1: Determínese qué tipo de escala de medida es la más adecuada para
cada una de las siguientes variables:
Variable Escala
a) Nuestro sistema de numeración cronológica
de los años, por ejemplo: 1492, 1650, 1949,
1985, 1991
Intervalo
b) La edad de los sujetos (entendiendo por
edad el tiempo de vida extra materna)
Razón
d) Los diferentes números de las camisetas de
los jugadores de equipos de fútbol
Nominal
e) La lista de éxitos discográficos del verano Nominal
f) El tiempo empleado por los pilotos de
automóviles en recorrer diez veces un circuito
Intervalo
g) Las marcas de paquetes de cigarrillos Nominal

12. Sumatoria, Razón, Proporción, Tasa y
Frecuencia
Sumatoria: se emplea para representar la suma de muchos o infinitos sumandos.
Razón: es el cociente entre dos números, en el que ninguno o sólo algunos elementos del
numerador están incluidos en el denominador. El rango es de 0 a infinito.
Proporción: es una razón en la cual los elementos del numerador están incluidos en el
denominador. Se utiliza como estimación de la probabilidad de un evento. El rango es de 0 a
1, o de 0 a 100%.
Tasa: es un tipo especial de razón o de proporción que incluye una medida de tiempo en el
denominador.
Frecuencia: es el número de veces ni que dicho evento se repite durante un experimento
o muestra estadística. Comúnmente, la distribución de la frecuencia suele visualizarse con el
uso de histogramas. Estas pueden ser: absolutas, relativas (fi), absolutas acumuladas (Ni),
y relativa acumulada (fi).

13. Ejemplo Sumatoria, Razón, Proporción, Tasa
y Frecuencia
 Ejemplo Nº1: Sumatoria
Hallar la sumatoria de la siguiente expresión:
 Ejemplo Nº2: Calcular razón, proporción y tasa
En el año 2002, según el Centro Nacional de Epidemiología se declararon los siguientes
casos de legionelosis:
Comunitario Nosocomial Total
Casos Defunciones Casos Defunciones Casos Defunciones
372 9 29 5 401 14
a) Legionelosis adquirida en la comunidad/ legionelosis nosocomiales= 372/29= 12,8. Por
cada caso de legionelosis nosocomial hay 12,8 casos comunitarios.
b) Defunciones por legionelosis adquirida en la comunidad/defunciones por legionelosis
nosocomiales= 9/5= 1,8. Por cada defunción por legionelosis nosocomial hay 1,8
defunciones por legionelosis adquirida en la comunidad.

14. Proporción
1. Casos de legionelosis comunitarias en relación al total del año 2002= 372/401= 0,93*
100= 93%. El 93% de las legionelosis declaradas en España en 2002 fueron adquiridas
en la comunidad.
2. Defunciones por legionelosis comunitarias en relación al total de las defunciones por
legionelosis del año 2002= 9/14= 0,64* 100= 64%. El 64% de las defunciones por
legionelosis declaradas en España en 2002 fueron por legionella adquirida en la
comunidad.
Ejemplo Sumatoria, Razón, Proporción, Tasa
y Frecuencia
Tasa
1. Tasa de legionelosis en el año 2002 en España= 401/41.837.894 =0,96*10-5
(*100.000)= 0,96 personas padecieron legionelosis en el año 2002 en España por cada
100.000 habitantes.
2. Tasa de mortalidad por legionelosis en España en 2002= 14/41.837.894= 3,3*10-7
(*100.000)= 0,033 personas fallecieron por legionelosis en España en 2002 por cada
100.000 habitantes.

15. Ejemplo Sumatoria, Razón, Proporción, Tasa
y Frecuencia
 Ejemplo Nº3: Frecuencia
Durante el mes de julio, en una ciudad se han registrado las siguientes temperaturas
máximas:
32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30, 30, 31,
30, 31, 34, 33, 33, 29, 29.
xi fi Fi ni Ni
27 1 1 0.032 0.032
28 2 3 0.065 0.097
29 6 9 0.194 0.290
30 7 16 0.226 0.516
31 8 24 0.258 0.774
32 3 27 0.097 0.871
33 3 30 0.097 0.968
34 1 31 0.032 1
31 1

16. Ejemplo General
La tabla siguiente nos muestra el resultado de una encuesta entre los alumnos de primer
curso, analizando el número de suspensos en la primera evaluación:
Realicemos un estudio estadístico completo. Se trata de una variable cuantitativa discreta.
Esto condicionará algunos procesos del cálculo estadístico.

17. Ejemplo General
Parámetros Estadísticos: Media, Varianza y Desviación Típica
Este tipo de tabla facilita los cálculos.
Media = 137 / 60 = 2,283
Varianza = (433 / 60) - media al cuadrado = 2'005
Desviación típica = raíz cuadrada de la varianza = 1'416
Moda = Valor de mayor frecuencia = 3

18. Bibliografía
 http://www.vitutor.com/estadistica/descriptiva/a_2.html
 http://www.rena.edu.ve/cuartaEtapa/metodologia/Tema6.html
 https://app.box.com/s/iird9pig9z4dk18n9723gb1j32p3yoz0
 http://recursostic.educacion.es/descartes/web/materiales_didacticos/EDAD_3eso_estadistica/3eso_qui
ncena11.pdf
 http://estadisticaparaadministracion.blogspot.com/2011/10/poblacion-y-muestra-parametro-y.html
 https://es.wikiversity.org/wiki/Medici%C3%B3n_en_estad%C3%ADstica.#Escalas_de_medici.C3.B3n
 http://www.monografias.com/trabajos96/practica-2-tipos-variables-y-escalas/practica-2-tipos-variables-
y-escalas.shtml
 http://www2.uca.es/serv/fag/fct/downloads/tema1.pdf
 http://www.ditutor.com/estadistica/sumatoria.html
 http://sameens.dia.uned.es/Trabajos7/Trabajos_Publicos/Trab_3/Gaspar_Garcia_3/razon.html
 https://es.wikipedia.org/wiki/Frecuencia_estad%C3%ADstica