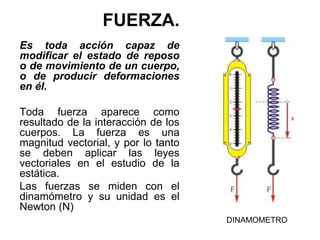
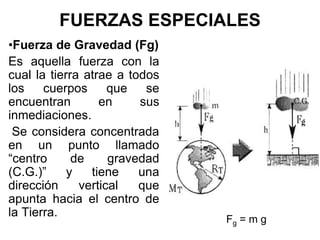
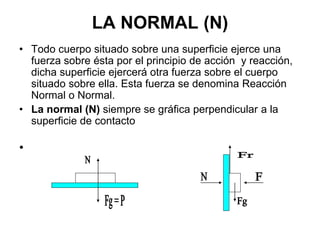
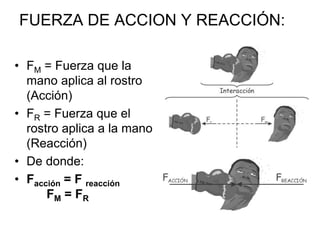
La estática es una rama de la mecánica que estudia las fuerzas que permiten que un cuerpo permanezca en equilibrio, sin considerar el movimiento. Se centra en fuerzas aplicadas a partículas y cuerpos rígidos, utilizando conceptos como la fuerza de gravedad, la normal y las condiciones de equilibrio traslacional y rotacional. Para resolver problemas estáticos, se debe aislando el cuerpo en análisis, contabilizando las fuerzas y aplicando condiciones de equilibrio mediante el uso de diagramas de cuerpo libre.

1. ESTÁTICA
• CONCEPTO
• “La estática es una parte de la mecánica que estudia
las condiciones que deben cumplir las fuerzas para
que al actuar sobre un cuerpo hagan que éste se
mantenga en una condición de equilibrio”
• Se ocupa de estudiar las fuerzas sin considerar el
movimiento que estas producen. Estudia las condiciones
de equilibrio de los sistemas de fuerzas.
• Se va a considerar fuerzas aplicadas solamente a
masas puntuales o partículas y cuerpos rígidos.

2. FUERZA.
Es toda acción capaz de
modificar el estado de reposo
o de movimiento de un cuerpo,
o de producir deformaciones
en él.
Toda fuerza aparece como
resultado de la interacción de los
cuerpos. La fuerza es una
magnitud vectorial, y por lo tanto
se deben aplicar las leyes
vectoriales en el estudio de la
estática.
Las fuerzas se miden con el
dinamómetro y su unidad es el
Newton (N)
DINAMOMETRO

3. FUERZAS ESPECIALES
•Fuerza de Gravedad (Fg)
Es aquella fuerza con la
cual la tierra atrae a todos
los cuerpos que se
encuentran en sus
inmediaciones.
Se considera concentrada
en un punto llamado
“centro de gravedad
(C.G.)” y tiene una
dirección vertical que
apunta hacia el centro de
la Tierra.
Fg = m g

4. LA NORMAL (N)
• Todo cuerpo situado sobre una superficie ejerce una
fuerza sobre ésta por el principio de acción y reacción,
dicha superficie ejercerá otra fuerza sobre el cuerpo
situado sobre ella. Esta fuerza se denomina Reacción
Normal o Normal.
• La normal (N) siempre se gráfica perpendicular a la
superficie de contacto
•

5. FUERZA DE ACCION Y REACCIÓN:
• FM = Fuerza que la
mano aplica al rostro
(Acción)
• FR = Fuerza que el
rostro aplica a la mano
(Reacción)
• De donde:
• Facción = F reacción
FM = FR

6. PRIMERA CONDICIÓN DE EQUILIBRIO
(Equilibrio traslacional)
“Un cuerpo se encuentra en equilibrio de
traslación si la fuerza resultante de todas las
fuerzas externas que actúan sobre él es nula”
 
 0
i
R F
F
0
0 
 RY
RX F
F
1
F
3
F
2
F
Matemáticamente se cumple
3
2
1 F
F
F
FR 


Donde:

7. FUERZAS EN EQUILIBRIO
(Teorema de Lamy)
"Si un cuerpo, bajo la
acción de tres fuerzas
coplanares y concurrentes,
se encuentra en equilibrio,
el valor de cada una de las
fuerzas es directamente
proporcional al seno del
ángulo que se le opone"
•
γ
Sen
F
β
Sen
F
α
Sen
F 3
2
1


1
F
α
 
3
F
2
F

8. DIAGRAMA DE CUERPO LIBRE
¿Graficar las fuerzas del bloque sobre el plano?
¿Con cuantos cuerpos interactúa el bloque colgante y
grafique sus fuerzas?
37º
A

9. EJEMPLO 1
Halla las tensiones en las cuerdas A y B. Si el bloque pesa
100 √3 N y el sistema está en equilibrio. Usar DCR Ver figura
º
30 º
60
B
A
P
º
30 º
60
B
T
P
A
T
Descomposición de fuerzas

10. MOMENTO DE UNA FUERZA O TORQUE (M)
Se denomina momento de una fuerza, o torque, a aquella
magnitud vectorial que es una medida de la capacidad de
rotación que dicha fuerza externa es capaz de producir a un
cuerpo, cuando este puede rotar alrededor de un eje de
rotación.
r
F
de
acción
de
Linea
rotación
de
Eje
F

d
O
F
O
M
Vectorial
F
x
r
MF
O 

sen
F
r
MF
O 
Escalar
d
F
MF
O 
Del grafico d = |r| sen θ
d = Brazo de palanca

11. DIRECCION DEL MOMENTO Mo
F
La dirección del momento de una fuerza Mo
F es
perpendicular al plano formado por r y F y su
sentido se determina por la regla de la mano
derecha
r
θ
Eje de rotación
o de giro
d = Distancia  del eje
de rotación a la línea de
acción de la fuerza

12. La dirección del torque Mo
F es perpendicular al plano
formado por r y F y su sentido se determina por la regla
de la mano derecha
Dirección del torque

13. CONVENCIÓN DE SIGNOS DEL MOMENTO
• Se considera el momento positivo si el cuerpo gira en sentido
antihorario, y el momento negativo si el cuerpo gira en sentido
horario
• Si la línea de acción de una fuerza pasa por el centro de rotación, o
centro de momentos, el momento producido por dicha fuerza es
nulo

14. Segunda Condición de Equilibrio
(Equilibrio rotacional)
“Un cuerpo se encuentra
en equilibrio de rotación
si el momento resultante
de todas las fuerzas que
actúan sobre él,
respecto de cualquier
punto, es nulo”
0
0
0
0
0
2
1




 N
F
F
F
R
M
M
M
M 
n
F
F
F
R
Donde 


 
2
1
:
R
0
0 
R
M

15. PASOS PARA RESOLVER UN
PROBLEMA DE ESTÁTICA
1. Dado un sistema aislar imaginariamente el cuerpo que
se desea analizar y realizar su diagrama de cuerpo
libre.
2. Contabilizar el número de fuerzas actuantes, recordar
que las fuerzas son el resultado de la interacción de los
cuerpos.
3. Aplicar la primera condición de equilibrio y el recurso
matemático necesario según sea el número de fuerzas.
4. Elegir el centro de momentos, de preferencia en donde
concurran la mayor cantidad de fuerzas desconocidas.
5. Aplicar la segunda condición de equilibrio respecto al
punto elegido.

16. Ejemplo 2
La barra de la figura pesa 20 N y permanece en posición
horizontal sobre B y C. Hallar las reacciones en los puntos
de apoyo. El bloque sobre la barra pesa 40 N.

17. Resolución: 2
• Se toman los momentos con respecto a los
puntos sobre los cuales se pueden girar:
• Primero:MB = 0 respecto al punto B
• RC . 6m – 40 N . 4m – 20 N . 2 m = 0
• RC = 33,33 N
• Segundo: MC = 0 respecto al punto C
• – RB . 6m + 20 N . 4 m + 40 N . 2m = 0
• RB = 26, 67N

18. APLICACIÓN 3
Una fuerza vertical de 100 lb se aplica en el extremo de una
palanca que está unida a una flecha en el pun to O. Determine
a) el momento de la fuerza de 100 lb con respecto a O;
b) la fuerza horizontal aplicada en A que origina el mismo
momento con respecto a O;
c) la fuerza mínima aplicada en A que origina el mismo
momento con respecto a O.
a) Momento con respecto a O

19. APLICACIÓN 3
Una fuerza vertical de 100 lb se aplica en el extremo de una
palanca que está unida a una flecha en el pun to O. Determine:
a) el momento de la fuerza de 100 lb con respecto a O;
b) la fuerza horizontal aplicada en A que origina el mismo
momento con respecto a O;
c) la fuerza mínima aplicada en A que origina el mismo
momento con respecto a O.
b) Momento con respecto A

20. APLICACIÓN 3
Una fuerza vertical de 100 lb se aplica en el extremo de una
palanca que está unida a una flecha en el pun to O. Determine
a) el momento de la fuerza de 100 lb con respecto a O;
b) la fuerza horizontal aplicada en A que origina el mismo
momento con respecto a O;
c) la fuerza mínima aplicada en A que origina el mismo
momento con respecto a O.
c) Fuerza mínima aplicada

21. APLICACIÓN 4
Una fuerza de 800 N actúa sobre la ménsula, como se
muestra en la figura. Determine el momento de la
fuerza con respecto a B.

22. APLICACIÓN 5
Una fuerza de 30 lb actúa sobre el extremo de una palanca
de 3 ft, como se muestra en la figura. Determine el momento
de la fuerza con respecto a O.

23. Ejemplo 6
Sobre la barra quebrada de peso despreciable se
aplica un sistema de fuerzas. Determinar el
momento resultante respecto del pasador en A.
Además: AB = BC = CD = DE = 2m
Calcule el torque neto alrededor del punto 0 para
las dos fuerzas aplicadas