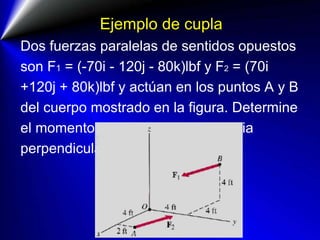
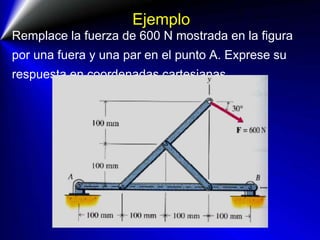
Este documento presenta conceptos fundamentales sobre fuerzas en física. Explica que una fuerza es un agente capaz de modificar la cantidad de movimiento o forma de los cuerpos, y que debe especificarse por su intensidad, dirección y punto de aplicación. Luego define elementos de la fuerza, clases de fuerzas, unidades de fuerza, descomposición y resultado de fuerzas, momento de una fuerza y principios relacionados con pares de fuerzas. Finalmente incluye ejemplos ilustrativos sobre estos temas.

1. UNIDAD EDUCATIVA
“PEDRO VICENTE MALDONADO”
CURSO: FISICA I
TEMA: FUERZAS - ESTATICA
Profesor: RAUL ASQUI VILLARROEL
RIOBAMBA 2015

2. I. FUERZA
●En física, la fuerza es todo agente capaz de
modificar la cantidad de movimiento o la forma de
los cuerpos. Es decir, la fuerza expresa la acción
mecánica de un cuerpo sobre otro.
●Siendo la fuerza una cantidad vectorial su
especificación completa requiere de: (a) una
intensidad, (b) una dirección y sentido, y (c) un
punto de aplicación.

3. ELEMENTOS DE LA FUERZA

4. I. FUERZA_1
La fuerza produce dos efectos:
A. Exteriores: En la estructura el efecto exterior de la
fuerza F = 500 N, es las reacciones que aparecen
sobre las varillas y sobre el perno.
B. Interiores: El efecto interior de la fuerza F es las
deformaciones y esfuerzos resultantes distribuidos
en el seno del material

5. I. FUERZA_2
Al estudiar la mecánica de los cuerpos rígidos
donde se tiene en cuenta el efector exterior
podemos considerar a la fuerza como un vector
deslizante es decir, goza del principio de
transmisibilidad, esto es, la fuerza puede
considerarse aplicada en cualquier punto de su
línea de acción sin que altere su efecto exterior
sobre el cuerpo

6. II. CLASES DE FUERZAS
1.FUERZAS DE
CONTACTO.
Se generan mediante el
contacto físico directo
entre dos cuerpos
2. FUERZAS MASICAS
se crean por acción a
distancia. Ejm. la fuerza
gravitacional, eléctrica y
magnética.

7. II. CLASES DE FUERZAS_2
1.FUERZAS
CONCENTRADAS .
Aquellas que se consideran
aplicada en un punto
2. FUERZAS DISTRIBUIDAS
Aquellas que se consideran
aplicadas en una línea, un
área o un volumen

8. III. UNIDADES DE FUERZA
●Una fuerza puede medirse comparándola con
otras fuerzas conocidas, recurriendo al equilibrio
mecánico, o por deformación calibrada de un
resorte.
●La unidad patrón de la fuerza en el SI de
unidades es el Newton (1 N)

9. III. FUERZA RESULTANTE
●Consideremos dos fuerzas actuando sobre un
cuerpo como se ve en la figura .
●Geométricamente se determina mediante la ley
del paralelogramo o triángulo. Su modulo y
dirección son

10. EJEMPLO O1
Determine el ángulo θ para conectar el elemento a
la placa tal que la resultante de las fuerzas FA y FB
esté dirigida horizontalmente a la derecha.
Determine además la magnitud de la fuerza
resultante

11. EJEMPLO O2
La resultante FR de las dos fuerzas que actúan
sobre el tronco de madera está dirigido a lo largo
del eje x positivo y tiene una magnitud de 10 kN.
Determine el ángulo θ que forma el cable unido a
B tal que la magnitud de la fuerza FB en este cable
sea un mínimo. ¿Cuál sería la magnitud de la
fuerza en cada cable para esta situación?

12. IV. DESCOMPOSICIÓN DE UNA FUERZA
1. EN DOS DIRECCIONES PERPENDICULARES EN EL
PLANO

13. Ejemplo
Calcule las componentes horizontal y vertical de las
fuerzas mostradas en la figura

14. IV. DESCOMPOSICIÓN DE UNA FUERZA
2. EN DOS DIRECCIONES NO PERPENDICULARES EN EL
PLANO

15. Ejemplo
Calcule las componentes de la fuerza de 260 N
representada en la figura, una de ellas actúa en la
dirección de AB mientras que la línea de acción de la
otra componente pasa por C

16. Ejemplo
Calcule las componentes de la fuerza de 100 N
representada en la figura , una de ellas actúa en la
dirección de AB y la otra paralela a BC.

17. EJEMPLO O2
La fuerza de 500 N que actúa sobre la armadura
ha de ser resuelta en dos componentes actuando
a lo largo de los ejes AB y AC de la estructura. Si
la componente de la fuerza a lo largo de AC es de
300 N dirigida de A C, determine la magnitud de la
fuerza actuante a l largo de AB y el ángulo θ de la
fuerza de 500 N

18. EJEMPLO O2
La fuerza F de 500 N está aplicada al poste
vertical tal como se indica . (a) Escribir F en
función de los vectores unitarios i y j e identificar
sus componentes vectoriales y escalares; (b)
hallar las componentes escalares de F en los ejes
x’ e y’; © hallar las componentes escalares de F en
los ejes x e y’.

19. IV. DESCOMPOSICIÓN DE UNA FUERZA
3. EN TRES DIRECCIONES PERPENDICULARES EN EL
ESPACIO

20. IV. DESCOMPOSICIÓN DE UNA FUERZA
3. DIRECCIONES DE LA FUERZA EN EL ESPACIO

21. V. FUERZA DEFINIDA POR SU MODULO Y DOS
PUNTOS DE SU LINEA DE ACCIÓN
En algunos caso la fuerza está definida por su
modulo y dos puntos de su línea de acción. En este
caso

22. EJEMPLO O2
Combinar las dos fuerza P y T, que actúan sobre
el punto B de la estructura fija, para obtener una
única fuerza R.

23. EJEMPLO O2
En el sistema de fuerzas mostrado en la figura
determine la magnitud y la dirección de la fuerza
resultante.

24. EJEMPLO O2
Expresar la fuerza F de 36 kN en función de los
vectores unitarios i, j y k. Hallar la proyección
sobre el eje x

25. EJEMPLO O2
Expresar la fuerza F de 400 N en función de los
vectores unitarios i, j y k. Hallar la proyección
sobre la recta OA.

26. EJEMPLO O2
Calcular las componentes rectangulares de la
fuerza de 110 N, representada en la figura, una es
paralela a AB y la otra es perpendicular a esta
línea.

27. MOMENTO DE UNA FUERZA
●En mecánica newtoniana, se denomina momento
de una fuerza (respecto a un punto dado) a una
magnitud vectorial, obtenida como producto
vectorial del vector de posición del punto de
aplicación de la fuerza con respecto al punto al
cual se toma el momento por la fuerza, en ese
orden. También se le denomina momento
dinámico o sencillamente momento.

28. MOMENTO DE UNA FUERZA
●El momento de una fuerza aplicada en un punto P
con respecto de un punto O viene dado por el
producto vectorial del vector de posición OP por el
vector fuerza F; esto es
●El momento es un vector perpendicular al plano de
r y F.
●La magnitud del momento esta dado por
●El sentido del momento se determina mediante la
regla de la mano derecha.

29. INTERPRETACIÓN DEL MOMENTO DE UNA
FUERZA●El momento de una fuerza con respecto a un eje
da a conocer en qué medida existe capacidad en
una fuerza o sistema de fuerzas para causar la
rotación del cuerpo alrededor de un eje que pase
por dicho punto.
●El momento tiende a provocar un giro en el cuerpo
sobre el cual se aplica y es una magnitud
característica en elementos que trabajan
sometidos a torsión (como los ejes de maquinaria)
o a flexión (como las vigas

30. COMPONETES RECTANGULARES DEL
MOMENTOEl momento de la fuerza respecto a
O es

31. COMPONETES RECTANGULARES DEL
MOMENTO RESPECTO A UN PUNTO
CUALQUIERA

32. COMPONETES RECTANGULARES DEL
MOMENTO EN EL PLANO

33. Ejemplo
●Determine el momento ejercido por el peso de
30 lbf con respecto a los puntos (a) E y (b) S

34. Ejemplo
Se aplica una fuerza vertical de 100 lb
al extremo de una palanca que está
unida a un eje en O. Determine:
(a) el momento de la fuerza de 100 lb
con respecto al punto O,
(b) el módulo de la fuerza horizontal
que aplicada en A produce el mismo
momento produce el mismo momento
respecto a O,
(c) la menor fuerza que aplicada en A
produce el mismo momento respecto a
O,

35. Parte (a) La magnitud del momento
de la fuerza de 100 lb se obtiene
multiplicando la fuerza por el brazo
de palanca esto es
La dirección de Mo es perpendicular
al plano que contiene F y d y su
SOLUCIÓN

36. Parte (b) La fuerza que aplcada en
A produce el mismo momento se
determina en la forma siguiente
SOLUCIÓN

37. Parte (b) Debido a que M = F d. el
mínimo valor de F corresponde al
máximo valor de d. Eligiendo la
fuerza perpendicular a OA se
encuentra que d = 24 in; entonces
SOLUCIÓN

38. Parte (b). En este caso Mo = Fd
obteniendo
SOLUCIÓN

39. Ejemplo
●La placa rectangular es soportada por dos pernos
en A y B y por un alambre CD. Conociendo que la
tensión e el alambre es 200 N. Determine el
momento con respecto al punto A de la fuerza
ejercida por el alambre en C
El momento MA de la
fuerza F ejercida por el
alambre es obtenido
evaluando el producto
vectorial
SOLUCIÓN

40. SOLUCIÓN

41. Ejemplo
La tensión en el cable AB es 150 N. Determine la
tensión en AC y CD tal que la suma de los momentos
alrededor del origen debido a la fuerza ejercida por
los cables en el punto A es cero.

42. Ejemplos

43. MOMENTO DE UNA FUERZA CON RESPECTO
A UN EJE QUE PASA POR EL ORIGEN
●Sabemos que el momento de
la fuerza F respecto al punto
O.
●El momento de la fuerza F
con respecto al eje OL es la
proyección ortogonal de Mo
sobre el eje OL.

44. MOMENTO DE UNA FUERZA CON
RESPECTO A UN EJE QUE PASA POR
UN PUNTO CUALQUIERA●El momento de una
fuerza alrededor de un
eje cualquiera es
●El resultado es
independiente del

45. Ejemplo
●Sobre un cubo de arista a
actúa una fuerza P, como
se muestra en la figura.
Determine el momento de
P:
(a) con respecto a A,
(b) con respecto a la arista
AB.
(c) Con respecto a la
diagonal AG

46. SOLUCIÓN
●Moment of P about A,
●Moment of P about AB,
La magnitud del momento respecto a AB es

47. SOLUCIÓN
(c) La magnitud del momento respecto a AG es

48. Ejemplo
●Se aplica una tensión
T de intensidad 10 kN
al cable amarrado al
extremo superior A
del mástil rígido y se
fija en tierra en B.
Hallar e momento Mz
de T respecto del eje
Z que pasa por la
base O del mástil.

49. Ejemplo
●La fuerza F tiene una
intensidad de 2 kN y
está dirigida de A
hacia B. Determine :
(a) La proyección FCD
de La fuerza F sobre
la recta CD (b) el
ángulo que θ que
forma la fuerza F y la
recta CD y (c) si el
modulo del momento

50. Ejemplo
●La tensión el cable es 143,4 N. Determine el
momento alrededor del eje x de esta fuerza de
tensión actuando en A. Compare su resultado con
el momento del peso de 15 kgf de la placa
uniforme alrededor del eje x. ¿Cuál es el momento
de fuerza de tensión actuando en A alrededor de la
línea OB

51. Ejemplo
●Una barra doblada está rígidamente fijada a una
pared en el punto (0,0,0). Una fuerza de magnitud
F = 7 lb actúa en su extremo libre con una línea de
acción que pasa por el origen, como se muestra en
la figura: Halle : (a) el momento de la fuerza
respecto al punto P, (b) el momento respecto a la
línea l que pasa por P con una pendiente 5/12 en
el plano yz.

52. PRINCIPIO DE MOMENTOS: Teorema de Varignon
Si un sistema de fuerzas concurrentes esta actuando
sobre un cuerpo como se muestra en la figura, el
momento de la fuerza resultante alrededor del punto
puede ser determinado mediante la suma de cada
uno de los momentos de las fueras individuales
respecto al mismo punto. Es decir:

53. CUPLA O PAR DE FUERZAS
La cupla o par de fuerzas es un sistema
formado por dos fuerzas F y –F que
tiene la misma magnitud, líneas de
acción paralelas pero de sentidos
opuestos.
●El momento de la cupla es,
El vector momento de la cupla es
un vector independiente del origen
o es decir es un vector libre

54. DIRECCIÓN Y SENTIDO DEL PAR
●La cupla es un vector libre perpendicular al plano
de la cupla y su sentido se determina mediante la
regla de la mano derecha

55. CUPLA O PAR DE FUERZAS
●Dos cuplas tendrán igual
momento si:
a)
b) Las dos cuplas se encuentran
ubicadas en planos paralelos
c) La dos cuplas tienen el mismo
sentido o la misma tendencia a
causar rotación y la misma
dirección

56. Ejemplo de cupla
●Determine el momento de la cupla
mostrada en la figura y la distancia
perpendicular entre las dos fuerzas

57. Ejemplo de cupla
Dos fuerzas paralelas de sentidos opuestos
son F1 = (-70i - 120j - 80k)lbf y F2 = (70i
+120j + 80k)lbf y actúan en los puntos A y B
del cuerpo mostrado en la figura. Determine
el momento de la cupla y la distancia
perpendicular entre las dos fuerzas

58. EQUIVALENCIA ENTRE LOS PARES
Dos sistemas de fuerzas son equivalentes (es decir producen
el mismo efecto sobre un sólido) si pueden transformarse el
uno en el otro mediante una o varias de las operaciones
siguientes:
1.Sustituyendo dos fuerzas que actúan sobre la misma
partícula por su resultante;
2.Descomponiendo una fuerza en dos componentes y
3.Anulando fuerzas iguales y opuestas que actúan sobre la
misma partícula
4.Aplicando a una partícula dos fuerzas iguales y opuestas
5.Moviendo una fuerza a lo largo de su recta soporte

59. SISTEMAS FUERZA CUPLA
Cualquier fuerza F aplicada a un sólido rígido puede ser
trasladada a un punto arbitrario B, sin más que añadir
una cupla cuyo momento sea igual al momento de F
respecto de B
No hay cambio en el
efecto externo
Cupla

60. Ejemplo
Remplace la fuerza de 350 N por una fuera y una
cupla en el punto B- Exprese su respuesta en
coordenadas cartesianas

61. solución
Se trazan dos fuerzas en B
como se ve en la figura . La
expresión vectorial de F es
El momento C será

62. Ejemplo
Remplace la fuerza de 600 N mostrada en la figura
por una fuera y una par en el punto A. Exprese su
respuesta en coordenadas cartesianas

63. Ejemplo
La tensión en el cable sujeto al extremo C del botalón
ajustable ABC es de 1000 N. Sustituir la fuerza que el
cable ejerce en C por un sistema fuerza-par equivalente :
(a) en A , (b) en B

64. Ejemplo
●Una fuerza de 700 N es aplicada en el punto A
de un miembro estructural. Sustituirla por: (a) un
sistema fuerza –par equivalente en C, (b) un
sistema equivalente compuesto por una fuerza
vertical en B y una segunda fuerza en D

65. Ejemplo
La fuerza horizontal P actúa como se muestra sobre la
palanca acodada. (a) sustituir P por un sistema fuerza-
par equivalente en B. Determinar las dos fuerzas
verticales en C y D equivalentes al par hallado en la parte
(a)

66. SISTEMAS FUERZA CUPLA
Paso 1 Paso 2 Paso 3
Seleccionar un
punto para
encontrar el
momento
Remplazar las
fuerzas por una
fuerza y un par en
el punto O
Sumar las fuerza y
cuplas
vectorialmente para
encontrar la
resultarte y el
momento resultante

67. Ejemplo
Reducir el sistema de fuerzas y momentos a una
fuerza un par actuando en A