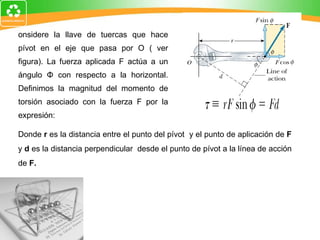
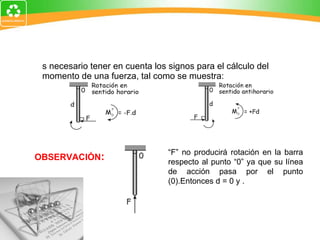
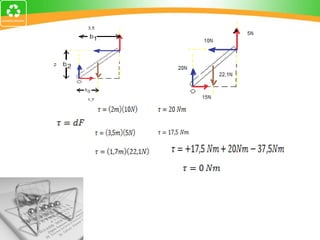
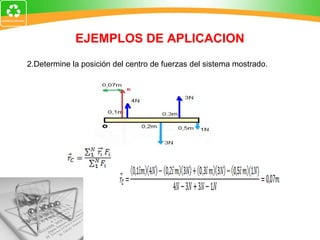
El documento resume conceptos fundamentales de la estática, incluyendo el momento de fuerza, equilibrio rotacional, centro de gravedad, teorema de Varignon, composición de fuerzas paralelas y cupla. Proporciona definiciones, fórmulas y ejemplos para ilustrar estos conceptos clave de la mecánica estática.

1. Lic. Fis. Carlos Lévano Huamaccto FISICA I

2. TORQUE O MOMENTO DE FUERZA

20. EJEMPLOS DE APLICACION 2.Determine la posición del centro de fuerzas del sistema mostrado.

21. 3.El sube y baja. Un tablón uniforme de 40N de peso soporta a dos niños que pesan uno 500N y el otro 350N , como se muestra en la figura. Si el soporte de apoyo está debajo el centro de gravedad del tablón y si la niña de 500N se encuentra a 1.5m del centro. Determine la fuerza hacia arriba n ejercida sobre el tablón por el soporte.

22. Para encontrar esta posición, debemos apelar a la segunda condición de equilibrio. Si se toma el centro de gravedad del tablón como el eje para nuestra ecuación de momento de torsión, vemos, que

29. El equilibrio es indiferente si el cuerpo siendo movido, queda en equilibrio en cualquier posición. En este caso el centro de gravedad coincide con el punto de suspensión.

30. COMPOSICION DE FUERZAS En general, un sistema de fuerzas que actúan sobre un cuerpo rígido no puede reducirse a una sola fuerza o resultante igual a la suma vectorial de las fuerzas. Cuando las fuerzas no se aplican al mismo punto sino que actúan en un cuerpo rígido, es necesario distinguir dos efectos : traslación y rotación. La traslación del cuerpo es determinada por la resultante (vector suma) de las fuerzas En este caso el punto de aplicación de R queda aún por determinarse. El efecto de rotación sobre el cuerpo está determinado por el vector suma de los torques de las fuerzas

31. CUPLA O PAR DE FUERZAS Se define como un sistema de dos fuerzas de igual magnitud pero de direcciones opuestas que actúan a lo largo de líneas paralelas.

32. Indicando que la cupla no produce efecto de traslación. Por otro lado la suma vectorial de los torque, teniendo en cuenta . donde b es el brazo de palanca de la cupla es dada por la cupla produce efecto de rotación

33. COMPOSICIÓN DE FUERZAS PARALELAS Consideremos un sistema de fuerzas paralelas a un vector unitario u . donde F i es positivo o negativo dependiendo de si la dirección de F i es la misma de u u opuesta a la de u . La suma vectorial es Y por tanto también paralelo a u. La magnitud de la resultante es entonces La suma vectorial es

34. La cual es perpendicular a u y por lo tanto también es perpendicular a R . Por este motivo, colocando R en la posición apropiada r c , es posible igualar su torque a  . Introduciendo las expresiones de R y  podemos escribir Esta ecuación se satisface si O sea, r c se denomina centro de fuerzas paralelas.

35. La ecuación vectorial se puede separar en sus tres componentes donde hemos designado por x c , y c , z c las coordenadas del punto definido por r c .

36. GRACIAS