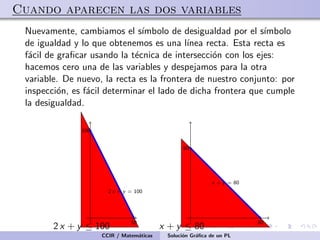
Este documento presenta el método gráfico para resolver problemas de programación lineal mediante la representación gráfica de la región factible y las curvas de nivel de la función objetivo. Se explica cómo graficar las restricciones y determinar la región factible, y luego cómo localizar el punto óptimo comparando las curvas de nivel con la región factible. Se incluyen seis ejemplos para ilustrar este método.

1. Soluci´on Gr´afica de un PL
CCIR / Matem´aticas
euresti@itesm.mx
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

2. El m´etodo gr´afico de soluci´on de problemas de programaci´on lineal
(PL) s´olo aplica a problemas con dos variables de decisi´on; sin
embargo, ilustra adecuadamente los conceptos que nos permitir´an
entender la naturaleza del problema PL y de all´ı entender los
m´etodos de soluci´on algebraicos.
Primeramente graficaremos la regi´on factible. Despu´es ilustraremos
el comportamiento de funciones lineales para entender c´omo
determinar los puntos ´optimos.
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

3. Ejemplo 1
Suponga que se desea resolver el problema PL:
Max z = 3 x + 2 y
sujeto a
2 x + y ≤ 100 R5
x + y ≤ 80 R4
x ≤ 40 R3
x ≥ 0 R1
y ≥ 0 R2
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

4. Nuestra primera meta es graficar en el plano la regi´on factible; es
decir, graficar la totalidad de puntos del plano que satisfacen las
restricciones. Notemos que las restricciones se deben cumplir
simult´aneamente. Es decir, que los puntos deben cumplir la
restricci´on R1, la restricci´on R2, y as´ı sucesivamente hasta la
restricci´on R5. Desde el punto de vista de teor´ıa b´asica de
conjuntos, la regi´on factible es la intersecci´on de los conjuntos que
satisfacen por separado cada una de las restricciones. Para avanzar
en nuestra meta, debemos saber c´omo determinar los puntos del
plano que satisfacen una desigualdad lineal. Distinguimos dos
casos:
cuando en la desigualdad s´olo aparece una variable de decisi´on
(es decir, la otra variable tiene coeficiente cero)
cuando en la desigualdad aparecen las dos variables de
decisi´on (es decir, ambas tienen coeficientes diferentes de cero
en tal desigualdad)
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

5. Cuando s´olo aparece una variable
En este caso, cuando cambiamos el s´ımbolo de desigualdad por el
s´ımbolo de igualdad lo que obtenemos es el conjunto frontera del
conjunto de puntos que cumple la desigualdad. En este caso, dicha
frontera es una l´ınea horizontal o vertical: por inspecci´on, es f´acil
determinar el lado de dicha frontera que cumple la desigualdad.
x = 0
x ≥ 0
y = 0
y ≥ 0
x = 40
x ≤ 40
40
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

6. Cuando aparecen las dos variables
Nuevamente, cambiamos el s´ımbolo de desigualdad por el s´ımbolo
de igualdad y lo que obtenemos es una l´ınea recta. Esta recta es
f´acil de graficar usando la t´ecnica de intersecci´on con los ejes:
hacemos cero una de las variables y despejamos para la otra
variable. De nuevo, la recta es la frontera de nuestro conjunto: por
inspecci´on, es f´acil determinar el lado de dicha frontera que cumple
la desigualdad.
2 x + y = 100
2 x + y ≤ 100
100
50
x + y = 80
x + y ≤ 80
80
80
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

7. Regi´on factible
Se forma haciendo una intersecci´on de los conjuntos de puntos que
hemos encontrado (El punto S(20, 60) se determina resolviendo el
sistema 2 x + y = 100 y x + y = 80; el punto R(20, 60) se
determina resolviendo el sistema 2 x + y = 100 y x = 40).
P(0, 0) Q(40, 0)
R(40, 20)
S(20, 60)
T(0, 80)
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

8. Crecimiento de z = 3 x + 2 y
De momento, nos olvidamos de la regi´on factible y vemos en qu´e
direcci´on crece la funci´on z: siendo el gradiente de la funci´on
z =< ∂z
∂x = 3, ∂z
∂y = 2 > determinamos que en tal direcci´on crece
z; direcciones perpendiculares a z (< 2, −3 >) dan las curvas de
nivel.
z
z = 0
z = 30
z = 60
z = 90
z = 120
z = 150
z = 180
z = 210
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

9. Localizaci´on del ´Optimo
Ahora graficamos las curvas de nivel de z encima de la regi´on
factible y determinamos aquel punto de la regi´on factible que
queda en la curva de nivel de mayor valor (caso de maximizaci´on).
z = 0
z = 30
z = 60
z = 90
z = 120
z = 150
z = 180
z = 210
z
P(0, 0) Q(40, 0)
R(40, 20)
S(20, 60), ´optimo con z = 180
T(0, 80)
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

10. Ejemplo 2
Se desea resolver el problema PL:
Min z = 4 x − y
sujeto a
−2 x + 3 y ≤ 90
3 x + 5 y ≤ 245
2 x + 2 y ≥ 40
x ≤ 40
x ≥ 0
y ≥ 0
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

11. Regi´on factible
Convertimos cada desigualdad en igualdad; trazamos las rectas
correspondientes buscando intersecciones y determinamos por
inspecci´on el lado de la recta que cumple la desigualdad.
P(20, 0) Q(40, 0)
R(40, 25)
S(15, 40)
T(0, 30)
U(0, 20)
X(81.6, 0)
Y (0, 49)
Z(−45, 0) O
x ≤ 40
3 x + 5 y ≤ 245
−2 x + 3 y ≤ 90
2 x + 2 y ≥ 40
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

12. Localizaci´on del ´optimo
En este caso el problema es de minimizaci´on; as´ı, en la direcci´on
opuesta al gradiente la funci´on se minimiza. Para determinar el
´optimo, debemos buscar la curva de nivel en la direcci´on opuesta al
gradiente de menor valor que toca a la regi´on factible.
P(20, 0) Q(40, 0)
R(40, 25)
S(15, 40)
T(0, 30)
U(0, 20)
O
z
z = −60
z = −30
z = 0
z = 30
z = 60
z = 90
z = 120
z = 150
z = 180
z = 210
M´ınimo con z = −30
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

13. Ejemplo 3
Suponga que se desea resolver el problema PL:
Max z = 2 x + y
sujeto a
2 x + y ≤ 100 R5
x + y ≤ 80 R4
x ≤ 40 R3
x ≥ 0 R1
y ≥ 0 R2
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

14. Regi´on factible
En este ejemplo, la regi´on factible es la misma que en el ejemplo 1.
Pero ha cambiando la funci´on objetivo; el gradiente es
z =< 2, 1 > y las curvas de nivel son tales que son paralelas a
uno de los lados de la regi´on factible. Y esa curva es la de mayor
valor en el problema de maximizaci´on. Por tanto, habr´a infinitas
soluciones: todos los puntos del segmento ¯SR son m´aximos.
P(0, 0) Q(40, 0)
R(40, 20)
S(20, 60)
T(0, 80)
z
z = 0
z = 20
z = 40
z = 60
z = 80
z = 100
z = 120
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

15. Ejemplo 4
Se desea resolver el problema PL:
Max z = x + y
sujeto a
6 x + 5 y ≥ 300
20 x + 20 y ≤ 100
y ≥ 30
x ≥ 0
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

16. Regi´on factible
Convertimos cada desigualdad en igualdad; trazamos las rectas
correspondientes buscando intersecciones y determinamos por
inspecci´on el lado de la recta que cumple la desigualdad. En este
ejemplo la regi´on factible es vac´ıa: no hay valores de x y de y
que satisfagan simult´aneamente todas las restricciones.
P(50, 0)
Q(0, 50)
R(0, 60)
T(0, 30)
O
y ≥ 30
6 x + 5 y ≥ 300
20 x + 20 y ≤ 100
x ≥ 0
x
y
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

17. Ejemplo 5
Se desea resolver el problema PL:
Max z = −3 x + y
sujeto a
−4 x + 3 y ≤ 60
2 x + 3 y ≥ 30
x − y ≤ 20
x ≥ 0
y ≥ 0
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

18. Regi´on factible
Convertimos cada desigualdad en igualdad; trazamos las rectas
correspondientes buscando intersecciones y determinamos por
inspecci´on el lado de la recta que cumple la desigualdad. En este
ejemplo la regi´on factible es infinita: se extiende
indefinidamente entre dos rectas que se abren.
P(20, 0)Q(15, 0)
R(0, 10)
T(0, 20)
O
x − y ≤ 20
2 x + 3 y ≥ 30
−4 x + 3 y ≤ 60
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

19. Obtenci´on del ´optimo
A pesar que la regi´on factible es no acotada, el gradiente crece en
una direcci´on hacia donde la regi´on est´a acotada: por tanto, el
´optimo existe y est´a en el punto T(0, 20).
P(20, 0)Q(15, 0)
R(0, 10)
T(0, 20)
O
z = −60
z = −40
z = −20
z = 0
z = 20
z = 40
z = 60
z = 80
z
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

20. Ejemplo 6
Se desea resolver el problema PL:
Max z = 3 x − y
sujeto a
−4 x + 3 y ≤ 60
2 x + 3 y ≥ 30
x − y ≤ 20
x ≥ 0
y ≥ 0
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

21. Obtenci´on del ´optimo
Este problema tiene la misma regi´on factible que el problema
previo pero la funci´on crece en direcci´on opuesta entonces es
posible encontrar puntos sobre la frontera x − y = 20 con
evaluaci´on cada vez mayor. El problema no tiene m´aximo; el valor
de la funci´on no es acotado.
P(20, 0)Q(15, 0)
R(0, 10)
T(0, 20)
Oz = −60
z = −40
z = −20
z = 0
z = 20 z
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

22. Aprendizajes?
Sobre la regi´on factible:
puede ser vac´ıa (ejemplo 4), acotada (ejemplos 1,2 y 3) o
infinita (ejemplos 5 y 6).
cuando no es vac´ıa. . .
es faceteada: sus caras son realizadas por cortes rectos;
por ello es que es convexa, es decir, no tiene partes sumidas;
por ello es que para dos puntos en la regi´on factible, el
segmento que los une est´a totalmente dentro de la regi´on
factible.
cuando es acotada y no vac´ıa. . .
los puntos extremos la definen completamente.
CCIR / Matem´aticas Soluci´on Gr´afica de un PL

23. Aprendizajes?
Una funci´on lineal definida sobre un segmento de recta se
convierte en una funci´on lineal en una variable; y por lo tanto,
toma sus valores m´aximos o m´ınimos en los extremos del
intervalo (a´un en el caso que sea constante la funci´on).
Al optimizar un PL que tiene regi´on factible acotada y no
vac´ıa, los valores m´aximos y m´ınimos los toma en un punto
extremo de la regi´on factible (en una esquina del poliedro que
es la regi´on factible).
Al optimizar un PL que tiene regi´on factible no acotada
pueden ocurrir dos posibilidades:
que el m´aximo o el m´ınimo lo tome en un punto extremo ´o
que el problema no sea acotado: es decir, que no es posible
encontrar un valor ´optimo porque siempre es posible encontrar
un punto en la regi´on factible con una evaluaci´on mejor.
CCIR / Matem´aticas Soluci´on Gr´afica de un PL