1. El documento habla sobre el primer principio de la termodinámica y conceptos relacionados como energía interna, trabajo, calor y cambios de estado. 2. Explica que la energía total se conserva y que el trabajo y el calor son formas de transferir energía entre un sistema y su entorno. 3. Define conceptos como energía interna, entalpía y capacidad calorífica, y establece las relaciones entre cambios en estas propiedades termodinámicas durante procesos y transferencias de trabajo y calor.


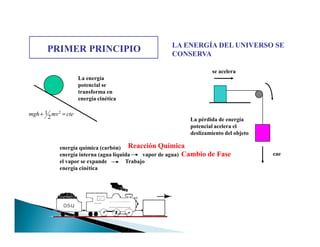
![PRIMER PRINCIPIO LA ENERGÍA DEL UNIVERSO SE
CONSERVA
Es imposible realizar un trabajo sin consumir una energía
.
uff, uff
Fuerza
2X
X
W Fdx= ∫
W=F x
Trabajo realizado
por el hombre
Fuerza aplicada
Distancia que
se desplaza
el objeto Fuerza
distanciaX1 X2
1X∫
Trabajo=área
[N.m=J]
Energía = Capacidad para realizar un trabajo](https://image.slidesharecdn.com/tema1-primerprincipio-101031170337-phpapp02/85/Primera-Ley-Diapositivas-3-320.jpg)
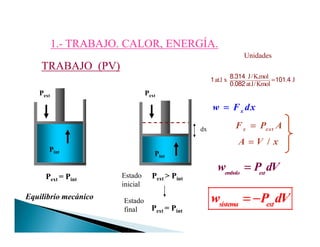
![( ) 0W P V V= − − <
TRABAJO (PV) Expansión-(Compresión)
Pext
dx
P 1Pext
2
P’
• Frente a Pext=P2 constante
2
1
V
extV
W P dV= −∫
2 2 1
( ) 0W P V V= − − <
Pext < Pint
Pint
Estado Inicial
1
VPint
Pext = Pint
Estado Final
2
[ ]1 2 2
'( ' ) ( ')W P V V P V V= − − + −
2 etapas
V’](https://image.slidesharecdn.com/tema1-primerprincipio-101031170337-phpapp02/85/Primera-Ley-Diapositivas-6-320.jpg)






![La energía es la capacidad para hacer un trabajo
1.1.-- TRABAJO. CALOR, ENERGÍA.TRABAJO. CALOR, ENERGÍA.
ENERGÍAENERGÍA
E = U+ E
E debida a la posición del sistema en un campo de
fuerzas (gravitacional, eléctrico, magnético) y a su
movimiento en conjunto: Eotras
Esistema= U+ Eotras
Energía Interna, U
característica del sistema (Et, Er, Ev de moléculas)
depende del estado de agregación del sistema
La energía es una función de estado
La energía es una propiedad extensiva
Unidades: Julio (J)
( , , )U f T P V≡≡≡≡
[[[[ ]]]]/J mol
U
U
n
====Puedo definir una propiedad intensiva](https://image.slidesharecdn.com/tema1-primerprincipio-101031170337-phpapp02/85/Primera-Ley-Diapositivas-14-320.jpg)




![Proceso a P = cte
3.3.-- ENTALPÍA.ENTALPÍA.
1º Principio ∆U=Q+W
2
V
U Q W Q P dV∆ = + = −∫
2
( )
V
Q P dV Q P V V= − = − −∫
2 2 1 1
( ) ( )P
Q U PV U PV= + − += + − += + − += + − +
H ≡≡≡≡ U + PV Entalpía
(H)
• Función de estado H≡≡≡≡f(T,P,V,U)
• Propiedad extensiva
• Unidades de energía (J)
• [ / ]
H
H J mol
n
≡≡≡≡
v
2
1
extV
U Q W Q P dV∆ = + = −∫ 1
2 1
( )ext VP PQ P dV Q P V V= − = − −∫
P=cte
H2 H1
= ∆∆∆∆HQP
∆U=U2-U1
•Nos da una forma de determinar ∆H](https://image.slidesharecdn.com/tema1-primerprincipio-101031170337-phpapp02/85/Primera-Ley-Diapositivas-19-320.jpg)

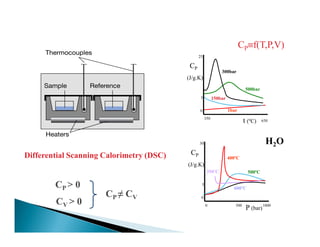
![4.4.-- CAPACIDAD CALORÍFICA.CAPACIDAD CALORÍFICA.
( , , ) 2 1( )T P VQ mC T T= −= −= −= −
2 1
lim
T T
Q q
C
T dT→→→→
≡ =≡ =≡ =≡ =
∆∆∆∆
El Q se definió como la energía trasferida
como consecuencia de una diferencia de T
Capacidad Calorífica
•si no hay cambio de fase
•ni reacción química
Capacidad calorífica de una sustancia: cantidad infinitesimal de calor
necesaria para elevar su T en una cantidad dT . [J⋅K-1]
• Depende de la naturaleza de la propia sustancia
• Puesto que Q depende de la trayectoria del cambio de estado,
para definir C hay que definir la trayectoria](https://image.slidesharecdn.com/tema1-primerprincipio-101031170337-phpapp02/85/Primera-Ley-Diapositivas-21-320.jpg)
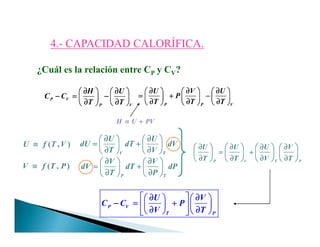
![4.4.-- CAPACIDAD CALORÍFICA.CAPACIDAD CALORÍFICA.
Puesto que Q = ∆U y Q = ∆H
Capacidad calorífica molar de una sustancia: cantidad de calor necesaria
para elevar la T de un mol de dicha sustancia un grado.
Calor específico de una sustancia: cantidad de calor necesaria para elevar la T
de un gramo de dicha sustancia un grado. [J⋅g-1⋅K-1]
[[[[ ]]]]/ .C J K mol≡≡≡≡
p
v
v
1 1
n n
1 1
n T n
P
P
V
q H
C
dT T
q U
C
d T
∂
= =
∂
∂
= =
∂
Capacidad calorífica molar a P cte
Capacidad calorífica molar a V cte
Puesto que QV = ∆U y QP = ∆H
en un sistema cerrado, en equilibrio o proceso reversible y sólo W(P-V) es
posible definir :
U,H≡f(T,P,V)
∂∂∂∂
∂∂∂∂
p. Intensivas
f=(T,P,V)](https://image.slidesharecdn.com/tema1-primerprincipio-101031170337-phpapp02/85/Primera-Ley-Diapositivas-22-320.jpg)