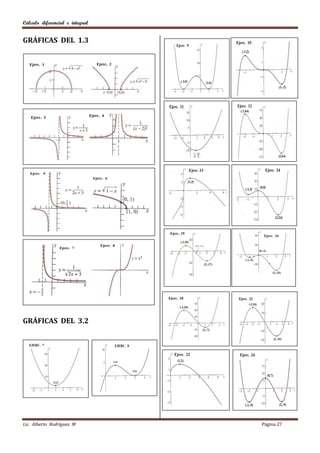
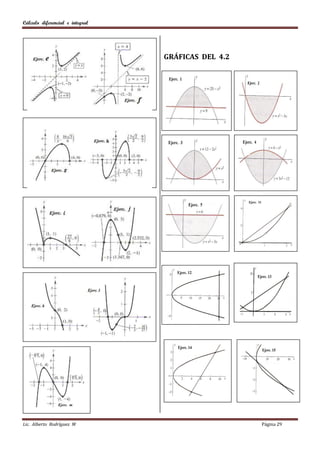
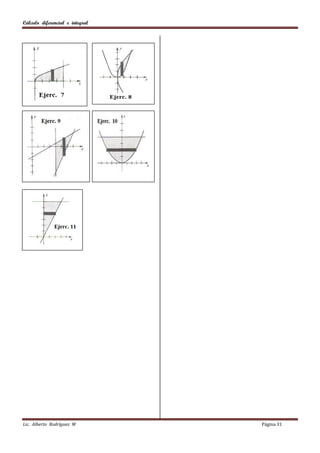
Este documento presenta problemas de cálculo diferencial e integral. En la primera sección, se pide encontrar el conjunto solución para 60 desigualdades. La segunda sección solicita determinar el dominio y la imagen para 21 funciones. Finalmente, la tercera sección pide graficar 10 funciones determinando su dominio e imagen.