El documento presenta un examen parcial de cálculo vectorial que consta de 3 preguntas. La primera pregunta solicita calcular el volumen de un sólido limitado por planos. La segunda pregunta pide calcular el volumen de otro sólido limitado por planos y un cilindro. La tercera pregunta requiere enumerar las seis posibles órdenes de integración para calcular el volumen de un sólido limitado por planos y una superficie cilíndrica.

1. UNIVERSIDAD SANTO TOMAS
´
DEPARTAMENTO DE CIENCIAS BASICAS
´
AREA DE MATEMATICAS
´
CALCULO VECTORIAL
PARCIAL IV
Nombre: C´digo:
o
Fecha: Grupo:
Lea cuidadosamente toda la prueba antes de comenzar a resolver. La prueba tiene una duraci´n de 1 hora 30 minutos.
o
Para las preguntas de selecci´n unica. Seleccione la respuesta correcta marc´ndola con esfero. Si la respuesta seleccionada
o ´ a
es correcta y es sustentada con un proceso adecuado el valor es de 1. Si la respuesta seleccionada es correcta y NO es
sustentada completamente con procesos que lleven a ella el valor es de 0,5. Si la respuesta seleccionada es correcta y NO
es sustentada el valor es de 0. Si la respuesta seleccionada es incorrecta y tiene un proceso adecuado el valor es de 0,5.
Si la respuesta seleccionada es incorrecta el valor es 0. El valor de cada enunciado aparece en negrilla y encerrado por [
]. No se permite el intercambio de objetos.
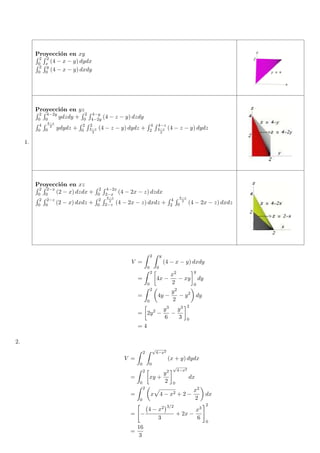
1. [1] El volumen del s´lido limitado por los planos y = x, y = 2, z = 0, x = 0
o
y z = 4 − x − y,es: (gr´fique la proyecci´n del s´lido con la que va a trabajar)
a o o
4
a) 6 b) 3 c) 4 d) 3
2. [1] El volumen del s´lido limitado por los planos x = 0,y = 0,z = 0,z = x+y
o
y el cilindro circular x2 + y 2 = 4 es:
8 20 16 14
a) 3 b) 3 c) 3 d) 3
3. [3] Dar los seis posibles ´rdenes de integraci´n para encontrar el volumen
o o
del s´lido limitado por los planos y = 0,x = 0, z = 0, z = 1 − y y el cilindro
o
x = 1 − y2.

2. Proyecci´n en xy
o
2 2
0 x (4 − x − y) dydx
2 y
0 0 (4 − x − y) dxdy
Proyecci´n en yz
o
2 4−2y 2 4−y
0 0 ydzdy + 0 4−2y (4 − z − y) dzdy
4−z
4 2 2 4 4−z
0 0
2
ydydz + 0 4−z (4 − z − y) dydz + 2 4−z (4 − z − y) dydz
2 2
1.
Proyecci´n en xz
o
2 2−x 2 4−2x
0 0 (2 − x) dzdx + 0 2−x (4 − 2x − z) dzdx
4−z 4−z
2 2−z 2 4
0 0 (2 − x) dxdz + 0 2−z (4 − 2x − z) dxdz + 2 0
2 2
(4 − 2x − z) dxdz
2 y
V = (4 − x − y) dxdy
0 0
2 y
x2
= 4x − − xy dy
0 2 0
2
y2
= 4y − − y 2 dy
0 2
2
y3 y3 2
= 2y − −
6 3 0
=4
2.
√
2 4−x2
V = (x + y) dydx
0 0
√
2 4−x2
y2
= xy + dx
0 2 0
2
x2
= x 4 − x2 + 2 − dx
0 2
3/2 2
4 − x2 x3
= − + 2x −
3 6
0
16
=
3

3. Proyecci´n en xy
√ o
1 1−x 1−y
0 0 0 dzdydx
1 1−y 2 1−y
0 0 0 dzdxdy
Proyecci´n en yz
o
1 1−y 1−y 2
0 0 0 dxdzdy
3. 1 1−z 1−y 2
0 0 0 dxdydz
Proyecci´n en xz
√ o √
1 1− 1−x 1−x 1 1 √ 1−z
0 0 0 dydzdx + 0 1− 1−x 0 (4 − z − y) dydzdx
√
1 1−(1−z)2 1−z 1 1 1−x
0 0 0 dydxdz + 0 1−(1−z)2 0 dydxdz