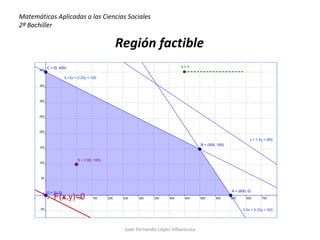
Una empresa fabrica dos modelos de guantes y desea maximizar sus beneficios sujeto a restricciones en las horas disponibles en sus departamentos de corte y costura, terminado y empaquetado. La solución óptima es fabricar 500 pares del modelo normal y 150 pares del modelo de lujo, obteniendo un beneficio máximo de 3,200 euros.

1. Programación lineal Matemáticas aplicadas a las Ciencias Sociales 2º Bachiller Juan Fernando López Villaescusa

2. Una empresa fabrica dos modelos de guantes: un modelo normal y un modelo de lujo. La empresa tiene 900 horas disponibles en su departamento de corte y costura, 300 horas en el departamento de terminado y 100 horas disponibles en el departamento de empaquetado. Las horas necesarias de cada departamento por par de guantes y sus beneficios, en euros, se dan en la siguiente tabla: ¿Cuántos pares de cada modelo debe fabricar para maximizar el beneficio? Problema de optimización Juan Fernando López Villaescusa Matemáticas Aplicadas a las Ciencias Sociales 2ª Bachiller Corte y costura Terminado Empaquetado Beneficios Normal 1 1/2 1/8 4 De lujo 3/2 1/3 1/4 8

3. Análisis de los datos Juan Fernando López Villaescusa Matemáticas Aplicadas a las Ciencias Sociales 2ª Bachiller El Beneficio es F(x,y) = 4 x + 8 y en euros. Normal De lujo Horas Nº pares guantes x y Corte y costura (h) 1 3/2 ≤ 900 Terminado (h) 1/2 1/3 ≤ 300 Empaquetado (h) 1/8 1/4 ≤ 100 Beneficio(€) 4 8 Min

4. F(x,y) = 4 x + 8 y Función objetivo Región factible Planteamiento del problema Averiguar para qué valores de x e y la expresión Se hace máxima , sujeto a las siguientes restricciones: Juan Fernando López Villaescusa Matemáticas Aplicadas a las Ciencias Sociales 2ª Bachiller

5. Región factible Juan Fernando López Villaescusa Matemáticas Aplicadas a las Ciencias Sociales 2ª Bachiller

6. Juan Fernando López Villaescusa Matemáticas Aplicadas a las Ciencias Sociales 2ª Bachiller Solución del problema

7. Solución del problema el valor máximo se alcanza en el segmento BC B=(500,150) y C=(0,400) El número de pares de guantes es entero. La solución es: x pares de guantes del modelo normal, siendo 0≤x≤500 y pares de guantes del modelo de lujo, siendo Con un beneficio máximo de 3.200 € Juan Fernando López Villaescusa Matemáticas Aplicadas a las Ciencias Sociales 2ª Bachiller