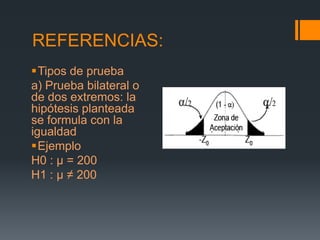
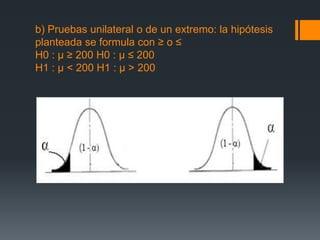
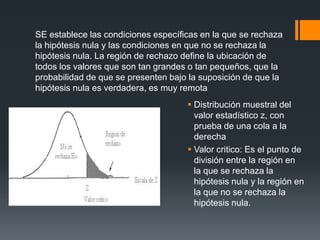
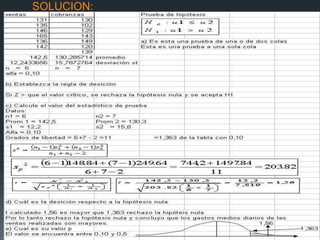
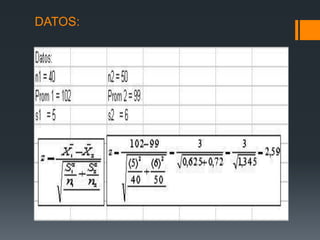
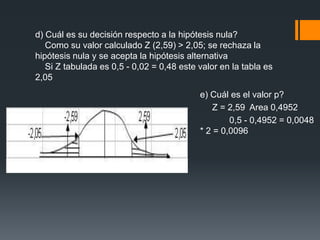
Este documento presenta diferentes problemas sobre pruebas de hipótesis, incluyendo definiciones de pruebas unilaterales y bilaterales, cómo calcular los valores estadísticos z y t, y cómo establecer regiones de rechazo. Luego, proporciona ejemplos numéricos y sus soluciones sobre temas como comparar medias poblacionales, proporciones y el tiempo que pasan juntos diferentes tipos de parejas.