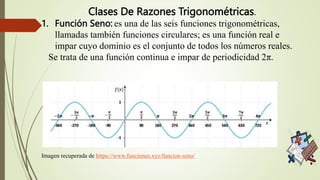
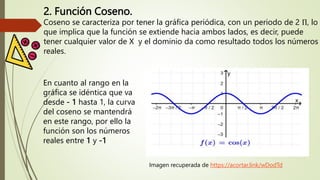
Este documento presenta información sobre la Unidad 2 de pensamiento variacional y trigonométrico. Explica definiciones clave como las funciones trigonométricas, relaciones trigonométricas y clases de razones trigonométricas. También cubre temas como identidades trigonométricas básicas, ejemplos de resolución de problemas trigonométricos y recomendaciones para resolver ecuaciones trigonométricas.

1. unidad 2:
Pensamiento
variacional y
trigonométrico.

2. Paso 3-Profundizar y contextualizar el conocimiento
de la Unidad 2.
Yeimi Rureli Acosta Gaviria
Grupo: 27
Algebra, Trigonometría y Geometría Analítica,
Código: 551108
Licenciatura en matemáticas

3. INTRODUCCIÓN
A continuación se dan a conocer temas acerca de unidad dos “Pensamiento
variacional y trigonométrico” donde se centra principalmente en las razones
trigonométricas y algunas identidades, las cuales son de vital importancia para dar la
correcta resolución a los ejercicios y operaciones que como futuros docentes debe
conocer.

4. 1. Definición de las Funciones Trigonométricas
Las razones trigonométricas son relaciones entre los lados de un triángulo,
sirven para determinar los elementos desconocidos en base a los que se
conocen, es así como a través de la trigonométrica se calcula valores o
medidas de precisión.
Haciendo una revisión socio-epistemológica, Buendía y Montiel (2008)
afirma que para Euler anteriormente el seno y coseno eran el objeto de
estudio, fueron las nuevas cantidades trigonométricas que llevaron a
considerarse líneas de un círculo, puesto que ayudan a desarrollar y describir
tareas específicas. Buendía y Montiel (2008)

5. Las razones trigo-métricas se pueden aplicar solo a los triángulos rectángulos
porque estos cumplen con unos criterios como:

6. Relaciones Trigonométricas.
A continuación se definen las siguientes relaciones trigonométricas
Relaciones principales
𝛿ⅇ𝑛(𝜃) =
𝑦
ℎ
Cos(𝜃) =
𝑥
ℎ
tan(𝜃) =
𝑦
𝑥
Relaciones Complementarias.
Csc (𝜃) =
ℎ
𝑦
Sec(𝜃) =
ℎ
𝑥
Cot(𝜃) =
𝑥
𝑦

7. Funciones Trigonométricas.
• Seno y su inversa
• La cosecante.
• Coseno y su inversa,
• la secante;
• Tangente y su inversa,
• La cotangente.

8. Clases De Razones Trigonométricas.
1. Función Seno: es una de las seis funciones trigonométricas,
llamadas también funciones circulares; es una función real e
impar cuyo dominio es el conjunto de todos los números reales.
Se trata de una función continua e impar de periodicidad 2π.
Imagen recuperada de https://www.funciones.xyz/funcion-seno/

9. 2. Función Coseno.
Coseno se caracteriza por tener la gráfica periódica, con un periodo de 2 Π, lo
que implica que la función se extiende hacia ambos lados, es decir, puede
tener cualquier valor de X y el dominio da como resultado todos los números
reales.
Imagen recuperada de https://acortar.link/wDodTd
En cuanto al rango en la
gráfica se idéntica que va
desde - 1 hasta 1, la curva
del coseno se mantendrá
en este rango, por ello la
función son los números
reales entre 1 y -1

10. 3. Función Tangente
Relación entre la hipotenusa, catetos y ángulos de un triángulo rectángulo.
Imagen recuperada de https://acortar.link/n1QUJF
Relación entre la hipotenusa,
catetos y ángulos de un triángulo
rectángulo. La función tangente
es una curva en un punto P, es
una recta que toca a la curva Solo
en dicho punto, el cual se le
conoce como tangencia

11. Funciones Complementarias.
Recuperada dedeRondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá D.C.: Universidad Nacional Abierta y a
Distancia. Páginas 237 - 265. https://acortar.link/797u7k

12. Ejemplo Razones
Trigonométricas.
Calcula las razones trigonométricas
seno, coseno y tangente de los
ángulos agudos (A y B) del triangulo
triangulo rectángulo.
Solución
Hallar el lado faltante mediante el teorema de Pitágoras.
𝑐2 = 𝑎2 + 𝑏2
𝑎2 = 𝑐2 − 𝑏2
𝑎2 = 4.52 − 42 = 4.25
𝑎 = 2.06
Resolver las propiedades trigonométricas con los valores
correspondientes del triangulo.
sin α =
𝑐𝑜
ℎ
=
𝑎
𝑐
= 0.45
cos α =
𝑐𝑎
ℎ
=
𝑏
𝑐
= 0.88
tan α =
𝑐𝑜
𝑐𝑎
=
𝑎
𝑐
= 0.51
sin β =
𝑐𝑜
ℎ
=
𝑏
𝑐
= 0.88
cos β =
𝑐𝑎
ℎ
=
𝑎
𝑐
= 0.45
tan β =
𝑐𝑜
𝑐𝑎
=
𝑏
𝑎
= 1.94

13. Para conocer qué es una identidad trigonométrica es necesario
conocer:
• Ecuación: se le conoce como una igualdad entre dos expresiones
que contienen una o más variables
• Identidad: Es una ecuación que es válida para todos los valores
la variable
• Ahora bien, que una Identidad trigonométrica, es una identidad
en la que se presentan funciones trigonométricas y se verifican
para cualquier valor del ángulo.
Identidades Trigonométricas.

14. Ejemplo:
s𝒆n 𝑎 → cos 𝑎
𝒔𝒆𝒏(4𝟓0) = 𝒄𝒐𝒔 (4𝟓0)
2
2
=
2
2
𝑻𝒂𝒏 𝑨 =
sin 𝑨
cos 𝑨
𝑻𝒂𝒏 800 =
sin 800
cos 800
30
3
=
30
3
Para que sea una identidad trigonométrica debe comprobarse con
todos los ángulos
Una identidad
contiene
solamente una
variable, en este
caso A

15. Existen las siguientes identidades básicas:
• Identidad Fundamental
• Identidades de Cociente
• Identidades Recíprocas
• Identidades Pitagóricas
• Identidades Pares – Impares
• Identidades de Cofunción
• Identidades Inversas
• IDENTIDADES DE SUMA Y DIFERENCIA
• IDENTIDADES DE ÁNGULO DOBLE
• IDENTIDADES DE ÁNGULO MITAD
• IDENTIDADES DE PRODUCTO – SUMA.
A continuación se darán a conocer las identidades básicas dentro de la trigonometría

16. Identidades Básicas.
Según Rondón, J. (2017), clasifica las entidades de la siguiente manera:
1. Identidad Fundamental: Partiendo del teorema de Pitágoras, la relación de los lados del
triángulo y el círculo trigonométrico, se puede obtener dicha identidad
Ejemplo:
𝑠ⅇ𝑛2
𝑥 + 𝑐𝑜𝑠2
(x)=1
Demostración : a partir del circulo trigonométrico unitario.
Recuperado de Rondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá D.C.: Universidad Nacional Abierta y a Distancia. Páginas 237 - 265.

17. 2. Identidades de Cociente:
Rondón, J. (2017) define las identidades trigonométricas así: “ se obtienen por la definición de las
relaciones trigonométricas” es decir se relaciona la tangente de un ángulo con el seno del ángulo
dividido por el coseno del ángulo
Ejemplo
Recuperado deRondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá D.C.: Universidad Nacional Abierta y a
Distancia. Páginas 237 - 265. https://acortar.link/797u7k

18. Ejemplo
Recuperado deRondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá D.C.: Universidad Nacional Abierta y a Distancia. Páginas 237 - 265.
https://acortar.link/797u7k

19. 3. Identidades Recíprocas:
Según Rondón, J. (2017) se les llama de esta manera debido a que a partir de la
definición, al aplicar el recíproco, se obtiene nuevos cocientes.
A continuación están las 8 identidades reciprocas:
𝒔𝒊𝒏 𝑎
𝒄𝒐𝒔 𝑎
𝒕𝒂𝒏 𝑎
𝒄𝒐𝒕 𝑎
s𝒆𝒄 𝑎
𝒄𝒔𝒕 𝑎
𝛿𝒆𝒏 𝒂 =
1
𝑐𝑠𝒄 𝑎
𝒄𝒐𝒔 𝒂 =
1
𝒔𝒆𝒄 𝑎
𝒕𝒂𝒏 𝒂 =
1
𝑐𝒐𝒕 𝑎
𝒄𝒐𝒕 𝒂 =
1
𝒕𝒂𝒏 𝑎
𝛿𝒆𝒄 𝒂 =
1
𝑐𝒐𝒔 𝑎
𝒄𝒔𝒄 𝒂 =
1
𝒔𝒆𝒏 𝑎
𝒕𝒂𝒏 𝒂 =
𝒔𝒆𝒏 𝒂
𝑐𝒐𝒔 𝑎
𝒄𝒐𝒕 𝒂 =
𝒄𝒐𝒔 𝒂
𝒔𝒆𝒏 𝑎

20.  Identidades Recíprocas:
Demostración:
cos 𝐵 =
𝐶𝑜𝑠 𝐵
𝑠ⅇ𝑛 𝐵
cos 𝐵
𝑠𝑒𝑛 𝐵
=
𝑐𝑎
ℎ
𝑐𝑜
ℎ
=
𝑐𝑎∗ℎ
ℎ∗𝑐𝑜
=
𝑐𝑎
𝑐𝑜
= Cot B
Recuperado deRondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá D.C.: Universidad Nacional Abierta y a Distancia. Páginas
237 - 265. https://acortar.link/797u7k

21. 4. Identidades Pitagóricas.
Las identidades trigonométricas pitagóricos se Dan a partir de la implementación del teorema
de Pitágoras. En este caso son tres identidades en total las cuales se cumplen para cualquier
valor del ángulo. Según Rondón, J. (2017) a partir de la identidad fundamental y las identidades
de cociente, se obtienen otras identidades llamadas pitagóricas.
Identidades Pitagóricas:
• 1 = 𝑠ⅇ𝑛2
𝜃 + cos2
𝜃
• 1 − 𝑠ⅇ𝑛2
𝜃 = cos2
𝜃
• 1 − 𝑐𝑜𝑠2
𝜃 + 𝑠ⅇ𝑛2
𝜃
• c𝑠𝑐2
𝜃 = 1 + co𝑡2
𝜃
• c𝑠𝑐2
𝜃 − 1 = co𝑡2
𝜃
• 𝑠ⅇ𝑐2
𝜃 = 𝑡𝑎𝑛2
𝜃 + 1
• 𝑠ⅇ𝑐2𝜃 − 1 = 𝑡𝑎𝑛2𝜃

22. 5. Identidades Pares - Impares:
Cuando se definió la simetría de las funciones trigonométricas, se hizo referencia a las
funciones pares e impares, de este hecho se obtiene las funciones pares e impares.
Recuperado de Rondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá D.C.: Universidad Nacional Abierta y a Distancia. Páginas
237 - 265. https://acortar.link/797u7k

23. 6. IDENTIDADES DE SUMA Y DIFERENCIA:
De acuerdo con Rondón, J. (2017). “En muchas ocasiones, un ángulo dado se
puede expresar como suma o diferencia de ángulo notables, por ejemplo
15 0 se puede expresar como (45 0 – 30 0), 75 0 como (30 0 + 45 0) y así
con otros”. Es decir que son fórmulas que me sirven para hallar ángulos no
especiales o notables sin usar las funciones trigonométricas.
Formulas para esta identidad:

24. Cómo Aplico Las Anteriores Formulas En Identidades De
Suma Y Diferencia:
Ejemplo:
Hallar sen de 105° utilizando ángulos notables.
Sen, (45° + 60°) = sen45° ∗ cos 60° + cos 45° ∗ sen 60°
=
2
2
⋅
1
2
+
2
2
⋅
3
2
=
2
4
+
6
4
=
2+ 6
4

25. Ejercicio 1:
Expresar en términos de sen 𝑎 y cos 𝑎
cos 𝑎 ⋅ tan 𝑎
=
cos 𝑎
1
⋅
𝑠ⅇ𝑛 𝑎
cos 𝑎
=
cos 𝑎 ∗ 𝑠ⅇ𝑛 𝑎
cos 𝑎
= 𝑠ⅇ𝑛 𝑎
Ejercicio 2:
Expresar en términos de sen 𝑎 y cos 𝑎
tan 𝑎
𝑠ⅇ𝑛 𝑎
𝛿ⅇ𝑛 𝑎
cos 𝑎
𝑠ⅇ𝑛 𝑎
1
𝑠𝑒𝑛 𝑎
cos 𝑎 ∗𝑠𝑒𝑛 𝑎
=
1
𝑐𝑜𝑠 𝑎

26. Recomendaciones según Rondón, J. (2017).
• “La resolución de ecuaciones trigonométricas requiere de un buen manejo
de las funciones trigonométricas inversas; además, de los principios de
álgebra y trigonometría”. Rondón, J. (2017).
• “Para que la ecuación sea más fácil de desarrollar, es pertinente reducir
toda la expresión a una sola función, generalmente seno o coseno, de tal
manera que se pueda obtener el ángulo o los ángulos solución. Es
importante aclarar que si no se dice otra cosa, la solución para nuestro
caso se dará solo para la circunferencia unidad: 0 ≤ x ≤ 2π. Algunos
autores acostumbrar a dar al solución general, recordemos que las
funciones trigonométricas son periódicas, ya que se repiten cada p
intervalo”. Rondón, J. (2017).

27. Referentes Bibliográficos
Castañeda, H. S. (2014). Matemáticas fundamentales para estudiantes de ciencias.
Bogotá, CO: Universidad del Norte. Páginas 153 – 171. https://elibro-
net.bibliotecavirtual.unad.edu.co/es/ereader/unad/69943?page=159
Rondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá D.C.:
Universidad Nacional Abierta y a Distancia. Páginas 237 -
265. https://repository.unad.edu.co/handle/10596/11583
Henao, A. (2012). Funciones
Trigonométricas Geogebra. https://repository.unad.edu.co/handle/10596/7691