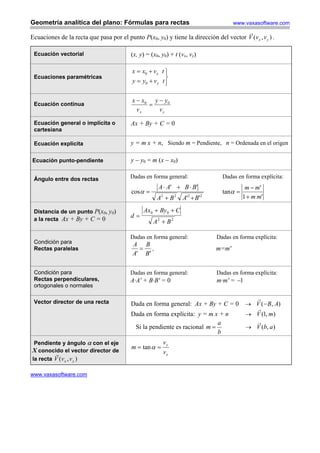
Este documento describe varias fórmulas para representar rectas en geometría analítica del plano, incluyendo ecuaciones vectoriales, paramétricas, generales, explícitas y punto-pendiente. También explica cómo calcular la distancia entre un punto y una recta, el ángulo entre dos rectas, y la pendiente y ángulo con el eje x a partir del vector director de una recta.

1. Geometría analítica del plano: Fórmulas para rectas www.vaxasoftware.com
r
Ecuaciones de la recta que pasa por el punto P(x0, y0) y tiene la dirección del vector V (v x , v y ) .
Ecuación vectorial (x, y) = (x0, y0) + t (vx, vy)
x = x0 + v x t ⎫
Ecuaciones paramétricas ⎬
y = y0 + v y t ⎭
x − x0 y − y0
Ecuación continua =
vx vy
Ecuación general o implícita o Ax + By + C = 0
cartesiana
Ecuación explícita y = m x + n, Siendo m = Pendiente, n = Ordenada en el origen
Ecuación punto-pendiente y − y0 = m (x − x0)
Ángulo entre dos rectas Dadas en forma general: Dadas en forma explícita:
A ⋅ A' + B ⋅ B' m − m'
cosα = tanα =
A +B
2 2
A' + B'
2 2 1 + m m'
Distancia de un punto P(x0, y0) Ax 0 + By 0 + C
a la recta Ax + By + C = 0
d=
A2 + B 2
Dadas en forma general: Dadas en forma explícita:
Condición para A B
Rectas paralelas = , m=m'
A' B'
Condición para Dadas en forma general: Dadas en forma explícita:
Rectas perpendiculares, A·A' + B·B' = 0 m·m' = −1
ortogonales o normales
r
Vector director de una recta Dada en forma general: Ax + By + C = 0 → V (− B, A)
r
Dada en forma explícita: y = m x + n → V (1, m)
a r
Si la pendiente es racional m = → V (b, a )
b
Pendiente y ángulo α con el eje vy
m = tan α =
X conocido el vector director de
r vx
la recta V (v x , v y )
www.vaxasoftware.com