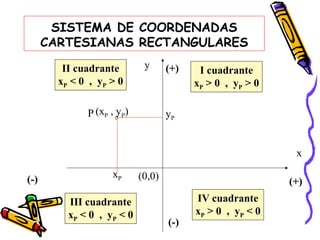
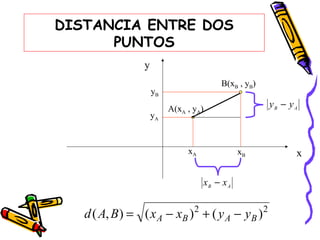
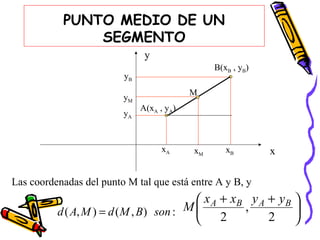
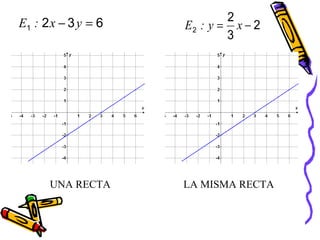
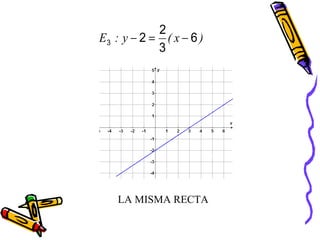
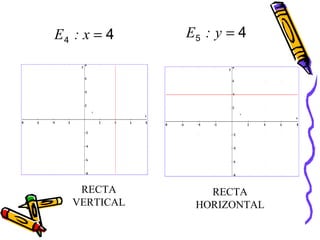
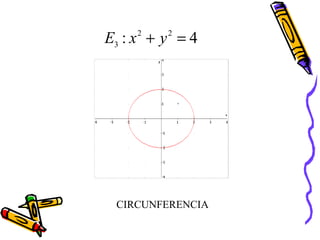
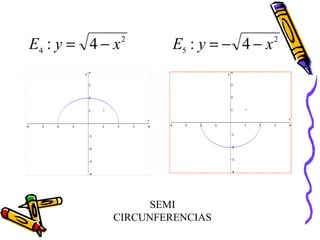
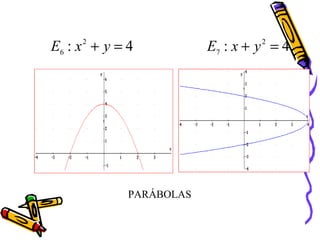
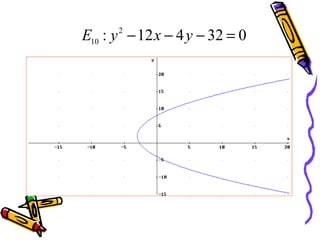
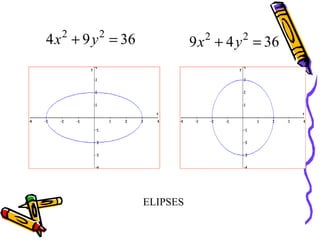
Este documento presenta conceptos básicos de coordenadas cartesianas como sistema para representar puntos en un plano, incluyendo cuadrantes, abscisas y ordenadas. También introduce la distancia entre puntos, el punto medio de un segmento, ecuaciones en dos variables y algunos ejemplos de ecuaciones de rectas, circunferencias, parábolas, elipses y funciones.

1. CAPÍTULO 3
FUNCIONES REALES
I M U 2011 – 2
Horario 0112 y 0125
Prof. José Henostroza G.
jhenost@pucp.edu.pe
http://macareo.pucp.edu.pe/~jhenost

2. TEMAS DE HOY:
• Sistema de coordenadas cartesianas en el
plano.
• Distancia entre dos puntos.
• Punto medio de un segmento.
• Ecuaciones en dos variables. Ecuaciones de
la Recta.

3. SISTEMA DE COORDENADAS
CARTESIANAS RECTANGULARES
II cuadrante y (+) I cuadrante
xP < 0 , yP > 0 xP > 0 , yP > 0
P (xP , yP) yP
x
(-) xP (0,0)
(+)
III cuadrante IV cuadrante
xP < 0 , yP < 0 xP > 0 , yP < 0
(-)

4. A cada punto P se le asocia una pareja
ordenada de números reales (xP , yP).
Dichas componentes se llaman las
coordenadas de P.
• xP es la primera componente o abscisa de P.
• yP es la segunda componente u ordenada de P.
EJEMPLOS:
•Ubicar puntos
•Localizar cuadrantes

5. y
Este sistema lo denotamos Inventó algo “muy simple”:
como R2 cruzar dos rectas numéricas
Nos permite relacionar el reales en el origen
Algebra y la Geometría.
x
Publicó estas ideas
como apéndice
de las “Reglas para la Buena
Dirección del Espíritu”? René Descartes
1596 - 1650

6. DISTANCIA ENTRE DOS
PUNTOS
y
B(xB , yB)
yB
A(xA , yA) yB − y A
yA
xA xB x
xB − x A
d ( A, B ) = ( x A − xB ) 2 + ( y A − yB ) 2

7. PUNTO MEDIO DE UN
SEGMENTO
y
B(xB , yB)
yB
M
yM
A(xA , yA)
yA
xA xM xB x
Las coordenadas del punto M tal que está entre A y B, y
 x A + xB y A + y B 
d ( A, M ) = d ( M , B) son : M  , 
 2 2 

8. ECUACIONES EN DOS
VARIABLES
• Una ecuación en R2 es una igualdad con
dos variables, de la forma E(x,y)=0
• Un par ordenado (x0 , y0) es una solución de
la ecuación E(x,y)=0 si los valores x= x0
y y= y0 satisfacen la igualdad.
• El conjunto de todos los puntos P(x , y) en
R2 cuyas coordenadas son soluciones de la
ecuación E(x,y)=0 es la gráfica de la
ecuación E(x,y)=0

9. EJEMPLOS DE ECUACIONES Y
SUS GRÁFICAS
RECTAS
(Introducción en el curso de IMU)

10. E1 : 2 x − 3 y = 6 2
E2 : y = x − 2
3
UNA RECTA LA MISMA RECTA

11. 2
E3 : y − 2 = ( x − 6 )
3
LA MISMA RECTA

12. E4 : x = 4 E5 : y = 4
RECTA RECTA
VERTICAL HORIZONTAL

13. OTRAS ECUACIONES Y SUS GRÁFICAS
(Se estudiarán en MB y CAL 1)

14. E3 : x + y = 4
2 2
CIRCUNFERENCIA

15. E4 : y = 4 − x 2
E5 : y = − 4 − x 2
SEMI
CIRCUNFERENCIAS

16. E6 : x + y = 4
2
E7 : x + y = 4
2
PARÁBOLAS

17. E10 : y − 12 x − 4 y − 32 = 0
2

18. 2 2
4 x + 9 y = 36 2 2
9 x + 4 y = 36
ELIPSES

19. 2x − 1
y = ( x − 1)( x + 2)( x − 3) y=
x +1
FUNCIÓN FUNCIÓN
POLINÓMICA RACIONAL
CÚBICA