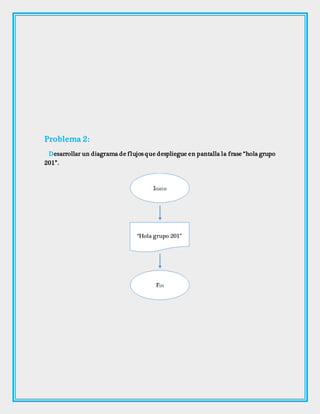
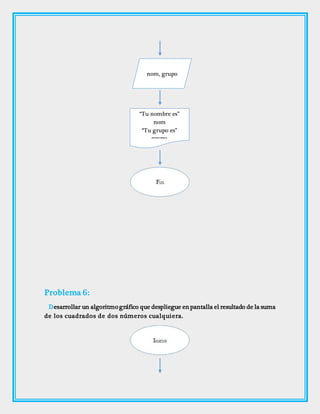
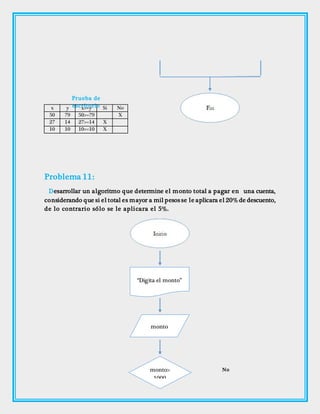
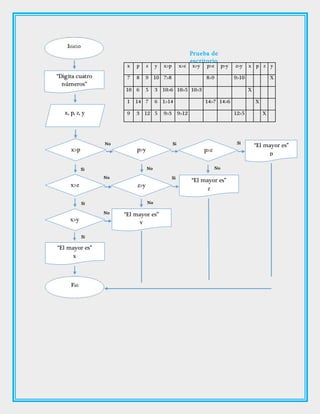
Este documento presenta 16 problemas para desarrollar diagramas de flujo que resuelven diferentes operaciones matemáticas y lógicas. Se explican los símbolos básicos para la creación de diagramas de flujo y se incluyen ejemplos de problemas resueltos como determinar el mayor de tres números o el orden de cuatro números de mayor a menor.

1. Conalep
Tlalnepantla 1
Maestro: Hugo Acosta Serna
Módulo: Manejo de técnicas de
programación
Alumno: Erik González Aldana
Grupo: 201
“Problemas de diagramas de flujo”

2. Problema 1:
Desarrollar un diagrama de flujo que despliegue en pantalla el valor de π.
Inicio
π= 3.1416
Fin
Este símbolo
nos servirá
para dar
inicio y fin a
un diagrama
de flujo.
Esta
flecha
nos
indicara
el orden
y
secuencia
del
algoritmo
.
Este símbolo
refleja el
resultado de
la
información
dada.

3. Problema 2:
Desarrollar un diagrama de flujos que despliegue en pantalla la frase “hola grupo
201”.
“Hola grupo 201”

4. Problema 3:
Desarrollar un diagrama de flujo que imprimaen pantalla el nombre que el usuario
indique.
“Digita tu nombre”
nom
“Tu nombre es”
nom
Este
símbolo
capta el
dato
provenient
e de algún
dispositivo
de
entrada.

5. Problema 4:
Desarrollar un diagrama de flujo que imprima en pantalla el doble de un número
dado.
“Dame un número”
num
Este
símbolo
genera o
desarrolla

6. Problema 5:
Desarrollar un diagrama de flujo que despliegue en pantalla el nombre y grupo
que el usuario indique.
res=num*2
“El doble del
número es”
res
r
“Digita tu nombre y
grupo”

7. Problema 6:
Desarrollar un algoritmo gráfico que despliegue en pantalla el resultado de la suma
de los cuadrados de dos números cualquiera.
nom, grupo
“Tu nombre es”
nom
“Tu grupo es”
grupo

8. Problema 7
Desarrollar un diagrama de flujo que muestre en pantalla el resultado de la
siguiente expresión matemática.
“Dame dos números
cualquiera”
x, y
res=x^2+y^2
“La suma de los
cuadrados de dos
números es”
res

9. “Dame dos
números”
h, i
res=((h+i)^3)/((h-i)^2)
“El resultado es”
res

10. Problema 8:
Desarrollar un algoritmo que determine si un número proporcionado por el
usuario es positivo o negativo. Considerando el 0 como positivo.
No
Si
Prueba de
escritorio
núm núm>=0 Positivo Negativo
5 5>=0 X
-13 -13>=0 X
0 0>=0 X
“Dame un número”
núm
núm>=0
“Positivo” “Negativo”
Este símbolo
sólo se utiliza
si se tienen
dos posibles
respuestas.
La prueba
de
escritorio es
una
herramienta
que
verificara si
el algoritmo
está muy
bien
desarrollado
.

11. Problema 9:
Desarrollar un diagrama de flujo que permita determinar si una persona es mayor
de edad o menor.
No
Si
“Digita tu edad”
edad
edad<=18
“Eres mayor” “Eres menor”

12. Problema 10
Desarrollar un algoritmo que permita determinar cuál es el mayor de dos números
dados.
edad edad>=18 Si No
18 18>=18 X
13 13>=18 X
23 23>=18 X
Prueba de
escritorio
No
Si
“Dame dos
números”
x, y
x>=y
“El mayor es”
x
“El mayor es”
y

13. Problema 11:
Desarrollar un algoritmo que determine el monto total a pagar en una cuenta,
considerando que si el total es mayor a mil pesos se le aplicara el 20% de descuento,
de lo contrario sólo se le aplicara el 5%.
x y x>=y Si No
50 79 50>=79 X
27 14 27>=14 X
10 10 10>=10 X
Prueba de
escritorio
No
“Digita el monto”
monto
monto>
1000

14. Problema 12:
Desarrollar un diagrama de flujo que determine el número mayor de tres números
diferentes.
Si
Prueba de
escritoriomonto Monto>1000 Si No
2000 2000>1000 X
1430 1400>1000 X
620 620>1000 X
Prueba de
escritorioa b c a>b a>c b>c a b c
3 4 5 3>4 4>5 X
6 7 4 6>7 7>4 X
10 4 2 10>4 10>2 X
Si
No
res=monto-
(monto*.20)
res=monto-
(monto*.05)
“El monto total es”
res
Inicio
“Digita tres
números”
a, b, c
a>b b>c
“El mayor es”
b

15. Problema 13:
Desarrollar un algoritmo que determine y muestre en pantalla el menor de dos
números dados.
Si No
No
Si
a>c
“El mayor es”
a
“El mayor es”
c
Fin
“Digita dos
números
cualquiera”
d, f

16. d f A<b Si No
15 30 15<30 X
14 5 14<5 X
10 10 10<10 X
Problema 14:
Desarrollar un algoritmo que permita ordenar de mayor a menor dos números
cualquiera dados.
No
Si
Prueba de
escritorio
d<f
“El menor es”
d
“El menor es”
f
“Digita dos
números”

17. Problema 15:
Desarrollar un algoritmo que permita determinar y mostrar en pantalla el número
mayor de cuatro números cualquiera.
No
Si
x y x>y Si No
3 19 3>19 X
14 10 14>10 X
7 7 7>7 X
Prueba de
escritorio
x, y
x>y
“El orden es”
x, y
“El orden es”
y, x

18. Prueba de
escritorio
x p z y x>p x>z x>y p>z p>y z>y x p z y
7 8 9 10 7>8 8>9 9>10 X
10 6 5 3 10>6 10>5 10>3 X
1 14 7 6 1>14 14>7 14>6 X
9 3 12 5 9>3 9>12 12>5 X
Si SiNo
No NoSi
SiNo
Si No
No
Si
“Digita cuatro
números”
x, p, z, y
x>p
x>z
x>y
“El mayor es”
x
“El mayor es”
y
z>y
p>y p>z
“El mayor es”
z
“El mayor es”
p

19. Problema 16:
Desarrollar un algoritmo que permita ordenar de mayor a menor tres números
diferentes dados.
Prueba de
escritorio
a b c a>b a>c b>c c>a “El orden es”
14 5 4 14>5 14>4 5>4 a, b, c
9 12 2 9>12 12>2 2>9 b, a, c
3 7 16 3>7 7>16 c, b, a
15 1 8 15>1 15>8 1>8 a, c, b
3 17 6 3>17 17>6 6>3 b, c, a
9 1 13 9>1 9>13 c, a, b
No
No Si Si
NoSi
No
Si
No
Si
“Dame tres
números”
a, b, c
a>b b>c c>a
“El orden es”
b, c, a
“El orden es”
c, b, a
a>c
“El orden es”
c, a, b
“El oren es”
b, a, c
b>c
“El orden es”
a, c, b
1
“El orden es”
a, b, c
1
Este símbolo nos ayuda a
seguir continuidad con el
diagrama de flujo, solo
puede haber una salida.