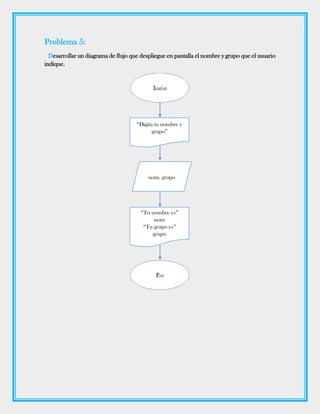
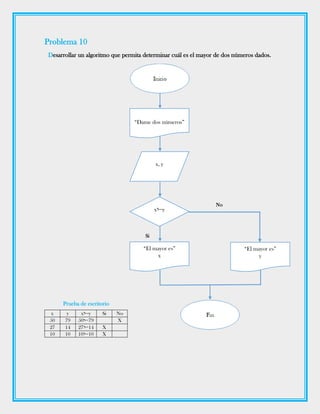
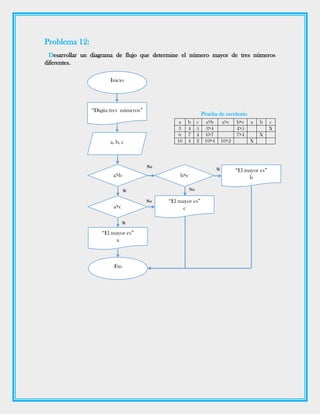
Este documento presenta 16 problemas para desarrollar diagramas de flujo que resuelven diferentes tareas matemáticas y lógicas, como mostrar el valor de pi, imprimir frases, calcular el doble de un número, determinar si un número es positivo o negativo, y ordenar y comparar números. Cada problema incluye una descripción de la tarea, un ejemplo de diagrama de flujo propuesto y una prueba de escritorio.

1. Conalep Tlalnepantla
1
Maestro: Hugo Acosta Serna
Módulo: Manejo de técnicas de programación
Alumno: Erik González Aldana
Grupo: 201
“Problemas de diagramas de flujo”

2. Problema 1:
Desarrollar un diagrama de flujo que despliegue en pantalla el valor de π.
Inicio
π= 3.1416
Fin
Este símbolo nos
servirá para dar
inicio y fin a un
diagrama de flujo.
Esta flecha
nos indicara
el orden y
secuencia del
algoritmo.
Este símbolo
refleja el
resultado de la
información dada.

3. Problema 2:
Desarrollar un diagrama de flujos que despliegue en pantalla la frase “hola grupo 201”.
“Hola grupo 201”

4. Problema 3:
Desarrollar un diagrama de flujo que imprima en pantalla el nombre que el usuario indique.
“Digita tu nombre”
nom
“Tu nombre es”
nom
Este símbolo
capta el dato
proveniente de
algún
dispositivo de
entrada.

5. Problema 4:
Desarrollar un diagrama de flujo que imprima en pantalla el doble de un número dado.
“Dame un número”
res=num*2
num
“El doble del número
es”
res
r
Este símbolo
genera o
desarrolla
cálculos
aritméticos.

6. Problema 5:
Desarrollar un diagrama de flujo que despliegue en pantalla el nombre y grupo que el usuario
indique.
“Digita tu nombre y
grupo”
nom, grupo
“Tu nombre es”
nom
“Tu grupo es”
grupo

7. Problema 6:
Desarrollar un algoritmo gráfico que despliegue en pantalla el resultado de la suma de los
cuadrados de dos números cualquiera.
“Dame dos números
cualquiera”
x, y
res=x^2+y^2
“La suma de los
cuadrados de dos
números es”
res

8. Problema 7
Desarrollar un diagrama de flujo que muestre en pantalla el resultado de la siguiente
expresión matemática.
“Dame dos números”
h, i
res=((h+i)^3)/((h-i)^2)
“El resultado es”
res

9. Problema 8:
Desarrollar un algoritmo que determine si un número proporcionado por el usuario es
positivo o negativo. Considerando el 0 como positivo.
No
Si
Prueba de escritorio
núm núm>=0 Positivo Negativo
5 5>=0 X
-13 -13>=0 X
0 0>=0 X
“Dame un número”
núm
núm>=0
“Positivo” “Negativo”
Este símbolo sólo se
utiliza si se tienen
dos posibles
respuestas.
La prueba de
escritorio es una
herramienta que
verificara si el
algoritmo está
muy bien
desarrollado.

10. Problema 9:
Desarrollar un diagrama de flujo que permita determinar si una persona es mayor de edad o
menor.
No
Si
edad edad>=18 Si No
18 18>=18 X
13 13>=18 X
23 23>=18 X
Prueba de escritorio
“Digita tu edad”
edad
edad<=18
“Eres mayor” “Eres menor”

11. Problema 10
Desarrollar un algoritmo que permita determinar cuál es el mayor de dos números dados.
No
Si
x y x>=y Si No
50 79 50>=79 X
27 14 27>=14 X
10 10 10>=10 X
Prueba de escritorio
“Dame dos números”
x, y
x>=y
“El mayor es”
x
“El mayor es”
y

12. Problema 11:
Desarrollar un algoritmo que determine el monto total a pagar en una cuenta, considerando
que si el total es mayor a mil pesos se le aplicara el 20% de descuento, de lo contrario sólo se
le aplicara el 5%.
No
Si
Prueba de escritorio
monto Monto>1000 Si No
2000 2000>1000 X
1430 1400>1000 X
620 620>1000 X
“Digita el monto”
monto
monto>
1000
res=monto-(monto*.20) res=monto-(monto*.05)
“El monto total es”
res

13. Problema 12:
Desarrollar un diagrama de flujo que determine el número mayor de tres números
diferentes.
Prueba de escritorio
a b c a>b a>c b>c a b c
3 4 5 3>4 4>5 X
6 7 4 6>7 7>4 X
10 4 2 10>4 10>2 X
Si
No
Si No
No
Si
Inicio
“Digita tres números”
a, b, c
a>b
a>c
“El mayor es”
a
b>c
“El mayor es”
c
“El mayor es”
b
Fin

14. Problema 13:
Desarrollar un algoritmo que determine y muestre en pantalla el menor de dos números
dados.
d f A<b Si No
15 30 15<30 X
14 5 14<5 X
10 10 10<10 X
No
Si
Prueba de escritorio
“Digita dos números
cualquiera”
d, f
d<f
“El menor es”
d
“El menor es”
f

15. Problema 14:
Desarrollar un algoritmo que permita ordenar de mayor a menor dos números cualquiera
dados.
No
Si
x y x>y Si No
3 19 3>19 X
14 10 14>10 X
7 7 7>7 X
Prueba de escritorio
“Digita dos números”
x, y
x>y
“El orden es”
x, y
“El orden es”
y, x

16. Problema 15:
Desarrollar un algoritmo que permita determinar y mostrar en pantalla el número mayor de
cuatro números cualquiera.
Prueba de escritorio
x p z y x>p x>z x>y p>z p>y z>y x p z y
7 8 9 10 7>8 8>9 9>10 X
10 6 5 3 10>6 10>5 10>3 X
1 14 7 6 1>14 14>7 14>6 X
9 3 12 5 9>3 9>12 12>5 X
Si SiNo
No NoSi
SiNo
Si No
No
Si
“Digita cuatro
números”
x, p, z, y
x>p
x>z
x>y
“El mayor es”
x
“El mayor es”
y
z>y
p>y p>z
“El mayor es”
z
“El mayor es”
p

17. Problema 16:
Desarrollar un algoritmo que permita ordenar de mayor a menor tres números diferentes
dados.
Prueba de escritorio
a b c a>b a>c b>c c>a “El orden es”
14 5 4 14>5 14>4 5>4 a, b, c
9 12 2 9>12 12>2 2>9 b, a, c
3 7 16 3>7 7>16 c, b, a
15 1 8 15>1 15>8 1>8 a, c, b
3 17 6 3>17 17>6 6>3 b, c, a
9 1 13 9>1 9>13 c, a, b
No
No Si Si
NoSi
No
Si
No
Si
“Dame tres números”
a, b, c
a>b b>c c>a
“El orden es”
b, c, a
“El orden es”
c, b, a
a>c
“El orden es”
c, a, b
“El oren es”
b, a, c
b>c
“El orden es”
a, c, b
1
“El orden es”
a, b, c
1
Este símbolo nos ayuda a seguir
continuidad con el diagrama de flujo,
solo puede haber una salida.