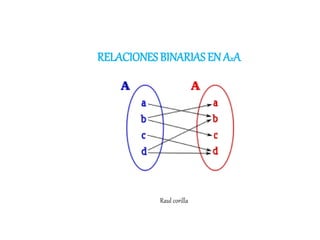
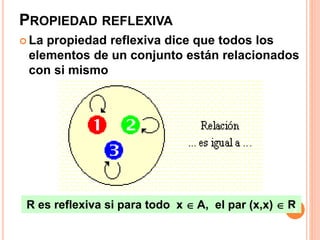
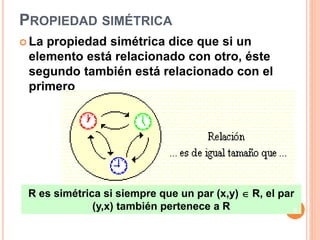
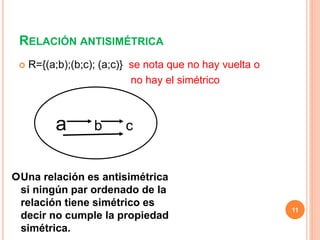
Este documento describe las relaciones binarias definidas en un solo conjunto. Explica que una relación binaria en un conjunto A es un subconjunto de A x A. Presenta ejemplos de relaciones binarias en conjuntos dados y describe las propiedades fundamentales que pueden cumplir una relación: reflexiva, simétrica, antisimétrica y transitiva. Finalmente, propone actividades para que el lector identifique estas propiedades en relaciones dadas.

1. RELACIONES BINARIAS EN AxA
Raul corilla

2. Propósito
• Sea capaz de construir relaciones binarias en
un mismo conjunto , con conceptos básicos
de matemática y por extensión con objetos
del entorno, en el cual actúan, desarrollando
el aprendizaje colaborativo

3. RELACIÓN BINARIA DEFINIDA EN UN SÓLO
CONJUNTO
 Cuando los conjuntos de partida y de llegada de
una relación R son el mismo conjunto A,
decimos que R es una relación binaria definida
en AxA, o, simplemente, una relación en A.
 Una relación R en A es entonces un
subconjunto de A2 = A x A
3

4. RELACIÓN BINARIA DEFINIDA EN UN CONJUNTO
 Ejemplo:
Sea A = { 2, 3, 4, 6, 8, 9, 12} y de plantea las
relaciones R de A en A.
R1: “x es la mitad de y”
R = { (2;4); (3;6); (4;8); (6;12)}
 Resolver las relaciones R2, R3,
R2: “x es el doble de y”
R3: “x es divisor y” 4

5.  Sea B = { 4, 6, 8, 9, 12, 15,18} y se plantea las
relaciones R de B en B.
Determinar los pares ordenados de R2, R3, R5 y
R7
R1: “x es la mitad de y”
R = {(4;8); (6;12);(9;18)}
R2: “x es el doble de y”
R3: “x es divisor y”
5

6. R4: “x es múltiplo de y” sin considerar consigo mismo
R = {(8,4);(12;4);(12,6);(18;6);(18;9)}
 R5: “x es el duplo de y”
 R6: “x es primo entre si con y”
R = { (4;9);(4;15); (8,9); (8;15)}
 R7: “x es el triple de y”
6

7. PROPIEDADES DE LAS RELACIONES DEFINIDAS
EN UN CONJUNTO
 Si establecemos una relación entre los
elementos de un mismo conjunto,
existen cuatro propiedades
fundamentales que pueden cumplirse en
esa relación
Propiedad reflexiva
Propiedad simétrica
Propiedad antisimétrica
Propiedad transitiva
7

8. PROPIEDAD REFLEXIVA
 La propiedad reflexiva dice que todos los
elementos de un conjunto están relacionados
con si mismo
R es reflexiva si para todo x  A, el par (x,x)  R
8

9. PROPIEDAD SIMÉTRICA
 La propiedad simétrica dice que si un
elemento está relacionado con otro, éste
segundo también está relacionado con el
primero
R es simétrica si siempre que un par (x,y)  R, el par
(y,x) también pertenece a R 9

10. PROPIEDAD SIMÉTRICA
 Ejemplo
 Dado A = {3, 4, 2} decir si las siguientes relaciones
en A2 son simétricas
R = {(2, 3), (3, 4), (4, 3), (3, 2), (4, 4)}
S = {(3, 2), (4, 3), (2, 2), (3, 4)}
T = {(3, 2), (4, 3), (2, 2), (3, 4), (2, 3), (3, 3), (4, 4)}
10

11. RELACIÓN ANTISIMÉTRICA
 R={(a;b);(b;c); (a;c)} se nota que no hay vuelta o
no hay el simétrico
11
a b c
Una relación es antisimétrica
si ningún par ordenado de la
relación tiene simétrico es
decir no cumple la propiedad
simétrica.

12. PROPIEDAD ANTISIMÉTRICA
 Ejemplo
 Dado A = {2, 4, 6} cuales de las siguientes
relaciones en A2 son antisimétricas
R = {(2, 2), (4, 4)}
S = {(2, 4)}
T ={(4, 6), (2, 2), (6, 4), (4, 2)}
V ={(4, 6), (2, 4), (2, 6)}
12

13. PROPIEDAD TRANSITIVA
 La propiedad transitiva dice que si un
elemento está relacionado con otro y éste
está a su vez relacionado con un tercero, el
primer elemento está relacionado con el
tercero.
R es transitiva si
x , y ,z , (x,y)  R  (y,z)  R  (x,z)  R
13

14. PROPIEDAD TRANSITIVA
 Ejemplo
 Dado A = {2, 4, 6, 3} decir si las siguientes relaciones en
A2 son transitivas
R = {(2, 2), (2, 3), (4, 6), (6, 2), (4, 2), (4, 3), (6, 3)}
S = {(2, 2), (4, 4), (4, 2), (2, 6), (6, 4), (6, 2)}
14

15. ACTIVIDADES:
 Proponga un conjunto C con 5 elementos y plantea
una relación reflexiva, una relación simétrica, una
relación antisimétrica y una relación transitiva.
 Enviar a la plataforma juntamente con los
anteriores
15