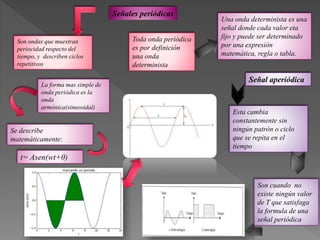
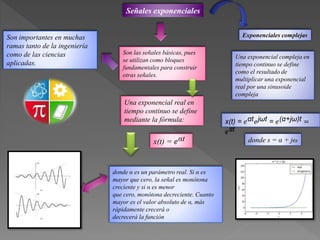
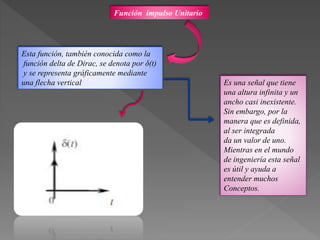
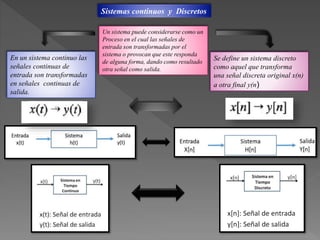
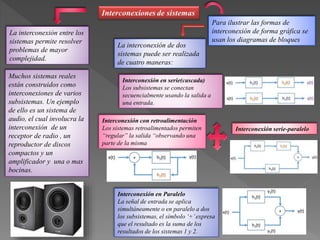
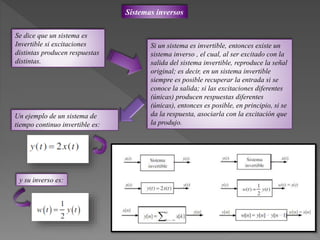
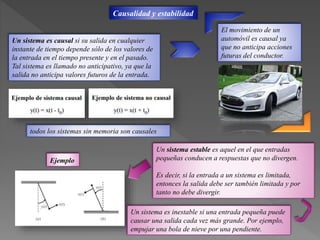
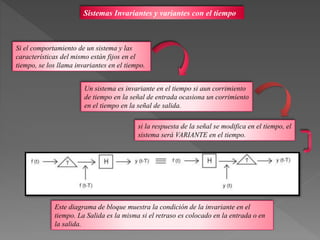
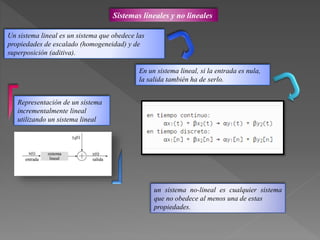
Este documento presenta diferentes tipos de señales y sistemas. Describe señales periódicas, aperiódicas, exponenciales, senoidales, impulso unitario y escalón unitario. También explica sistemas continuos y discretos, e interconexiones de sistemas como en serie, paralelo y retroalimentación. Además, distingue sistemas con y sin memoria, invertibles, causales, estables, invariantes y variantes en el tiempo, y lineales frente a no lineales.

1. Republica Bolivariana De Venezuela
Ministerio del Poder popular Para la educación
Instituto universitario de Tecnología
″Antonio José de Sucre″
Extensión Barquisimeto
Integrante:
Marianyeli Méndez
Semestre:5to
Carrera: Electrónica
Materia: Análisis de señales
Profesora: Ing. Ranielina RondónBarquisimeto, 09 febrero del 2019
Representación de Señales

2. Señales periódicas
Son ondas que muestran
periocidad respecto del
tiempo, y describen ciclos
repetitivos
Toda onda periódica
es por definición
una onda
determinista
Una onda determinista es una
señal donde cada valor eta
fijo y puede ser determinado
por una expresión
matemática, regla o tabla.
La forma mas simple de
onda periódica es la
onda
armónica(sinusoidal)
Se describe
matemáticamente:
t= Asen(wt+θ)
Señal aperiódica
Esta cambia
constantemente sin
ningún patrón o ciclo
que se repita en el
tiempo
Son cuando no
existe ningún valor
de T que satisfaga
la formula de una
señal periódica

3. Señales exponenciales
Son importantes en muchas
ramas tanto de la ingeniería
como de las ciencias
aplicadas.
Una exponencial real en
tiempo continuo se define
mediante la fórmula:
x(t) = 𝑒αt
donde α es un parámetro real. Si α es
mayor que cero, la señal es monótona
creciente y si α es menor
que cero, monótona decreciente. Cuanto
mayor es el valor absoluto de α, más
rápidamente crecerá o
decrecerá la función
Exponenciales complejas
Una exponencial compleja en
tiempo continuo se define
como el resultado de
multiplicar una exponencial
real por una sinusoide
compleja
x(t) = 𝑒αt 𝑒jωt = 𝑒(α+jω)t =
𝑒st
donde s = α + jω
Son las señales básicas, pues
se utilizan como bloques
fundamentales para construir
otras señales.

4. Señales senoidales
Señales senoidales con
diferentes frecuencias
Este hecho fue
establecido en 1822
por el matemático
Joseph Fourier.
Es el valor de la tensión de la
Corriente alterna a través de un
tiempo continuamente variable, en
un par de ejes cartesianos
marcados en amplitud y tiempo
Su formula viene dada por una
función trigonométrica del tiempo
(seno,coseno) dada la relación entre
estos con el ángulo se expresaría de
esta forma:
Fase (φ)
Una señal senoidal puede estar
desplazada en el eje horizontal, es
decir en tiempo. La fase es un
valor que representa el ángulo
inicial de la señal y se mide en
radianes o en grados.
Período (T)
El período es la duración de un
ciclo completo de una señal
alterna. Se mide en segundos (con
sus prefijos correspondientes).
Frecuencia (f)
Es la inversa del período y
corresponde a la cantidad de
ciclos por unidad de tiempo de
una señal alterna. Se mide en
hertz. Un hertz equivale a un ciclo
completo en un segundo.
Velocidad angular (ω)
La velocidad angular o pulsación
se calcula como 2 π multiplicado
por la frecuencia. Representa la
velocidad de variación del ángulo
de giro.

5. Función impulso Unitario
Esta función, también conocida como la
función delta de Dirac, se denota por δ(t)
y se representa gráficamente mediante
una flecha vertical Es una señal que tiene
una altura infinita y un
ancho casi inexistente.
Sin embargo, por la
manera que es definida,
al ser integrada
da un valor de uno.
Mientras en el mundo
de ingeniería esta señal
es útil y ayuda a
entender muchos
Conceptos.

6. La función escalón de Heaviside o Función escalón unitario
Expresado matemáticamente
seria de la forma:
Esta función normalmente se
utiliza para presentar variables que
se interrumpen en algún instante de
tiempo , para esto se multiplica la
función escalón unitario por la
función que define la variable en el
tiempo.
En ingeniería es común encontrar funciones
que corresponden a estados de sí o no, o bien
activo o inactivo, Para tratar de forma
efectiva con estas funciones discontinuas
conviene introducir una función especial
llamada función escalón unitario.
Es una función discontinua
cuyo valor es 0 para cualquier
argumento negativo, y 1 para
cualquier argumento positivo
Debe su nombre al
matemático inglés Oliver
Heaviside.

7. Sistemas continuos y Discretos
Un sistema puede considerarse como un
Proceso en el cual las señales de
entrada son transformadas por el
sistema o provocan que este responda
de alguna forma, dando como resultado
otra señal como salida.
En un sistema continuo las
señales continuas de
entrada son transformadas
en señales continuas de
salida.
Se define un sistema discreto
como aquel que transforma
una señal discreta original x(n)
a otra final y(n)

8. La interconexión entre los
sistemas permite resolver
problemas de mayor
complejidad.
Muchos sistemas reales
están construidos como
interconexiones de varios
subsistemas. Un ejemplo
de ello es un sistema de
audio, el cual involucra la
interconexión de un
receptor de radio , un
reproductor de discos
compactos y un
amplificador y una o mas
bocinas.
Para ilustrar las formas de
interconexión de forma gráfica se
usan los diagramas de bloques
La interconexión de dos
sistemas puede ser realizada
de cuatro maneras:
Interconexión en serie(cascada)
Los subsistemas se conectan
secuencialmente usando la salida a
una entrada.
Interconexión en Paralelo
La señal de entrada se aplica
simultáneamente o en paralelo a dos
los subsistemas, el símbolo ‘+’expresa
que el resultado es la suma de los
resultados de los sistemas 1 y 2.
Interconexión serie-paralelo
Interconexión con retroalimentación
Los sistemas retroalimentados permiten
“regular” la salida “observando una
parte de la misma

9. Sistemas con y sin memoria
Sistema con memoria
Incorpora algún mecanismo que
almacena información sobre valores de la
entrada correspondientes a distintos
valores de la variable independiente
Sistema sin memoria
La salida para cada valor de la variable
independiente es función exclusivamente
del valor de la entrada para dicho valor
de la variable.
Si la salida de un sistema depende solo del
valor aplicado en la entrada para un tiempo
cualquiera, se dice que el sistema es sin
memoria. El ejemplo más común es un
sistema con un resistor.
Si el sistema depende de los valores
anteriores de la entrada, se lo considera
con memoria.
Tal es el caso de un capacitor, cuyo valor
de salida depende de lo acumulado
desde el tiempo -∞ hasta t.
Los sistemas sin memoria también se conocen como
instantáneos, que son un caso particular de los
sistemas dinámicos (con memoria).

10. Sistemas inversos
Se dice que un sistema es
Invertible si excitaciones
distintas producen respuestas
distintas.
Si un sistema es invertible, entonces existe un
sistema inverso , el cual, al ser excitado con la
salida del sistema invertible, reproduce la señal
original; es decir, en un sistema invertible
siempre es posible recuperar la entrada si se
conoce la salida; si las excitaciones diferentes
(únicas) producen respuestas diferentes
(únicas), entonces es posible, en principio, si se
da la respuesta, asociarla con la excitación que
la produjo.
Un ejemplo de un sistema de
tiempo continuo invertible es:
y su inverso es:

11. Causalidad y estabilidad
Un sistema es causal si su salida en cualquier
instante de tiempo depende sólo de los valores de
la entrada en el tiempo presente y en el pasado.
Tal sistema es llamado no anticipativo, ya que la
salida no anticipa valores futuros de la entrada.
El movimiento de un
automóvil es causal ya
que no anticipa acciones
futuras del conductor.
todos los sistemas sin memoria son causales
Un sistema estable es aquel en el que entradas
pequeñas conducen a respuestas que no divergen.
Es decir, si la entrada a un sistema es limitada,
entonces la salida debe ser también limitada y por
tanto no debe divergir.
Ejemplo
Un sistema es inestable si una entrada pequeña puede
causar una salida cada vez más grande. Por ejemplo,
empujar una bola de nieve por una pendiente.

12. Sistemas Invariantes y variantes con el tiempo
Si el comportamiento de un sistema y las
características del mismo están fijos en el
tiempo, se los llama invariantes en el tiempo.
Un sistema es invariante en el tiempo si aun corrimiento
de tiempo en la señal de entrada ocasiona un corrimiento
en el tiempo en la señal de salida.
si la respuesta de la señal se modifica en el tiempo, el
sistema será VARIANTE en el tiempo.
Este diagrama de bloque muestra la condición de la invariante en el
tiempo. La Salida es la misma si el retraso es colocado en la entrada o en
la salida.

13. Sistemas lineales y no lineales
En un sistema lineal, si la entrada es nula,
la salida también ha de serlo.
Representación de un sistema
incrementalmente lineal
utilizando un sistema lineal
Un sistema lineal es un sistema que obedece las
propiedades de escalado (homogeneidad) y de
superposición (aditiva).
un sistema no-lineal es cualquier sistema
que no obedece al menos una de estas
propiedades.