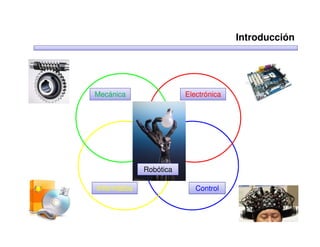
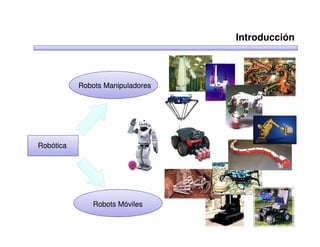
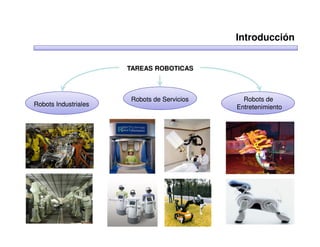
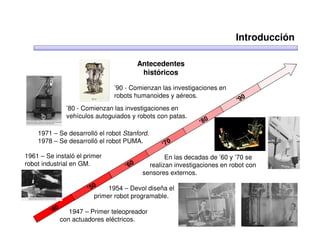
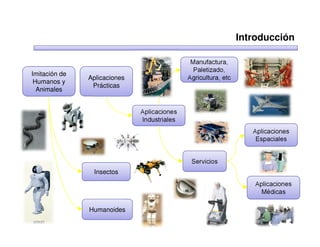
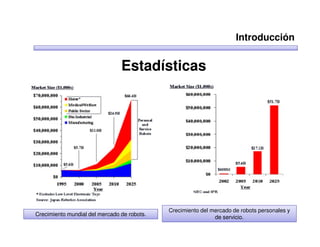
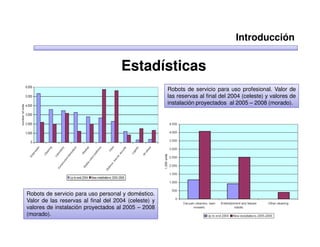
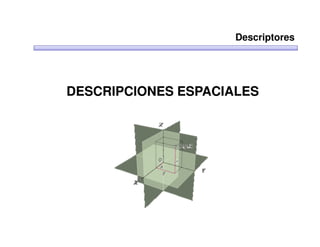
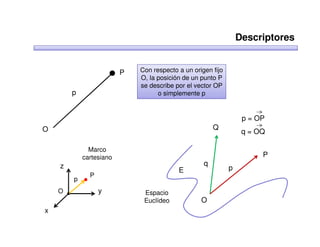
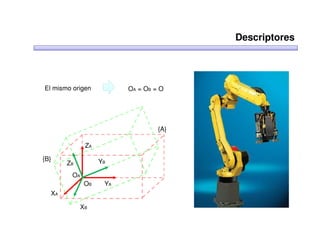
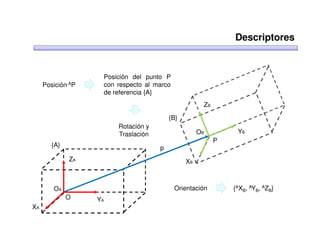
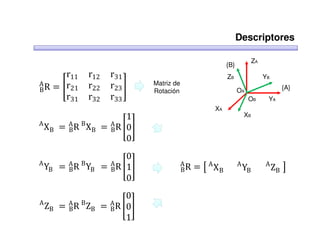
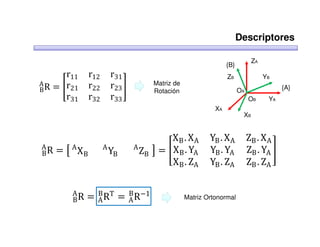
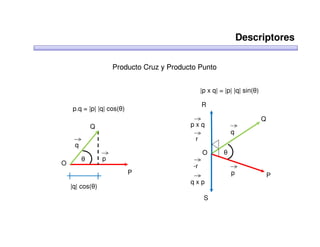
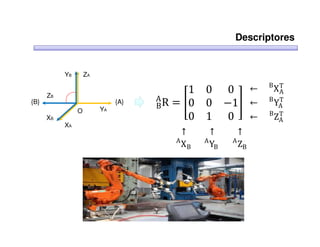
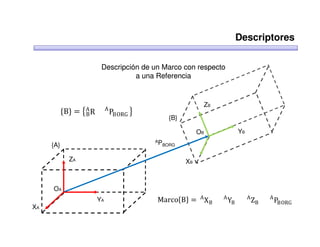
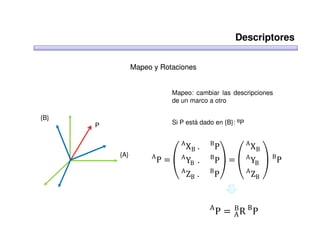
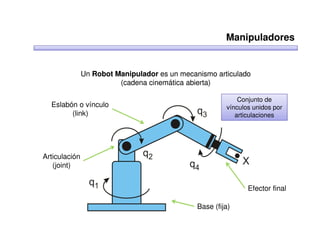
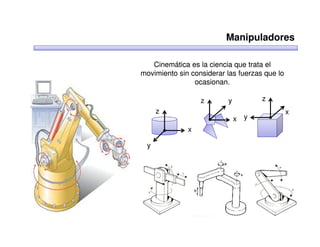
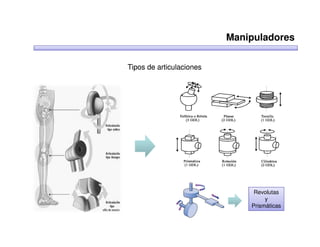
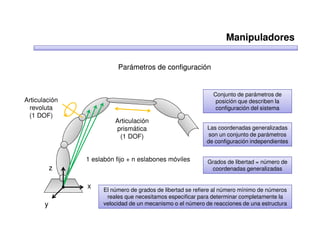
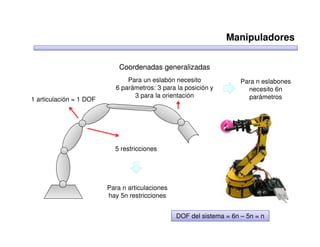
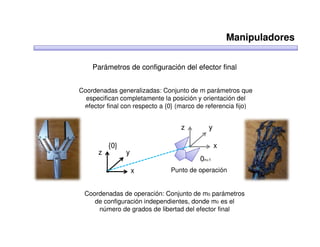
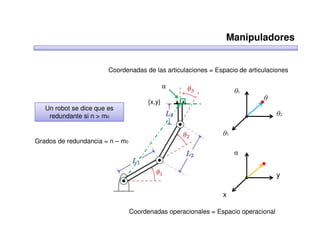
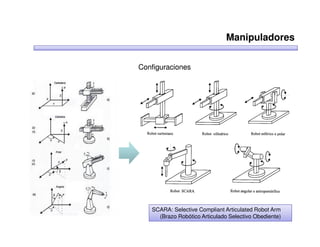
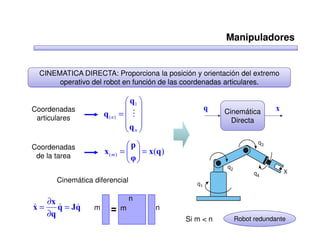
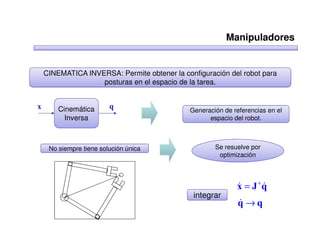
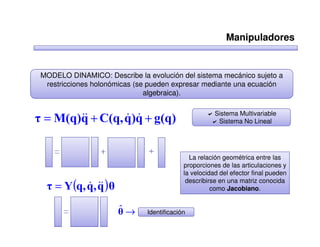
Este documento trata sobre robótica. Explica que la robótica involucra mecánica, electrónica, informática y control. Describe robots manipuladores y móviles, y cómo se usan descriptores espaciales como posición, orientación y matrices de rotación para controlar los movimientos de los robots.

1. ROBÓTICA
Manipuladores
Andrés Rosales

2. Robótica
CONTENIDO
• Introducción
• Definiciones
• Tareas
• Estadísticas
• Robots Manipuladores
• Definiciones
• Control
• Robots Móviles
• Definiciones
• Control

3. Robótica
INTRODUCCIÓN

4. Introducción
Mecánica Electrónica
Robótica
Informática Control

5. Introducción
Robots Manipuladores
Robótica
Robots Móviles

6. Introducción
Definiciones
Robótica:
Es la conexión inteligente entre percepción y acción. (Brady, 1985).

7. Introducción
Definiciones
Manipuladores:
Robot Institute of America: Un robot es un manipulador reprogramable
multifuncional diseñado para mover materiales, piezas o dispositivos
especializados a través de movimientos programados variables para la
realización de una diversidad de tareas (Schlussel, 1985).
Japón: Cualquier dispositivo que reemplaza el trabajo humano. (Sosoka,
1985).

8. Introducción
Definiciones
Robot móvil:
Cualquier robot que posee movilidad con respecto al medio
Cualquier sistema el cual es:
Móvil - todo el sistema se desplaza con respecto al ambiente.
Autónomo - limitada interacción con el hombre.
Inteligente - sensa y reacciona a su entorno.

9. Introducción
TAREAS ROBOTICAS
Robots de Servicios Robots de
Robots Industriales Entretenimiento

10. Introducción
Antecedentes
históricos
’90 - Comienzan las investigaciones en
robots humanoides y aéreos.
’80 - Comienzan las investigaciones en
vehículos autoguiados y robots con patas.
1971 – Se desarrolló el robot Stanford.
1978 – Se desarrolló el robot PUMA.
1961 – Se instaló el primer En las decadas de ’60 y ’70 se
robot industrial en GM. realizan investigaciones en robot con
sensores externos.
1954 – Devol diseña el
primer robot programable.
1947 – Primer teleopreador
con actuadores eléctricos.

11. Introducción
Manufactura,
Paletizado,
Imitación de
Aplicaciones Agricultura, etc
Humanos y
Prácticas
Animales
Aplicaciones
Industriales
Aplicaciones
Espaciales
Servicios
Insectos
Aplicaciones
Médicas
Humanoides

12. Introducción
Estadísticas
Crecimiento del mercado de robots personales y
Crecimiento mundial del mercado de robots.
de servicio.

13. Introducción
Estadísticas
Robots de servicio para uso profesional. Valor de
las reservas al final del 2004 (celeste) y valores de
instalación proyectados al 2005 – 2008 (morado).
Robots de servicio para uso personal y doméstico.
Valor de las reservas al final del 2004 (celeste) y
valores de instalación proyectados al 2005 – 2008
(morado).

14. Introducción
Estadísticas
Para el 2011 habrá más de 1.2 millones de Robots
industriales en todo el mundo, la gráfica izquierda está
basada en un estudio del número de robots por país por
cada 10.000 trabajadores, donde Japón ocupa el primer
lugar con 295 robots de producción por cada 10.000
empleados, seguido de Singapur con 169, Corea 164 y
Alemania 163.
Los robots industriales tendrán su mayor
producción en el sector automotriz, mientras
que según su aplicación el mayor porcentaje los
robots que manejan materiales y procesos.

15. Descriptores
DESCRIPCIONES ESPACIALES

16. Descriptores
P Con respecto a un origen fijo
O, la posición de un punto P
se describe por el vector OP
p o simplemente p
p = OP
O Q
q = OQ
Marco
cartesiano P
z q
E p
P
p
O y Espacio
Euclídeo O
x

17. Descriptores
El mismo origen OA = OB = O
{A}
ZA
{B} YB
ZB
OA
OB YA
XA
XB

18. Descriptores
Posición del punto P
Posición AP con respecto al marco
de referencia {A}
ZB
{B}
Rotación y
Traslación OB YB
P
{A} p
ZA XB
OA Orientación {AXB, AYB, AZB}
O YA
XA

19. Descriptores
r11 r12 r31
ZA
{B}
r
B R = ൥ 21
A r22 r23 ൩
ZB YB
r31 r32 r33
Matriz de
OA {A}
Rotación
OB YA
1
XA
A
XB = A R BXB = A R ൥0൩
XB
B B
0
0
YB = A R B YB = A R ൥1൩ BR = ൣ A XB YB ZB ൧
A A A A
B B
0
0
A
ZB = A R B ZB
B = A R ൥0൩
B
1

20. Descriptores
r11 r12 r31
ZA
{B}
r
B R = ൥ 21
A r22 r23 ൩
ZB YB
r31 r32 r33
Matriz de
OA {A}
Rotación
OB YA
XA
XB
XB . XA YB . X A ZB . X A
BR
A
= ൣ A XB A
YB A
ZB ൧ = ൥ X B . YA YB . YA ZB . YA ൩
X B . ZA YB . ZA ZB . ZA
BR = A RT = A R−1
A B B Matriz Ortonormal

21. Descriptores
Producto Cruz y Producto Punto
|p x q| = |p| |q| sin(θ)
R
p.q = |p| |q| cos(θ)
Q
Q pxq
q
r
q
O θ
θ p
O -r
P p P
qxp
|q| cos(θ)
S

22. Descriptores
1 0 0 ← XA
B T
YB ZA
B R = ൥0 0 −1൩ ←
A
YA
B T
0 1 0 ←
ZB
ZA
B T
{B} {A}
O YA
↑ ↑ ↑
XB
XA
A
XB A
YB A
ZB

23. Descriptores
Descripción de un Marco con respecto
a una Referencia
ሼBሽ = ൛AR
B
A
PBORG ൟ
ZB
{B}
OB YB
AP
{A} BORG
ZA XB
MarcoሼBሽ = A X B A
YB A
ZB A
PBORG
OA
YA
XA

24. Descriptores
Mapeo y Rotaciones
Mapeo: cambiar las descripciones
de un marco a otro
{B}
P Si P está dado en {B}: BP
A
XB . B
P A
XB
A
P = ൮ A YB . B
P൲ = ൮ A YB ൲ B P
{A}
A
ZB . B
P A
ZB
A
P = A R BP
B

25. Manipuladores
ROBOTS MANIPULADORES

26. Manipuladores
Un Robot Manipulador es un mecanismo articulado
(cadena cinemática abierta)
Conjunto de
Eslabón o vínculo vínculos unidos por
(link) articulaciones
Articulación
(joint)
Efector final
Base (fija)

27. Manipuladores
Cinemática es la ciencia que trata el
movimiento sin considerar las fuerzas que lo
ocasionan.
z y z
z x
x y
x
y

28. Manipuladores
Tipos de articulaciones
Revolutas
y
Prismáticas

29. Manipuladores
Parámetros de configuración
Conjunto de parámetros de
Articulación posición que describen la
revoluta configuración del sistema
(1 DOF)
Articulación
prismática Las coordenadas generalizadas
(1 DOF) son un conjunto de parámetros
de configuración independientes
1 eslabón fijo + n eslabones móviles Grados de libertad = número de
z coordenadas generalizadas
x El número de grados de libertad se refiere al número mínimo de números
reales que necesitamos especificar para determinar completamente la
y velocidad de un mecanismo o el número de reacciones de una estructura

30. Manipuladores
Coordenadas generalizadas
Para un eslabón necesito Para n eslabones
6 parámetros: 3 para la posición y necesito 6n
3 para la orientación parámetros
1 articulación = 1 DOF
5 restricciones
Para n articulaciones
hay 5n restricciones
DOF del sistema = 6n – 5n = n

31. Manipuladores
Parámetros de configuración del efector final
Coordenadas generalizadas: Conjunto de m parámetros que
especifican completamente la posición y orientación del
efector final con respecto a {0} (marco de referencia fijo)
z y
{0} x
z y
0n+1
x Punto de operación
Coordenadas de operación: Conjunto de m0 parámetros
de configuración independientes, donde m0 es el
número de grados de libertad del efector final

32. Manipuladores
Coordenadas de las articulaciones = Espacio de articulaciones
α
θ1
θ
{x,y}
Un robot se dice que es
redundante si n > m0 θ2
θ3
Grados de redundancia = n – m0
α
y
x
Coordenadas operacionales = Espacio operacional

33. Manipuladores
Configuraciones
SCARA: Selective Compliant Articulated Robot Arm
(Brazo Robótico Articulado Selectivo Obediente)

34. Manipuladores
CINEMATICA DIRECTA: Proporciona la posición y orientación del extremo
operativo del robot en función de las coordenadas articulares.
 q1 
Coordenadas   q x
q(n) = M  Cinemática
articulares Directa
q 
 n
Coordenadas p
de la tarea
x( m) =   = x(q)
φ
 
Cinemática diferencial
∂x n
&
x= & &
q = Jq m m n
∂q
Si m < n Robot redundante

35. Manipuladores
CINEMATICA INVERSA: Permite obtener la configuración del robot para
posturas en el espacio de la tarea.
x Cinemática q Generación de referencias en el
Inversa espacio del robot.
No siempre tiene solución única Se resuelve por
optimización
x = J +q
& &
integrar
&
q→q

36. Manipuladores
MODELO DINAMICO: Describe la evolución del sistema mecánico sujeto a
restricciones holonómicas (se pueden expresar mediante una ecuación
algebraica).
Sistema Multivariable
&& & &
τ = M(q)q + C(q, q)q + g(q) Sistema No Lineal
La relación geométrica entre las
proporciones de las articulaciones y
la velocidad del efector final pueden
τ = Y(q, q, q )θ
describirse en una matriz conocida
& && como Jacobiano.
ˆ
θ→ Identificación